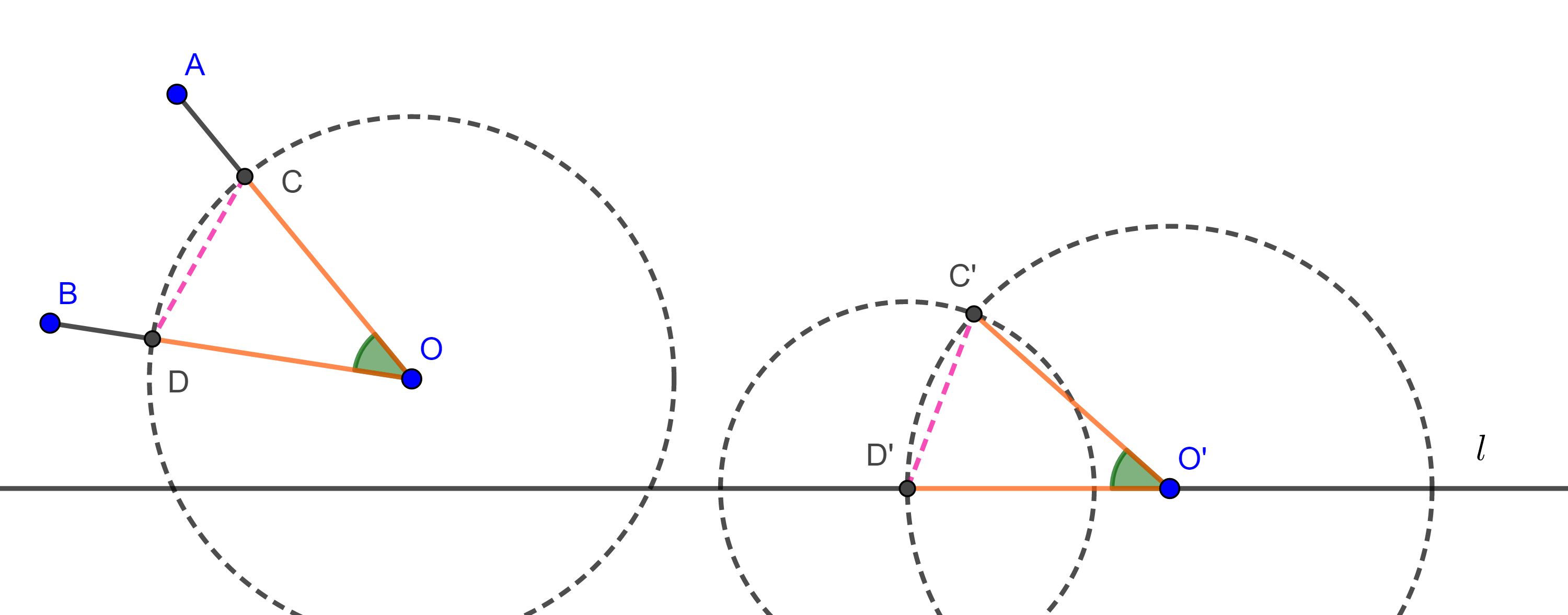Introducción

En esta ocasión estudiaremos una propiedad muy importante de los triángulos, la desigualdad del triángulo que básicamente nos dice que la distancia mas corta entre dos puntos es el segmento de recta que los une, también veremos lo que es un lugar geométrico y mostraremos un par de ejemplos importantes.

Desigualdad del triángulo

Proposición 1. En todo triángulo al mayor de los lados se opone el mayor de los ángulos.

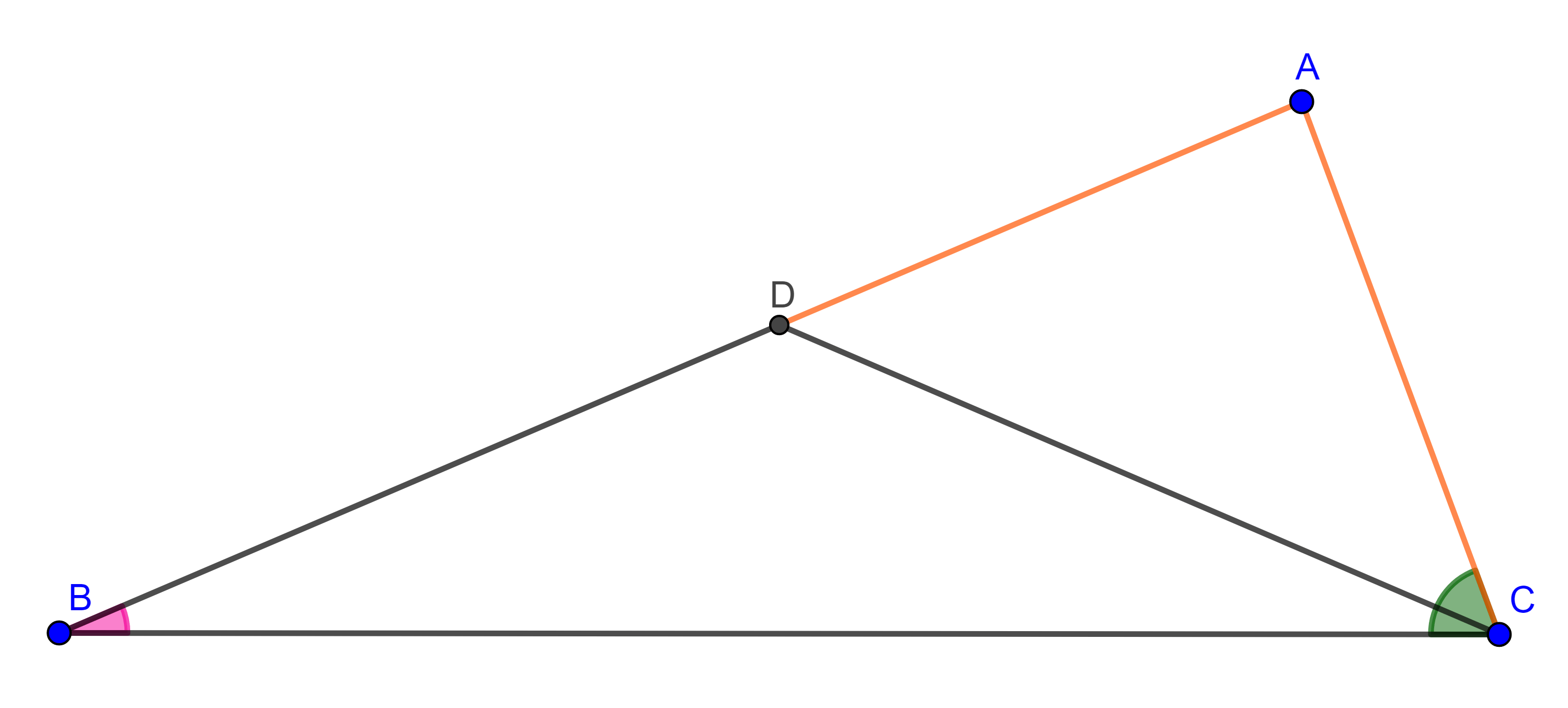
Demostración. Sea $\triangle ABC$ tal que $AB > AC$, debemos mostrar que $\angle C > \angle B$.

Como $AB > AC$, podemos construir un punto $D \in AB$ tal que $AD = AC$, ya que $\triangle ADC$ es isósceles, por la proposición de la entrada anterior, se cumple $\angle CDA = \angle ACD$, de aquí se sigue que:

$\begin{equation} \angle C = \angle ACB > \angle ACD = \angle DCA. \end{equation}$

Como $\angle ADC$ es un ángulo exterior de $\triangle DBC$, entonces $\angle ADC$ es mayor que los ángulos internos de $\triangle DBC$, no adyacentes a él, en particular

$\begin{equation} \angle ADC > CBD = \angle B. \end{equation}$

De $(1)$ y $(2)$ se sigue que $\angle C > \angle B$.

$\blacksquare$

Corolario. En todo triángulo el ángulo mayor es opuesto al lado mayor.

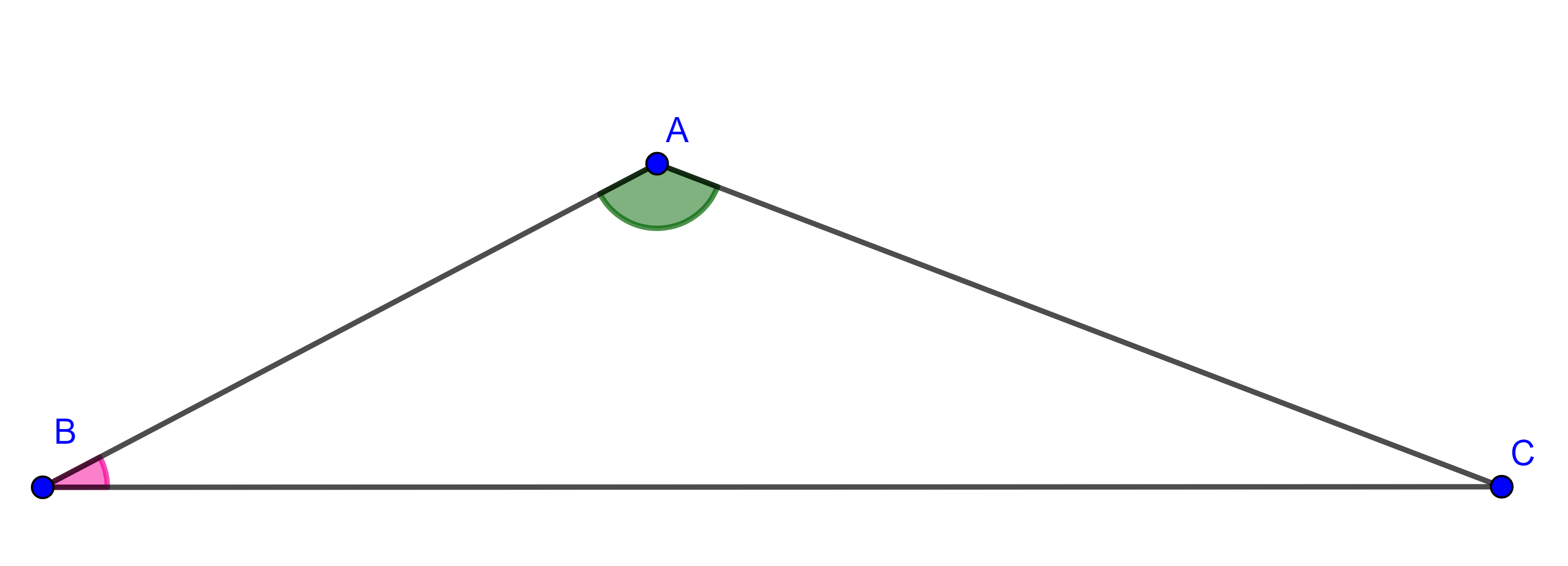
Demostración. Sea $\triangle ABC$ tal que $\angle A > \angle B$, por demostrar que $BC > AC$. Supongamos lo contrario.

Caso 1. Si $BC = AC$, entonces $\triangle ABC$ es isósceles por lo que $\angle A = \angle B$, lo que es una contradicción a nuestra hipótesis.

Caso2. Si $BC < AC$, entonces por la proposición anterior $\angle B > \angle A$, esto nuevamente contradice la hipótesis.

Por lo tanto, no queda otra opción más que $\angle A > \angle B$.

$\blacksquare$

Proposición 2. Si dos lados de un triángulo son iguales a dos lados de un segundo triángulo, pero el ángulo comprendido entre el primer par de lados es mayor que el ángulo formado por los lados del segundo triangulo, entonces el lado restante del primer triángulo será mayor al tercer lado del segundo triangulo.

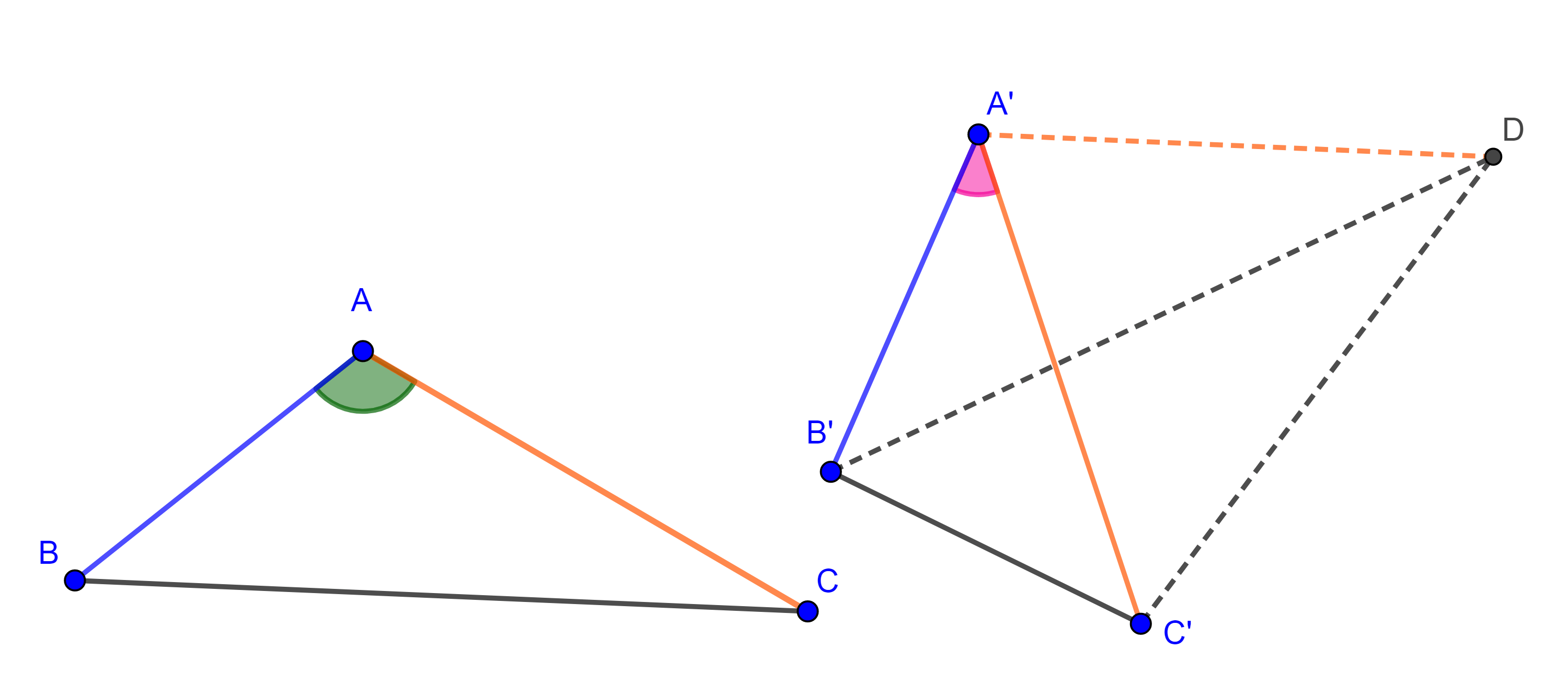
Demostración. Sean $\triangle ABC$ y $\triangle A’B’C’$ tales que $AB = A’B’$, $AC = A’C’$ y $\angle A > \angle A’$, por demostrar que $BC > B’C’$.

Sobre $A’B’$ y tomando como vértice $A’$ construimos un ángulo igual a $\angle A$, y construimos $D$ tal que $A’D = AC$, entonces por criterio LAL, $\triangle ABC \cong \triangle A’B’D$ por lo que $B’D = BC$.

Notemos que $\triangle C’A’D$ es isósceles, entonces $\angle DC’A = \angle A’DC’$.

Ahora en $\triangle DC’B’$ tenemos $\angle DC’B’ = \angle A’C’B’ + \angle DC’A$,
$\Rightarrow \angle DC’B’ > \angle DC’A = \angle A’DC’$.

Pero $\angle A’DC’ = \angle A’DB’ + \angle B’DC’$,
$\Rightarrow \angle A’DC’ > \angle B’DC’$.

Por transitividad, $\angle DC’B’ > \angle B’DC’$.

Aplicando el corolario obtenemos $B’D > B’C’$, pero $B’D = BC$,
$\Rightarrow BC > B’C’$.

$\blacksquare$

Teorema 1, desigualdad del triángulo. Para todo triangulo se cumple que la suma de cualesquiera dos de sus lados es mayor al lado restante.

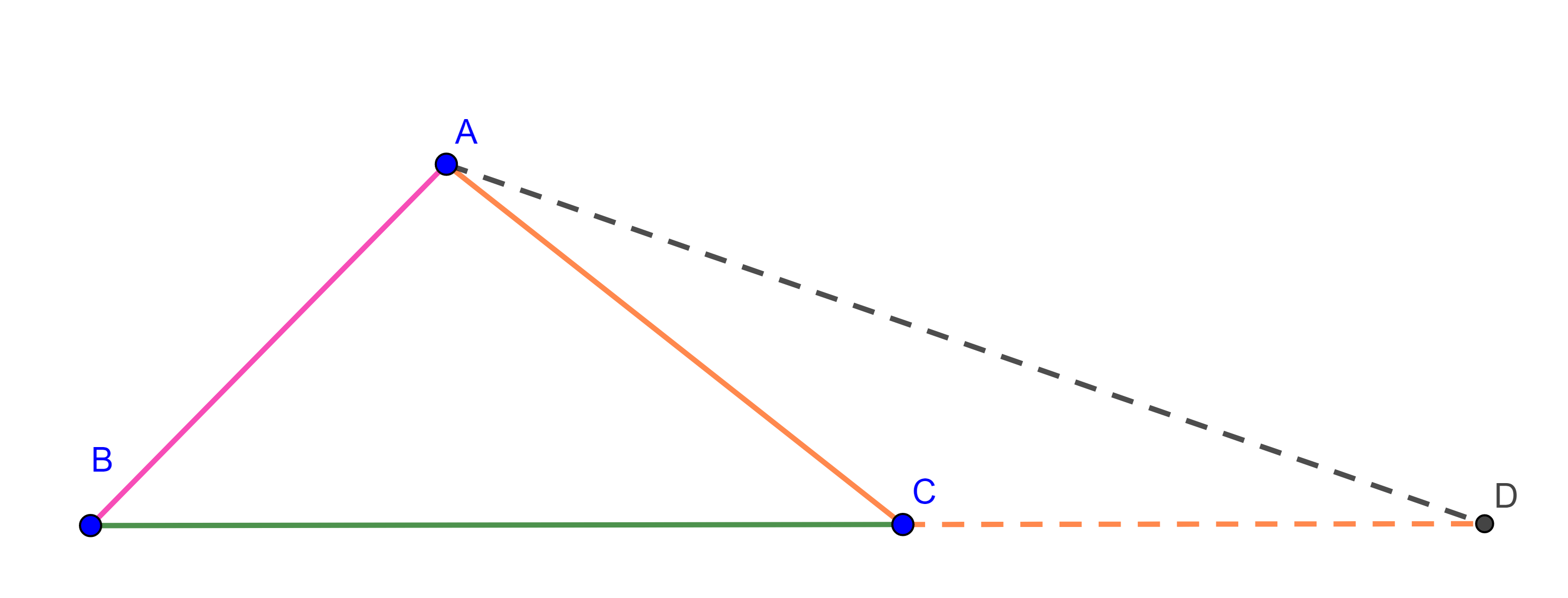
Demostración. Sea $\triangle ABC$, sobre la recta que pasa por $B$ y $C$, construimos un punto $D$ tal que $CD = AC$.

Como $\triangle ACD$ es isósceles, $\angle CAD = \angle ADC$, entonces en $\triangle ABD$ tenemos $\angle BAD > \angle CAD = \angle ADC = \angle ADB$, por el corolario anterior $BD > AB$.

Pero $BD = BC + CD = BC + AC$, por lo tanto, $AC + BC > AB$.

Las otras desigualdades, $AB + BC > AC$ y $AB + AC > BC$, se muestran de manera similar.

$\blacksquare$

El reciproco de este teorema también es cierto y lo mostramos a continuación.

Construcción de un triángulo y un ángulo

Teorema 2. Si $a$, $b$ y $c$ son tres números positivos tales que $a + b > c$, $a + c > b$ y $b + c > a$, entonces es posible construir un triángulo de lados $a$, $b$ y $c$.

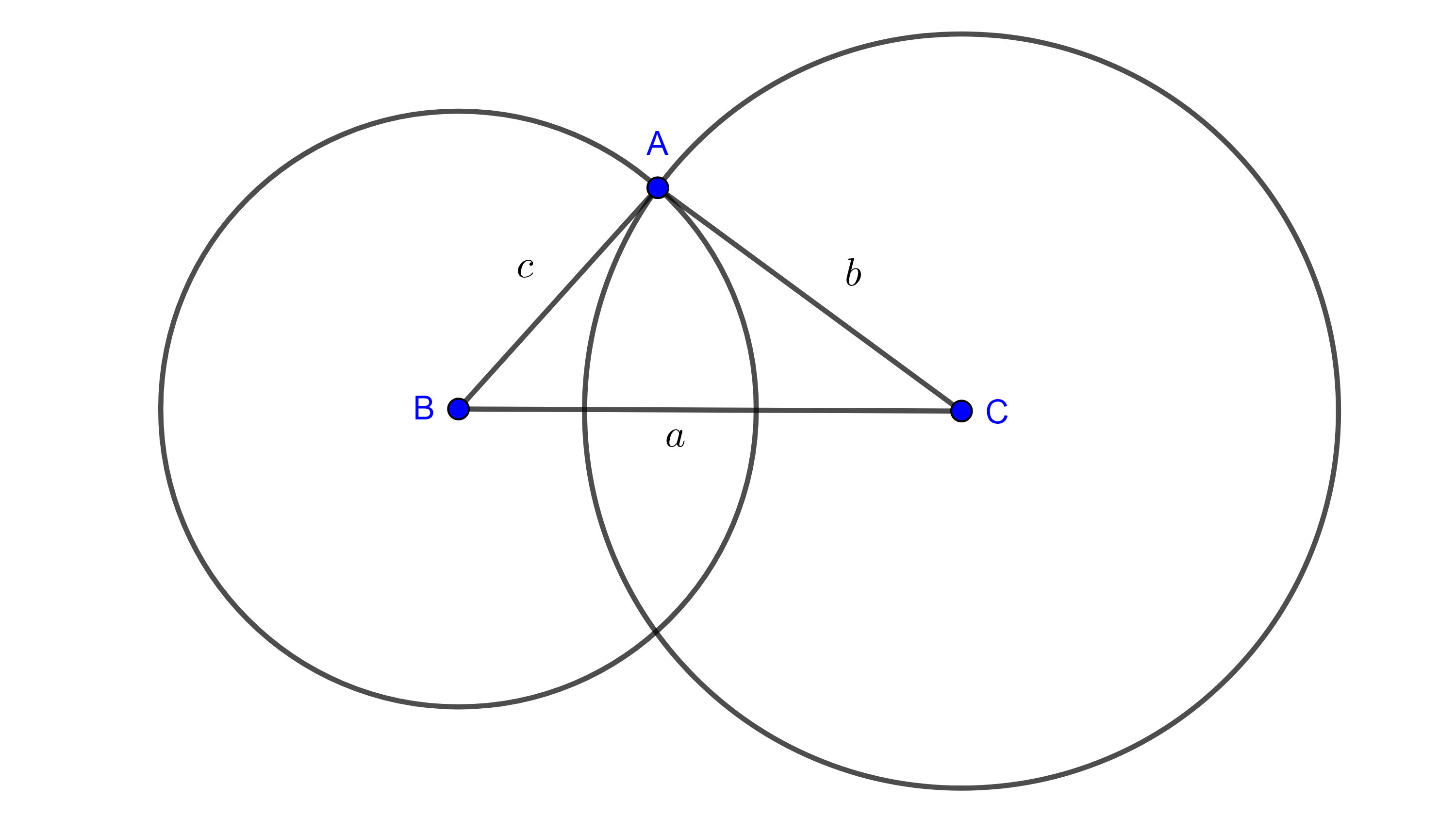
Demostración. Construyamos un segmento $BC$ de longitud $a$, trazamos una circunferencia con centro en $B$ y radio $c$ $(B, c)$, trazamos otra circunferencia con centro en $C$ y radio $b$ $(C, b)$.

$(B, c)$ y $(C, b)$ se intersecan en dos puntos, sea $A$ uno de estos puntos. $AB = c$ por ser radio de $(B, c)$, $AC = b$ por ser radio de $(C, b)$ y $BC = a$ por construcción.

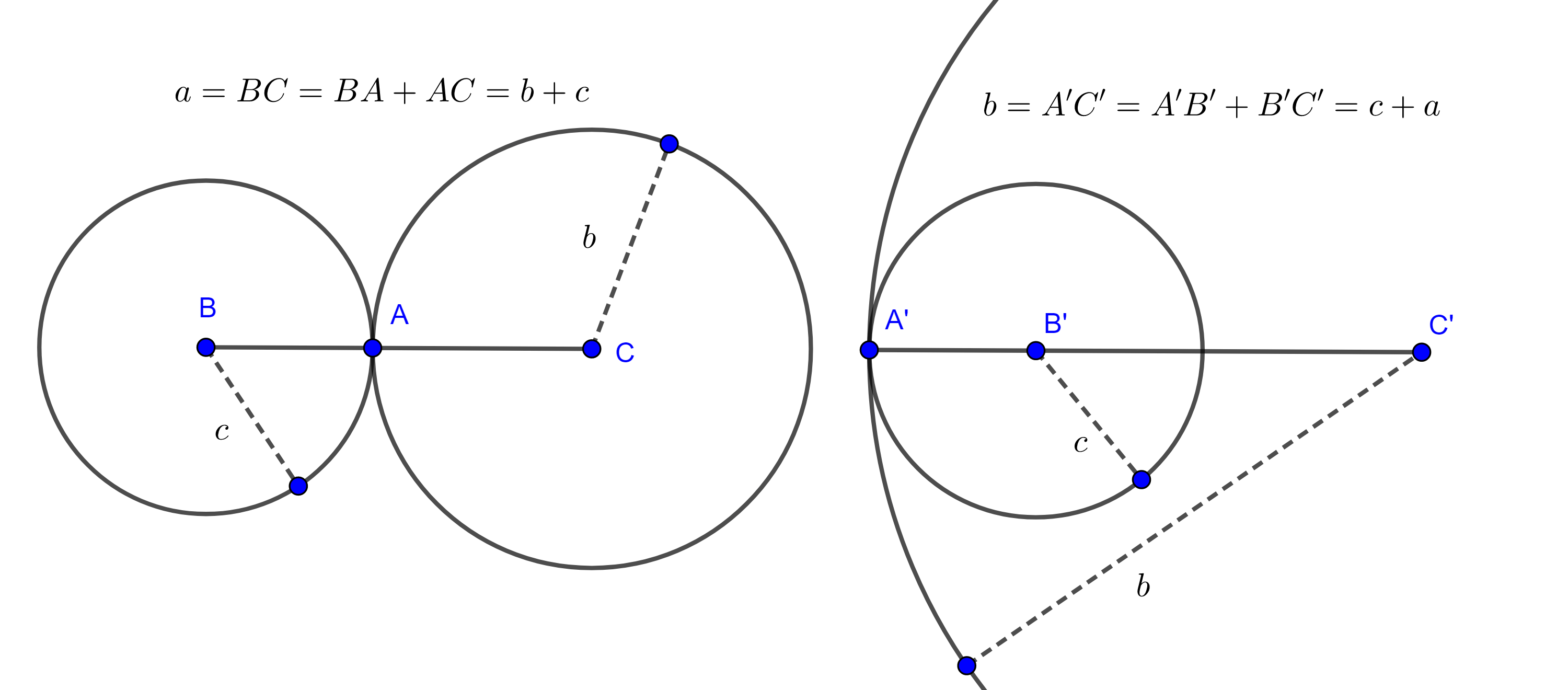
Notemos que si $(B, c)$ y $(C, b)$ se intersecaran en un solo punto entonces la intersección estaría sobre $BC$ o su extensión, y en tal caso se tendría alguna de las siguientes igualdades
$a = b + c$, $b = a + c$ o $c = a + b$, figura 6.

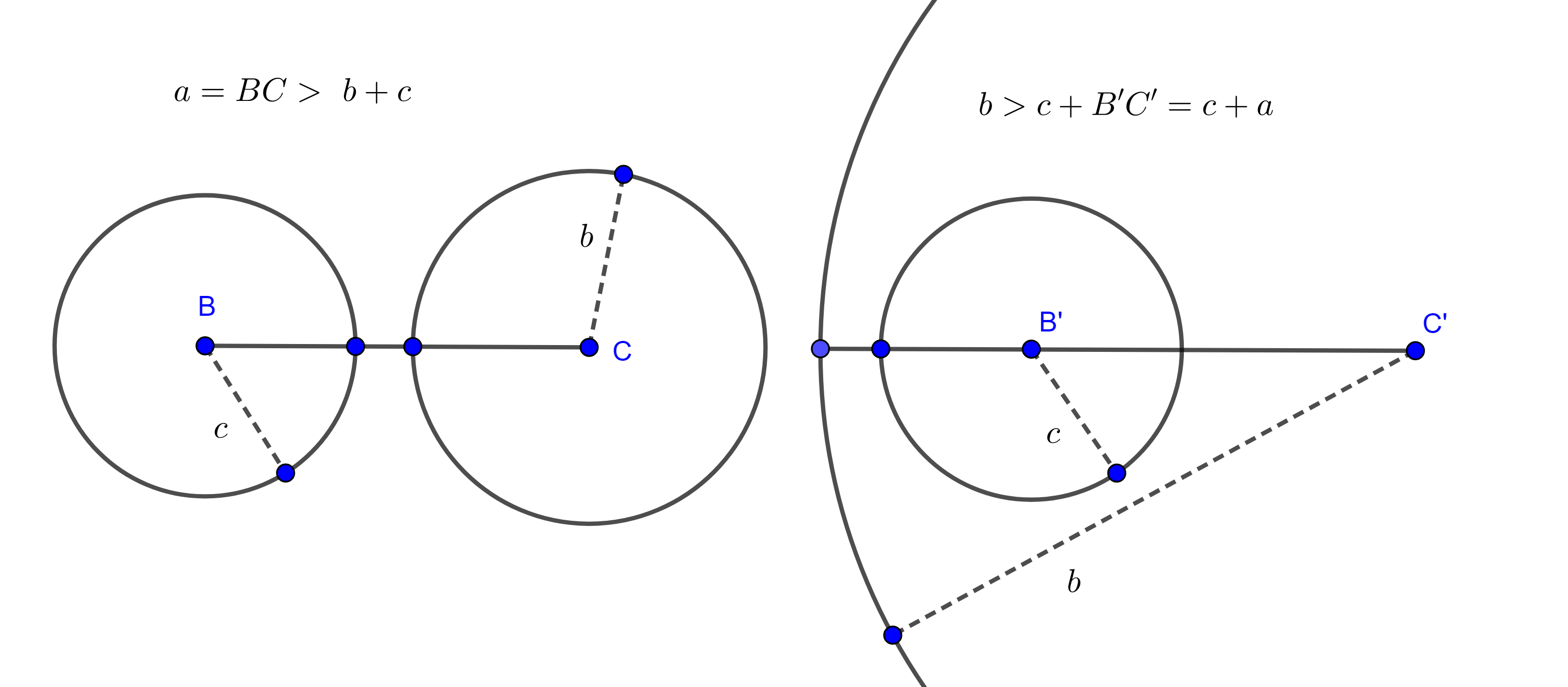
Y si $(B, c) \cap (C, b) = \varnothing$, entonces alguna de las cantidades seria mayor que la suma de las otras dos, $a > b + c$, $b > a + c$ o $c > a + b$, figura 7, lo que sería una contradicción a nuestras hipótesis.

Por lo tanto, $\triangle ABC$ es el triángulo buscado.

$\blacksquare$

Problema. Sobre una recta dada construir un ángulo igual a un ángulo dado.

Solución. Sea $\angle AOB$ el ángulo dado y $l$ la recta dada.

Con centro en $O$ y radio arbitrario $r > 0$ trazamos una circunferencia $(O, r)$ que corte a $OA$ en $C$ y a $OB$ en $D$.

Tomamos $O’ \in l$ y construimos una circunferencia con centro en $O’$ y radio $r$, $(O’, r)$, tomamos una de las intersecciones de $l$ con $(O’, r)$, digamos $D’$, trazamos otra circunferencia con centro en $D’$ y radio $CD$, $(D’, CD)$, sea $C’$ una de las intersecciones de $(O’, r)$ con $(D´, CD)$, entonces por criterio LLL $\triangle COD \cong \triangle C’O’D’$

Por lo tanto, $\angle AOB = \angle C’O’D’$.

$\blacksquare$

Lugar geométrico

Un lugar geométrico es un conjunto de puntos que cumplen un conjunto de condiciones dadas. Para probar que una figura geométrica es un lugar geométrico por lo general la prueba se divide en dos partes.

• Probar que todos los puntos que satisfacen las condiciones pertenecen a la figura.
• Probar que todos los puntos que pertenecen a la figura satisfacen las condiciones.

Teorema 3. El lugar geométrico de los puntos que equidistan a dos puntos dados, es la mediatriz del segmento que une los puntos dados.

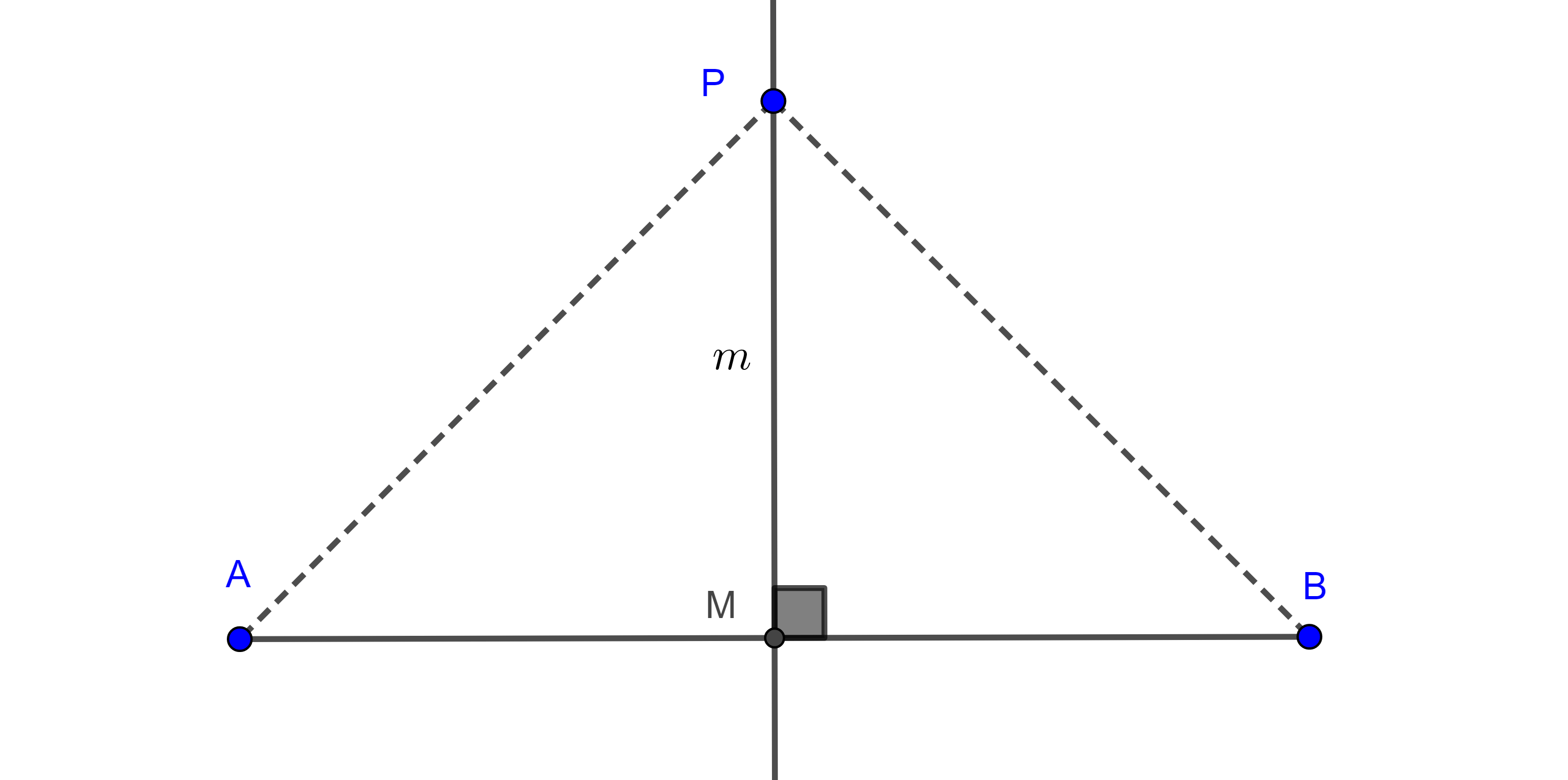
Demostración. Sean $AB$ un segmento dado, $M$ el punto medio y $m$ la mediatriz de $AB$ respectivamente.

Primero vemos que los puntos en la mediatriz de $AB$  equidistan de $A$ y $B$.

Sea $P \in m$, por definición de mediatriz, $m \cap AB = M$ y $l \perp AB$.

Entonces por criterio LAL (lado, ángulo, lado), $\triangle PMA \cong \triangle PMB$, en consecuencia, $PA = PB$.

$\blacksquare$

Ahora veamos que todos los puntos que equidistan de $A$ y $B$, son los puntos en la mediatriz $m$ de $AB$.

Sea $P$ un punto que satisface las condiciones dadas, entonces $PA = PB$ y así $\triangle APB$ es isósceles, en la entrada anterior vimos que la mediatriz de un triángulo isósceles, pasa por el vértice que comparten los lados iguales, por lo tanto, $P \in m$.

$\blacksquare$

Definición. Definimos la distancia de un punto $P$ a una recta $l$ como la distancia entre $P$ y el pie de la perpendicular trazada desde $P$ a $l$.

Teorema 4. El lugar geométrico de los puntos que equidistan a dos rectas que se intersecan son las bisectrices de los ángulos formados por las rectas.

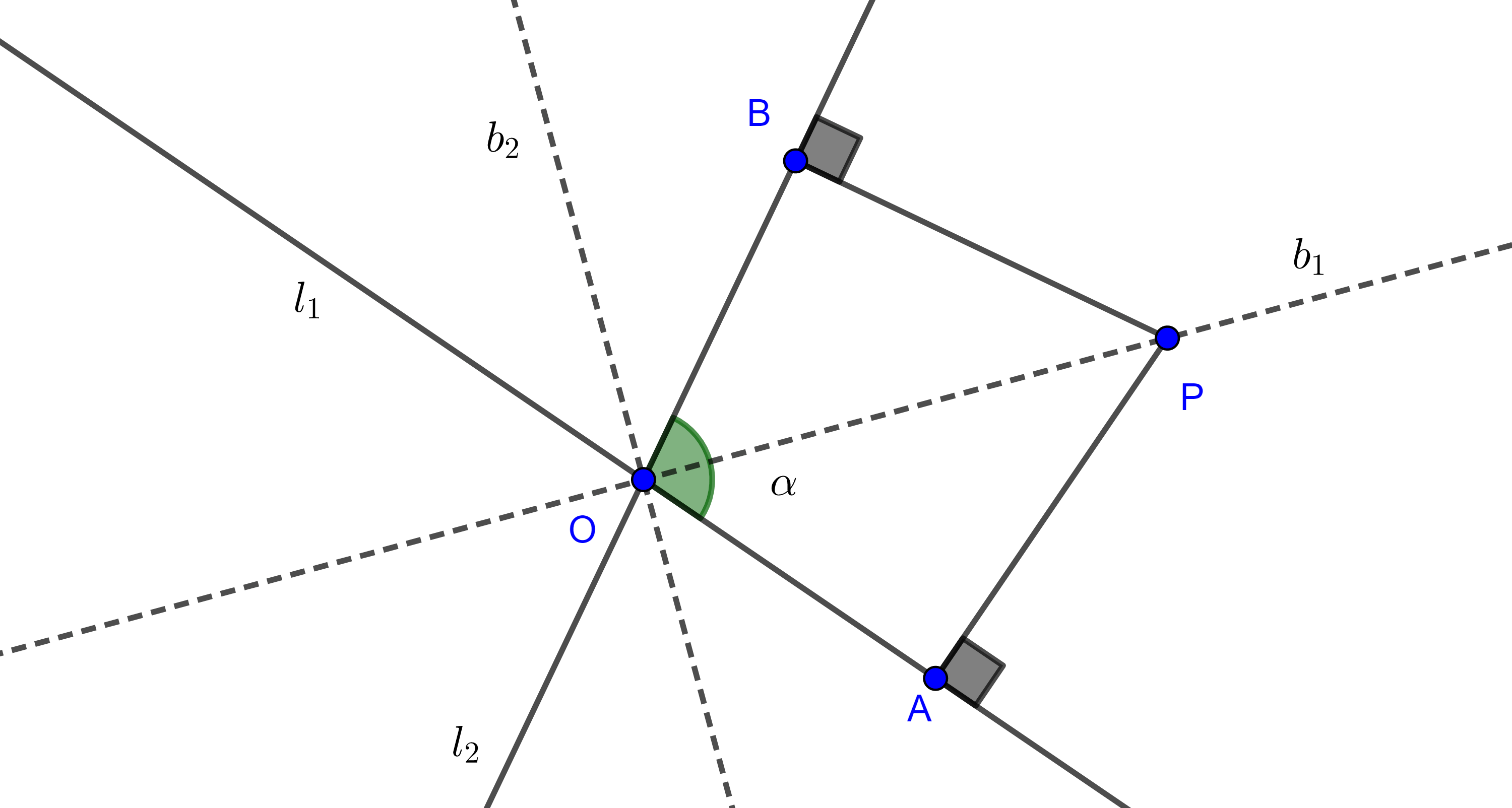
Demostración. Sean $l_{1}$ y $l_{2}$, dos rectas que se intersecan en $O$, consideremos $b_{1}$ la bisectriz de uno de los ángulos formados por $l_{1}$ y $l_{2}$, digamos $\alpha$, y sea $b_{2}$ la bisectriz del ángulo suplementario a $\alpha$.

Primero veamos que todos los puntos en la bisectriz de $\alpha$ equidistan a $l_{1}$ y $l_{2}$.

Sea $P \in b_{1}$, y sean $A$ y $B$ las intersecciones de las perpendiculares trazadas desde $P$ a $l_{1}$ y $l_{2}$ respectivamente.

Como $b_{1}$ es bisectriz, $\angle AOP = \angle POB$, además $\angle PAO = \angle OBP = \dfrac{\pi}{2}$, como la suma de los ángulos internos de todo triángulo es constante entonces $\angle OPA = \angle BPO$.

Entonces en los triángulos $\triangle PAO$ y $\triangle PBO$, $\angle AOP = \angle POB$, $\angle OPA = \angle BPO$ y $OP$ es un lado común.

Por criterio LAL, $\triangle PAO \cong \triangle PBO$, por lo tanto $PA = PB$, así la distancia de $P$ a $l_{1}$ y a $l_{2}$ es la misma.

De manera análoga podemos ver que los puntos en $b_{2}$ son equidistantes a $l_{1}$ y $l_{2}$.

$\blacksquare$

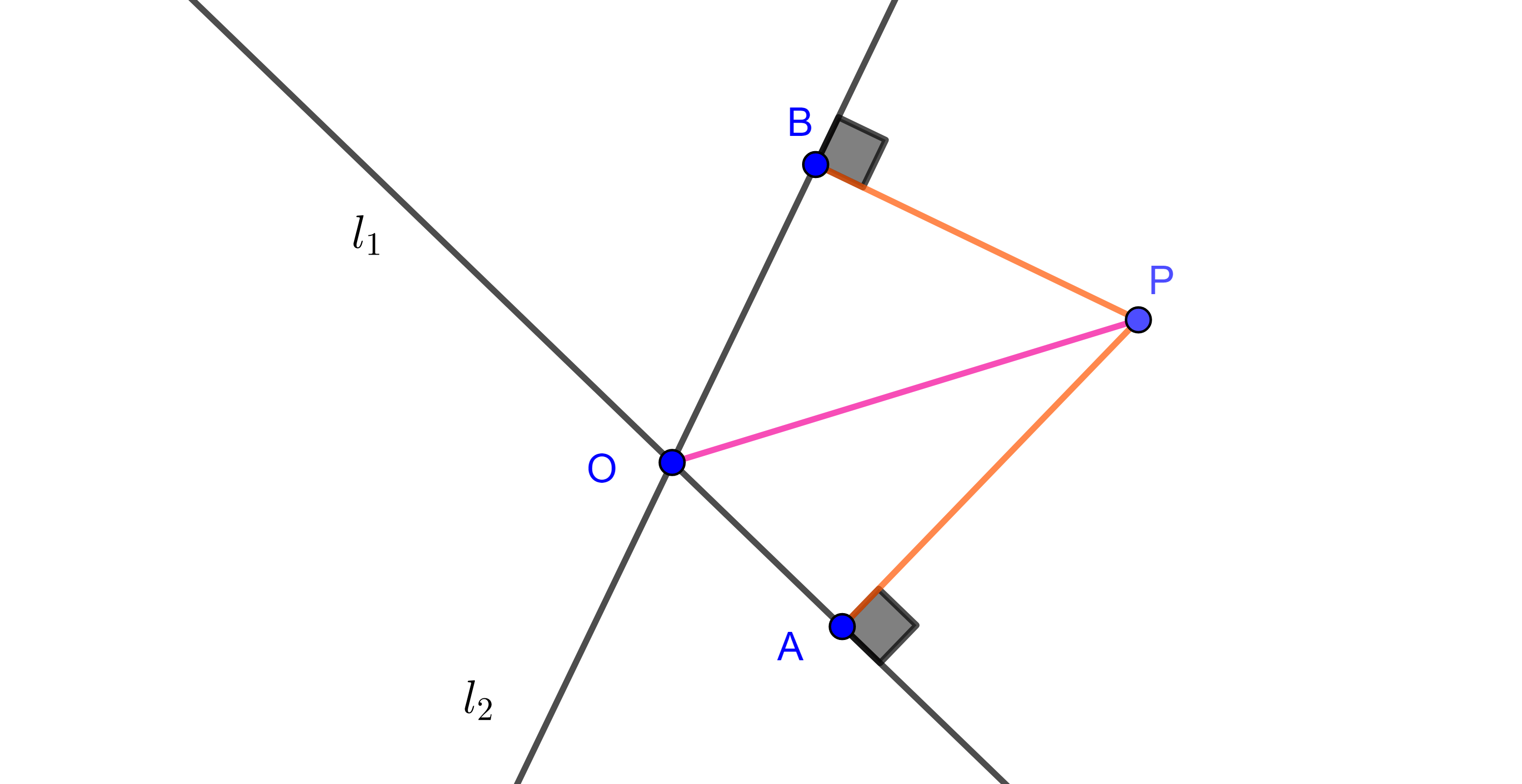
Ahora mostremos que todos los puntos que son equidistantes a $l_{1}$ y $l_{2}$ pertenecen a $b_{1}$ o $b_{2}$.

Sea $P$ un punto que satisface que $PA = PB$, donde $A$ y $B$ son los pies de las perpendiculares trazadas desde $P$ a $l_{1}$ y $l_{2}$ respectivamente.

Entonces $\triangle PAO$ y $\triangle PBO$ son triángulos rectángulos donde la hipotenusa es la misma, y por hipótesis tienen un cateto igual, $PA = PB$, por criterio hipotenusa – cateto $\triangle PAO \cong \triangle PBO$, en particular $\angle AOP =\angle POB$.

Notemos que las dos rectas dividen al plano en cuatro regiones distintas y en cada región podemos hacer el mismo procedimiento, pero dos rectas que se intersecan solo tienen dos bisectrices distintas.

Por lo tanto si $PA = PB$, entonces $P \in b_{1}$ o $P \in b_{2}$.

$\blacksquare$

Más adelante…

En al siguiente entrada estudiaremos a los paralelogramos y sus propiedades.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

1. Sean $\triangle ABC$ y $\triangle A’B’C’$ tales que $AB = A’B’$, $AC = A’C’$ y $BC > B’C’$, muestra que $\angle A > \angle A’$.
2. Sea $\square ABCD$ un cuadrado y $O$ un punto en el plano muestra que $OA < OB + OC + OD$.
3. Sean $\triangle ABC$ y $A’$ un punto en el interior del triángulo, muestra que $AB + AC > A’B + A’C$ y que $\angle BA’C > \angle BAC$.
4. En un poblado situado junto a un rio, cuyo borde es totalmente recto, hay un incendio en un punto $A$, la estación de bomberos se encuentra en un punto $B$ del mismo lado del río donde se dio el incendio, los bomberos necesitan pasar primero por el río para abastecerse de agua. ¿Qué punto $P$ en el borde del río hace que el trayecto $BP + PA$ sea mínimo?
5. Muestra que si dos circunferencias se intersecan en un solo punto entonces el punto pertenece al segmento que une los centros o a su extensión.
6. $i)$ Dados una recta y un punto en ella construye la perpendicular a la recta por el punto dado.
   $ii)$ Dados una recta y un punto fuera de ella construye la paralela a la recta por el punto dado.
   $iii)$ Dados una recta y un punto fuera de ella construye la perpendicular a la recta por el punto dado.
7. $i)$ Dados una recta y un numero $a > 0$ encuentra el el lugar geométrico de los puntos cuya distancia a la recta es $a$.
   $ii)$ ¿Cuál es el lugar geométrico de los puntos cuya distancia a una circunferencia dada $(O, r)$ es una constante dada $b > 0$?
   

Entradas relacionadas

• Ir a Geometría Moderna I
• Entrada anterior del curso: Congruencia de triángulos.
• Siguiente entrada del curso: Paralelogramos.

Fuentes

• Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 9-12, 44-54.
• Cárdenas, S., Notas de Geometría. México: Ed. Prensas de Ciencias, 2013, pp 16-18.
• Geometría interactiva
• Geometry Help

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»