Archivo de la etiqueta: recta de Euler

Geometría Moderna I: Puntos de Fermat y triángulos de Napoleón

Por Rubén Alexander Ocampo Arellano

Deja un comentario

Introducción

En esta ocasión veremos algunos resultados sobre los puntos de Fermat y los triángulos de Napoleón, objetos que aparecen al construir triángulos equiláteros sobre los lados de un triángulo cualquiera.

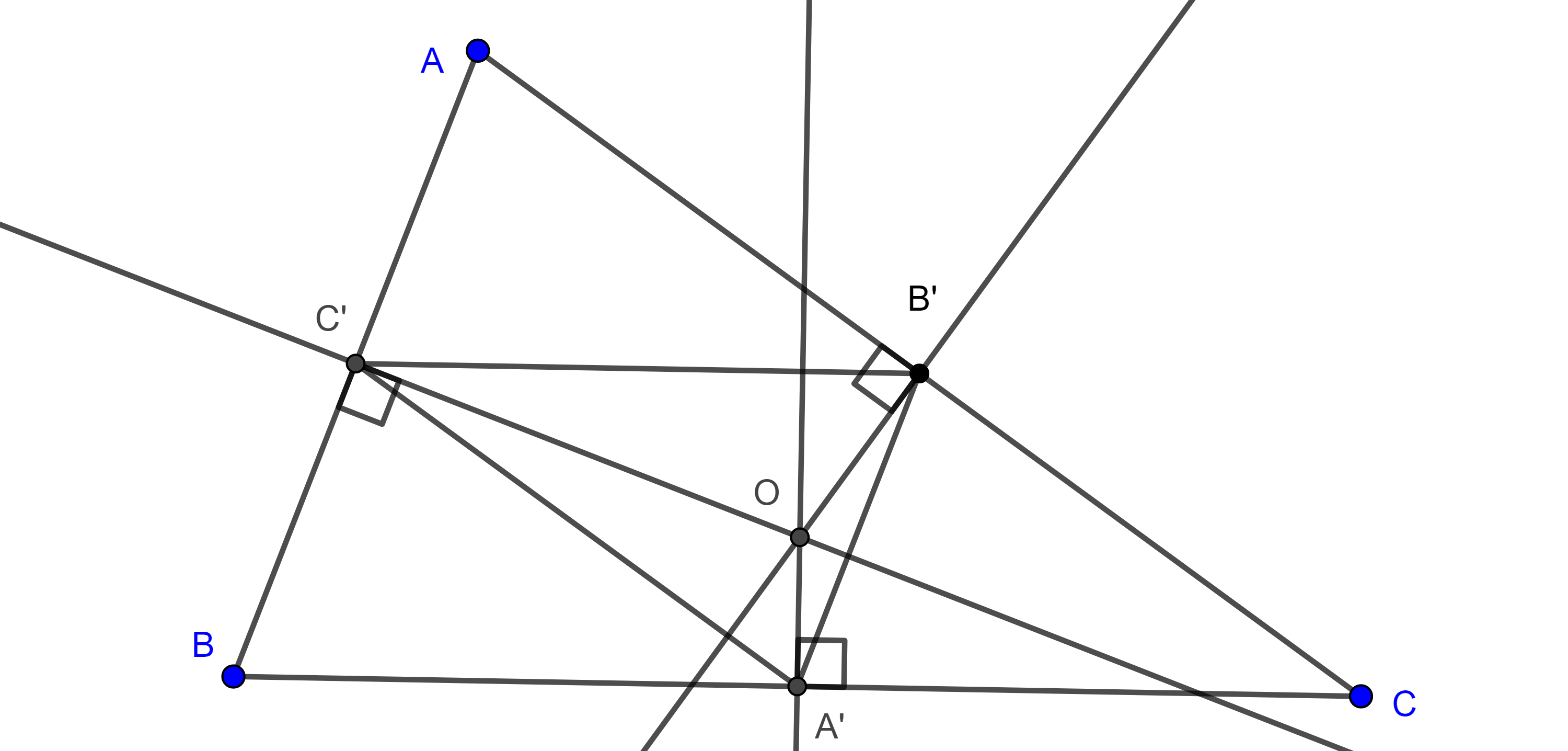
Definición. Sean $\triangle ABC$ y puntos $A’$, $B’$, $C’$ tales que los triángulos $\triangle A’BC$, $\triangle AB’C$ y $\triangle ABC’$ son equiláteros y ninguno se traslapa con $\triangle ABC$, decimos que $ABCA’B’C’$ es una configuración externa de Napoleón.

De manera análoga definimos una configuración interna de Napoleón, si los triángulos $\triangle A’BC$, $\triangle AB’C$ y $\triangle ABC’$ son equiláteros y todos se traslapan con $\triangle ABC$.

Puntos de Fermat

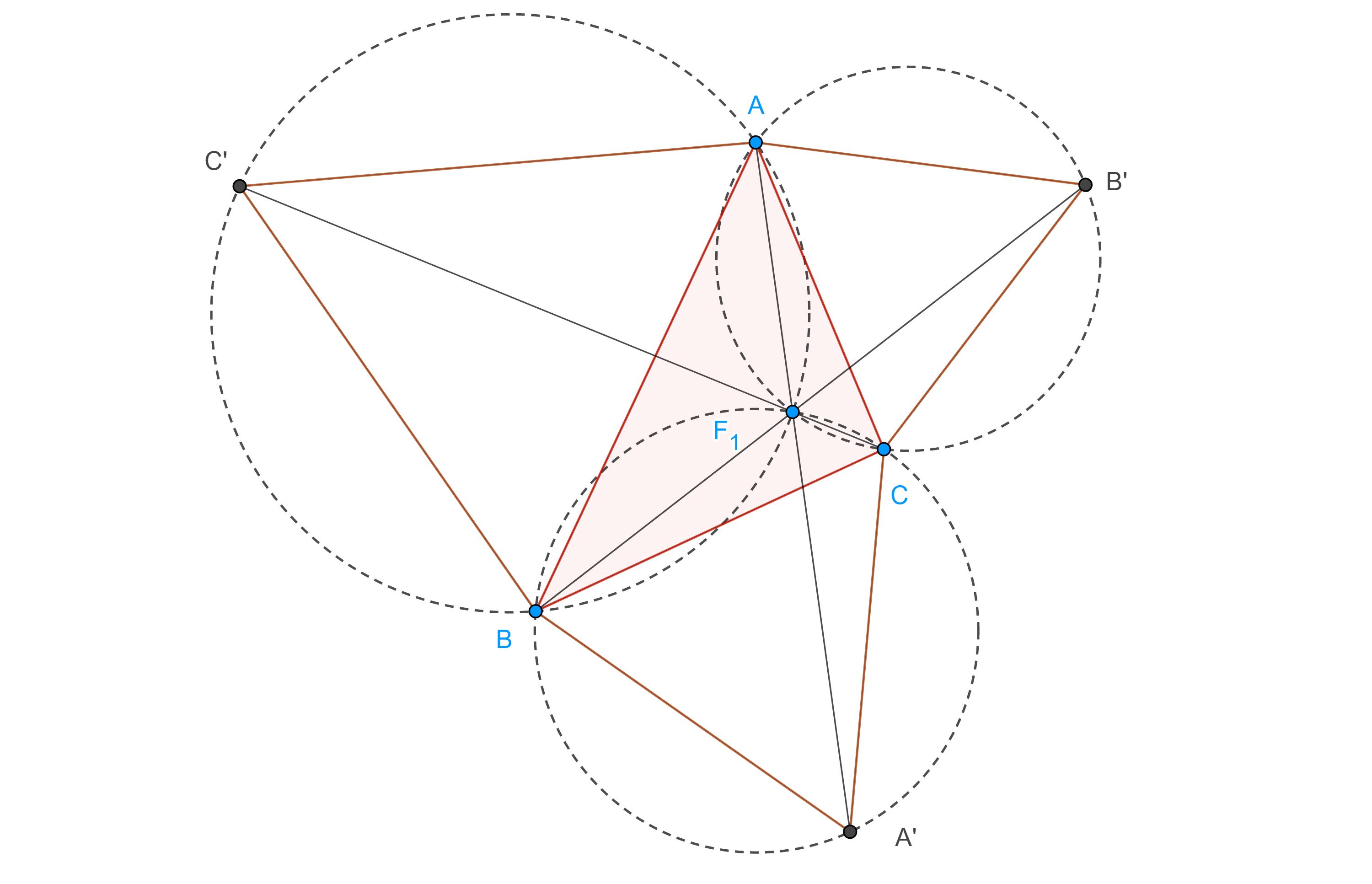
Teorema 1. Sea $ABCA’B’C’$ una configuración externa de Napoleón, entonces
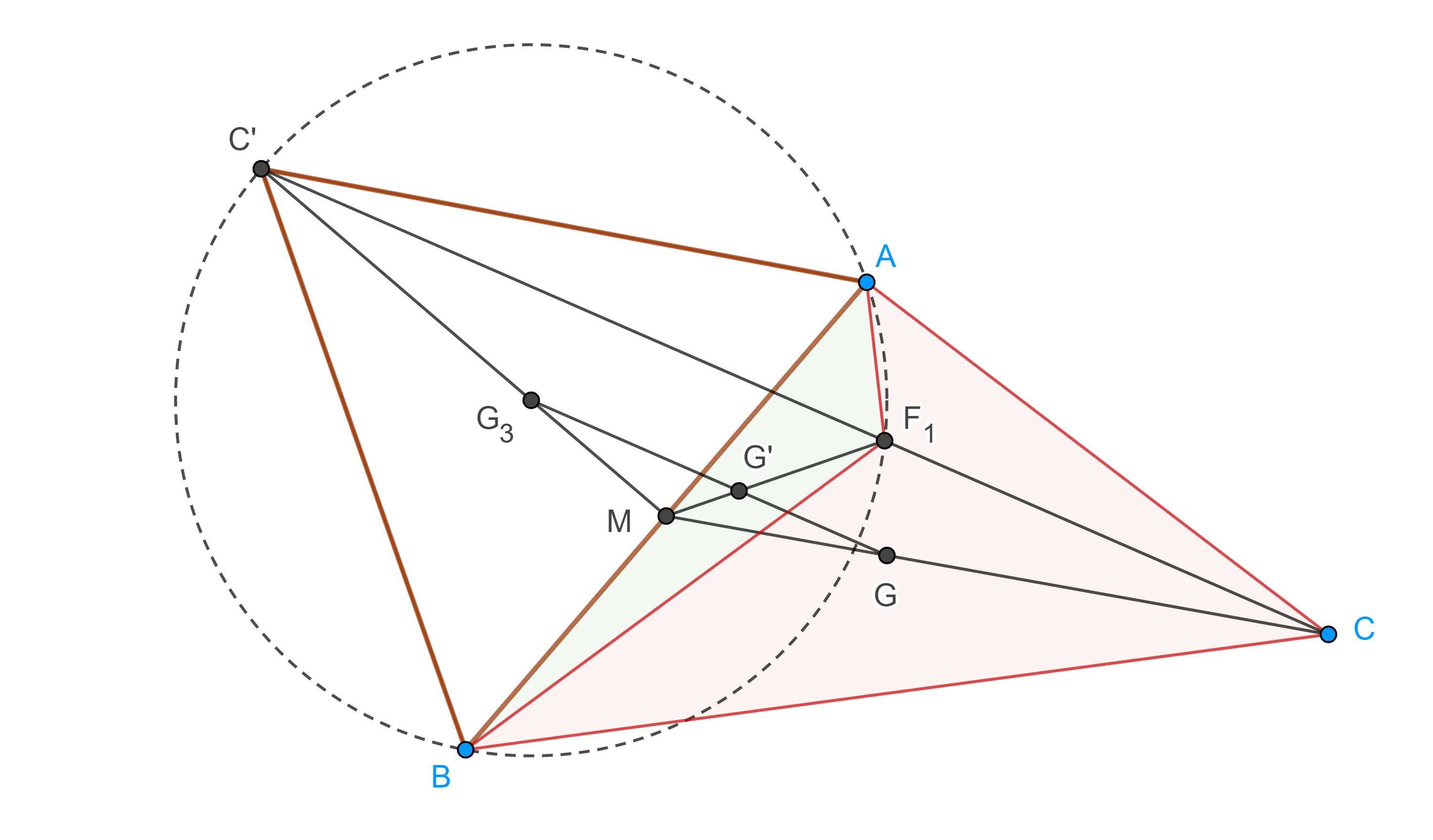
$i)$ los circuncírculos de $\triangle A’BC$, $\triangle AB’C$, $\triangle ABC’$ y las rectas $AA’$, $BB’$, $CC’$ son concurrentes, al punto de concurrencia se le conoce como primer punto de Fermat,
$ii)$ $AA’ = BB’ = CC’$.

Demostración. Sea $F_1 = \Gamma(AB’C) \cap \Gamma(ABC’)$ la intersección de los circuncírculos de $\triangle AB’C$ y $\triangle ABC’$ respectivamente.

Como $\square AF_1CB’$ y $\square AF_1BC’$ son cíclicos entonces los pares de ángulos $\angle BC’A$, $\angle AF_1B$ y $\angle AB’C$, $\angle CF_1A$ son suplementarios, por lo tanto, $\angle AF_1B = \angle CF_1A = \dfrac{2\pi}{3}$.

Figura 1

En consecuencia, $\angle BF_1C = \dfrac{2\pi}{3}$, por lo tanto, $\angle BF_1C$ y $\angle PA’B$ son suplementarios, así, $\square F_1BA’C$ es cíclico, es decir $F_1 \in \Gamma(A’BC)$.

Por otra parte, $\angle BF_1A’ = \angle BCA$, pues abarcan el mismo arco, entonces, $\angle AF_1B + \angle BF_1A’ = (\pi – \angle BC’A) + \angle BCA’ = \pi – \dfrac{\pi}{3} + \dfrac{\pi}{3} = \pi$, por lo tanto, $F_1 \in AA’$.

Igualmente podemos ver que $F_1 \in BB’$ y $F_1 \in CC’$.

Finalmente, hagamos una rotación de $\dfrac{\pi}{3}$ en sentido contrario al de las manecillas y centro en $B$, entonces $A$ toma el lugar de $C’$ y $A’$ toma el lugar de $C$, por lo tanto, $AA’ = CC’$.

Con una rotación de $\dfrac{\pi}{3}$ en el sentido de las manecillas, con centro en $C$, $A’$ toma el lugar de $B$ y $A$ el de $B’$, por lo tanto, $CC’ = AA’ = BB’$.

$\blacksquare$

Nota. Si $ABCA’B’C’$ es una configuración interna de Napoleón, los mismos resultados son ciertos y al punto de concurrencia le llamamos segundo punto de Fermat.

Problema de Fermat

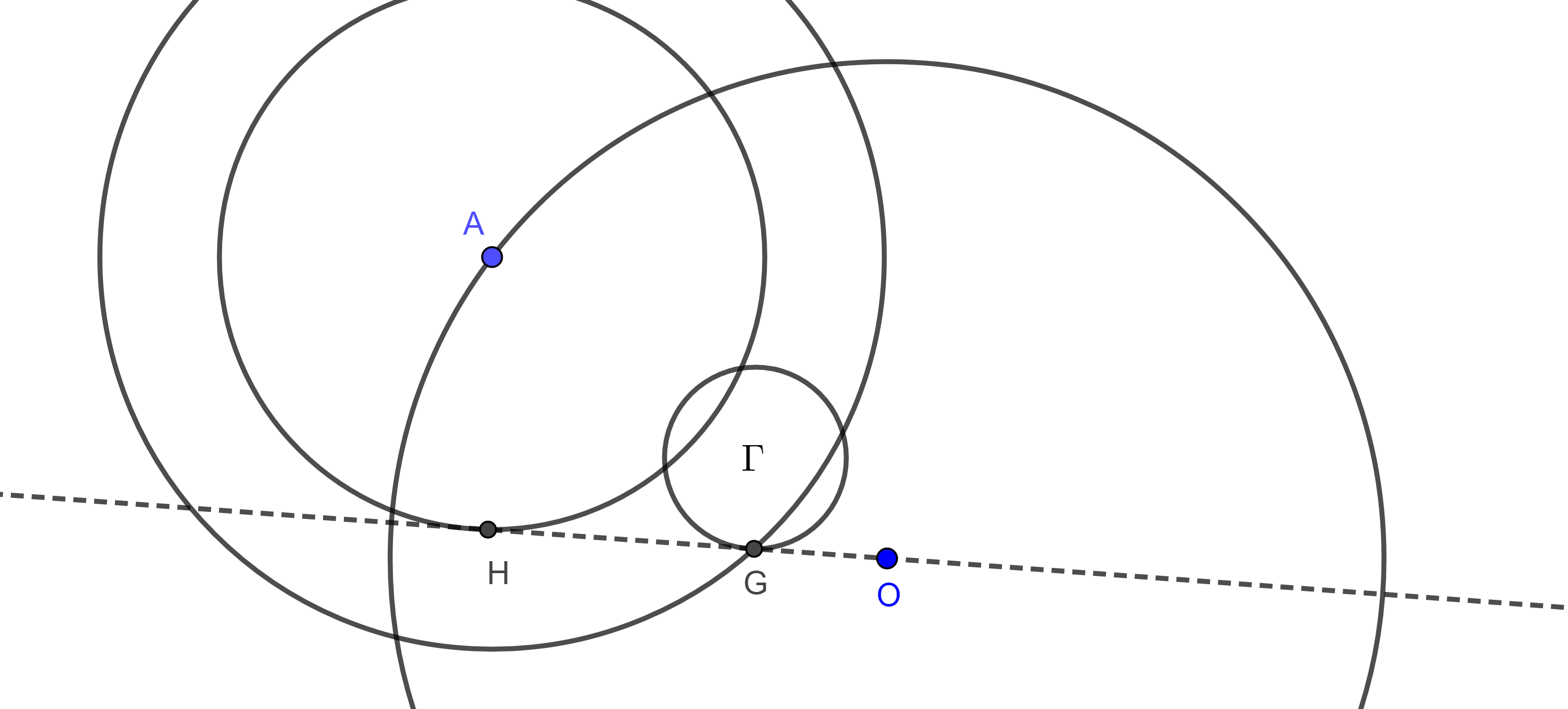
Problema de Fermat. Dado un triángulo $\triangle ABC$ tal que ninguno de sus ángulos internos es mayor a $\dfrac{2\pi}{3}$, encuentra el punto $P$ que minimiza la suma de las distancias a los vértices de $\triangle ABC$, $PA + PB + PC$.

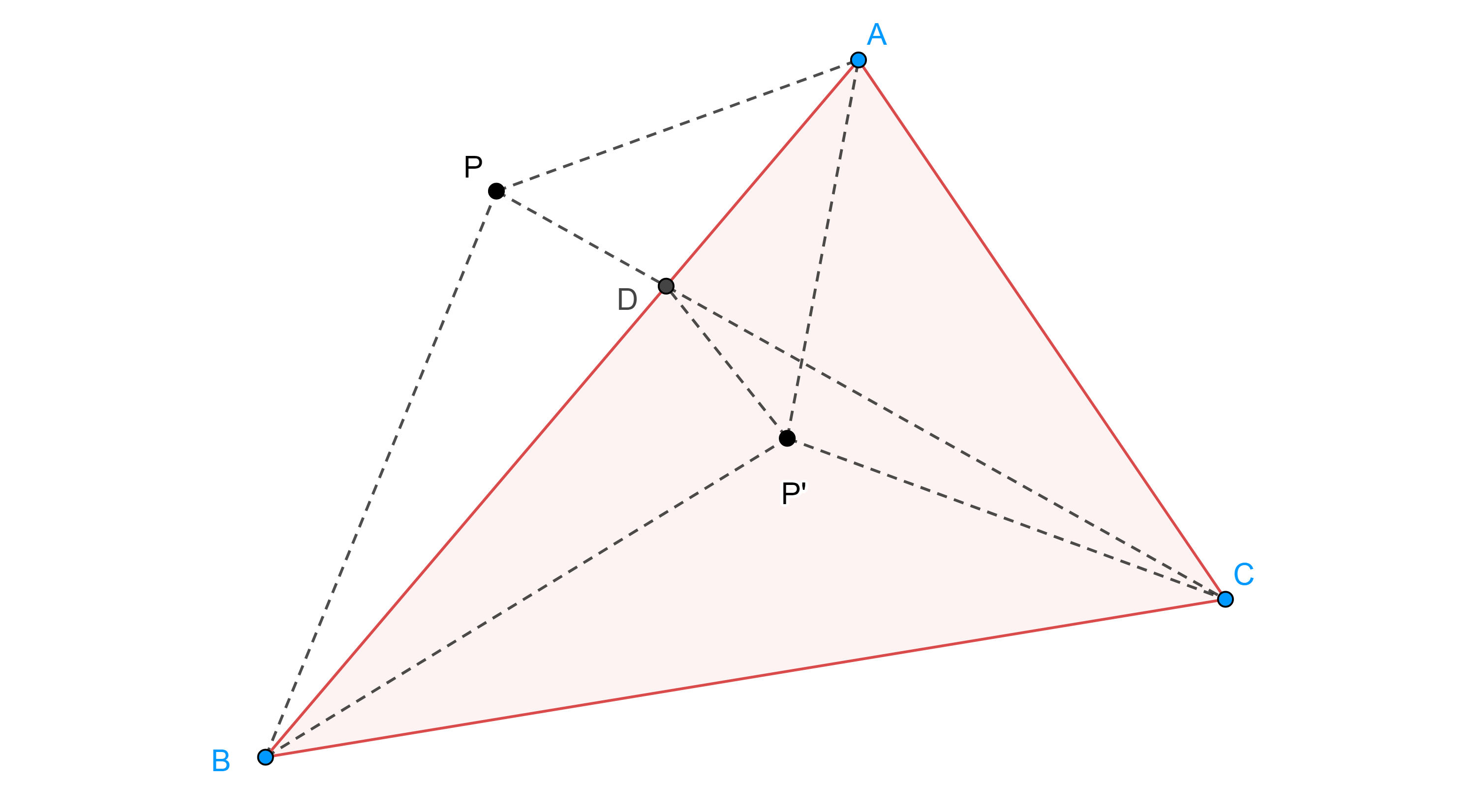
Solución. Sea $P$ un punto fuera de $\triangle ABC$ (figura 2), sin pérdida de generalidad supongamos que $P$ y $C$ se encuentran en lados contrarios respecto de $AB$.

Sea $D = PC \cap AB$ aplicando la desigualdad del triángulo tenemos lo siguiente
$PA + PB + PC = P’A + P’B + PC$
$= P’A + P’B + PD + DC$
$= P’A + P’B + P’D + DC$
$\geq P’A + P’B + P’C$.

Figura 2

De lo anterior concluimos que el punto buscado debe estar dentro de $\triangle ABC$.

Ahora supongamos que $P$ está dentro de $\triangle ABC$ (figura 3), sea $\triangle BC’P’$ la imagen de $\triangle BAP$ bajo una rotación de $\dfrac{\pi}{3}$ en sentido contrario al de las manecillas y centro en $B$.

Como $BP = BP’$ y $\angle PBP’ = \dfrac{\pi}{3}$ entonces $\triangle BPP’$ es equilátero y tenemos lo siguiente
$PA + PB + PC = P’C’ + PP’ + PC \geq CC’$.

Figura 3

Por lo tanto, para que la suma de distancias sea mínima es necesario que $P \in CC’$, pero por un razonamiento análogo también es necesario que $P \in AA’$ y $P \in BB’$, donde $ABCA’B’C’$ es una configuración externa de Napoleón.

Por el teorema 1, $P = F_1$, es el primer punto de Fermat.

Sin embargo, notemos que, $\angle BPC = \pi – \angle P’PB = \dfrac{2\pi}{3}$, por lo tanto, por el ejercicio 3 de la entrada desigualdad del triángulo, cualquier ángulo interno de $\triangle ABC$ debe ser menor o igual que $\dfrac{2\pi}{3}$, si esto se cumple entonces $F_1$ es el punto buscado.

$\blacksquare$

Triángulos de Napoleón

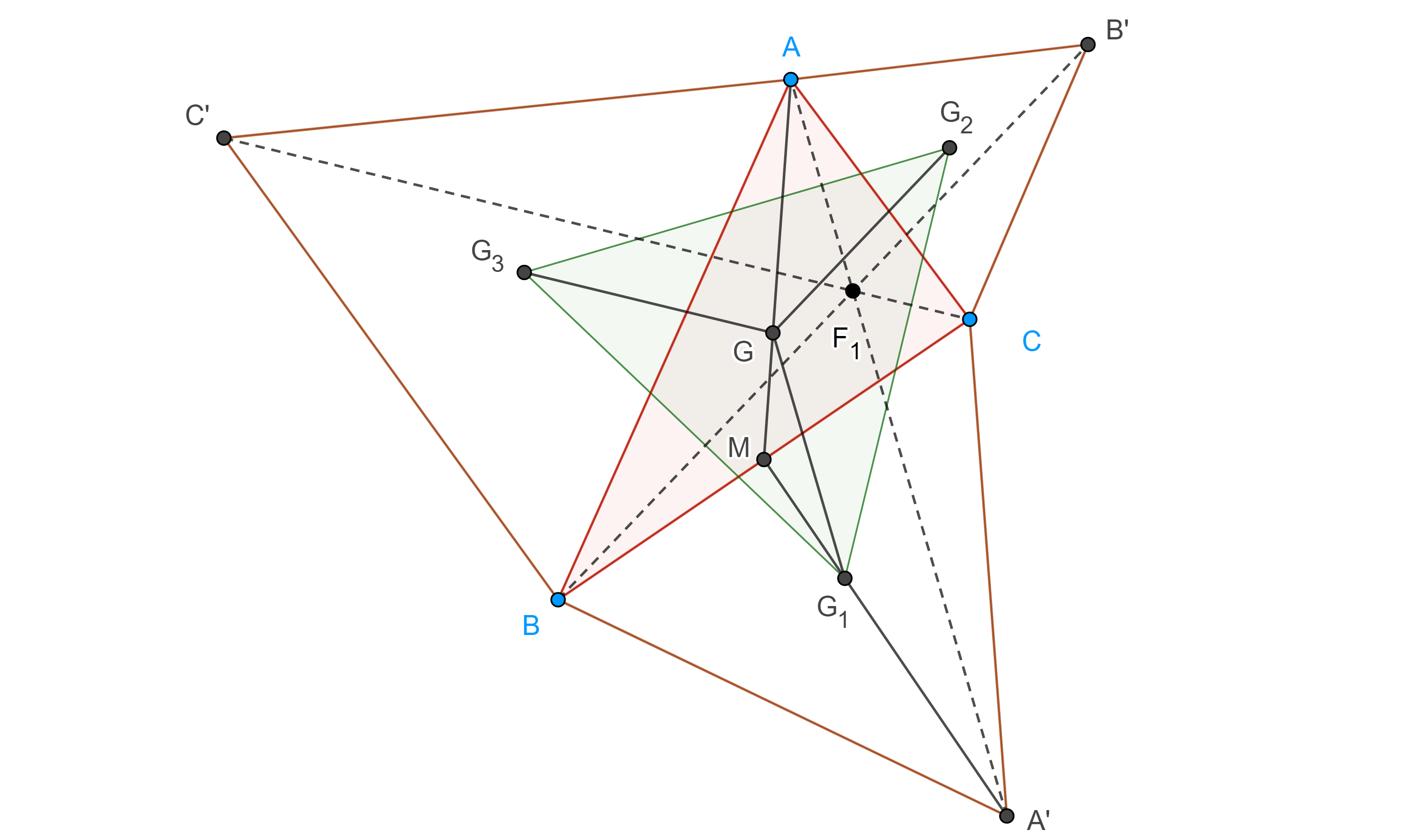
Teorema 2, de Napoleón. Sea $ABCA’B’C’$ una configuración externa de Napoleón, entonces los centroides de $\triangle A’BC$, $\triangle AB’C$ y $\triangle ABC’$ son los vértices de un triángulo equilátero, conocido como triángulo exterior de Napoleón y su centroide coincide con el centroide de $\triangle ABC$.

Demostración. Sean $G_1$, $G_2$ y $G_3$ los centroides de $\triangle A’BC$, $\triangle AB’C$ y $\triangle ABC’$ respectivamente, $G$ el centroide de $\triangle ABC$ y $M$ el punto medio de $BC$.

Figura 4

Como $\dfrac{MA}{MG} = \dfrac{MA’}{MG_1} = 3$ por el reciproco del teorema de Tales $GG_1 \parallel AA’$, además $AA’ = 3GG_1$.

Igualmente podemos ver que $GG_2 \parallel BB’$, $BB’ = 3GG_2$ y $GG_3 \parallel CC’$ y $CC’ = 3GG_3$.

Como $AA’ = BB’ = CC’$, entonces $GG_1 = GG_2 = GG_3$, por lo tanto, $G$ es el circuncentro de $\triangle G_1G_2G_3$.

Por el teorema 1, $\angle A’F_1B’ = \dfrac{2\pi}{3}$, por lo tanto, $\angle G_1GG_2 = \dfrac{2\pi}{3}$.

Igualmente vemos que $\angle G_2GG_3 = \angle G_3GG_1 = \dfrac{2\pi}{3}$.

Por criterio de congruencia LAL, $\triangle GG_1G_2 \cong \triangle GG_2G_3 \cong \triangle GG_1G_3$.

En consecuencia, $\triangle G_1G_2G_3$ es equilátero, como en un triángulo equilátero el circuncentro y el centroide coinciden entonces $G$ es el centroide de $\triangle G_1G_2G_3$.

$\blacksquare$

Nota. Si $ABCA’B’C’$ es una configuración interna de Napoleón se obtienen los mismos resultados y al triángulo formado por los centroides se le conoce como triángulo interior de Napoleón.

Área del triángulo externo de Napoleón

Teorema 3. El área del triangulo externo de Napoleón es igual a la la mitad del área de su triángulo de referencia mas un sexto de la sumas de las áreas de los triángulos equiláteros construidos.

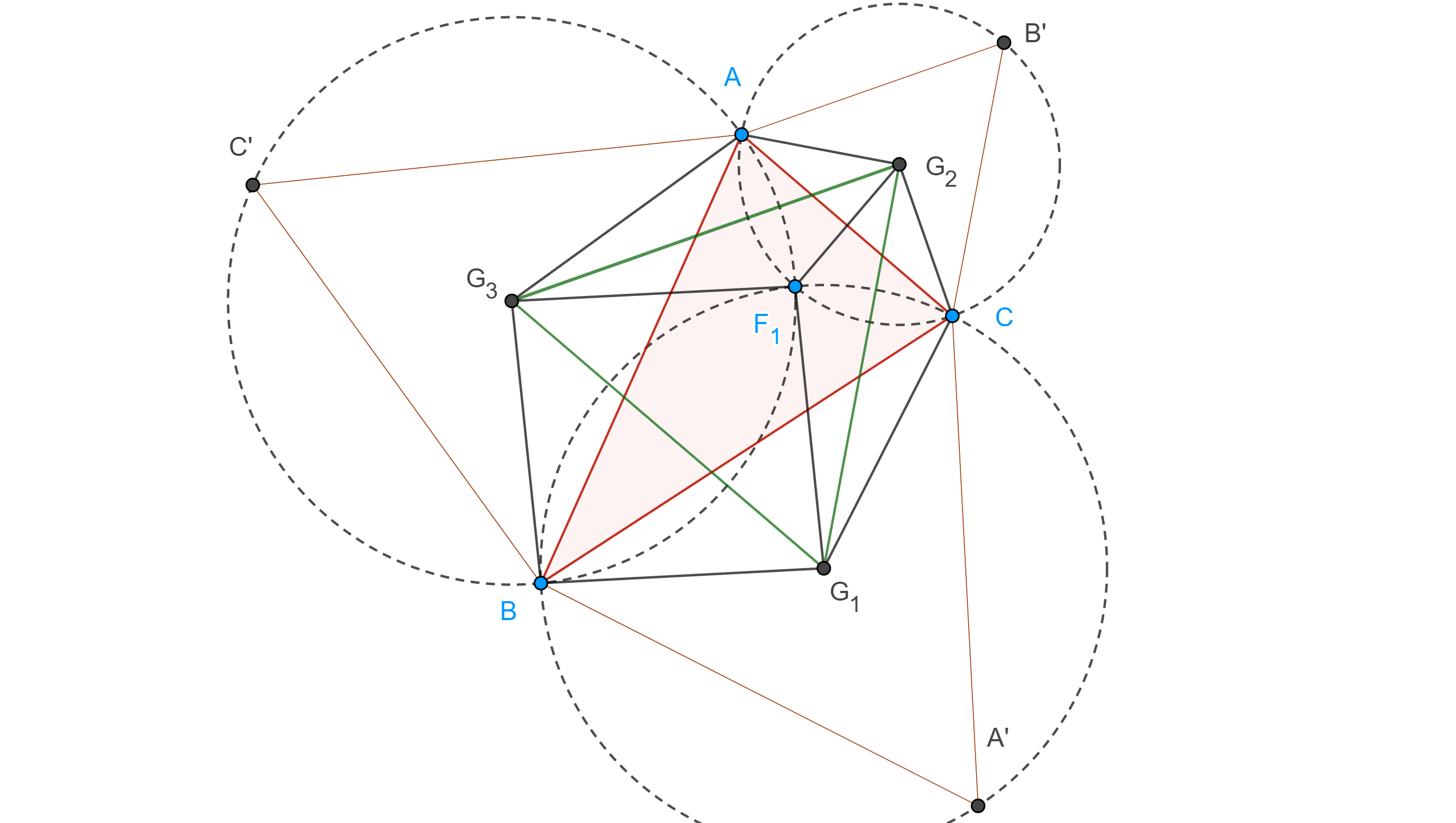
Demostración. Sea $ABCA’B’C’$ una configuración externa de Napoleón y $G_1$, $G_2$, $G_3$ los centroides de $\triangle A’BC$, $\triangle AB’C$, $\triangle ABC’$ respectivamente.

Figura 5

Sean $F_1$ el primer punto de Fermat, como $AF_1$ es una cuerda común de $\Gamma(ABC’)$ y $\Gamma(AB’C)$, entonces $G_2G_3$ es la mediatriz de $AF_1$, es decir, la reflexión de $A$ en $G_2G_3$ es $F_1$.

Por lo tanto, $\triangle AG_2G_3$ y $\triangle F_1G_2G_3$ son congruentes.

Similarmente vemos que $\triangle BG_1G_3 \cong \triangle F_1G_1G_3$ y $\triangle CG_1G_2 \cong \triangle F_1G_1G_2$.

Esto implica que,
$(\triangle G_1G_2G_3) = \dfrac{(AG_3BG_1CG_2)}{2} $
$= \dfrac{1}{2} ((\triangle ABC) + (\triangle ABG_3) + (\triangle BCG_1) + (\triangle ACG_2))$
$= \dfrac{1}{6} ((\triangle ABC’) + (\triangle A’BC) + (\triangle AB’C)) + \dfrac{(\triangle ABC)}{2}$.

$\blacksquare$

Área del triángulo interno de Napoleón

Teorema 3. El área del triangulo interno de Napoleón es igual a menos la mitad del área de su triángulo de referencia mas un sexto de la sumas de las áreas de los triángulos equiláteros construidos.

Demostración. Sea $ABCA’’B’’C’’$ una configuración interna de Napoleón, $F_2$ el segundo punto de Fermat y $G’_1$, $G’_2$, $G’_3$ los centroides de $\triangle A’’BC$, $\triangle AB’’C$, $\triangle ABC’’$ respectivamente.

Sea $F_2$ el segundo punto de Fermat, siguiendo un razonamiento análogo al teorema anterior tenemos
$(\triangle G’_1G’_2G’_3) $
$= (\triangle F_2G’_1G’_3) + (\triangle F_2G’_3G’_2) – (\triangle F_2G’_1G’_2)$
$\begin{equation} = (\triangle BG’_1G’_3) + (\triangle AG’_3G’_2) – (\triangle CG’_1G’_2). \end{equation}$.

Figura 6

Por otro lado,
$\dfrac{1}{3}((\triangle A’BC) + (\triangle AB’C) + (\triangle ABC’))$
$\begin{equation} = (\triangle G’_1BC) + (\triangle AG’_2C) + (\triangle ABG’_3). \end{equation}$.

Sean, $E = AB \cap G’_1G’_3$, $D = BC \cap G’_1G’_3$, $J = BC \cap G’_2G’_3$ e $I = G’_1C \cap G’_2G’_3$, entonces tenemos lo siguiente:

$(\triangle G’_1BC) = (\triangle BED) + (\triangle BEG’_1) + (\triangle CJI) + (\square G’_1DJI)$.

$(\triangle ABG’_3) = (\triangle BEG’_3) + (\triangle AG’_2G’_3) + (AEDJG’_2) + (\triangle DG’_3J)$.

Sustituyendo en $(2)$
$\dfrac{1}{3}((\triangle A’BC) + (\triangle AB’C) + (\triangle ABC’)) $
$= ((\triangle BEG’_3) + (\triangle BEG’_1)) + (\triangle AG’_2G’_3) + ((\triangle BED) + (AEDJG’_2)$
$+ (\triangle CJI) + (\triangle AG’_2C)) + ((\triangle DG’_3J) + (\square G’_1DJI))$
$= (\triangle BG’_1G’_3) + (\triangle AG’_2G’_3) + ((\triangle ABC) – (\triangle CIG’_2)) + (\triangle IG’_1G’_3)$
$= (\triangle BG’_1G’_3) + (\triangle AG’_2G’_3) + ((\triangle ABC) – (\triangle CIG’_2)) + ((\triangle G’_1G’_2G’_3) – (\triangle G’_1G’_2I))$
$ = (\triangle ABC) + ((\triangle BG’_1G’_3) + (\triangle AG’_2G’_3) – (\triangle CG’_1G’_2)) + (\triangle G’_1G’_2G’_3)$.

Usando $(1)$
$\dfrac{1}{3}((\triangle A’BC) + (\triangle AB’C) + (\triangle ABC’))$
$= (\triangle ABC) + 2(\triangle G’_1G’_2G’_3)$.

Por lo tanto,
$(\triangle G’_1G’_2G’_3) = \dfrac{1}{6} ((\triangle ABC’) + (\triangle A’BC) + (\triangle AB’C)) –  \dfrac{(\triangle ABC)}{2}$.

$\blacksquare$

Corolario. La diferencia entre el área del triángulo externo de Napoleón y el área del triángulo interno de Napoleón es igual al área de su triángulo de referencia.

Como consecuencia de los teorema 3 y 4 tenemos,
$(\triangle G_1G_2G_3) – (\triangle G’_1G’_2G’_3) = (\triangle ABC)$.

$\blacksquare$

Rectas de Euler concurrentes

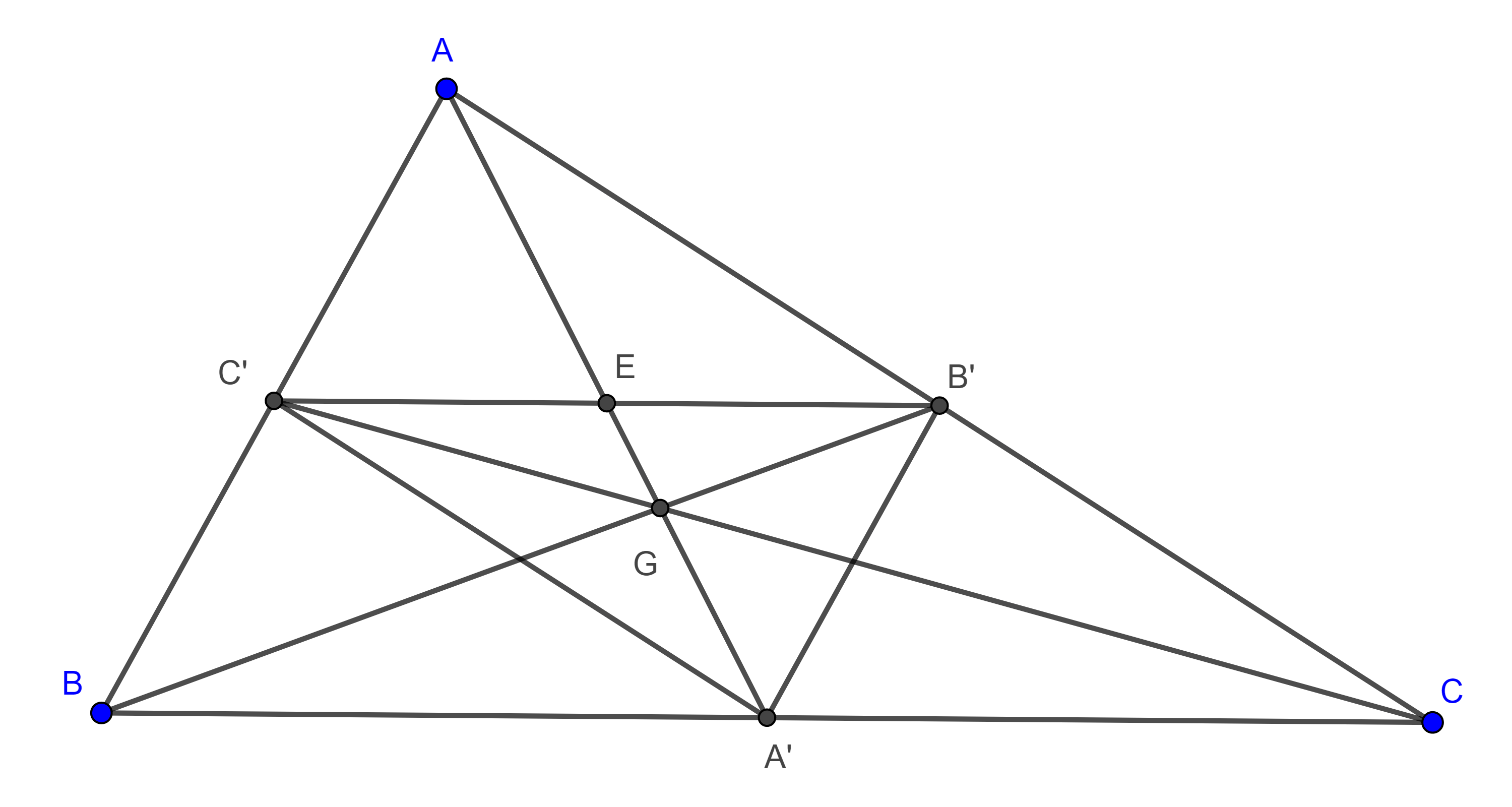
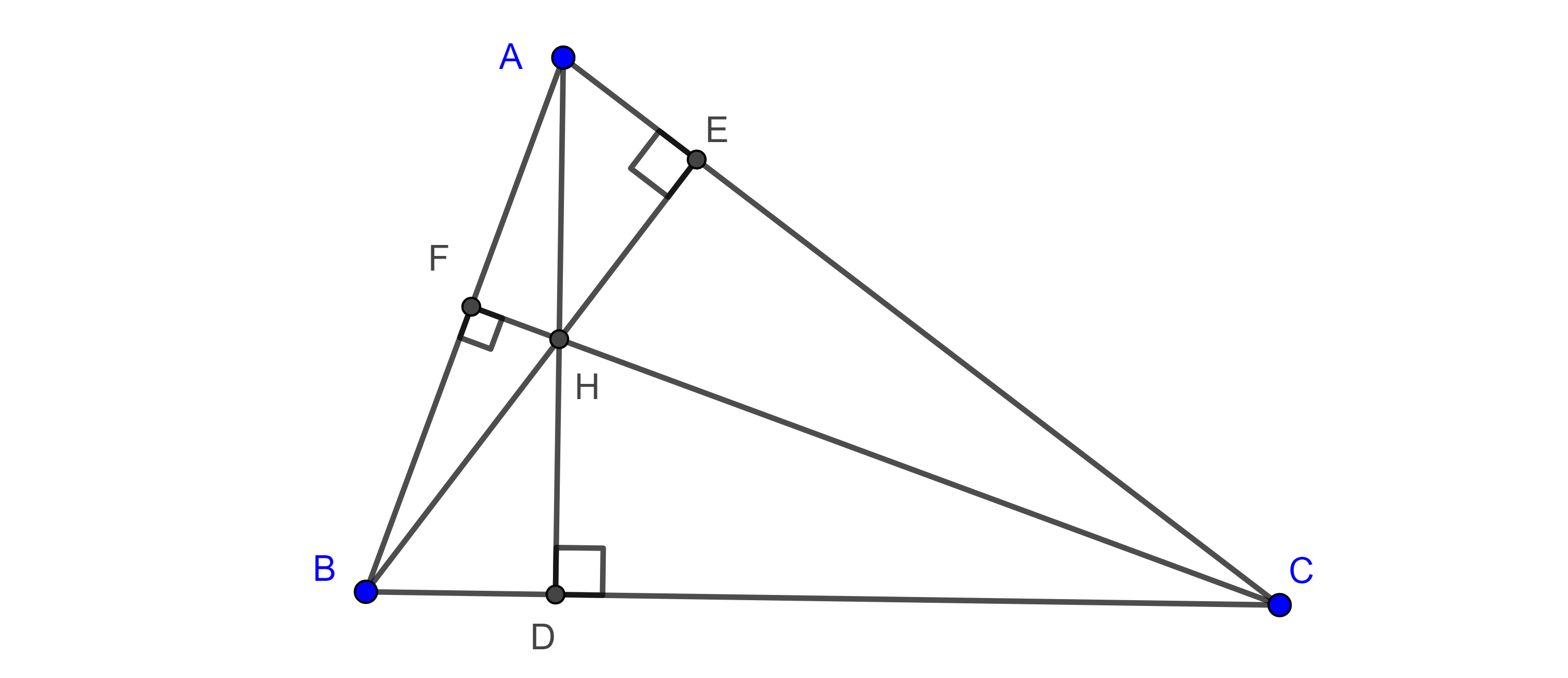
Proposición 1. Sea $ABCA’B’C’$ una configuración externa de Napoleón y $F_1$ el primer punto de Fermat, entonces las rectas de Euler de $\triangle ABF_1$, $\triangle AF_1C$ y $\triangle F_1BC$ concurren en el centroide de $\triangle ABC$.

Demostración. Sean $G$, $G’$ y $G_3$ los centroides de $\triangle ABC$, $\triangle ABF_1$ y $\triangle ABC’$ respectivamente, consideremos el $M$ el punto medio de $AB$.

Figura 7

Por el teorema 1, $G_3$ es el circuncentro de $\triangle ABF_1$ y $C$, $F_1$ y $C’$ son colineales, como $G_3$, $G’$ y $G$ son los centroides de $\triangle ABC’$, $\triangle AF_1$ y $\triangle ABC$ entonces
$\dfrac{MG_3}{MC’} = \dfrac{MG’}{MF_1} = \dfrac{MG}{MC} = \dfrac{1}{3}$.

Por el reciproco del teorema de Tales $G_3G’ \parallel C’F_1$ y $G’G \parallel F_1C$.

Por lo tanto, $G_3$, $G’$ y $G$ son colineales, y $G_3G’$ es la recta de Euler de $\triangle ABF_1$.

Igualmente podemos ver que las rectas de Euler de $\triangle AF_1C$ y $\triangle F_1BC$ pasan por el centroide de $\triangle ABC$.

$\blacksquare$

Hexágono de Napoleón

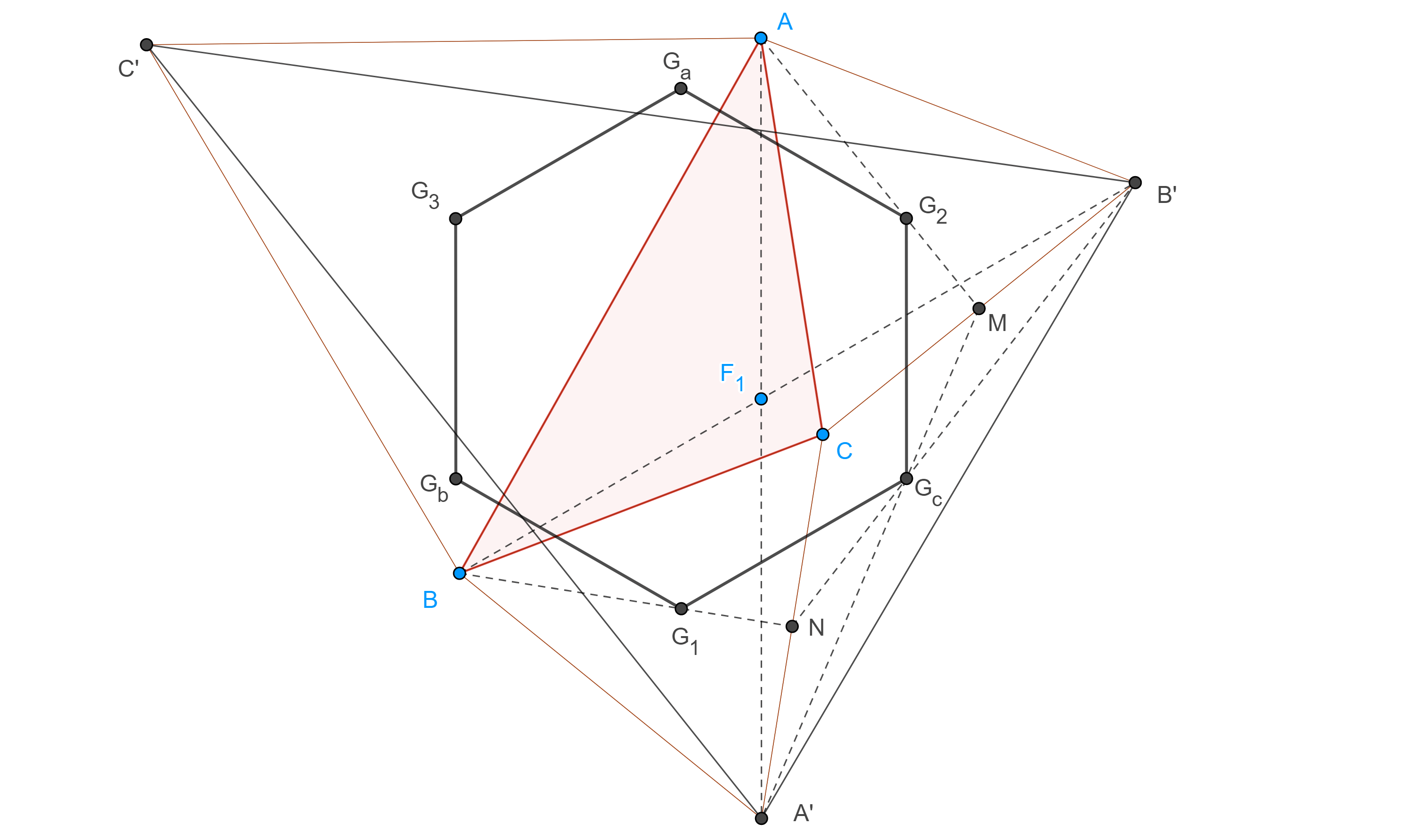
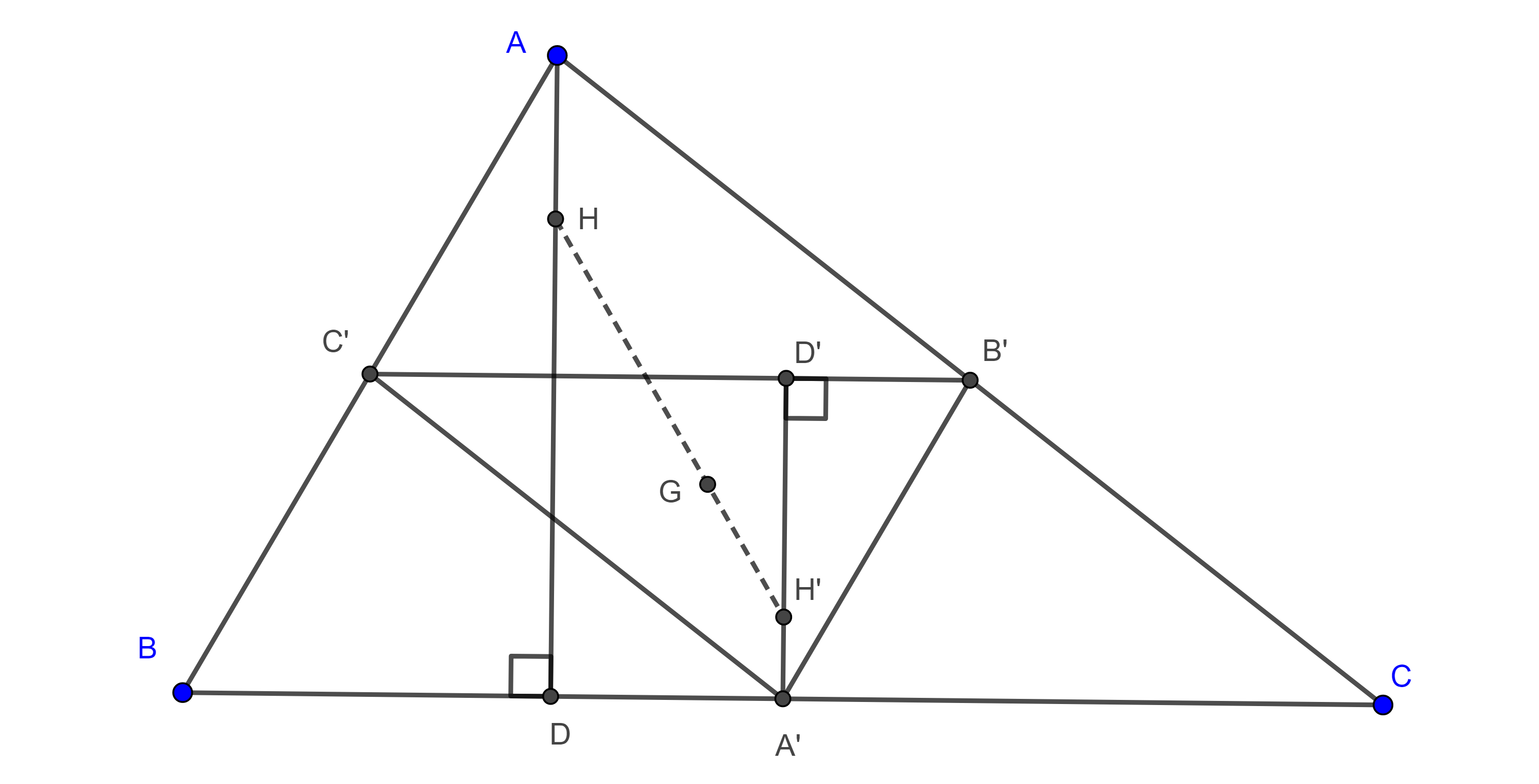
Proposición 2. Sea $ABCA’B’C’$ una configuración externa de Napoleón, sean $G_1$, $G_2$, $G_3$ los centroides de $\triangle A’BC$, $\triangle AB’C$, $\triangle ABC’$ y $G_a$, $G_b$, $G_c$ los centroides de $\triangle AB’C’$, $\triangle A’BC’$, $\triangle A’B’C$, entonces $G_aG_3G_1G_bG_2G_c$ es un hexágono regular.

Demostración. Sea $M$ el punto medio de $CB’$, en $\triangle MAA’$ tenemos
$\dfrac{MG_2}{MA} = \dfrac{MG_c}{MA’} = \dfrac{1}{3}$.

Por lo tanto, $G_2G_c \parallel AA’$ y $3G_2G_c = AA’$.

Figura 8

Análogamente consideremos $N$ el punto medio de $CA’$, en $\triangle NBB’$ tenemos
$\dfrac{NG_c}{NB’} = \dfrac{NG_1}{NB} = \dfrac{1}{3}$.

Por lo tanto, $G_1G_c \parallel BB’$ y $3G_1G_c = BB’$.

Por el teorema 1, $AA’ = BB’$, por lo que $G_1G_c = G_cG_2$, sea $F_1$ el primer punto de Fermat entonces $\angle G_1G_cG_2 = \angle BF_1A = \dfrac{2\pi}{3}$.

Igualmente podemos ver que los demás lados del hexágono son iguales y que el ángulo entre ellos es de $\dfrac{2\pi}{3}$.

En conclusión, $G_aG_3G_1G_bG_2G_c$ es un hexágono regular.

$\blacksquare$

Más adelante…

Con la siguiente entrada daremos inicio a la unidad III y con la ayuda de segmentos dirigidos mostraremos el teorema de Menelao, que nos dice cuando tres puntos sobre los lados de un triángulo son colineales.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Sea $ABCA’B’C’$ una configuración interna de Napoleón (figura 6), para los ejercicios 1, 2 y 3 demuestra lo siguiente:
    $i)$ los circuncírculos de $\triangle A’BC$, $\triangle AB’C$, $\triangle ABC’$ y las rectas $AA’$, $BB’$, $CC’$ son concurrentes,
    $ii)$ $AA’ = BB’ = CC’$.
  2. Prueba que los centroides de $\triangle A’BC$, $\triangle AB’C$ y $\triangle ABC’$ son los vértices de un triángulo equilátero y que su centroide coincide con el centroide de $\triangle ABC$ (figura 6).
  3. Considera $F_2$, el segundo punto de Fermat, muestra que las rectas de Euler de $\triangle ABF_2$, $\triangle AF_2C$ y $\triangle F_2BC$ concurren en el centroide de $\triangle ABC$ (figura 6).
  4. Sean $ABCA’B’C’$ una configuración externa de Napoleón y $ABCA’’B’’C’’$ una configuración interna de Napoleón, demuestra que
    $i)$ el punto medio de $CC»$ coincide con el punto medio de $A’B’$,
    $ii)$ el punto medio de $CC’$ coincide con el punto medio de $A»B»$.
  5. Sea $ABCA’B’C’$ una configuración externa de Napoleón demuestra que el centroide de $\triangle A’B’C’$ coincide con el centroide de $\triangle ABC$.
  6. Divide los lados de un triángulo en tres partes iguales, sobre el tercio de en medio de cada lado del triángulo, construye externamente (internamente) triángulos equiláteros, muestra que los terceros vértices construidos son los vértices de un triángulo equilátero (figura 9).
Figura 9
  1. Sea $ABCA’B’C’$ una configuración externa de Napoleón, considera los arcos $\overset{\LARGE{\frown}}{BC}$, $\overset{\LARGE{\frown}}{CA}$ y $\overset{\LARGE{\frown}}{AB}$ de los circuncírculos de $\triangle A’BC$, $\triangle AB’C$ y $\triangle ABC’$ respectivamente que no contienen a los vértices de $\triangle ABC$ (figura 1), sean $P \in \overset{\LARGE{\frown}}{AB}$ arbitrario y $Q = PA \cap \overset{\LARGE{\frown}}{CA}$, muestra que la intersección $R$ de $PB$ y $QC$ esta en el arco $\overset{\LARGE{\frown}}{BC}$ y que $\triangle PQR$ es equilátero.

Entradas relacionadas

Fuentes

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Geometría Moderna I: Triángulo medial y recta de Euler

Por Rubén Alexander Ocampo Arellano

2 respuestas

Introducción

Continuando con el estudio de las propiedades del centroide, en esta entrada veremos que es colineal con el ortocentro y el circuncentro, y que además triseca al segmento que une dichos puntos. Para establecer estos resultados, veremos primero algunos resultados del triángulo medial de un triángulo dado.

Triángulo medial

Definición 1. Al triángulo que tiene como vértices los puntos medios de un triángulo dado se le conoce como triángulo medial o triángulo complementario del triángulo dado.

Teorema 1. Un triángulo y su triángulo medial son homotéticos además comparten el mismo centroide.

Demostración. Sean $\triangle ABC$, $A’$, $B’$ y $C’$ los puntos medios de $BC$, $AC$ y $AB$ respectivamente.

Por el teorema del segmento medio, los lados del triángulo medial $\triangle A’B’C’$ son paralelos a los lados de $\triangle ABC$ y por lo tanto son homotéticos.

Ya que las rectas determinadas por dos puntos homólogos, $AA’$, $BB’$ y $CC’$ son las medianas de $\triangle ABC$, entonces el centroide $G$ es el centro de homotecia y sabemos que $AG = 2GA’$, por lo que la razón de homotecia es $\dfrac{-1}{2}$, donde el signo menos indica que dos puntos homólogos de esta homotecia se encuentran en lados opuestos respecto del centro de homotecia.

Figura 1

Como $BC$ y $B’C’$ son rectas homotéticas, entonces el punto homólogo de $A’ \in BC$ es $E = A’G \cap B’C’$, y como $A’$ es el punto medio de $BC$ entonces $E$ es el punto medio de $B’C’$, pues la homotecia preserva las proporciones.

Por lo tanto, $A’G$ es mediana de $\triangle A’B’C’$, de manera similar podemos ver que $B’G$ y $C’G$ son medianas de $\triangle A’B’C’$, por lo tanto, $G$ es el centroide de $\triangle A’B’C’$.

$\blacksquare$

Proposición 1. El circuncentro de un triángulo es el ortocentro de su triángulo medial.

Demostración. Se sigue del hecho de que las mediatrices de un triángulo son las alturas de su triángulo medial, esto es así porque los vértices del triángulo medial son, por definición, los puntos medios de un triángulo dado y los lados del triángulo medial son paralelos a los lados del triángulo dado.

$\blacksquare$

Figura 2

Triángulo anticomplementario

Definición 2. Dado un triángulo, al triángulo formado por las rectas paralelas a los lados del triángulo dado a través de los respectivos vértices opuestos, se le conoce como triángulo anticomplementario del triángulo dado.

Proposición 2. Un triángulo y su triángulo anticomplementario son homotéticos y tienen el mismo centroide.

Demostración. Consideremos $\triangle ABC$ y $\triangle A’’B’’C’’$ su triángulo anticomplementario.

Figura 3

Como $\square C’’BCA$ y $\square ABCB’’$ son paralelogramos entonces $C’’A = BC = AB’’$, por lo tanto, $A$ es el punto medio de $B’’C’’$. De manera análoga vemos que $B$ y $C$ son puntos medio de $A’’C’’$ y $A’’B’’$ respectivamente,

Por lo tanto, $\triangle ABC$ es el triángulo medial de $\triangle A’’B’’C’’$ y por el teorema 1 se tiene el resultado.

$\blacksquare$

Circunferencia de Droz Farny

Proposición 3. El producto de los segmentos en que el ortocentro divide a la altura de un triángulo es igual para las tres alturas del triángulo.

Demostración. Sean $\triangle ABC$ y $D$, $E$ y $F$ los pies de las alturas por $A$, $B$ y $C$ respectivamente y $H$ el ortocentro.

Figura 4

Notemos que $\triangle AFH \sim \triangle CDH$ y $\triangle AEH \sim \triangle BDH$ (son semejantes) pues son triángulos rectángulos y comparten un ángulo opuesto por el vértice, por lo tanto
$\dfrac{AH}{CH} = \dfrac{FH}{DH}$ $\Rightarrow AH \times DH = CH \times HF$,
$\dfrac{AH}{BH} = \dfrac{EH}{DH}$ $\Rightarrow AH \times DH = BH \times HE$.

De esto se sigue que
$CH \times HF = AH \times DH = BH \times HE$.

$\blacksquare$

Teorema 2. Si tomamos los vértices de un triángulo como centros de circunferencias del mismo radio, estas cortaran a los respectivos lados de su triángulo medial en tres pares de puntos que son equidistantes del ortocentro del triángulo.

Demostración. Sean $\triangle ABC$ y $\triangle A’B’C’$ su triángulo medial, tracemos tres circunferencias del mismo radio $(A, r)$, $(B, r)$ y $(C, r)$ las cuales intersecan a $B’C’$, $A’C’$ y $A’B’$ en $P$, $P’$; $Q$, $Q’$ y $R$, $R’$, respectivamente.

Sean $D \in BC$ el pie de la altura por $A$, y $M = AD \cap B’C’$, por el teorema de Pitágoras en $\triangle AMP$ y $\triangle HMP$ tenemos
$AP^2 – AM^2 = MP^2 = HP^2 – HM^2$
$\Rightarrow AP^2 – HP^2 = AM^2 – HM^2 = (AM + HM)(AM – HM)$.

Figura 5

Como $\triangle AC’B’ \cong \triangle C’BA’$ son congruentes por criterio LLL entonces sus alturas desde $A$ y $C’$, respectivamente, son iguales , por lo tanto $AM = MD$,
$\Rightarrow AP^2 – HP^2 = (MD + HM)AH = HD \times AH$.

Por otra parte, $\triangle PAP’$ es isósceles y como $AM$ es altura entonces $AM$ es mediatriz de $PP’$, por lo tanto $HP = HP’$$\Rightarrow$
$\begin{equation} HP’^2 = HP^2 = AP^2 – AH \times HD. \end{equation}$.

Si consideramos $E$ y $F$ los pies de las alturas por $B$ y $C$ respectivamente podemos encontrar fórmulas análogas
$\begin{equation} HQ’^2 = HQ^2 = BQ^2 – BH \times HE, \end{equation} $
$\begin{equation} HR’^2 = HR^2 = CR^2 – CH \times HF. \end{equation} $.

Como $(A, r)$, $(B, r)$ y $(C, r)$ tienen el mismo radio, entonces $AP = BQ = CR$ y por la proposición 3, $AH \times DH = BH \times HE = CH \times HF$.

Tomando lo anterior en cuenta y a las ecuaciones $(1)$, $(2)$ y $(3)$ se sigue que
$HP = HP’ = HQ = HQ’ = HR = HR’$.

$\blacksquare$

Recta de Euler

Teorema 3. El circuncentro, el centroide y el ortocentro de todo triangulo son colineales, con el centroide siempre en medio, a la recta determinada por estos tres puntos se le conoce como recta de Euler del triángulo, además $HG = 2GO$.

Demostración. Sean $\triangle ABC$ y $\triangle A’B’C’$ su triángulo medial, por el teorema 1, $\triangle ABC$ y $\triangle A’B’C’$ están en homotecia desde $G$, el centroide, que es el mismo para ambos triángulos, y la razón de homotecia es $\dfrac{-1}{2}$.

Consideremos la altura $AD$ de $\triangle ABC$, la homotecia de $AD$ es una recta paralela a ella y que pasa por el punto homólogo de $A$, $A’$, es decir la homotecia de una altura de $\triangle ABC$ es una altura de $\triangle A’B’C’$.

Figura 6

Como el ortocentro $H$ de $\triangle ABC$ es la intersección de sus alturas, entonces su punto homologo bajo la homotecia estará en la intersección de las alturas de $\triangle A’B’C’$, esto es, el ortocentro de $\triangle A’B’C’$, $H’$.

Con esto tenemos que el ortocentro de $\triangle A’B’C’$ es colineal con $G$ el centroide y el ortocentro de $\triangle ABC$ respectivamente, además, debido a la razón de homotecia, $HG = 2GH’$.

Por la proposición 1, el ortocentro del triángulo medial $\triangle A’B’C’$ es el circuncentro $O$ de $\triangle ABC$.

Así, $O$, $G$ y $H$ son colineales y $HG = 2GO$.

$\blacksquare$

Observación. Notemos que si el triángulo es equilátero el ortocentro, el centroide y el circuncentro son el mismo punto y por lo tanto la recta de Euler degenera en un punto.

Problema. Construye un triángulo $\triangle ABC$ dados el vértice $A$, el circuncentro $O$ y las distancias de $A$ al ortocentro $AH$, y al centroide $AG$.

Solución. El centroide $G$ se encuentra en la circunferencia con centro en $A$ y radio $AG$, $(A, AG)$, el ortocentro $H$ se encuentra en la circunferencia con centro en $A$ y radio $H$, $(A, AH)$.

Por el teorema 3 sabemos que $H$, $G$ y $O$ son colineales y que $HO = 3GO$, por lo que $H$ y $G$ se encuentran en homotecia desde $O$.

Entonces, a $(A, AH)$ le aplicamos una homotecia con centro en $O $ y razón $\dfrac{1}{3}$, esto será una circunferencia $\Gamma$ y $G$ resultara de la intersección de $\Gamma$ con $(A, AG)$.

Figura 7

Teniendo a $G$ construido, como tenemos el circuncírculo $(O, OA)$ y un vértice del triángulo, el problema se reduce a la solución del problema 2 de la entrada anterior.

$\blacksquare$

Distancia entre puntos notables

Teorema 4. Para un triángulo con lados $a$, $b$, $c$, ortocentro $H$, centroide $G$, y circuncírculo $(O, R)$ tenemos:
$OH^2 = 9R^2 – (a^2 + b^2 + c^2)$,
$HG^2 = 4R^2 – \dfrac{4}{9}( a^2 – b^2 + c^2)$.

Demostración. Por el teorema 3 sabemos que $OH = 3OG$ y $HG = 2GO$, además en la entrada anterior calculamos
$OG^2 = R^2 – (\dfrac{a^2 + b^2 + c^2}{9})$.

Por lo tanto,
$OH^2 = 9OG^2 = 9R^2 – (a^2 + b^2 + c^2)$,
$HG^2 = 4OG^2 = 4R^2 – \dfrac{4}{9}(a^2 + b^2 + c^2)$.

$\blacksquare$

Corolario. Podemos calcular la suma de los cuadrados de las distancias del ortocentro a los vértices del triángulo en función del circunradio y los lados del triángulo con la siguiente fórmula.
$HA^2 + HB^2 + HC^2 = 12R^2 + (a^2 + b^2 + c^2)$.

Demostración. Por el teorema 4, y usando las fórmulas encontradas en la entrada anterior
$HA^2 + HB^2 + HC^2 = GA^2 + GB^2 + GC^2 + 3HG^2$,
$GA^2 + GB^2 + GC^2 = \dfrac{a^2 + b^2 + c^2}{3}$ .

Esto implica que,
$HA^2 + HB^2 + HC^2 = \dfrac{a^2 + b^2 + c^2}{3} + 12R^2 – \dfrac{4}{3}(a^2 + b^2 + c^2)$
$= 12R^2 – (a^2 + b^2 + c^2)$.

$\blacksquare$

Más adelante…

En la siguiente entrada estudiaremos otro triángulo asociado a un triángulo dado, aquel cuyos vértices son los pies de las alturas del triángulo dado.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Muestra que el triángulo complementario y el triángulo anticomplementario de un triángulo dado son homotéticos, encuentra el centro y la razón de homotecia.
  2. Sea $\triangle ABC$ y $P$ un punto en el plano, considera $A’$, $B’$ y $C’$ los pies de las perpendiculares dese $P$ a $BC$, $AC$ y $AB$ respectivamente. Desde los puntos medios de $A’B’$, $A’C’$ y $B’C’$ traza perpendiculares a los lados de $AB$, $AC$ y $BC$ respectivamente, muestra que este último conjunto de perpendiculares son concurrentes.
  3. Sean $D$, $D’ \in BC$ de un triangulo $\triangle ABC$, tal que el punto medio de $BC$ es el punto medio de $DD’$, sea $E = AD \cap B’C’$, donde $B’$ y $C’$ son los puntos medios de $AC$ y $AB$ respectivamente, muestra que $ED’$ pasa por el centroide de $\triangle ABC$.
  4. Muestra que la recta de Euler de un triángulo pasa por uno de los vértices del triángulo si y solo si el triángulo es isósceles o rectángulo.
  5. Prueba que la recta que une el centroide de un triangulo con un punto $P$ en su circuncírculo biseca al segmento que une el punto diametralmente opuesto a $P$ con el ortocentro.
  6. Sean $H$, $G$, $(O, R)$ y $(I, r)$, el ortocentro, el centroide, el circuncírculo y el incírculo de un triángulo, muestra que:
    $i)$ $HI^2 + 2OI^2 = 3(IG^2 + 2OG^2)$,
    $ii)$ $3(IG^2 + \dfrac{HG^2}{2}) – IH^2 = 2R(R – 2r)$.

Entradas relacionadas

Fuentes

  • Altshiller, N., College Geometry. New York: Dover, 2007, pp 68-69, 94-96, 101-102.
  • Coxeter, H. y Greitzer, L., Geometry Revisited. Washington: The Mathematical Association of America, 1967, pp 18-19.
  • Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 65-68.

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»