Introducción
En esta entrada estudiamos el tema de homotecia, se trata de una transformación que lleva una figura del plano a otra semejante, con lados correspondientes paralelos y vértices correspondientes concurrentes, esto nos permite entre otras cosas, abordar algunos problemas de construcciones geométricas.
Definición 1. Considera un punto $H$, un conjunto de puntos $F$ y $k$ un numero real, para cada $X \in F$ sea $X’$ tal que $X’$, $X$ y $H$ son colineales y $\dfrac{HX’}{HX} = k$.
Sea $F’$ el conjunto de puntos $X’$, diremos que los conjuntos $F$ y $F’$ son figuras homotéticas y los puntos $X$ y $X’$ son puntos homólogos.
$H$ se llama centro de homotecia, $k$ es la razón de homotecia y la relación entre $F$ y $F’$ es una homotecia con centro en $H$ y razón $k$. Por convención el centro de homotecia $H$ es su propio punto homólogo.
Si puntos homólogos de una homotecia están del mismo lado del centro de homotecia decimos que los conjuntos son directamente homotéticos y la razón de homotecia es positiva, si los puntos homólogos están en lados opuestos respecto del centro de homotecia decimos que las figuras son inversamente homotéticas y la razón de homotecia será negativa.
Homotecia de una recta
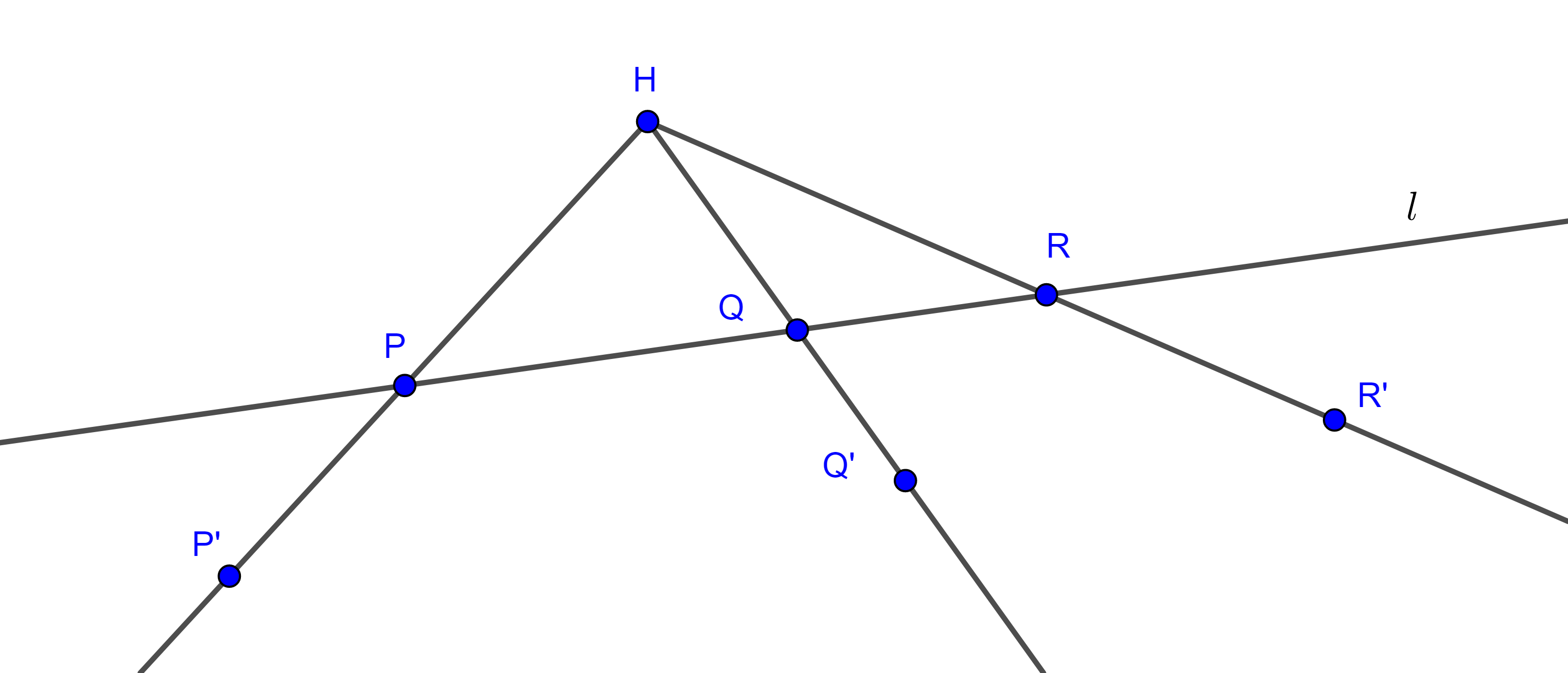
Teorema 1. La homotecia de una recta que no pasa por el centro de homotecia es una recta paralela.
Demostración. Sean $H$ y $k$ el centro y la razón de homotecia, y sea $l$ una recta que no pasa por $H$. Tomemos tres puntos arbitrarios $P$, $Q$, $R \in l$, sean $P’$, $Q’$ y $R’$ sus correspondientes puntos homólogos.
Como $\dfrac{HP’}{HP} = k = \dfrac{HQ’}{HQ}$, por el reciproco del teorema de Tales, $PQ \parallel P’Q’$.
Análogamente vemos que $QR \parallel Q’R’$ y $PR \parallel P’R’$.
Supongamos que $P’$, $Q’$ y $R’$ no son colineales, entonces $\triangle P’Q’R’$ es un triángulo y así $\triangle PQR$ es un triángulo con lados paralelos a los de $\triangle P’Q’R’$, lo cual es una contradicción, pues $PQR$ es una recta.
Si fijamos $P$ y $Q$, y tomamos $R$ como variable, entonces $P’$ y $Q’$ son fijos y $R’$ es variable, así todos los puntos $R’$ son colineales con $P’$ y $Q’$.
Por lo tanto, la homotecia de una recta es una recta paralela a esta.
$\blacksquare$
Definición 2. Decimos que dos polígonos $ABCD…$ y $A’B’C’D’…$ son semejantes si los correspondientes lados son proporcionales $\dfrac{AB}{A’B’} = \dfrac{BC}{B’C’} =…$ y los ángulos correspondientes son iguales $\angle A = \angle A’$, $\angle B = \angle B’$, $…$
Corolario. Dos polígonos homotéticos son semejantes.
Demostración. Sean $A$, $B$ y $C$ vértices de un polígono $ABCD…$
Por el teorema anterior, los lados del triángulo $\triangle A’B’C’$, formado por los puntos homólogos de $A$, $B$ y $C$, son paralelos a los lados correspondientes de $\triangle ABC$, por lo tanto, los triángulos son semejantes y así los ángulos correspondientes son iguales y los lados correspondientes son proporcionales.
$\blacksquare$
Polígonos homotéticos
Teorema 2. Si los lados correspondientes de dos polígonos son proporcionales y paralelos entonces los polígonos son homotéticos.
Demostración. Sean $ABCD…$ y $A’B’C’D’…$ dos polígonos que cumplen las condiciones dadas, sea $H$ la intersección de las rectas $AA’$ y $BB’$ y supongamos que $CC’$ no pasa por $H$, entonces sea $H’ = CC’ \cap BB’$.
Como $AB \parallel A’B’$ y $BC \parallel B’C’$ entonces $\triangle HAB \sim \triangle HA’B’$ y $\triangle H’BC \sim \triangle H’B’C’$
$\Rightarrow \dfrac{AB}{A’B’} = \dfrac{HB}{HB’}$ y $\dfrac{BC}{B’C’} = \dfrac{H’B}{H’B’}$.
Ya que los lados correspondientes de $ABCD…$ son proporcionales a los de $A’B’C’D’…$, entonces
$ \dfrac{HB}{HB’} = \dfrac{AB}{A’B’} = \dfrac{BC}{B’C’} = \dfrac{H’B}{H’B’} $
$\Rightarrow \dfrac{HB}{HB’} – 1= \dfrac{H’B}{H’B’} – 1 \Rightarrow \dfrac{HB – HB’}{HB’} = \dfrac{H’B – H’B’}{H’B’}$
$\Rightarrow \dfrac{B’B}{HB’} = \dfrac{B’B}{H’B’} \Rightarrow HB’ = H’B’$.
Por lo tanto, $H = H’$.
Así, $AA’$, $BB’$ y $CC’$ son concurrentes y $\dfrac{HA’}{HA} = \dfrac{HB’}{HB} = \dfrac{HC’}{HC}$, es análogo ver que las demás rectas que unen vértices correspondientes concurren en $H$.
Por tanto, $ABCD…$ y $A’B’C’D’…$ se encuentran en homotecia desde $H$ y por el corolario 1, $ABCD…$ y $A’B’C’D’…$, son semejantes, la razón de homotecia es la razón de semejanza, $\dfrac{HA’}{HA} = \dfrac{AB}{A’B’} = \dfrac{BC}{B’C’} =…$
$\blacksquare$
Observación 1. Si la razón de homotecia es 1, los lados correspondientes de las figuras $ABCD…$ y $A’B’C’D’…$ son congruentes y así $\square AA’B’B$ es un paralelogramo, es decir, $AA’$ y $BB’$ no pueden ser concurrentes.
Observación 2. En el caso particular cuando los polígonos son triángulos, solo es necesario pedir que los lados correspondientes sean paralelos, pues esto asegura la semejanza y por tanto la condición de proporcionalidad.
Rectas concurrentes
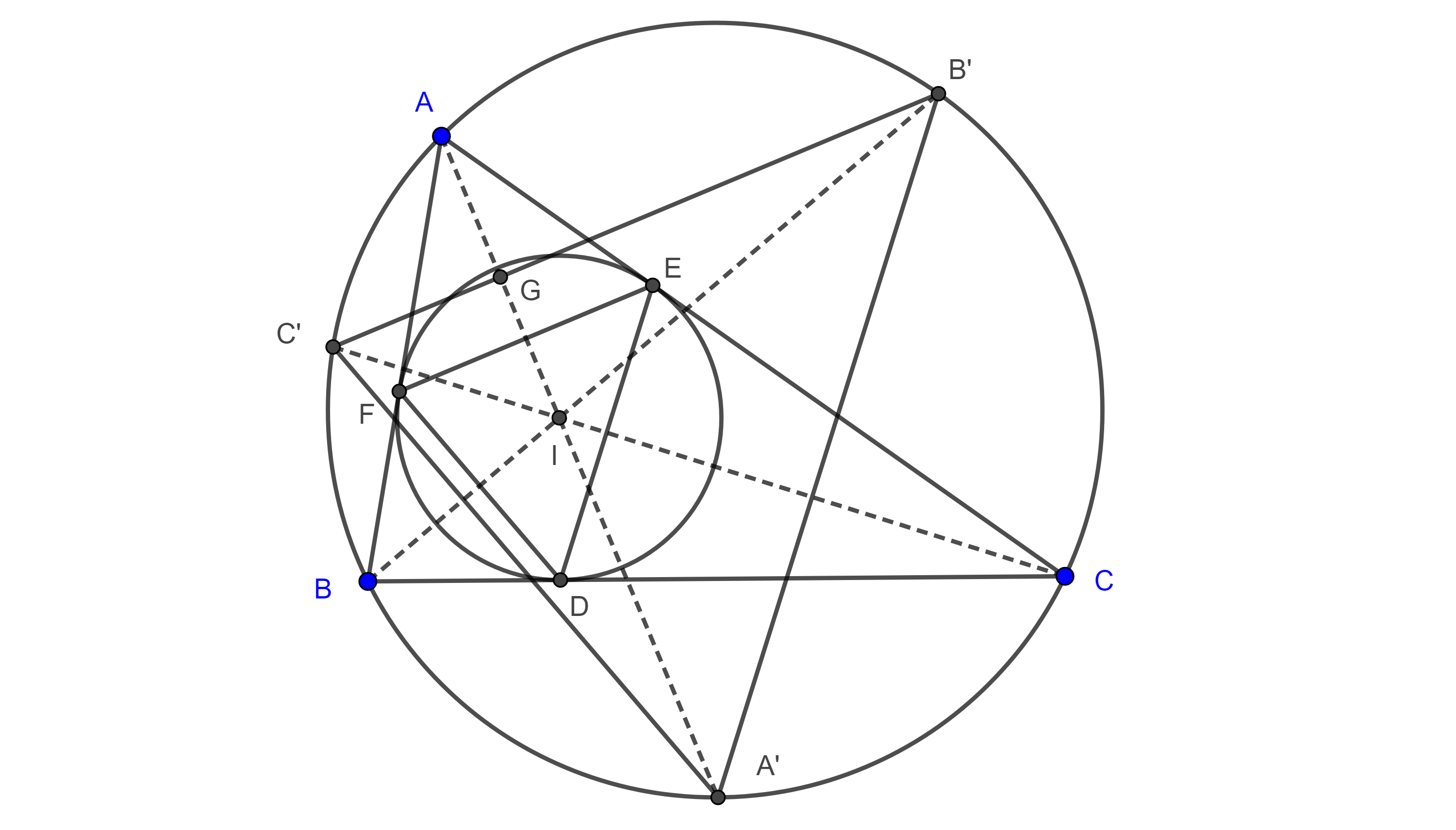
Proposición. Sea $\triangle ABC$ un triángulo y sean $D$, $E$ y $F$ los puntos de tangencia del incírculo $(I, r)$ de $\triangle ABC$, con los lados $BC$, $AC$ y $AB$ respectivamente, sean $A’$, $B’$ y $C’$ la intersección de las rectas $AI$, $BI$ y $CI$ con el circuncírculo del triángulo $\triangle ABC$, entonces la rectas $A’D$, $B’E$ y $C’F$ son concurrentes.
Demostración. Notemos que $AF = AE$, pues son las tangentes trazadas desde $A$ a $(I, r)$ , como $\triangle AEF$ es isósceles entonces la bisectriz de $A$ es perpendicular a $EF$, $AI \perp EF$.
Por otro lado, tenemos que $\angle C’B’B = \angle C’CB = \dfrac{\angle C}{2}$ pues abarcan el mismo arco; el ángulo $\angle B’IA$ es un ángulo exterior del triángulo $\triangle AIB$, entonces
$\angle B’IA = \angle BAI + \angle IBA = \dfrac{\angle A + \angle B}{2}$.
Sea $G = AI \cap C’B’$, en el triángulo $\triangle GIB’$ tenemos que
$\angle IGB’ = \pi – (\angle C’B’B + \angle B’IA) $
$= \pi – \dfrac{\angle A + \angle B + \angle C}{2} = \dfrac{\pi}{2}$.
Por lo tanto, $AI \perp B’C’$ $\Rightarrow EF \parallel B’C’$, de manera análoga podemos ver que $ED \parallel B’A’$ y $DF \parallel A’C’$.
De lo anterior se sigue que $\triangle DEF \sim \triangle A’B’C’$, y por el teorema 2, $A’D$, $B’E$ y $C’F$ concurren en algún punto $H$ que es el centro de homotecia de los triángulos $\triangle DEF$ y $\triangle A’B’C’$.
$\blacksquare$
Inscribir un triángulo en otro triángulo dado
Problema. 1 En un triángulo dado inscribir un triángulo cuyos lados sean perpendiculares a los lados del triángulo dado.
Solución. Sea $\triangle ABC$ el triángulo dado, la idea es construir una homotecia desde uno de los vértices, tomemos $D \in BC$, distinto de $B$, $C$ y también diferente al pie de la altura por $A$.
Por $D$ trazamos la perpendicular a $BC$ que interseca a $AC$ en $E$, por $E$ trazamos la perpendicular a $AC$ que interseca a $AB$ en $F$.
Por $F$ trazamos la perpendicular a $AB$ que interseca a $DE$ en $G$.
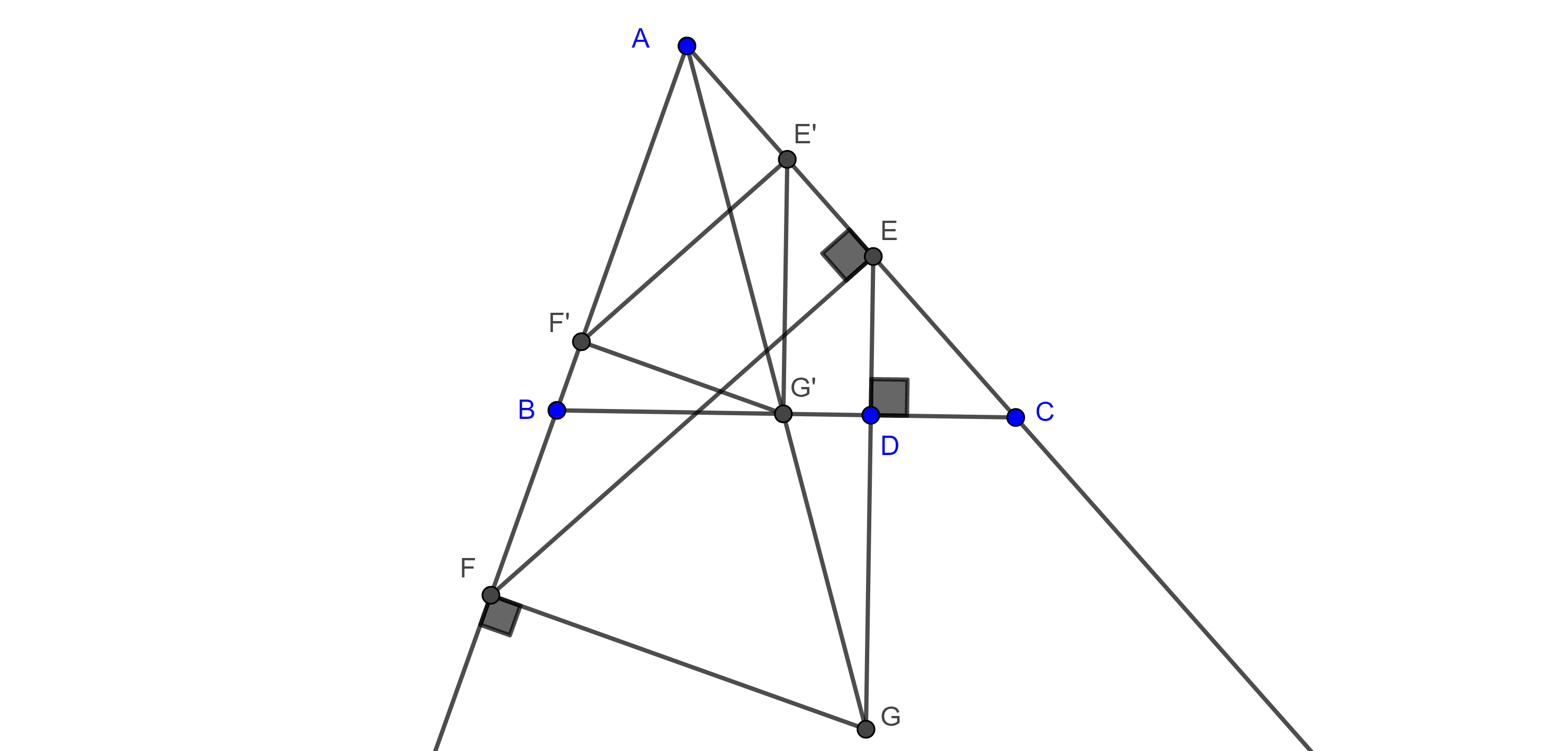
Sea $G’ = BC \cap AG$, por $G’$ trazamos la paralela a $GE$ que interseca a $AC$ en $E’$, también trazamos la paralela a $GF$ por $G’$ que interseca a $AB$ en $F’$.
Por construcción $EE’$, $FF’$ y $GG’$ concurren en $A$, $G’F’ \perp AB$ y $G’E’ \perp AC$.
Como $\triangle AF’G’ \sim \triangle AFG$ y $\triangle AG’E’ \sim \triangle AGE$
$\dfrac{AF’}{AF} = \dfrac{AG’}{AG} = \dfrac{AE’}{AE}$.
Por tanto, $E’$, $F’$ y $G’$ son puntos homólogos de $E$, $F$ y $G$ respectivamente, con centro de homotecia en $A$.
Por el teorema 1, $E’F’ \parallel EF$ y así $E’F’ \perp AC$.
$\blacksquare$
Observación. Notemos que construimos $DE \perp BC$ y tal que $E \in AC$, pero pudimos haber construido $E \in AB$ de lo que resultaría un triangulo distinto $\triangle E’F’G’$ y por lo tanto tenemos dos soluciones.
Inscribir un cuadrado en un triángulo dado
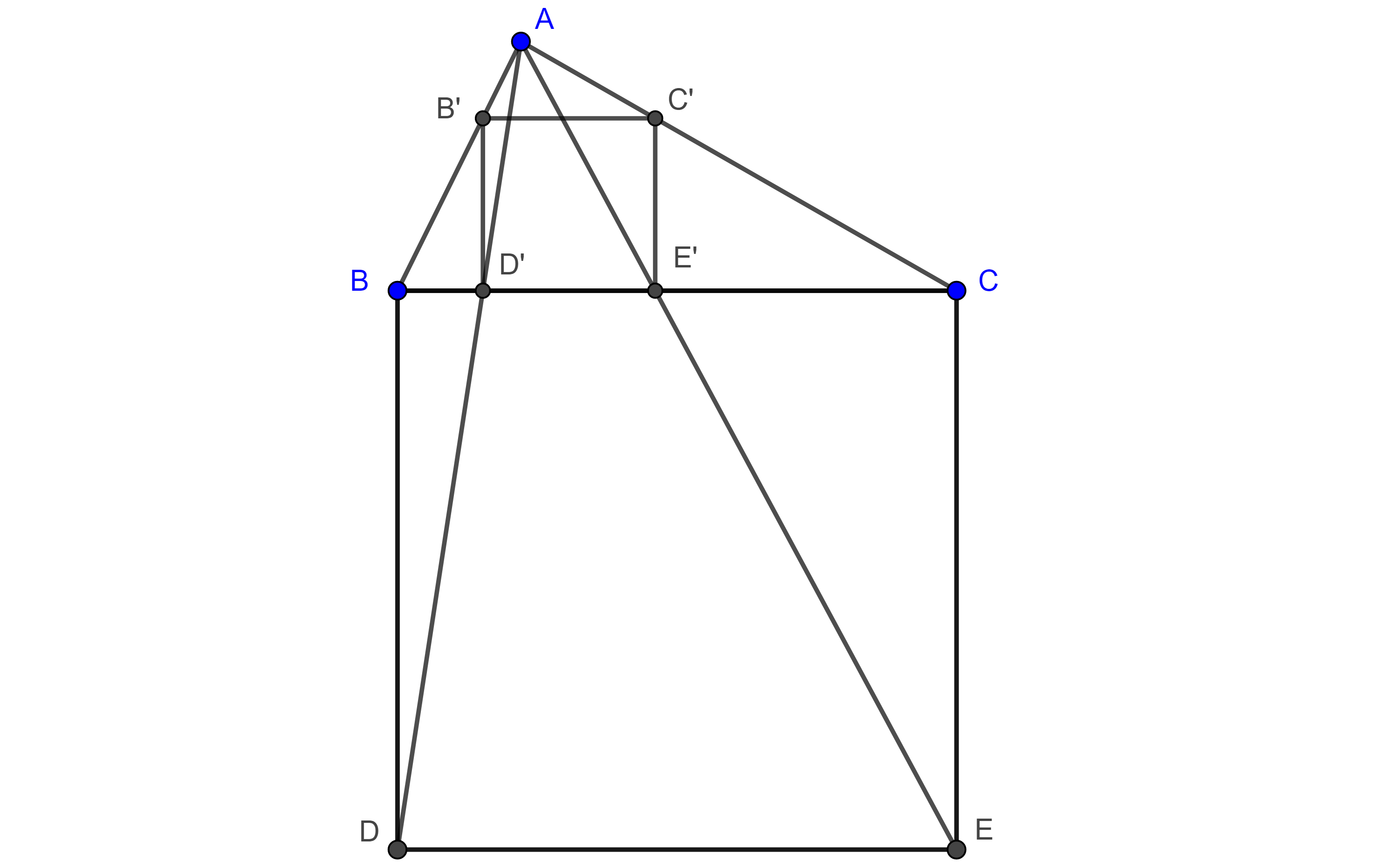
Problema 2. Dado un triángulo, inscribir un cuadrado en el triángulo dado.
Solución. Sea $\triangle ABC$ el triángulo dado, construimos un cuadrado exteriormente $\square BDEC$ sobre $BC$, sean $D’ = AD \cap BC$ y $E’ = AE \cap BC$.
Como $BC \parallel DE$ entonces $D’$ y $E’$ son puntos homólogos de $D$ y $E$ respectivamente con centro de homotecia en $A$.
Por $D’$ trazamos una paralela a $BD$ que interseca a $AB$ en $B’$ y por $E’$ trazamos una paralela a $CE$ que interseca a $AC$ en $C’$.
Como $B’D’$ es transversal a $AB$ y a $AD$ y es paralela a $BD$ entonces $\dfrac{AB’}{AB} =\dfrac{AD’}{AD}$ y por tanto, $B$ y $B’$ son puntos homólogos, de manera similar podemos ver que $C$ y $C’$ son puntos homólogos.
Como $\square BDEC$ y $\square B’D’E’C’$ son figuras homotéticas entonces, por el corolario, son semejantes, por lo tanto, $\square B’D’E’C’$ es un cuadrado.
$\blacksquare$
Observación. Si alguno de los ángulos $\angle B$ o $\angle C$ es obtuso, entonces una de las rectas $AD$ o $AE$ intersecaría a $BC$ por fuera y no seria posible la construcción.
Así, si nuestro triángulo $\triangle ABC$ es obtusángulo tenemos que tomar como centro de homotecia el vértice del ángulo obtuso.
Si $\triangle ABC$ es acutángulo existen tres soluciones, una por cada vértice como centro de homotecia, y si es rectángulo hay dos soluciones.
Construir una secante a un triángulo dado
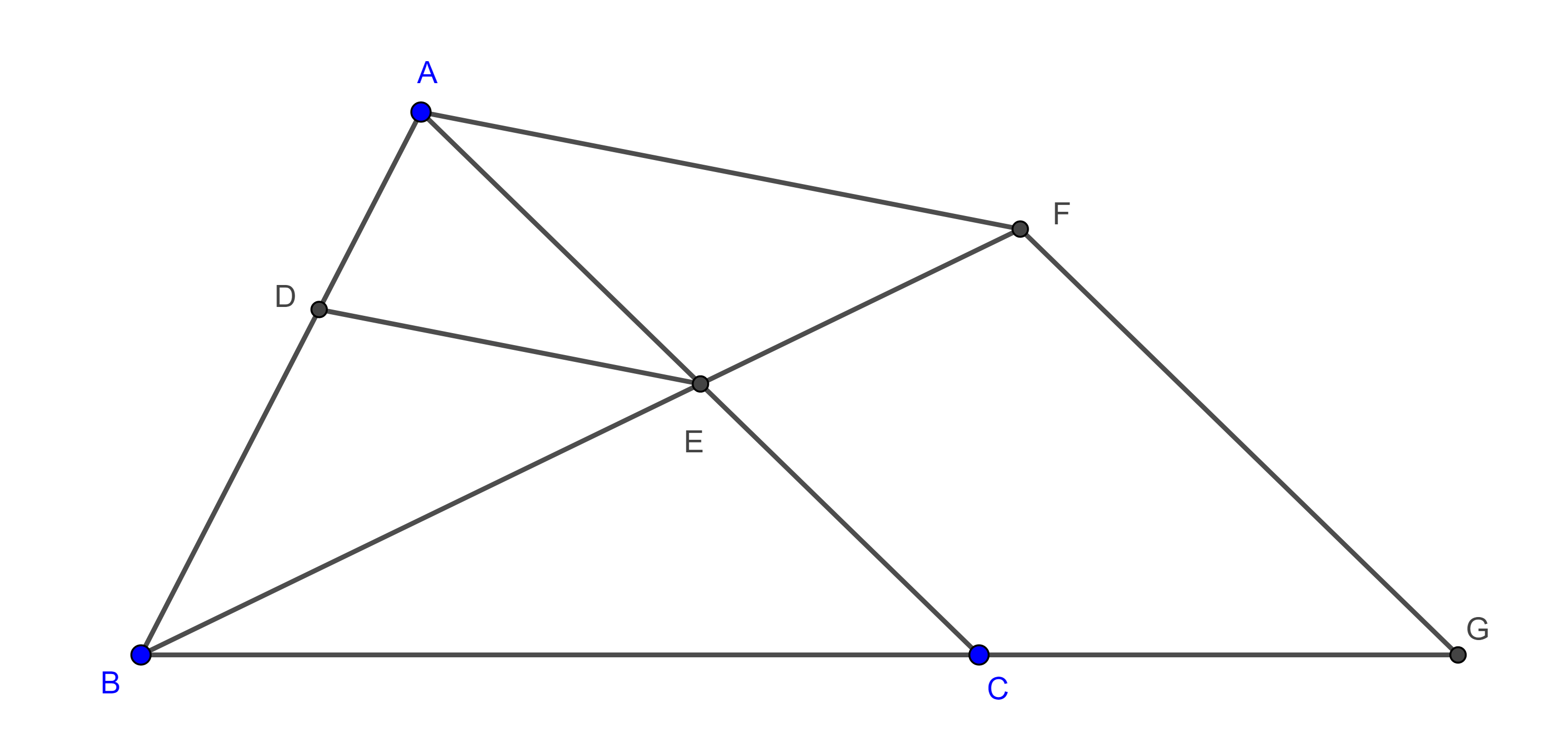
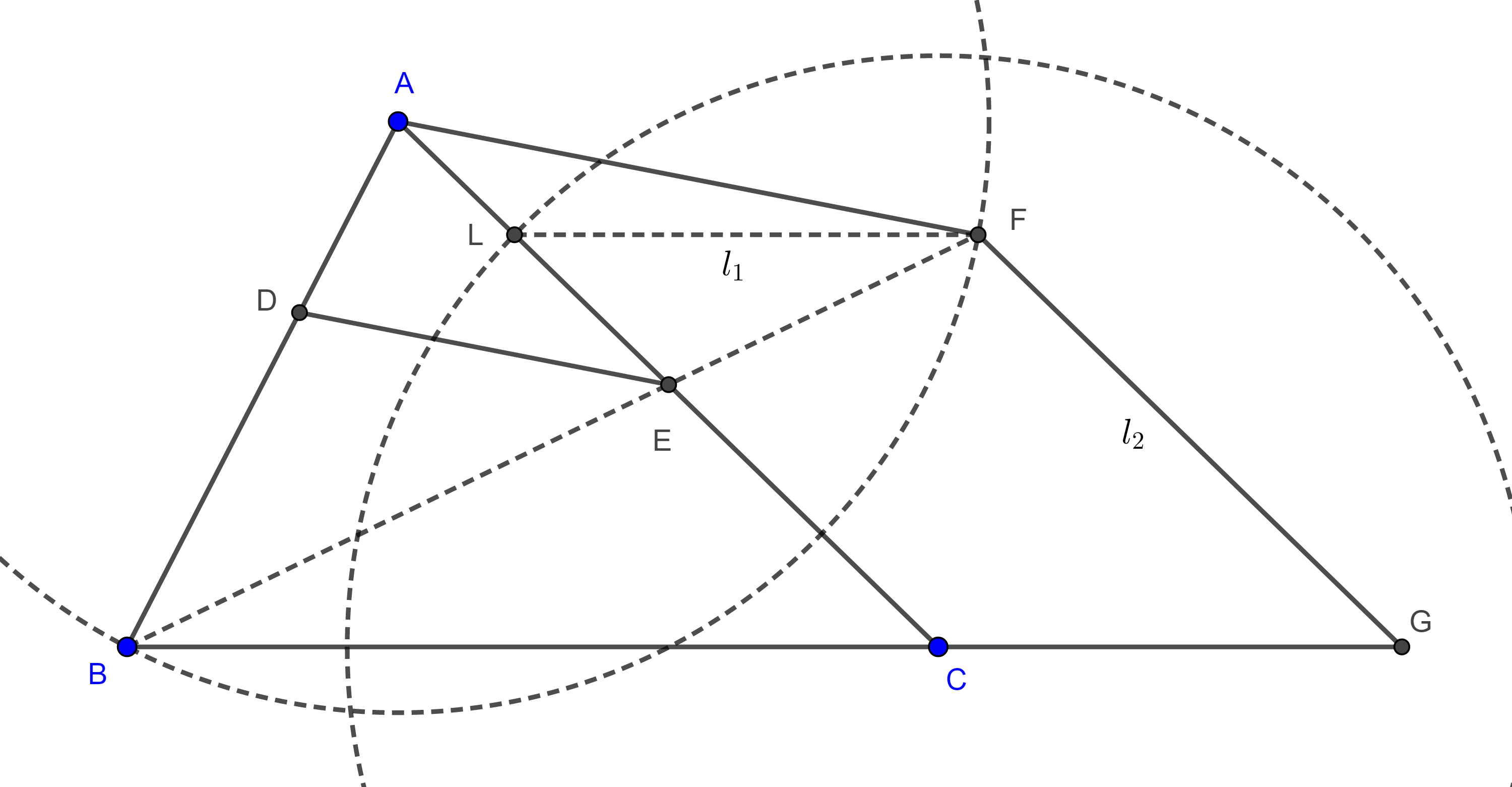
Problema 3. Dado un triángulo $\triangle ABC$, construye $D \in AB$ y $E \in AC$ tal que $BD = DE = EC$.
Solución. Supongamos que ya tenemos la figura requerida (figura 6). Por $A$ trazamos una paralela a $DE$ que interseca a $BE$ en $F$, por $F$ trazamos una paralela a $AC$ que interseca a $BC$ en $G$.
Como $AF \parallel DE$ y $FG \parallel EC$, por el teorema de Tales, tenemos
$\dfrac{BA}{BD} = \dfrac{BF}{BE} = \dfrac{BG}{BC}$.
Así que $(A, D)$, $(F, E)$ y $(G, C)$ son pares de puntos homólogos, con centro en $B$.
Inversamente, para construir el cuadrilátero auxiliar $\square BAFG$ hacemos lo siguiente (figura 7), trazamos una circunferencia con centro en $A$ y radio $AB$, $(A, AB)$, construimos $L \in AC$ tal que $LC = AB$, trazamos una paralela $l_1$ a $BC$ por $L$, sea $F = (A, AB) \cap l_1$, trazamos una paralela $l_2$ a $AC$ por $F$, sea $G = BC \cap l_2$.
Como $\square LCGF$ es un paralelogramo entonces $FG = LC = AB = AF$.
Finalmente, sean $E = AC \cap BF$ y $D$ la intersección de la paralela por $E$ a $AF$ con $AB$.
Por construcción $\square BDEC$ y $\square BAFG$ son homotéticos, con centro de homotecia en $B$, y tenemos que $\dfrac{BD}{BA} = \dfrac{DE}{AF} = \dfrac{EC}{FG}$ $\Rightarrow BD = DE = EC$.
$\blacksquare$
Más adelante…
Continuando con el tema de homotecia, en la próxima entrada veremos circunferencias homotéticas.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Sean $B$, $B’$ y $C$, $C’$ pares de puntos homólogos de dos figuras homotéticas $F$ y $F’$, considera $A \in F$, por $B’$ y $C’$ tracemos paralelas a $AB$ y $AC$ respectivamente, sea $A’$ la intersección de estas dos últimas rectas, prueba que $A$ y $A’$ son puntos homólogos.
- Si dos triángulos están en homotecia muestra que sus incentros, circuncentros, ortocentros y centroides son puntos homólogos, y que sus bisectrices, mediatrices, alturas y medianas son rectas homotéticas.
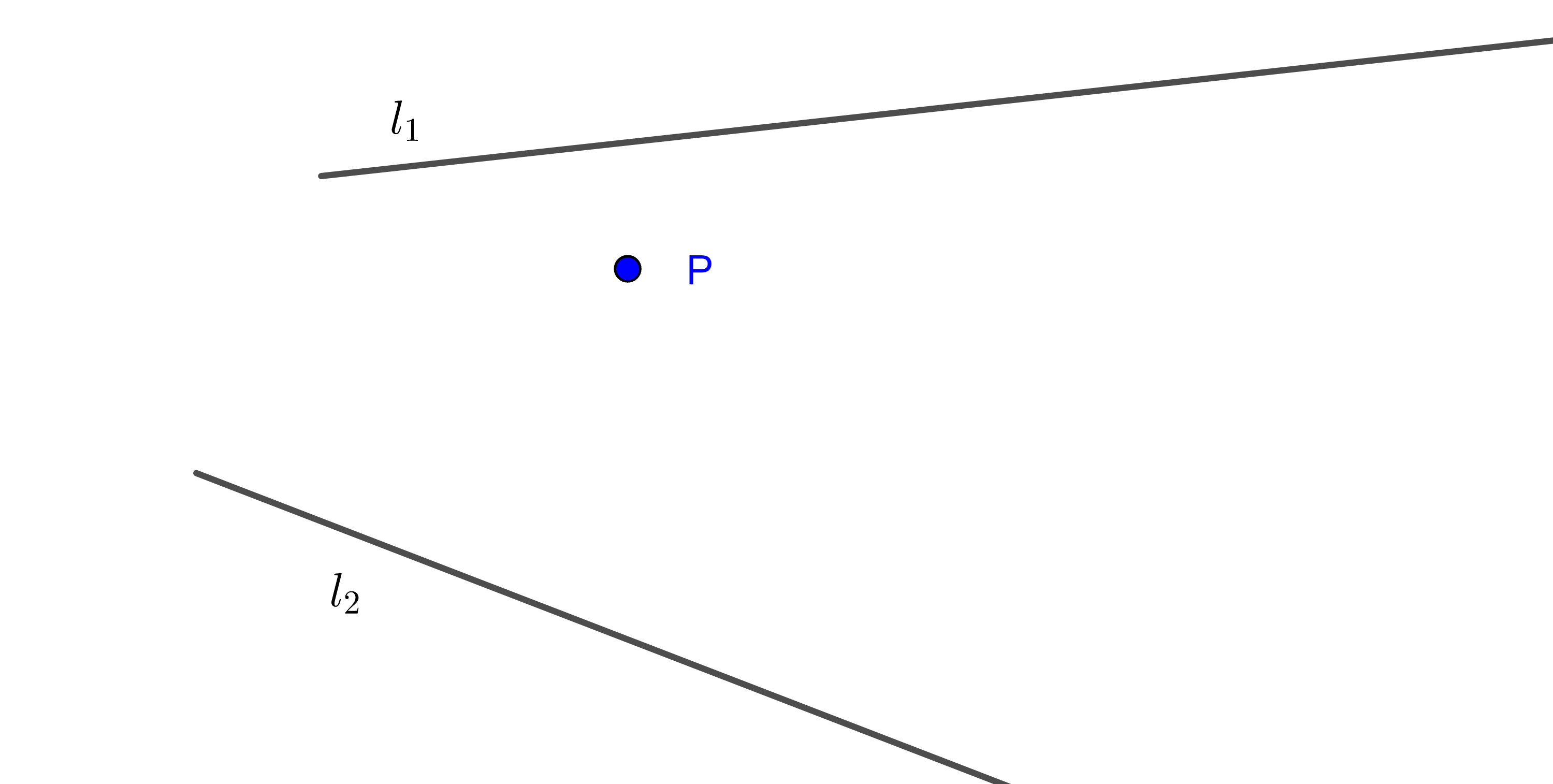
- Dadas dos rectas $l_1$ y $l_2$ que se intersecan en un punto inaccesible, trazar una recta que pase por un punto dado $P$ y la intersección de las rectas dadas (figura 8).
- En un triangulo dado inscribir un triangulo cuyos lados sean paralelos a las bisectrices internas del triangulo dado.
- En un triangulo dado $\triangle ABC$, construir un cuadrado tal que un vértice este en la extensión de $AB$, otro en la exención de $AC$ y los otros dos vértices en $BC$.
- Construir un triangulo $\triangle ABC$ dados $\angle A$, $AB + BC$ y $AC + BC$.
Entradas relacionadas
- Ir a Geometría Moderna I.
- Entrada anterior del curso: Construcciones geométricas.
- Siguiente entrada del curso: Circunferencias homotéticas.
- Otros cursos.
Fuentes
- Altshiller, N., College Geometry. New York: Dover, 2007, pp 38-45.
- Andreescu, T., Korsky, S. y Pohoata, C., Lemmas in Olympiad Geometry. USA: XYZ Press, 2016, pp 199-200.
- Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 110-111.
- Cut the Knot
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»