Introducción
La simediana es un tipo especial de ceviana relacionada con la mediana de un triángulo, veremos algunas caracterizaciones y propiedades.
Simediana, primera caracterización
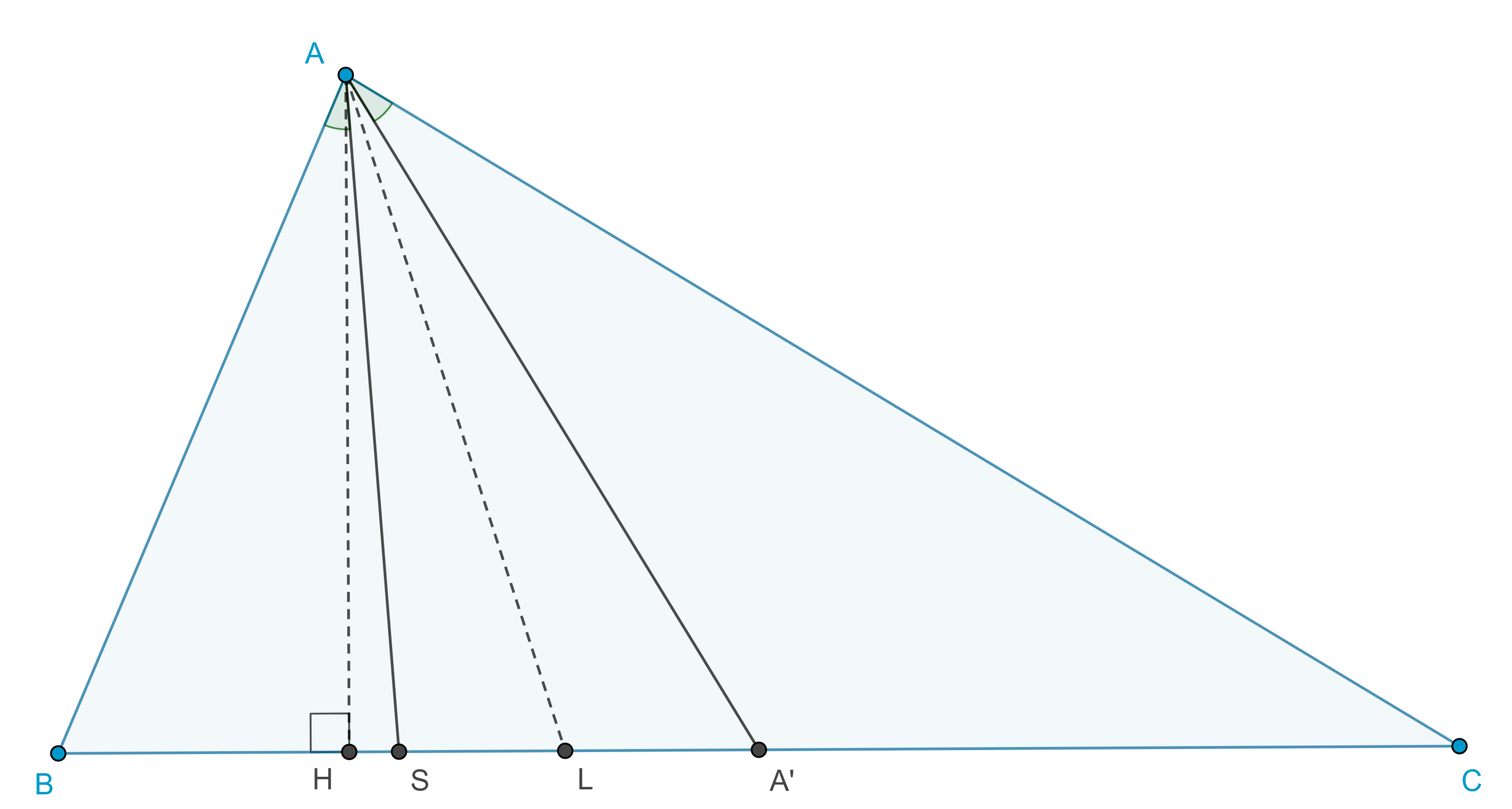
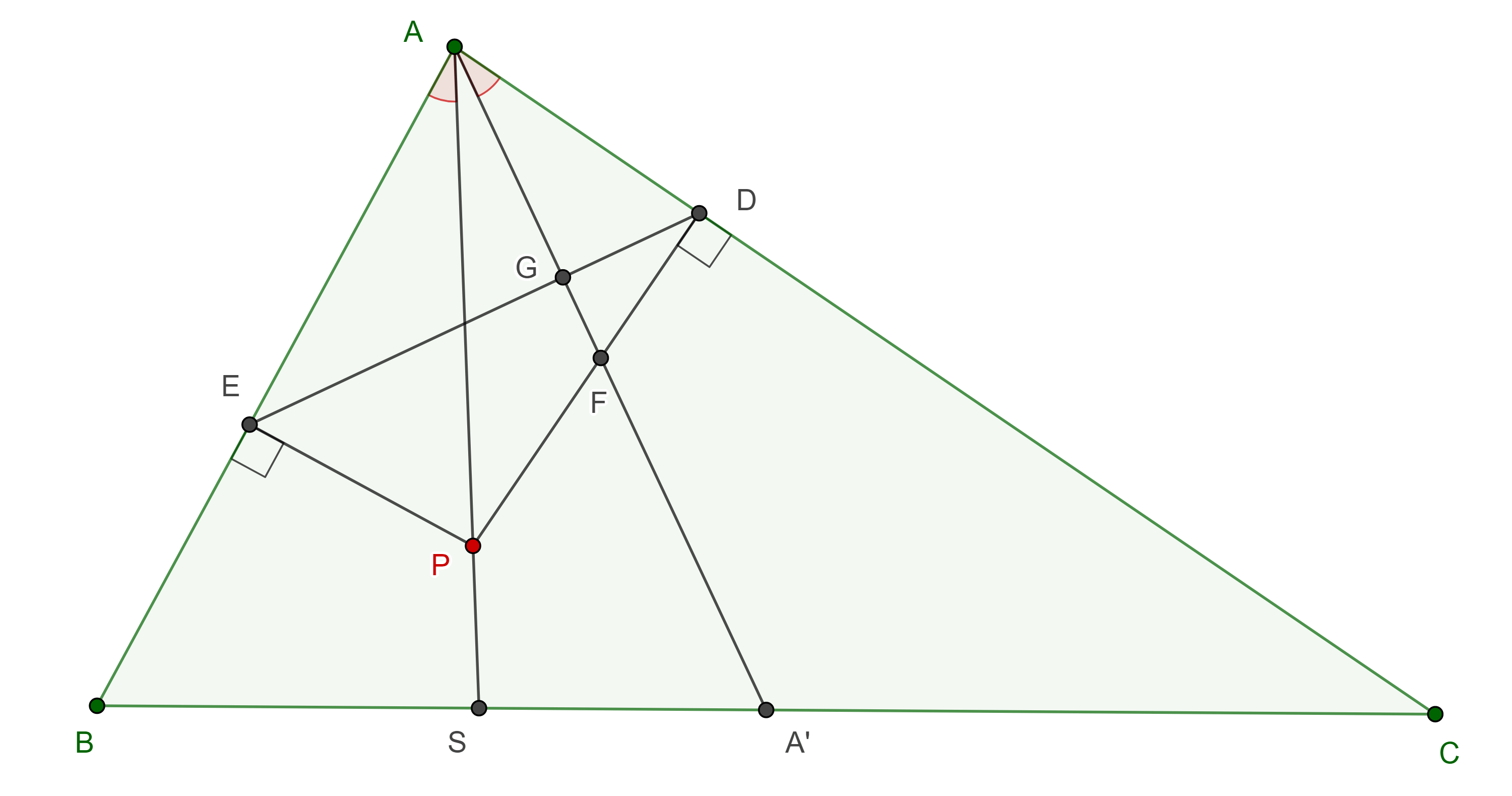
Definición 1. Una simediana de un triángulo es la reflexión de una mediana respecto de la bisectriz interna que pasa por el mismo vértice. Un triángulo tiene tres simedianas.
Notación. Denotaremos a la intersección de una simediana con el lado opuesto como $S$.
Teorema 1. Una ceviana de un triángulo divide internamente al lado opuesto en la razón de los cuadrados de los lados adyacentes si y solo si es simediana.
Demostración. Sean $AA’$ la mediana y $AS$ la simediana en un triángulo $\triangle ABC$.
Sea $H$ el pie de la altura por $A$, calculamos las áreas de los triángulos $\triangle BAS$, $\triangle BAA’$, $\triangle SAC$ y $\triangle A’AC$.
$\begin{equation} (\triangle BAS) = \dfrac{BS \times AH}{2} = \dfrac{BA \times AS \sin \angle BAS}{2}, \end{equation}$
$\begin{equation} (\triangle BAA’) = \dfrac{BA’ \times AH}{2} = \dfrac{BA \times AA’ \sin \angle BAA’}{2}, \end{equation}$
$ \begin{equation} (\triangle SAC) = \dfrac{SC \times AH}{2} = \dfrac{SA \times AC \sin \angle SAC}{2}, \end{equation}$
$\begin{equation} (\triangle A’AC) = \dfrac{A’C \times AH}{2} = \dfrac{AA’ \times AC \sin \angle A’AC}{2}. \end{equation}$
Sea $L$ la intersección de la bisectriz de $A$ con $BC$, entonces
$\begin{equation} \angle BAS = \angle BAL – \angle SAL = \angle LAC – \angle LAA’ = \angle A’AC, \end{equation}$
$\angle BAA’ = \angle BAL + \angle LAA’ = \angle LAC + \angle SAL = \angle SAC.$
Haciendo el cociente de $(1)$ con $(4)$ y de $(2)$ con $(3)$ obtenemos
$\dfrac{BS}{A’C} = \dfrac{BA \times AS}{AA’ \times AC}$,
$\dfrac{BA’}{SC} = \dfrac{BA \times AA’}{SA \times AC}$.
Multiplicando estas dos ecuaciones obtenemos el resultado esperado
$\dfrac{BS}{SC} = \dfrac{BA^2}{AC^2}$.
El reciproco también es cierto, pues el punto $S$ que divide a $BC$ en la razón $\dfrac{BA^2}{AC^2}$, es único.
$\blacksquare$
Exsimediana
Definición 2. Las tangentes al circuncírculo de un triángulo por sus vértices se conocen como simedianas externas o exsimedianas.
Corolario. La simediana y la exsimediana que pasan por el mismo vértice de un triángulo son conjugadas armónicas respecto de los lados del triángulo que forman dicho vértice.
Demostración. En la entrada teorema de Menelao mostramos que la exsimediana de un triángulo divide externamente al lado opuesto en la razón de los cuadrados de los lados que pasan por el mismo vértice.
El resultado se sigue del hecho de que el conjugado armónico es único y el teorema 1.
$\blacksquare$
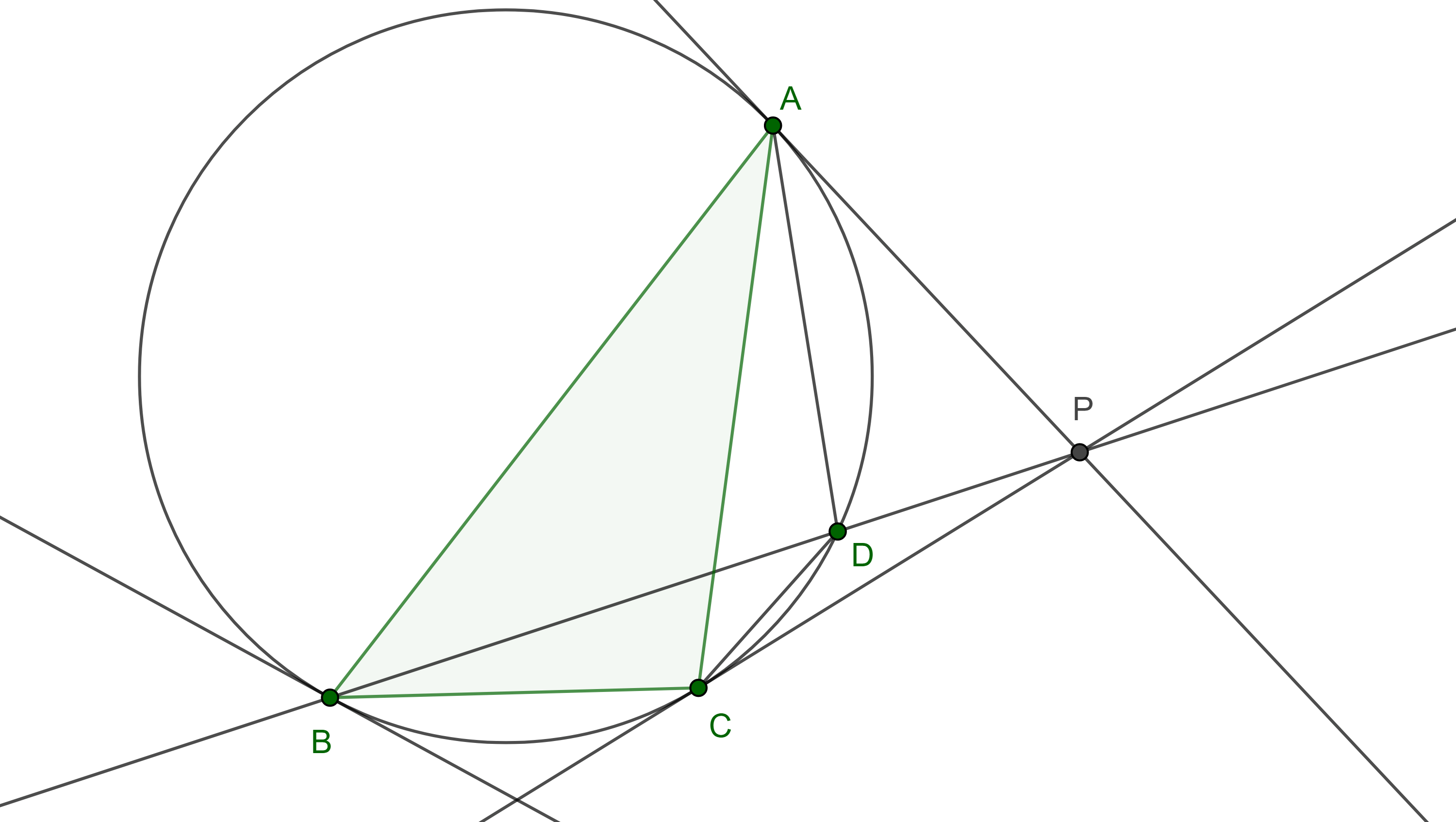
Teorema 2. Una simediana y las exsimedianas que pasan por vértices distintos son concurrentes, al punto de concurrencia se le conoce como punto exsimediano.
Demostración. En $\triangle ABC$, $AP$ y $CP$ son tangentes al circuncírculo $\Gamma$ de $\triangle ABC$ en $A$ y en $C$ respectivamente y se cortan en $P$ (figura 2).
Sea $D = BP \cap \Gamma$, $D \neq B$, por la proposición 5 de la entrada anterior, $\square ABCD$ es un cuadrilátero armónico.
Entonces, por el teorema 2 de la entrada anterior, el Haz $B(BCDA)$ es armónico, es decir, la tangente a $\Gamma$ en $B$, y $BD$ son conjugadas armónicas respecto de $BA$ y $BC$.
Como el conjugado armónico es único, $BP$ es simediana de $\triangle ABC$, por el corolario anterior.
$\blacksquare$
Antiparalelas (1)
Teorema 3. La $B$-simediana de un triángulo $\triangle ABC$ es el lugar geométrico de los puntos que bisecan a las antiparalelas de $AC$ respecto a $AB$ y $BC$.
Demostración. Sean $D \in AB$ y $E \in BC$ tales que $AC$ y $DE$ son antiparalelas respecto a $AB$ y $BC$, entonces $\square ADEC$ es cíclico.
Por lo tanto, $\angle ACE$ y $\angle EDA$ son suplementarios, en consecuencia, $\angle ACB = \angle ACE = \angle BDE$.
Sea $TB$ tangente al circuncírculo de $\triangle ABC$ en $B$, entonces $\angle ABT = \angle ACB$ pues abarcan el mismo arco, por lo tanto, la $B$-exsimediana y $DE$ son paralelas.
Sea $BS$ una ceviana de $\triangle ABC$, entonces por la proposición 2 de la entrada anterior $BS$ biseca a $DE$ si y solo si el haz $B(TCSA)$ es armónico.
En consecuencia, como el conjugado armónico de $BT$ respecto de $BC$ y $BA$ es la $B$-simediana, $BS$ biseca a $DE$ si y solo si $BS$ es simediana de $\triangle ABC$.
$\blacksquare$
Antiparalelas (2)
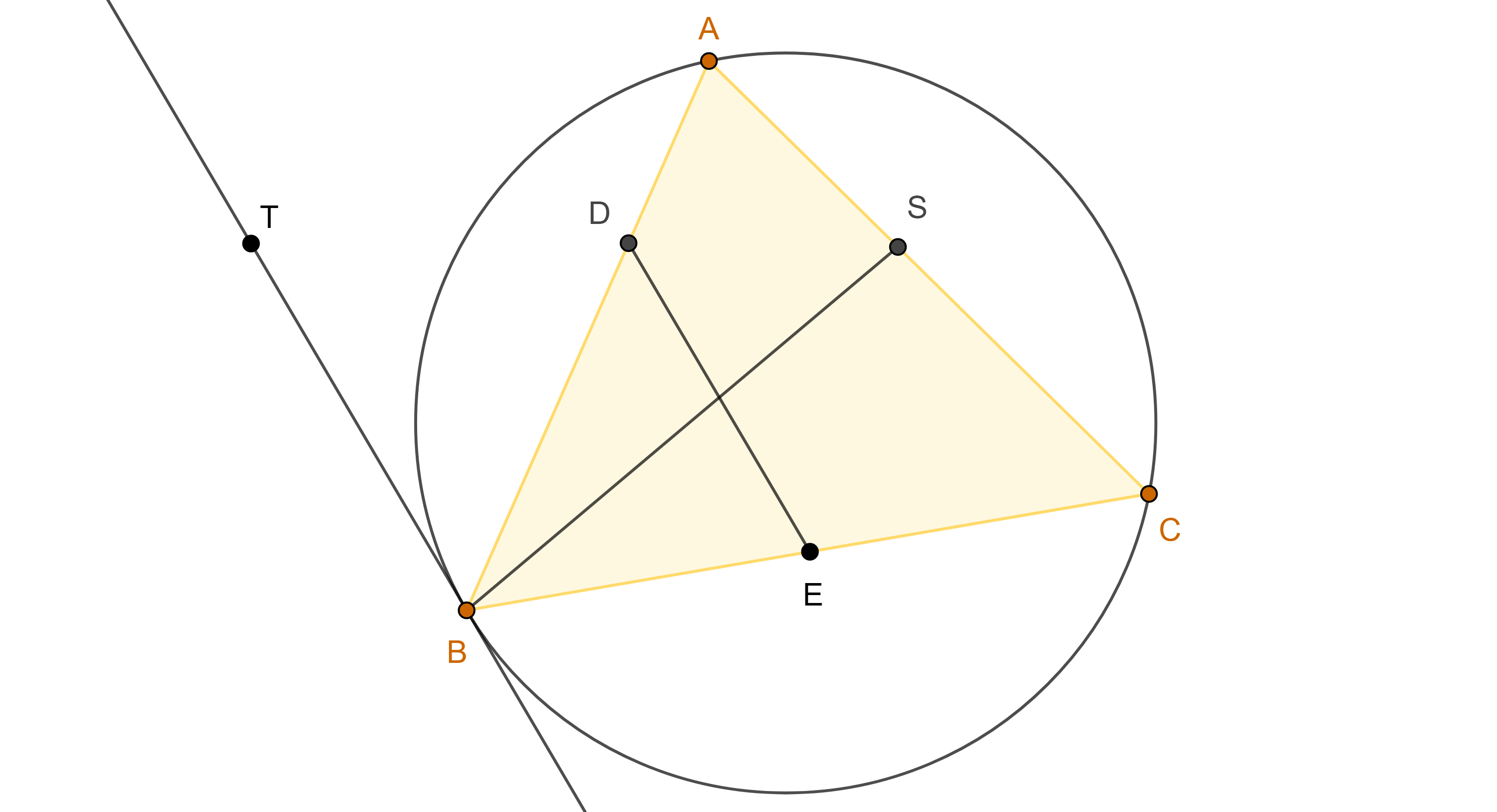
Proposición. 1 Si dos antiparalelas a dos de los lados de un triángulo tienen la misma longitud, entonces estas se intersecan en la simediana relativa al tercer lado, el reciproco también es cierto.
Demostración. Sean $\triangle ABC$, $E$, $G \in BC$, $F \in AB$ y $H \in CA$, tales que $EF$, $AC$ son antiparalelas respecto a $AB$ y $BC$; $AB$, $GH$ son antiparalelas respecto a $BC$ y $CA$, y $EF = GH$.
Como $\square AFEC$ y $\square ABGH$ son cíclicos, entonces, $\angle FEB = \angle BAC = \angle CGH$, por lo tanto $PG = PE$.
Sea $P = EF \cap GH$, dado que $FE = GH$ entonces $FP = HP$.
Si $S = AP \cap BC$, considera $I \in AB$, $J \in CA$, tales que $IS \parallel FE$ y $JS \parallel GH$, entonces $\triangle ASI \sim \triangle APF$ y $\triangle ASJ \sim \triangle APH$.
Por lo tanto, $\dfrac{SI}{PF} = \dfrac{AS}{AP} = \dfrac{SJ}{PH}$, como $PF = PH$ entonces $SI = SJ$.
Por otro lado $\triangle SBI \sim \triangle ABC \sim \triangle SJC$, esto es
$\dfrac{SB}{SI} = \dfrac{AB}{AC}$ y $\dfrac{SJ}{SC} = \dfrac{AB}{AC}$.
Como resultado de multiplicar estas dos ecuaciones obtenemos
$\dfrac{BS}{SC} = \dfrac{AB^2}{AC^2}$.
Por el teorema 1, esto implica que $AS$ es la $A$-simediana de $\triangle ABC$.
Notemos que el reciproco también es cierto, esto es, si dos antiparalelas a dos de los lados de un triángulo se intersecan en la simediana relativa al tercer lado, entonces estas tienen la misma longitud.
Esto lo podemos ver tomando la prueba anterior en sentido contrario.
$\blacksquare$
Otra caracterización importante
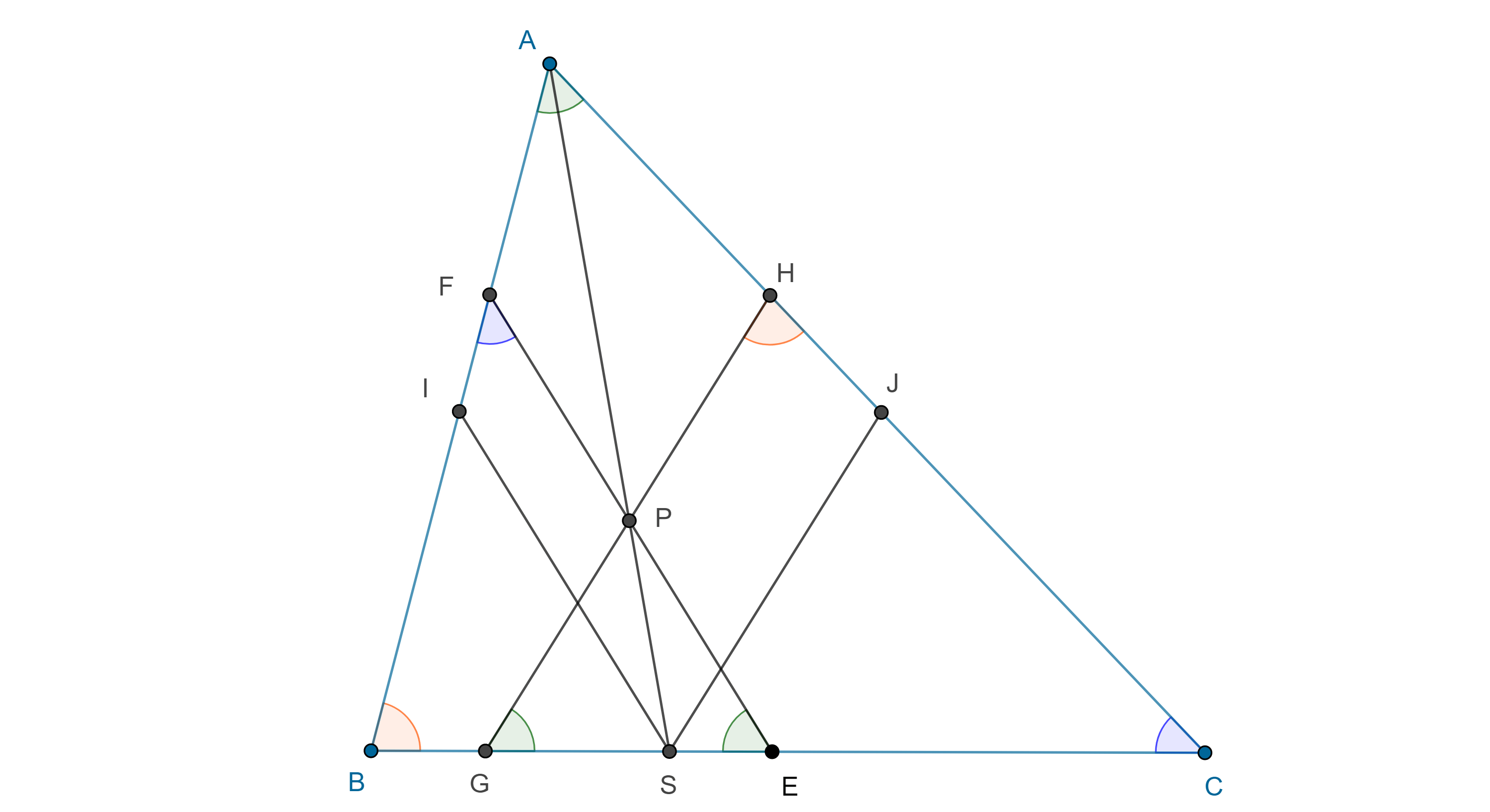
Teorema 4. Una simediana es el lugar geométrico de los puntos (dentro de los ángulos internos del triángulo o sus ángulos opuestos por el vértice) tales que la razón de sus distancias a los lados adyacentes a la simediana, es igual a la razón entre esos lados.
Demostración. Sean $\triangle ABC$, $A’$ el punto medio de $BC$ y $P \in AA’$, considera las proyecciones $P_c$, $P_b$ de $P$ en $AB$ y $AC$ respectivamente y $A’_c$, $A’_b$, las correspondientes de $A’$.
Como $\triangle APP_c \sim \triangle AA’A’_c$ y $\triangle APP_b \sim \triangle AA’A’_b$ entonces
$\dfrac{PP_c}{A’A’_c} = \dfrac{AP}{AA’} = \dfrac{PP_b}{A’A’_b}$.
Tomando en cuenta que los triángulos $\triangle ABA’$ y $\triangle AA’C$ tienen la misma altura desde $A$, tenemos lo siguiente:
$\dfrac{AC}{AB} = \dfrac{PP_c}{PP_b} = \dfrac{A’A’_c}{A’A’_b}$
$\Leftrightarrow AC \times A’A’_b = AB \times A’A’_c$
$\Leftrightarrow (\triangle AA’C) = (\triangle AA’B)$
$ \Leftrightarrow A’C = BA’$.
Por lo tanto, la mediana de un triángulo es el lugar geométrico de los puntos tales que la razón de sus distancias a los lados adyacentes a la mediana es el inverso de la razón entre dichos lados.
Denotamos la distancia de un punto $P$ a una recta $l$ como $d(P, l)$.
Para $P \in AA’$ considera $P’ \in AS$ su reflexión respecto de la bisectriz de $\angle BAC$, entonces
$\dfrac{d(P’, AB)}{d(P’, AC)} = \dfrac{d(P, AC)}{d(P’, AB)} = \dfrac{AB}{AC}$.
$\blacksquare$
Proposición 2. La recta que une las proyecciones de un punto en la simediana (mediana) de un triángulo, sobre los lados adyacentes, es perpendicular a la mediana (simediana) que pasa por el mismo vértice.
Demostración. En un triángulo $\triangle ABC$ sean $AA’$ la mediana y $AS$ la simediana, considera $P \in AS$ y $D$, $E$, las proyecciones de $P$ en $CA$ y $AB$ respectivamente.
Como $\angle PEA + \angle ADP = \pi$ entonces $\square AEPD$ es cíclico, así que $\angle EAP = \angle EDP$, por la ecuación $(5)$, $\angle EAP = \angle A’AD$.
Sean $F = PD \cap AA’$ y $G = DE \cap AA’$, en los triángulos $\triangle ADF$ y $\triangle DGF$, $\angle FAD = \angle GDF$ y $\angle DFG$ es un ángulo común, por lo tanto son semejantes.
Como $PD \perp AC$ entonces $DE \perp AA’$.
El caso para la mediana es análogo.
$\blacksquare$
Más adelante…
Así como las medianas de un triángulo son concurrentes, las simedianas también son concurrentes, pero dicho punto tiene propiedades importantes por si mismo, y de eso hablaremos en la próxima entrada.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Muestra que las segundas intersecciones de una mediana y su correspondiente simediana con el circuncírculo del triángulo, determinan una recta paralela al lado del triángulo relativo a la mediana considerada.
- Sea $\triangle ABC$ un triángulo acutángulo, $D$ y $A’$ las proyecciones de $A$ y $O$, el circuncírculo de $\triangle ABC$, en $BC$ respectivamente, sean $E = BO \cap AD$, $F = CO \cap AD$ y considera $P$ el segundo punto en común entre los circuncírculos de $\triangle ABE$ y $\triangle AFC$, demuestra que $AP$ es la $A$-simediana de $\triangle ABC$.
- Sea $P$ un punto dentro de un triángulo isósceles $\triangle ABC$ con $AB = AC$, tal que $\angle PBC = \angle ACP$, si $A’$ es el punto medio de $BC$, muestra que $\angle BPA’$ y $\angle CPA$ son suplementarios.
- Sean $\triangle ABC$, $D \in AB$ y $E \in CA$ tal que $DE \parallel BC$, considera $P = BE \cap CD$, los circuncírculos de $\triangle BDP$ y $\triangle CEP$ se intersecan en $P$ y $Q$, muestra que $\angle BAQ = \angle PAC$.
- La $A$-simediana $AS$ y la $A$-meidnana $AA’$ de un triángulo $\triangle ABC$ intersecan otra vez a su circuncírculo en $S’$ y $L$ respectivamente, prueba que la rectas de Simson de $S’$ y $L$ son perpendiculares a $AA’$ y a $AS$ respectivamente.
- Muestra que las exsimedianas de un triángulo tienen la misma propiedad que se señala en el teorema 4 respecto a las simedianas, pero esta vez para los puntos dentro de los ángulos externos del triángulo.
Entradas relacionadas
- Ir a Geometría Moderna I.
- Entrada anterior del curso: Haz armónico.
- Siguiente entrada del curso: Punto simediano.
- Otros cursos.
Fuentes
- Altshiller, N., College Geometry. New York: Dover, 2007, pp 247-252.
- Lozanovski, S., A Beautiful Journey Through Olympiad Geometry. Version 1.4. 2020, pp 86-92.
- Andreescu, T., Korsky, S. y Pohoata, C., Lemmas in Olympiad Geometry. USA: XYZ Press, 2016, pp 129-145.
- Shively, L., Introducción a la Geómetra Moderna. México: Ed. Continental, 1961, pp 66-70.
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»