Archivo de la etiqueta: centro de los nueve puntos

Geometría Moderna I: Cuadrángulo ortocéntrico

Por Rubén Alexander Ocampo Arellano

Introducción

En esta entrada veremos que los cuatro triángulos que se forman con los vértices de un cuadrángulo ortocéntrico, tienen la misma circunferencia de los nueve puntos y derivaremos algunas otras propiedades.

Cuadrángulo ortocéntrico

Definición. Un cuadrángulo ortocéntrico es el conjunto de puntos formado por los vértices de un triángulo y su ortocentro.

Nos referiremos a los cuatro triángulos que se pueden formar con los cuatro puntos de un cuadrángulo ortocéntrico como grupo ortocéntrico de triángulos.

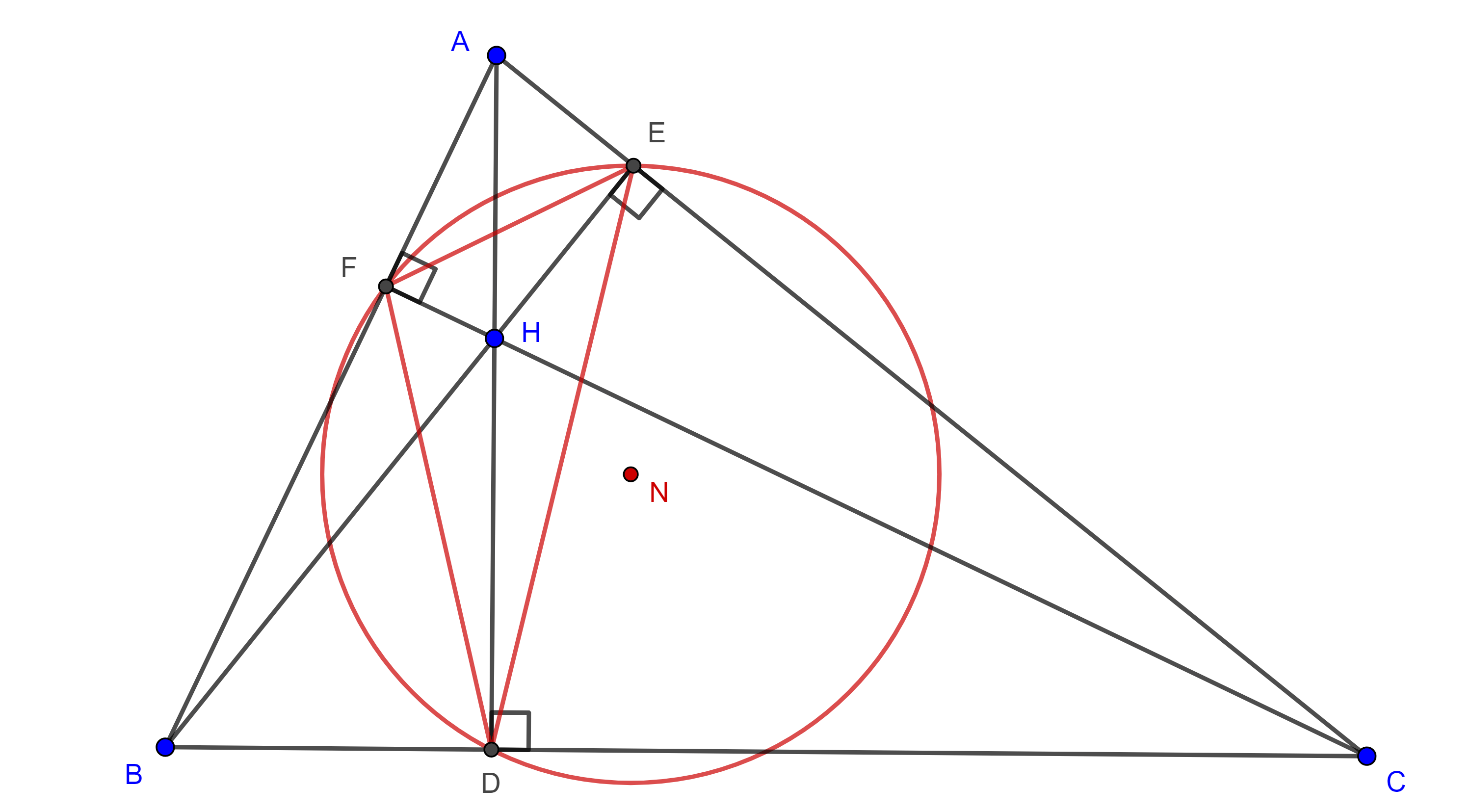
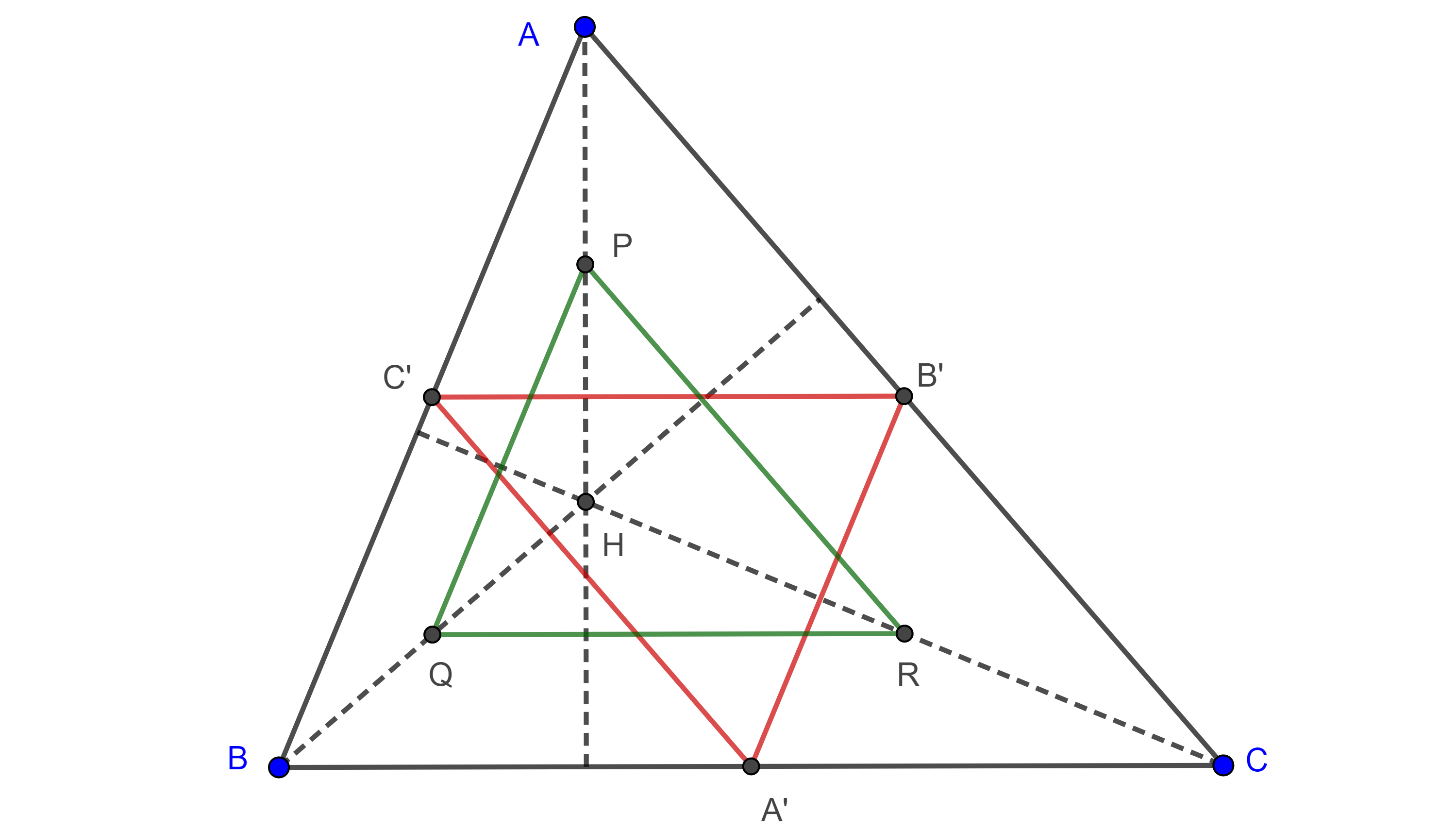
Teorema 1. Cualquier punto de un cuadrángulo ortocéntrico es el ortocentro del triángulo formado por los otros tres puntos y los triángulos de este grupo ortocéntrico tienen el mismo triangulo órtico.

Demostración. Sea $△ A B C$ y $H$ su ortocentro.

Notemos que el ortocentro de $△ B H C$ es $A$ pues $A B ⊥ H C$ , $A H ⊥ B C$ y $A C ⊥ H B$ .

De manera análoga podemos ver que $B$ es el ortocentro de $△ A H C$ y $C$ es el ortocentro de $△ A H B$ .

Por otro lado, los pares de rectas perpendiculares $A H$ , $B C$ ; $B H$ , $A C$ y $C H$ , $A B$ , se intersecan en $D$ , $E$ y $F$ , respectivamente.

Por lo tanto, estos tres puntos son fijos, así el triángulo órtico es el mismo para los cuatro triángulos $△ A B C$ , $△ H A B$ , $△ H A C$ y $△ H B C$ .

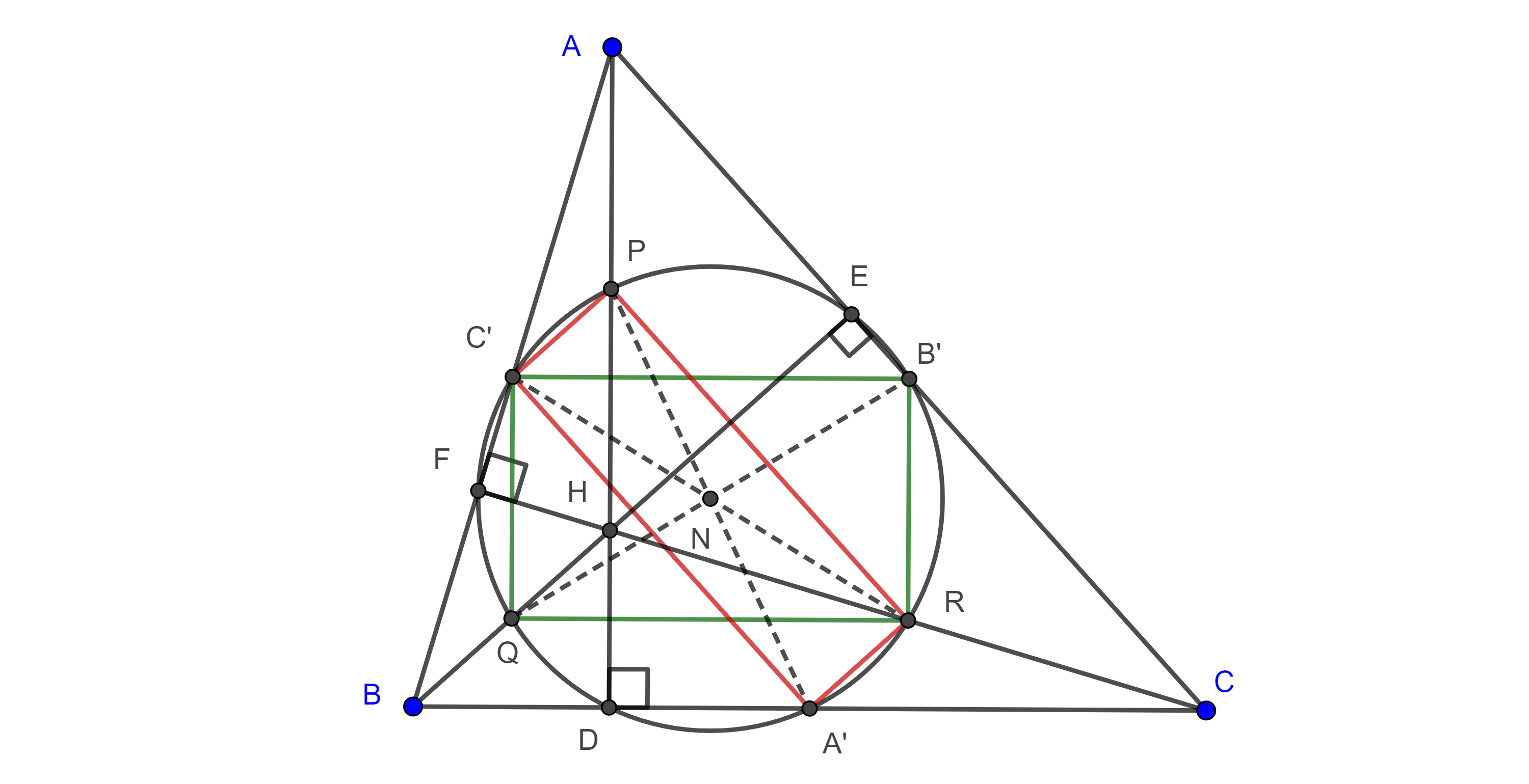
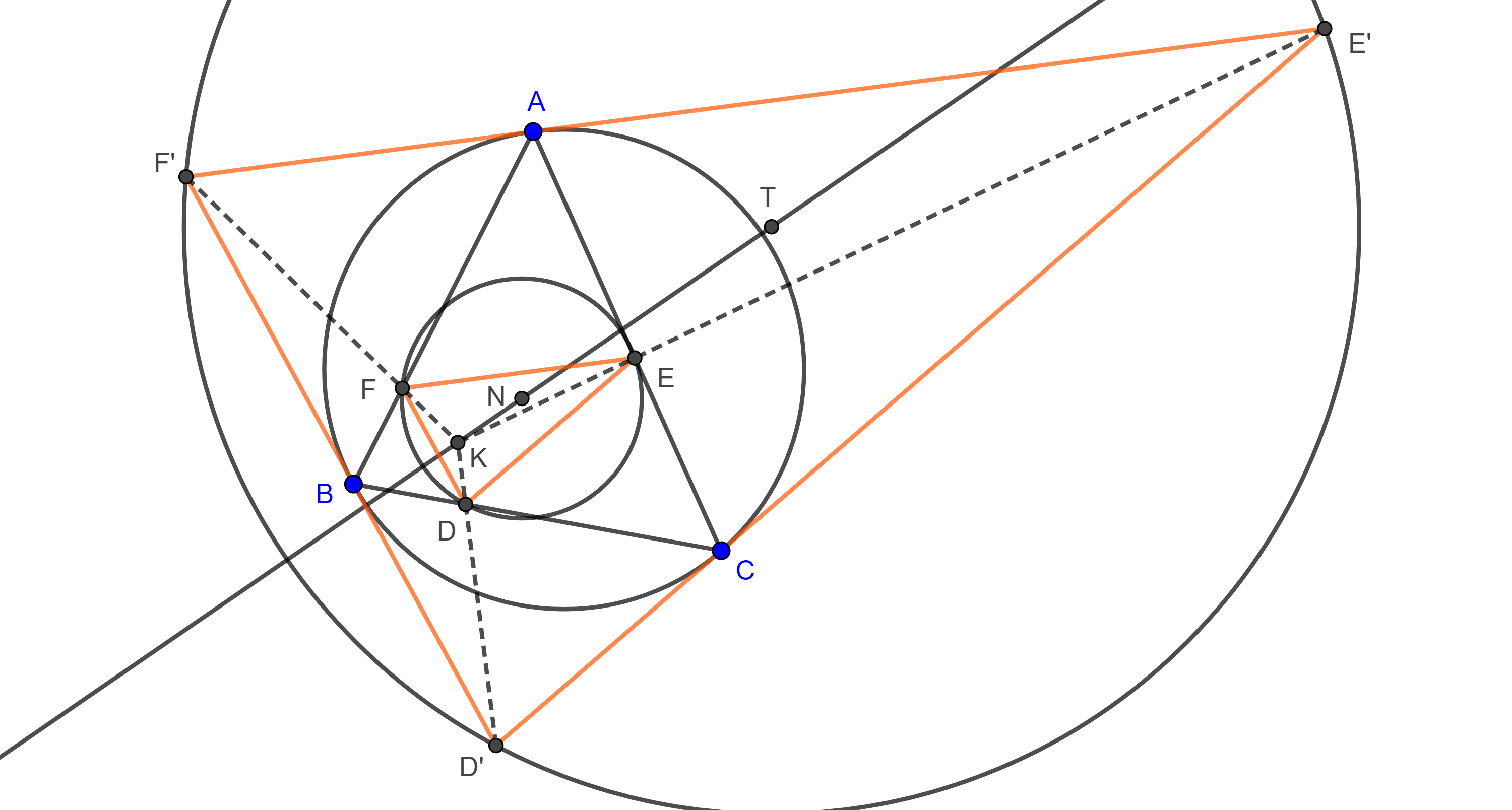
Corolario 1. Las circunferencias de los nueve puntos de un grupo ortocéntrico de triángulos coinciden y sus circunradios son iguales.

Demostración. Como el circuncírculo del triángulo órtico de un triángulo dado es la circunferencia de los nueve puntos, por el teorema 1, los triángulos de un grupo ortocéntrico tienen la misma circunferencia de los nueve puntos.

En la entrada anterior vimos que el radio de la circunferencia de los nueve puntos es igual a la mitad del circunradio de su triángulo de referencia.

Por lo tanto, $△ A B C$ , $△ H A B$ , $△ H A C$ y $△ H B C$ tienen el mismo circunradio (figura 1).

Circuncentros

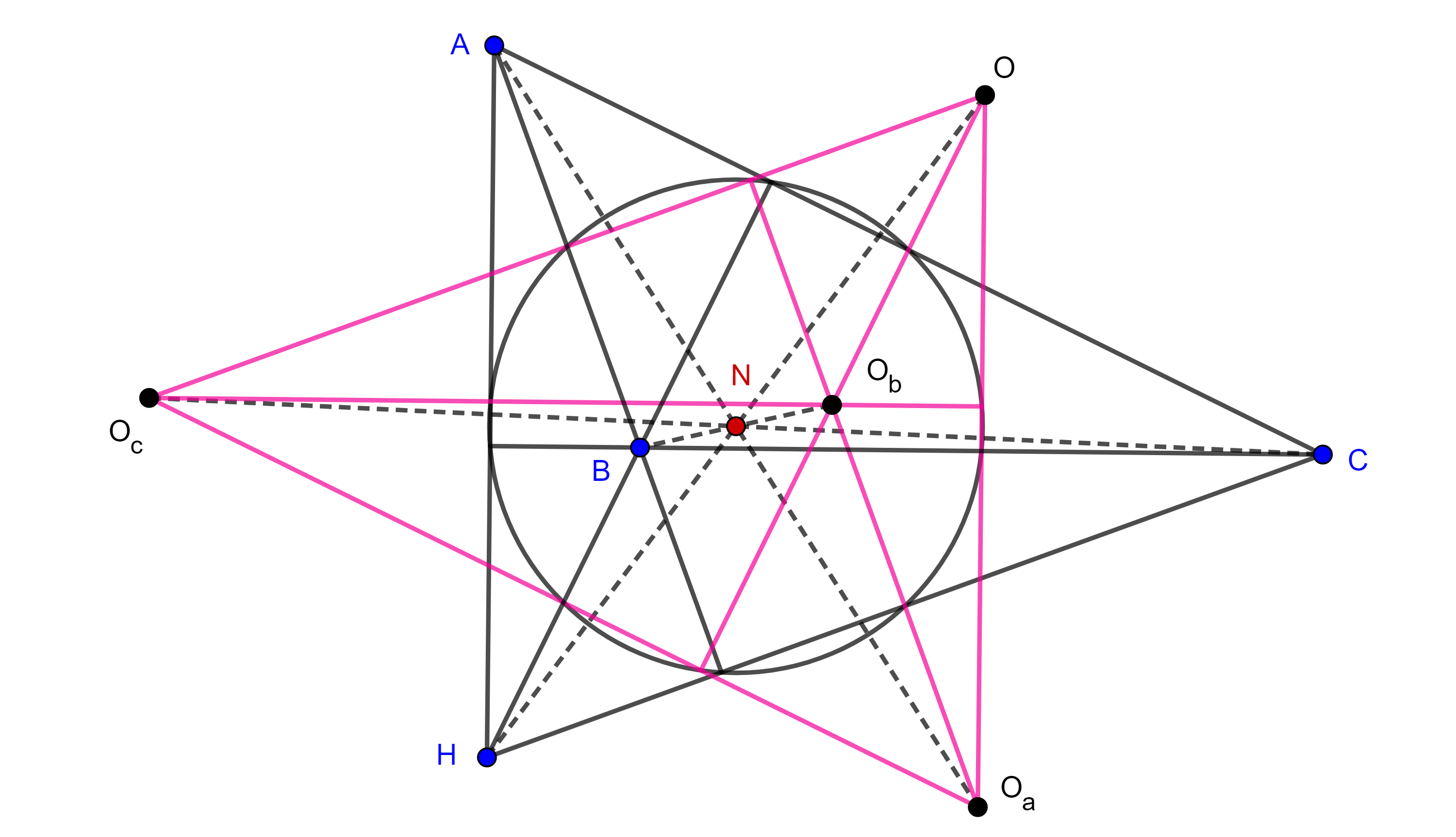
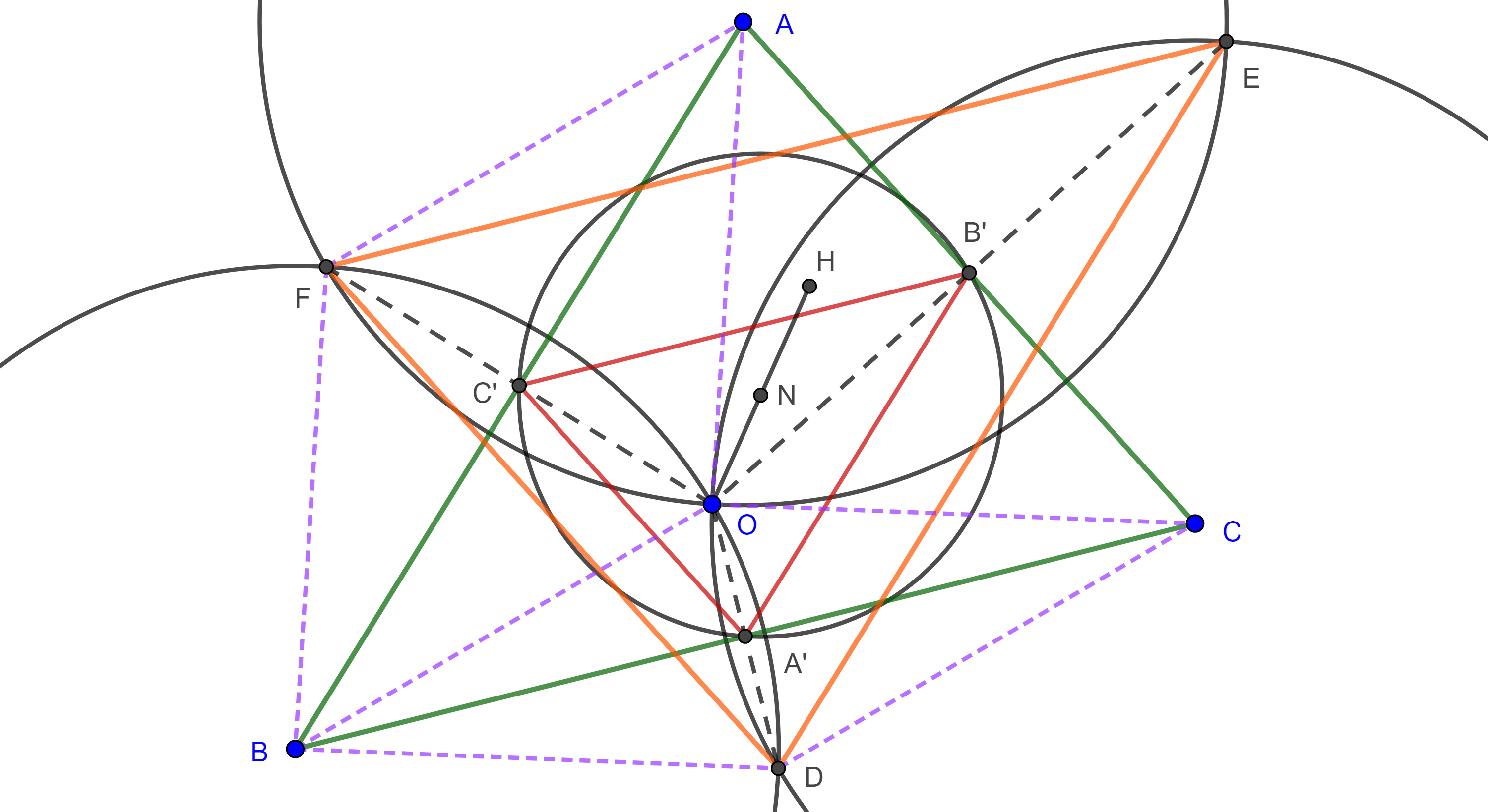
Teorema 2. Los circuncentros de un grupo ortocéntrico de triángulos forman un cuadrángulo ortocéntrico.

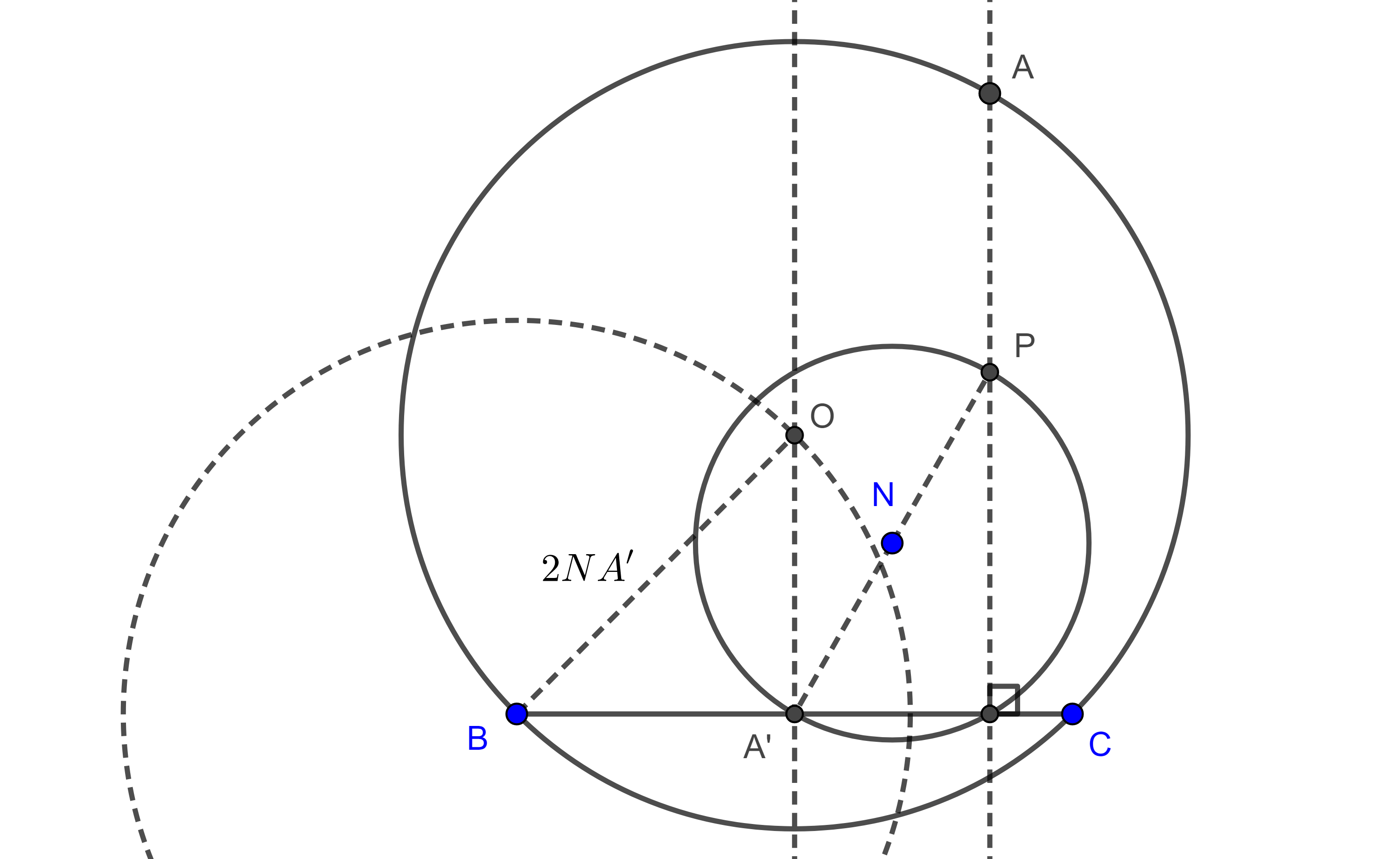
Demostración. Por el teorema 2 de la entrada anterior, sabemos que el circuncentro de un triángulo es la reflexión de su ortocentro respecto de $N$ , el centro de los nueve puntos.

Como los triángulos de un grupo ortocéntrico tienen el mismo centro de los nueve puntos, los circuncentros $O_{a}$ , $O_{b}$ , $O_{c}$ y $O$ de $△ H B C$ , $△ H A C$ , $△ H A B$ y $△ A B C$ son las reflexiones de $A$ , $B$ , $C$ y $H$ respectivamente respecto a $N$ .

Dado que una reflexión es una homotecia de razón $- 1$ entonces las figuras $A B C H$ y $O_{a} O_{b} O_{c} O$ son congruentes y por lo tanto $O_{a} O_{b} O_{c} O$ es un cuadrángulo ortocéntrico.

Corolario 2. Un grupo ortocéntrico de triángulos y el grupo ortocéntrico de triángulos formado por sus circuncentros tienen la misma circunferencia de los nueve puntos.

Demostración. Como las figuras $A B C H$ y $O_{a} O_{b} O_{c} O$ son simétricas respecto a $N$ entonces también sus circunferencias de los nueve puntos son simétricas respecto a $N$ .

Como $N$ es el centro de una de estas circunferencias, entonces coinciden.

Observación. Notemos que como $O_{a} O_{b} O_{c} O$ es un grupo ortocéntrico de triángulos, entonces la reflexión de sus ortocentros respecto al centro de los nueve puntos $N$ será el conjunto de sus circuncentros.

Entonces $A$ , $B$ , $C$ y $H$ son los circuncentros de $△ O_{b} O_{c} O$ , $△ O_{a} O_{c} O$ , $△ O_{a} O_{b} O$ y $△ O_{a} O_{b} O_{c}$ respectivamente.

Problema. Construye un triángulo $△ A B C$ dados el centro de los nueve puntos $N$ y los circuncentros $O_{b}$ y $O_{c}$ de los triángulos $△ C A H$ y $△ A B H$ respectivamente donde $H$ es el ortocentro de $△ A B C$ .

Solución. $O_{b}$ y $O_{c}$ son los ortocentros de $△ O_{a} O_{c} O$ y $△ O_{a} O_{b} O$ respectivamente y si los reflejamos respecto a $N$ obtendremos a los circuncentros de sus respectivos triángulos, estos son los vértices $B$ y $C$ del triángulo requerido.

Ahora tenemos dos vértices y el centro de los nueve puntos, este problema lo resolvimos en la entrada anterior.

Centroices

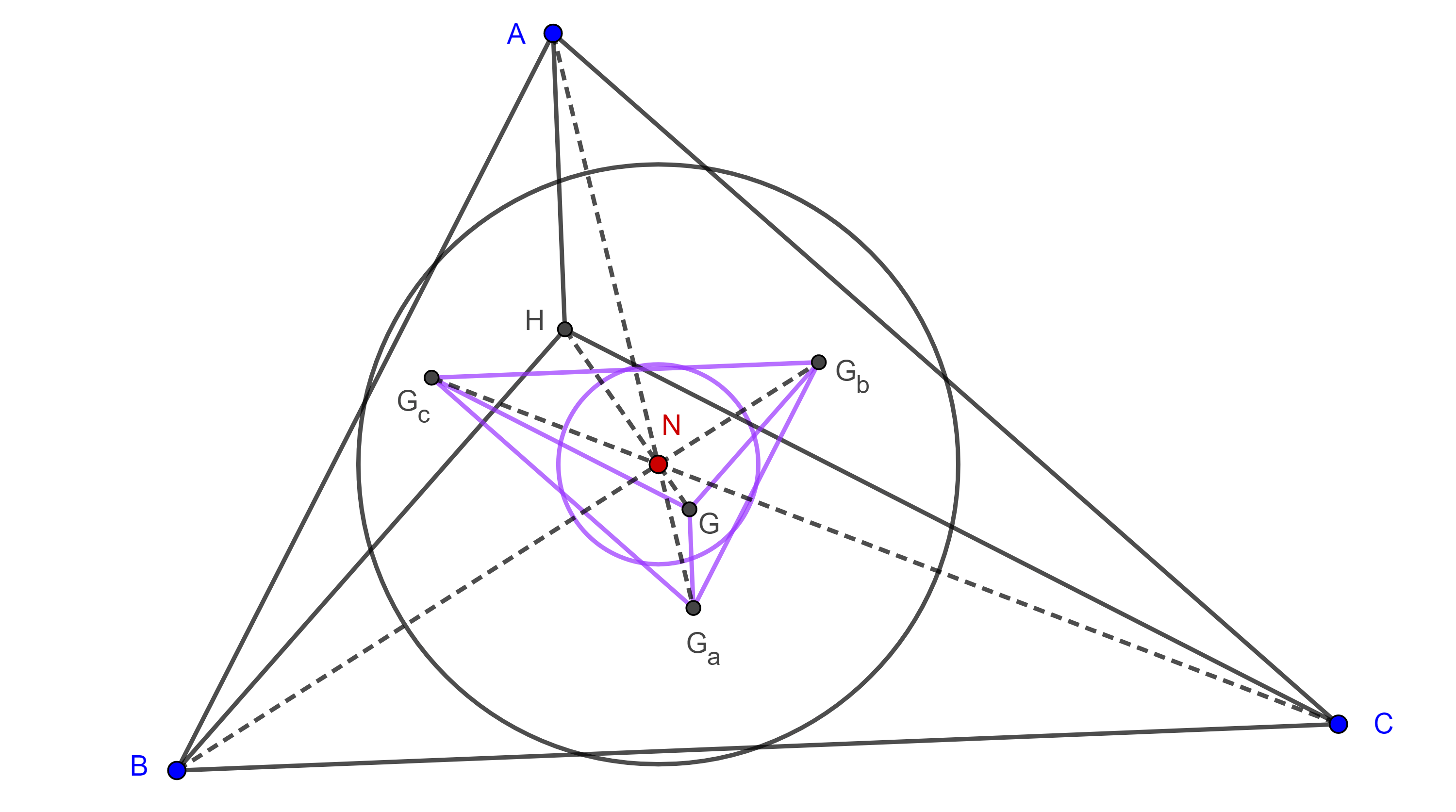
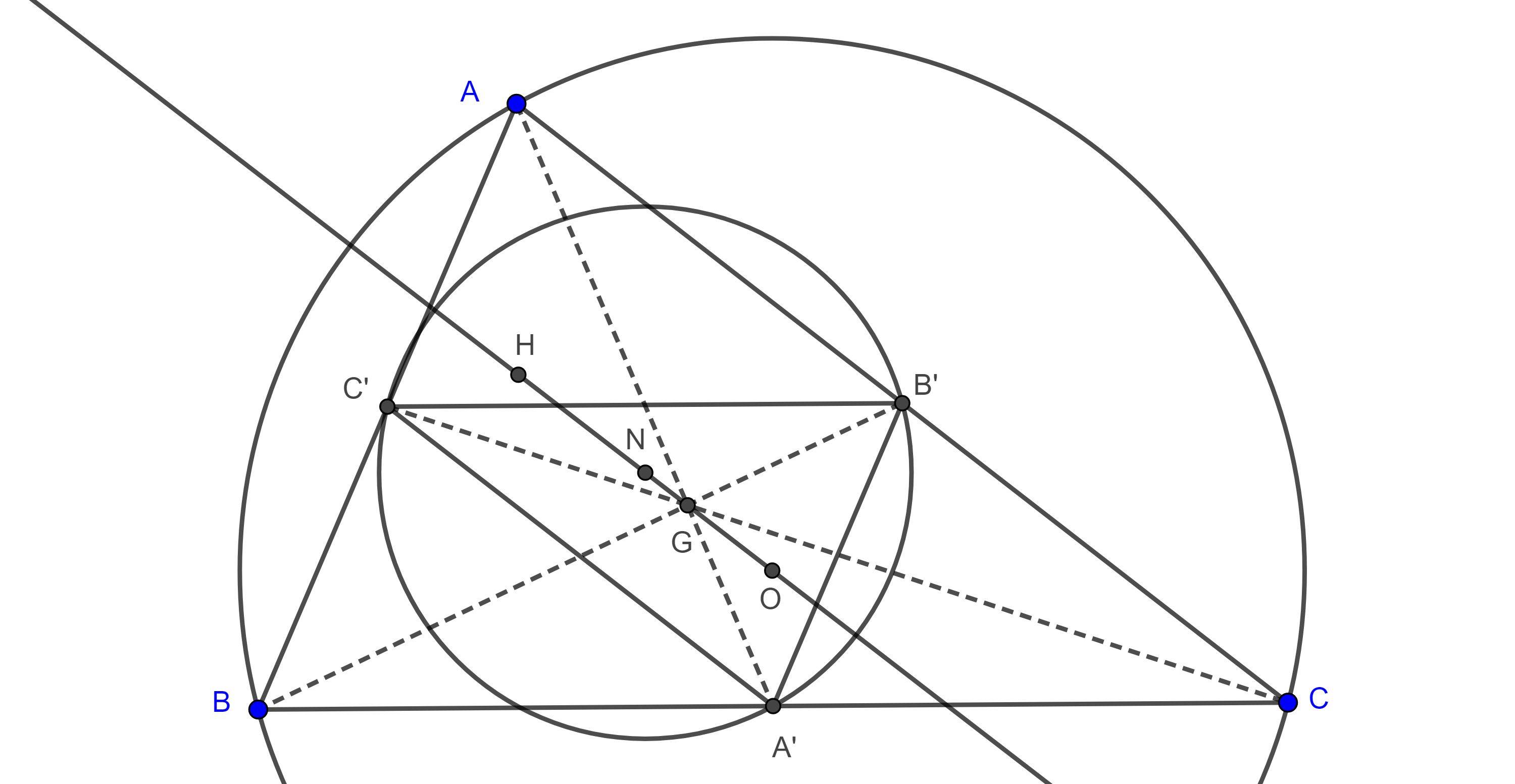
Teorema 3. Los cuatro centroides de un grupo ortocéntrico de triángulos forman un cuadrángulo ortocéntrico.

Demostración. Sea $△ A B C$ y $H$ su ortocentro.

Sabemos que el centro de los nueve puntos $N$ de $△ A B C$ divide internamente al segmento $H G$ en razón $3 : 1$ , donde $G$ es el centroide de $△ A B C$ .

Como el grupo ortocéntrico de triángulos $△ A B C$ , $△ H B C$ , $△ H A C$ , $△ H A B$ tienen el mismo centro de los nueve puntos $N$ , entonces sus respectivos centroides $G$ , $G_{a}$ , $G_{b}$ , $G_{c}$ están en homotecia con $H$ , $A$ , $B$ , $C$ respectivamente desde $N$ y la razón de homotecia es $- 3$ .

Como dos figuras homotéticas son semejantes, entonces $G G_{a} G_{b} G_{c}$ es un cuadrángulo ortocéntrico.

Corolario 3. La circunferencia de los nueve puntos de un grupo ortocéntrico de triángulos y la circunferencia de los nueve puntos del grupo ortocéntrico formado por sus centroides son concéntricas.

Demostración. Como las figuras $H A B C$ y $G G_{a} G_{b} G_{c}$ están en homotecia desde el centro de los nueve puntos $N$ de $△ A B C$ entonces sus respetivas circunferencias de los nueve puntos también están en homotecia desde $N$ .

Como $N$ es el centro de una de ellas, entonces son concéntricas.

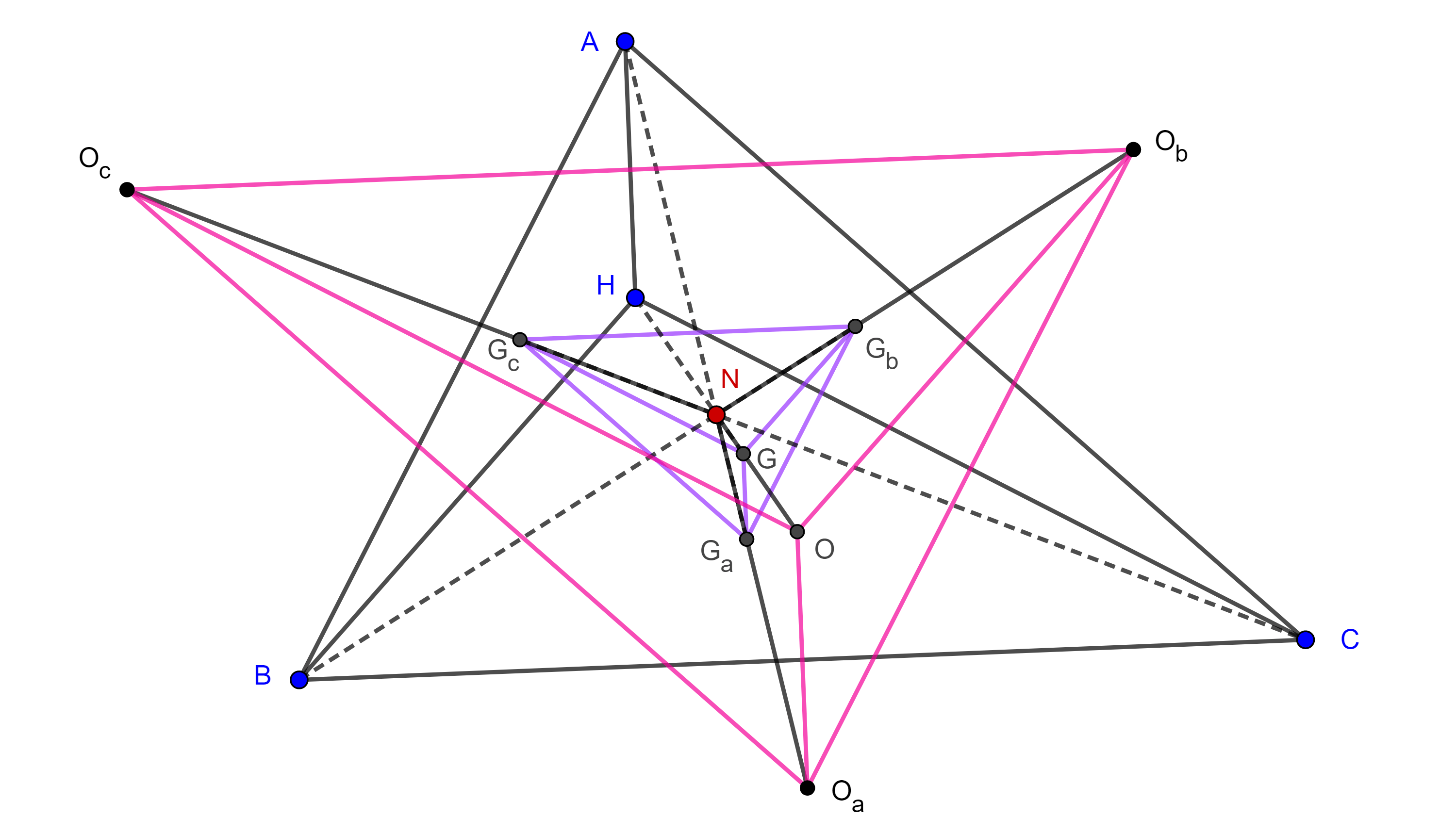
Corolario 4. Dado un cuadrángulo ortocéntrico, el cuadrángulo ortocéntrico formado por sus circuncentros y el cuadrángulo ortocéntrico formado por sus centroides tienen el mismo centro de los nueve puntos y además existe una homotecia entre ellos con centro en este punto.

Demostración. Por los corolarios 2 y 3, $O O_{a} O_{b} O_{c}$ y $G G_{a} G_{b} G_{c}$ tienen el mismo centro de los nueve puntos que $H A B C$ y son homotéticos con este último precisamente desde $N$ en razón $- 1$ y $- 3$ respectivamente.

Por lo tanto, existe una homotecia con centro en $N$ y razón $3$ que lleva a $G G_{a} G_{b} G_{c}$ en $O O_{a} O_{b} O_{c}$ .

Incentro y excentros

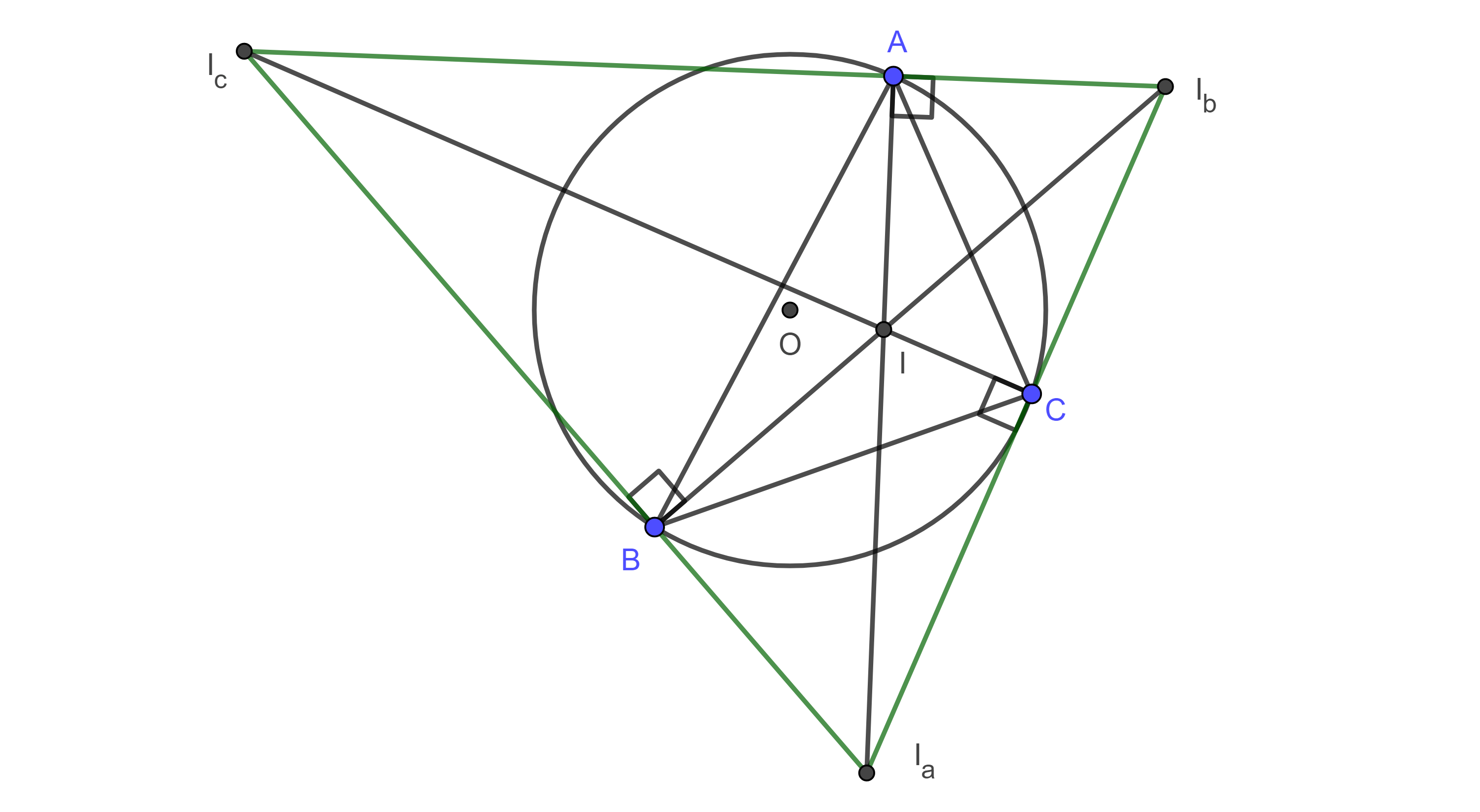
Teorema 4. El incentro y los excentros de un triángulo dado forman un cuadrángulo ortocéntrico y el circuncírculo del triángulo dado es la circunferencia de los nueve puntos de este grupo ortocéntrico de triángulos.

Demostración. Como las bisectrices interna y externa de los ángulos de un triángulo $△ A B C$ son perpendiculares entre si entonces el incentro $I$ es el ortocentro del triángulo formado por los excentros $△ I_{a} I_{b} I_{c}$ y el triángulo $△ A B C$ es el triángulo órtico de $△ I_{a} I_{b} I_{c}$ .

Entonces, por el teorema 1 y corolario 1, $I_{a} I_{b} I_{c} I$ es un grupo ortocéntrico de puntos y su circunferencia de los nueve puntos es el circuncírculo de $△ A B C$ .

Proposición. El segmento que une el ortocentro de un triángulo dado con el circuncentro del triángulo formado por los excentros del triángulo dado es bisecado por el incentro del triángulo medial del triángulo dado.

Demostración. Sea $△ A B C$ un triángulo, $I$ , $I_{a}$ , $I_{b}$ , $I_{c}$ , el incentro y sus respectivos excentros, $O$ y $O_{e}$ los circuncentros de $△ A B C$ y $△ I_{a} I_{b} I_{c}$ respectivamente.

Por el teorema anterior, $I$ y $O$ son el ortocentro y el centro de los nueve puntos respectivamente de $△ I_{a} I_{b} I_{c}$ , por lo tanto, $O$ es el punto medio de $I O_{e}$ .

Sean $H$ y $G$ el ortocentro y el centroide respectivamente de $△ A B C$ , como $H$ , $G$ y $O$ son colineales y $G$ triseca el segmento $O H$ , entonces, $G$ es el centroide de $△ I O_{e} H$ .

Por lo tanto, $I G$ biseca a $O_{e} H$ en $I^{'}$ y $\frac{I G}{2} = G I^{'}$ .

Por otro lado, sabemos que existe una homotecia con centro en $G$ y razón $\frac{- 1}{2}$ , que lleva a $△ A B C$ , a su triangulo medial $△ A^{'} B^{'} C^{'}$ , por lo que sus respectivos incentros $I$ y $I_{m}$ son puntos homólogos de esta homotecia, es decir $I$ , $G$ y $I_{m}$ son colineales y $G$ triseca al segmento $I I_{m}$ .

Como $I^{'}$ cumple con estas características entonces $I^{'} = I_{m}$ .

Más adelante…

En la próxima entrada estudiaremos otra recta notable del triángulo, la recta de Simson, veremos que la intersección de dos rectas de Simson se intersecan en la circunferencia de los nueve puntos y que cierto conjunto de rectas de Simson forman un cuadrángulo ortocéntrico.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Muestra que las rectas de Euler de los cuatro triángulos de un grupo ortocéntrico son concurrentes.
Demuestra que el simétrico del circuncentro de un triángulo con respecto a uno de los lados del triángulo coincide con el simétrico del vértice opuesto al lado considerado respecto al centro de los nueve puntos del triángulo.
Muestra que los vértices de un grupo ortocéntrico de triángulos pueden ser considerados como los centroides de otro grupo ortocéntrico de triángulos.
Sea $△ A B C$ un triángulo rectángulo con $∠ A = \frac{π}{2}$ , $D$ el pie de la altura por $A$ , las bisectrices de $∠ B A D$ y $∠ D A C$ intersecan a $B C$ en $P$ y $P^{'}$ respectivamente. Las bisectrices de $∠ D B A$ y $∠ A C D$ intersecan a $A D$ en $Q$ y $Q^{'}$ respectivamente.
$i)$ Muestra que $P P^{'} Q Q^{'}$ es un cuadrángulo ortocéntrico,
$i i)$ si $I$ , $J$ y $K$ son los incentros de $△ A B C$ , $△ A B D$ y $△ A D C$ , muestra que $A I J K$ es un cuadrángulo ortocéntrico.
Prueba que la suma de los cuadrados de dos segmentos no adyacentes que unen vértices de un cuadrángulo ortocéntrico es igual al cuadrado del circundiámetro de los triángulos de este grupo ortocéntrico.
Construye un triángulo $△ A B C$ dados su circuncentro $O$ , y los circuncentros de los triángulos $△ I I_{b} I_{c}$ y $△ I I_{a} I_{c}$ , donde $I$ , $I_{a}$ , $I_{b}$ y $I_{c}$ es el incentro y los excentros de $△ A B C$ .

Entradas relacionadas

Ir a Geometría Moderna I.
Entrada anterior del curso: Circunferencia de los nueve puntos.
Siguiente entrada del curso: Recta de Simson.
Otros cursos.

Fuentes

Altshiller, N., College Geometry. New York: Dover, 2007, pp 109-115.
Johnson, R., Advanced Euclidean Geometry. New York: Dover, 2007, pp 165-167.
Shively, L., Introducción a la Geómetra Moderna. México: Ed. Continental, 1961, pp 58.

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Geometría Moderna I: Circunferencia de los nueve puntos

Por Rubén Alexander Ocampo Arellano

Deja un comentario

Introducción

En esta ocasión veremos que nueve puntos notables del triángulo son concíclicos, a saber, los puntos medios de los lados, los pies de las alturas y los puntos medios de los segmentos que unen al ortocentro con los vértices del triángulo. A esta circunferencia se le conoce como circunferencia de los nueve puntos y su centro se encuentra en la recta de Euler del triángulo considerado.

Triángulo de Euler

Definición 1. A los puntos medios de los segmentos que unen los vértices de un triángulo dado con su ortocentro se les conoce como puntos de Euler, y el triángulo que tiene como vértices los puntos de Euler es el triángulo de Euler del triángulo dado.

Observación. Por la definición anterior, un triángulo y su triángulo de Euler son homotéticos (figura 1), con centro de homotecia en el ortocentro y razón de homotecia $\frac{1}{2}$ .

Proposición 1. El triángulo de Euler y el triángulo medial de todo triángulo son congruentes y sus respectivos lados son paralelos.

Demostración. Sean $△ A^{'} B^{'} C^{'}$ el triángulo medial y $△ P Q R$ el triángulo de Euler de $△ A B C$ , (figura 1).

$C^{'}$ y $B^{'}$ son puntos medios de $A B$ y $A C$ respectivamente, así que $C^{'} B^{'}$ es un segmento medio de $△ A B C$ , de igual manera $Q R$ es un segmento medio de $△ H B C$ , donde $H$ es el ortocentro de $△ A B C$ .

Por lo tanto, $C^{'} B^{'} ∥ B C ∥ Q R$ , y $2 C^{'} B^{'} = B C = 2 Q R$ .

De manera análoga podemos ver que $A^{'} C^{'} = R P$ y $A^{'} B^{'} = Q P$ , por criterio de congruencia LLL, $△ A^{'} B^{'} C^{'} ≅ △ P Q R$ .

Circunferencia de los nueve puntos

Teorema 1. El triángulo de Euler, el triángulo medial y el triángulo órtico de todo triángulo tienen el mismo circuncírculo.

Demostración. Por la proposición 1 y empleando la misma notación de esta, sabemos que $C^{'} Q R B^{'}$ es un paralelogramo (figura 2).

$C^{'} Q$ es un segmento medio de $△ B A H$ , así que $C^{'} Q ∥ A H$ $\Rightarrow C^{'} Q ⊥ B C$ .

Y como $Q R ∥ B C$ , entonces, $C^{'} Q R B^{'}$ es un rectángulo, lo que significa que las diagonales $C^{'} R$ y $Q B^{'}$ tienen la misma longitud y se cortan en su punto medio, $N$ .

De manera análoga podemos probar que $P C^{'} A^{'} R$ es un rectángulo y que $P A^{'}$ y $C^{'} R$ tienen la misma longitud y se cortan en su punto medio.

Como el punto medio de $C^{'} R$ es $N$ , entonces, los puntos $A^{'}$ , $B^{'}$ , $C^{'}$ , $P$ , $Q$ y $R$ son equidistantes a $N$ .

Sean $D$ , $E$ y $F$ los pies de las alturas por $A$ , $B$ y $C$ respectivamente.

Como $A^{'} P$ , $B^{'} Q$ y $C^{'} R$ son diámetros de esta circunferencia y además $∠ A^{'} D P = ∠ Q E B^{'} = ∠ R F C^{'} = \frac{π}{2}$ , es decir estos diámetros subtienden ángulos rectos en los puntos $D$ , $E$ y $F$ respectivamente, entonces $D$ , $E$ y $F$ se encuentran en la misma circunferencia.

Definición 2. Nos referiremos al centro de la circunferencia de los nueve puntos de un triángulo como el centro de los nueve puntos y los denotaremos como $N$ .

Teorema 2. El radio de la circunferencia de los nueve puntos de un triángulo es igual a la mitad del circunradio y el centro de los nueve puntos biseca al segmento que une al circuncentro con el ortocentro.

Demostración. Recordemos que todo triángulo está en homotecia con su triángulo medial, esto implica que son semejantes, con razón $\frac{- 1}{2}$ y centro de homotecia en el centroide $G$ del triángulo.

Por lo tanto, el radio de la circunferencia de los nueve puntos de un triángulo es la mitad del circunradio de este.

De la relación de homotecia también tenemos que $G$ triseca el segmento $O N$ de los circuncentros $O$ y $N$ de $△ A B C$ y $△ A^{'} B^{'} C^{'}$ , su triángulo medial, esto es, $O G = 2 G N$ .

Y sabemos que $2 O G = G H$ , donde $H$ es el ortocentro.

Por lo tanto, $H N = O N$ .

Triángulo tangencial

Teorema 3. El circuncentro del triángulo tangencial de un triángulo dado se encuentra en la recta de Euler del triángulo dado.

Demostración. Recordemos que el triángulo tangencial $△ D^{'} E^{'} F^{'}$ y el triángulo órtico $△ D E F$ de un triángulo $△ A B C$ están en homotecia desde un punto $K$ que se encuentra en la recta de Euler de $△ A B C$ .

Ahora, como los circuncentros de los triángulos tangencial y el triángulo órtico, $T$ y $N$ , respectivamente, son puntos correspondientes de esta homotecia, entonces $T$ es colineal con $N$ y $K$ .

Por el teorema 2, $N$ esta en la recta de Euler de $△ A B C$ , por lo tanto, $T$ está en la recta de Euler de $△ A B C$ .

Corolario 1. El circuncentro de un triángulo dado se encuentra en la recta de Euler del triángulo formado por los puntos de tangencia del incírculo con los lados del triángulo dado.

Demostración. Notemos que todo triángulo es el triángulo tangencial del triángulo formado por los puntos de tangencia de su incírculo con sus lados.

El resultado se sigue al aplicar el teorema 3.

Corolario 2. El cuadrado del circunradio de un triángulo es dos veces el producto del inradio de su triángulo órtico por el circunradio de su triángulo tangencial.

Demostración. Sean $R$ , $p$ y $q$ los circunradios de $△ A B C$ , de su triángulo tangencial $△ D^{'} E^{'} C^{'}$ y el inradio de su triángulo órtico $△ D E F$ , respectivamente.

Como $△ D^{'} E^{'} F^{'}$ y $△ D E F$ son homotéticos entonces la razón entre sus inradios y la razón entre sus circunradios son iguales a su razón de homotecia y por lo tanto son iguales entre si, además por el teorema 2, $R$ es dos veces el circunradio de $△ D E F$ .

$\frac{R}{q} = \frac{p}{\frac{R}{2}}$
$\Rightarrow R^{2} = 2 p q$

Ejemplos

Proposición 2. La recta determinada por el ortocentro de un triángulo y el punto medio de uno de sus lados pasa por el punto diametralmente opuesto, en su circuncírculo, al vértice opuesto del lado considerado.

Demostración. Sean $△ A B C$ , $(O, R)$ su circuncírculo, $X$ el punto diametralmente opuesto a $A$ , $H$ el ortocentro, $A^{'}$ el punto medio de $B C$ y $P$ el punto de Euler entre $A$ y $H$ .

$P O$ es un segmento medio de $△ A H X$ , por lo tanto, $H X ∥ P O$ .

Por la proposición 6 de la entrada anterior tenemos que $P H = O A^{'}$ y ambos son perpendiculares a $B C$ , por lo tanto, $P H A^{'} O$ es un paralelogramo, es decir, $H A^{'} ∥ P O$ .

Como la paralela a una recta por un punto exterior a ella es única, entonces $H$ , $A^{'}$ y $X$ son colineales.

Proposición 3. Sean $A$ , $B$ y $C$ los centros de tres circunferencias distintas, con el mismo radio y que tienen un punto $O$ en común.

Consideremos los otros puntos en común, $D = (B, r) \cap (C, r)$ , $E = (A, r) \cap (C, r)$ y $F = (A, r) \cap (B, r)$ , entonces el circunradio de $△ D E F$ es igual al de las tres circunferencias dadas y su circuncentro es el ortocentro de $△ A B C$ .

Demostración. Notemos primero que $O A = O B = O C = r$ , por lo tanto, el circuncentro de $△ A B C$ es $O$ y su circunradio es $r$ .

Como $A F B O$ y $O B D C$ son rombos entonces $A F = B O = C D$ y $A F ∥ B O ∥ C D$ .

Por tanto, $A F D C$ es paralelogramo y así $\Rightarrow A C = D F$ y $A C ∥ D F$ .

De manera análoga podemos ver que $A B = D E$ , $A B ∥ D E$ y $B C = E F$ y $B C ∥ E F$

Por lo tanto, $△ A B C$ y $△ D E F$ son congruentes por criterio LLL y sus respectivos lados son paralelos.

Como $O B D C$ es un rombo entonces, $O D ⊥ B C$ además $O D$ y $B C$ se intersecan en su punto medio, $A^{'}$ .

De manera análoga podemos ver $A B ⊥ O F$ , se bisecan en $C^{'}$ y $A C ⊥ O E$ , se bisecan en $B^{'}$ .

De lo anterior se sigue que $△ A^{'} B^{'} C^{'}$ es el triángulo medial de $△ A B C$ , que $D O$ , $E O$ y $F O$ son las alturas de $△ D E F$ .

Por lo tanto $O$ es el ortocentro de $△ D E F$ y $△ A^{'} B^{'} C^{'}$ es el triángulo de Euler de $△ D E F$ .

En consecuencia, la circunferencia de los nueve puntos es la misma para $△ A B C$ y $△ D E F$ , por el teorema 2, se sigue que sus circunradios son iguales, por lo tanto, el circunradio de $△ D E F$ es $r$ .

También por el teorema 2, sabemos que el centro de los nueve puntos biseca al segmento que une ortocentro con el circuncentro.

Como el centro de los nueve puntos es el mismo para $△ A B C$ y $△ D E F$ , y ya que el circuncentro de $△ A B C$ coincide con el ortocentro de $△ D E F$ entonces el circuncentro de $△ A B C$ coincide con el ortocentro de $△ D E F$ .

Problema. Construir un triángulo $△ A B C$ dados dos vértices $B$ , $C$ y el centro de los nueve puntos, $N$ .

Solución. Trazamos $B C$ y su punto medio $A^{'}$ ,

Con el radio $N A^{'}$ de la circunferencia de los nueve puntos, obtenemos el circunradio de $△ A B C$ , $2 N A^{'}$ .

Ahora podemos encontrar al circuncentro de $△ A B C$ que se encuentra en la mediatriz de $B C$ , trazando una circunferencia con centro en $B$ o en $C$ y radio $2 N A^{'}$ .

El simétrico de $A^{'}$ respecto a $N$ será $P$ , el punto de Euler que se encuentra entre $N$ y el vértice buscado. Como la perpendicular a $B C$ por $P$ es la altura por $A$ , entonces su intersección con el circuncírculo $(O, 2 N A^{'})$ de $△ A B C$ , es el vértice faltante.

Más adelante…

En la próxima entrada veremos como cierto conjunto de triángulos al que llamaremos grupo ortocéntrico de triángulos tienen la misma circunferencia de los nueve puntos y otros resultados relacionados.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Muestra que el triángulo de Euler $△ P Q R$ y el triangulo $△ C^{'} B^{'} D$ son congruentes, (figura 2).
Por los puntos medios de un triángulo dado traza paralelas a las bisectrices externas de los correspondientes ángulos opuestos. Prueba que el triángulo formado por estas paralelas y el triángulo dado tienen la misma circunferencia de los nueve puntos.
Muestra que las paralelas a las bisectrices internas de un triángulo dado trazadas por los respectivos puntos de Euler del triángulo dado son concurrentes, también prueba que la recta que pasa por el punto de concurrencia y el centro de los nueve puntos del triángulo dado es paralela con la recta que pasa por el circuncentro y el incentro del triángulo dado.
Demuestra que la circunferencia de los nueve puntos biseca cualquier segmento que une al ortocentro con un punto en el circuncírculo.
Construye un triángulo dados un vértice, el ortocentro y el centro de los nueve puntos.

Entradas relacionadas

Ir a Geometría Moderna I.
Entrada anterior del curso: Triángulo órtico.
Siguiente entrada del curso: Cuadrángulo ortocéntrico.
Otros cursos.

Fuentes

Altshiller, N., College Geometry. New York: Dover, 2007, pp 103-105.
Coxeter, H. y Greitzer, L., Geometry Revisited. Washington: The Mathematical Association of America, 1967, pp 20-22.
Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 69-70.

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

El blog de Leo

Aprendiendo, creando y compartiendo matemáticas

Archivo de la etiqueta: centro de los nueve puntos

Geometría Moderna I: Cuadrángulo ortocéntrico

Introducción

Cuadrángulo ortocéntrico

Circuncentros

Centroices

Incentro y excentros

Más adelante…

Tarea moral

Entradas relacionadas

Fuentes

Agradecimientos

Geometría Moderna I: Circunferencia de los nueve puntos

Introducción

Triángulo de Euler

Circunferencia de los nueve puntos

Triángulo tangencial

Ejemplos

Más adelante…

Tarea moral

Entradas relacionadas

Fuentes

Agradecimientos