Archivo de la etiqueta: triángulo pedal

Geometría Moderna I: Rectas isogonales

Por Rubén Alexander Ocampo Arellano

Deja un comentario

Introducción

En esta ocasión hablaremos sobre un tipo mas general de pares de rectas que las medianas y simedianas, estas son las rectas isogonales, esto nos permitirá hablar sobre pares de puntos mas generales que el centroide y el punto simediano, nos referimos a los puntos conjugados isogonales y a sus triángulos pedales.

Rectas isogonales

Definición 1. Dos rectas que pasan por el vértice de un ángulo tales que una es la reflexión de la otra respecto a la bisectriz del ángulo, se llaman rectas isogonales.

Teorema 1. Las distancias a los lados de un ángulo desde dos puntos en dos rectas que pasan por el vértice del ángulo son inversamente proporcionales si y solo si las rectas son isogonales.

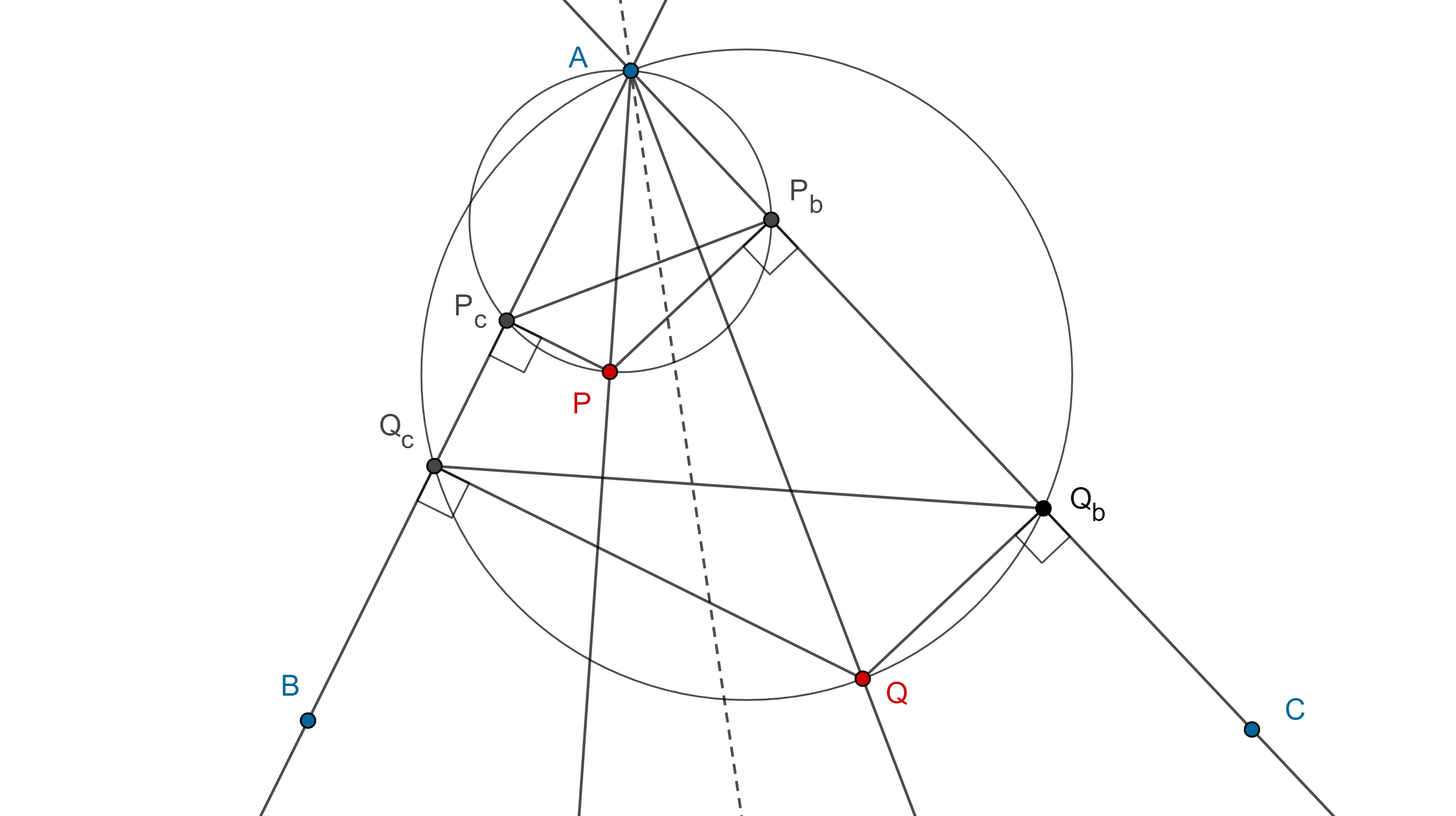
Demostración. Si $AP$ y $AQ$ son dos rectas isogonales respecto del ángulo $\angle BAC$, considera $P_c$, $Q_c$, las proyecciones de $P$ y $Q$ en $AB$, y $P_b$, $Q_b$, las proyecciones de $P$ y $Q$ en $AC$.

Figura 1

Como $AP$, $AQ$ son isogonales entonces $\angle BAP = \angle QAC$ y tenemos las siguientes semejanzas $\triangle APP_c \sim \triangle AQQ_b$, $\triangle APP_b \sim \triangle AQQ_c$ por lo tanto,
$\dfrac{PP_c}{QQ_b} = \dfrac{AP}{AQ} = \dfrac{PP_b}{QQ_c}$.

$\blacksquare$

Ahora supongamos que las distancias a los lados del ángulo, desde $P$ y $Q$, son inversamente proporcionales.

Notemos que los cuadriláteros $\square AP_cPP_b$, $\square AQ_cQQ_b$ son cíclicos, por lo tanto, los pares de ángulos $\angle BAC$, $\angle P_bPP_c$ y $\angle BAC$, $\angle Q_bQQ_c$ son suplementarios, entonces $\angle P_bPP_c = \angle Q_bQQ_c$.

Por hipótesis tenemos que $PP_c \times QQ_c = PP_b \times QQ_b$
$\Rightarrow \dfrac{PP_c}{QQ_b} = \dfrac{PP_b}{QQ_c}$.

Por criterio de semejanza LAL, $\triangle PP_bP_c \sim \triangle QQ_cQ_b$,  y como$\square AP_cPP_b$, $\square AQ_cQQ_b$ son cíclicos, entonces
$\angle BAP = \angle P_cP_bP = \angle QQ_cQ_b = \angle QAC$.

Por lo tanto $AP$ y $AQ$ son isogonales.

$\blacksquare$

Puntos conjugados isogonales

Teorema 2. Si tres cevianas de un triángulo son concurrentes, entonces sus rectas isogonales respecto de los ángulos del triángulo son concurrentes, los puntos de concurrencia se llaman conjugados isogonales respecto al triángulo considerado.

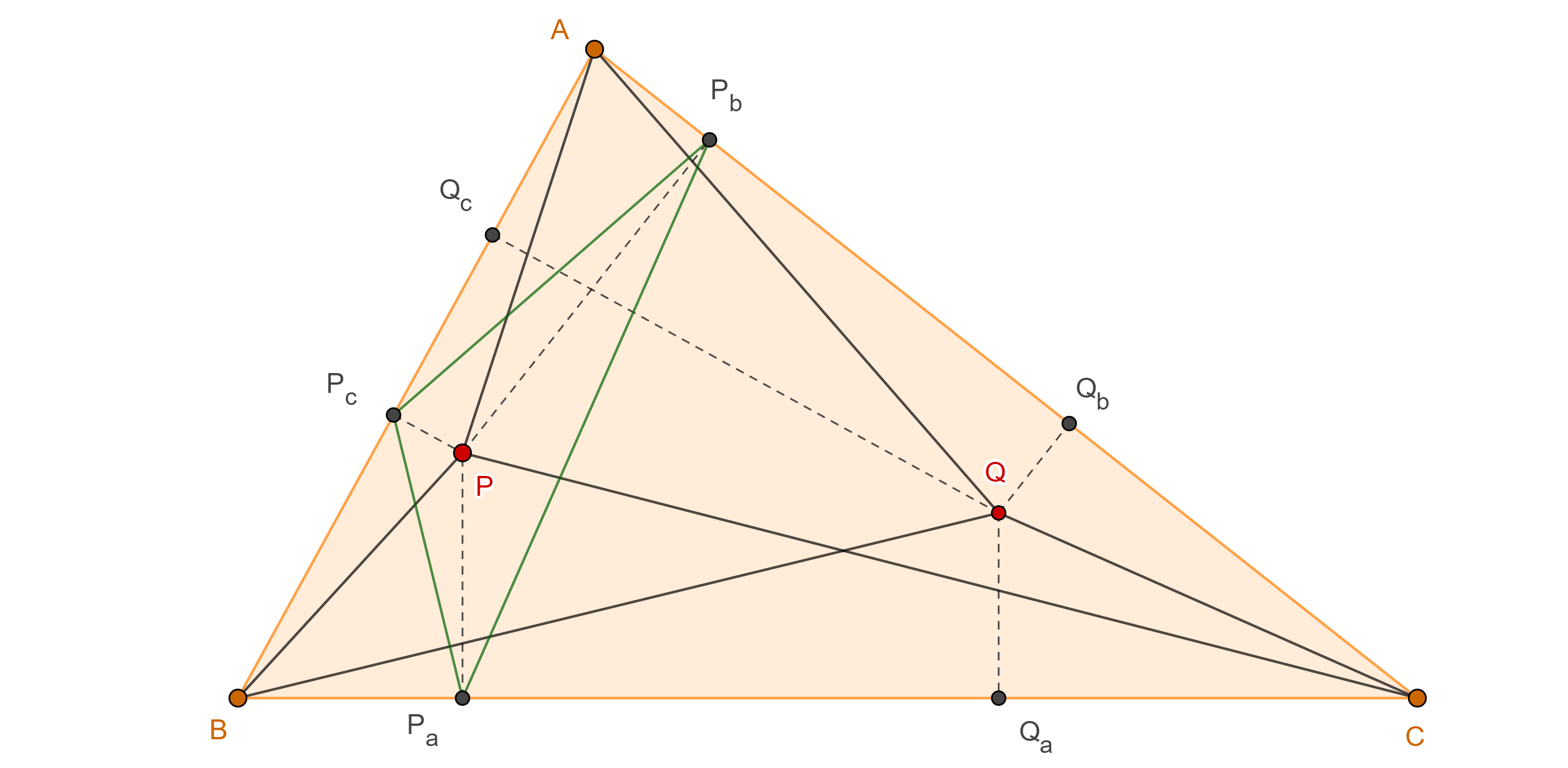
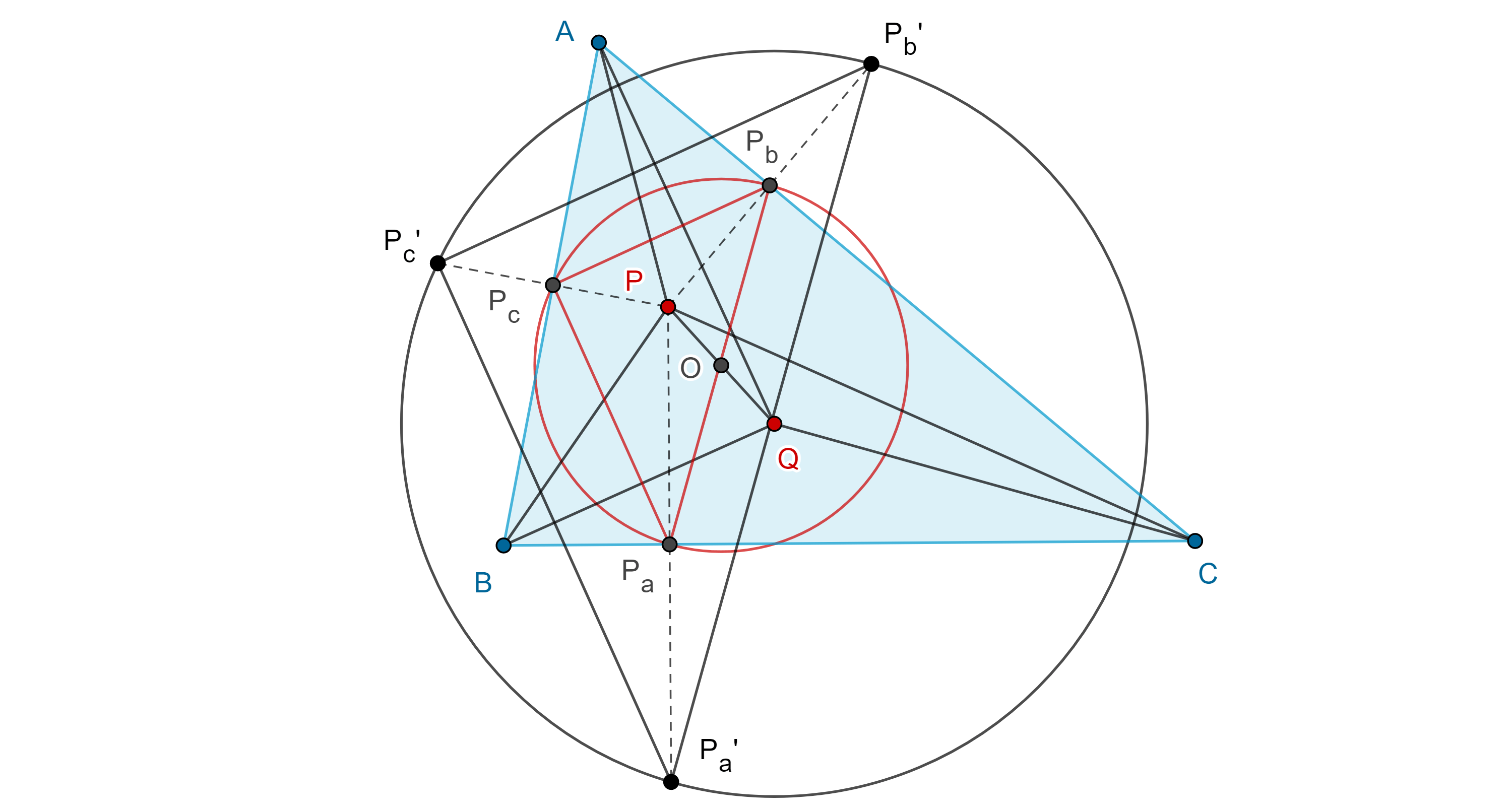
Si en $\triangle ABC$, $AP$, $BP$, $CP$ son tres cevianas concurrentes, consideremos $Q$ la intersección de las isogonales $BQ$, $CQ$ de $BP$ y $CP$ respectivamente, sean $P_a$, $P_b$, $P_c$; $Q_a$, $Q_b$, $Q_c$, las proyecciones de $P$ y $Q$ en $BC$, $CA$ y $AB$ respectivamente.

Figura 2

Por el teorema 1, $\dfrac{PP_a}{PP_c} = \dfrac{QQ_c}{QQ_a}$ y $\dfrac{PP_b}{PP_a} = \dfrac{QQ_a}{QQ_b}$.

Como resultado, $PP_c \times QQ_c = PP_a \times QQ_a = PP_b \times QQ_b$.

Por el teorema 1, $P$ y $Q$ están sobre rectas isogonales repecto de $\angle BAC$.

$\blacksquare$

Proposición 1. Dados un ángulo y un punto, la recta que une las proyecciones del punto a los lados del ángulo, es perpendicular a la isogonal a la recta que une el vértice del ángulo con el punto dado.

Demostración. En la entrada simediana probamos la misma proposición, pero para simedianas y medianas, la demostración permanece igual para el caso general.

$\blacksquare$

Corolario. Dados un triángulo $\triangle ABC$ y un punto $P$, las perpendiculares desde los vértices del triángulo a los lados del triángulo pedal de $P$ respecto de $\triangle ABC$, concurren en el conjugado isogonal de $P$ respecto de $\triangle ABC$.

Demostración. Aplicamos la proposición anterior a los tres ángulos del triángulo y recordamos que las tres isogonales a $AP$, $BP$ y $CP$ son concurrentes (figura 2).

$\blacksquare$

Proposición 2. El conjugado isogonal de un punto respecto a un triángulo es un punto al infinito si y solo si el punto se encuentra en el circuncírculo del triángulo.

Demostración. Sean $\triangle ABC$, y $P$ un punto, recordemos que el triángulo pedal de $P$ respecto de $\triangle ABC$ degenera en una recta, la recta de Simson, sí y solo si $P$ esta en el circuncírculo de $\triangle ABC$.

Figura 3

Por la proposición 1, las rectas isogonales a $AP$, $BP$, $CP$, respecto de los ángulos de $\triangle ABC$ son perpendiculares a los lados del triángulo pedal, por lo tanto estas rectas son paralelas si y solo si las proyecciones de $P$ en los lados de $\triangle ABC$ son colineales.

Ya que las rectas paralelas se intersecan en un punto ideal y las isogonales a $AP$, $BP$, $CP$ se intersecan en el conjugado isogonal a $P$, se tiene el resultado.

$\blacksquare$

Circulo pedal de conjugados isogonales

Proposición 3. Las proyecciones a los lados de un ángulo desde dos puntos en dos rectas isogonales son cíclicos y el centro de la circunferencia es el punto medio entre $P$ y $Q$.

Demostración. En la demostración del teorema 1, vimos que se tienen la siguientes semejanzas, $\triangle APP_c \sim \triangle AQQ_b$, $\triangle APP_b \sim \triangle AQQ_c$, es decir,
$\dfrac{AP_c}{AQ_b} = \dfrac{AP}{AQ} = \dfrac{AP_b}{AQ_c}$
$\Rightarrow AP_c \times AQ_c = AP_b \times AQ_b$.

Figura 4

Por el teorema de las cuerdas, $\square P_cQ_bP_bQ_c$ es un cuadrilátero cíclico.

Por otra parte, en $\triangle P_cQ_cP$, la mediatriz de $P_cQ_c$ es paralela a $P_cP$ y pasa por el punto medio de $P_cQ_c$, por lo tanto pasa por el punto medio de $PQ_c$.

En $\triangle PQ_cQ$ la mediatriz de $P_cQ_c$ es paralela a $Q_cQ$ y pasa por el punto medio de $PQ_c$ por lo tanto pasa por el punto medio de $PQ$.

Igualmente vemos que la mediatriz de $P_bQ_b$ pasa por el punto medio de $PQ$.

Como $P_cQ_c$ y $P_bQ_b$ son cuerdas de la circunferencia sus mediatrices se intersecan en el centro, por lo tanto este coincide con el punto medio de $PQ$.

$\blacksquare$

Teorema 3. Los triángulos pedales de dos puntos que son conjugados isogonales respecto a un triángulo tienen el mismo circuncírculo y su centro es el punto medio entre los puntos isogonales, esta circunferencia se conoce como circulo pedal de los puntos conjugados isogonales.

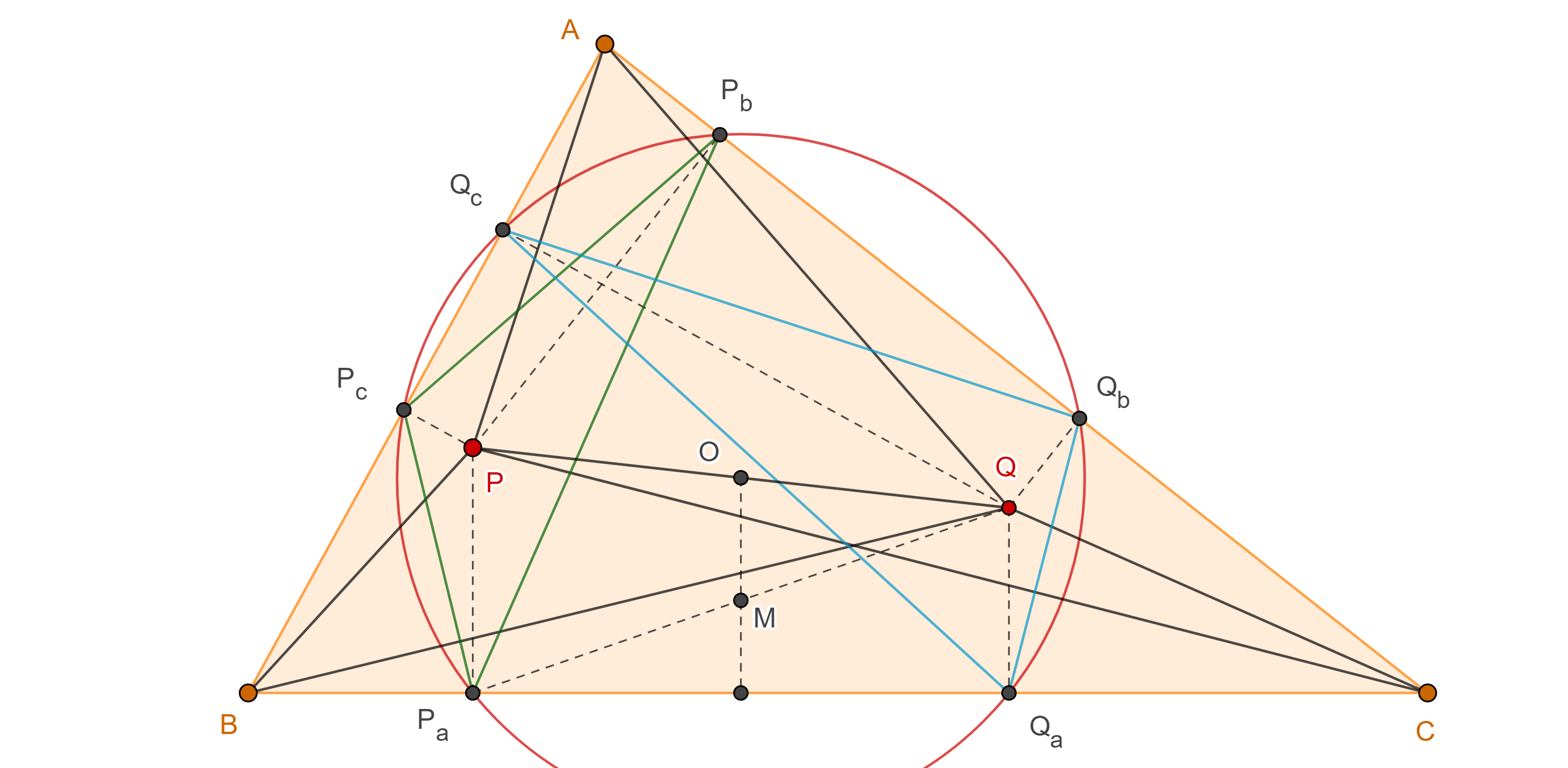
Demostración. Sean $O$ el punto medio de $PQ$ y $\triangle P_aP_bP_c$, $\triangle Q_aQ_bQ_c$, los triángulos pedales de $P$ y $Q$.

Por la proposición anterior, $\square Q_cP_CQ_bP_b$ es cíclico, con centro en $O$, $\square Q_cP_cP_aQ_a$ es cíclico con centro en $O$, $\square P_bP_aQ_aQ_b$ es cíclico con centro en $O$.

Figura 5

Como estas tres circunferencias son concéntricas y tienen el mismo radio, son la misma.

$\blacksquare$

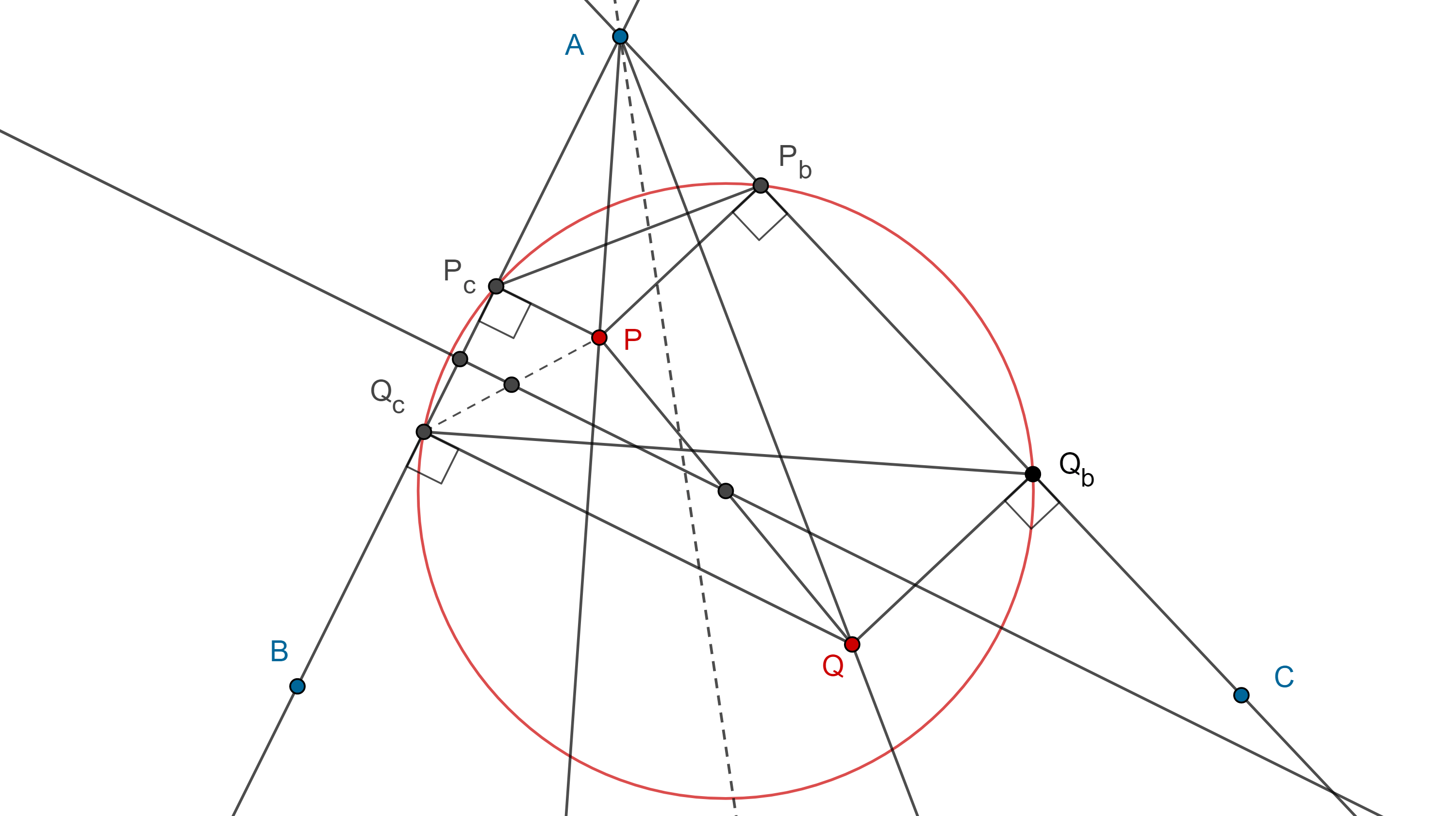
Teorema 4. Dado un triángulo $\triangle ABC$ y un punto $P$, el circuncírculo del triángulo pedal de $P$ respecto de $\triangle ABC$, corta a los lados de $\triangle ABC$ en los vértices del triángulo pedal del conjugado isogonal de $P$ respecto a $\triangle ABC$.

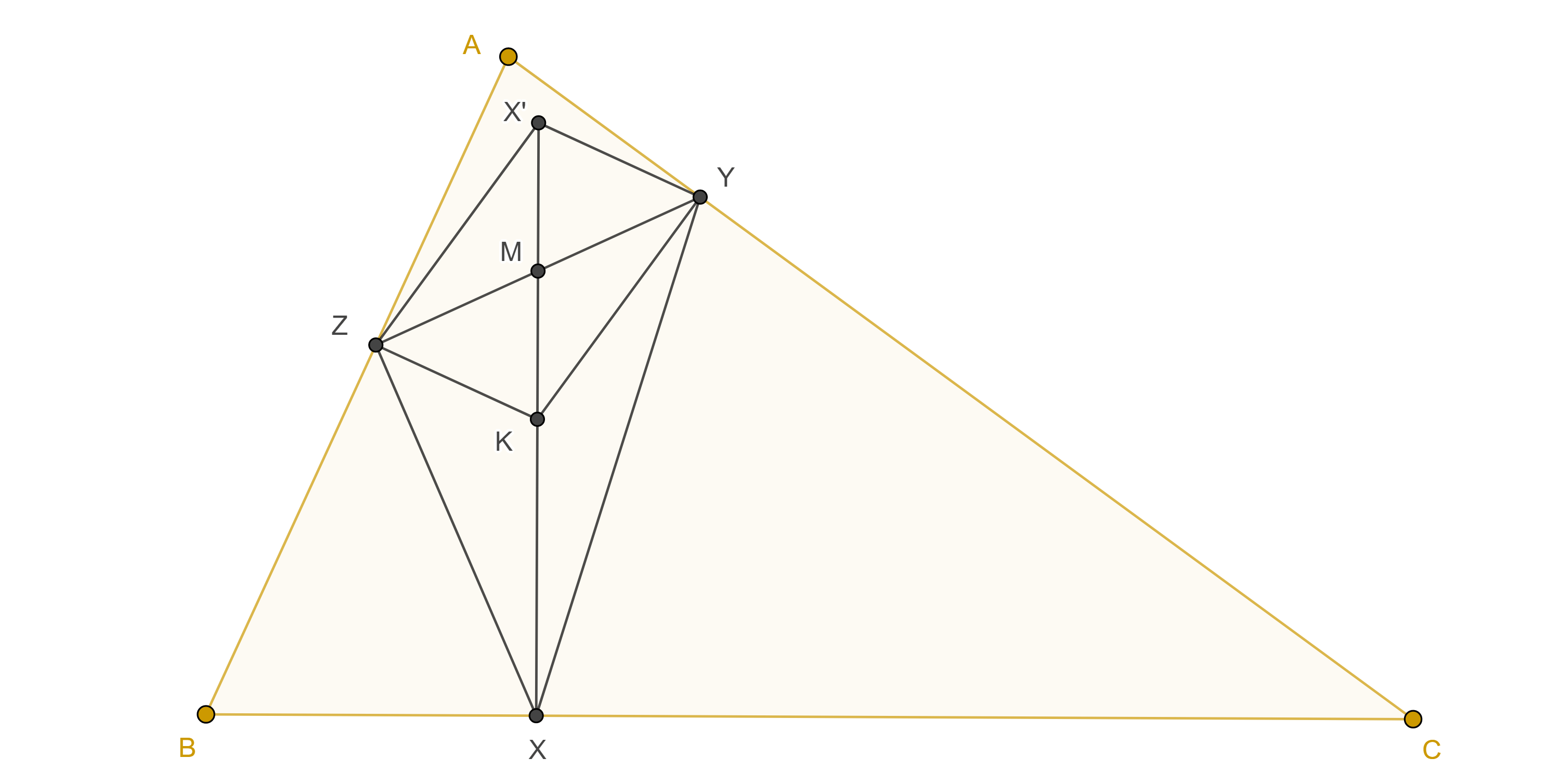
Demostración. Si $\triangle P_aP_bP_c$ es el triángulo pedal de $P$ (figura 5), sean $Q_a \in BC$, $Q_b \in CA$, $Q_c \in AB$, las otras tres intersecciones de $\Gamma(O)$, el circuncírculo de $\triangle P_aP_bP_c$ con $\triangle ABC$, consideremos $Q$ el conjugado isogonal de $P$ respecto $\triangle ABC$ y $OM \parallel PP_a$, con $M \in P_aQ$.

Como $OM \parallel PP_a$ y pasa por el punto medio de $PQ$ entonces $M$ es el punto medio de $P_aQ$.

Como $OM \perp P_aQ_a$ y pasa por $O$ entonces es la mediatriz de $P_aQ_a$ y por lo tanto biseca a $P_aQ_a$.

Ya que $OM$ biseca a $P_aQ_a$ y $P_aQ$ entonces $OM \parallel QQ_a$.

Por lo tanto, $QQ_a \perp BC$, igualmente vemos que $QQ_b \perp CA$, $QQ_c \perp AB$.

En consecuencia, $\triangle Q_aQ_bQ_c$ es el triángulo pedal de $Q$.

$\blacksquare$

Proposición 4. Dado un triángulo $\triangle ABC$ y un punto $P$, el centro del circuncírculo del triángulo cuyos vértices son las reflexiones de $P$ respecto de los lados de $\triangle ABC$, es el conjugado isogonal de $P$ respecto de $\triangle ABC$.

Demostración. Sean $P_a’$, $P_b’$, $P_c’$, las respectivas reflexiones de $P$ respecto de $BC$, $CA$ y $AB$, considera $\triangle P_aP_bP_c$ el triángulo pedal de $P$ respecto de $\triangle ABC$.

Figura 6

Por construcción, $P$ es el centro de homotecia entre $\triangle P_aP_bP_c$ y $\triangle P_a’P_b’P_c’$ con razón de homotecia $2$, por lo tanto, sus respectivos circuncírculos y sus circuncentros también están en homotecia con centro en $P$ y razón $2$.

En consecuencia, si $O$ es el circuncentro de $\triangle P_aP_bP_c$, entonces el circuncentro de $\triangle P_a’P_b’P_c’$ se encuentra en la reflexión $Q$, de $P$ respecto de $O$.

Por el teorema 3, $Q$ el conjugado isogonal de $P$ respecto de $\triangle ABC$.

$\blacksquare$

Triángulo antipedal

Definición 2. Dado un triángulo $\triangle ABC$ y un punto $P$, el triángulo $\triangle A’B’C’$ formado por las perpendiculares a $AP$, $BP$, $CP$, por los vértices de $\triangle ABC$ se llama triángulo antipedal de $P$ respecto de $\triangle ABC$

Notemos que $\triangle ABC$ es el triángulo pedal de $P$ respecto de $\triangle A’B’C’$.

Proposición 5. Sean $\triangle ABC$ y $P$ un punto, entonces el triángulo antipedal de $P$ respecto de $\triangle ABC$ y el triángulo pedal del conjugado isogonal de $P$ respecto de $\triangle ABC$ son homotéticos.

Figura 7

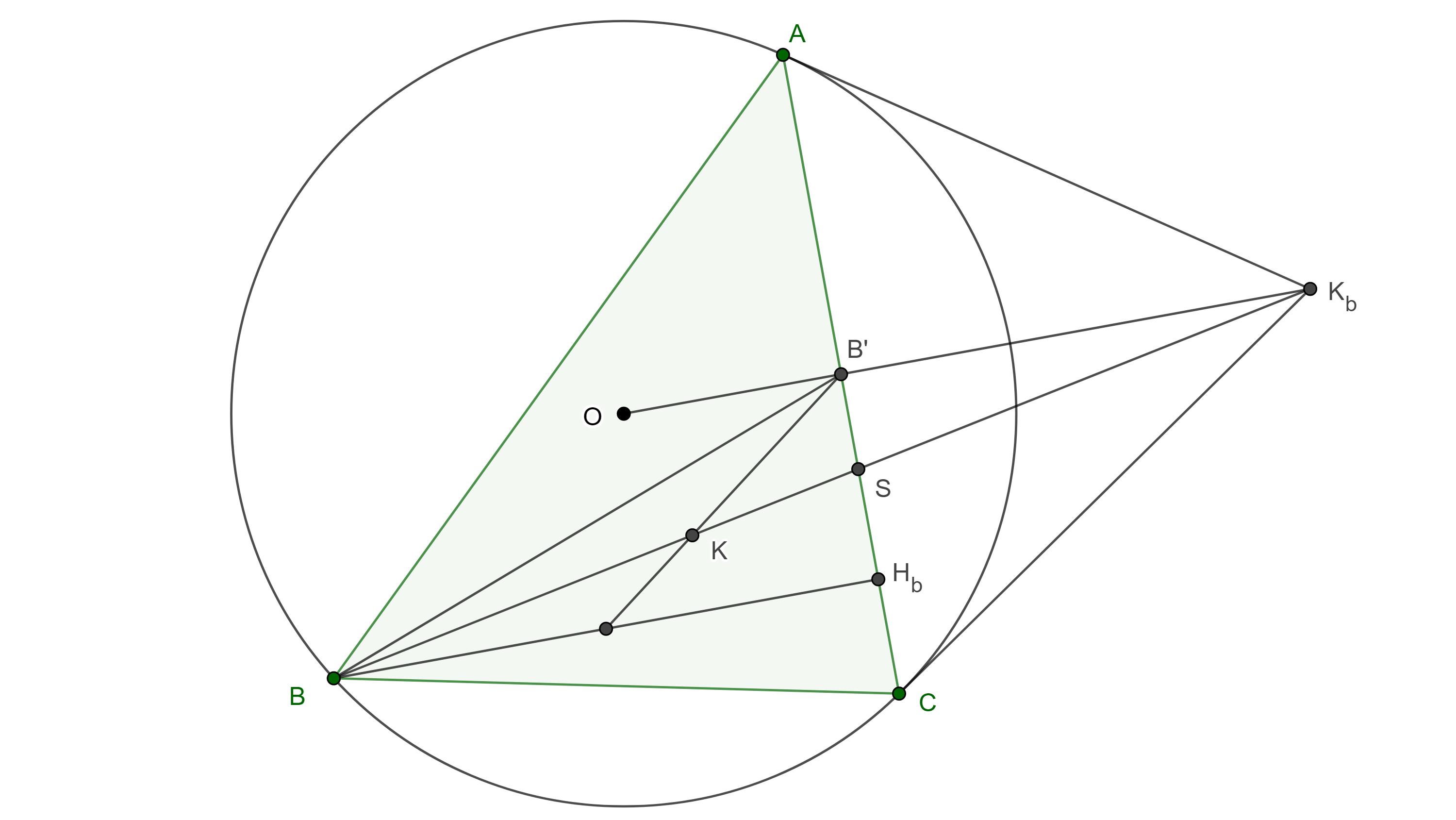
Demostración. Sea $Q$ el conjugado isogonal de $P$ respecto de $\triangle ABC$, consideremos $Q_a \in BC$, $Q_b \in CA$, $Q_c \in AB$, las proyecciones de $Q$ en lados de $\triangle ABC$.

Por la proposición 1, la isogonal $CP$, de $CQ$, es perpendicular a $Q_aQ_b$ entonces $A’B’ \parallel Q_aQ_b$ (figura 7).

Igualmente vemos que $B’C’ \parallel Q_bQ_c$ y $C’A’ \parallel Q_cQ_a$.

Por lo tanto, existe una homotecia entre $\triangle A’B’C’$ y $\triangle Q_aQ_bQ_c$.

$\blacksquare$

Área del triangulo pedal

Teorema 5, de Euler. Sean $\triangle ABC$ y $P$ un punto, considera $\triangle P_aP_bP_c$ el triángulo pedal de $P$ respecto de $\triangle ABC$ y $(O, R)$ el circuncírculo de $\triangle ABC$, entonces podemos calcular el área de $\triangle P_aP_bP_c$ mediante la siguiente formula:
$(\triangle P_aP_bP_c) = \dfrac{|R^2 – OP^2|}{4R^2} (\triangle ABC)$.

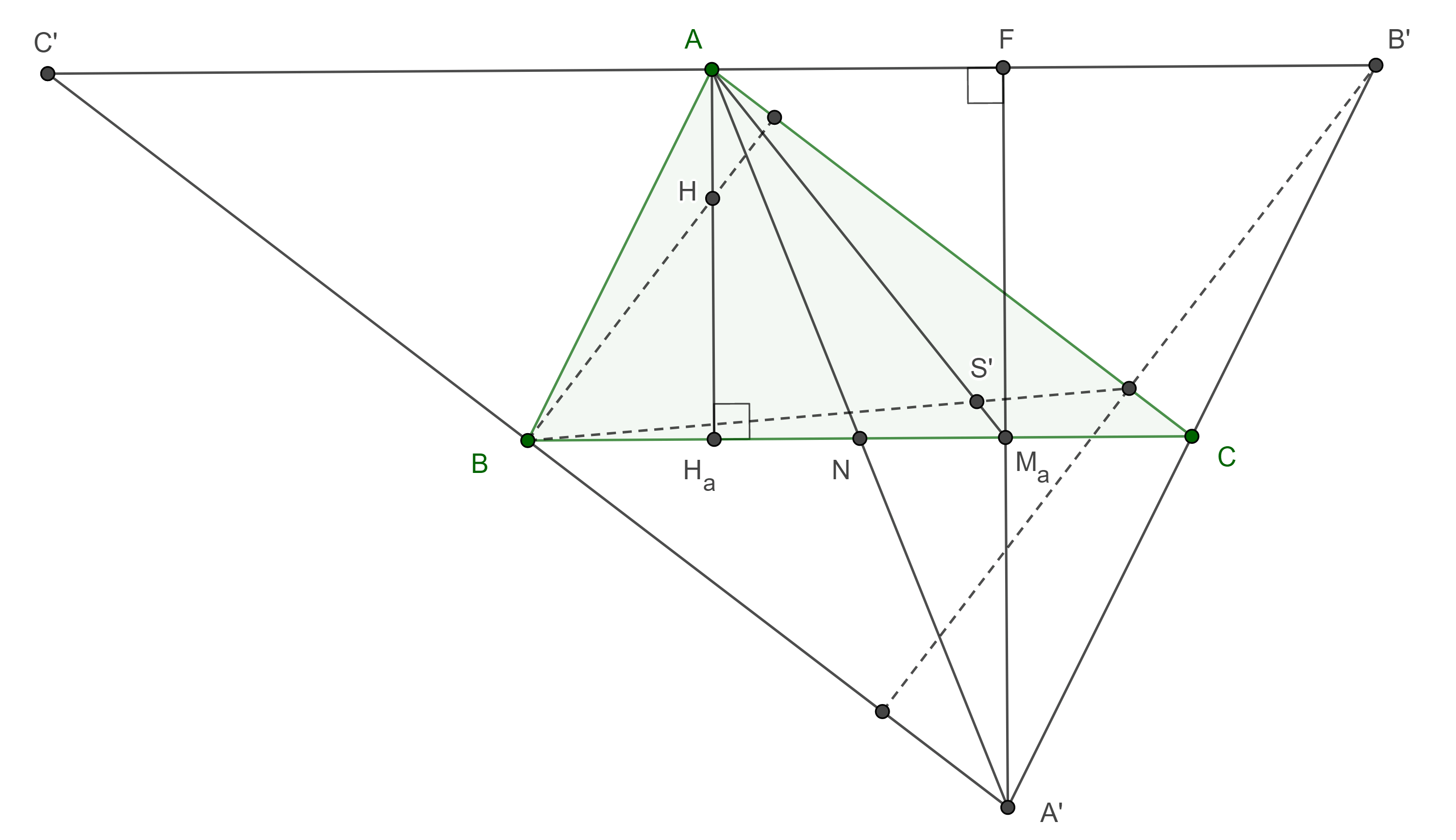
Demostración. Sean $D$, $E$, $F$ las segundas intersecciones de $AP$, $BP$, $CP$ con $(O, R)$, veamos que $\triangle P_aP_bP_c$ y $\triangle DEF$ son semejantes.

Figura 8

Tomando en cuenta que $\square PP_cP_bA$ y $\square PBP_aP_c$ son cíclicos tenemos:
$\angle DFE = \angle DFP + \angle PFE $
$= \angle DAC + \angle CBE = \angle PAP_b + \angle P_aBP $
$= (\pi – \angle P_bP_cP) + (\pi – \angle PP_cP_a)$
$ = 2\pi – \angle P_bP_cP_a = \angle P_aP_cP_b$.

De manera similar vemos que $\angle EDF = \angle P_bP_aP_c$ y $\angle FED = \angle P_cP_bP_a$, $\Rightarrow \triangle P_aP_bP_c \sim \triangle DEF$.

Al triángulo $\triangle DEF$ se le conoce como triángulo circunscrito de Ceva de $P$ respecto de $\triangle ABC$.

Recordemos que podemos calcular el área de un triángulo como el producto de sus lados entre cuatro veces su circunradio, si $R_p$ es el circunradio de $\triangle P_aP_bP_c$, entonces

$\begin{equation} \dfrac{(\triangle P_aP_bP_c)}{(\triangle ABC)} = \dfrac{P_aP_b}{AB} \times \dfrac{P_bP_c}{BC} \times \dfrac{P_cP_a}{CA} \times \dfrac{R}{R_p}. \end{equation}$

Con el fin de calcular la última ecuación, consideremos los siguientes argumentos.

Como $\triangle P_aP_bP_c \sim \triangle DEF$ entonces $\dfrac{R}{R_p} = \dfrac{DE}{P_aP_b}$.

Ya que $\square ABDE$ es cíclico, entonces $\triangle PAB \sim \triangle PED$, esto es
$\dfrac{PA}{PE} = \dfrac{AB}{ED}$.

También, como $\square PP_cP_bA$ y $\square PBP_aP_c$ $\square PP_aCP_b$ son cíclicos y aplicando la ley extendida de los senos tenemos,
$P_bP_c = PA \sin \angle A$ y $P_cP_a = PB \sin \angle B$.

Ahora, aplicamos la ley extendida de los senos en $\triangle ABC$,
$\dfrac{\sin \angle A}{BC} =\dfrac{1}{2R} = \dfrac{\sin \angle B}{AC}$.

Finalmente, la potencia de $P$ respecto de $(O, R)$ es $PB \times PE = |R^2 – OP^2|$.

Sustituyendo lo anterior en $(1)$ obtenemos:

$\dfrac{(\triangle P_aP_bP_c)}{(\triangle ABC)} = \dfrac{P_aP_b}{AB} \times \dfrac{PA \sin \angle A}{BC} \times \dfrac{PB \sin \angle B}{CA} \times \dfrac{DE}{P_aP_b}$
$= \dfrac{PE}{PA} \times \dfrac{PA \times PB}{(2R)(2R)}$
$= \dfrac{|R^2 – OP^2|}{4R^2}$.

$\blacksquare$

Más adelante…

En la siguiente entrada hablaremos sobre un par de puntos conjugados isogonales en particular, se trata de los puntos de Brocard, que tienen algunas propiedades especiales dentro de un triángulo.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Muestra que:
    $i)$ el ortocentro y el circuncentro de un triángulo son conjugados isogonales,
    $ii)$ el incentro y los excentros de un triángulo son sus propios conjugados isogonales.
  2.  Sea $P$ un punto dentro de un triangulo $\triangle ABC$, considera a $Q$ su conjugado isogonal, muestra que $\angle BPC + \angle BQC = \pi + \angle BAC$.
  3. Sean $P$ y $Q$ puntos conjugados isogonales respecto a un triangulo $\triangle ABC$, prueba que $\dfrac{AP \times AQ}{AB \times AC} + \dfrac{BP \times BQ}{BA \times BC} + \dfrac{CP \times CQ}{CA \times CB} = 1$.
  4. Sean $\triangle ABC$ y $P$ un punto en su interior, considera $\triangle P_aP_bP_c$ el triángulo pedal de $P$ respecto $\triangle ABC$, supón que $P_aP_b \perp P_aP_c$, muestra que el conjugado isogonal de $P$ respecto de $\triangle ABC$ es el ortocentro de $\triangle AP_bP_c$.
  5. En la figura 7, muestra que el producto de los triángulos homotéticos es igual al cuadrado del área de $\triangle ABC$.

Entradas relacionadas

Fuentes

  • Altshiller, N., College Geometry. New York: Dover, 2007, pp 267-273.
  • Andreescu, T., Korsky, S. y Pohoata, C., Lemmas in Olympiad Geometry. USA: XYZ Press, 2016, pp 95-108.
  • Lozanovski, S., A Beautiful Journey Through Olympiad Geometry. Version 1.4. 2020, pp 169-176.
  • Johnson, R., Advanced Euclidean Geometry. New York: Dover, 2007, pp 153-157.

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Geometría Moderna I: Punto simediano

Por Rubén Alexander Ocampo Arellano

2 respuestas

Introducción

El punto simediano es el punto en el que concurren las simedianas de un triángulo, es otro punto notable del triángulo, en esta entrada veremos algunas de sus propiedades.

Punto simediano

Teorema 1. Las tres simedianas de un triángulo son concurrentes, al punto de concurrencia se le conoce como punto simediano o punto de Lemoine a menudo denotado con la letra $K$.

Demostración. En la entrada teorema de Menelao mostramos que un triángulo $\triangle ABC$ y su triangulo tangencial $\triangle K_aK_bK_c$, están en perspectiva desde una recta, conocida como eje de Lemoine.

Por el teorema de Desargues, $\triangle ABC$ y $\triangle K_aK_bK_c$ están en perspectiva desde un punto, es decir, $AK_a$, $BK_b$ y $CK_c$ concurren en un punto $K$.

Figura 1

Por el teorema 2 de la entrada anterior, dos exsimedianas (los lados del triángulo tangencial $\triangle K_aK_bK_c$) y una simediana, que pasan por vértices distintos de $\triangle ABC$ concurren en un punto exsimediano, es decir, $AK_a$, $BK_b$, $CK_c$ son las simedianas de $\triangle ABC$.

$\blacksquare$

Observación. Como el eje de Lemoine de $\triangle ABC$ es el eje de Gergonne de $\triangle K_aK_bK_c$, entonces el punto de Lemoine de $\triangle ABC$ es el punto de Gergonne de $\triangle K_aK_bK_c$, su triángulo tangencial.

Corolario 1. Sea $S = AK \cap BC$ entonces $AKSK_a$ es una hilera armónica de puntos.

Demostración. Por el corolario de la entrada anterior $B(AK_bCK_a)$ es un haz armónico de rectas y como $AD$ es transversal entonces sus intersecciones con el haz forman una hilera armónica.

$\blacksquare$

Triángulo pedal del punto simediano

Definición. Dados un triángulo $\triangle ABC$ y un punto $P$, el triángulo pedal de $P$ respecto de $\triangle ABC$, es aquel cuyos vértices son las proyecciones de $P$ en los lados de $\triangle ABC$. Por ejemplo, el triángulo órtico es el triángulo pedal del ortocentro.

Teorema 2, de Lemoine. El punto simediano es el único punto del plano que es el centroide de su propio triángulo pedal.

Demostración. Sean $\triangle ABC$ y $K$ su punto simediano, considera $X$, $Y$ y $Z$ las proyecciones de $K$ en $BC$, $CA$ y $AB$ respectivamente, sea $X’ \in KX$ tal que $YX’ \parallel KZ$.

Figura 2

Entonces $\triangle ABC \sim \triangle YX’K$, pues sus respectivos lados son perpendiculares, esto es
$\dfrac{AB}{AC} = \dfrac{YX’}{YK}$.

Pero $\dfrac{AB}{AC} = \dfrac{KZ}{KY}$ pues $K$ esta en la $A$-simediana, por lo tanto $KZ = YX’$.

En consecuencia, $\square X’ZKY$ es un paralelogramo y por lo tanto $KX’$ biseca a $YZ$.

Como resultado tenemos que $XK$ es mediana de $\triangle XYZ$.

De manera análoga vemos que $YK$, $ZK$ son medianas de $\triangle XYZ$, por lo tanto, $K$ es el centroide de su triangulo pedal.

$\blacksquare$

Recíprocamente, supongamos que $K$ es el centroide de su triángulo pedal $\triangle XYZ$ respecto a $\triangle ABC$, con $X \in BC$, $Y \in CA$, $Z \in AB$, sea $M$ el punto medio de $YZ$, extendemos $KM$ hasta un punto $X’$ tal que $KM = MX’$.

Como $YZ$ y $KX’$ se bisecan entonces $\square X’ZKY$ es un paralelogramo, entonces $YX’ = KZ$ y $YX’ \parallel KZ$.

Ya que los lados de $\triangle YX’K$ son perpendiculares a los lados de $\triangle ABC$, entonces son semejantes, esto es
$\dfrac{AB}{AC} = \dfrac{YX’}{YK} = \dfrac{KZ}{KY}$.

Por lo tanto, $K$ está en la $A$-simediana, igualmente vemos que $K$ pertenece a las $B$ y $C$-simedianas.

En consecuencia, $K$ es el punto simediano de $\triangle ABC$.

$\blacksquare$

Conjugado isotómico del punto simediano

Teorema 3. Las rectas que unen el punto medio del lado de un triángulo con el punto medio de la altura perpendicular a ese lado concurren en el punto simediano del triángulo.

Demostración. Sean $\triangle ABC$, $K$ el punto simediano, $K_b$ el punto exsimediano opuesto al vértice $B$, $S = BK_b  \cap CA$.

Figura 3

Por el corolario 1, $BKSK_b$ es una hilera armónica, por lo tanto, $B’(BKSK_b)$ es un haz armónico, donde $B’$ es el punto medio de $CA$.

Considera $O$ el circuncentro de $\triangle ABC$ y $H_b$ el pie de la altura por $B$, notemos que $O$, $B’$ y $K_b$ son colineales, por lo tanto, $B’K_b$ es perpendicular a $CA$ y así $BH_b \parallel B’K_b$.

Como $BH_b$ es paralela a una de las rectas del haz armónico, entonces las otras tres rectas del haz dividen a $BH_b$ en dos segmentos iguales, es decir $B’K$ biseca a $BH_b$.

Igualmente vemos que $A’K$ y $C’K$ bisecan a $AH_a$ y $CH_c$ respectivamente, y de esto concluimos la concurrencia de las rectas mencionadas.

$\blacksquare$

Proposición 1. El ortocentro de un triángulo y el punto simediano de su triángulo anticomplementario son conjugados isotómicos respecto del triángulo original.

Demostración. Sean $\triangle ABC$ y $\triangle A’B’C’$ su triángulo anticomplementario.

Como $AB$ y $AC$ son segmentos medios de $\triangle A’B’C’$, entonces $\square ABA’C$ es un paralelogramo, por lo tanto, $\triangle ABC$ y $\triangle A’CB$ son congruentes, además $AA’$ y $BC$ se intersecan en su punto medio $N$.

Figura 4

Sean $H_a$, $M_a$ los pies de las alturas desde $A$ y $A’$ respectivamente en $BC$, como $\triangle ABC \cong \triangle A’CB$, entonces $AH_a = M_aA’$.

Por criterio de congruencia ALA, $\triangle AH_aN \cong \triangle A’M_aN$, por lo que $H_aN = NM_a$, es decir, el punto medio de $H_a$ y $M_a$ coincide con el punto medio de $BC$,

Por lo tanto, $H_a$ y $M_a$ son puntos isotómicos respecto de $\triangle ABC$.

Sea $F$ el pie de la altura por $A’$ en $\triangle A’B’C’$, como $\square AH_aM_aF$ es un rectángulo entonces $M_aA’ = AH_a = FM_a$, y así $M_a$ es el punto medio de la altura $A’F$.

Por lo tanto, el segmento $AM_a$ une los puntos medios de un lado y una altura de $\triangle A’B’C’$.

De manera análoga vemos que los pies de las alturas en $\triangle ABC$, $H_b$, $H_c$ son isotómicos a los puntos medios de las alturas en $\triangle A’B’C’$, $M_b$, $M_c$, respectivamente.

Como las alturas de $\triangle ABC$ concurren en el ortocentro $H$ y, por el teorema 3, los segmentos $AM_a$, $BM_b$, $CM_c$ concurren en el punto simediano $S’$ de $\triangle A’B’C’$, entonces estos puntos son conjugados isotómicos respecto de $\triangle ABC$.

$\blacksquare$

Construcción de un triángulo dado su punto simediano

Problema. Construye un triángulo dados dos vértices $B$, $C$, y su punto simediano $K$.

Solución. Supongamos que $\triangle ABC$ es el triángulo requerido y consideremos $G$ y $A’$ el centroide y el punto medio de $BC$ respectivamente.

Sean $B’$, $C’ \in BC$, tales que $B’A \parallel BG$ y $AC’ \parallel GC$.

Figura 5

Por el teorema de Tales tenemos
$\dfrac{1}{2} = \dfrac{A’G}{GA} = \dfrac{A’B}{BB’} = \dfrac{A’C}{CC’}$.

Por lo tanto, $BB’ = CC’ = 2A’B = BC$, así que $B’$ y $C’$ pueden ser construidos teniendo $B$ y $C$.

Por otro lado, como $B’A \parallel BG$ y $AC’ \parallel GC$ y tomando en cuenta que $K$ esta en las reflexiones de $BG$ y $CG$ respecto de las bisectrices de $\angle B$ y $\angle C$ respectivamente, tenemos lo siguiente:

$\angle B’AB = \angle GBA = \angle KBC$ y $\angle CAC’ = \angle ACG = \angle KCB$.

Y estos ángulos son conocidos.

Entonces $B’B$ y $CC’$ subtienden ángulos conocidos en $A$, por lo que podemos trazar los arcos de circunferencia que son el lugar geométrico de los puntos que subtienden estos ángulos.

Así que de la intersección de estos dos arcos resultara en el vértice faltante.

Notemos que los arcos pueden tener dos intersecciones, ser tangentes o no intersecarse, por lo tanto, existen dos, una o cero soluciones.

$\blacksquare$

Distancia del punto simediano a los lados del triángulo

Proposición 2. El punto simediano de un triángulo es el único punto dentro del triángulo cuyas distancias a los lados del triángulo son proporcionales a los respectivos lados.

Demostración. Sean $\triangle ABC$ y $K$ su punto simediano, considera $X$, $Y$ y $Z$ las proyecciones de $K$ en $BC$, $CA$ y $AB$ respectivamente, denotemos $BC = a$, $CA = b$, $AB = c$.

Figura 6

Dado que $K$ está en las tres simedianas del triángulo, por el teorema 4 de la entrada anterior, las razones de sus distancias a los lados del triángulo son proporcionales a estos:

$\begin{equation} \dfrac{KZ}{KY} = \dfrac{c}{b}, \end{equation}$
$\begin{equation} \dfrac{KY}{KX} = \dfrac{b}{a}, \end{equation}$
$ \begin{equation} \dfrac{KX}{KZ} = \dfrac{a}{c}. \end{equation}$

Por $(1)$, $(2)$ y $(3)$
$\dfrac{KX}{a} = \dfrac{KY}{b} = \dfrac{KZ}{c} = q$.

Por lo tanto,
$KZ = \dfrac{cKY}{b} = cq$,
$KY = \dfrac{b KX}{a} = bq$,
$KX = \dfrac{a KZ}{c} = aq$.

La unicidad se da por que solo los puntos en las simedianas cumplen esa propiedad y solo $K$ se encuentra en las tres simedianas.

$\blacksquare$

Corolario. 2 $KX = a \dfrac{2(ABC)}{a^2 + b^2 + c^2}$.

Demostración. Calculamos el área de $\triangle ABC$ en función de áreas menores (figura 6).

$(\triangle ABC) = (\triangle KBC) + (\triangle KCA) + (\triangle KAB) $
$= \dfrac{1}{2}(aKX + bKY + cKZ)$
$= \dfrac{q}{2}(a^2 + b^2 + c^2)$.

Por lo tanto, $KX = aq = a \dfrac{2(ABC)}{a^2 + b^2 + c^2}$.

$\blacksquare$

Teorema 4. La suma de los cuadrados de las distancias de un punto a los lados de un triángulo dado, es mínima si el punto es el punto simediano del triángulo.

Demostración. Sean $a$, $b$, $c$, $x$, $y$, $z$ seis números reales entonces la siguiente igualdad es cierta:

 $(a^2 + b^2 + c^2)(x^2 + y^2 + z^2) = (ax + by + cz)^2 + (ay – bx)^2 + (az – cx)^2 + (bz – cy)^2$.

Para comprobarlo solo hace falta realizar los productos.

Podemos pensar estas cantidades como los lados de un triángulo $\triangle ABC$, $BC = a$, $CA = b$, $AB = c$, y $x$, $y$, $z$, las distancias de un punto $K$, a los lados de $\triangle ABC$.

Notemos $ax + by + cz$ representa al menos dos veces el área del triángulo $\triangle ABC$, $2(\triangle ABC)$, que junto con $(a^2 + b^2 + c^2)$ son constantes.

Como las cantidades $(ay – bx)^2$, $(az – cx)^2$, $(bz – cy)^2$ son mayores o iguales a cero, entonces el mínimo se alcanza si se satisfacen las siguientes igualdades:
$\begin{equation} (ay – bx)^2 = (az – cx)^2 = (bz – cy)^2 = 0, \end{equation}$
$\begin{equation} ax + by + cz = 2(\triangle ABC). \end{equation}$

Por otra parte, por las ecuaciones $(1)$, $(2)$ y $(3)$ sabemos que el punto simediano cumple $(4)$ y por el corolario 2 cumple $(5)$, también podemos calcular directamente,

$KX^2 + KY^2 + KZ^2 = \dfrac{(2(\triangle ABC))^2}{a^2 + b^2 + c^2}$.

Por lo tanto, si $K$ es el punto simediano de $\triangle ABC$, se alcanza el mínimo.

$\blacksquare$

Más adelante…

En la próxima entrada veremos otra propiedad del punto simediano, o punto de Lemoine, que amerita su propia entrada, se trata de un conjunto de circunferencias asociadas a este punto.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Si $K$ es el punto simediano de $\triangle ABC$, sea $X$ la proyección de $K$ en $BC$, muestra que la reflexión de $X$ respecto de $K$ esta en la mediana que pasa por $A$.
  2.  Encuentra el punto simediano de un triángulo rectángulo.
  3. Sobre los lados de un triángulo $\triangle ABC$ construye cuadrados externamente, muestra que los lados (de los cuadrados) opuestos a los lados de $\triangle ABC$ se intersecan formando un triángulo homotético a $\triangle ABC$, con centro de homotecia el punto simediano de $\triangle ABC$.
  4. Si las simedianas de $\triangle ABC$ intersecan a su circuncírculo en $D$, $E$ y $F$ muestra que $\triangle ABC$ y $\triangle DEF$ tienen el mismo punto simediano.
  5. $i)$ Muestra que las distancias a los lados de un triángulo desde sus puntos exsimedianos son proporcionales a las longitudes de los lados del triángulo,
    $ii)$ calcula dichas distancias.
  6. Prueba que de entre todos los triángulos inscritos en un triángulo dado, el triángulo pedal del punto simediano, es el que tiene la propiedad de que la suma de los cuadrados de sus lados es mínima.

Entradas relacionadas

Fuentes

  • Altshiller, N., College Geometry. New York: Dover, 2007, pp 252-257.
  • Andreescu, T., Korsky, S. y Pohoata, C., Lemmas in Olympiad Geometry. USA: XYZ Press, 2016, pp 129-145.
  • Johnson, R., Advanced Euclidean Geometry. New York: Dover, 2007, pp 215-218.

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»