Introducción
Ya que hemos visto el concepto de función, en esta entrada veremos cómo están definidas las operaciones de suma, producto y cociente. De igual modo, definiremos la composición entre un par de funciones. Para dejar más claras dichas operaciones, daremos ejemplos.
Operaciones de funciones
Definición (operaciones): Sean $f: D_{f}\subseteq \r \rightarrow \r$, $\quad g: D_{g}\subseteq \r \rightarrow \r$. Definimos las siguientes operaciones como:
- $f+g: D_{f} \cap D_{g} \subseteq \r \rightarrow \r$
$$(f+g)(x)= f(x)+g(x)\quad \text{.}$$ - $\alpha f: D_{f}\subseteq \r \rightarrow \r \quad$ y $\quad \alpha \in \r$
$$(\alpha f)(x)= \alpha f(x)\quad \text{.}$$ - $fg: D_{f} \cap D_{g} \subseteq \r \rightarrow \r$
$$(fg)(x)= f(x)g(x)\quad \text{.}$$ - $\begin{multline*} \frac{f}{g}: D_{f/g} \subseteq \r \rightarrow \r \end{multline*}$
\begin{equation*}
\left(\frac{f}{g}\right)(x)=\frac{f(x)}{g(x)}\quad \text{.}
\end{equation*}
donde $D_{f/g}=D_{f} \cap (D_{g} – \left\{x \in D_{g}: g(x)=0 \right\})$
Notación: Cuando escribamos $f-g$ hacemos referencia a:
$$f-g=f+ (-g) \quad \text{.}$$
Ejemplos
Consideremos a las siguientes funciones:
\begin{align*}
f: \r – \left\{-1\right\} &\rightarrow \r & g: \r &\rightarrow \r & h: \r &\rightarrow \r^{+}
\end{align*}
\begin{align*}
f(x)&= \frac{1}{x+1}& g(x)&= x^{3}+3 & h(x)&=x^{2}+2x+1
\end{align*}
Notación: Usamos $\r^{+}$ para referirnos al conjunto de los números reales positivos.
Realizaremos las siguientes operaciones para ejemplificar lo visto anteriormente:
- $$(f+g)(x)= f(x)+g(x)= \frac{1}{x+1} + x^{3}+3$$
con $D_{f+g}=D_{f} \cap D_{g}= \r \cap (\r- \left\{-1\right\})= \r- \left\{-1\right\}$ - $$(fg)(x)= f(x)g(x)=\left(\frac{1}{x+1}\right)(x^{3}+3)=\frac{x^{3}+3}{x+1}$$
con $D_{fg}=D_{f} \cap D_{g}= \r \cap (\r- \left\{-1\right\})= \r- \left\{-1\right\}$ - Si $\alpha = – 4$:
$$(\alpha g)(x)= \alpha g(x)= -4(x^{3}+3)=-4x^{3}-12$$
con $D_{\alpha g}= D_{g}= \r$ - $$\left(\frac{g}{h}\right)(x)=\frac{g(x)}{h(x)}=\frac{x^{3}+3}{x^{2}+2x+1}$$
como $D_{g/h}=D_{g} \cap (D_{h} – \left\{x \in D_{h}: h(x)=0 \right\})$
Observemos que $x^{2}+2x+1 = (x+1)^{2}$ por lo que $(x+1)^{2}=0$ cuando $x=-1$.
Así el dominio sería:
$$D_{g/h}=\r \cap (\r- \left\{-1 \right\})= \r – \left\{-1\right\}$$ - $$(h-g)(x)=h(x)-g(x)=x^{2}+2x+1-(x^{3}+3)=x^{2}+2x+1-x^{3}-3$$
con $D_{h-g}= D_{h} \cap D_{g}= \r \cap \r= \r$
Composición de funciones
Definición (composición): Consideremos a las funciones $g: A \rightarrow B$ y $f: B \rightarrow C$ definimos a la composición de $g$ seguida de $f$ como:
$$f \circ g: A \rightarrow C$$
$$(f \circ g)(x)= f(g(x)),$$
observamos que la composición sólo está definida si $Im_g \subseteq D_f$, por lo que $g(x) \in B$.
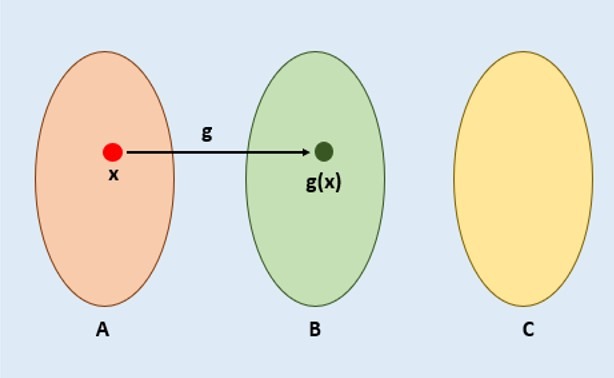
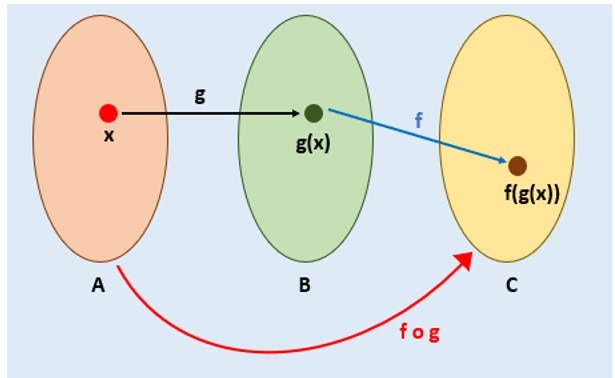
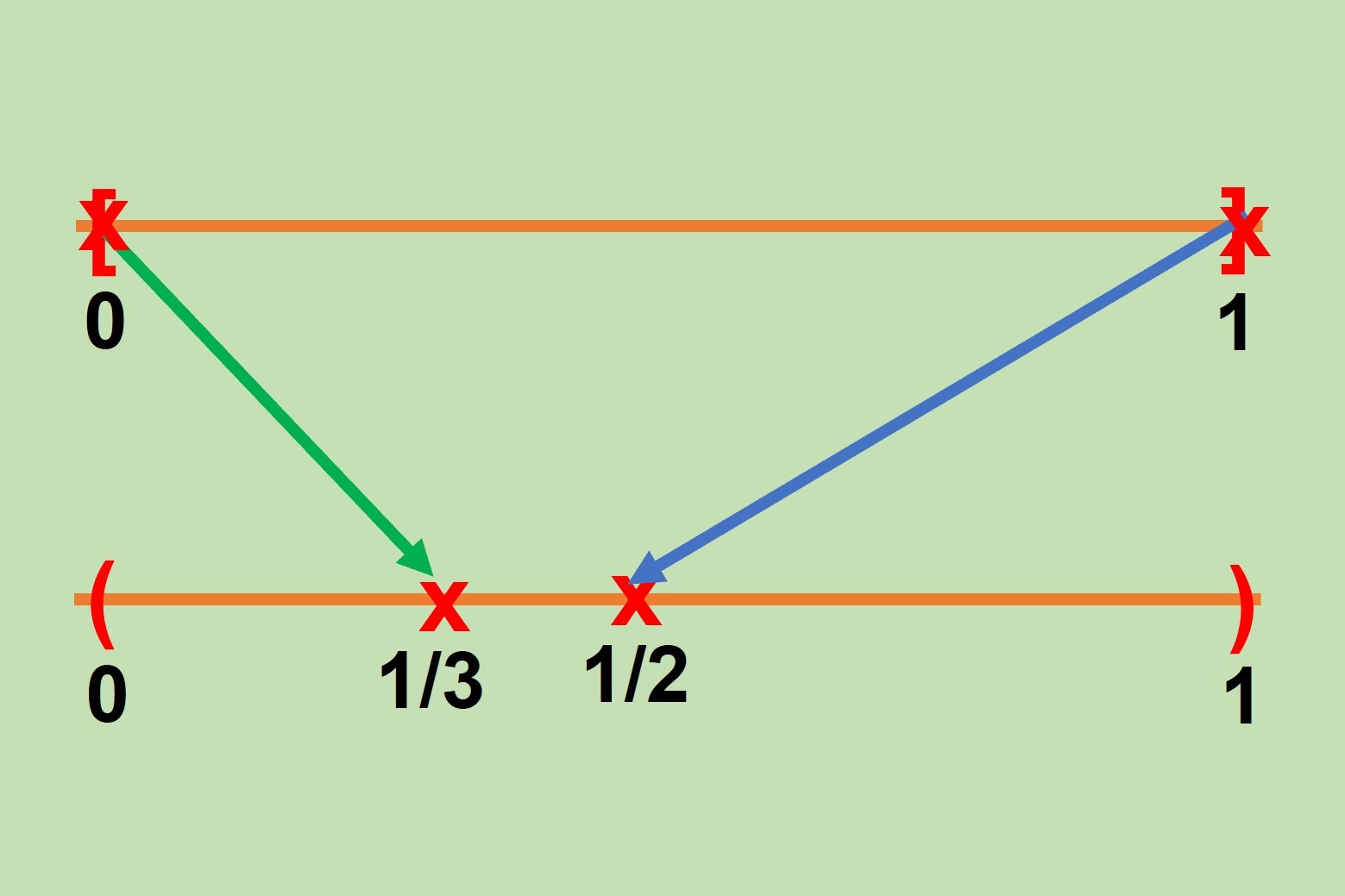
En el siguiente diagrama podemos ver más claramente cómo funciona la composición $f \circ g$:
Primero tomamos $x \in A$ a la cual le aplicamos la función $g$ para así obtener $g(x) \in B$.
Ahora tomamos a $g(x) \in B$ para aplicarle la función $f$ y finalmente obtener $f(g(x)) \in C$.
Así la composición de $f \circ g$ se vería como en el diagrama anterior.
Observación: La composición no es conmutativa, es decir, ocurre que:
$$f \circ g \neq g \circ f\quad \text{.}$$
Ejemplos
Retomando las funciones:
\begin{align*}
f(x)&= \frac{1}{x+1}& g(x)&= x^{3}+3 & h(x)&=x^{2}+2x+1
\end{align*}
Realicemos las siguientes composiciones de funciones para tener más claro cómo funciona lo antes explicado:
- Ejemplo 1:
\begin{align*}
(g \circ f)(x)&= g(f(x))\\
&= g\left(\frac{1}{x+1} \right)\\
&= \left( \frac{1}{x+1} \right)^{3} +3\\
&= \frac{1}{(x+1)^{3}}+3
\end{align*}
Así tenemos que la composición obtenida es:
\begin{equation*}
(g \circ f)(x)=\frac{1}{(x+1)^{3}}+3
\end{equation*} - Ejemplo 2:
\begin{align*}
(f \circ h)(x)&= f(h(x))\\
&= f((x^{2}+2x+1))\\
&= \frac{1}{(x^{2}+2x+1)+1}\\
&=\frac{1}{x^{2}+2x+2}
\end{align*}
Por lo que la composición quedaría como:
\begin{equation*}
(f \circ h)(x) = \frac{1}{x^{2}+2x+2}
\end{equation*}
Más adelante
Ahora que ya hemos definido las operaciones entre funciones y la composición, en la siguiente entrada veremos qué características debe cumplir una función para poder determinar si es inyectiva, sobreyectiva o biyectiva. Del mismo modo, examinaremos el concepto de función inversa, donde haremos uso de la composición de funciones y algunas condiciones.
Tarea moral
- Si tenemos a las funciones $f : \r \rightarrow \r$ y $g : \r \rightarrow \r^{+}$ definidas como siguen:
$$ f(x) = x-8$$
$$g(x)= x^{4}$$
Realiza las siguientes operaciones:- $f + g$
- $f – g$
- $fg$
- $\frac{g}{f}$
- $g \circ f$
- Da una función $f$ y una función $g$ que ejemplifiquen que la composición no es conmutativa:
$$f \circ g \neq g \circ f\quad \text{.}$$ - Demuestra que la composición es asociativa, es decir,
$$f\circ (g \circ h)= (f\circ g) \circ h\quad \text{.}$$
Entradas relacionadas
- Ir a: Cálculo Diferencial e Integral I
- Entrada anterior del curso: Cálculo Diferencial e Integral I: Concepto de función
- Entrada siguiente del curso: Cálculo Diferencial e Integral I: Funciones inyectivas, sobreyectivas y biyectivas. Función inversa.
- Resto de cursos: Cursos
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»