Archivo de la etiqueta: álgebra

1.4. SUBESPACIO: definición y ejemplos

Por Jennyfer Paulina Bennetts Castillo

Deja un comentario

INTRODUCCIÓN

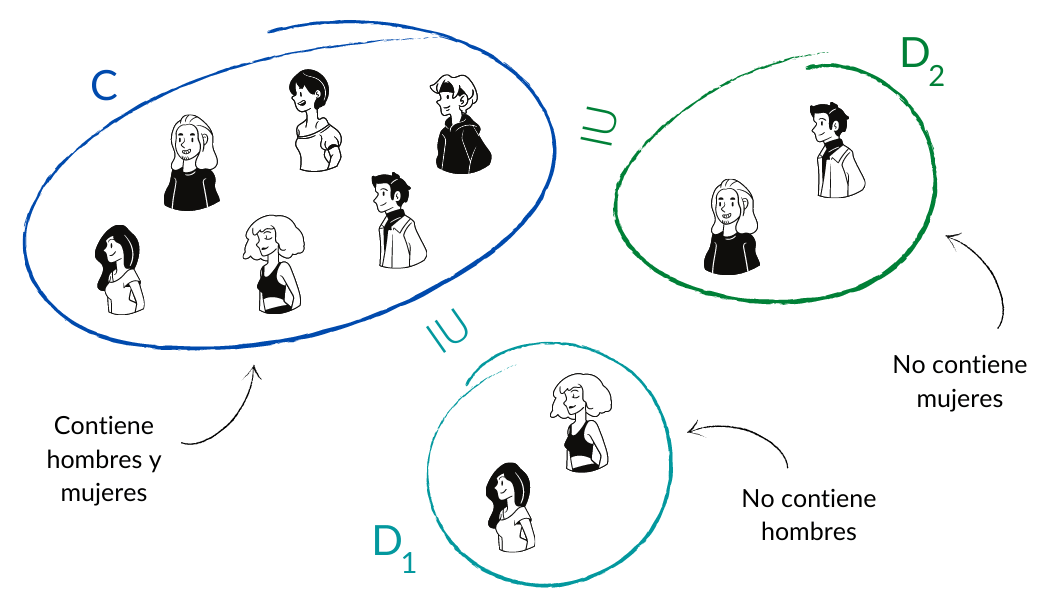
Si tenemos un conjunto $C$ con ciertas propiedades de nuestro interés, no forzosamente todo subconjunto de $C$ va a conservar esas propiedades, pero nos interesa encontrar condiciones suficientes (y de preferencia también necesarias) para saber si un subconjunto $D$ de $C$ dado tiene o no las propiedades que queremos.

Si $C$ es un conjunto que contiene a hombres y a mujeres, podemos definir un subconjunto que no contenga hombres y un subconjunto que no tenga mujeres, con lo que ya no preservan la propiedad deseada.

En esta entrada analizaremos qué se requiere para que un subconjunto de un espacio vectorial, tenga también estructura de espacio vectorial. Veremos que aunque aparentemente se requiere pedir muchas condiciones, en realidad éstas se pueden reducir sólo a unas cuantas.

SUBESPACIO

Definición: Sea $V$ un $K$ – espacio vectorial y $W$ un subconjunto de $V$. Decimos que $W$ es un subespacio de $V$, y se le denota como $W\leqslant V$ si:

i) $W$ contiene al neutro del espacio $V$,
i.e. $\theta_V\in W$

ii) La suma es cerrada en $W,$
i.e. $\forall u,v\in W:$
$u+v\in W$

iii) El producto por escalar es cerrado en $W$,
i.e. $\lambda\in K$, $w\in W:$
$\lambda w\in W$

Veamos una equivalencia a esta definición que nos facilitará demostrar si un subconjunto dado de un espacio vectorial es por sí mismo un espacio vectorial.

Proposición: Sean $V$ un $K$ – espacio vectorial y $W$ un subconjunto de $V$. Se cumple que $W\leqslant V$ si y sólo si $W$ con las operaciones restringidas de $V$ es un $K$ – espacio vectorial.

Demostración: Veamos que se cumplen ambas implicaciones.

$\Longrightarrow )$ Sup. que $W\leqslant V$.
Por ii) y iii) la suma y el producto por escalar son cerrados en $W$, entonces las operaciones restringidas de $V$ dan una suma y un producto por escalar en $W$.
Propiedades $1$, $2$, $5$, $6$, $7.1$ y $7.2$ de espacio vectorial: Como $u+v=v+u$ para cualesquiera $u,v\in V$, en particular $u+v=v+u$ para toda $u,v\in W$. Por lo tanto, la suma en $W$ es conmutativa.
Nota: Decimos en este caso que la conmutatividad de la suma se hereda de $V$.
Análogamente se heredan la asociatividad de la suma en $W$ y las propiedades $5$, $6$, $7.1$ y $7.2$ de espacio vectorial.
Propiedad $4$ de espacio vectorial: Para cada $w\in W$ se cumple que $-w=(-1_K)w\in W$ ya que el producto es cerrado en $W$.
Propiedad $5$ de espacio vectorial: Por hipótesis $\theta_V\in W$ y como es el neutro en $V$, $\theta_V+v=v+\theta_V=v$ para todo $v\in V$, en particular $\theta_V+w=w+\theta_V=w$ para todo $w\in W$, así $\theta_V$ funciona como neutro en $W$.
$\therefore W$ con las operaciones restringidas de $V$ es un $K$ – espacio vectorial.

$\Longleftarrow )$ Sup. que $W$ es un $K$ – espacio vectorial con las operaciones restringidas de $V$.
Entonces la suma y el producto por escalar son cerrados en $W$, es decir, se cumplen ii. y iii.
Además $W$ tiene un neutro, digamos $\theta_W\in W$.
Por un lado $\theta_V+\theta_W=\theta_W$ en $V$, pues $\theta_V$ es neutro en $V$.
Por otro lado $\theta_W+\theta_W=\theta_W$ en $W$, pues $\theta_W$ es neutro en $W$.
Así, $\theta_V+\theta_W=\theta_W+\theta_W$ en $V$ y por cancelación en $V$, $\theta_V=\theta_W$.
De donde $\theta_V\in W$
$\therefore W\leqslant V$ .

Obs. Sean $V$ un $K$ – espacio vectorial, $W$ un subconjunto de $V$. Resulta que
$W\leqslant V$ si y sólo si se cumple que: a) $W\not=\emptyset$ y b) $\forall u,v\in W$ $\forall\lambda\in K(\lambda u+v\in W)$.

La implicación de ida es muy directa y queda como ejercicio. Para justificar el regreso sup. que se cumplen a) y b). Dados $u,v\in W$ se tiene que $u+v=1_Ku+v$ y gracias a b) sabemos que $1_Ku+v\in W$, así se cumple la propiedad ii). Por otro lado, como se cumple a) podemos asegurar que existe $v \in W$, y por la propiedad b) $\theta_V=-v+v=(-1_K)v+v\in W$, por lo que $\theta_V\in W$ y se cumple i). Finalmente dados $u\in W, \lambda \in K$ como $\theta_V\in W$, usando b) se tiene que $\lambda u=\lambda u+\theta_V\in W$ por lo que se cumple la propiedad iii).

Ejemplos:

  • $\{ (x,y,0)|x,y\in\mathbb{R}\}$ es un subespacio de $\mathbb{R}^3.$
  • $\{\begin{pmatrix}a&b\\b&a\end{pmatrix}|a,b\in\mathbb{R}\}$ es un subespacio de $\mathcal{M}_{2\times 2}(\mathbb{R})$.
  • $\mathcal{P}_n(\mathbb{R})$ (el conjunto de polinomios de grado mayor o igual a $n$ con coeficientes en $\mathbb{R}$) es un subespacio de $\mathbb{R}[x]$
  • $\{ f:\mathbb{R}\longrightarrow\mathbb{R}| f$ es continua$\}$ es un subespacio de $\{ f|f:\mathbb{R}\longrightarrow\mathbb{R}\}.$
  • $\{(x,y,z)|x=y=z\in \mathbb{R}\}$ es un subespacio de $\mathbb{R}^3.$

EJEMPLO SISTEMA HOMOGÉNEO

Sean $V=\mathcal{M}{n\times 1}(K)$ y $A\in\mathcal{M}{m\times n}(K)$.
$W={X\in V|AX=0}$$\leqslant V$.

Recordemos que si tenemos el sistema de ecuaciones homogéneo de $m$ ecuaciones con $n$ incógnitas:

\begin{align*}
\begin{matrix}a_{11}x_1 & +a_{12}x_2 & \cdots & +a_{1n}x_n=0\\ a_{21}x_1 & +a_{22}x_2 & \cdots & +a_{2n}x_n=0 \\ \vdots & & \ddots & \vdots \\ a_{m1} x_1& +a_{m2}x_2 & \cdots & +a_{mn}x_n=0, \end{matrix} \end{align*}
entonces su forma matricial es:
\begin{align*}
AX=\begin{pmatrix}a_{11} & a_{12} & \cdots & a_{1n}\\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{pmatrix} \begin{pmatrix}x_1\\ \vdots\\ x_n\end{pmatrix}
= \begin{pmatrix}0\\ \vdots\\ 0\end{pmatrix} = 0 \end{align*}
Recordemos que estamos usando al $0$ para denotar a la matriz $n\times 1$ con todas sus entradas iguales al cero del campo. Veamos que las soluciones del sistema homogéneo dado por $A$ es un subespacio del espacio vectorial de matrices de $n\times 1$ con entradas en el campo $K$.

DEMOSTRACIÓN

Vamos a ver que $W$ cumple las tres condiciones suficientes y necesarias (por definición) para ser subespacio de $V$:

Sean $X,Y\in W$, $\lambda\in K$.

  1. P.D. $W$ tiene al neutro de $V$
    $i.e.$ $\theta_V\in W.$

Sabemos que $A\theta_V=A0=0$.
$\therefore\theta_V\in W.$

  1. P.D. La suma es cerrada en $W$
    $i.e.$ $X+Y\in W$.

Como $X,Y\in W$, $AX=AY=0$ y por lo tanto, $AX+AY=0+0=0$.
Basta recordar que por distributividad en las matrices $A(X+Y)=AX+AY$ para obtener que $A(X+Y)=0$.
$\therefore X+Y\in W.$

  1. P.D. El producto por escalar es cerrado en $W$
    $i.e.$ $\lambda X\in W$.

Como $X\in W$, $AX=0$ y por lo tanto, $\lambda (AX)=0$.
Basta recordar que por propiedad del producto por escalar en matrices $A(\lambda X)=\lambda(AX)$ para obtener que $A(\lambda X)=0$
$\therefore\lambda X\in W.$

Así, concluimos que $W=\{X\in V|AX=0\}$, donde $A\in\mathcal{M}_{m\times n}(K)$, es un subespacio de $V=\mathcal{M}_{n\times 1}(K)$.

Proposición: La intersección de una familia no vacía de subespacios es un subespacio.

Demostración: Sean $V$ un $K$ – espacio vectorial y $W=\{W_i|i\in I\}$ una familia no vacía de subespacios de $V$.

Sean $V$ un $K$ – espacio vectorial y $W=\{W_i|i\in I\}$ una familia no vacía de subespacios de $V$. Vamos a ver que $W$ cumple las tres condiciones suficientes y necesarias (por definición) para ser subespacio de $V$:

Sean $u,v\in W$, $\lambda\in K$.

  1. P.D. $W$ contiene al neutro de $V$
    $i.e.$ $\theta_V\in W.$

Sabemos que $\forall i\in I(\theta_V\in W_i)$ porque todos los $W_i$ son subespacios de $V$.
$\displaystyle\therefore\theta_V\in\bigcap_{i\in I}W_i.$

  1. P.D. La suma es cerrada en $W$
    $i.e.$ $u+v\in W$.

Dado que $u,v\in W$, $\forall i\in I(u,v\in W_i)$ y como todos los $W_i$ son subespacios de $V$, entonces $\forall i\in I(u+v\in W_i)$.
$\displaystyle\therefore u+v\in\bigcap_{i\in I}W_i.$

  1. P.D. El producto por escalar es cerrado en $W$
    $i.e.$ $\lambda u\in W$.

Dado que $u\in W$, $\forall i\in I(u\in W_i)$ y como todos los $W_i$ son subespacios de $V$, entonces $\forall i\in I(\lambda u\in W_i)$.
$\displaystyle\therefore\lambda u\in\bigcap_{i\in I}W_i.$

Concluimos así que $W\leqslant V.$

Tarea Moral

  1. Dado $V$ un $K$ – espacio vectorial. Sean $W_1, W_2\leqslant V$. Demuestra que si $W_1\bigcup W_2\leqslant V$, entonces $W_1\subseteq W_2$, o bien, $W_2\subseteq W_1$.
    Para lograrlo se te sugiere lo siguiente:
    • Sup. que $W_1 \nsubseteq W_2$.
    • Observamos que para cualesquiera $w_1\in W_1\backslash W_2$ y $w_2\in W_2$, tenemos que $w_1,w_2\in W_1\bigcup W_2$. Y como $W_1\bigcup W_2\leqslant V$, entonces $w_1+w_2\in W_1\bigcup W_2$. Además, gracias a la primera proposición de esta entrada, sabemos que $W_1$ y $W_2$ son $K$ – espacios vectoriales, de modo que los inversos aditivos de $w_1$ y $w_2$ son elementos de $W_1$ y $W_2$ respectivamente.
    • Ahora argumenta por qué $w_1+w_2\notin W_2$ para concluir que $w_1+w_2\in W_1$.
    • Por último argumenta por qué gracias a que $w_1+w_2\in W_1$, obtenemos que $w_2\in W_1$ para concluir que $W_2\subseteq W_1$.
  1. Sean $K=\mathbb{R}$ y $V=\{a+bx+cx^2+dx^3\mid a,b,c,d\in\mathbb{R}\}$.
    Determina si $U=\{p(x)\in V|p(1)=0\}$ y $T=\{p(x)\in V|p'(1)=0\}$ son subespacios de $V$ y encuentra $U\cap T$.

MÁS ADELANTE…

Definiremos y analizaremos un nuevo concepto que dará lugar a un nuevo subespacio muy peculiar y central en el Álgebra Lineal.

Entradas relacionadas

Geometría Analítica I: Polinomios cuadráticos y curvas cuadráticas

Por Leonardo Ignacio Martínez Sandoval

Deja un comentario

Introducción

Lo primero que queremos determinar en un problema de clasificación es cuáles son los objetos que clasificaremos. En esta entrada los definimos con toda precisión: serán los polinomios cuadráticos en dos variables y las curvas cuadráticas.

Los primeros son expresiones algebraicas que mezclan a dos variables $x$ y $y$ mediante sumas y productos, pero teniendo grado dos. Las segundas son aquellos conjuntos del plano en donde se anula un polinomio cuadrático.

Polinomios cuadráticos en dos variables

Comencemos con una definición algebraica.

Definición. Un polinomio cuadrático en dos variables $P$ es una función $P:\mathbb{R}^2\to \mathbb{R}$ de la forma $$P((x,y))=Ax^2+Bxy+Cy^2+Dx+Ey+F,$$ para algunos reales $A,B,C,D,E,F$, en donde alguno de $A$, $B$ ó $C$ es distinto de cero.

En ocasiones, para abreviar «polinomio cuadrático en dos variables» simplemente usaremos las siglas «PCDV».

Ejemplo. Todas las expresiones que aparecen en las cónicas canónicas que hemos estudiado son PCDVs. Por ejemplo, la ecuación canónica de la elipse $$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$ puede reescribirse como $$b^2x^2+a^2y^2-a^2b^2=0.$$ Del lado izquierdo de esta igualdad tenemos un PCDV. De manera similar, la ecuación canónica de la parábola $y^2=4px$ puede reescribirse como $y^2-4px=0$. Una vez más al lado izquierdo nos aparece un PCDV.

$\triangle$

Ejemplo. Si consideramos las dos rectas $3x+5y+1=0$ y $2x-2y+1=0$ y «multiplicamos» sus ecuaciones, entonces obtenemos de nuevo un PCDV pues el producto es:

\begin{align*}
(3x+5y+1)(2x-2y+1)&=6x^2-6xy+3x+10xy-10y^2+5y+2x-2y+1\\
&=6x^2+4xy-10y^2+5x+3y+1.
\end{align*}

$\triangle$

Curvas cuadráticas

Cuando tenemos una expresión algebraica que depende de dos variables $x$ y $y$, entonces podemos preguntarnos por cómo es la figura geométrica que se obtiene al considerar los puntos $(x,y)$ del plano que hacen que la expresión algebraica sea igual a cero. Un ejemplo de esto es cuando consideramos las expresiones del estilo $Ax+By+C$. Las parejas $(x,y)$ que hacen que esta expresión sea igual a cero forman una recta en el plano. En efecto, forman la recta en forma normal dada por la ecuación $(A,B)\cdot (x,y)=-C$, como puedes verificar.

Esta idea es mucho más general. A partir de los polinomios cuadráticos en dos variables también podemos hacernos la misma pregunta: ¿cómo se ven las parejas $(x,y)$ que anulan un polinomio cuadrático? La respuesta será importante, así que las figuras que se construyen así les damos su propio nombre.

Definición. Una curva cuadrática es el conjunto de puntos $(x,y)$ del plano que anulan a un polinomio cuadrático en dos variables $P$. En otras palabras, es un conjunto de la forma $$\mathcal{C}:=\{(x,y)\in \mathbb{R}^2: Ax^2+Bxy+Cy^2+Dx+Ey+F = 0\}.$$

A $P$ le llamamos el polinomio asociado a $\mathcal{C}$. A $\mathcal{C}$ le llamamos la curva descrita (o dada) por $P$. Quizás usaremos terminología un poco distinta, pero que siga dejando evidente que $P$ y $\mathcal{C}$ están relacionados.

Ejemplo. Ya hemos estudiado anteriormente algunas curvas cuadráticas: las cónicas canónicas. Por ejemplo, si tomamos el PCDV $P((x,y))=4x^2-9y^2-36$ y nos preguntamos para cuáles parejas $(x,y)$ esto es igual a cero, como respuesta tenemos que son aquellas parejas $(x,y)$ tales que $ 4x^2-9y^2-36=0$, lo cual podemos reescribir como $$\frac{x^2}{9}-\frac{y^2}{4}=1.$$ Esta es la hipérbola canónica de semieje mayor $3$ y semieje menor $2$. Podemos verla en la siguiente figura.

$\triangle$

Ejemplo. ¿Qué sucede si nos fijamos en la curva descrita por el polinomio cuadrático en dos variables $$ 6x^2+4xy-10y^2+5x+3y+1$$ que construimos en un ejemplo anterior? Si recuerdas, obtuvimos este polinomio cuadrático en dos variables a partir de multiplicar dos expresiones. De esta forma, tenemos que $$ 6x^2+4xy-10y^2+5x+3y+1=0$$ si y sólo si $$ (3x+5y+1)(2x-2y+1) =0.$$ Pero el producto de dos cosas es igual a cero si y sólo si alguna es igual a cero. Así, alguna de las expresiones $3x+5y+1$ y $2x-2y+1$ debe ser igual a cero. Si la primera es cero, entonces $(x,y)$ es un punto en la recta normal $\ell_1$ de ecuación $(3,5)\cdot (x,y) = -1$. Si la segunda es cero, entonces $(x,y)$ es un punto en la recta normal $\ell_2$ de ecuación $(2,-2)\cdot(x,y) = -1$. Así, la curva cuadrática descrita por el PCDV es la unión de $\ell_1$ con $\ell_2$. Podemos verla en la siguiente figura.

$\triangle$

Forma matricial de polinomios cuadráticos en dos variables

Cuando trabajamos con rectas, nos convenía tener varias formas de expresarlas: la forma paramétrica ayudaba a determinar fácilmente el paralelismo, la forma baricéntrica nos daba fórmulas sencillas para los puntos medios, la forma normal nos permitía encontrar distancias, etc. Así mismo, cuando trabajamos con polinomios cuadráticos en dos variables es de ayuda tener más de una expresión.

Podemos reescribir un polinomio cuadrático en dos variables $$P((x,y))=Ax^2+Bxy+Cy^2+Dx+Ey+F$$ de una manera más compacta usando multiplicación matricial. Para ello, definimos $$M=\begin{pmatrix} A & \frac{B}{2} \\ \frac{B}{2} & C \end{pmatrix}, k=\begin{pmatrix} D \\ E \end{pmatrix}, v=\begin{pmatrix} x \\ y \end{pmatrix}.$$ Con esta notación, e interpretando a las matrices de $1\times 1$ como reales, tenemos que $P$ se puede reescribir de la siguiente manera: $$P(v)=v.$$

En efecto, al realizar las operaciones en el lado derecho obtenemos:

\begin{align*}
v^t M v + k^t v + F &=\begin{pmatrix} x & y \end{pmatrix} \begin{pmatrix} A & \frac{B}{2} \\ \frac{B}{2} & C \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} + \begin{pmatrix} D & E \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} + F\\
&=\begin{pmatrix} x & y \end{pmatrix} \begin{pmatrix} Ax + \frac{B}{2} y \\ \frac{B}{2} x + C y \end{pmatrix} + Dx + Ey + F\\
&=Ax^2 + Bxy + Cy^2+Dx+Ey+F.
\end{align*}

Observa que cuando pasamos un polinomio cuadrático en dos variables a forma matricial entonces siempre obtenemos una matriz $M$ simétrica.

Ejemplo. La forma matricial del PCDV que encontramos anteriormente $$6x^2+4xy-10y^2+5x+3y+1$$ es

$$ \begin{pmatrix} x & y \end{pmatrix} \begin{pmatrix} 6 & 2 \\ 2 & 10 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} + \begin{pmatrix} 5 & 3 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} + 1.$$

nota que el coeficiente de $xy$ se tuvo que dividir entre $2$ para llegar a las entradas de la matriz. Es importante recordar esto al pasar de la forma en coordenadas a la forma matricial.

$\triangle$

En caso de ser necesario, también podemos pasar fácilmente de la forma matricial de un polinomio cuadrático en dos variables a su forma en coordenadas.

Ejemplo. Si comenzamos con el polinomio cuadrático en dos variables con forma matricial $$ \begin{pmatrix} x & y \end{pmatrix} \begin{pmatrix} 2 & -1 \\ -1 & 3 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} + \begin{pmatrix} 0 & -3 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} – 1, $$

entonces su forma en coordenadas es $$2x^2-2xy+3y^2 – 3y -1.$$

Observa que las entradas $-1$ fuera de la diagonal principal de la matriz al salir se duplican para conformar el coeficiente de $xy$. Es importante recordar esto al pasar de forma matricial a forma en coordenadas.

$\triangle$

Más adelante…

En esta entrada definimos qué son los polinomios cuadráticos en dos variables y qué son las curvas cuadráticas.

Por un lado, mencionamos que todas las ecuaciones de cónicas canónicas que hemos visto tienen polinomios cuadráticos en dos variables. ¿Será que todas las ecuaciones de cónicas también tienen polinomios cuadráticos en dos variables? Por otro lado, vimos que algunas curvas cuadráticas son cónicas. Pero nos pasó algo un poco raro: en un ejemplo salieron dos rectas que se intersectan, que quizás estrictamente no pensamos como una cónica usual (elipse, hipérbola, parábola).

¿Cómo serán todas las curvas cuadráticas? ¿Serán sólo las cónicas usuales y algunas excepciones o podrán tener formas muy extrañas? Eso lo estudiaremos después.

También en esta entrada vimos la forma matricial de un polinomio cuadrático en dos variables. De momento, no hemos hablado de la utilidad que tiene pensar a un PCDV así. Sin embargo, en la siguiente entrada veremos que esta expresión es fundamental para ver qué sucede cuando «combinamos» un polinomio cuadrático con una transformación afín.

Tarea moral

  1. Usa alguna herramienta tecnológica (como GeoGebra) para trazar las curvas cuadráticas descritas por los siguientes polinomios cuadráticos en dos variables:
    • $x^2-2xy+3y^2+x-5y+7$
    • $3y^2+5y+x$
    • $x^2+y^2-5x-5y+3$
    • $xy-x-y+7$
    • $-x^2+2xy-3y^2-x+5y-7$
  2. Sea $P:\mathbb{R}^2\to \mathbb{R}$ dada por $P((x,y))=(Ax+By+C)(Dx+Ey+F)$. Demuestra que $P$ es un polinomio cuadrático en dos variables. Luego, demuestra que:
    1. Si $AE-BD\neq 0$, entonces la curva cuadrática dada por $P$ es la unión de dos rectas que se intersectan.
    2. Si $AE-BD=0$, entones la curva cuadrática dada por $P$ es la unión de dos rectas paralelas (no necesariamente distintas).
  3. Demuestra que la intersección de una recta con una curva cuadrática sólo puede ser:
    1. Vacía,
    2. Un punto,
    3. Dos puntos, o
    4. Una infinidad de puntos.
  4. Demuestra que cualquier curva cuadrática $\mathcal{C}$ puede ser descrita a través de una infinidad de polinomios cuadráticos en dos variables.
  5. Considera la gráfica de la función $f(x)=\sin(x)$. ¿Será que esta gráfica es una curva cuadrática? Intenta demostrar por qué sí o por qué no.

Entradas relacionadas

Álgebra Lineal II: Otras aplicaciones de formas canónicas de Jordan

Por Elizabeth Chalnique Ríos Alvarado

Deja un comentario

Introducción

En las notas anteriores desarrollamos teoría interesante acerca de las formas canónicas de Jordan, ahora vamos a ver algunos ejemplos de todo eso.

Ejemplo 1

Considera la matriz $$A = \begin{pmatrix}1 & 0 & 0 & 0 & 2 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ -1 & 0 & 0 & 0 & -2 \end{pmatrix}$$

Calculamos $\chi_{A}(X)$ expandiendo $det(XI_{5} – A)$ con respecto a la tercera fila y obtenemos (usando de nuevo la expansión respecto a la segunda fila en el nuevo determinante) \begin{align*} \chi_{A}(X) &= X \begin{vmatrix} X-1 & 0 & 0 & -2 \\ 0 & X & 0 & 0 \\ 0 & -1 & X & 0 \\ 1 & 0 & 0 & X+2 \end{vmatrix} \\ &= X^{2} \begin{vmatrix} X-1 & 0 & 2 \\ 0 & X & 0 \\ 1 & 0 & X+2 \end{vmatrix} \\ &= X^{3} \begin{vmatrix} X-1 & -2 \\ 1 & X+2 \end{vmatrix} \\ &= X^{4} (X+1) \end{align*}

El eigenvalor $-1$ tiene multiplicidad algebraica 1, por lo que hay un solo bloque de Jordan asociado con este eigenvalor, de tamaño 1. Ahora, veamos qué pasa con el eigenvalor 0 que tiene multiplicidad algebraica 4. Sea $N_{m}$ el número de bloques de Jordan de tamaño $m$ asociados con ese eigenvalor. Por el Teorema visto en la nota anterior tenemos que $$N_{1} = rango(A^{2}) – 2rango(A) + 5,$$ $$N_{2} = rango(A^{3}) – 2rango(A^{2}) + rango(A)$$ etcétera. Puedes checar fácilmente que $A$ tiene rango 3.

Luego, calculemos $A^{2} = \begin{pmatrix} -1 & 0 & 0 & 0 & -2 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 & 2 \end{pmatrix}$, $A^{3} = \begin{pmatrix} 1 & 0 & 0 & 0 & 2 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ -1 & 0 & 0 & 0 & -2 \end{pmatrix}$.

Nota que $A^{2}$ tiene rango 2 (pues una base del generado por sus filas está dada por la primera y cuarta fila) y $A^{3}$ tiene rango 1. De donde, $$N_{1} = 2-2 \cdot 3 + 5 = 1,$$ por lo que hay un bloque de Jordan de tamaño 1 y $$N_{2} = 1-2 \cdot 2 + 3 = 0,$$ entonces no hay un bloque de Jordan de tamaño 2. Dado que la suma de los tamaños de los bloques de Jordan asociados con el eigenvalor 0 es 4, y como ya sabemos que hay un bloque de tamaño 1 y no hay de tamaño 2, deducimos que hay un bloque de tamaño 3 y que la forma canónica de Jordan de $A$ es $$\begin{pmatrix} -1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1& 0 \\ 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0\end{pmatrix}.$$

Ejemplo 2

Más adelante…

Con esto finalizamos el curso de Álgebra Lineal II, lo que sigue es el maravilloso mundo del Álgebra Moderna.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Usa el Teorema de Jordan para probar que cualquier matriz $A \in M_{n}(\mathbb{C})$ es similar a su transpuesta.
  2. Prueba que si $A \in M_{n}(\mathbb{C})$ es similar a $2A$, entonces $A$ es nilpotente.
  3. Usa el teorema de Jordan para probar que si $A \in M_{n}(\mathbb{C})$ es nilpotente, entonces $A$ es similar a $2A$.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Álgebra Lineal II: Clasificación de matrices por similaridad

Por Elizabeth Chalnique Ríos Alvarado

Deja un comentario

Introducción

En las notas anteriores hemos desarrollado el Teorema de Jordan, y ahora veremos cómo podemos clasificar matrices por similaridad.

Sección

Supongamos que $A$ es una matriz similar a $$\begin{pmatrix} J_{k_{1}}(\lambda_{1}) & 0 & \cdots & 0 \\ 0 & J_{k_{2}}(\lambda_{2}) & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & J_{k_{d}}(\lambda_{d}) \end{pmatrix}$$

Entonces el polinomio característico de $A$ es $$\chi_{A}(X) = \prod_{i=1}^{d}\chi_{J_{k_{i}}} (\lambda_{i})(X).$$

Ahora, dado que $J_{n}$ es nilpotente tenemos $\chi_{J_{k_{i}}}(X) = X^{n}$ y así $$\chi_{J_{n}(\lambda)}(X) = (X – \lambda)^{n}.$$

Se sigue que $$\chi_{A}(X) = \prod_{i=1}^{d} (X – \lambda_{i})^{k_{i}}$$ y así necesariamente $\lambda_{1}, \ldots, \lambda_{d}$ son todos eigenvalores de $A$. Nota que no asumimos que $\lambda_{1}, \ldots, \lambda_{d}$ sean distintos a pares, por lo que no podemos concluir de la igualdad anterior que $k_{1}, \ldots, k_{d}$ sean las multiplicidades algebráicas de los eigenvalores de $A$. Esto no es verdad en general: varios bloques de Jordan correspondientes a un dado eigenvalor pueden aparecer. El problema de la unicidad se resuelve completamente por el siguiente:

Teorema: Supongamos que una matriz $A \in M_{n}(F)$ es similar a $$\begin{pmatrix} J_{k_{1}}(\lambda_{1}) & 0 & \cdots & 0 \\ 0 & J_{k_{2}}(\lambda_{2}) & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & J_{k_{d}}(\lambda_{d}) \end{pmatrix}$$ para algunos enteros positivos $k_{1}, \ldots, k_{d}$ que suman $n$ y algunas $\lambda_{1}, \ldots, \lambda_{d} \in F$. Entonces

  1. Cada $\lambda_{i}$ es un eigenvalor de $A$.
  2. Para cada eigenvalor $\lambda$ de $A$ y cada entero positivo $m$, el número de bloques de Jordan $J_{m}(\lambda)$ entre $J_{k_{1}}(\lambda_{1}), \ldots, J_{k_{d}}(\lambda_{d})$ is $$N_{m}(\lambda) = rango(A – \lambda I_{n})^{m+1} – 2 rango(A – \lambda I_{n})^{m} + rango(A – \lambda I_{n})^{m-1}$$ y depende sólo en la clase de similaridad de $A$.

Demostración. Ya vimos el inciso 1. La prueba del inciso 2 es muy similar a la solución del Problema __. Más precisamente, sea $B = A – \lambda I_{n}$ y observa que $B^{m}$ es similar a $\begin{pmatrix} (J_{k_{1}}(\lambda_{1}) – \lambda I_{k_{1}})^{m} & 0 & \cdots & 0 \\ 0 & (J_{k_{2}}(\lambda_{2}) – \lambda I_{k_{2}})^{m} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & (J_{k_{d}}(\lambda_{d}) – \lambda I_{k_{d}})^{m}\end{pmatrix}$, por lo que $\displaystyle rango(B^{m}) = \sum_{i=1}^{d} rango(J_{k_{i}} (\lambda_{i}) – \lambda I_{k_{i}})^{m}$.

Ahora, el rango de $(J_{n}(\lambda) – \mu I_{n})^{m}$ es

  • $n$ si $\lambda \neq \mu$, como en este caso $$J_{n}(\lambda) – \mu I_{n} = J_{n} + (\lambda – \mu) I_{n}$$ es invertible,
  • $n-m$ para $\lambda = \mu$ y $m \leq n$, como se sigue del Problema __.
  • 0 para $\lambda = \mu$ y $m > n$, dado que $J^{n}_{n} = O_{n}$.

De ahí, si $N_{m}(\lambda)$ es el número de bloques de Jordan $J_{m}(\lambda)$ entre $J_{k_{1}}(\lambda_{1}), \ldots, J_{k_{d}}(\lambda_{d})$, entonces $$rango(B^{m}) = \sum_{\substack{\lambda_{i} = \lambda \\ k_{i} \geq m}} (k_{i} – m) + \sum_{\lambda_{i} \neq \lambda} k_{i},$$ luego sustrayendo esas igualdades para $m-1$ y $m$ se tiene que $$rango(B^{m-1}) – rango(B^{m}) = \sum_{\substack{\lambda_{i} = \lambda \\ k_{i} \geq m}} 1$$ y finalmente \begin{align*} rango(B^{m-1}) – 2rango(B^{m}) + rango(B^{m+1}) = \\ (rango(B^{m-1}) – rango(B^{m})) – (rango(B^{m}) – rango(B^{m+1})) = \\ \sum_{\substack{\lambda_{i} = \lambda \\ k_{i} = m}} 1 = N_{m}(\lambda) \end{align*} como queríamos.

$\square$

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. ¿Cuáles son las posibles formas canónicas de Jordan de una matriz cuyo polinomio característico es $(X-1)(X-2)^{2}$?
  2. Considera una matriz $A \in M_{6}(\mathbb{C}) de rango 4 cuyo polinomio mínimo es $X(X-1)(X-2)^{2}$.
    1. ¿Cuáles son los eigenvalores de $A$?
    2. ¿$A$ es diagonalizable?
    3. ¿Cuáles son las posibles formas canónicas de Jordan de $A$?

Más adelante…

En la siguiente nota veremos algunos ejemplos de cómo funciona todo esto.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Álgebra Lineal II: Existencia de la forma canónica de Jordan para nilpotentes

Por Elizabeth Chalnique Ríos Alvarado

Deja un comentario

Introducción

En la entrada anterior estudiamos de manera un poco más sistemática las matrices y transformaciones lineales nilpotentes. Lo que haremos ahora es enunciar el teorema de la forma canónica de Jordan para matrices nilpotentes. Este es un teorema de existencia y unicidad. En esta entrada demostraremos la parte de la existencia. En la siguiente entrada hablaremos de la unicidad y de cómo encontrar la forma canónica de Jordan de matrices nilpotentes de manera práctica.

El teorema de Jordan para nilpotentes

El teorema que queremos demostrar tiene dos versiones: la de transformaciones y la matricial. La versión en transformaciones dice lo siguiente.

Teorema. Sea $V$ un espacio vectorial de dimensión finita $n$ y $T:V\to V$ una transformación lineal nilpotente. Entonces existen únicos enteros $k_1,\ldots,k_d$ tales que \begin{align*} &k_1+k_2+\ldots+k_d = n,\\ &k_1\leq k_2 \leq \ldots \leq k_d,\end{align*} y para los cuales existe una base de $V$ en la cual $T$ tiene como forma matricial a la siguiente matriz de bloques:

$$\begin{pmatrix} J_{0,k_1} & 0 & \cdots & 0 \\ 0 & J_{0,k_2} & \cdots & 0 \\ \vdots & & \ddots & \vdots \\ 0 & 0 & \cdots & J_{0,k_d}\end{pmatrix}.$$

La versión en forma matricial dice lo siguiente.

Teorema. Sea $A$ una matriz nilpotente en $M_n(F)$. Entonces existen únicos enteros $k_1,\ldots,k_d$ tales que \begin{align*} &k_1+k_2+\ldots+k_d = n,\\ &k_1\leq k_2 \leq \ldots \leq k_d,\end{align*} y para los cuales $A$ es similar a la siguiente matriz de bloques: $$\begin{pmatrix} J_{0,k_1} & 0 & \cdots & 0 \\ 0 & J_{0,k_2} & \cdots & 0 \\ \vdots & & \ddots & \vdots \\ 0 & 0 & \cdots & J_{0,k_d}\end{pmatrix}.$$

A esta matriz de bloques (ya sea para una transformación, o para una matriz) le llamamos la forma canónica de Jordan de $A$.

En vista de que dos matrices son similares si y sólo si representan a la misma transformación lineal en distintas bases, entonces ambos teoremas son totalmente equivalentes. Así, basta enfocarnos en demostrar una de las versiones. Haremos esto con la versión para transformaciones lineales.

Trasnformaciones nilpotentes y unos vectores linealmente independientes

En esta sección enunciaremos un primer resultado auxiliar para demostrar la existencia de la forma canónica de Jordan. Veremos que a partir de una transformación lineal nilpotente podemos obtener algunos vectores linealmente independientes.

Proposición. Sea $V$ un espacio vectorial de dimensión finita y $T:V\to V$ una transformación lineal de índice $k$. Sea $v$ un vector tal que $T^{k-1}(v)\neq 0$, el cual existe ya que $T^{k-1}$ no es la transformación lineal cero. Entonces:

  1. Los vectores $v$, $T(v)$, $\ldots$, $T^{k-1}(v)$ son linealmente independientes.
  2. El subespacio $W$ que generan es de dimensión $k$ y es estable bajo $T$.
  3. La transformación $T$ restringida a $W$ en la base $T^{k-1}(v)$, $T^{k-2}(v)$, $\ldots$, $T(v)$, $v$ tiene como matriz al bloque de Jordan $J_{0,k}$. Ojo. Aquí los vectores los escribimos en orden contrario, empezando con la mayor potencia de $T$ aplicada.

Demostración. Probemos las afirmaciones una por una. Para empezar, supongamos que para ciertos escalares $\alpha_0,\ldots,\alpha_{k-1}$ tenemos que $$\alpha_0v+\alpha_1T(v)+\ldots+\alpha_{k-1}T^{k-1}(v)=0.$$

Vamos a probar inductivamente de $0$ a $k-1$ que $\alpha_k=0$. Para mostrar que $\alpha_0=0$, aplicamos $T^{k-1}$ a la combinación lineal anterior para obtener:

\begin{align*}
0&=\alpha_0T^{k-1}(v)+\alpha_1T^k(v)+\ldots+\alpha_{k-1}T^{2k-2}(v)\\
&=\alpha_0T^{k-1}(v).
\end{align*}

Aquí estamos usando en todos los sumandos, excepto el primero, que $T^k=0$. Como $T^{k-1}(v)\neq 0$, concluimos que $\alpha_0=0$. Suponiendo que ya hemos mostrado $\alpha_0=\ldots=\alpha_l=0$, la combinación lineal con la que empezamos queda como $$\alpha_{l+1}T^{l+1}(v)+\alpha_{l+2}T^{l+2}(v)+\ldots+\alpha_{k-1}T^{k-1}(v)=0.$$ Aplicando $T^{k-l-2}$ y usando un argumento similar al anterior se llega a que $\alpha_{l+1}=0$. Esto muestra que la única combinación lineal de los vectores que da cero es la combinación lineal trivial, así que son linealmente independientes.

De manera inmediata obtenemos entonces que esos $k$ vectores generan un subespacio $W$ de dimensión $k$. Para ver que $W$ es $T$ estable, tomemos un elemento $w$ en $W$, es decir $$w=\alpha_0v+\alpha_1T(v)+\ldots+\alpha_{k-1}T^{k-1}(v)$$ para algunos escalares $\alpha_0,\ldots,\alpha_{k-1}$. Debemos ver que $T(w)$ está nuevamente en $W$. Haciendo las cuentas y usando nuevamente que $T^k=0$ obtenemos:

\begin{align*}
T(w)&=T(\alpha_0v+\alpha_1T(v)+\ldots+\alpha_{k-1}T^{k-1}(v))\\
&= \alpha_0T(v)+\alpha_1T^2(v)+\ldots+\alpha_{k-2}T^{k-1}(v)+\alpha_{k-1}T(v)\\
&= \alpha_0T(v)+\alpha_1T^2(v)+\ldots+\alpha_{k-2}T^{k-1}(v)\\
\end{align*}

Este vector de nuevo es combinación lineal de los vectores que nos interesan, así que $T(w)$ está en $W$, como queríamos.

La afirmación de la forma matricial es inmediata pues precisamente

$$T(T^{j}(v))=0\cdot T^{n-1}(V)+\ldots+1\cdot T^{j+1}(v)+\ldots+0\cdot T(v) + 0\cdot v,$$ de donde se lee que las columnas de dicha forma matricial justo son las del bloque de Jordan $J_{0,k}$.

$\square$

El teorema anterior da otra demostración de algo que ya habíamos mostrado en la entada anterior: el índice de una matriz en $M_n(F)$ (o de una transformación nilpotente en un espacio vectorial de dimensión $n$) no puede exceder $n$.

Encontrar un subespacio complementario y estable

Ahora veremos otro resultado auxiliar que necesitaremos para demostrar la existencia de la forma canónica de Jordan. A partir de él podemos conseguirnos un «subespacio complementario y estable» que en la prueba de la existencia nos ayudará a proceder inductivamente. Este truco ya lo hemos visto antes en la clasificación de matrices ortogonales y el la demostración del teorema espectral.

Proposición. Sea $V$ un espacio vectorial de dimensión finita $n$ y $T:V\to V$ una transformación lineal nilpotente de índice $k$. Tomemos $v$ un vector tal que $T^{k-1}(v)\neq 0$. Sea $W$ el subespacio generado por $v,T(v),\ldots,T^{k-1}(v)$. Entonces, existe un subespacio $W’$ estable bajo $T$ y tal que $T=W\oplus W’$.

La principal dificultad para probar esta proposición es una cuestión creativa: debemos saber de dónde sacar el espacio $W’$. Para ello, haremos uso de la transformación transpuesta y de un espacio ortogonal por dualidad. Como recordatorio, si $T:V\to V$ es una transformación lineal, entonces su transformación transpuesta es una transformación lineal $^tT:V^\ast \to V^\ast$ para la cual $^tT(\ell)(u)=\ell(T(u))$ para cualquier forma lineal $\ell$ y cualquier vector $u$ en $V$.

Demostración. Primero, nos enfocamos en construir $W’$. Para ello procedemos como sigue. Como $T^{k-1}(v)\neq 0$, entonces existe una forma lineal $\ell$ tal que $\ell(T^{k-1}(v))\neq 0$. Se puede mostrar que $S:=\text{ }^t T$ también es nilpotente de índice $k$. Por la proposición de la sección anterior, tenemos entonces que $\ell, S(\ell),\ldots,S^{k-1}(\ell)$ son $k$ vectores linealmente independientes en $V^\ast$ y por lo tanto que generan un subespacio $Z$ de dimensión $k$. El espacio $W’$ que propondremos será $Z^\bot$.

Debemos mostrar que:

  1. En efecto $V=W\oplus W’$.
  2. En efecto $W’$ es $T$ estable.

Para la primer parte, usando teoría de espacios ortogonales tenemos que $$\dim(W’)=\dim(Z^\bot)=n-\dim(Z)=n-k,$$ así que los subespacios tienen la dimensión correcta para ser complementarios. Además, si $u\in W\cap W’$, entonces $u$ es combinación lineal de $v, T(v),\ldots, T^{k-1}(v),$ digamos $$u=\alpha_0v+\ldots+\alpha_{k-1}T^{k-1}(v)$$ y se anula por $\ell, S(\ell),\ldots,S^{k-1}(\ell)$, lo que quiere decir que se anula por $\ell, \ell\circ T, \ldots, \ell \circ T^{k-1}$. Esto permite probar iterativamente que $\alpha_0=\ldots=\alpha_{k-1}=0$, de modo que $u=0$. Con esto, $W$ y $W’$ son de intersección trivial y dimensiones complementarias, lo cual basta para que $V=W\oplus W’$.

Para terminar, debemos ver que $W’$ es $T$ estable. Tomemos un $u$ en $W’$, es decir, tal que se anula por $\ell, \ell\circ T, \ldots, \ell \circ T^{k-1}$. Al aplicar $T$, tenemos que $T(u)$ también se anula por todas estas transformaciones. Esto se debe a que para $\ell \circ T^j$ con $j\leq k-2$ se anula ya que $\ell\circ T^j(T(u))=\ell\circ T^{j+1}(u)=0$ por cómo tomamos $u$ y para $\ell \circ T^{k-1}$ se anula pues $T$ es nilpotente de índice $k$.

$\square$

Existencia de forma canónica de Jordan para nilpotentes

La idea para encontrar la forma canónica de Jordan debe ser clara a estas alturas: se procederá por inducción, el caso base será sencillo, asumiremos la hipótesis inductiva y para hacer el paso inductivo descomponeremos al espacio $V$ mediante la proposición de la sección anterior. Veamos los detalles.

Demostración (existencia de forma canónica de Jordan para nilpotentes). Estamos listos para probar la existencia de la forma canónica de Jordan para una transformación lineal nilpotente $T:V\to V$ con $V$ un espacio vectorial de dimensión finita $n$. Procederemos por inducción en la dimensión. Si $n=1$, entonces $V$ es generado por un vector $v$ y la transformación lineal $T$ debe mandarlo al vector $0$ para ser nilpotente. En esta base, $T(v)=0$ y la matriz que representa a $T$ es entonces $(0)=J_{0,1}$.

Supongamos que existe la forma canónica de Jordan para cuando $V$ es de cualquier dimensión menor a un entero positivo dado $n$. Tomemos $V$ un espacio vectorial de dimensión $n$ y $T:V\to V$ una transformación lineal nilpontente. Si $T$ es de índice $n$, entonces $T^{n-1}(v),\ldots,T(v),v$ son linealmente independientes y por lo tanto son una base de $V$. La forma matricial de $T$ en esta base es el bloque de Jordan $J_{0,n}$, en cuyo caso terminamos.

De otra forma, el índice es un número $k<n$. Entonces, $T^{k-1}(v),\ldots,T(v),v$ generan un subespacio estable $W$ de dimensión $k$. Por la proposición de la sección anterior, podemos encontrar un subespacio complementario $W’$ de dimensión $n-k<n$ y estable bajo $T$. Como la restricción de $T$ a $W’$ tiene codominio $W’$, es nilpotente y $\dim(W)<\dim(V)$, entonces por hipótesis inductiva $W’$ tiene una base $\beta$ bajo la cual la restricción de $T$ a $W’$ tiene como forma matricial una matriz diagonal por bloques con puros bloques de Jordan del estilo $J_{0,k_j}$. Al completar $\beta$ con $T^{k-1}(v),\ldots,T(v),v$ , obtenemos una base de $V$ en la cual $T$ tiene como forma matricial una matriz diagonal por bloques con puros bloques de Jordan del estilo $J_{0,k_j}$ (que vienen de la hipótesis inductiva) y un bloque de Jordan $J_{0,k}$. Salvo quizás un reordenamiento de la base para ordenar los $k_j$ y $k$, obtenemos exactamente lo buscado.

$\square$

Más adelante…

Ya demostramos una parte fundamental del teorema que nos interesa: la existencia de la forma canónica de Jordan para transformaciones (y matrices) nilpotentes. Nos falta otra parte muy importante: la de la unicidad. Las demostraciones de unicidad típicamente son sencillas, pero en este caso no es así. Para decir de manera explícita cuál es la forma canónica de Jordan de una transformación (o matriz) nilpotente, deberemos hacer un análisis cuidadoso del rango de las potencias de la transformación (o matriz). Veremos esto en las siguientes entradas.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Verifica que la siguiente matriz es nilpotente: $$\begin{pmatrix}13 & 6 & -14 & -5\\ 2 & 0 & -4 & -2 \\ 29 & 12 & -34 & -13 \\ -45 & -18 & 54 & 21\end{pmatrix}.$$
    Siguiendo las ideas de la demostración de existencia de esta entrada, ¿cómo podrías dar la forma canónica de Jordan de esta matriz? Intenta hacerlo.
  2. Sea $V$ un espacio vectorial de dimensión finita y $T:V\to V$ una transformación lineal nilpotente de índice $k$. Demuestra que $^tT$ también es una transformación lineal nilpotente de índice $k$. ¿Cuál sería el resultado análogo para matrices?
  3. Sea $V$ un espacio vectorial de dimensión finita y $T:V \to V$ una transformación lineal tal que para cualquier $v$ en $V$ existe algún entero $n$ tal que $T^n(v)=0$. Estos $n$ pueden ser distintos para distintos $v$. Muestra que $T$ es nilpotente.
  4. Considera el subespacio $V$ de polinomios reales con grado a lo más $4$ y $D:V\to V$ la transformación lineal derivar. Da, de manera explícita, espacios $W$ y $W’$ como en las proposición de encontrar el subespacio complementario estable.
  5. Hay varios detalles que quedaron pendientes en las demostraciones de esta entrada. Revisa la entrada para encontrarlos y da las demostraciones correspondientes.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»