Introducción
En la entrada anterior empezamos a hablar del teorema de la función inversa. Dimos su enunciado y probamos varias herramientas que nos ayudarán ahora con su demostración.
Recordemos que lo que queremos demostrar es lo siguiente.
Teorema (de la función inversa). Sea $f:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}^{n}$ de clase $C^{1}$ en el abierto $S$. Si $Df(\bar{a})$ es invertible, entonces, existe $\delta >0$ tal que:
- $B_{\delta}(\bar{a})\subseteq S$ y $f$ es inyectiva en $B_{\delta}(\bar{a})$.
- $f^{-1}:f(B_{\delta}(\bar{a}))\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}^{n}$ es continua en $f(B_{\delta}(\bar{a}))$.
- $f(B_{\delta}(\bar{a}))\subseteq \mathbb{R}^{n}$ es un conjunto abierto.
- $f^{-1}$ es de clase $C^{1}$ en $f(B_{\delta}(\bar{a}))$ y además, si $\bar{x}=f(\bar{v})\in f(B_{\delta}(\bar{a}))$, entonces, $Df^{-1}(\bar{x})=Df^{-1}(f(\bar{v}))=(Df(\bar{v}))^{-1}$.
La herramienta más importante que probamos en la entrada anterior nos dice que si una función $f:S\subseteq \mathbb{R}^n\to \mathbb{R}^n$ es de clase $C^1$, $\bar{a}\in S$ y $DF(\bar{a})$ es invertible, entonces existe una $\delta>0$ tal que $B_\delta(\bar{a})\subseteq S$ y $Df(\bar{b})$ es invertible para todo $\bar{b}\in B_\delta(\bar{a})$. Veremos cómo esta herramienta y otras que desarrollaremos en el transcurso de esta entrada nos permiten demostrar el teorema.
La función $f$ es inyectiva en una vecindad de $\bar{a}$
Vamos a enfocarnos en el punto $(1)$ del teorema. Veremos que existe la $\delta$ que hace que la función restringida a la bola de radio $\delta$ centrada en $\bar{a}$ es inyectiva. En esta parte de la prueba es conveniente que recuerdes que la norma infinito de un vector $(x_1,\ldots,x_n)\in \mathbb{R}^n$ es $$||\bar{x}||_{\infty}:=máx\{ |x_{1}|,\dots ,|x_{n}|\}.$$
Además, cumple para todo $\bar{x}\in \mathbb{R}^{n}$ que $$||\bar{x}||\leq \sqrt{n} ||\bar{x}||_{\infty}.$$
Veamos que bajo las hipótesis del problema se puede acotar $||f(\bar{u})-f(\bar{v})||$ en términos de $||\bar{u}-\bar{v}||$ dentro de cierta bola.
Proposición. Sea $f:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}^{n}$ de clase $C^{1}$ en el conjunto abierto $S$, y $\bar{a}\in S$. Si $Df(\bar{a})$ es invertible, entonces existe $\delta >0$ y $\varepsilon>0$ tal que $B_{\delta}(\bar{a})\subseteq S$ y $||f(\bar{u})-f(\bar{v})||\geq \varepsilon||\bar{u}-\bar{v}||$ para cualesquiera $\bar{u},\bar{v}\in B_{\delta}(\bar{a})$.
Demostración. Por la diferenciabilidad de $f$ en $\bar{a}$, tenemos
\[ Df(\bar{a})(\bar{x})=\begin{pmatrix} \triangledown f_{1}(\bar{a})\cdot \bar{x} \\ \vdots \\ \triangledown f_{n}(\bar{a})\cdot \bar{x}\end{pmatrix} \]
para cada $\bar{a}\in S$ y cada $\bar{x}\in \mathbb{R}^{n}$.
Como $Df(\bar{a})$ es invertible, por los resultados de la entrada anterior existe un $m>0$ tal que
\[ ||Df(\bar{a})(\bar{x})||\geq m||\bar{x}|| \]
para todo $\bar{x}\in \mathbb{R}^{n}$.
También por resultados de la entrada anterior, para $\epsilon:=\frac{m}{2\sqrt{n}}>0$ existe $\delta >0$ tal que si $\bar{b}\in B_{\delta}(\bar{a})\subseteq S$ entonces
\[||(Df(\bar{b})-Df(\bar{a}))(\bar{x})||\leq \frac{m}{2\sqrt{n}}||\bar{x}||\]
para todo $\bar{x}\in \mathbb{R}^{n}$.
Usaremos en un momento estas desigualdades, pero por ahora fijemos nuestra atención en lo siguiente. Dados $\bar{u},\bar{v}\in B_{\delta}(\bar{a})$, tomemos el $k\in \{1,\dots ,n\}$ tal que $$||Df(\bar{a})(\bar{u}-\bar{v})||_{\infty}=|\triangledown f_{k}(\bar{a})\cdot (\bar{u}-\bar{v})|.$$
Para dicho $k$, tenemos
\begin{align*}
|\triangledown f_{k}(\bar{a})\cdot (\bar{u}- \bar{v})|&=||Df(\bar{a})(\bar{u}-\bar{v})||_{\infty}\\
&\geq \frac{1}{\sqrt{n}}||Df(\bar{a})(\bar{u}-\bar{v})||.
\end{align*}
¿Cómo podemos seguir con nuestras desigualdades? Necesitamos usar el teorema del valor medio. Bastará el que demostramos para campos escalares. Aplicándolo a $f_k$ en los puntos $\bar{u},\bar{v}$ cuyo segmento se queda en la bola convexa $B_\delta(\bar{a})$, podemos concluir que existe un vector $\bar{w}$ en el segmento $\bar{\bar{u}\bar{v}}$ que cumple
$$f_k(\bar{u})-f_k(\bar{v})=\triangledown f(\bar{w}) \cdot (\bar{u}-\bar{v}).$$
Sabemos que para cualquier vector el valor absoluto de cualquiera de sus coordenadas es en valor menor o igual que la norma del vector. Además, demostramos inicialmente unas desigualdades anteriores. Juntando esto, obtenemos la siguiente cadena de desigualdades:
\begin{align*}
||f(\bar{u})-f(\bar{v})||&\geq |f_{k}(\bar{u})-f_{k}(\bar{v})|\\
&=|\triangledown f(\bar{w}) \cdot (\bar{u}-\bar{v})|\\
&\geq |\triangledown f_k(\bar{a})\cdot (\bar{u}-\bar{v})|-|\triangledown f_k(\bar{w}) \cdot (\bar{u}-\bar{v})-\triangledown f_k(\bar{a})\cdot (\bar{u}-\bar{v})|\\
&\geq \frac{1}{\sqrt{n}}||Df(\bar{a})(\bar{u}-\bar{v})|| – ||Df(\bar{w})(\bar{u}-\bar{v})-Df(\bar{a})(\bar{u}-\bar{v})||\\
&\geq \frac{1}{\sqrt{n}}(m||\bar{u}-\bar{v}||)-\frac{m}{2\sqrt{n}}||\bar{u}-\bar{v}||\\
&=\frac{m}{2\sqrt{n}}||\bar{u}-\bar{v}||\\
&=\varepsilon||\bar{u}-\bar{v}||.
\end{align*}
La gran conclusión de esta cadena de desigualdades es que $$||f(\bar{u})-f(\bar{v})||\geq \varepsilon||\bar{u}-\bar{v}||,$$ que es lo que buscábamos.
$\square$
¡Esto es justo lo que nos pide el primer punto! Hemos encontrado una bola alrededor de $\bar{a}$ dentro de la cual si $\bar{u}\neq \bar{v}$, entonces $||f(\bar{u})-f(\bar{v})||\geq \varepsilon ||\bar{u}-\bar{v}||>0$, de modo que $f(\bar{u})\neq f(\bar{v})$. ¡La función restringida en esta bola es invertible! En términos geométricos el último teorema nos dice lo siguiente: Si $f$ es diferenciable en un abierto $S$, y $Df(\bar{a})$ es invertible, entonces hay una vecindad alrededor de $\bar{a}$ en donde $f$ «no se pega», es decir $f$ es inyectiva.

Ya vimos cómo encontrar una bola $B_\delta(\bar{a})$ dentro de la cual $f$ es inyectiva. Si pensamos que el contradominio es exactamente $f(B_\delta(\bar{a}))$, entonces la función también es suprayectiva. Esto hace que sea biyectiva y por tanto que tenga inversa $f^{-1}$.
La función inversa es continua
Veamos ahora que la función inversa es continua. De hecho, mostraremos algo un poco más fuerte.
Teorema. Sea $f:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}^{n}$ de clase $C^{1}$ en el abierto $S$, y $\bar{a}\in S$. Si $Df(\bar{a})$ es invertible, entonces existe $\delta >0$ tal que $B_{\delta}(\bar{a})\subseteq S$, $f$ es inyectiva en $B_{\delta}(\bar{a})$ y además $f^{-1}:f(B_{\delta}(\bar{a}))\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}^{n}$ es uniformemente continua en su dominio.
Demostración. La primera parte y la existencia de $f^{-1}:f(B_\delta(a))\subseteq \mathbb{R}^n \to \mathbb{R}^n$ se debe a la discusión de la sección anterior. De hecho, lo que mostramos es que existe $\delta >0$ y $\varepsilon>0$ tal que $||f(\bar{v})-f(\bar{u})||\geq \varepsilon||\bar{v}-\bar{u}||$ para todo $\bar{u},\bar{v}\in B_{\delta}(\bar{a})$.
Supongamos que nos dan un $\varepsilon^\ast$. Tomemos $\delta^\ast=\varepsilon^\ast \varepsilon$. Tomemos $\bar{x},\bar{y}$ en $f(B_\delta(\bar{a}))$ tales que $||\bar{y}-\bar{x}||<\delta ^{\ast}$. Como $\bar{x}$ y $\bar{y}$ están en dicha bola, podemos escribirlos como $\bar{x}=f(\bar{u})$, $\bar{y}=f(\bar{v})$ con $\bar{u},\bar{v}\in B_{\delta}(\bar{a})$. Notemos entonces que
\begin{align*}
||f^{-1}(\bar{y})-f^{-1}(\bar{x})||&=||\bar{v}-\bar{u}||\\
&\leq \frac{1}{\varepsilon}||f(\bar{v})-f(\bar{u})||\\
&= \frac{1}{\varepsilon}||\bar{y}-\bar{x}||\\
&<\frac{\varepsilon^\ast\varepsilon}{\varepsilon}\\
&=\varepsilon^\ast.
\end{align*}
Tenemos entonces que $f^{-1}$ es uniformemente continua en $f(B_\delta(\bar{a}))$.
$\square$
Esto demuestra el punto $(2)$ de nuestro teorema. La prueba de que el conjunto $f(B_\delta(\bar{a}))$ es abierto no es para nada sencilla como parecería ser. Una demostración muy instructiva, al nivel de este curso, se puede encontrar en el libro Cálculo diferencial de varias variables del Dr. Javier Páez Cárdenas editado por la Facultad de Ciencias de la Universidad Nacional Autónoma de México (UNAM) en las páginas 474-476.
La función inversa es diferenciable
Resta hacer la demostración de $(4)$. En esta sección veremos que la inversa $f^{-1}$ es derivable y que la derivada es precisamente lo que propone el teorema. En la siguiente sección veremos que la inversa es $C^1$.
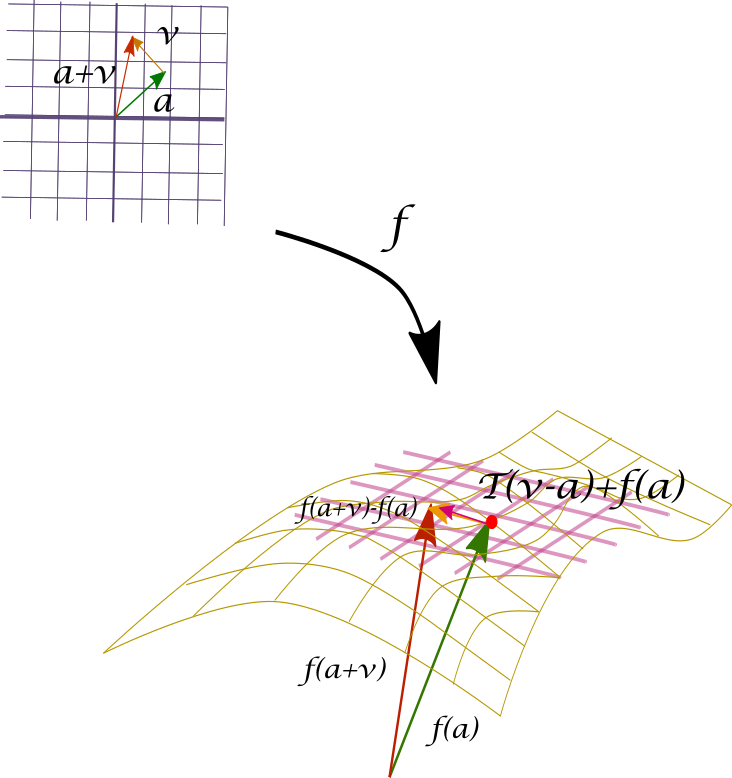
Tomemos un punto $\bar{x}_0=f(\bar{v}_0)\in f(B_{\delta}(\bar{a}))$. Mostraremos que, en efecto, $T=(Df(\bar{v}_0))^{-1}$ es la derivada de $f^{-1}$ en $\bar{x}_0$, lo cual haremos por definición verificando que
\[ \lim\limits_{\bar{x}\to \bar{x}_{0}}\frac{f^{-1}(\bar{x})-f^{-1}(\bar{x}_{0})-T(\bar{x}-\bar{x}_{0})}{||\bar{x}-\bar{x}_{0}||}=0.\]
Para ello, introducimos la siguiente función auxiliar $g:B_{\delta}(\bar{a})\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}^{n}$ dada por:
\[ g(\bar{v})=\left\{ \begin{matrix} \frac{\bar{v}-\bar{v}_{0}-T(f(\bar{v})-f(\bar{v}_{0}))}{||f(\bar{v})-f(\bar{v}_{0})||} & \bar{v}\neq \bar{v}_{0} \\ \bar{0} & \bar{v}=\bar{v}_{0}. \end{matrix} \right. \]
Esta función está bien definida, pues $f$ es inyectiva en la bola $B_{\delta}(\bar{a})$. La composición $g\circ f^{-1}$ también está bien definida en el abierto $f(B_{\delta}(\bar{a}))$ y
\[ (g\circ f^{-1})(\bar{x})=\left\{ \begin{matrix} \frac{f^{-1}(\bar{x})-f^{-1}(\bar{x}_{0})-T(\bar{x}-\bar{x}_{0})}{||\bar{x}-\bar{x}_{0}||} & \bar{x}\neq \bar{x}_{0} \\ \bar{0} & \bar{x}=\bar{x}_{0} \end{matrix} \right.\]
para todo $\bar{x}\in f(B_{\delta}(\bar{a}))$. Esto nos permite poner el límite buscado como el límite de una composición de la siguiente forma:
\[ \lim\limits_{\bar{x}\to \bar{x}_{0}}\frac{f^{-1}(\bar{x})-f^{-1}(\bar{x}_{0})-T(\bar{x}-\bar{x}_{0})}{||\bar{x}-\bar{x}_{0}||}=\lim\limits_{\bar{x}\to \bar{x}_{0}}(g\circ f^{-1})(\bar{x}) \]
Como $f^{-1}$ es continua en $\bar{x}_{0}$, basta demostrar que $g$ es continua en $\bar{v}_{0}=f^{-1}(\bar{x}_{0})$. Esto equivale a probar que
\[ \lim\limits_{\bar{v}\to \bar{v}_{0}}g(\bar{v})=\lim\limits_{\bar{v}\to \bar{v}_{0}}\frac{\bar{v}-\bar{v}_{0}-(Df(\bar{v}_{0}))^{-1}(f(\bar{v})-f(\bar{v}_{0})))}{||f(\bar{v})-f(\bar{v}_{0})||}=0.\]
Hay que demostrar este último límite. Reescribimos la expresión
$$\frac{\bar{v}-\bar{v}_{0}-(Df(\bar{v}_{0}))^{-1}(f(\bar{v})-f(\bar{v}_{0}))}{||f(\bar{v})-f(\bar{v}_{0})||}$$ como
$$\frac{(Df(\bar{v}_{0}))^{-1}[Df(\bar{v}_{0})(\bar{v}-\bar{v}_{0})-(f(\bar{v})-f(\bar{v}_{0}))]}{||f(\bar{v})-f(\bar{v}_{0})||},$$
y luego multiplicamos y dividimos por $||\bar{v}-\bar{v}_0||$ y reorganizamos para obtener
\[ -\frac{||\bar{v}-\bar{v}_{0}||}{||f(\bar{v})-f(\bar{v}_{0})||}(Df(\bar{v}_{0}))^{-1}\left( \frac{f(\bar{v})-f(\bar{v}_{0})-Df(\bar{v}_{0})(\bar{v}-\bar{v}_{0})}{||\bar{v}-\bar{v}_{0}||}\right).\]
Como $(Df(\bar{v}_{0}))^{-1}$ es continua (por ser lineal) y $f$ es diferenciable en $\bar{v}_{0}$, se tiene que
\begin{align*}
\lim\limits_{\bar{v}\to \bar{v}_{0}}(Df(\bar{v}_{0}))&^{-1}\left( \frac{f(\bar{v})-f(\bar{v}_{0})-Df(\bar{v}_{0})(\bar{v}-\bar{v}_{0})}{||\bar{v}-\bar{v}_{0}||}\right)\\
&=(Df(\bar{v}_{0}))^{-1}\left( \lim\limits_{\bar{v}\to \bar{v}_{0}}\frac{f(\bar{v})-f(\bar{v}_{0})-Df(\bar{v}_{0})(\bar{v}-\bar{v}_{0})}{||\bar{v}-\bar{v}_{0}||}\right)\\
&=(Df(\bar{v}_{0}))^{-1}(\bar{0})\\
&=\bar{0}.
\end{align*}
El factor que nos falta entender es $\frac{||\bar{v}-\bar{v}_{0}||}{||f(\bar{v})-f(\bar{v}_{0})||}$. Pero por la primera proposición de esta entrada, sabemos que existe una $\epsilon>0$ que acota este factor superiormente por $\frac{1}{\epsilon}$. De esta manera,
\[ \lim\limits_{\bar{v}\to \bar{v}_{0}}g(\bar{v})=\cancelto{acotado}{\lim\limits_{\bar{v}\to \bar{v}_{0}}\frac{-||\bar{v}-\bar{v}_{0}||}{||f(\bar{v})-f(\bar{v}_{0})||}}\cancelto{0}{(Df(\bar{v}_{0}))^{-1}\left( \frac{f(\bar{v})-f(\bar{v}_{0})-Df(\bar{v}_{0})(\bar{v}-\bar{v}_{0})}{||\bar{v}-\bar{v}_{0}||}\right)}=0.\]
Esto nos dice entonces que $g$ es continua en $\bar{v}_0$ y por lo tanto:
\begin{align*}
\lim\limits_{\bar{x}\to \bar{x}_{0}}(g\circ f^{-1})(\bar{x}) &= g\left(\lim_{\bar{x}\to \bar{x}_0} f^{-1}(\bar{x})\right)\\
&=g(f^{-1}(\bar{x}_0))\\
&=g(\bar{v}_0)\\
&=\bar{0}.
\end{align*}
Por lo tanto $f^{-1}$ es diferenciable en $\bar{x}_{0}$ mediante la derivada que propusimos, es decir,
\[ Df^{-1}(\bar{x}_{0})=Df^{-1}(f(\bar{v}_{0}))=(Df(\bar{v}_{0}))^{-1}=(Df(f^{-1}(\bar{x}_{0})))^{-1} \]
para todo $\bar{x}_0\in f(B_{\delta}(\bar{a}))$.
La función inversa es de clase $C^1$
Resta verificar que $f^{-1}$ es de clase $C^{1}$ en $f(B_{\delta}(\bar{a}))$. Lo haremos con la caracterización de la entrada anterior. Tomemos una $\mu>0$. Nos gustaría ver que si $\bar{x}$ y $\bar{x}_0$ están suficientemente cerca, entonces
$$||Df^{-1}(\bar{x})(\bar{z})-Df^{-1}(\bar{x}_{0})(\bar{z})||<\mu ||\bar{z}||$$
para toda $\bar{z} \in \mathbb{R}^n$.
Recordemos que por la entrada anterior hay una $m>0$ tal que para todo $\bar{z}$ en $\mathbb{R}^n$ se cumple
\begin{equation}
\label{eq:clasec1}
\frac{1}{m}||\bar{z}||=\frac{1}{m}|Df(\bar{v})((Df(\bar{v}))^{-1})(\bar{z})||\geq ||(Df(\bar{v}))^{-1}(\bar{z})||
\end{equation}
También notemos que, si $X,Y$ son matrices invertibles en $M_n(\mathbb{R})$, tenemos:
$$X^{-1}(Y-X)Y^{-1}=X^{-1}YY^{-1}-X^{-1}XY^{-1}=X^{-1}-Y^{-1}.$$
Tomando $X=Df(\bar{v})$ y $Y=Df(\bar{v}_0)$, aplicando la igualdad anterior en un punto $\bar{x}$ en $\mathbb{R}^n$, sacando normas y usando la desigualdad \eqref{eq:clasec1}, obtenemos:
\begin{align*}
||(X^{-1}-Y^{-1})(\bar{z})||&=||(X^{-1}(Y-X)Y^{-1})(\bar{z})||\\
&\leq \frac{1}{m} ||((Y-X)Y^{-1})(\bar{z})||\\
&=\frac{1}{m}||((Df(\bar{v}_0)-Df(\bar{v}))Df^{-1}(f(\bar{v}_0)))(\bar{z})||.
\end{align*}
Como $f$ es de clase $C^1$, por la entrada anterior podemos construir una $\delta^\ast$ tal que $B_{\delta^\ast}(\bar{v}_0)\subseteq B_\delta(\bar{a})$ y para la cual si $\bar{v}$ está en $B_{\delta^\ast}(\bar{v}_0)$, entonces:
\[ \begin{equation}||(Df(\bar{v}_{0})-Df(\bar{v}))(\bar{z})||\leq m^{2}\mu||\bar{z}||\end{equation}.\]
Para todo $\bar{x}\in \mathbb{R}^{n}$.
Finalmente, como $f^{-1}$ es continua en $f(B_{\delta}(\bar{a}))$, si $\bar{x}$ y $\bar{x}_0$ están suficientemente cerca, digamos $||\bar{x}-\bar{x}_0||<\nu$, entonces
\[ \begin{equation}||f^{-1}(\bar{x})-f^{-1}(\bar{x}_{0})||=||\bar{v}-\bar{v}_{0}||<\delta ^\ast.\end{equation}.\]
Usamos todo lo anterior para establecer la siguiente cadena de desigualdades cuando $||\bar{x}-\bar{x}_0||<\nu$:
\begin{align*}
||Df^{-1}(\bar{x})(\bar{z})-Df^{-1}(\bar{x}_{0})(\bar{z})||&=||Df^{-1}(f(\bar{v}))(\bar{z})-Df^{-1}(f(\bar{v}_{0}))(\bar{z})||\\
&\leq \frac{1}{m}||[Df(\bar{v}_{0})-Df(\bar{v})](Df^{-1}(f(\bar{v}_{0})))(\bar{z})||\\
&\leq \frac{1}{m}\left( m^{2}\mu ||Df^{-1}(f(\bar{v}_{0}))(\bar{z})||\right) \\
&=m\mu ||Df^{-1}(f(\bar{v}_{0}))(\bar{z})||\\
&\leq m\mu \left( \frac{1}{m}||\bar{z}||\right)\\
&=\mu||\bar{z}||.
\end{align*}
Esto implica que $f^{-1}$ es de clase $C^1$. Como tarea moral, revisa los detalles y di explícitamente qué resultado de la entrada anterior estamos usando.
$\square$
Ejemplo del teorema de la función inversa
Ejemplo. Consideremos $\xi :\mathbb{R}^{3}\rightarrow \mathbb{R}^{3}$ dada por $\xi (r,\theta, \phi)=(r\hspace{0.15cm}sen \phi \hspace{0.15cm}cos\theta ,r\hspace{0.15cm} sen \phi \hspace{0.15cm}sen\theta ,r\hspace{0.15cm}cos \phi)$. Se tiene que $\xi$ es diferenciable en todo su dominio pues cada una de sus derivadas parciales es continua. Esta es la función de cambio de coordenadas de esféricas a rectangulares o cartesianas. La matriz jacobiana está dada como sigue.
\[ D\xi (r,\theta ,\phi )=\begin{pmatrix} sen\phi \hspace{0.1cm}cos\theta & -r\hspace{0.1cm}sen\phi \hspace{0.1cm}sen\theta & r\hspace{0.1cm}cos\phi \hspace{0.1cm}cos\theta \\ sen\phi \hspace{0.1cm}sen\theta & r\hspace{0.1cm}sen\phi \hspace{0.1cm}cos\theta & r\hspace{0.1cm}cos\phi \hspace{0.1cm}sen\theta \\ cos\phi & 0 & -r\hspace{0.1cm}sen\phi \end{pmatrix}.\]
Luego $\det(D\xi (r,\theta ,\phi ))=-r^{2}\hspace{0.1cm}sen\phi$ entonces $D\xi$ es invertible cuando $r\neq 0$ y $\phi \neq k\pi$, $k\in \mathbb{Z}$. Su inversa es:
\[ (D\xi (r,\theta ,\phi ))^{-1}=\begin{pmatrix} sen\phi \hspace{0.1cm}cos\theta & sen\phi \hspace{0.1cm}sen\theta & cos\phi \\ -\frac{sen\theta}{r\hspace{.01cm}sen\phi} & \frac{cos\theta}{r\hspace{0.1cm}sen\phi} & 0 \\ \frac{1}{r}\hspace{0.1cm}cos\theta \hspace{0.1cm}cos\phi & \frac{1}{r}\hspace{0.1cm}cos\phi \hspace{0.1cm}sen\theta & -\frac{1}{r}\hspace{0.1cm}sen\phi \end{pmatrix}.\]
El teorema de la función inversa nos garantiza la existencia local de una función $\xi ^{-1}$. En este caso, sería la función de cambio de coordenadas rectangulares a esféricas. Si $f:S\subseteq \mathbb{R}^{3}\rightarrow \mathbb{R}$ es una función $C^{1}$ dada en coordenadas esféricas; podemos asumir que $f\circ \xi ^{-1}$ es la misma función pero en términos de coordenadas rectangulares.
$\triangle$
Más adelante…
¡Lo logramos! Hemos demostrado el teorema de la función inversa, uno de los resultados cruciales de nuestro curso. El siguiente tema es el teorema de la función implícita, que será otro de nuestros resultados principales. Uno podría pensar que nuevamente tendremos que hacer una demostración larga y detallada. Pero afortunadamente la demostración del teorema de la función implícita se apoya fuertemente en el teorema de la función inversa que ya demostramos. En la siguiente entrada enunciaremos y demostraremos nuestro nuevo resultado y una entrada más adelante veremos varios ejemplos para profundizar en su entendimiento.
Tarea moral
- En el ejemplo que dimos, verifica que el determinante en efecto es $-r^2\sin\phi$. Verifica también que la inversa es la matriz dada.
- Repasa cada una de las demostraciones de esta entrada y asegúrate de entender por qué se siguen cada una de las desigualdades. Explica en qué momentos estamos usando resultados de la entrada anterior.
- Da la función inversa de la transformación de cambio de coordenadas polares a rectangulares $g(r,\theta)=(r\hspace{0.1cm}cos\theta , r\hspace{0.1cm}sen\theta )$.
- Demuestra que para todo $\bar{x}\in \mathbb{R}^{n}$ se tiene $||\bar{x}||\leq \sqrt{n}||\bar{x}||_{\infty}.$
- Verifica que en efecto $||\cdot||_{\infty}$ es una norma.
Entradas relacionadas
- Ir a Cálculo Diferencial e Integral III
- Entrada anterior del curso: Introducción al teorema de la función inversa
- Entrada siguiente del curso: Teorema de la función implícita y demostración