Introducción
En esta entrada abordaremos los conceptos de conexidad y compacidad para caracterizar a los conjuntos de $\mathbb{C}$, además de que veremos que tanto la conexidad como la compacidad son invariantes respecto a una función continua, es decir, son propiedades topológicas, concluyendo así que entre espacios métricos homeomorfos los conjuntos conexos y compactos están en correspondencia biunívoca.
Intuitivamente al hablar de un conjunto conexo pensamos en conjuntos que están constituidos por una sola pieza, conjuntos que no están formados por piezas separadas. Esta característica nos devuelve muchas propiedades importantes que se obtienen al trabajar con este tipo de conjuntos.
Mientras que el concepto de conjunto conexo es fácil de interpretar intuitivamente, el concepto de conjunto compacto no lo es, sin embargo podemos pensar a la compacidad como una generalización topológica de conjunto finito, lo cual es de suma utilidad pues nos permite dotar de propiedades importantes, que se cumplen en conjuntos finitos, a los conjuntos compactos.
Conexidad en un espacio métrico
Definición 10.1. (Subespacio métrico.)
Si $(X,d_X)$ es un espacio métrico y $A\subset X$ se define para todo $x,y\in A$ la métrica inducida por $d_X$ como:
\begin{equation*}
d_A(x,y) = d_X(x,y).
\end{equation*} Esta es claramente una métrica en $A$. Al conjunto $A$ dotado con está métrica se le llama un subespacio métrico de $X$ y lo denotamos como $(A, d_A)$.
Definición 10.2. (Conexidad.)
Un espacio métrico $(X,d_X)$ se dice que es conexo si los únicos subconjuntos de $X$ tales que ambos son abiertos y cerrados en $X$ son el conjunto $\emptyset$ y $X$. Si $A\subset X$, entonces $A$ es un subconjunto conexo de $X$ si el subespacio métrico $(A, d_A)$ es conexo.
Equivalentemente, un espacio métrico $X$ se dice que no es conexo o que es disconexo si existen subconjuntos $A$ y $B$ de $X$, ambos abiertos en $X$ y tales que: \begin{equation*}
A\neq\emptyset, \,\, B\neq\emptyset, \,\, A\cap B = \emptyset \,\,\, \text{y} \,\,\, X = A \cup B.
\end{equation*} Considerando estas condiciones se tiene que $A$ y $B$ son también cerrados en $X$ desde que $A=X\setminus B$ y $B=X\setminus A$.
Ejemplo 10.1.
a) Dado que $\mathbb{C}$ y $\emptyset$ son los únicos subconjuntos abiertos y cerrados en $\mathbb{C}$, ejemplo 7.1(d), tenemos que $(\mathbb{C},d)$ es conexo.
b) Los números reales $\mathbb{R}$ dotados con la métrica euclidiana dada por el valor absoluto, es decir para $a, b\in\mathbb{R}$ se define $d(a,b) = |a\,-\,b|$, forman un espacio métrico conexo.
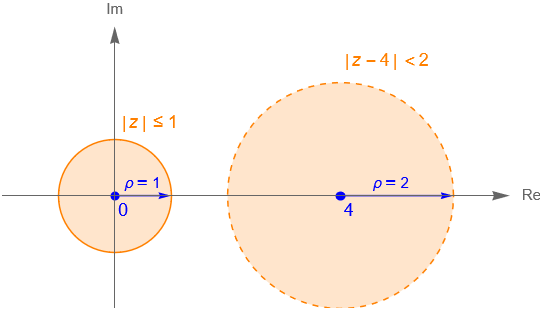
c) Sea $X = A \cup B$ donde $ A = \{ z\in\mathbb{C} : |\,z\,| \leq 1 \} $ y $B = \{ z\in\mathbb{C} : |\,z – 4\,| < 2\}$, dotado con la métrica euclidiana. Veamos que el subespacio métrico $(X,d_X)$ es disconexo, figura 48.
Solución. Dado que $X\subset\mathbb{C}$ está dotado con la métrica euclidiana, entonces $(X, d_X)$ es un espacio métrico. Por lo que $A = \overline{B}(0,1)$ es un conjunto cerrado en $X$ y $B = B(4,2)$ es un conjunto abierto en $X$. Veamos que $A$ también es abierto. Sea $w \in A$, notemos que para todo $\rho \in (0,1)$ se cumple que:
\begin{equation*}
B(w,\rho) = \{ z \in X \, : \, |z-w|<\rho \} \subset A,
\end{equation*} por lo que $A$ es abierto.
Es claro que $A\neq \emptyset$, $B\neq \emptyset$, $A \cap B = \emptyset$ y $X = A \cup B$. Dado que $A$ y $B$ son abiertos en $X$, entonces $(X, d_X)$ es disconexo.
Recordemos el siguiente resultado del espacio métrico $(\mathbb{R}, d)$, donde $d(a,b)=|a\,-\,b|$ para $a,b\in\mathbb{R}$.
Proposición 10.1.
Un conjunto $I\subset \mathbb{R}$ es conexo si y sólo si $I$ es un intervalo.
Demostración. Ejercicio.
$\blacksquare$
Definición 10.3. (Región o dominio.)
Un conjunto $U\subset\mathbb{C}$ abierto y conexo se llama región o dominio.
Ejemplo 10.2.
a) El conjunto $\mathbb{C}$ es una región.
b) Dado $z_0\in\mathbb{C}$, se tiene que para todo $\rho>0$ una $\rho$-vecindad de $z_0$ es una región, figura 41(a).
c) El conjunto $X = \{z\in\mathbb{C} \, : \, 1 < \operatorname{Re}(z) + \operatorname{Im}(z) < 4\} \cap \{ z\in\mathbb{C} \, : \, |\,\operatorname{Re}(z) – \operatorname{Im}(z)\,|< 2\}$ es una región, figura 49.
Definición 10.4. (Segmento de recta.)
Sean $z_1,z_2\in\mathbb{C}$, entonces el segmento de recta que va de $z_1$ a $z_2$, denotado por $[z_1, z_2]$, se define como:
\begin{equation*}
[z_1, z_2] = \{ z_1 + t(z_2 -z_1) \, : \, 0\leq t \leq 1 \}
\end{equation*}
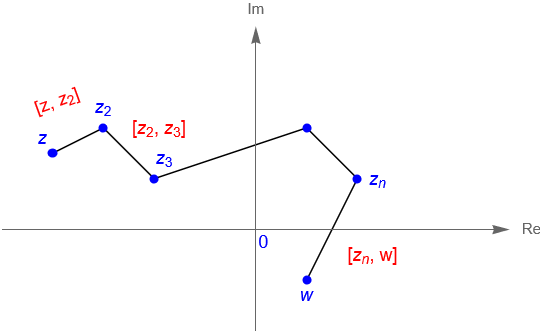
Definición 10.5. (Polígono o poligonal.)
Sean $z,w\in\mathbb{C}$, con $z\neq w$. Un polígno o poligonal de $z$ a $w$ se define como el conjunto de $n$-segmentos de recta que unen a dichos puntos, es decir: \begin{align*}
P & = \bigcup\limits_{k=1}^{n} [z_k, w_k]\\
& = [z, z_2, \ldots , z_n, w],
\end{align*} donde $z=z_1$, $w=w_n$ y $w_k = z_{k+1}$ para $1\leq k \leq n-1$.
Definición 10.6. (Poligonal conexo.)
Un conjunto $S\subset\mathbb{C}$ se llama poligonal conexo si para cualesquiera dos puntos $z, w\in S$ existe un polígono de $z$ a $w$ tal que está totalmente contenido en $S$.
Ejemplo 10.3.
Sean $\rho_1, \rho_2, \rho_3 \in (0,\infty)$ con $\rho_1 < \rho_2 < \rho_3$ y $z_0 \in \mathbb{C}$ un punto fijo. Consideremos a los siguientes conjuntos de $\mathbb{C}$:
a) $X = \overline{B}(z_0,\rho_1) \cup \left( \, \overline{B}(z_0,\rho_3) \setminus \overline{B}(z_0,\rho_2) \right)$, figura 51(a).
b) $Y = B(z_0,\rho_2) \setminus B(z_0,\rho_1)$, figura 51(b).
Figura 51: El conjunto $X$ no es poligonal conexo, mientras que el conjunto $Y$ sí es poligonal conexo..
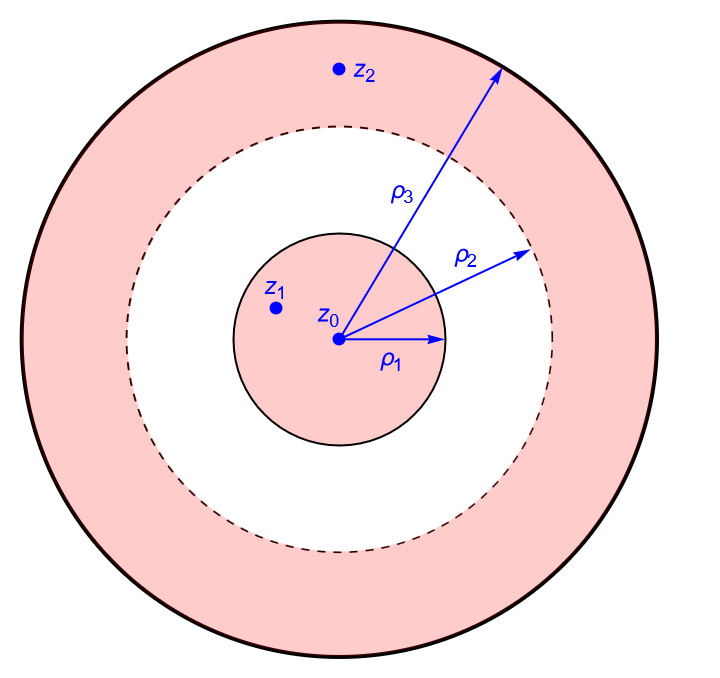
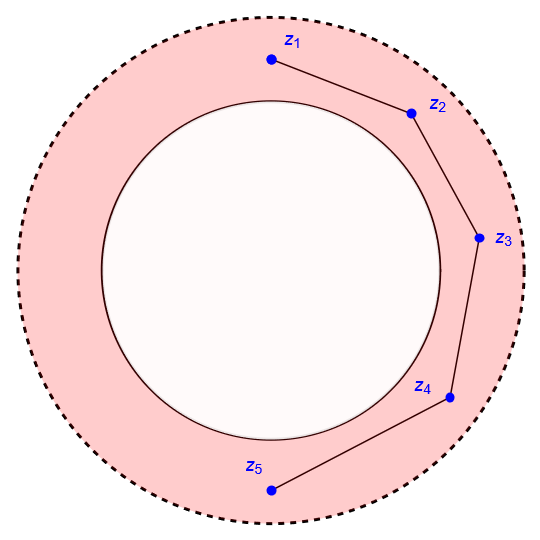
De acuerdo con la figura 51(a) podemos ver que el conjunto $X$ no es poligonal conexo, ya que si tomamos a $z_1 \in \overline{B}(z_0,\rho_1)$ y $z_2 \in \overline{B}(z_0,\rho_3) \setminus \overline{B}(z_0,\rho_2)$, entonces no es posible trazar una poligonal que una a dichos puntos.
Por otra parte, considerando la figura 51(b) es claro que para cualesquiera dos puntos en $Y$ es posible encontrar una poligonal que los una y que se quede contenida en $Y$, por lo que dicho conjunto sí es poligonal conexo.
Teorema 10.1.
Un conjunto $S \subset \mathbb{C}$ abierto es conexo si y solo si es poligonal conexo.
Demostración.
$\Rightarrow)$
Supongamos que $S$ es un dominio y sea $\zeta \in S$ un punto fijo. Dar una construcción explícita de un polígono $P$ que vaya de $\zeta$ a un punto $w \in S$ tal que $P\subset S$, puede resultar un tanto complicado. Sin embargo solo basta con garantizar que existe dicho polígono. Definamos el siguiente conjunto: \begin{equation*} A = \{w \in S \, : \, \text{existe un polígono} \, \, P \,\, \text{de} \, \, \zeta \,\, \text{a} \,\, w \,\, \text{tal que} \,\, P \subset S \}. \end{equation*} Notemos que $A\neq\emptyset$ ya que $\zeta\in A$.
Veamos que $A$ es abierto en $S$. Sea $w\in A$ y sea $P = [\zeta, z_2, \ldots, z_n, w]$ un polígono de $\zeta$ a $w$ tal que $P\subset S$. Dado que $S$ es abierto entonces existe $\rho>0$ tal que $B(w,\rho)\subset S$. Notemos que si $z\in B(w,\rho)$, entonces se cumple que $[w,z] \subset B(w,\rho)$ (¿por qué?) Así el polígono $Q = P \cup [w,z]$ es un polígono de $\zeta$ a $z$ tal que $Q \subset S$, por lo que $z \in A$. Entonces $B(w,\rho) \subset A$, es decir $A$ es abierto.
Es claro que si $A = S$, entonces $S\setminus A = \emptyset$ es abierto, por lo que $A$ es cerrado y en tal caso no habría nada que probar.
Supongamos entonces que existe $z \in S\setminus A$. Dado que $S$ es abierto entonces existe $\rho>0$ tal que $B(z,\rho) \subset S$. Si suponemos que existe $w\in B(z,\rho) \cap A$, entonces podemos construir un polígono $Q = [\zeta, z_2, \ldots, z_n, w] \cup [w, z]$ que va de $\zeta$ a $z$ tal que $Q\subset S$, pero entonces $z \in A$, lo cual es una contradicción. Entonces no existe $w\in B(z,\rho) \cap A$, es decir $B(z,\rho) \cap A = \emptyset$. Por lo que $B(z,\rho) \subset S\setminus A$, de donde concluimos que $S\setminus A$ es abierto. Por lo tanto $A$ es cerrado en $S$.
Como $S$ es conexo y considerando que $A$ es abierto y cerrado en $S$, con $A \neq \emptyset$, entonces concluimos que $A = S$. Por lo tanto $S$ es poligonal conexo.
$(\Leftarrow$
Supongamos que $S$ es poligonal conexo, procedemos por reducción al absurdo. Supongamos que $S$ no es conexo, entonces existen $A\neq\emptyset$ y $B\neq\emptyset$ abiertos tales que $S = A \cup B$, $A \cap B = \emptyset$. Sea $z \in A$ y $w \in B$, por hipótesis sabemos que existe un polígono $P$ que va de $z$ a $w$ tal que $P \subset S$. Desde que $P \subset A \cup B $ y $A \cap B = \emptyset$ al menos uno de los segmentos que forman a $P$ debe tener un punto final en $A$, digamos $z_k$, y otro punto final en $B$, digamos $w_k$. Entonces dicho segmento es $[z_k, w_k]$. Definamos los siguientes conjuntos:
\begin{align*}
T_1 = \{ \lambda \in[0,1] \, : \, z_k + \lambda(w_k – z_k) \in A \},\\
T_2 = \{ \alpha \in[0,1] \, : \, z_k + \alpha(w_k – z_k) \in B \}.
\end{align*} Notemos que $0 \in S$ y $1\in T$, además dado que $A \cap B = \emptyset$ y $[z_k, w_k] \subset P \subset A \cup B$ es fácil ver que $S \cap T = \emptyset$ y $S \cup T = [0,1]$.
Lema 10.1.
Los conjuntos $S$ y $T$ son abiertos en $[0,1]\subset\mathbb{R}$ con la métrica euclidiana.
Demostración. Se deja como ejercicio al lector.
$\blacksquare$
De acuerdo con lo anterior y considerando el lema 10.1 tenemos que $[0,1] = T \cup S$ es disconexo, lo cual contradice la proposición 10.1. Por lo tanto $S$ es conexo.
$\blacksquare$
Observación 10.1.
Notemos que en la prueba del teorema 10.1, al probar que un conjunto poligonal conexo es conexo no utilizamos que $S$ es abierto, entonces ¿un conjunto conexo es poligonal conexo?
Proposición 10.2.
Sea $(X,d_X)$ un espacio métrico. Entonces las siguientes condiciones son equivalentes:
- $(X,d_X)$ es disconexo.
- Existe una función sobreyectiva y continua de $(X,d_X)$ en el espacio métrico discreto de dos elementos $(X_0,d_{X_0})$, donde $X_0 = \{0,1\}$ y $d_{X_0}$ es la métrica discreta, es decir $d_{X_0}(0,1) = 1$.
Demostración.
1. $\Rightarrow)$ 2.
Sea $X = A\cup B$, donde $A$ y $B$ son dos subconjuntos de $X$ abiertos no vacíos tales que $A \cap B = \emptyset$. Definimos la función $f:X \to X_0$ dada por:
\begin{equation*}
f(x)= \left\{ \begin{array}{lcc}
0 & \text{si} & x \in A,\\
1 & \text{si} & x \in B.
\end{array} \right.
\end{equation*} Es claro que la función $f$ es suprayectiva. Notemos que los conjuntos abiertos de $X_0$ son (¿por qué?): \begin{equation*}
\emptyset, \{0\}, \{1\}, X_0.
\end{equation*} Notemos que $f^{-1}\left(\emptyset\right) = \emptyset$, $f^{-1}\left(X_0\right) = X$, y sabemos que los conjuntos $X$ y $\emptyset$ son abiertos en $X$. Por otra parte, tenemos que $f^{-1}\left(\{0\}\right) = A$ y $f^{-1}\left(\{1\}\right) = B$, los cuales con conjuntos abiertos en $X$. Entonces por la proposición 9.2 se sigue que $f$ es continua en $X$.
2. $\Rightarrow)$ 1.
Sea $f:X \to X_0$ una función continua y sobreyectiva. Dado que $f$ es sobreyectiva tenemos que los conjuntos $A = f^{-1}\left(\{0\}\right)$ y $B = f^{-1}\left(\{1\}\right)$ son dos subconjuntos de $X$ no vacíos. Notemos que $A,B$ son abiertos en $X$, ya que los conjuntos $\{0\}$ y $\{1\}$ son abiertos en $X_0$, por lo que al ser $f$ una función continua se sigue de la proposición 9.2 que sus imágenes inversas son abiertas en $X$. Más aún, se tiene que los conjuntos $A$ y $B$ son tales que $X = A \cup B$ y $A \cap B = \emptyset$, por lo que $(X, d_X)$ es disconexo.
$\blacksquare$
Podemos reformular el resultado anterior y obtener el siguiente:
Corolario 10.1
Sea $(X, d_X)$ un espacio métrico. Las siguientes condiciones son equivalentes:
- $(X, d_X)$ es conexo.
- Las únicas funciones continuas de $(X, d_X)$ en $(X_0, d_{X_0})$ son las funciones constantes, es decir las funciones $f(x) = 1$ para todo $x\in X$ y $g(x) = 0$ para todo $x\in X$.
$\blacksquare$
Proposición 10.3.
Sean $(X, d_X)$ y $(Y, d_Y)$ dos espacios métricos y sea $f: X \to Y$ una función continua. Si $(X, d_X)$ es conexo, entonces el subespacio métrico $(f(X), d^*)$, donde $d^*$ es la métrica inducida por $d_Y$, es conexo.
Demostración. Dadas las hipótesis, procedamos por reducción al absurdo, supongamos que $(f(X), d^*)$ es disconexo. Entonces por la proposición 10.2 tenemos que existe una funcion sobreyectiva y continua, digamos $g$, entre $(f(X), d^*)$ y $(X_0, d_{X_0})$. Entonces por la proposición 9.3 se sigue que la función $g \circ f : X \to X_0$ es continua y como $g$ es sobreyectiva se tiene que $g(f(X))=X_0$, lo cual contradice la conexidad de $(X, d_X)$ de acuerdo con el corolario 10.1.
Por lo tanto $(f(X), d^*)$ es conexo.
$\blacksquare$
Un resultado importante que se prueba en Cálculo es el teorema del valor intermedio, el cual resulta ser un caso particular de la proposición 10.3.
Teorema 10.2. (Teorema del valor intermedio.)
Si $f:[a,b] \to \mathbb{R}$ es una función continua en $[a,b]$ con $f(a)<f(b)$, entonces para todo $y$ tal que $f(a) \leq y \leq f(b)$ existe $x\in[a, b]$ tal que $f(x) = y$.
Demostración. Dadas las hipótesis, tomemos a $y\in\mathbb{R}$ tal que $f(a) \leq y \leq f(b)$.
Como $[a, b]\subset\mathbb{R}$ es un intervalo, por la proposición 10.1 se sigue que $([a, b], \,d)$ es conexo, donde $d$ es la métrica inducida por el valor absoluto en $\mathbb{R}$. Dado que $f$ es una función continua y $([a, b], \, d)$ es conexo, por la proposición 10.3 se tiene que $(f([a, b]), \, d^*)$ es conexo, donde $d^*$ es la métrica inducida por el valor absoluto en $\mathbb{R}$. Por la proposición 10.1 tenemos que el conjunto $f([a,b])$ es un intervalo en $\mathbb{R}$. Es claro que dicho intervalo es no vacío desde que $f(a)$ y $f(b)$ pertenecen a dicho conjunto.
Dado que $f(a) \leq y \leq f(b)$ y $f(a),f(b)\in f([a,b])$ entonces se sigue que $y\in f([a,b])$. Por lo tanto existe algún $x\in[a, b]$ tal que $f(x) = y$. Como $y$ era arbitrario se sigue el resultado para todo $y\in\mathbb{R}$ tal que $f(a) \leq y \leq f(b)$.
$\blacksquare$
Proposición 10.4.
Sea $(X, d_X)$ un espacio métrico. Si $Y\subset X$ es conexo en $X$, entonces cualquier conjunto $Z$ tal que $Y \subset Z \subset \overline{Y}$ es conexo.
Demostración. Dadas las hipótesis, supongamos que $Z$ no es conexo. Entonces existen $A\neq \emptyset$ y $B\neq \emptyset$ tales que $Z = A\cup B$ y $A \cap B = \emptyset$.
Como $Y \subset Z \subset \overline{Y}$, entonces $\overline{Y} \subset \overline{Z}$, de donde se sigue que $Y$ es denso en $Z$, por lo que $Y \cap A \neq \emptyset$ y $Y \cap B \neq \emptyset$ son conjuntos abiertos en $Y$ (¿por qué?), además se tiene que: \begin{align*}
(Y \cap A) \cup (Y \cap B) = Y,\\
(Y \cap A) \cap (Y \cap B) = \emptyset,
\end{align*} lo cual contradice la conexidad de $Y$, por lo tanto $Z$ es conexo.
$\blacksquare$
Observación 10.2.
Dado que $Y\subset \overline{Y} \subset \overline{Y}$, de la proposición 10.4 se tiene que $\overline{Y}$ es conexo si $Y$ es conexo en $(X, d_X)$.
Proposición 10.5.
Sea $(X, d_X)$ un espacio métrico y sea $\{Y_j \,:\, j\in J\}$, con $J$ un conjunto de índices, una familia de conjuntos conexos en dicho espacio métrico tal que $\bigcap_{j\in J} Y_j \neq \emptyset$. Entonces $Y = \bigcup_{j\in J} Y_j$ es conexo.
Demostración. Dadas las hipótesis, procedamos por reducción al absurdo. Supongamos que $Y$ no es conexo. Entonces existen subconjuntos no vacíos de $Y$, digamos $A$ y $B$, los cuales son abiertos en $Y$ y tales que $Y = A\cup B$ y $A \cap B \neq \emptyset$. Sea $y \in \bigcap_{j\in J} Y_j \neq \emptyset$. Sin pérdida de generalidad supongamos que $y\in A$. Por hipótesis tenemos que $B\neq \emptyset$, por lo que debe existir al menos algún $j\in J$ tal que $B \cap Y_j \neq \emptyset$. Entonces $y\in A \cap Y_j$, es decir $A \cap Y_j \neq \emptyset$. Es claro que los conjuntos $A \cap Y_j$ y $B \cap Y_j$ son abiertos en $Y_j$ y además notemos que: \begin{align*}
(A \cap Y_j) \cup (B \cap Y_j) = Y_j,\\
(A \cap Y_j) \cap (B \cap Y_j) = \emptyset,
\end{align*} lo cual contradice la conexidad de $Y_j$.
Por lo tanto $Y = \bigcup_{j\in J} Y_j$ es conexo.
$\blacksquare$
De este resultado se deduce por inducción el siguiente:
Corolario 10.2.
Sea $(X, d_X)$ un espacio métrico y sea $\{Y_j\}_{1\leq j \leq n}$ una sucesión de conjuntos conexos en dicho espacio métrico tal que $Y_j \cap Y_{j+1} \neq \emptyset$, con $1 \leq j \leq n-1$. Entonces $\bigcup_{j=1}^n Y_j$ es conexo en $(X, d_X)$.
$\blacksquare$
Definición 10.7. (Componente conexa.)
Sea $(X,d_X)$ un espacio métrico y $z\in X$. La componente conexa de $z$ es el conjunto: \begin{equation*}
C(z) = \bigcup \{A \subset X \, : \, z\in A \,\, \text{y}\,\, A \,\, \text{es conexo}\}. \end{equation*}
Observación 10.3.
De la definición y de la proposición 10.4 es claro que $C(z)$ es el subconjunto conexo máximo de $X$.(¿Por qué?)
Por otra parte notemos que un espacio métrico disconexo puede ser descompuesto únicamente en sus componentes conexas.
Ejemplo 10.4.
- Si $X$ es conexo, entonces $C(z) = X$ para todo $z\in X$.
- Sea $X = (0, 2) \setminus \{1\}$ dotado con la métrica inducida por el valor absoluto en $\mathbb{R}$. Las componentes conexas de $X$ son los intervalos $(0, 1)$ y $(1, 2)$.
- Consideremos al conjunto $U = \left\{z\in\mathbb{C} \,:\, \operatorname{Re}(z)\neq0\right\}$. Sus componentes conexas son: \begin{equation*} D_1 = \left\{z\in\mathbb{C} \,:\, \operatorname{Re}(z) > 0\right\}, \quad D_2 = \left\{z\in\mathbb{C} \,:\,\operatorname{Re}(z) < 0\right\}.
\end{equation*} - Sea $V = \{ z\in\mathbb{C} \,:\, \operatorname{Re}(z)\not\in\mathbb{Z}\}$. Entonces sus componentes conexas son $G_n = \{z\in\mathbb{C} \,:\, n< \operatorname{Re}(z) < n+1\}$, para cada $n\in\mathbb{Z}$.
Proposición 10.6.
Sea $(X, d_X)$ un espacio métrico. Entonces se cumple lo siguiente.
- Cada subconjunto conexo de $(X, d_X)$ está contenido únicamente en una componente conexa.
- Cada subconjunto conexo y no vacío de $(X, d_X)$ que es abierto y cerrado en $X$ es una componente de $(X, d_X)$.
- Cada componente de $(X, d_X)$ es cerrada.
Demostración.
- Primeramente notemos que para $z,y \in X$, si $C(z) \cap C(y) \neq \emptyset$, entonces por la proposición 10.5 se tiene que $C(z) \cup C(y)$ es conexo lo cual contradice la maximalidad de $C(z)$ a menos de que $C(z) = C(y)$. Es decir, si $C(z) \neq C(y)$, entonces $C(z) \cap C(y) = \emptyset$. Sea $A \subset X $ un conjunto conexo tal que $z\in A$. Por la maximalidad de $C(z)$ es claro que $A \subset C(z)$. Dado que dos componentes distintas son ajenas entre sí, es claro que cada conjunto $A\subset X$ conexo tal que $z \in A$ únicamente está contenido en una componente conexa.
- Sea $A \subset X$ un conjunto conexo abierto y cerrado en $(X, d_X)$ y sea $z \in A$. Tenemos que $A \subset C(z)$, por lo que $A$ es abierto y cerrado en $(C(z), d_{C(z)})$ (¿por qué?), por lo que por la conexidad de $C(z)$ se debe cumplir que $C(z) = A$.
- Sea $z\in X$. Sabemos que $C(z) \subset \overline{C(z)}$. De acuerdo con la proposición 10.4 y la observación 10.2, tenemos que al ser $(C(z), d_{C(z)})$ un subespacio conexo, entonces $\overline{C(z)}$ es también conexo, por lo que por la maximalidad de $C(z)$ se cumple que $\overline{C(z)} \subset C(z)$, por lo que $\overline{C(z)} = C(z)$, es decir $C(z)$ es cerrado.
$\blacksquare$
Observación 10.4.
El inciso 1 de la proposición 10.6 nos dice que el conjunto $X$ se puede expresar como la unión de sus componentes conexas.
Observación 10.5.
Notemos que una componente conexa no necesariamente tiene que ser un conjunto abierto en $(X, d_X)$. Consideremos al siguiente conjunto: \begin{equation*}
X = \{0\} \cup \left\{\frac{1}{n} \,:\, n\in\mathbb{N}^+\right\},
\end{equation*} dotado con la métrica inducida por el valor absoluto en $\mathbb{R}$. No es díficil convencerse de que cada componente conexa de $X$ es un punto y cada punto es una componente. Además cada componente ${\frac{1}{n}}$ es un conjunto abierto en $X$, mientras que la componente conexa ${0}$ es cerrada en $X$ desde que su complemento es abierto en $X$, pero no es abierta ya que dada cualquier $\varepsilon$-vecindad de 0 a esta siempre pertenecerá $\frac{1}{n}$ para algún $n\in\mathbb{N}^+$.
Compacidad en un espacio métrico
Definición 10.8. (Cubierta abierta.)
Sea $(X,d)$ un espacio métrico y $K\subset X$. Una familia de subconjuntos de $X$, digamos $\mathcal{G} = \{G_i : i\in I\}$, donde $I$ es un conjunto arbitrario de índices, tal que: \begin{equation*}
K \subset \bigcup_{i \in I} G_i,
\end{equation*} se llama una cubierta de $K$. Si además cada conjunto de $\mathcal{G}$ es un conjunto abierto en $X$, entonces diremos que es una cubierta abierta de $K$.
Definición 10.9.
Sea $(X,d)$ un espacio métrico. Se dice que un conjunto $K\subset X$ es compacto si toda cubierta abierta $\mathcal{G}$ contiene un subconjunto finito $\{G_1, G_2, \ldots, G_n\} \subset \mathcal{G}$ tal que: \begin{equation*}
K \subset G_1 \cup G_2 \cup \cdots \cup G_n.
\end{equation*}
Ejemplo 10.5.
- El conjunto vacío y todo conjunto finito son compactos.
- El conjunto $B(0,1) = \left\{ z\in\mathbb{C} : |\,z\,|<1\right\}$ no es un conjunto compacto. Sea $G_n = \{z\in\mathbb{C} : |\,z\,| < 1 – \frac{1}{n+1}\}$ para toda $n\in\mathbb{N}^+$, entonces $\{G_1, G_2, G_3, \ldots \}$ es una cubierta abierta de $B(0,1)$, pero no existe una subcubierta finita.
Para el espacio métrico $(\mathbb{C},d)$ consideraremos válida en el curso las siguientes caracterizaciones de subconjuntos compactos de $(\mathbb{R}^2, d)$, donde $d$ es la distancia usual de $\mathbb{R}^2$.
Proposición 10.7.
Sea $ S \subset \mathbb{C}$. Las siguientes condiciones son equivalentes:
- $S$ es compacto.
- Todo subconjunto infinito de puntos de $S$ tiene algún punto de acumulación en $S$.
- Toda sucesión de números complejos $\{z_n\}_{n\geq 1}$ de $S$ tiene alguna subsucesión convergente a un punto $z\in S$.
- $S$ es cerrado y acotado. (Teorema de Heine – Borel.)
$\blacksquare$
Del mismo modo, para un espacio métrico $(X,d)$ consideraremos válidos los siguientes resultados. Para una prueba detallada de estos se puede consultar algún texto como Topología de espacios métricos de Ignacio L. Iribarren o Metric Spaces de Satish Shirali y Harkrishan L. Vasudeva.
Proposición 10.8.
Sea $(X,d)$ un espacio métrico compacto, entonces $(X,d)$ es completo.
Proposición 10.9.
Sean $(X, d_X)$ y $(Y, d_Y)$ dos espacios métricos y sea $f: X \to Y$ una función continua. Si $X$ es compacto, entonces $f(X)$ es un subconjunto compacto de $Y$.
Proposición 10.10.
Sea $(X, d_X)$ un espacio métrico, sea $K\subset X$ y sea $f: K \to \mathbb{R}$ una función continua. Si $K$ es un conjunto compacto, entonces $f$ alcanza sus valores máximo y mínimo y ambos son finitos.
Proposición 10.11. (Teorema de Cantor.)
Sean $(X, d)$ un espacio métrico y $\{K_n\}_{n\geq1}$ una sucesión de subconjuntos compactos no vacíos de $X$ tales que $K_1 \supset K_2 \supset K_3 \supset \cdots$. Entonces $\bigcap\limits_{n=1}^{\infty} K_n \neq \emptyset$.
Proposición 10.12.
Sean $(X, d_X)$ y $(Y, d_Y)$ dos espacios métricos. Si para todo $K\subset X$ conjunto compacto la restricción $f:K \to Y$ es una función continua, entonces $f: X \to Y$ es función continua.
Ejemplo 10.6.
Sea $z_0\in\mathbb{C}$ fijo y sea $\rho>0$. Todo disco cerrado $\overline{B}(z_0, \rho)$ es compacto.
Tarea moral
- Realiza la demostración de la proposición 10.1.
- Prueba el lema 10.1. Hint: Considera la función $\gamma:[0,1] \to\mathbb{C}$ tal que $\gamma(t) = z + t(w-z)$, con $z,w\in\mathbb{C}$ y utiliza la proposición 9.2.
- Considera la definición 10.4. Sean $z,w\in\mathbb{C}$. Demuestra que el segmento de recta $[z,w]$ es un conjunto conexo. Hint: Considera la proposición 10.3 y el ejercicio anterior.
- Consideremos el conjunto dado en el ejercicio 8 de la entrada 7, es decir: \begin{equation*}
S = \{z\in\mathbb{C} \,:\, |\,\operatorname{Im}(z)\,|<|\operatorname{Re}(z)|\}. \end{equation*} Prueba que dicho conjunto dotado con la métrica euclidiana de $\mathbb{C}$ no es conexo. Determina sus componentes conexas. - Consideremos a $(\mathbb{C}, d)$, donde $d$ es la métrica euclidiana. Sean $X,Y\subset \mathbb{C}$ dos conjuntos conexos. Supon que $X \cap Y \neq \emptyset$, entonces ¿el conjunto $X \cap Y$ es necesariamente conexo? Realiza la prueba o da un contraejemplo.
- Da un bosquejo de la demostración de la proposición 10.7.
- Considera los siguientes conjuntos:
a) $X = \left\{ \frac{1}{n} + i \frac{1}{m} \,: \, n,m\in\mathbb{N}^+ \right\}$.
b) $Y = \{z\in\mathbb{C} \,:\, \operatorname{Re}(z), \operatorname{Im}(z) \in \mathbb{Q}\}$.
c) $W = \bigcup_{n\in\mathbb{Z}} B(n, 1/2)$.
Determina sus componentes conexas. - ¿Cuáles de los siguientes subconjutnos de $\mathbb{C}$, dotados con la métrica inducida por el módulo complejo, son conexos?
a) $A = \{z\in\mathbb{C} \,:\, |\,z\,|\leq 1\} \cup \{z\in\mathbb{C} \, : \, |\,z-2\,|<1\}$.
b) $B = [0, 1) \cup \left\{1+\frac{1}{n} \, : \, n\in\mathbb{N}^+ \right\}$.
Si alguno no es conexo determina sus componentes conexas. - Sea $U\subset\mathbb{C}$ un conjunto abierto. Muestra que $U$ se puede ver como una unión disjunta numerable de dominios en el plano complejo, es decir, $U$ es la unión numerable de componentes conexas distintas.
Más adelante…
En esta entrada hemos abordado los conceptos de conexidad y compacidad para conjuntos de algún espacio métrico, con lo cual logramos caracterizar a los conjuntos de $\mathbb{C}$ mediante dichos conceptos. Es importante mencionar que existen muchos más resultados para los conjuntos con estas propiedades, sin embargo aquí únicamente mencionamos algunos de los cuales nos serán de utilidad a lo largo del curso. Asimismo solo hemos trabajado con las definiciones que requeriremos, por lo que es importante complementar estos temas con bibliografía adicional sobre espacios métricos.
La siguiente entrada abordaremos el concepto del infinito desde la perspectiva de los números complejos, por lo que realizaremos una extensión de $\mathbb{C}$ dotando a este campo con un nuevo elemento y considerando un nuevo modelo, la Esfera de Riemann, el cual nos permitirá trabajar de forma idónea con este nuevo elemento llamado el punto al infinito e inducir una nueva métrica.
Entradas relacionadas
- Ir a Variable Compleja I.
- Entrada anterior del curso: Continuidad en un espacio métrico.
- Siguiente entrada del curso: El plano complejo extendido $\mathbb{C}_{\infty}$.