Archivo de la etiqueta: construcciones geométricas

Geometría Moderna I: Homotecia

Por Rubén Alexander Ocampo Arellano

Deja un comentario

Introducción

En esta entrada estudiamos el tema de homotecia, se trata de una transformación que lleva una figura del plano a otra semejante, con lados correspondientes paralelos y vértices correspondientes concurrentes, esto nos permite entre otras cosas, abordar algunos problemas de construcciones geométricas.

Definición 1. Considera un punto $H$, un conjunto de puntos $F$ y $k$ un numero real, para cada $X \in F$ sea $X’$ tal que $X’$, $X$ y $H$ son colineales y $\dfrac{HX’}{HX} = k$.

Sea $F’$ el conjunto de puntos $X’$, diremos que los conjuntos $F$ y $F’$ son figuras homotéticas y los puntos $X$ y $X’$ son puntos homólogos.

$H$ se llama centro de homotecia, $k$ es la razón de homotecia y la relación entre $F$ y $F’$ es una homotecia con centro en $H$ y razón $k$. Por convención el centro de homotecia $H$ es su propio punto homólogo.

Si puntos homólogos de una homotecia están del mismo lado del centro de homotecia decimos que los conjuntos son directamente homotéticos y la razón de homotecia es positiva, si los puntos homólogos están en lados opuestos respecto del centro de homotecia decimos que las figuras son inversamente homotéticas y la razón de homotecia será negativa.

Homotecia de una recta

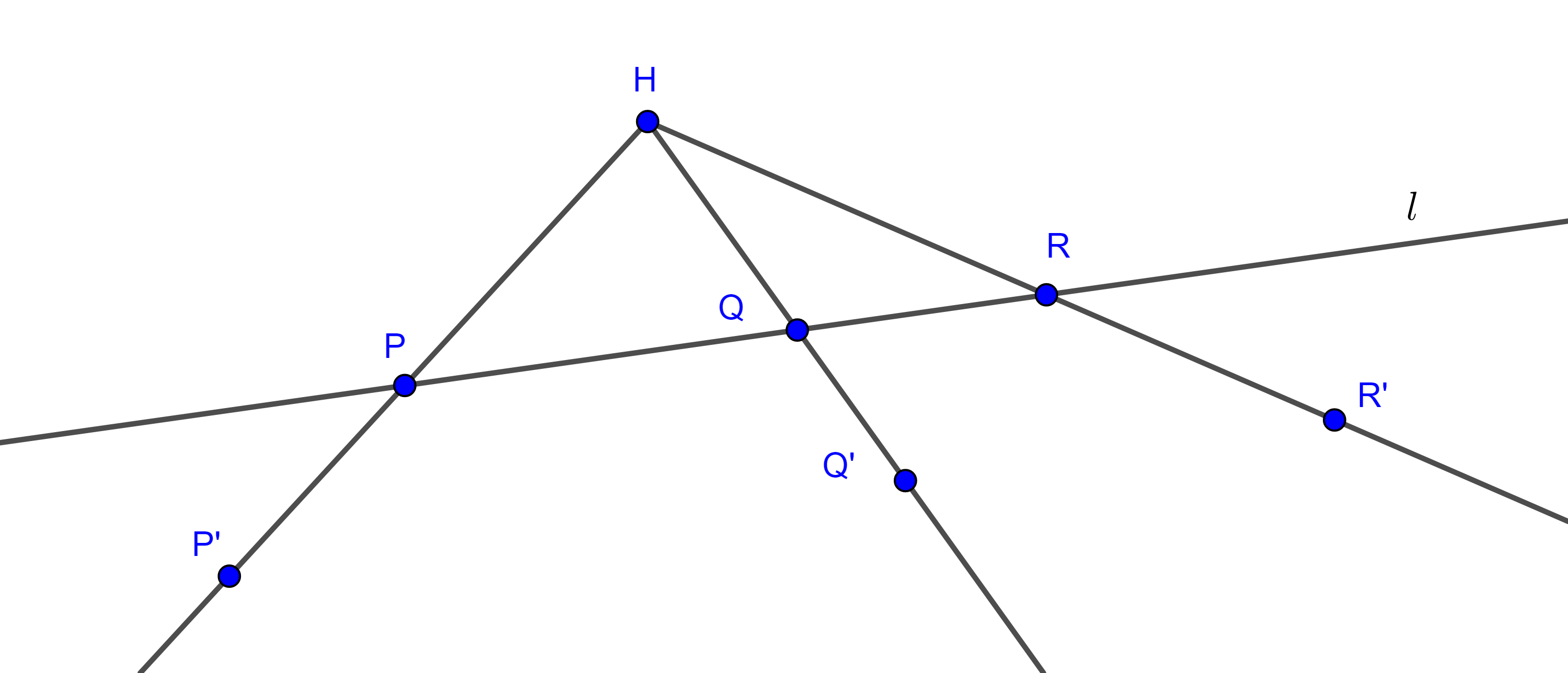
Teorema 1. La homotecia de una recta que no pasa por el centro de homotecia es una recta paralela.

Demostración. Sean $H$ y $k$ el centro y la razón de homotecia, y sea $l$ una recta que no pasa por $H$. Tomemos tres puntos arbitrarios $P$, $Q$, $R \in l$, sean $P’$, $Q’$ y $R’$ sus correspondientes puntos homólogos.

Figura 1

Como $\dfrac{HP’}{HP} = k = \dfrac{HQ’}{HQ}$, por el reciproco del teorema de Tales, $PQ \parallel P’Q’$.

Análogamente vemos que $QR \parallel Q’R’$ y $PR \parallel P’R’$.

Supongamos que $P’$, $Q’$ y $R’$ no son colineales, entonces $\triangle P’Q’R’$ es un triángulo y así $\triangle PQR$ es un triángulo con lados paralelos a los de $\triangle P’Q’R’$, lo cual es una contradicción, pues $PQR$ es una recta.

Si fijamos $P$ y $Q$, y tomamos $R$ como variable, entonces $P’$ y $Q’$ son fijos y $R’$ es variable, así todos los puntos $R’$ son colineales con $P’$ y $Q’$.

Por lo tanto, la homotecia de una recta es una recta paralela a esta.

$\blacksquare$

Definición 2. Decimos que dos polígonos $ABCD…$ y $A’B’C’D’…$ son semejantes si los correspondientes lados son proporcionales $\dfrac{AB}{A’B’} = \dfrac{BC}{B’C’} =…$ y los ángulos correspondientes son iguales $\angle A = \angle A’$, $\angle B = \angle B’$, $…$

Corolario. Dos polígonos homotéticos son semejantes.

Demostración. Sean $A$, $B$ y $C$ vértices de un polígono $ABCD…$

Por el teorema anterior, los lados del triángulo $\triangle A’B’C’$, formado por los puntos homólogos de $A$, $B$ y $C$, son paralelos a los lados correspondientes de $\triangle ABC$, por lo tanto, los triángulos son semejantes y así los ángulos correspondientes son iguales y los lados correspondientes son proporcionales.

$\blacksquare$

Polígonos homotéticos

Teorema 2. Si los lados correspondientes de dos polígonos son proporcionales y paralelos entonces los polígonos son homotéticos.

Demostración. Sean $ABCD…$ y $A’B’C’D’…$ dos polígonos que cumplen las condiciones dadas, sea $H$ la intersección de las rectas $AA’$ y $BB’$ y supongamos que $CC’$ no pasa por $H$, entonces sea $H’ = CC’ \cap BB’$.

Figura 2

Como $AB \parallel A’B’$ y $BC \parallel B’C’$ entonces $\triangle HAB \sim \triangle HA’B’$ y $\triangle H’BC \sim \triangle H’B’C’$
$\Rightarrow \dfrac{AB}{A’B’} = \dfrac{HB}{HB’}$ y $\dfrac{BC}{B’C’} = \dfrac{H’B}{H’B’}$. 

Ya que los lados correspondientes de $ABCD…$ son proporcionales a los de $A’B’C’D’…$, entonces
$ \dfrac{HB}{HB’} = \dfrac{AB}{A’B’} = \dfrac{BC}{B’C’} = \dfrac{H’B}{H’B’} $
$\Rightarrow \dfrac{HB}{HB’} – 1= \dfrac{H’B}{H’B’} – 1 \Rightarrow \dfrac{HB – HB’}{HB’} = \dfrac{H’B – H’B’}{H’B’}$
$\Rightarrow \dfrac{B’B}{HB’} = \dfrac{B’B}{H’B’} \Rightarrow HB’ = H’B’$.

Por lo tanto, $H = H’$.

Así, $AA’$, $BB’$ y $CC’$ son concurrentes y $\dfrac{HA’}{HA} = \dfrac{HB’}{HB} = \dfrac{HC’}{HC}$, es análogo ver que las demás rectas que unen vértices correspondientes concurren en $H$.

Por tanto, $ABCD…$ y $A’B’C’D’…$ se encuentran en homotecia desde $H$ y por el corolario 1, $ABCD…$ y $A’B’C’D’…$, son semejantes, la razón de homotecia es la razón de semejanza, $\dfrac{HA’}{HA} = \dfrac{AB}{A’B’} = \dfrac{BC}{B’C’} =…$

$\blacksquare$

Observación 1. Si la razón de homotecia es 1, los lados correspondientes de las figuras $ABCD…$ y $A’B’C’D’…$ son congruentes y así $\square AA’B’B$ es un paralelogramo, es decir, $AA’$ y $BB’$ no pueden ser concurrentes.

Observación 2. En el caso particular cuando los polígonos son triángulos, solo es necesario pedir que los lados correspondientes sean paralelos, pues esto asegura la semejanza y por tanto la condición de proporcionalidad.

Rectas concurrentes

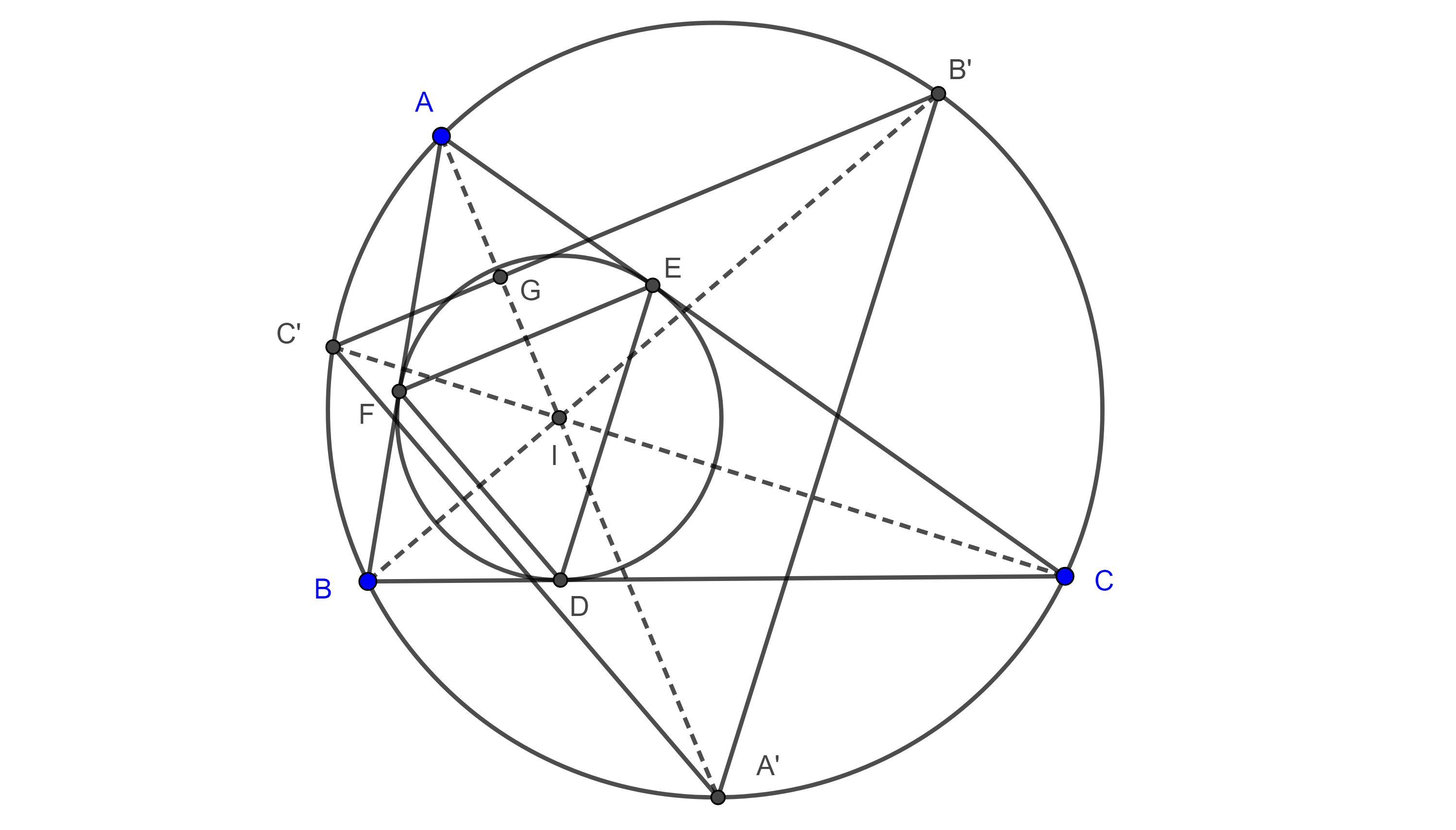
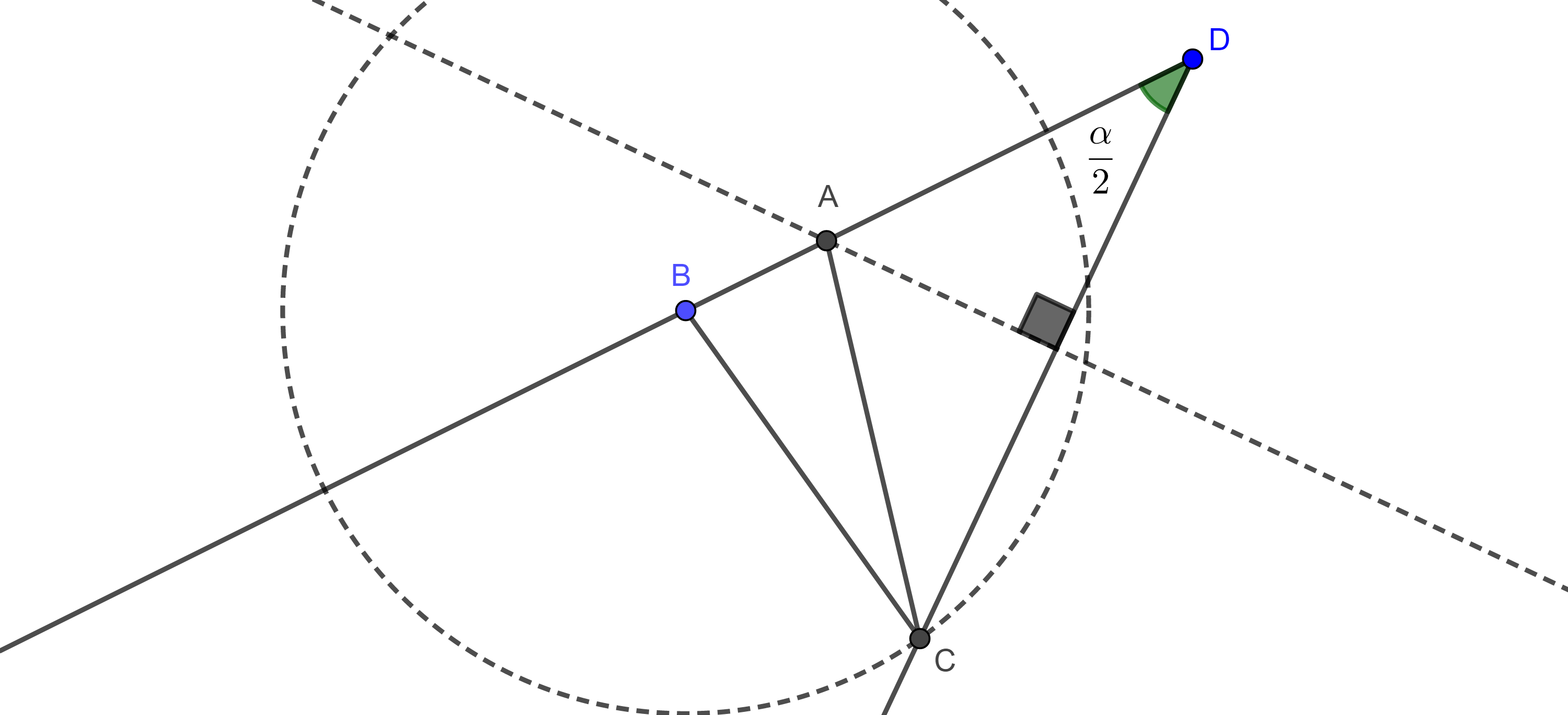
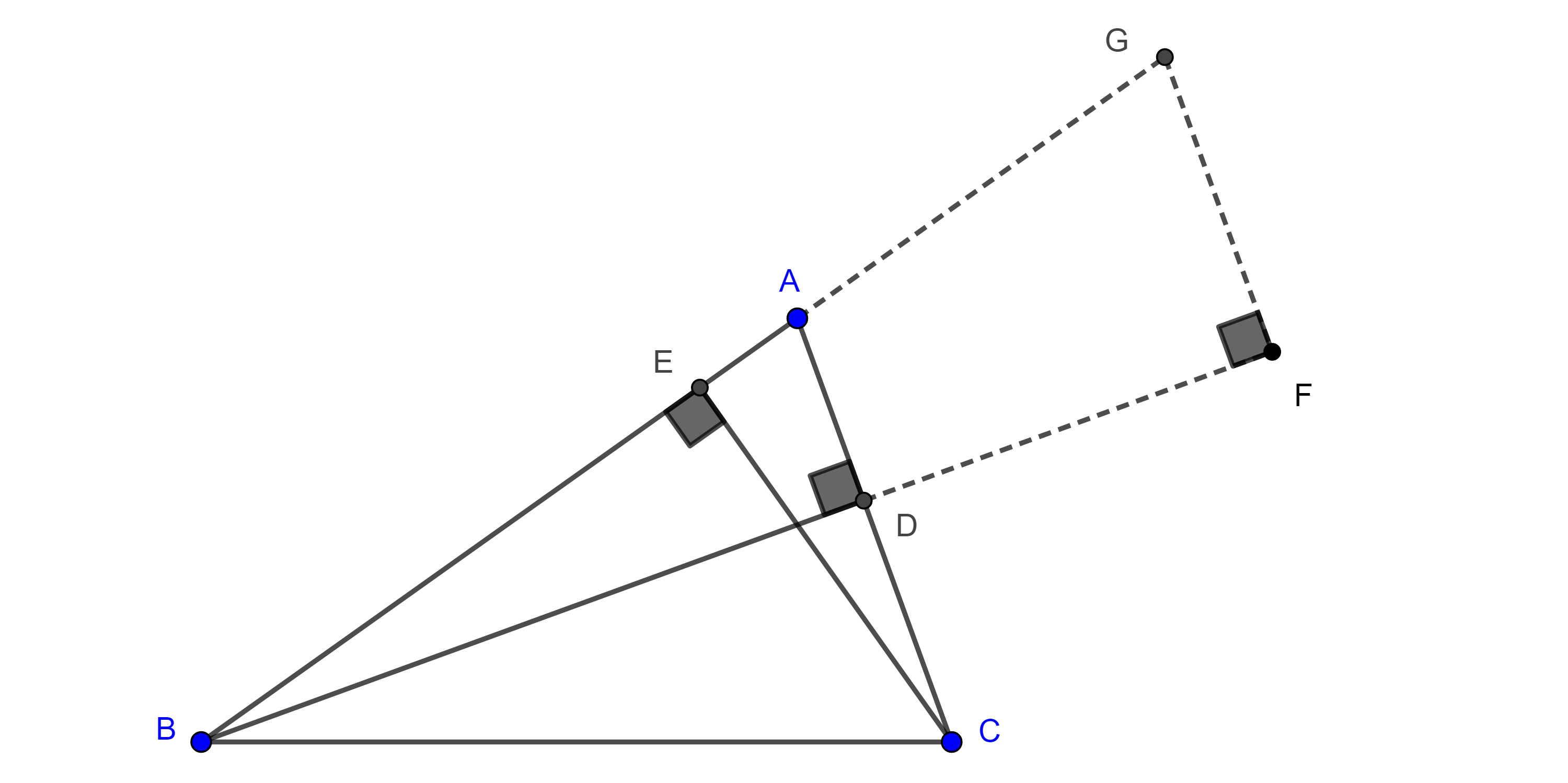
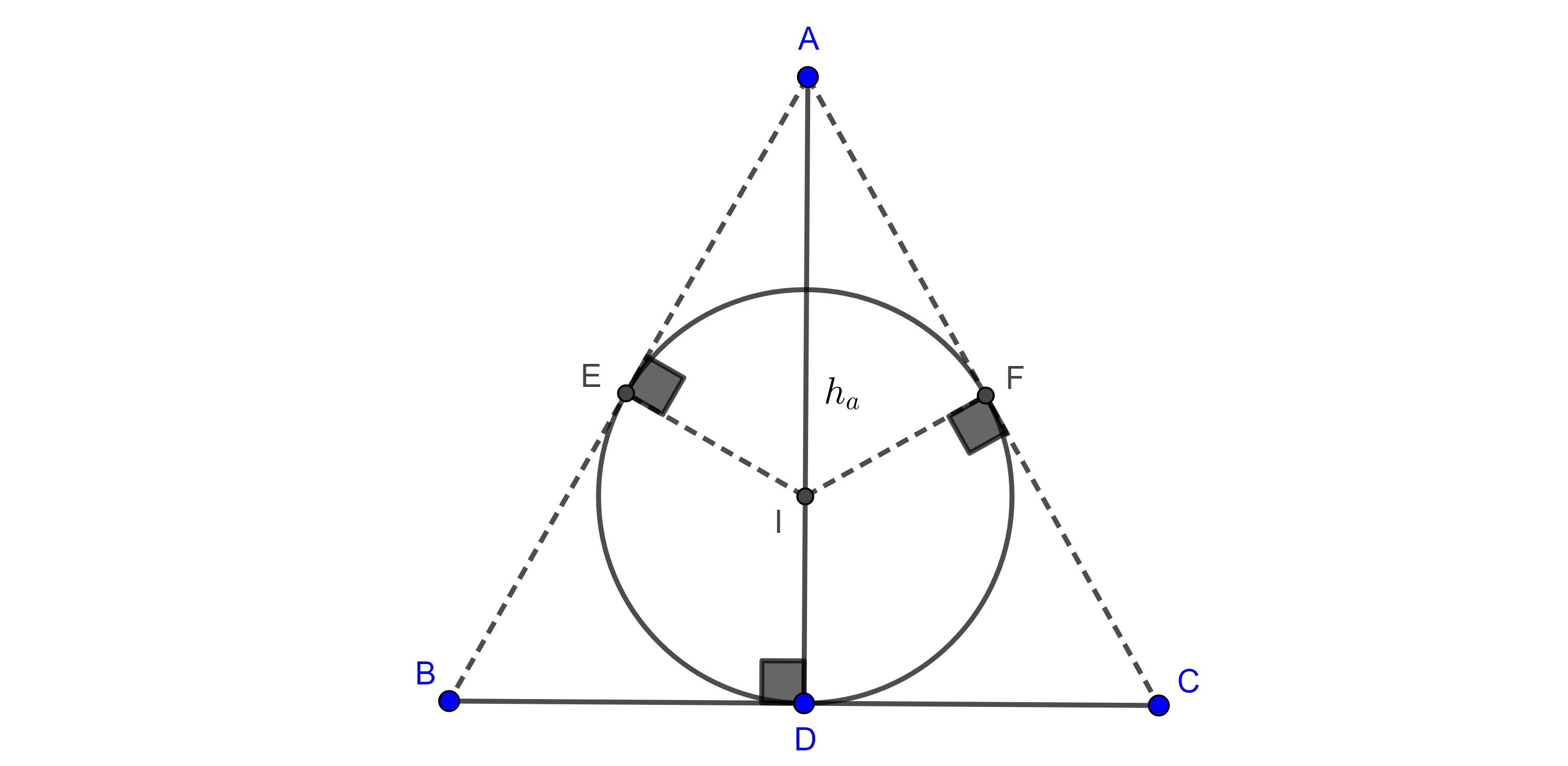
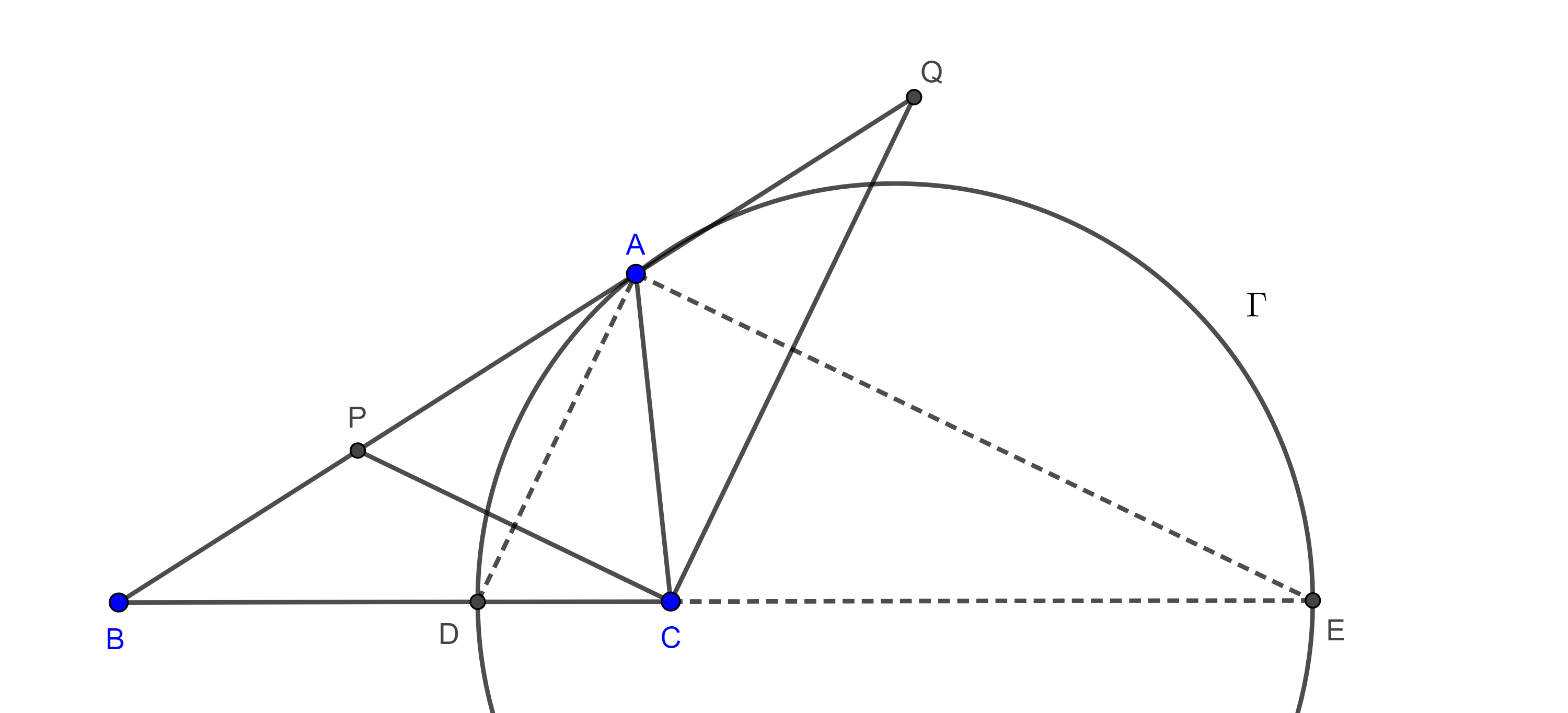
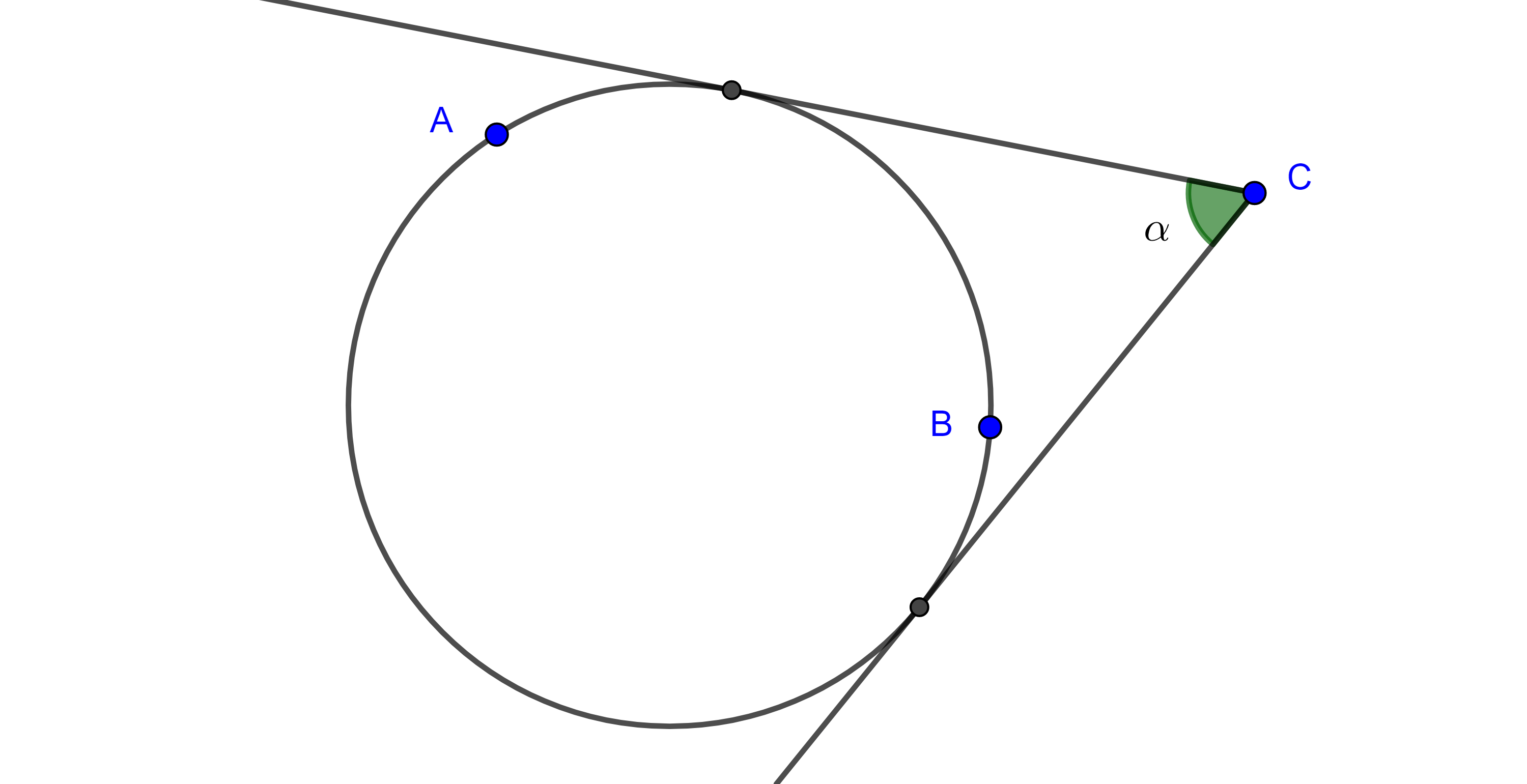
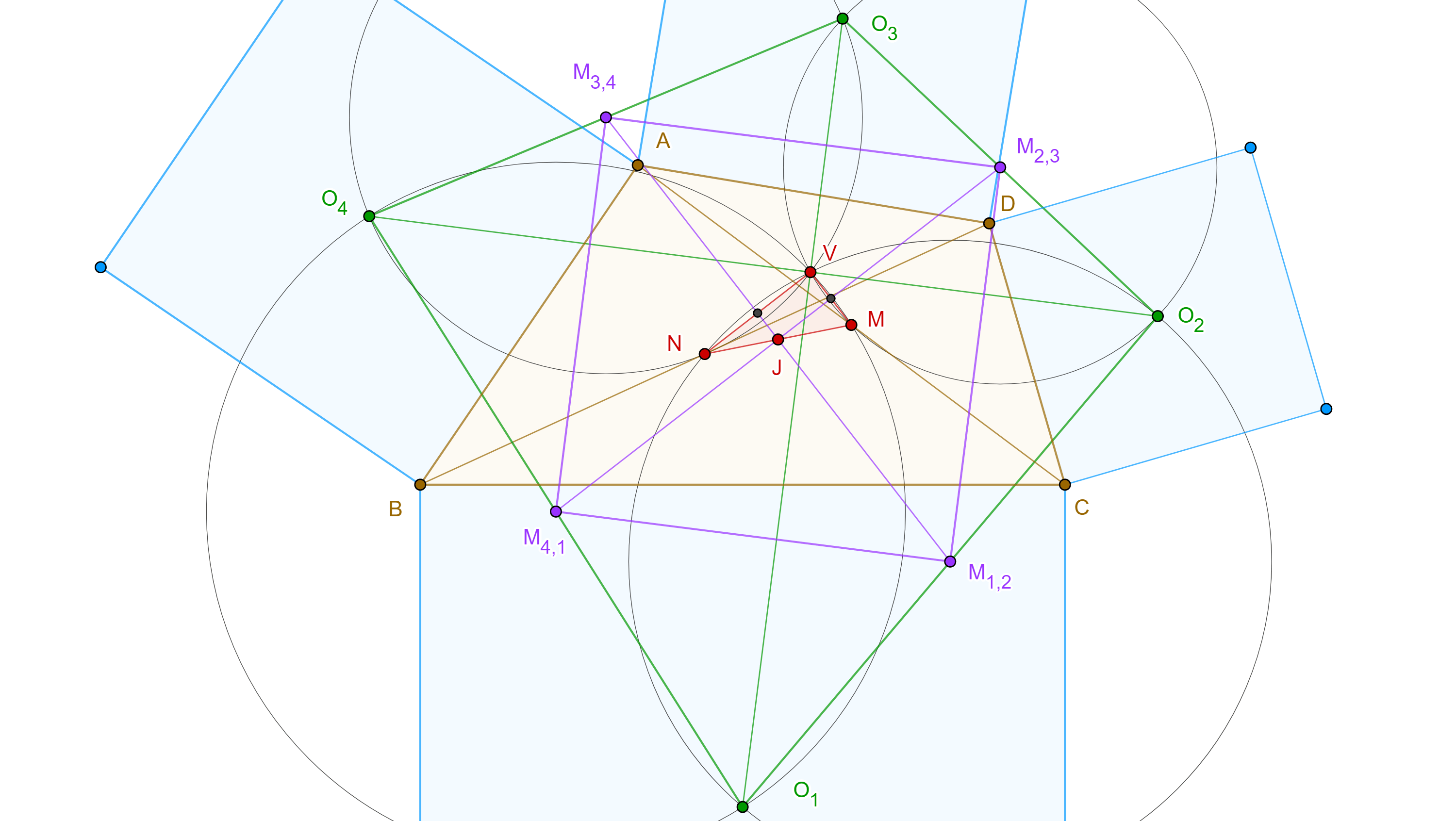
Proposición. Sea $\triangle ABC$ un triángulo y sean $D$, $E$ y $F$ los puntos de tangencia del incírculo $(I, r)$ de $\triangle ABC$, con los lados $BC$, $AC$ y $AB$ respectivamente, sean $A’$, $B’$ y $C’$ la intersección de las rectas $AI$, $BI$ y $CI$ con el circuncírculo del triángulo $\triangle ABC$, entonces la rectas $A’D$, $B’E$ y $C’F$ son concurrentes.

Demostración. Notemos que $AF = AE$, pues son las tangentes trazadas desde $A$ a $(I, r)$ , como $\triangle AEF$ es isósceles entonces la bisectriz de $A$ es perpendicular a $EF$, $AI \perp EF$.

Figura 3

Por otro lado, tenemos que $\angle C’B’B = \angle C’CB = \dfrac{\angle C}{2}$ pues abarcan el mismo arco; el ángulo $\angle B’IA$ es un ángulo exterior del triángulo $\triangle AIB$, entonces
$\angle B’IA = \angle BAI + \angle IBA = \dfrac{\angle A + \angle B}{2}$.

Sea $G = AI \cap C’B’$, en el triángulo $\triangle GIB’$ tenemos que
$\angle IGB’ = \pi – (\angle C’B’B + \angle B’IA) $
$= \pi – \dfrac{\angle A + \angle B + \angle C}{2} = \dfrac{\pi}{2}$.

Por lo tanto, $AI \perp B’C’$ $\Rightarrow EF \parallel B’C’$, de manera análoga podemos ver que $ED \parallel B’A’$ y $DF \parallel A’C’$.

De lo anterior se sigue que $\triangle DEF \sim \triangle A’B’C’$, y por el teorema 2, $A’D$, $B’E$ y $C’F$ concurren en algún punto $H$ que es el centro de homotecia de los triángulos $\triangle DEF$ y $\triangle A’B’C’$.

$\blacksquare$

Inscribir un triángulo en otro triángulo dado

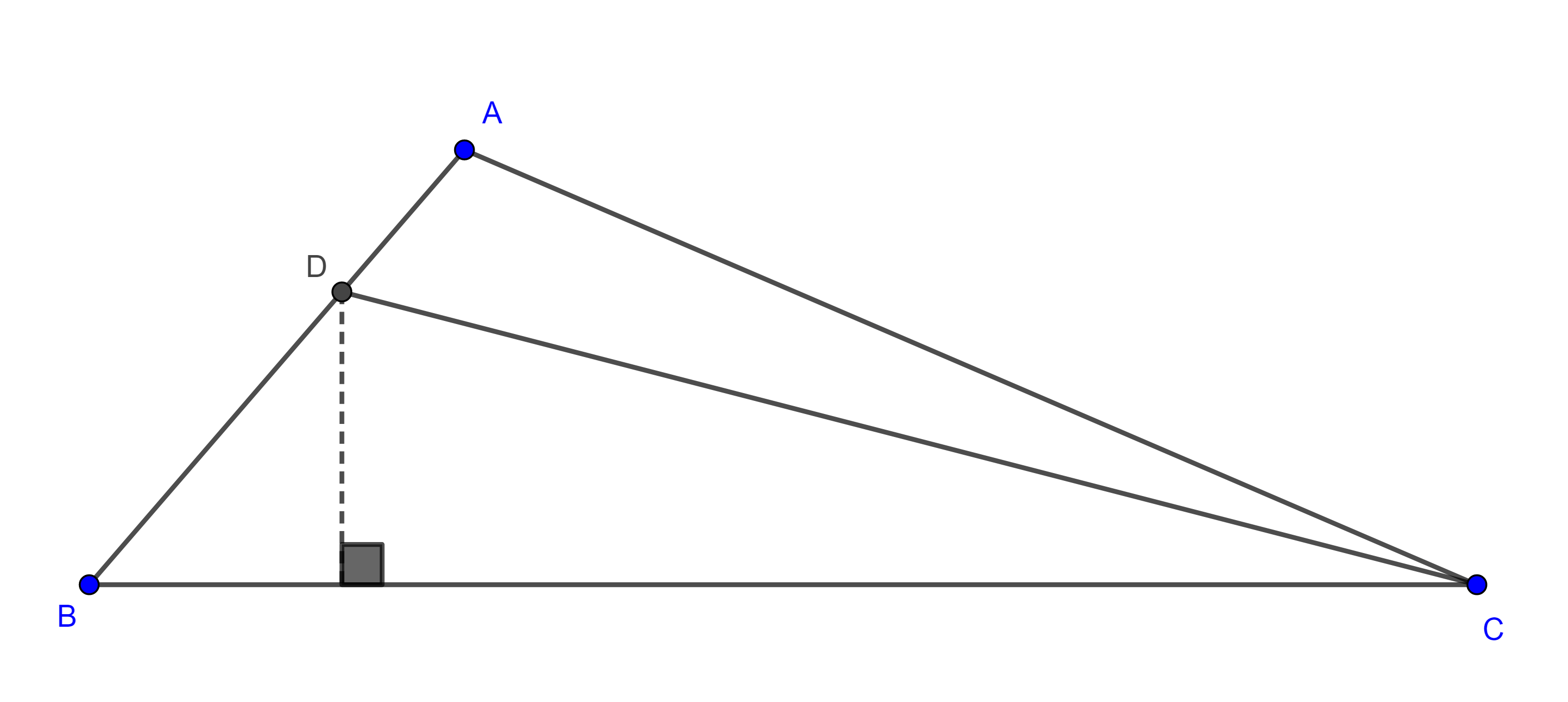
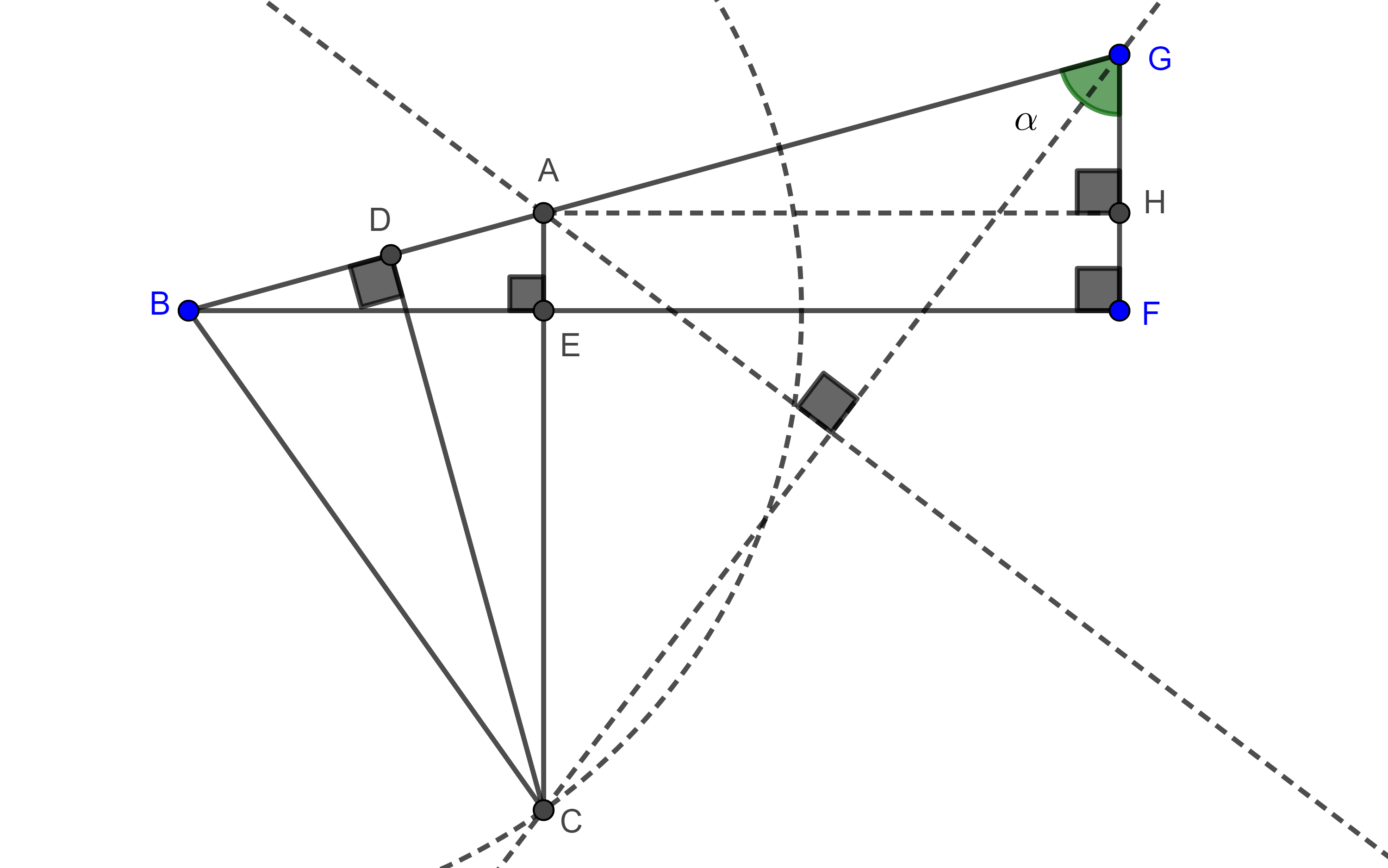
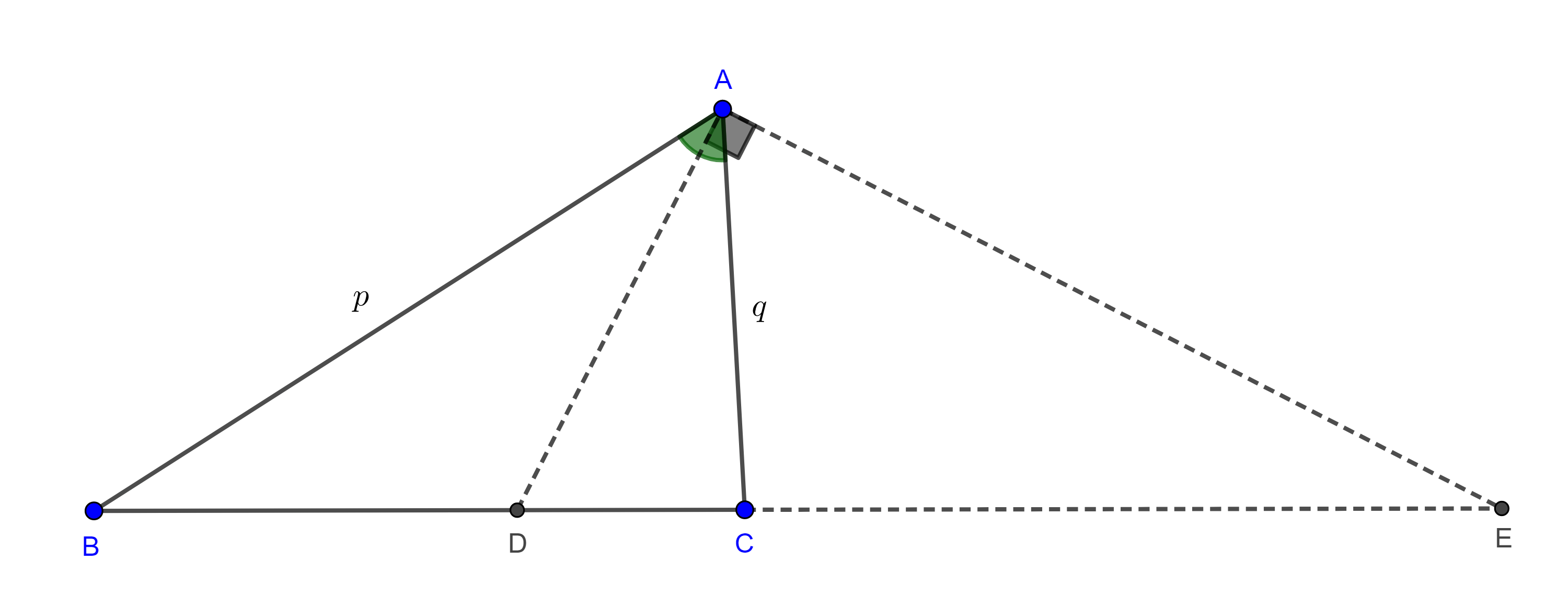
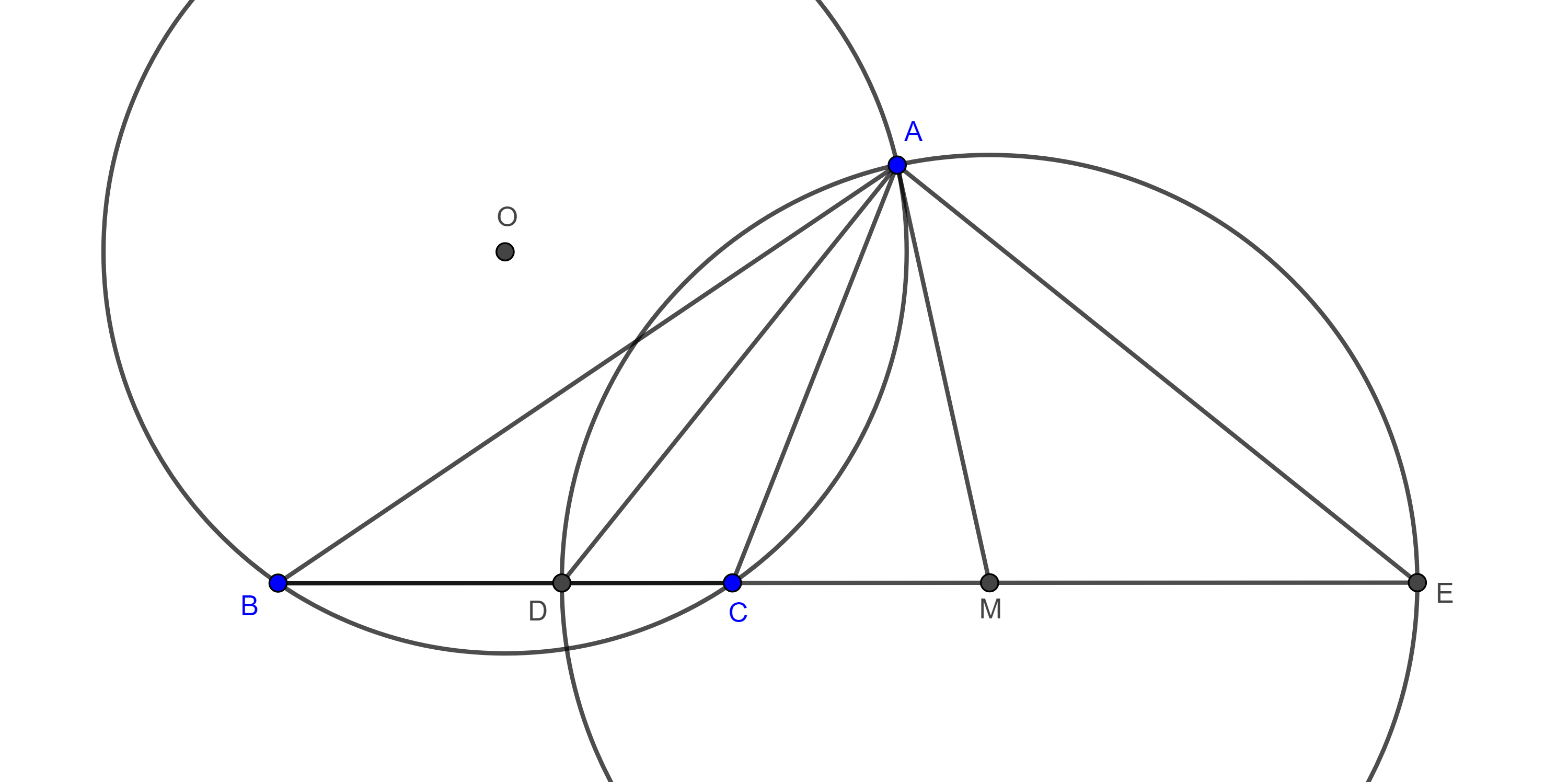
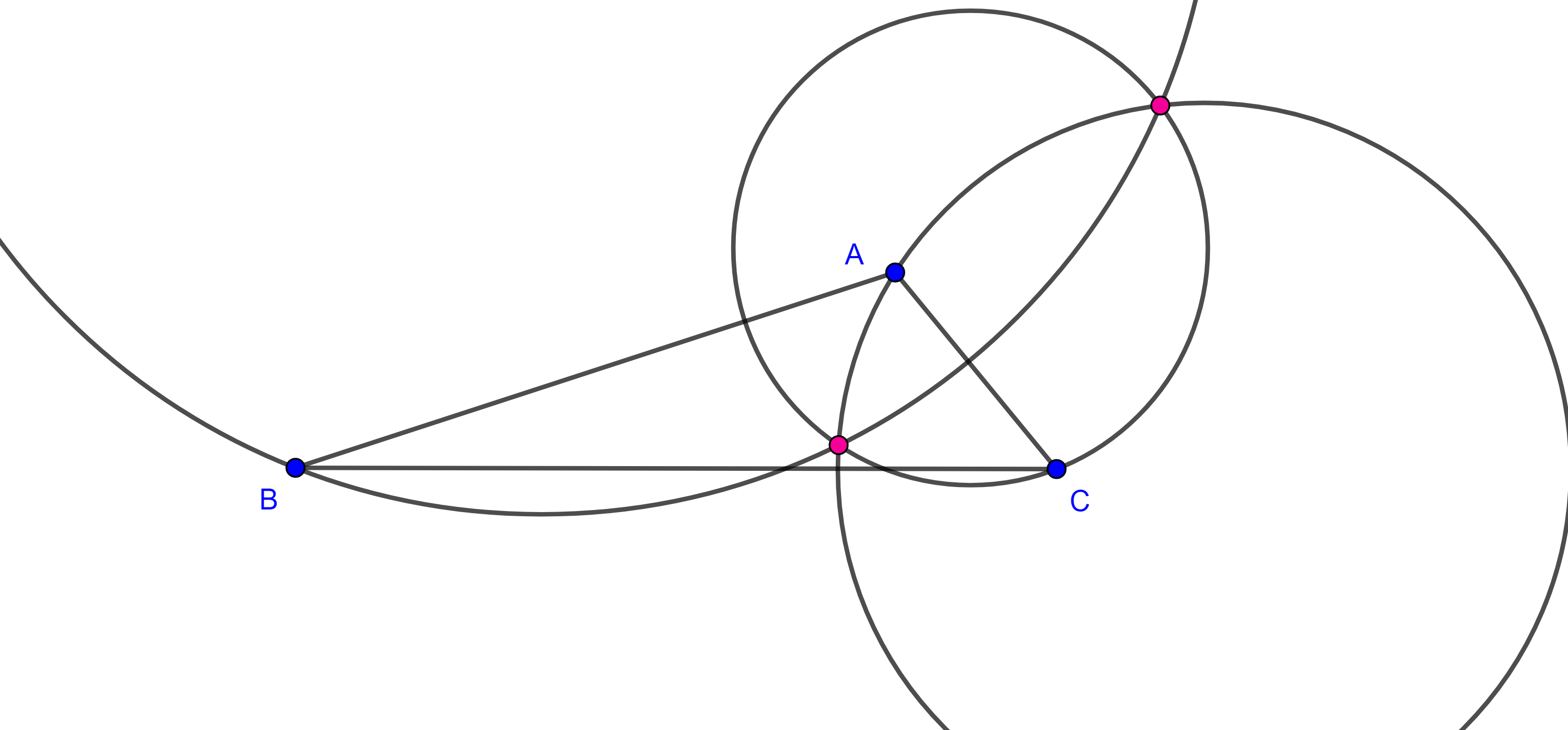
Problema. 1 En un triángulo dado inscribir un triángulo cuyos lados sean perpendiculares a los lados del triángulo dado.

Solución. Sea $\triangle ABC$ el triángulo dado, la idea es construir una homotecia desde uno de los vértices, tomemos $D \in BC$, distinto de $B$, $C$ y también diferente al pie de la altura por $A$.

Por $D$ trazamos la perpendicular a $BC$ que interseca a $AC$ en $E$, por $E$ trazamos la perpendicular a $AC$ que interseca a $AB$ en $F$.

Por $F$ trazamos la perpendicular a $AB$ que interseca a $DE$ en $G$.

Figura 4

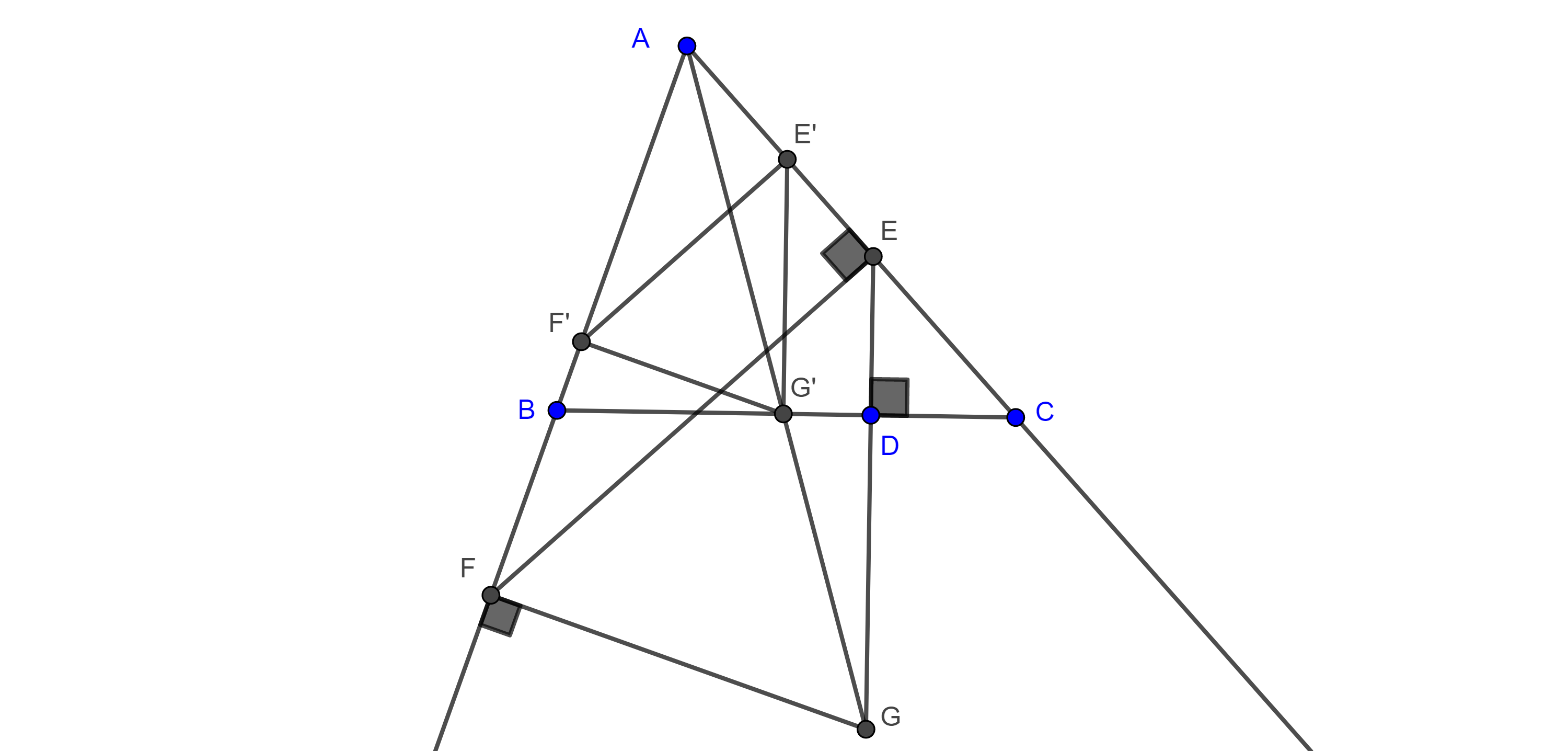
Sea $G’ = BC \cap AG$, por $G’$ trazamos la paralela a $GE$ que interseca a $AC$ en $E’$, también trazamos la paralela a $GF$ por $G’$ que interseca a $AB$ en $F’$.

Por construcción $EE’$, $FF’$ y $GG’$ concurren en $A$, $G’F’ \perp AB$ y $G’E’ \perp AC$.

Como $\triangle AF’G’ \sim \triangle AFG$ y $\triangle AG’E’ \sim \triangle AGE$
$\dfrac{AF’}{AF} = \dfrac{AG’}{AG} = \dfrac{AE’}{AE}$.

Por tanto, $E’$, $F’$ y $G’$ son puntos homólogos de $E$, $F$ y $G$ respectivamente, con centro de homotecia en $A$.

Por el teorema 1, $E’F’ \parallel EF$ y así $E’F’ \perp AC$.

$\blacksquare$

Observación. Notemos que construimos $DE \perp BC$ y tal que $E \in AC$, pero pudimos haber construido $E \in AB$ de lo que resultaría un triangulo distinto $\triangle E’F’G’$ y por lo tanto tenemos dos soluciones.

Inscribir un cuadrado en un triángulo dado

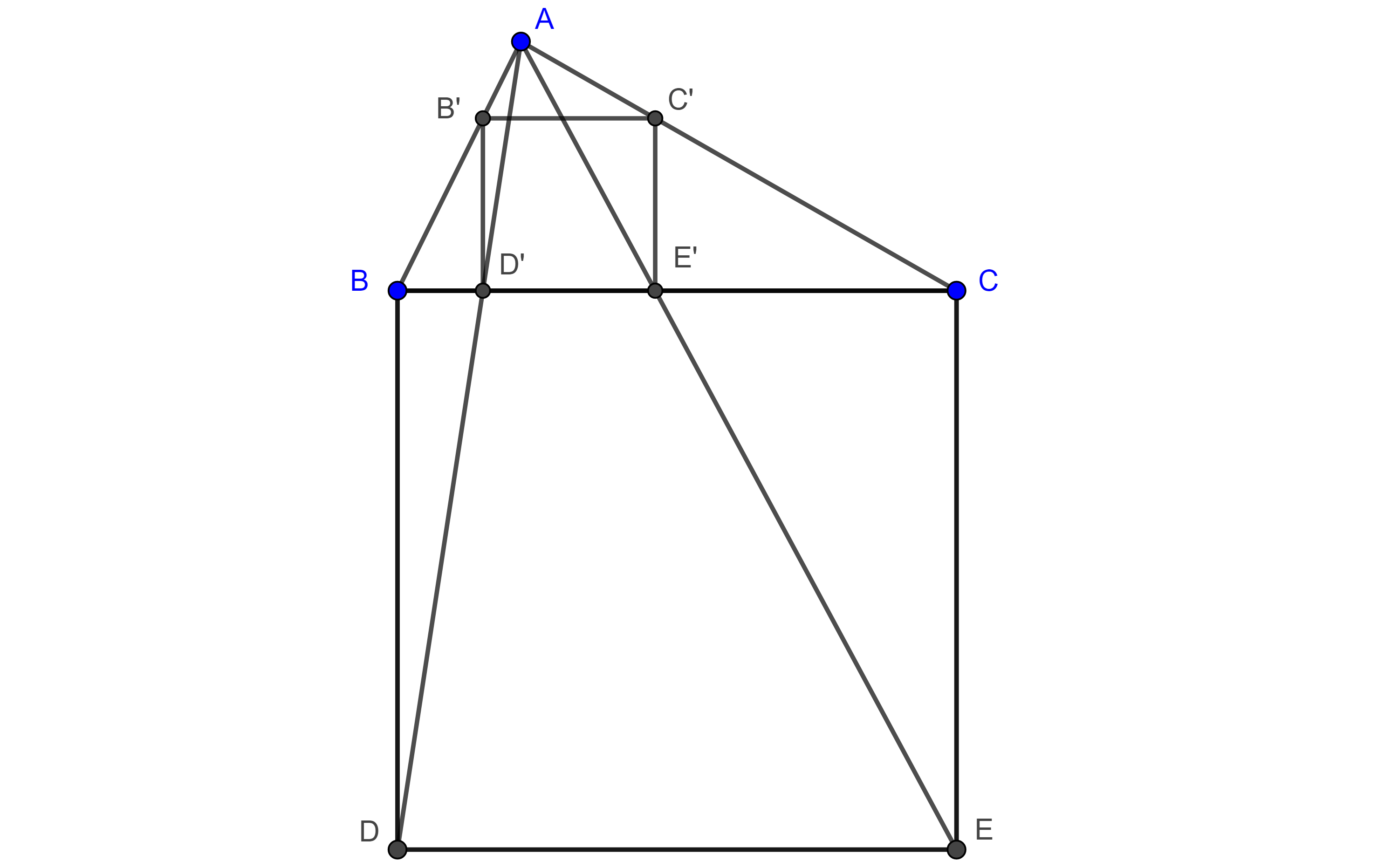
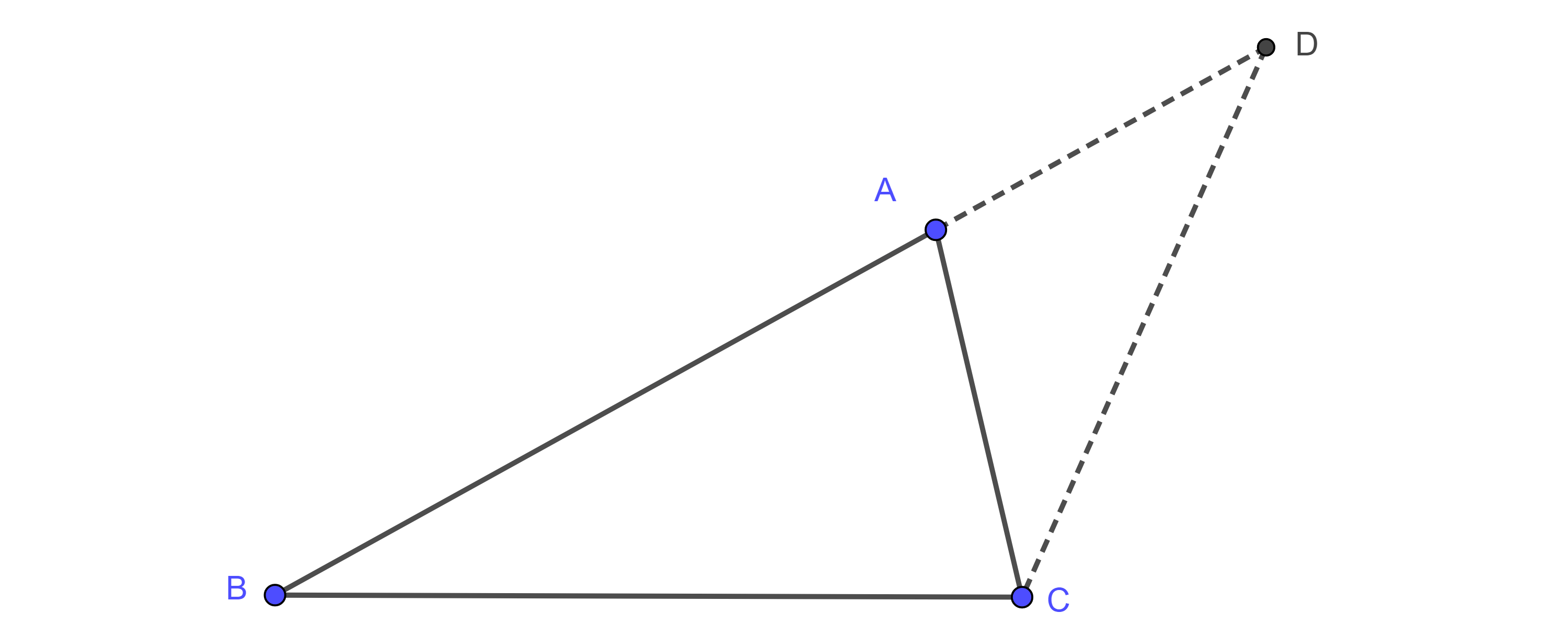
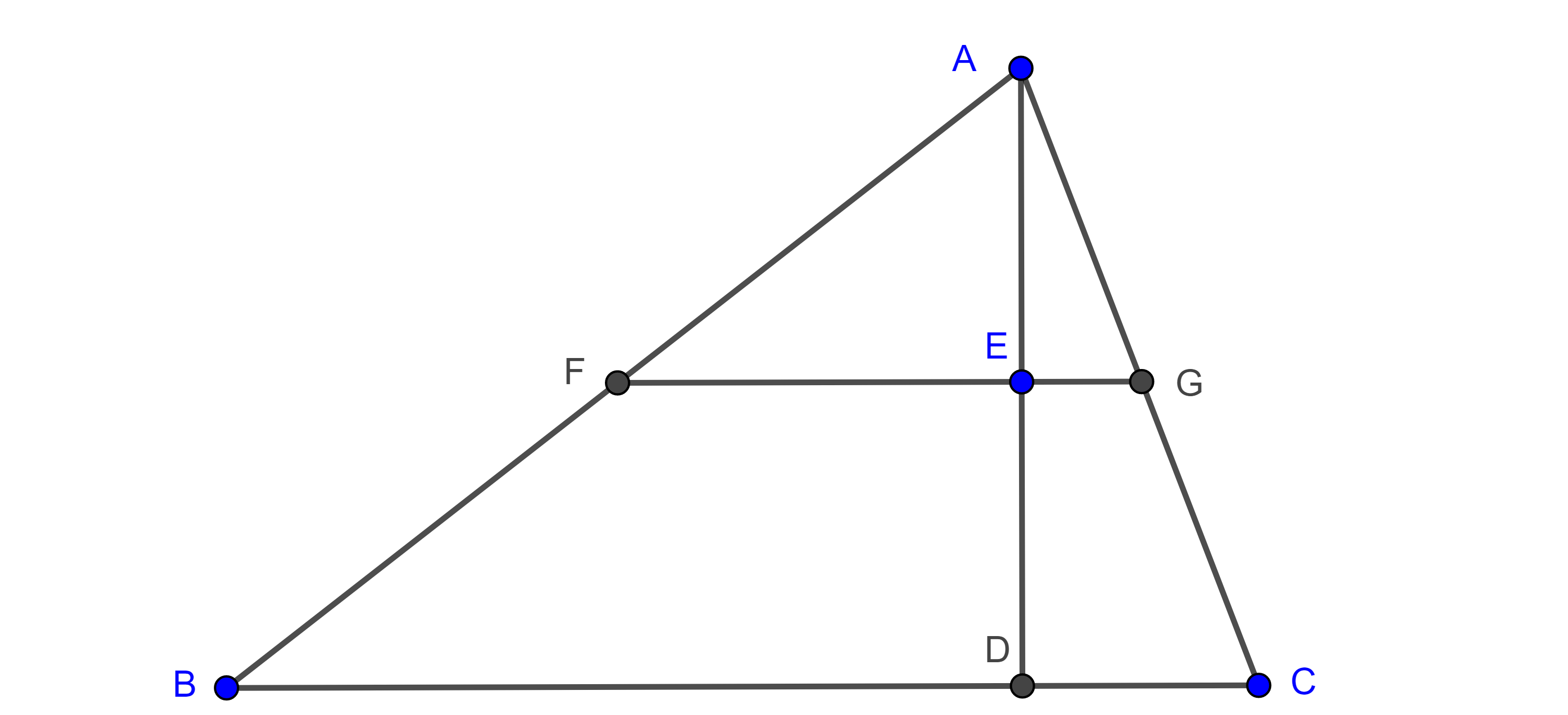
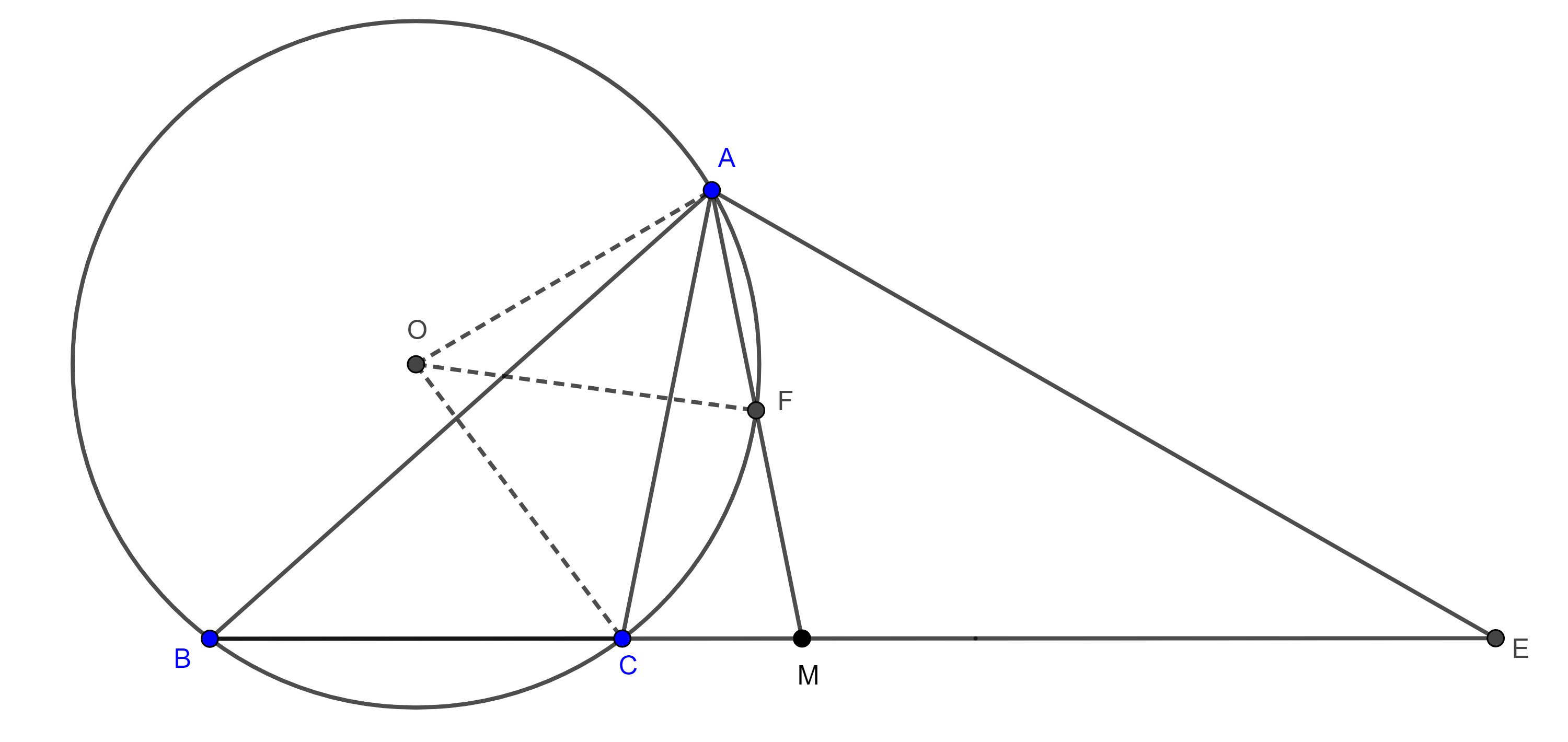
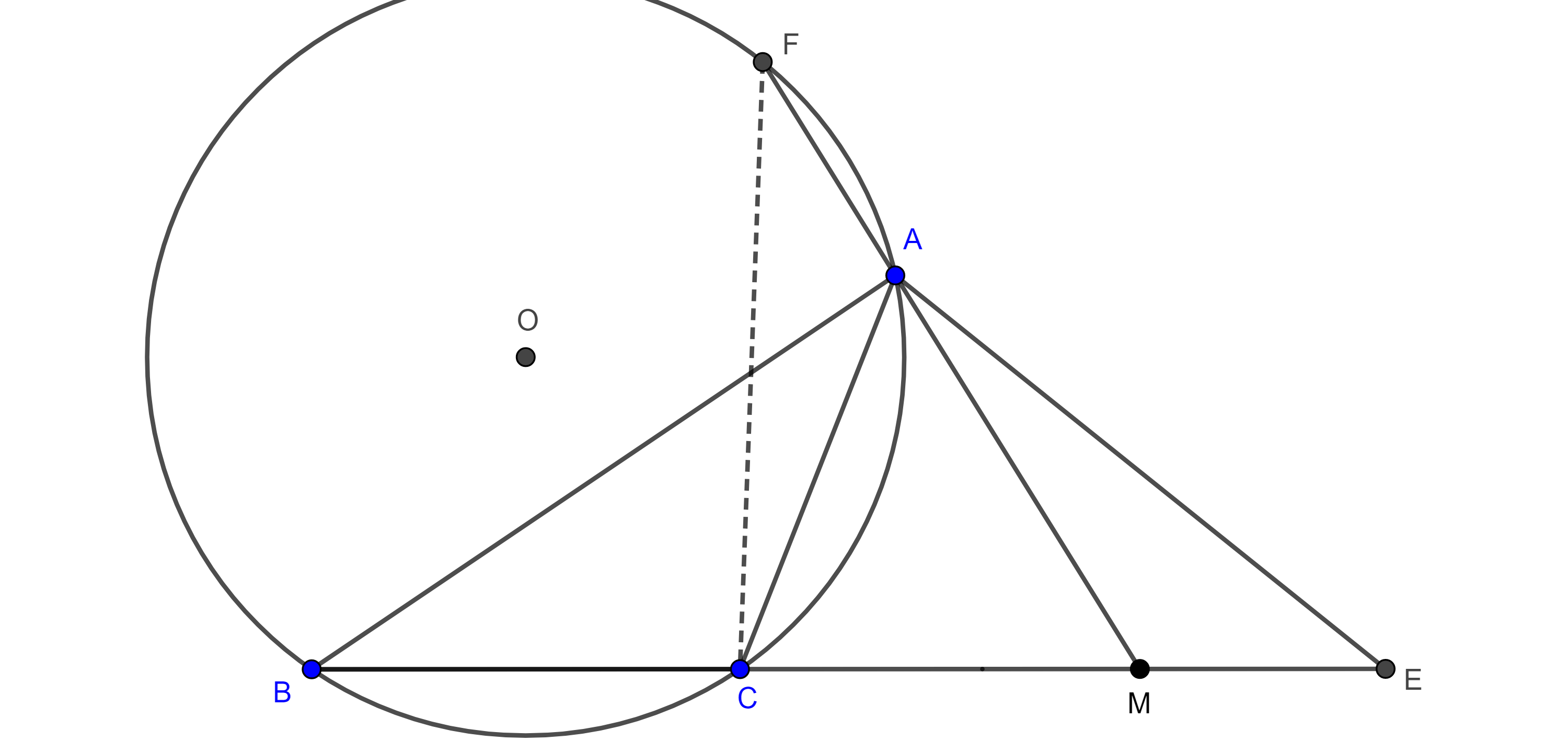
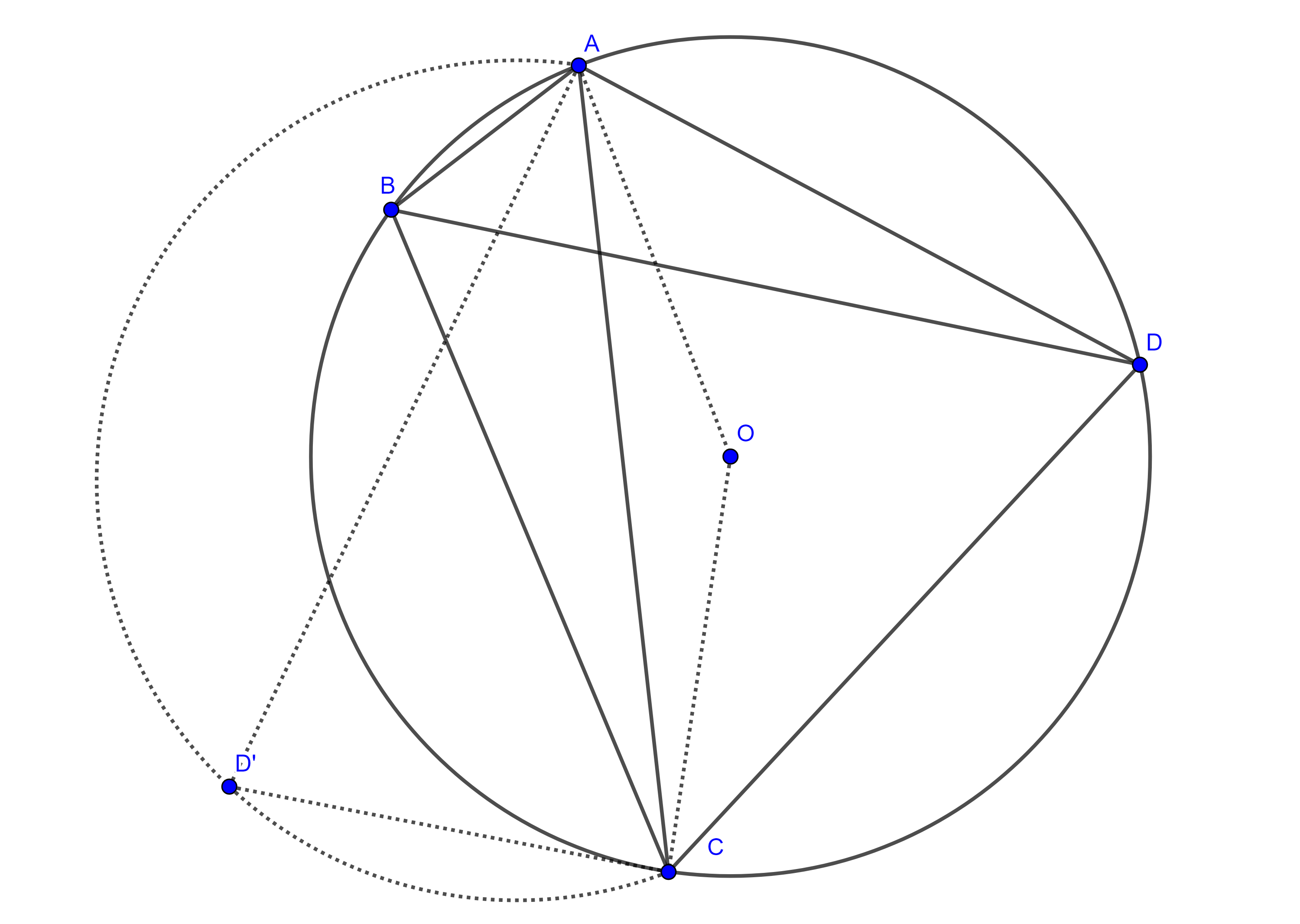
Problema 2. Dado un triángulo, inscribir un cuadrado en el triángulo dado.

Solución. Sea $\triangle ABC$ el triángulo dado, construimos un cuadrado exteriormente $\square BDEC$ sobre $BC$, sean $D’ = AD \cap BC$ y $E’ = AE \cap BC$.

Como $BC \parallel DE$ entonces $D’$ y $E’$ son puntos homólogos de $D$ y $E$ respectivamente con centro de homotecia en $A$.

Por $D’$ trazamos una paralela a $BD$ que interseca a $AB$ en $B’$ y por $E’$ trazamos una paralela a $CE$ que interseca a $AC$ en $C’$.

Figura 5

Como $B’D’$ es transversal a $AB$ y a $AD$ y es paralela a $BD$ entonces $\dfrac{AB’}{AB} =\dfrac{AD’}{AD}$ y por tanto, $B$ y $B’$ son puntos homólogos, de manera similar podemos ver que $C$ y $C’$ son puntos homólogos.

Como $\square BDEC$ y $\square B’D’E’C’$ son figuras homotéticas entonces, por el corolario, son semejantes, por lo tanto, $\square B’D’E’C’$ es un cuadrado.

$\blacksquare$

Observación. Si alguno de los ángulos $\angle B$ o $\angle C$ es obtuso, entonces una de las rectas $AD$ o $AE$ intersecaría a $BC$ por fuera y no seria posible la construcción.

Así, si nuestro triángulo $\triangle ABC$ es obtusángulo tenemos que tomar como centro de homotecia el vértice del ángulo obtuso.

Si $\triangle ABC$ es acutángulo existen tres soluciones, una por cada vértice como centro de homotecia, y si es rectángulo hay dos soluciones.

Construir una secante a un triángulo dado

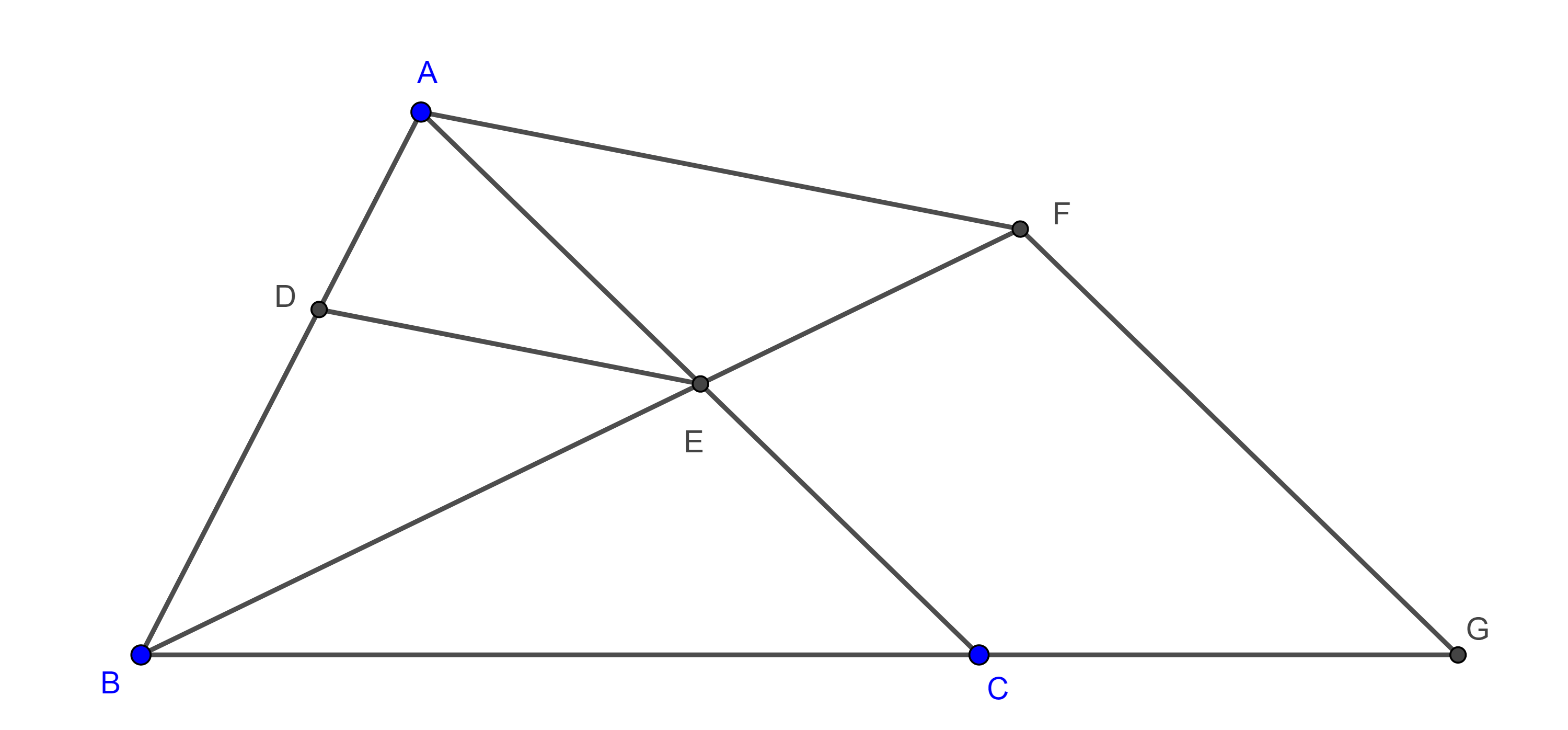
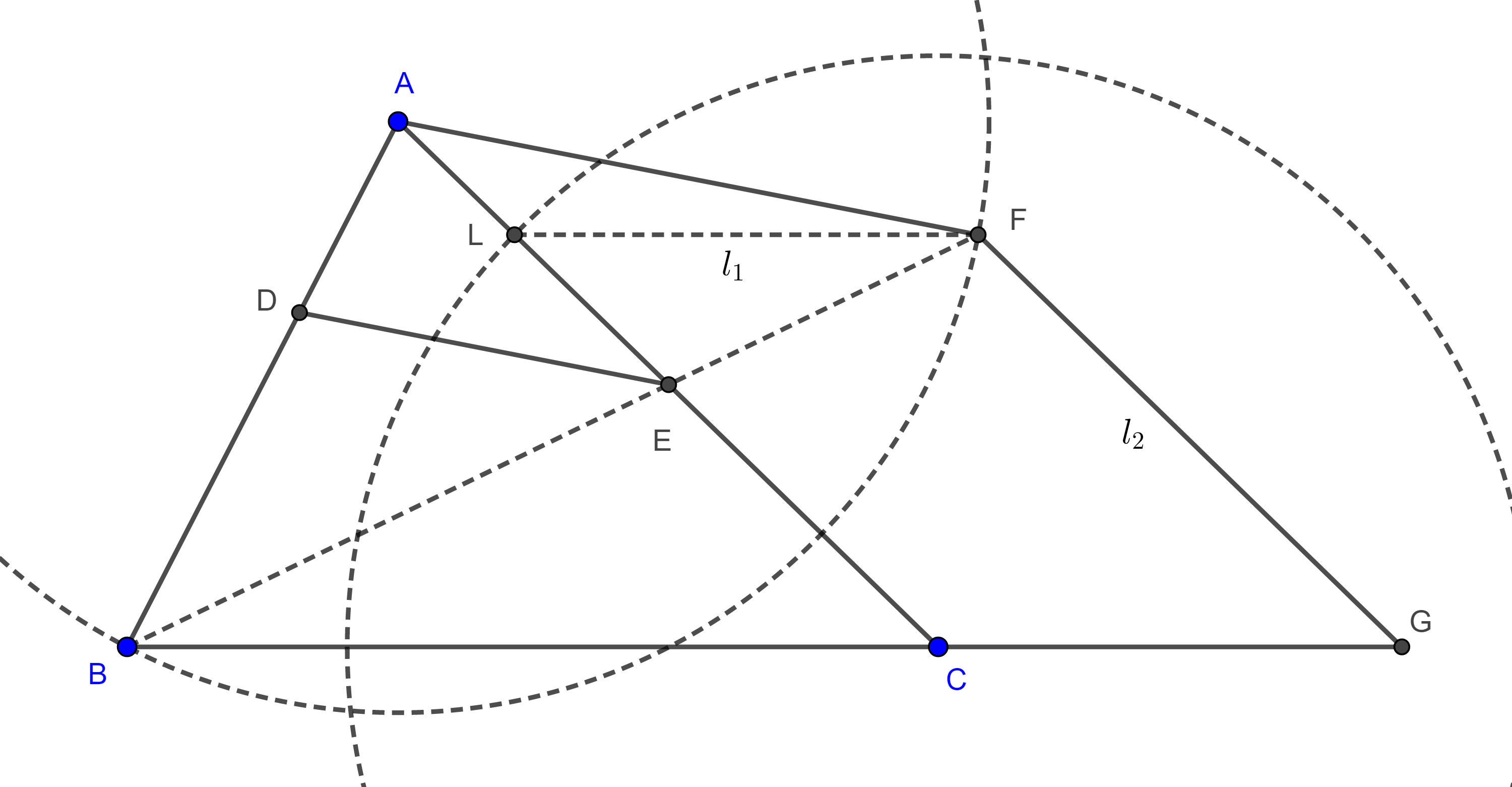
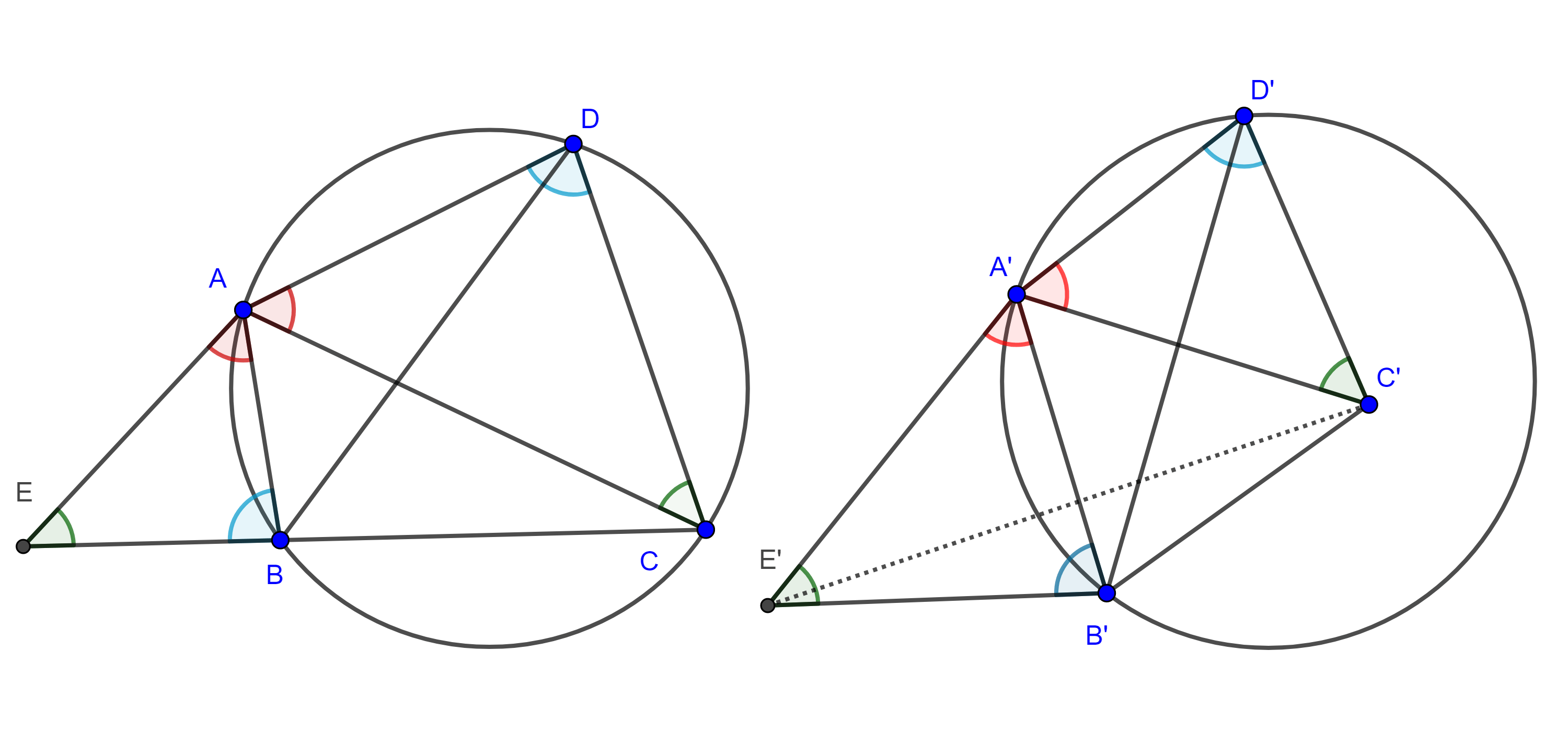
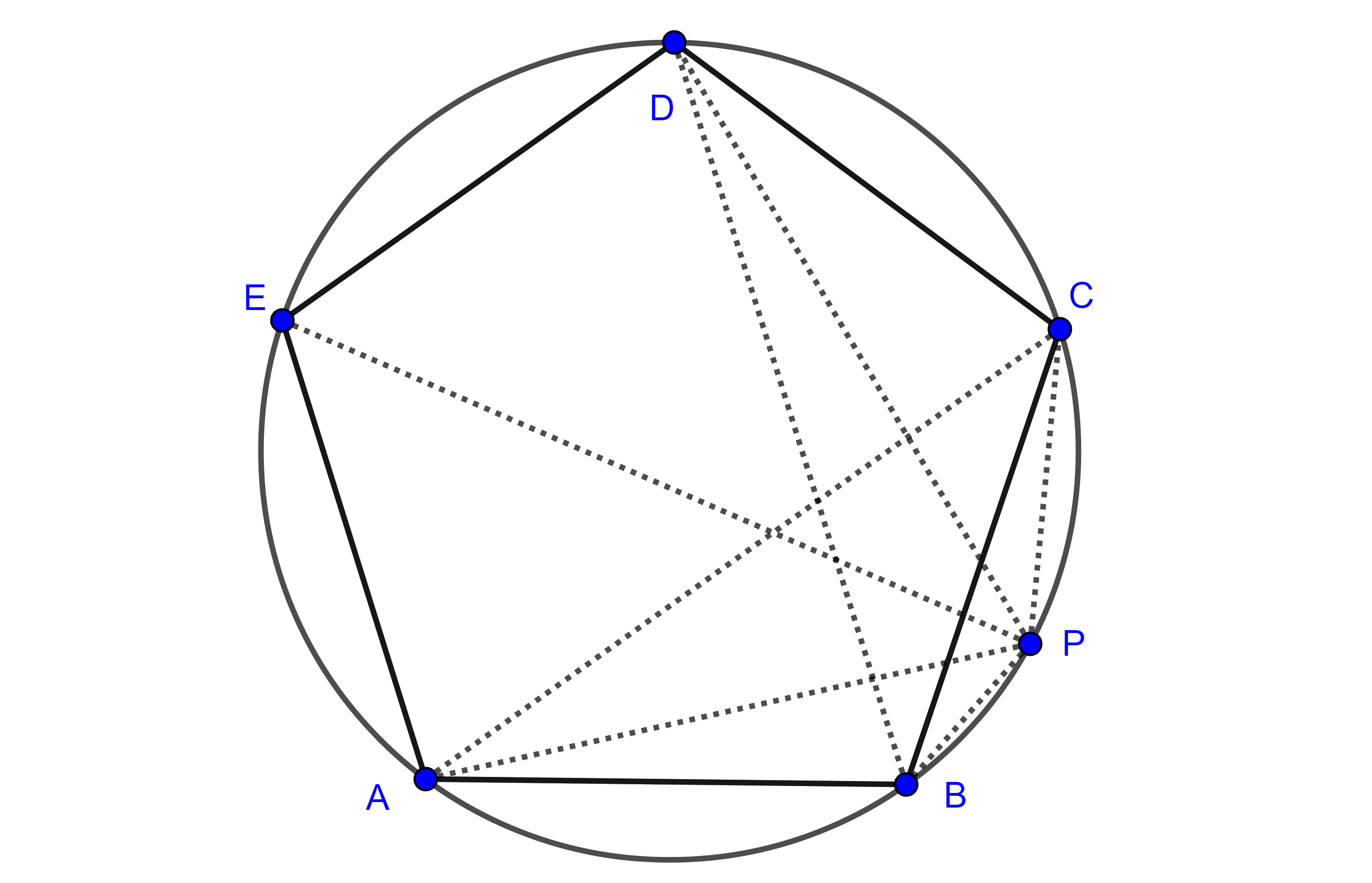
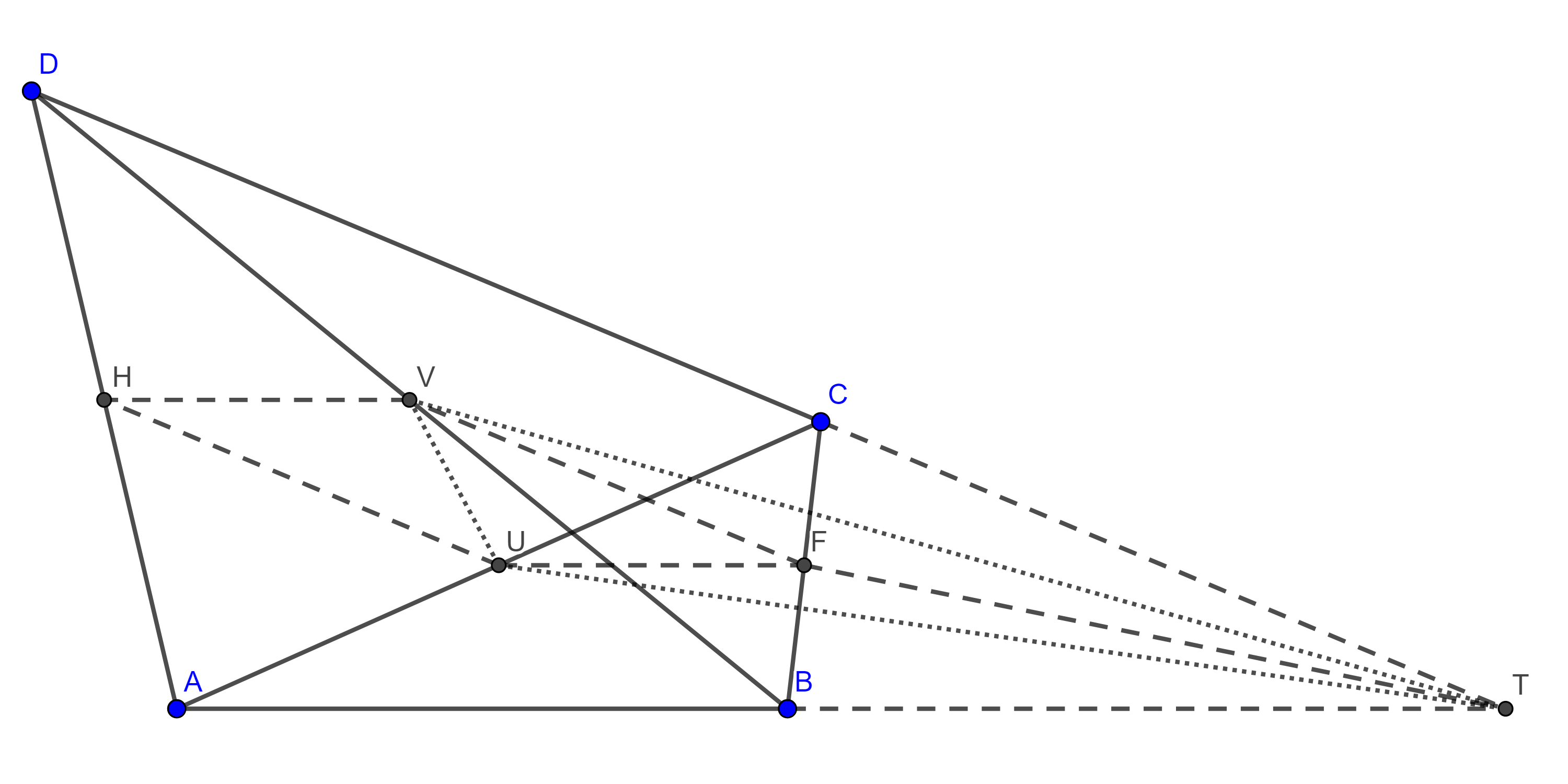
Problema 3. Dado un triángulo $\triangle ABC$, construye $D \in AB$ y $E \in AC$ tal que $BD = DE = EC$.

Solución. Supongamos que ya tenemos la figura requerida (figura 6). Por $A$ trazamos una paralela a $DE$ que interseca a $BE$ en $F$, por $F$ trazamos una paralela a $AC$ que interseca a $BC$ en $G$.

Figura 6

Como $AF \parallel DE$ y $FG \parallel EC$, por el teorema de Tales, tenemos
$\dfrac{BA}{BD} = \dfrac{BF}{BE} = \dfrac{BG}{BC}$.

Así que $(A, D)$, $(F, E)$ y $(G, C)$ son pares de puntos homólogos, con centro en $B$.

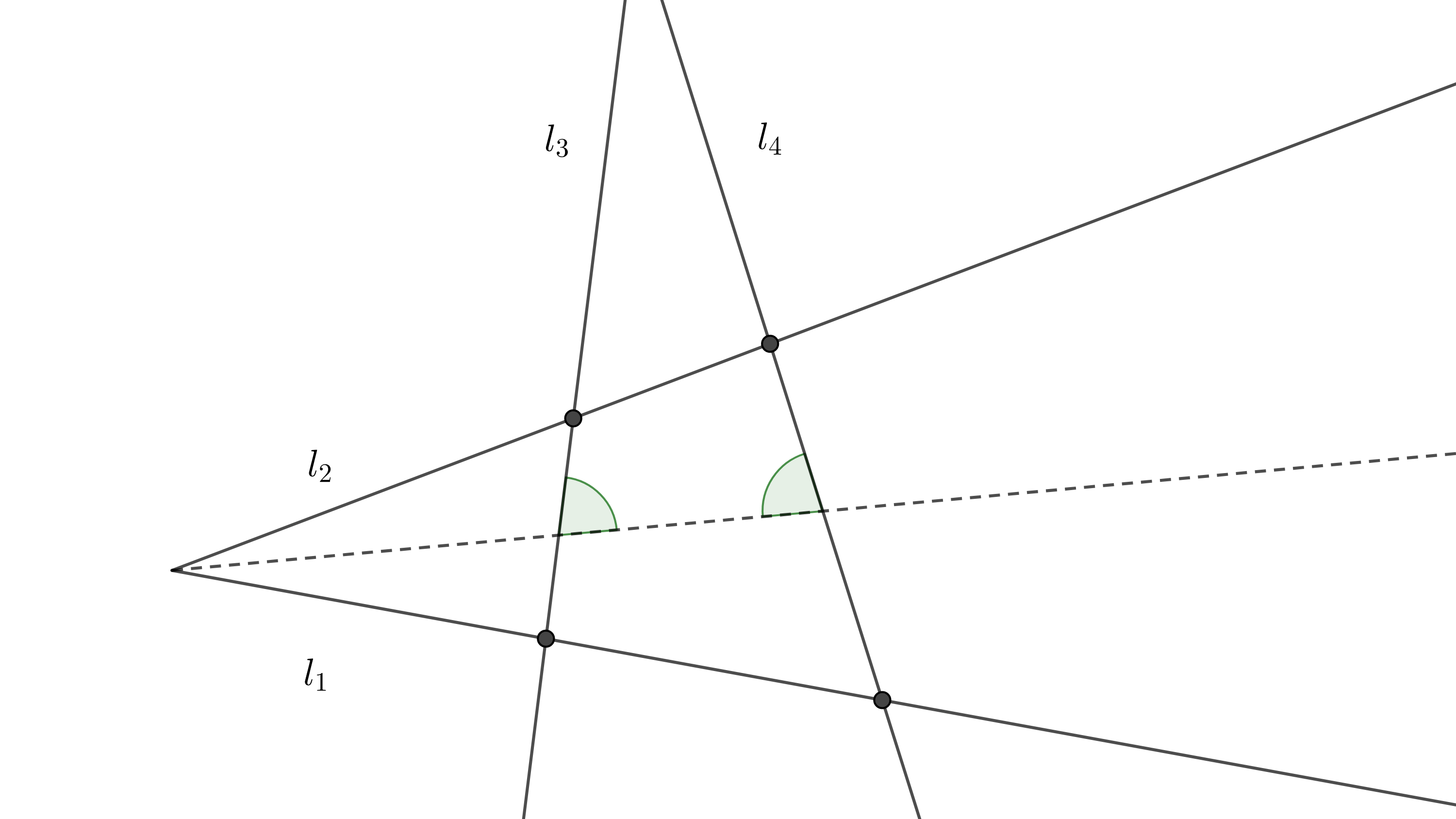
Inversamente, para construir el cuadrilátero auxiliar $\square BAFG$ hacemos lo siguiente (figura 7), trazamos una circunferencia con centro en $A$ y radio $AB$, $(A, AB)$, construimos $L \in AC$ tal que $LC = AB$, trazamos una paralela $l_1$ a $BC$ por $L$, sea $F = (A, AB) \cap l_1$, trazamos una paralela $l_2$ a $AC$ por $F$, sea $G = BC \cap l_2$.

Figura 7

Como $\square LCGF$ es un paralelogramo entonces $FG = LC = AB = AF$.

Finalmente, sean $E = AC \cap BF$ y $D$ la intersección de la paralela por $E$ a $AF$ con $AB$.

Por construcción $\square BDEC$ y $\square BAFG$ son homotéticos, con centro de homotecia en $B$, y tenemos que $\dfrac{BD}{BA} = \dfrac{DE}{AF} = \dfrac{EC}{FG}$ $\Rightarrow BD = DE = EC$.

$\blacksquare$

Más adelante…

Continuando con el tema de homotecia, en la próxima entrada veremos circunferencias homotéticas.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Sean $B$, $B’$ y $C$, $C’$ pares de puntos homólogos de dos figuras homotéticas $F$ y $F’$, considera $A \in F$, por $B’$ y $C’$ tracemos paralelas a $AB$ y $AC$ respectivamente, sea $A’$ la intersección de estas dos últimas rectas, prueba que $A$ y $A’$ son puntos homólogos.
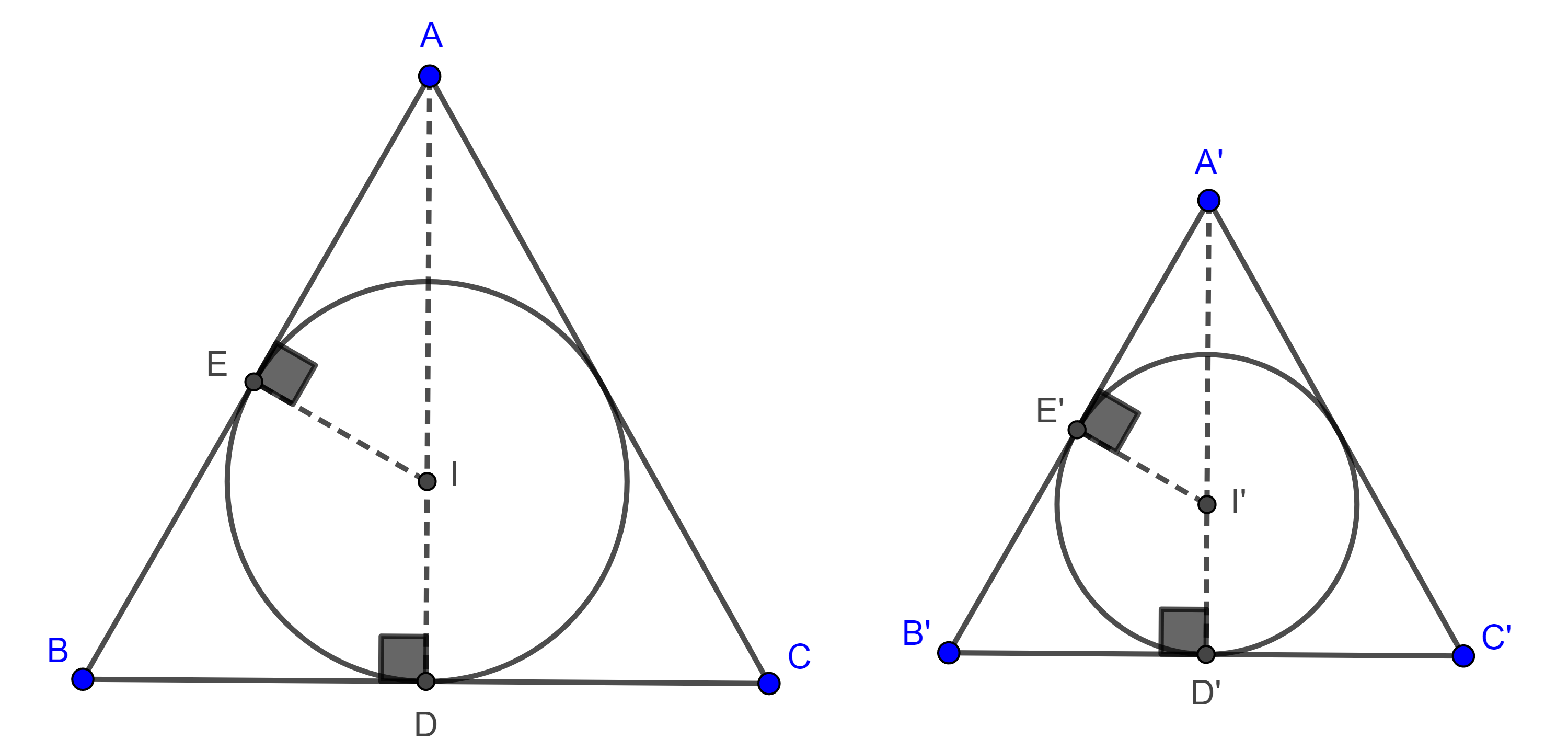
  2. Si dos triángulos están en homotecia muestra que sus incentros, circuncentros, ortocentros y centroides son puntos homólogos, y que sus bisectrices, mediatrices, alturas y medianas son rectas homotéticas.
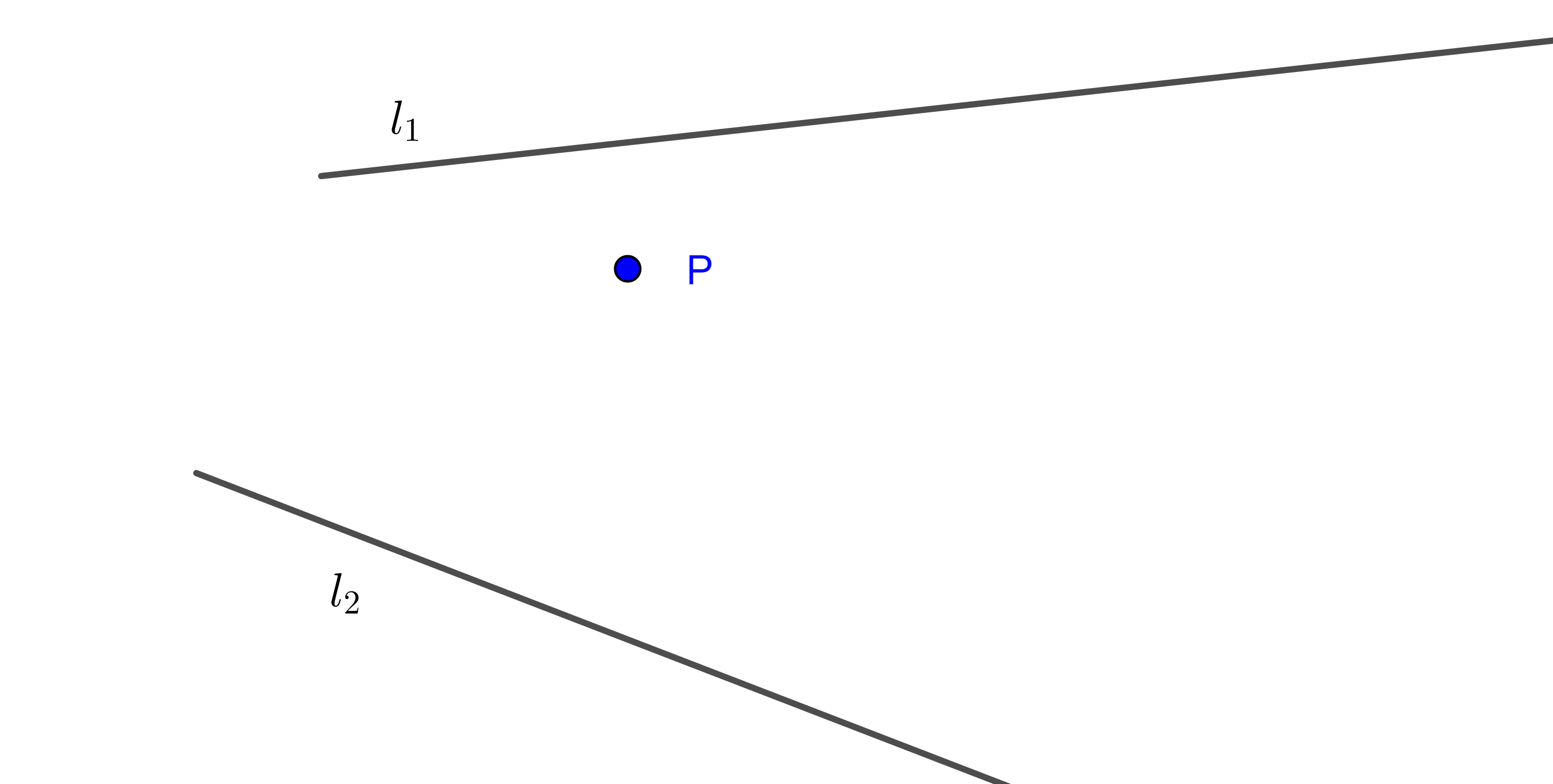
  3. Dadas dos rectas $l_1$ y $l_2$ que se intersecan en un punto inaccesible, trazar una recta que pase por un punto dado $P$ y la intersección de las rectas dadas (figura 8).
Figura 8
  1. En un triangulo dado inscribir un triangulo cuyos lados sean paralelos a las bisectrices internas del triangulo dado.
  2. En un triangulo dado $\triangle ABC$, construir un cuadrado tal que un vértice este en la extensión de $AB$, otro en la exención de $AC$ y los otros dos vértices en $BC$.
  3. Construir un triangulo $\triangle ABC$ dados $\angle A$, $AB + BC$ y $AC + BC$.

Entradas relacionadas

Fuentes

  • Altshiller, N., College Geometry. New York: Dover, 2007, pp 38-45.
  • Andreescu, T., Korsky, S. y Pohoata, C., Lemmas in Olympiad Geometry. USA: XYZ Press, 2016, pp 199-200.
  • Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 110-111.
  • Cut the Knot

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Geometría Moderna I: Construcciones geométricas

Por Rubén Alexander Ocampo Arellano

Deja un comentario

Introducción

En esta entrada estudiamos dos procedimientos generales que pueden ser útiles en la resolución de algunas construcciones geométricas.

Método analítico

Para problemas de construcciones geométricas en los cuales no es muy claro que pasos seguir, nos puede ayudar el método analítico el cual se divide en los siguientes pasos:

Análisis. Empezamos asumiendo que ya tenemos la figura que satisface las condiciones del problema y hacemos un dibujo aproximado de esta. A partir de esta figura indagamos que tipo de relación hay entre los datos que conocemos y los que no.

Construcción. Con la información obtenida llevamos a cabo nuestra construcción.

Demostración. Probamos que en efecto nuestra construcción nos lleva a la figura requerida.

Discusión. Hablamos sobre las condiciones bajo las cuales el problema puede ser resuelto, el número de soluciones posibles y otras observaciones.

A continuación, veremos un par de ejemplos.

($a$, $\angle A$, $b + c$)

Proposición 1. La mediatriz de un lado en todo triangulo siempre interseca al mayor de los lados restantes.

Demostración. Por contradicción, sea $\triangle ABC$ tal que $AC > AB$ y supongamos que la mediatriz de $BC$ interseca a $AB$ en $D$.

$\triangle DBC$ es isósceles, pues $D$ equidista a $B$ y a $C$,
$\Rightarrow \angle CBD = \angle DCB < \angle ACB$.

Figura 2

Por otro lado, sabemos que en todo triangulo al mayor de los lados siempre se opone el mayor de los ángulos, $\Rightarrow \angle CBD = \angle CBA > ACB$.

Lo cual es una contradicción, por tanto, $D \in AC$.

$\blacksquare$

Problema 1. Construir un triángulo $\triangle ABC$ dados la base, el ángulo opuesto a la base y la suma de los lados restantes ($BC = a$, $\angle A = \alpha$, $AB + AC= c + b$).

Análisis. Supongamos que $\triangle ABC$ es el triángulo requerido, sea $D$ en la recta $AB$ tal que $AD = AC$. $\angle BAC$ es un ángulo exterior del triángulo isósceles $\triangle ACD$,
$\Rightarrow BAC = \angle D + \angle DCA = 2\angle D$
$\Rightarrow \angle D = \dfrac{\angle BAC}{2} = \dfrac{\alpha}{2}$.

Figura 3

Con estos elementos podemos construir el triángulo auxiliar $\triangle DBC$ y a partir de este a $\triangle ABC$.

Construcción. Sobre un punto $D$ construimos el ángulo $\dfrac{\alpha}{2}$, sea $B$ sobre uno de los lados del ángulo tal que $DB = b + c$, dibujamos una circunferencia con centro en $B$ y radio $a$, $(B, a)$.

Figura 4

Sea $C$ la intersección de $(B, a)$ con el otro lado del ángulo $\dfrac{\alpha}{2}$.

Finalmente, el vértice $A$ de $\triangle ABC$, se encuentra en la intersección del lado $DB$, con la mediatriz de $CD$.

Demostración. Como $A$ es un punto en la mediatriz de $CD$, entonces $AD = AC$, y como $\triangle ADC$ es isósceles $\Rightarrow \angle DCA = \angle ADC = \dfrac{\alpha}{2}$.

Ya que $\angle BAC$ es ángulo exterior de $\triangle ADC$, es igual a la suma de los ángulos interiores no adyacentes a el $\Rightarrow \angle BAC = \angle DCA + \angle ADC = \alpha$.

Por otro lado, $BC = a$ y $AB + AC = AB + AD = b + c$, por construcción.

$\blacksquare$

Discusión. Por la proposición 2, notamos que es necesario que en el triángulo auxiliar $\triangle DBC$ se cumpla $DB > BC$, es decir $b + c > a$, para que la mediatriz de $CD$ interseque a $BD$.

También observamos que en la construcción de $\triangle DBC$, necesitamos que el radio de $(B, a)$ sea mayor o igual a la distancia de $B$ al segundo lado del ángulo $\alpha$, pues en caso contrario no es posible construir a $C$ y no habrá solución.

Finalmente, de cumplirse esta última condición puede haber una o dos soluciones distintas.

($a$, $\angle A$, $h_b + h_c$)

Problema 2. Construye un triángulo $\triangle ABC$ dados la base, el ángulo opuesto y la suma de las alturas perpendiculares a los otros dos lados ($BC = a$, $\angle A = \alpha$, $BD + CE = h_b + h_c$).

Análisis. Supongamos que $\triangle ABC$ es el triángulo requerido, y sean $BD = h_b$ y $CE = h_c$ las alturas por $B$ y $C$ respectivamente.

Figura 5

Sea $F$ sobre la recta $BD$ tal que $BF = BD + CE = h_b + h_c$.

Por $F$ trazamos una recta paralela a $AC$, la cual interseca a $AB$ en $G$, entonces $\angle BGF = \angle BAC = \alpha$ y $\angle GFB = \angle ADB = \dfrac{\pi}{2}$ por ser ángulos correspondientes.

Construcción. De manera similar a la construcción del triángulo auxiliar $\triangle DBC$ del problema anterior, con la información que resulta del análisis ($BF = h_b + h_c$ y $\angle BGF = \alpha$), podemos construir el triángulo rectángulo auxiliar $\triangle BFG$.

Figura 6

Luego, trazamos una circunferencia con centro $B$ y radio $a$, $(B, a)$.

La intersección de $(B, a)$ con la bisectriz interior de $\angle BGF$ será el vértice $C$ y la intersección de $GB$ con la mediatriz de $GC$ será el vértice $A$.

Demostración. Por construcción $BC = a$, como $A$ está en la mediatriz de $GC$ entonces $\triangle AGC$ es isósceles por lo que $\angle GCA = \angle AGC$, pero $\angle AGC = \angle CGF$ pues $GC$ es bisectriz de $\angle AGF$,
$\Rightarrow \angle GCA = \angle CGF$ $\Rightarrow AC \parallel FG$
$\Rightarrow  \angle BAC = \angle BGF = \alpha$

Como $AC \parallel FG$ entonces $BF \perp AC$.

Sean $BE$ y $CD$ las alturas de $\triangle ABC$ trazadas por $B$ y $C$ respectivamente.

Por $A$ trazamos una perpendicular a $AC$ que corta a $GF$ en $H$, como $\square AEFH$ es un rectángulo entonces $AH = EF$.

En los triángulos rectángulos $\triangle ADC$ y $\triangle GHA$ tenemos $AC = AG$ y $\angle DAC = \angle AGH$, por criterio de congruencia ALA $\triangle ADC \cong \triangle GHA$  $\Rightarrow CD = AH = EF$.

Por lo tanto, $BE + CD = BE + EF = BF = h_b + h_c$, por construcción.

$\blacksquare$

Discusión. Si el ángulo dado es obtuso entonces el triángulo rectángulo auxiliar $\triangle BFG$ incluirá al ángulo suplementario a $\angle A$ y el procedimiento será muy similar.

Notemos que $(B, a)$ puede intersecar a la bisectriz de $\angle BGF$ en cero, uno o dos puntos y por lo tanto existen cero, una o dos posibles soluciones.

Método de semejanza

Este método consiste en construir una figura semejante a la figura requerida omitiendo una de las condiciones dadas, la figura requerida se deriva a partir de la semejanza.

Ilustramos este método con un par de ejemplos.

($b$, $c$, $\dfrac{a}{h_a}$)

Problema 3. Construye un triangulo $\triangle ABC$ dados dos lados y la razón entre el tercer lado y la altura por el vértice opuesto ($AB = c$, $AC = b$, $\dfrac{BC}{AD} = \dfrac{a}{h_a}$).

Análisis. Supongamos que $\triangle ABC$ es el triángulo requerido, consideremos $D$, el pie de la altura desde $A$.

Sea $E \in AD$ tal que $AE = h_a$, por $E$ trazamos la paralela a $BC$ que interseca a $AB$ y a $AC$ en $F$ y $G$ respectivamente.

Figura 7

Como $\triangle ABC \sim \triangle AFG$, entonces
$\begin{equation} \dfrac{AF}{AG} = \dfrac{AB}{AC} = \dfrac{c}{b} \end{equation}$
y $\dfrac{FG}{AE} = \dfrac{BC}{AD} = \dfrac{a}{h_a}$,
como $AE = h_a \Rightarrow FG = a$

Construcción. Podemos construir el triángulo auxiliar $\triangle AFG$ con los siguientes datos, la base $FG = a$, la altura $AE = h_a$ y la razón entre los lados restantes $\dfrac{AF}{AG} = \dfrac{c}{b}$, este problema lo resolvimos en la entrada anterior.

Luego, sobre $AF$ construimos $B$ tal que $AB = c$ y sobre $AG$ construimos $C$ tal que $AC = b$.

Demostración. Por construcción se da la ecuación $(1)$, y por el reciproco del teorema de tales, esto implica $FG \parallel BC$ y $\triangle ABC \sim \triangle AFG$,

Sea $D = BC \cap AE$, el pie de la altura por $A$, entonces, $\dfrac{BC}{AD} = \dfrac{FG}{AE} = \dfrac{a}{h_a}$.

$\blacksquare$

Discusión. Debido a la construcción del triángulo auxiliar $\triangle AFG$ el problema tiene $0$, $1$ o $2$ soluciones posibles.

Construir un triángulo isósceles dado su incírculo

Proposición. 2 Dos triángulos isósceles son semejantes si la razón entre las alturas perpendiculares a las bases es igual a la razón entre sus inradios.

Demostración. Sean $\triangle ABC$ y $\triangle A’B’C’$ triángulos isósceles con $AB = AC$ y $A’B’ = A’C’$, $D$ y $D’$ los pies de las alturas desde $A$ y $A’$ respectivamente, consideremos $(I, r)$ y $(I’, r’)$ los incuncírculos de $\triangle ABC$ y $\triangle A’B’C’$ respectivamente.

Figura 8

Si $\dfrac{r}{r’} = \dfrac{AD}{A’D’} = \dfrac{h_a}{h_a’}$
$\Rightarrow h_a – r = \dfrac{rh_a’}{r’} – \dfrac{rr’}{r’} = \dfrac{r}{r’}(h_a’ – r’)$
$\Rightarrow \dfrac{AI}{A’I’} = \dfrac{h_a – r}{h’_a – r’} = \dfrac{r}{r’} = \dfrac{IE}{I’E’}$,

donde $E$ y $E’$ son los puntos de tangencia de $(I, r)$ y $(I’, r’)$ en $AB$ y $A’B’$ respectivamente.

Por criterio de semejanza hipotenusa-cateto, $\triangle AIE \sim \triangle A’I’E’$ $\Rightarrow$ $\angle EAI = \angle E’A’I’$, como $AI$ y $A’I’$ son bisectrices de $ \angle A$ y $ \angle A’$ respectivamente $\Rightarrow \angle A = \angle A’$.

Como $\angle B = \angle C$ y $\angle B’ = \angle C’$, obtenemos $2\angle B = 2\angle B’$, por cierto de semejanza AA, $\triangle ABC \sim \triangle A’B’C’$.

$\blacksquare$

Problema 4. Dada una circunferencia $(I, r)$, construir un triángulo isósceles tal que $(I, r)$ es incírculo del triángulo y el cociente entre uno de los lados iguales del triángulo y la base es igual a una razón dada $\dfrac{p}{q}$.

Construcción. Construimos un triángulo $\triangle A’B’C’$ con $A’B’ = A’C’ = p$ y $B’C’ = q$, de este triangulo tomamos $h_a’$ la altura trazada desde $A’$ y $r’$ el inradio.

Ahora construimos $h_a = \dfrac{rh_a’}{r’}$.

Por un punto arbitrario $D \in (I, r)$ trazamos la tangente $l$ a $(I, r)$, en la recta $DI$, tomamos $A$ tal que $AD = h_a$, finalmente trazamos tangentes desde $A$ a $(I, r)$ y las intersecciones con $l$ serán los vértices $B$ y $C$.

Figura 9

Demostración. Sean $E$ y $F$ los puntos de tangencia de $AB$ y $AC$ respectivamente con $(I, r)$, por criterio de congruencia hipotenusa-cateto, $\triangle AIE \cong \triangle AIF$ por lo que $\angle BAI = \angle IAC$.

Como $AD \perp BC$, por criterio de congruencia ALA, $\triangle ADB \cong \triangle ADC$ $\Rightarrow  AB = AC$, por lo tanto $\triangle ABC$ es un triángulo isósceles.

Dado que $\dfrac{h_a}{h_a’} = \dfrac{r}{r’}$, por la proposición 3, $\triangle ABC \sim \triangle A’B’C’$ y por tanto $\dfrac{AB}{BC}  = \dfrac{A’B’}{B’C’} = \dfrac{p}{q}$.

$\blacksquare$

Más adelante…

La siguiente entrada tratara sobre homotecia, una transformación en el plano que agranda o achica una figura e incluso la invierte pero no cambia su forma, esta herramienta será muy útil en posteriores entradas.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Dados tres segmentos de longitudes $a$, $b$ y $c$ decimos que $x$ es la cuarta proporcional de $a$, $b$ y $c$ si $\dfrac{x}{a} = \dfrac{b}{c}$. Construir la cuarta proporcional de tres segmentos.
  2. Construye un triangulo dados la base, el ángulo opuesto a la base y la diferencia de los lados restantes ($a$, $\angle A$, $b – c$).
  3. Con los siguientes datos construye un triángulo, la base, el ángulo opuesto a la base y la diferencia de las alturas perpendiculares a los lados restantes ($a$, $\angle A$, $h_b – h_c$).
  4. Construye un cuadrado dada la suma de su lado $l$ y su diagonal $d$, $l + d$.
  5. Construye un triángulo dados un ángulo, la bisectriz del ángulo dado y la razón en que la bisectriz divide al lado opuesto.

Entradas relacionadas

Fuentes

  • Altshiller, N., College Geometry. New York: Dover, 2007, pp 17-37.
  • Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 45-50.
  • Cut the Knot

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Geometría Moderna I: Circunferencia de Apolonio

Por Rubén Alexander Ocampo Arellano

Deja un comentario

Introducción

En esta entrada veremos dos lugares geométricos importantes, uno es la caracterización de arco de circunferencia y el otro la circunferencia de Apolonio.

Arco de circunferencia

Teorema 1. Dados un segmento $BC$ y un ángulo $\alpha < \pi$ el lugar geométrico de los puntos $A$ que están sobre un mismo lado de la recta $BC$ y tal que el ángulo $\angle BAC = \alpha$, es un arco de circunferencia que pasa por $B$ y $C$.

Demostración. Sea $A$ un punto tal que $\angle BAC = \alpha$, consideremos el circuncírculo $\Gamma (O)$ de $\triangle ABC$.

Todos los puntos $A’$ en el arco $\overset{\LARGE{\frown}}{CB}$  cumplen que $\angle BA’C =\alpha$ pues $\angle BAC$ y $\angle BA’C$ abarcan el mismo arco $\overset{\LARGE{\frown}}{BC}$.

Figura 1

Por lo tanto, el arco $\overset{\LARGE{\frown}}{CB}$ es parte del lugar geométrico.

$\blacksquare$

Ahora tomemos $A’$ del mismo lado que $A$ respecto de $BC$  pero $A’ \notin \overset{\LARGE{\frown}}{CB}$ y consideremos $B’ =  A’B \cap \overset{\LARGE{\frown}}{CB}$ y $C’ = A’C \cap \overset{\LARGE{\frown}}{CB}$.

Si $A’$ está dentro del circuncírculo de $\triangle ABC$ (izquierda figura 2), entonces los teoremas de la medida del ángulo interior y el ángulo inscrito nos dicen que
$\angle BA’C = \dfrac{\angle BOC + \angle B’OC’}{2} > \dfrac{\angle BOC}{2} = \angle BAC$.

Por tanto, $A’$ no está en el lugar geométrico.

Figura 2

Si $A’$ esta fuera del circuncírculo de $\triangle ABC$ (derecha figura 2) , entonces la medida del ángulo exterior es
$\angle BA’C = \dfrac{\angle BOC – \angle C’OB’}{2} < \dfrac{\angle BOC}{2} = \angle BAC$.

En consecuencia no existe $A’$ en el lugar geométrico fuera del arco $\overset{\LARGE{\frown}}{CB}$ y así queda demostrado el teorema.

$\blacksquare$

Observación. Si quitamos la condición de que los puntos $A$ estén de un mismo lado respecto de $BC$ entonces obtendremos dos arcos de circunferencia que son simétricos respecto de $BC$.

Corolario. Dados un segmento $BC$  el lugar geométrico de los puntos $A$ tal que el ángulo $\angle BAC = \dfrac{\pi}{2}$, es una circunferencia de diámetro $BC$.

Demostración. Por el teorema 1 y la observación, el lugar geométrico son dos arcos de circunferencia simétricos respecto de $BC$, además, por el teorema de Tales, $BC$ es diámetro de cada uno de estos arcos, por tanto los dos arcos forman una misma circunferencia.

$\blacksquare$

Circunferencia de Apolonio

Teorema 2. El lugar geométrico de los puntos $A$ tales que la razón de las distancias a dos puntos fijos $B$ y $C$ es igual a una razón dada $\dfrac{p}{q}$, es una circunferencia llamada circunferencia de Apolonio.

Demostración. Sea $BC = a$, construimos un triángulo de lados $p$, $q$ y $a$, si $p + q < a$ entonces tomamos un múltiplo $mp$ y $mq$ tal que $m(p + q) > a$.

Figura 3

Sea $A$ el vértice construido tal que $AB = p$ y $AC = q$, por el teorema de la bisectriz, las bisectrices interna $AD$ y externa $AE$ de $\angle A$ dividen al segmento $CB$ en la razón dada
$\dfrac{p}{q} = \dfrac{AB}{AC} = \dfrac{BD}{DC} = \dfrac{BE}{CE}$.

De esta manera, hemos encontrado dos putos $D$ y $E$ en la recta $BC$ del lugar geométrico.

Sea $A’$ cualquier punto en el lugar geométrico, entonces $\dfrac{A’B}{A’C} = \dfrac{p}{q} = \dfrac{BD}{DC} = \dfrac{BE}{CE}$.

Por el reciproco del teorema de la bisectriz esto implica que las cevianas $AD$ y $AE$ son las bisectrices interna y externa del ángulo $\angle BA’C$.

Figura 4

Como las bisectrices interna y externa de todo ángulo son perpendiculares entre si tenemos que $\angle DA’C = \dfrac{\pi}{2}$.

Por el corolario anterior, $A’ \in \Gamma$, la circunferencia cuyo diámetro es $DE$.

$\blacksquare$

Ahora, sea $A \in \Gamma$, entonces $AD \perp AE$ ya que $DE$ es diámetro.

Figura 5

Por $C$ trazamos las paralelas a $AE$ y $AD$ las cuales intersecan a $AB$ en $P$ y en $Q$ respectivamente, como $AD \perp AE$ entonces $PC \perp CQ$.

Aplicando el teorema de Tales a $\triangle BQC$ y $\triangle BAE$ tenemos
$\begin{equation} \dfrac{AB}{AQ} = \dfrac{BD}{DC} \end{equation}$
$\begin{equation} \dfrac{AB}{AP} = \dfrac{BE}{CE}. \end{equation}$

Por construcción $\dfrac{BD}{DC} = \dfrac{BE}{CE}$
$\Rightarrow \dfrac{AB}{AQ} = \dfrac{AB}{AP} \Rightarrow AP = AQ$.

Es decir, $A$ es el punto medio de la hipotenusa en el triángulo rectángulo $\triangle CPQ$, por tanto, equidista a los tres vértices del triangulo
$\Rightarrow AP = AQ = AC$

Reemplazando en las ecuaciones $(1)$ y $(2)$ obtenemos
$\dfrac{AB}{AC} = \dfrac{BD}{DC} = \dfrac{BE}{CE} = \dfrac{p}{q}$.

Por tanto, $A$ está en el lugar geométrico.

$\blacksquare$

Observación 1. Notemos que, si la razón dada es $1$, el lugar geométrico son los puntos que equidistan a los puntos dados, esto es la mediatriz del segmento que une los puntos dados.

Observación 2. Si $B$, $C$ son los puntos fijos y $\dfrac{p}{q}$ es la razón dada, los puntos $A$ tales que $\dfrac{AB}{AC} = \dfrac{p}{q}$, describen una circunferencia de Apolonio, pero los puntos $A’$ tales que $\dfrac{A’C}{A’B} = \dfrac{p}{q}$ también describen una circunferencia de Apolonio, estos dos lugares no coinciden a menos que $\dfrac{p}{q} = 1$.

En consecuencia, para un segmento dado y una razón dada tenemos dos circunferencias de Apolonio.

Construcción de un triangulo ($a$, $h_a$, $\dfrac{c}{b}$)

Problema. Construye un triángulo $\triangle ABC$ dados la base, la altura trazada por el vértice opuesto y la razón entre los lados restantes ($BC = a$, $AD = h_a$, $\dfrac{AB}{AC} = \dfrac{c}{b}$).

Solución. Construimos un segmento $BC$ de longitud $a$ y trazamos la circunferencia de Apolonio $\Gamma$ de los puntos $P$ tales que la razón de las distancias a $B$ y a $C$ es la razón dada, $\dfrac{PB}{PC} = \dfrac{c}{b}$.

Figura 6

Luego trazamos una recta $l$ paralela a $BC$ y a una distancia $h_a$. Una de las intersecciones de $l$ con $\Gamma$ es el tercer vértice del triángulo $\triangle ABC$.

Sea $D$ el pie de la perpendicular a $BC$ trazado desde $A$, entonces por construcción $BC = a$, $AD = h_a$ y $\dfrac{AB}{AC} =\dfrac{c}{b}$.

$\blacksquare$

Círculos de Apolonio de un triángulo

Definición 1. Consideremos un triángulo $\triangle ABC$, el lugar geométrico de los puntos $P$ tales que $\dfrac{PB}{PC} = \dfrac{AB}{AC}$, es la $A$-circunferencia de Apolonio de $\triangle ABC$. De esta manera todo triangulo tiene tres circunferencias de Apolonio asociadas a él, una que pasa por cada vértice.

Definición 2. Decimos que dos circunferencias son ortogonales si se intersecan y los radios trazados desde el punto de intersección son perpendiculares.

Proposición. Cada circunferencia de Apolonio asociada a un triángulo es ortogonal con el circuncírculo del triángulo.

Demostración. Sean $\triangle ABC$, $D$ y $E$ los pies de la bisectriz interior y exterior respectivamente de $\angle A$, consideremos $M$ el punto medio de $DE$.

La circunferencia con centro $M$ y radio $AM$, $(M, AM)$ es la $A$-circunferencia de Apolonio de $\triangle ABC$.

Figura 7

Tenemos lo siguiente
$\dfrac{\pi}{2} = \angle DAE = \angle DAC + \angle CAM + \angle MAE = \dfrac{\angle BAC}{2} + \angle CAM + \dfrac{\angle AMB}{2}$.

$\Rightarrow \pi = \angle BAC + 2\angle CAM + \angle AMB = \angle BAM + \angle AMB + \angle CAM$
$\Rightarrow \angle CBA = \pi – (\angle BAM + \angle AMB)$
$\begin{equation} = \angle CAM. \end{equation}$

Ahora consideremos el circuncírculo $(O, AO)$ de $\triangle ABC$, y supongamos que $AM$ es secante a $(O, AO)$ en $A$ y $F$, tenemos dos casos:

  • $F$ esta entre $A$ y $M$,
Figura 8

$\Rightarrow \angle CBA = \dfrac{\angle COA}{2} > \dfrac{\angle COF}{2} = \angle CAF = \angle CAM$.

  • $A$ esta entre $F$ y $M$,
Figura 9

$\Rightarrow \angle CAM > \angle CFA = \angle CBA$.

Ninguno de los dos casos anteriores es posible, puesto que por la ecuación $(3)$, $\angle CBA = \angle CAM$, por lo tanto, $A$ es tangente a $(O, AO)$ y así $(O, AO)$ y $(M, AM)$ son ortogonales.

La prueba para las otras dos circunferencias de Apolonio de $\triangle ABC$ es análoga.

$\blacksquare$

Más adelante…

En la siguiente entrada estudiaremos un par de métodos generales que nos pueden ayudar a resolver problemas de construcciones geométricas.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Dada una circunferencia, muestra que el lugar geométrico de los puntos medios de las cuerdas que pasan por un punto dado es una circunferencia, si el punto esta dentro o en la circunferencia. Analiza el caso cuando el punto se encuentra fuera de la circunferencia.
  2. Dados dos segmentos consecutivos $AB$ y $BC$ sobre una misma recta encuentra el lugar geométrico de los puntos $P$ tales que $\angle APB = \angle BPC$.
  3. Dados tres puntos $A$, $B$, $C$ y un ángulo $\alpha$, construye una circunferencia que pase por $A$ y $B$ y tal que el ángulo entre las tangentes trazadas desde $C$ a la circunferencia sea igual a $\alpha$.
Figura 10
  1. Construye un triangulo, dados:
    $i)$ la base, la mediana trazada desde el vértice opuesto y la razón entre los lados restantes,
    $ii)$ la base, la bisectriz del ángulo opuesto y la razón entre los lados restantes.
  2. Muestra que las tres circunferencias de Apolonio de un triangulo concurren en dos puntos.
Figura 11

Entradas relacionadas

Fuentes

  • Altshiller, N., College Geometry. New York: Dover, 2007, pp 11-16.
  • Andreescu, T., Korsky, S. y Pohoata, C., Lemmas in Olympiad Geometry. USA: XYZ Press, 2016, pp 275-276.
  • Santos, J., Tesis Geometría del Cuadrilátero. 2010, pp 135-137.
  • Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 38-39.

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Geometría Moderna I: Teorema de Ptolomeo

Por Rubén Alexander Ocampo Arellano

2 respuestas

Introducción

El teorema de Ptolomeo nos da una caracterización del cuando un cuadrilátero convexo es cíclico en términos de los productos entre sus lados y sus diagonales. Necesitaremos antes una caracterización diferente de cuadrilátero cíclico.

Cuadriláteros cíclicos

Definición. Si los vértices de un polígono están en una misma circunferencia decimos que está inscrito en ella o que es cíclico.

Teorema 1. Un cuadrilátero convexo es cíclico si y solo si los ángulos opuestos son suplementarios.

Demostración. Sea $\square ABCD$ un cuadrilátero cíclico inscrito en $(O, r)$, la circunferencia con centro en $O$.

Los ángulos opuestos $\angle ADC$ y $\angle CBA$ son subtendidos por los arcos $AC$ y $CA$ respectivamente y por el teorema de la medida del ángulo inscrito tenemos que
$\angle ADC + \angle CBA = \dfrac{\angle AOC}{2} + \dfrac{\angle COA}{2} = \dfrac{2\pi}{2} = \pi$.

Figura 1

De manera análoga se ve que $\angle BAD$ y $\angle DCB$ son suplementarios.

Por lo tanto, los ángulos opuestos de un cuadrilátero cíclico son suplementarios.

$\blacksquare$

Ahora supongamos que los ángulos opuestos $\angle ADC$ y $\angle CBA$ de $\square ABCD$ son suplementarios.

Consideremos el circuncírculo de $\triangle ABC$, entonces todos los puntos en el arco $\overset{\LARGE{\frown}}{CA}$ que no contiene a $B$ subtienden un ángulo $\angle ADC$ suplementario a $\angle CBA$, pero este lugar geométrico es único.

Por lo tanto $D \in \overset{\LARGE{\frown}}{CA}$ y en consecuencia $\square ABCD$ es cíclico.

$\blacksquare$

Teorema de Ptolomeo

Teorema 2, desigualdad de Ptolomeo. En todo cuadrilátero convexo la suma de los productos entre lados opuestos es mayor o igual al producto de las diagonales, y la igualdad se da si y solo si es el cuadrilátero es cíclico.

Demostración. Sea $\square ABCD$ un cuadrilátero convexo, construyamos sobre el segmento $AB$ (figura 2), un triángulo $\triangle ABE$ semejante a $\triangle ADC$ tal que $\angle ABE = \angle ADC$ y $\angle BAE = \angle CAD$ entonces

$\begin{equation} \dfrac{EA}{CA} = \dfrac{BA}{DA} \Leftrightarrow \dfrac{EA}{BA} = \dfrac{CA}{DA}. \end{equation}$

Figura 2

Dado que $\angle CAE = \angle BAD$ y por $(1)$, por criterio lado, ángulo, lado, los triángulos $\triangle EAC$ y $\triangle BAD$ son semejantes, entonces de la primera y segunda relaciones de semejanza tenemos que
$\dfrac{EB}{CD} = \dfrac{AB}{AD}$ y $\dfrac{EC}{BD} = \dfrac{AC}{AD}$
$\Leftrightarrow$ $EB = \dfrac{AB \times CD}{AD}$ y $EC = \dfrac{AC \times BD}{AD}$.

Ahora notemos que tenemos dos casos:

Caso 1. (izquierda figura 2)
$B \in EC$ $\Leftrightarrow$ $\angle CBA + \angle ADC = \angle CBA + \angle ABE = \pi$ $\Leftrightarrow$ $\square ABCD$ es cíclico,
y en tal caso $EC = EB + BC$ $\Leftrightarrow$ $\dfrac{AC \times BD}{AD} = \dfrac{AB \times CD}{AD} + BC$
$\Leftrightarrow$ $AC \times BD = AB \times CD + AD \times BC$.

Caso 2. (derecha figura 2)
$E$, $B$ y $C$ son tres puntos no colineales $\Leftrightarrow$ $\angle CBA + \angle ADC = \angle CBA + \angle ABE \ne \pi$ $\Leftrightarrow$ $\square ABCD$ no es cíclico, entonces aplicando la desigualdad del triángulo a $\triangle EBC$ tenemos que
$EC < EB + BC$ $\Leftrightarrow$ $AC \times BD < AB \times CD + AD \times BC$.

De lo anterior se sigue que $AB \times CD + AD \times BC \geq AC \times BD$, con la igualdad si y solo si $\square ABCD$ es cíclico.

$\blacksquare$

Construcción del cuadrilátero cíclico

Problema 1. Construir un cuadrilátero convexo y cíclico dados sus cuatro lados $a$, $b$, $c$ y $d$.

Solución. Notemos primero que es necesario que la suma de cualesquiera tres de los lados dados sea mayor que el lado restante.

Si un lado es mayor que la suma de los otros tres no es posible construir ningún cuadrilátero y si es igual entonces solo es posible construir un cuadrilátero degenerado donde todos los vértices están alineados.

Supongamos que $AB = a$, $BC = b$, $CD = c$ y $DA = d$, la prueba del teorema de Ptolomeo nos sugiere una manera de resolver este problema.

Trazamos el segmento $BC$ y lo extendemos del lado de $B$ hasta un punto $E$ tal que $EB = \dfrac{ac}{d}$, el cual es posible construir pues podemos construir el producto de dos magnitudes y el inverso de una magnitud dadas.

Aquí usaremos que $B \in EC$ $\Leftrightarrow$ $\square ABCD$ es cíclico y que los triángulos $\triangle ABE$ y $\triangle ADC$ son semejantes, como en la prueba anterior.

La razón de semejanza está dada por $\dfrac{AE}{AC} = \dfrac{BE}{CD} = \dfrac{ac}{dc} = \dfrac{a}{d}$.

Esto último nos dice que la razón entre las distancias de $A$ a los puntos $E$ y $C$ es una razón fija por lo tanto $A$ esta en la circunferencia de Apolonio determinada por $E$, $C$ y la razón $\dfrac{a}{d}$.

Por otro lado, el vértice $A$ se encuentra en la circunferencia con centro en $B$ y radio $a$, por lo tanto, $A$ esta determinado por la intersección de $(B, a)$ y la circunferencia de Apolonio mencionada.

Ahora que conocemos la diagonal $AC$ podemos completar el triángulo $\triangle ACD$ trazando circunferencias $(A, d)$ y $(C, c)$, una de las intersecciones será el cuarto vértice del cuadrilátero buscado.

Figura 3

Por construcción $\triangle ABE$ y $\triangle ADC$ son semejantes por lo que $\angle CBA$ y $\angle ADC$ son suplementarios.

Por lo tanto $\square ABCD$ es cíclico.

$\blacksquare$

Distancia de los vértices de un polígono cíclico a un punto del circuncírculo

Problema 2. Sean $\triangle ABC$ isósceles con $AB = AC$ y $P$ un punto en el arco $\overset{\LARGE{\frown}}{BC}$ del circuncírculo de $\triangle ABC$, muestra que $\dfrac{PA}{PB + PC} = \dfrac{AC}{BC}$.

Figura 4

Solución. Aplicando el teorema de Ptolomeo a $\square ABPC$ tenemos que
$PA \times BC = AB \times PC + AC \times PB $
$= AC \times PC + AC \times PB = AC(PC + PB)$.

Por lo tanto, $\dfrac{PA}{PB + PC} = \dfrac{AC}{BC}$.

$\blacksquare$

Problema 3. Sean $ABCDE$ un pentágono regular inscrito en una circunferencia y $P$ un punto en el arco $\overset{\LARGE{\frown}}{BC}$, muestra que $PA + PD = PB + PC + PE$.

Solución. Como el pentágono es regular, entonces sus diagonales tienen la misma longitud.

Figura 5

Aplicando el teorema de Ptolomeo a $\square ABPC$  y $\square BPCD$ obtenemos
$BC \times PA = AB \times PC + AC \times PB = BC \times PC + AC \times PB$
$BC \times PD = PB \times CD + PC \times BD = PB \times BC + PC \times AC$.

Sumando estas dos últimas igualdades tenemos
$\begin{equation} BC(PA + PD) = BC(PB + PC) + AC(PB + PC). \end{equation}$

Por otra parte dado que $\triangle BEC$ es isósceles podemos aplicar el resultado del problema anterior y obtenemos $\dfrac{PE}{PB + PC} = \dfrac{EC}{BC}$

$\Leftrightarrow$ $\begin{equation} \dfrac{PE \times BC}{PB + PC} = EC = AC. \end{equation}$

Sustituyendo $(3)$ en $(2)$ resulta
$BC(PA + PD) = BC(PB + PC) + \dfrac{PE \times BC}{PB + PC} (PB + PC)$.

Por lo tanto, $PA + PD = PB  + PC + PE$.

$\blacksquare$

Hexágono cíclico

Problema 4. Sea $ABCDEF$ un hexágono convexo inscrito en una circunferencia. Consideremos las diagonales que dividen al hexágono en dos cuadriláteros cíclicos, $AD = d$, $CF = e$ y $BE = f$ y los lados del hexágono que no comparten vértices con dichas diagonales $BC = a$, $EF = a’$, $DE = b$, $AB = b’$, $AF = c$, $CD = c’$ respectivamente, entonces $def = aa’d + bb’e + cc’f + abc +a’b’c’$.

Figura 6

Demostración. Aplicando el teorema de Ptolomeo a $\square ABCD$ y $\square BCDE$ obtenemos
$ad + b’c’ = AC \times BD$ y $ab + c’f = BD \times CE$.

Multiplicamos por $a’$ y $c$ respectivamente y después sumamos el resultado y obtenemos:
$aa’d + a’b’c’ + abc + cc’f $
$= a’(AC \times BD) + c(BD \times CE) = BD(a’AC + cCE)$.

Aplicando Ptolomeo a $\square ACEF$ obtenemos $a’AC + cCE = eAE$.

Por lo tanto $aa’d + a’b’c’ + abc + cc’f = BD(eAE) = e (BD \times AE)$.

Ahora consideramos $\square ABDE$ y por el teorema de Ptolomeo obtenemos
$BD \times AE = df -bb’$.

En consecuencia tenemos $aa’d + a’b’c’ + abc + cc’f = e(df – bb’)$.

Por lo tanto, $def = aa’d + bb’e + cc’f + abc +a’b’c’$.

$\blacksquare$

Más adelante…

En la próxima entrada estudiaremos trigonometría y mostraremos algunas identidades trigonométricas aplicando el teorema de Ptolomeo.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Muestra que un cuadrilátero convexo es cíclico si y solo si:
    $i)$ un ángulo interno formado con una diagonal y un lado es igual al ángulo interno formado con la otra diagonal y el lado opuesto,
    $ii)$ las mediatrices de los lados del cuadrilátero son concurrentes.
  2. Sean $l_{1}$, $l_{2}$ y $l_{3}$, $l_{4}$ dos pares de rectas tales que la bisectriz del primer par es transversal al segundo par y forma ángulos internos iguales entonces decimos que $l_{3}$ y $l_{4}$ son antiparalelas respecto a $l_{1}$ y $l_{2}$. Muestra que un cuadrilátero convexo es cíclico si y solo si un par de lados opuestos es antiparalelo respecto al otro par de lados opuestos.
Figura 7
  1. Como podrás haber notado nuestra construcción del cuadrilátero cíclico no es única pues partimos de una suposición arbitraria, que $AB = a$, $BC = b$, $CD = c$ y $DA = d$ para $a$, $b$, $c$ y $d$ dados. Muestra que es posible construir tres cuadriláteros cíclicos diferentes con los mismos lados y que de estos se obtienen tres diagonales diferentes.
  2. Expresa la razón de las diagonales de un cuadrilátero cíclico en términos de sus lados.
  3. Considera $\triangle ABC$ equilátero y $P$ un punto en el arco $\overset{\LARGE{\frown}}{BC}$ del circuncírculo de $\triangle ABC$, prueba que $PA = PB + PC$.
  4. Sean $\square ABCD$ un cuadrado y $P \in \overset{\LARGE{\frown}}{BC}$ del circuncírculo de $\square ABCD$, muestra que $\dfrac{PA +PC}{PD + PB} = \dfrac{PD}{PA}$.
  5. Si $ABCDEF$ es un hexágono regular y $P \in \overset{\LARGE{\frown}}{BC}$ del circuncírculo de $ABCDEF$, muestra que $PE + PF = PA + PB + PC + PD$.
  6. Sean $\triangle ABC$ equilátero, $P \in \overset{\LARGE{\frown}}{BC}$ del circuncírculo de $\triangle ABC$ y $D$ la intersección de $BC$ con $AP$, demuestra que $\dfrac{1}{PD} = \dfrac{1}{PB} + \dfrac{1}{PC}$.

Entradas relacionadas

Fuentes

  • Altshiller, N., College Geometry. New York: Dover, 2007, pp 127-131.
  • Santos, J., Tesis Geometría del Cuadrilátero. 2010, pp 15-19, 31-34.
  • Posamentier, A. y Salkind, C; Challenging Problems in Geometry. New York: Dover, 1996, pp 33-35.
  • Johnson, R., Advanced Euclidean Geometry. New York: Dover, 2007, pp 62-66.

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Geometría Moderna I: Teoremas de Varignon y Van Aubel

Por Rubén Alexander Ocampo Arellano

Deja un comentario

Introducción

Con esta entrada damos inicio a la cuarta unidad que tratará sobre cuadriláteros. Comenzaremos hablando sobre el paralelogramo de Varignon y el teorema de Van Aubel.

Área del cuadrilátero

A partir de la ubicación de las diagonales de un cuadrilátero podemos establecer una clasificación de estos.

Un cuadrilátero es convexo si sus dos diagonales se encuentran dentro de él, es cóncavo si tiene una diagonal dentro y otra fuera de él, y es cruzado si las dos diagonales se ubican fuera del cuadrilátero.

El teorema de Varignon nos habla sobre el área de un cuadrilátero en general y ya que no es tan intuitivo definir el área de un cuadrilátero cruzado es necesario introducir el concepto de área orientada.

Consideraremos el área de un triángulo como positiva si recorremos sus vértices en el sentido opuesto a las manecillas del reloj y como negativa en caso contrario.

De esta manera tenemos que para un triángulo $\triangle ABC$,
$(\triangle ABC) = (\triangle BCA) = (\triangle CAB) $
$= – (\triangle CBA) = – (\triangle ACB) = – (\triangle BAC)$.

Figura 1

Definición 1. Definimos el área de un cuadrilátero $\square ABCD$ como la suma de las áreas de los triángulos que se forman al considerar una de sus diagonales, esto es,
$(\square ABCD) = (\triangle ABC) + (\triangle CDA)$.

Notemos que como resultado de esta definición el área del cuadrilátero cruzado resulta ser la diferencia de las áreas de los triángulos que se forman al considerar la intersección cruzada de los lados.

Paralelogramo de Varignon

Teorema 1, de Varignon.
$i)$ Los puntos medios de los lados de un cuadrilátero convexo son los vértices de un paralelogramo, conocido como paralelogramo de Varignon, cuyo perímetro es la suma de las diagonales del cuadrilátero,
$ii)$ el área del paralelogramo de Varignon es la mitad del área del cuadrilátero.

Demostración. Sean $\square ABCD$ un cuadrilátero convexo y $M_{ab}$, $M_{bc}$, $M_{cd}$ y $M_{da}$ los puntos medios de $AB$, $BC$, $CD$ y $DA$ respetivamente.

Figura 2

Notemos que $M_{ab}M_{bc}$ y $M_{cd}M_{da}$ son segmentos medios de $\triangle ABC$ y $\triangle DAC$ por lo que $M_{ab}M_{bc} \parallel CA \parallel M_{cd}M_{da}$ y $2M_{ab}M_{bc} = CA = 2M_{cd}M_{da}$.

De manera análoga podemos ver que $M_{ab}M_{da} \parallel DB \parallel M_{bc}M_{cd}$ y $2M_{ab}M_{da} = BD = 2M_{bc}M_{cd}$.

Por lo tanto los lados opuestos de $\square M_{ab}M_{bc}M_{cd}M_{da}$ son paralelos y $M_{ab}M_{bc} + M_{bc}M_{cd} + M_{cd}M_{da} + M_{da}M_{ab} = \dfrac{CA + BD + CA +BD}{2} = CA + BD$.

Para calcular el área de  $\square M_{ab}M_{bc}M_{cd}M_{da}$ primero notemos que $\triangle AM_{ab}M_{da}$ y $\triangle ABD$ son semejantes pues $M_{ab}M_{da} \parallel BD$.

También sabemos que $M_{ab}M_{da} = \dfrac{BD}{2}$, por lo que las alturas desde $A$, $h$ y $h’$ de $\triangle AM_{ab}M_{da}$ y $\triangle ABD$ respectivamente, también cumplirán que $h = \dfrac{h’}{2}$.

Por lo tanto,
$(\triangle AM_{ab}M_{da}) = \dfrac{M_{ab}M_{da} \times h}{2}$
$= \dfrac{\frac{1}{2}DBD \times \frac{1}{2}h’}{2} = \dfrac{1}{4} \dfrac{BD \times h’}{2} $
$= \dfrac{1}{4} (\triangle ABD)$.

De manera similar podemos encontrar las áreas de $\triangle BM_{bc}M_{ab}$, $\triangle CM_{cd}M_{bc}$ y $\triangle DM_{da}M_{cd}$.

En consecuencia,
$(\square M_{ab}M_{bc}M_{cd}M_{da}) = (\square ABCD) – (\triangle AM_{ab}M_{da}) – (\triangle BM_{bc}M_{ab}) – (\triangle CM_{cd}M_{bc}) – (\triangle DM_{da}M_{cd})$
$= (\square ABCD) – \dfrac{1}{4} ((\triangle ABD) + (\triangle BCD) + (\triangle CDB) + (\triangle DAC))$
$= (\square ABCD) – \dfrac{2}{4}(\square ABCD) $
$ = \dfrac{(\square ABCD)}{2}$.

$\blacksquare$

Corolario. Sea $\square ABCD$ un cuadrilátero convexo, entonces su cuadrilátero de Varignon
$i)$ es un rombo si y solo si $AC = BD$,
$ii)$ es un rectángulo si y solo si $AC \perp BD$,
$iii)$ es un cuadrado si y solo si $AC = BD$ y $AC \perp BD$.

Demostración. Sean $E$, $F$, $G$, $H$, los puntos medios de $BC$, $CD$, $DA$, $AB$, respectivamente como $EF$ y $FG$ son segmentos medios de $\triangle DBC$ y $\triangle ADC$, entonces, $2EF = BD$, $EF \parallel BD$ y $2FG = AC$, $FG \parallel AC$.

Figura 3

$i)$ $\square EFGH$ es un rombo, entonces por definición $EF = FG \Leftrightarrow AC = BD$.

$ii)$ $\square EFGH$ es un rectángulo, entonces por definición $EF \perp FG \Leftrightarrow AC \perp BD$.

$iii)$ Es consecuencia de $i)$ y $ii)$.

$\blacksquare$

Centroide de un cuadrilátero

Definición 2. Los segmentos que unen los puntos medios de los lados opuestos de un cuadrilátero se llaman bimedianas.

Al segmento que une los puntos medios de las diagonales de un cuadrilátero se le conoce como recta de Newton.

Teorema 2. Las bimedianas de un cuadrilátero convexo y su recta de Newton son concurrentes y se bisecan entre sí, el punto de concurrencia es el centroide del cuadrilátero.

Demostración. Sea $\square ABCD$ un cuadrilátero convexo y $M_{ab}$, $M_{bc}$, $M_{cd}$, $M_{da}$, $M$, $N$, los puntos medios de $AB$, $BC$, $CD$, $DA$, $AC$, $BD$, respectivamente.

$M_{ab}M_{cd}$ y $M_{bc}M_{da}$ son las diagonales del paralelogramo de Varignon, por lo tanto, se intersecan en $J$ su punto medio.

Figura 4

Por otra parte, $M_{ab}M$ es un segmento medio de $\triangle ABC$, por lo que $M_{ab}M \parallel BC$; $NM_{cd}$ es un segmento medio de $\triangle DBC$, por lo tanto, $NM_{cd} \parallel BC$, y así $NM_{cd} \parallel M_{ab}M$.

Igualmente vemos que $M_{ab}N \parallel MM{cd}$.

Por lo tanto, $\square M_{ab}NM_{cd}M$ es un paralelogramo, en consecuencia las diagonales $M_{ab}M_{cd}$ y $NM$ se intersecan en $J$ su punto medio.

En conclusión, $J$ es el punto medio de $M_{ab}M_{cd}$, $M_{bc}M_{da}$ y $NM$.

$\blacksquare$

Construcción de un cuadrilátero

Problema. Construye un cuadrilátero $\square ABCD$ conociendo $AB$, $BC$, $CD$, $DA$ y $M_{ab}M_{cd}$ donde $M_{ab}$ y $M_{cd}$ son los puntos medios de $AB$ y $CD$ respectivamente.

Solución. Primero construimos el paralelogramo $\square M_{ab}NM_{cd}M$, donde $M$ y $N$ son los puntos medios de las diagonales $AC$ y $BD$, de la siguiente manera.

De la demostración del teorema 2 sabemos que $M_{ab}M = NM_{cd} = \dfrac{BC}{2}$ y $M_{ab}N = MM_{cd} = \dfrac{AD}{2}$ (figura 4).

También sabemos que la diagonal de un paralelogramo lo divide en dos triángulos congruentes, por lo que basta construir un triángulo de lados $M_{ab}M_{cd}$, $\dfrac{BC}{2}$  y $\dfrac{AD}{2}$ y luego trazar paralelas por $M_{ab}$ y $M_{cd}$ a los lados del triángulo construido completando así el paralelogramo.

De manera similar construimos el paralelogramo $\square M_{ab}M_{bc}M_{cd}M_{da}$ donde $M_{bc}$ y $M_{da}$ serían los puntos medios de $BC$ y $AD$ respectivamente.

Sabemos también que $M_{bc}M \parallel AB$ por lo que trazamos la paralela $AB$ a $M_{bc}M$ por $M_{ab}$ tal que $AM_{ab} = M_{bc}B = \dfrac{AB}{2}$.

Con $A$ y $B$ construidos, por $M_{bc}$ trazamos $ABC$ tal que $BM_{bc} = M_{bc}C = \dfrac{BC}{2}$, similarmente construimos $D$.

$\blacksquare$

Teorema de Van Aubel

Teorema 3, de Van Aubel. Los segmentos que unen los centros de cuadrados construidos externamente sobre lados opuestos de un cuadrilátero convexo son perpendiculares y tienen la misma longitud.

Demostración. Sean $\square ABCD$ un cuadrilátero convexo y $\square EFBA$, $\square BGHC$, $\square DCIJ$, $\square LADK$, cuadrados construidos externamente sobre los lados de $\square ABCD$ y $O_1$, $O_2$, $O_3$, $O_4$, sus respectivos centros.

Figura 5

Sea $M = LB \cap ED$, como $AL = AD$ y $AB = AE$ y $\angle LAB = \angle DAE$, por criterio de congruencia LAL, $\triangle LAB \cong \triangle DAE$,
$\Rightarrow LB = DE$ y $\angle AEM = \angle ABM$.

Por lo tanto, $\square MEBA$ es cíclico, así, $\angle EMB = \angle EAB$, es decir $LB \perp DE$.

Considera $N$ el punto medio de $BD$, $NO_4$ y $NO_3$ son segmentos medios de $\triangle BDE$ y $\triangle DBL$ respectivamente.

Esto implica que $2NO_4 = DE$ y $NO_4 \parallel DE$ y $2NO_3 = LB$ y $NO_4 \parallel LB$.

Por lo tanto, $NO_4 = NO_3$ y $NO_4 \perp NO_3$.

Igualmente vemos que $NO_1 = NO_2$ y $NO_1 \perp NO_2$.

Sea $V = O_1O_3 \cap O_2O_4$, por criterio de congruencia LAL, $NO_1O_3 \cong NO_2O_4$,
$\Rightarrow O_1O_3 = O_2O_4$ y $\angle VO_1N = \angle VO_2N$.

Por lo tanto, $\square VNO_1O_2$ es cíclico, y así $O_1O_3 \perp O_2O_4$.

$\blacksquare$

Definición 3. Nos referiremos al cuadrilátero $\square O_1O_1O_3O_4$ como cuadrilátero externo de Van Aubel y a la intersección de sus diagonales como punto externo de Van Aubel.

Centroide del cuadrilátero de Van Aubel

Teorema 4. Un cuadrilátero y su cuadrilátero externo de Van Aubel tienen el mismo centroide.

Demostración. Sean $\square ABCD$ y $\square O_1O_2O_3O_4$ su cuadrilátero externo de Van Aubel, $M$ y $N$ los puntos medios de $AC$ y $BD$, y $V$ el punto externo de Van Aubel.

Figura 6

En el teorema anterior vimos que $NV$ es una cuerda común a las circunferencias cuyos diámetros son $O_1O_2$ y $O_3O_4$, por lo tanto la línea que une sus centros $M_{1,2}M_{3,4}$ biseca a $NV$ y $M_{1,2}M_{3,4} \perp NV$.

De manera análoga podemos ver que $MV$ es una cuerda común a las circunferencias cuyos diámetros son $O_2O_3$ y $O_4O_1$ y por lo tanto la línea que une sus centros $M_{2,3}M_{4,1}$ biseca a $MV$ y $M_{2,3}M_{4,1} \perp MV$.

Por otra parte, por el teorema de Van Aubel las diagonales del cuadrilátero de Van Aubel son perpendiculares y tienen la misma longitud. Entonces por el corolario, su paralelogramo de Varignon $\square M_{1,2}M_{2,3}M_{3,4}M_{4,1}$ es un cuadrado, en particular, $M_{1,2}M_{3,4} \perp M_{2,3}M_{4,1}$.

En consecuencia, en $\triangle MNV$, $M_{1,2}M_{2,3} \parallel MV$ y $M_{1,2}M_{2,3}$ pasa por el punto medio de $NV$, por lo tanto $M_{1,2}M_{2,3}$ biseca a $MN$.

Igualmente podemos ver que $M_{2,3}M_{4,1}$ biseca a $MN$.

Por el teorema 2 sabemos que el punto medio $J$ de $MN$ es el centroide de $\square ABCD$ y que la intersección de las bimedianas $M_{1,2}M_{3,4}$ y $M_{2,3}M_{4,1}$ es el centroide de $\square O_1O_2O_3O_4$.

$\blacksquare$

Más adelante…

En la siguiente entrada continuaremos el estudio de los cuadriláteros cíclicos que comenzamos en la entada teorema de Ptolomeo.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Muestra que un cuadrilátero es dividido por una de sus diagonales en dos triángulos de igual área si y solo si la diagonal biseca a la otra diagonal.
  2.  Verifica que el teorema de Varignon se cumple para los cuadriláteros cóncavo y cruzado.
  3. Sean $\square ABCD$ un cuadrilátero $U$ y $V$ los puntos medios de $\overline{AC}$ y $\overline{BD}$ respectivamente y $T$ la intersección de $\overline{AB}$ con $\overline{CD}$. Prueba que $(\triangle TUV) = \dfrac{(\square ABCD)}{4}$.
    Sugerencia. Considera $H$ y $F$ los puntos medios de $\overline{AD}$ y $\overline{BC}$ y los cuadriláteros $\square ACBD$, $\square CUFT$ y $\square BVFT$ para calcular el área de los triángulos $\triangle UVF$, $\triangle UFT$ y $\triangle VFT$.
Figura 7
  1. Construye un cuadrilátero dados dos ángulos opuestos, la longitud de las diagonales y el ángulo entre las diagonales.
  2. Verifica que el teorema de Van Aubel se cumple cuando los cuadrados son construidos internamente, y también para los para los cuadriláteros cóncavo y cruzado.
  3. Muestra que en un cuadrilátero convexo los puntos medios de sus diagonales y los puntos medios de las diagonales de su cuadrilátero externo de Van Aubel, forman un cuadrado, y que el punto externo de Van Aubel pertenece al circuncírculo de este cuadrado.

Entradas relacionadas

Fuentes

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»