Archivo de la etiqueta: razón de homotecia

Geometría Moderna I: Circunferencias homotéticas

Por Rubén Alexander Ocampo Arellano

Introducción

Esta es la segunda parte de la entrada anterior, donde presentamos el concepto de homotecia, en esta entrada nos enfocaremos en circunferencias homotéticas.

Homotecia de una circunferencia

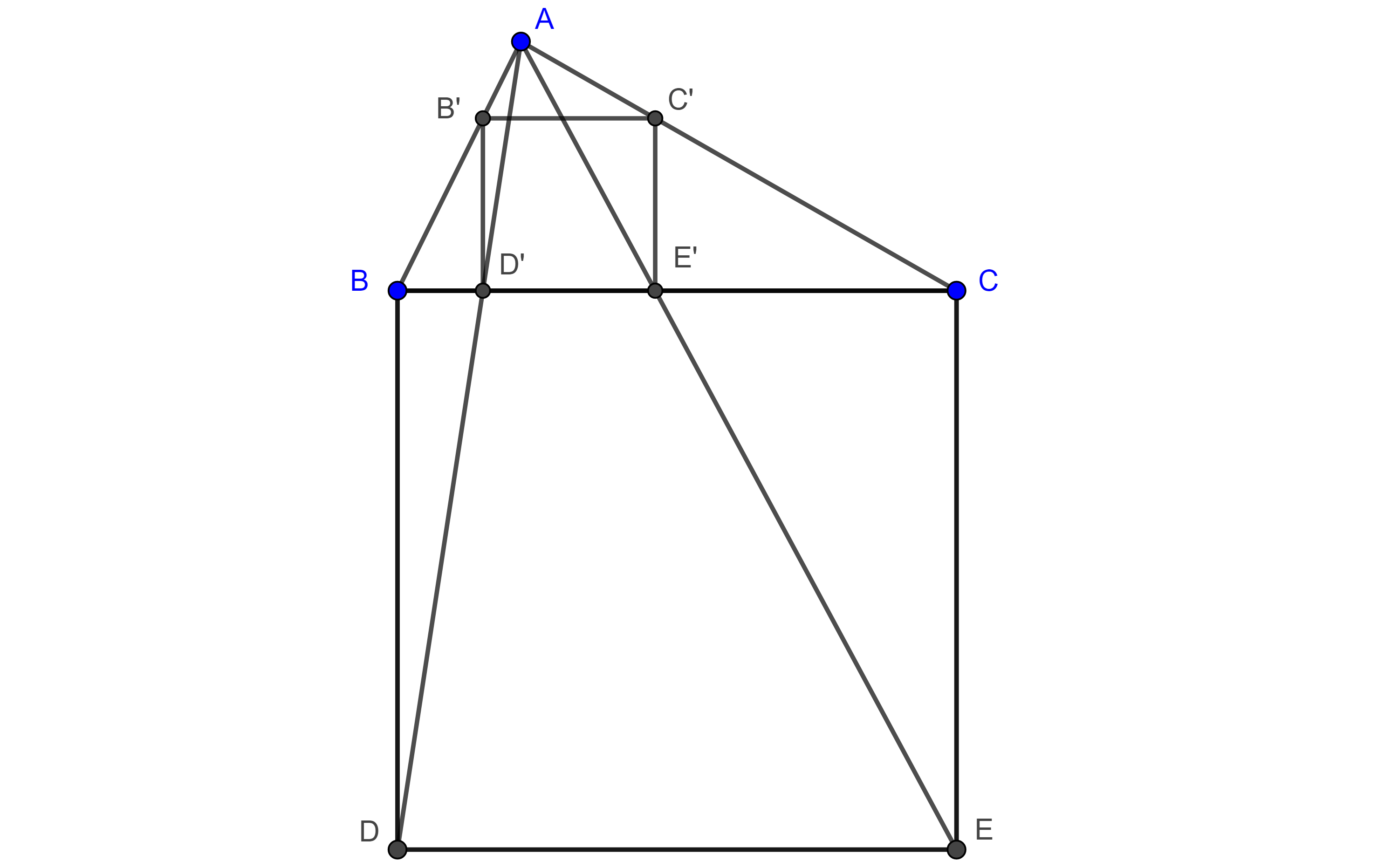
Teorema 1. La homotecia de una circunferencia es una circunferencia.

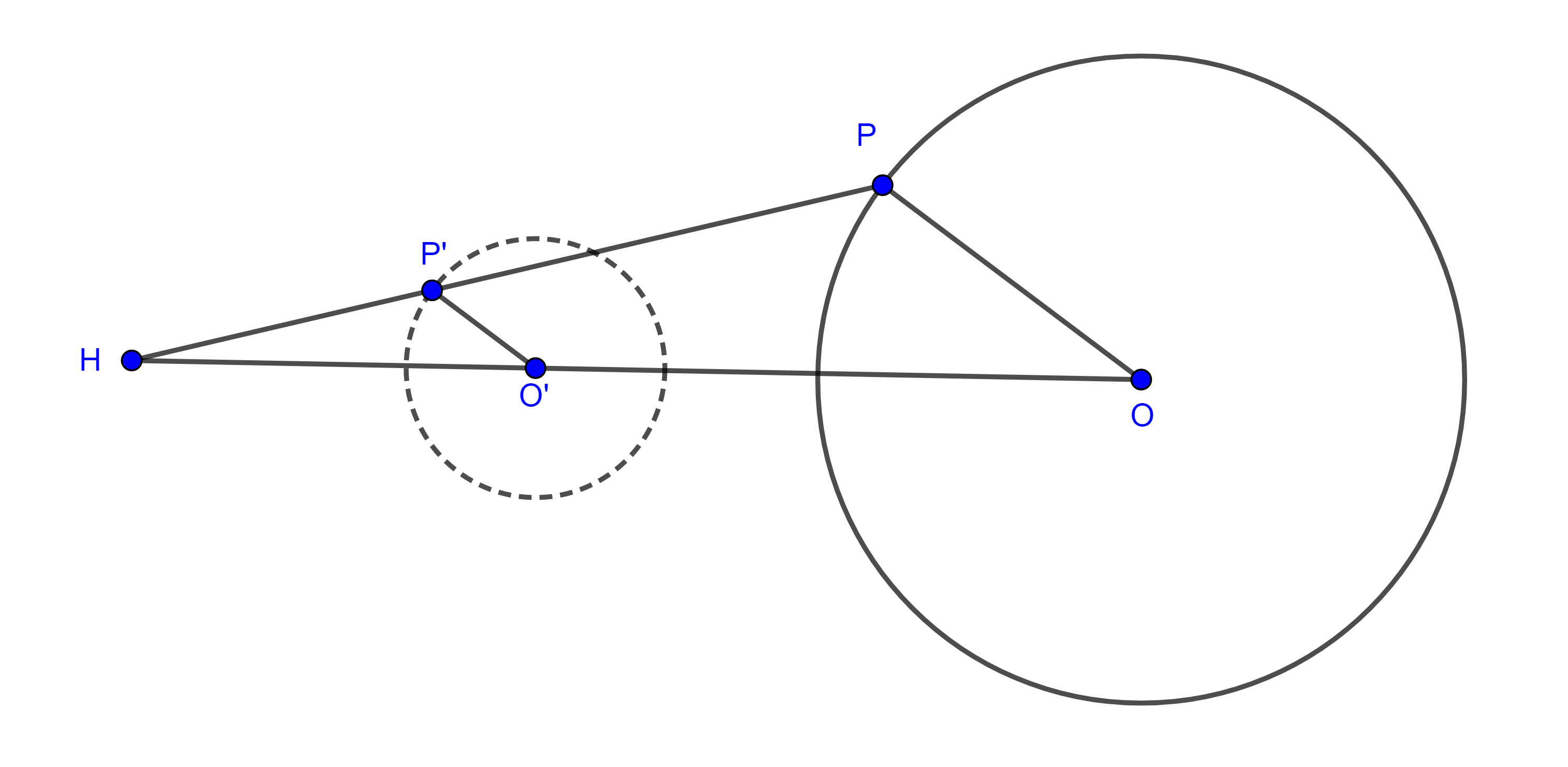
Demostración. Sea $(O, r)$ una circunferencia y consideremos una homotecia con centro en $H$ y razón $k$ . Tomemos $P \in (O, r)$ , y sean $P^{'}$ y $O^{'}$ los puntos homólogos de $P$ y $O$ respectivamente.

Como $P^{'} O^{'} ∥ P O$ entonces $△ H O^{'} P^{'} \sim △ H O P$
$\Rightarrow \frac{O^{'} P^{'}}{O P} = \frac{H P^{'}}{H P} = k$
$\Rightarrow O^{'} P^{'} = k \times O P = k r$

Por lo tanto, si $P$ describe una circunferencia, su punto homologo $P^{'}$ , se mueve a una distancia fija $k r$ de un punto fijo $O^{'}$ , esto es una circunferencia con centro en $O^{'}$ y radio $r^{'} = k r$ , $(O^{'}, r^{'})$ .

Observaciones. Notemos que los respectivos centros $O$ y $O^{'}$ son puntos homólogos y que la razón entre los radios de las circunferencias homotéticas es la razón de homotecia.

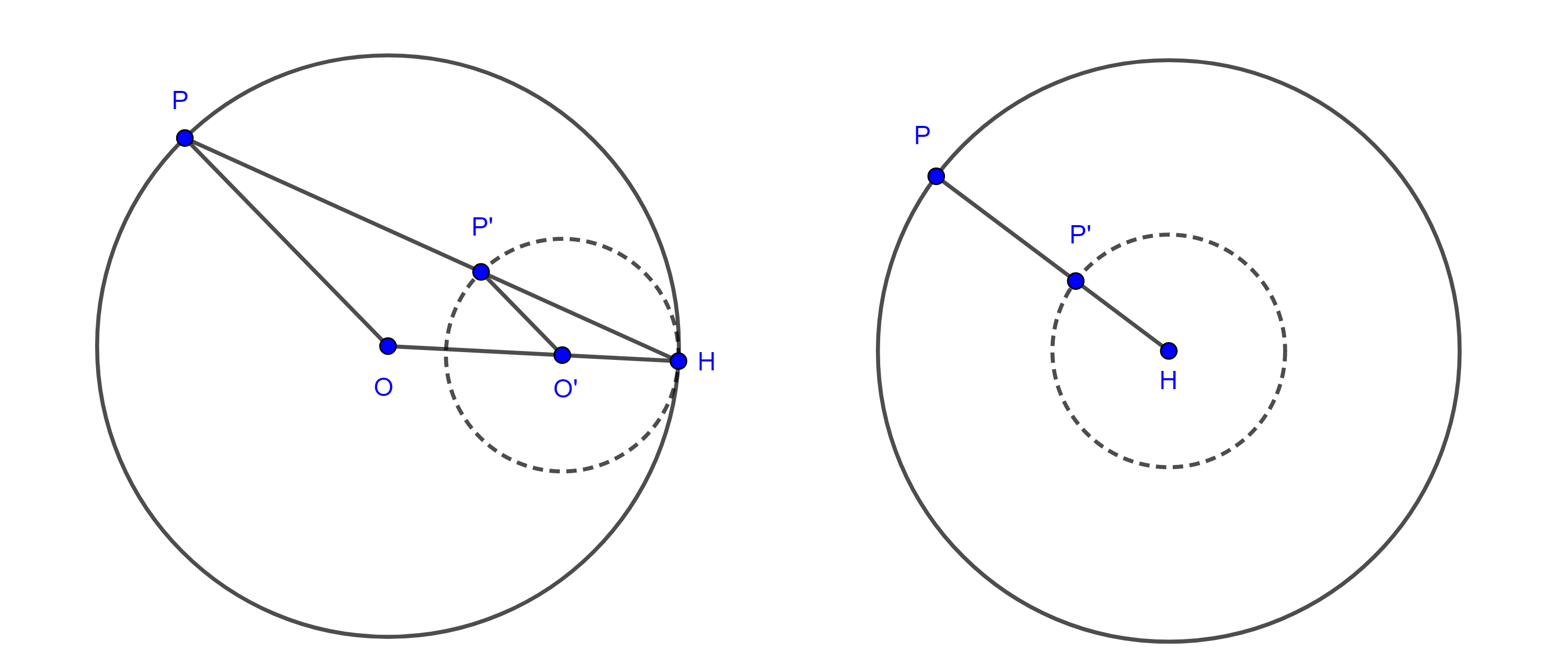
Recordemos que por convención, el punto homólogo del centro de homotecia es el mismo y como el centro de homotecia es colineal con los centros de las circunferencias homotéticas, si una de las circunferencias pasa por el centro de homotecia $H$ , entonces la otra circunferencia también pasara por $H$ y ambas serán tangentes en $H$ .

Si tomamos como centro de una circunferencia el centro de homotecia entonces las circunferencias homotéticas serán concéntricas.

Un triangulo variable

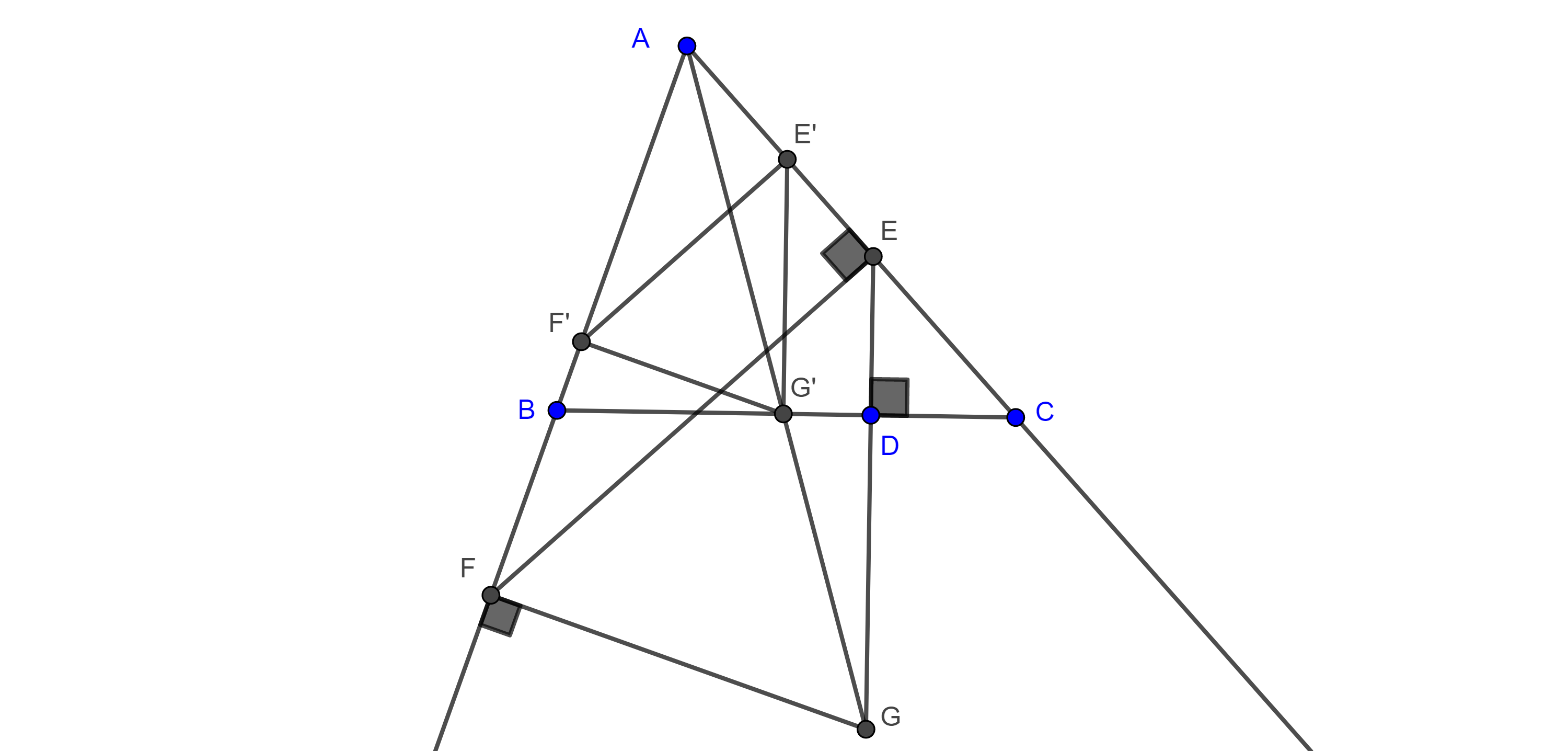
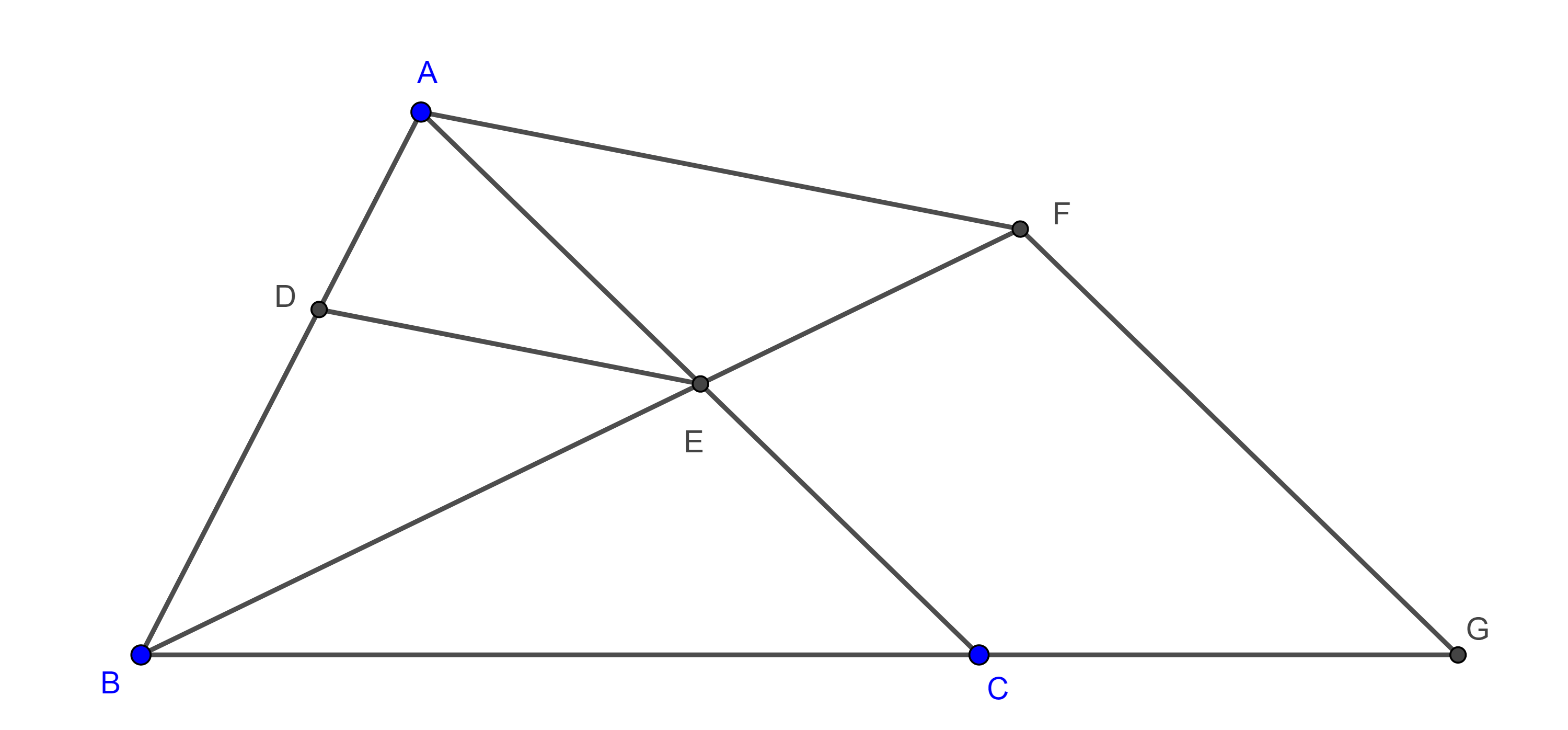
Teorema 2. Si un vértice de un triángulo variable esta sobre un punto fijo, un segundo vértice esta sobre una circunferencia dada y el triángulo variable siempre es semejante a un triángulo dado, entonces el tercer vértice del triángulo describe una circunferencia.

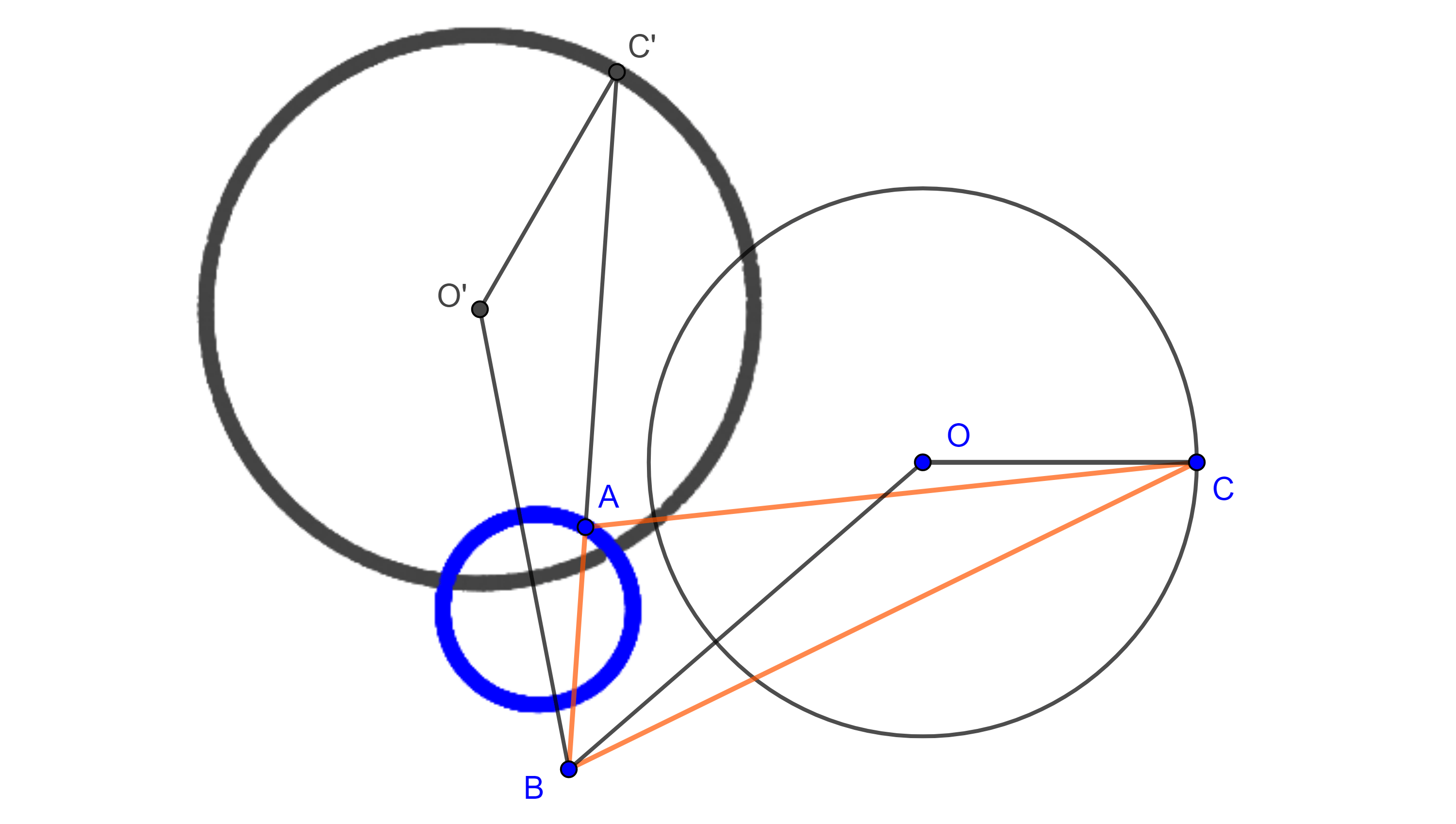
Demostración. Sea $△ A B C$ una de las posiciones del triángulo variable, donde $B$ es el punto fijo y $C$ está en $(O, r)$ , la circunferencia dada.

Sea $C^{'} \in A B$ tal que $B C^{'} = B C$ , sobre $B C^{'}$ construimos un triángulo $△ B O^{'} C^{'}$ congruente a $△ B O C$ , de tal manera que sea posible a través de una rotación con centro en $B$ superponer $△ B O C$ con $△ B O^{'} C^{'}$ .

Como $∠ O B C = ∠ O^{'} B C^{'}$ entonces $∠ O B O^{'} = ∠ C B C^{'} = ∠ C B A$ , este último ángulo es fijo por lo que la dirección de la recta $B O^{'}$ es fija.

$B O^{'} = B O$ entonces $O^{'}$ es un punto fijo para cualquier otra posición del triángulo variable $△ A B C$ .

Como $C O^{'} = C O = r$ , entonces todos los puntos $C^{'}$ se mueven a una distancia fija $r$ de un punto fijo $O^{'}$ , por lo tanto, $C^{'}$ describe una circunferencia.

Ya que $\frac{B A}{B C^{'}} = \frac{B A}{B C}$ y esta última razón es fija, pues todos los triángulos $△ A B C$ son semejantes entre sí, $A$ y $C^{'}$ son puntos homólogos de una homotecia con centro en $B$ y razón $\frac{B A}{B C}$ , y como $C^{'}$ describe una circunferencia, entonces por el teorema 1, $A$ también describe una circunferencia.

Observación. Notemos que en el punto fijo se puede construir cualquiera de los tres ángulos dados, así, en el vértice que esta en el circulo dado tenemos otras dos elecciones, y el tercer vértice lo podemos construir a ambos lados del segmento $B C$ , con lo que en total existen $12$ circunferencias diferentes que puede describir el tercer vértice.

Homotecia entre dos circunferencias dadas

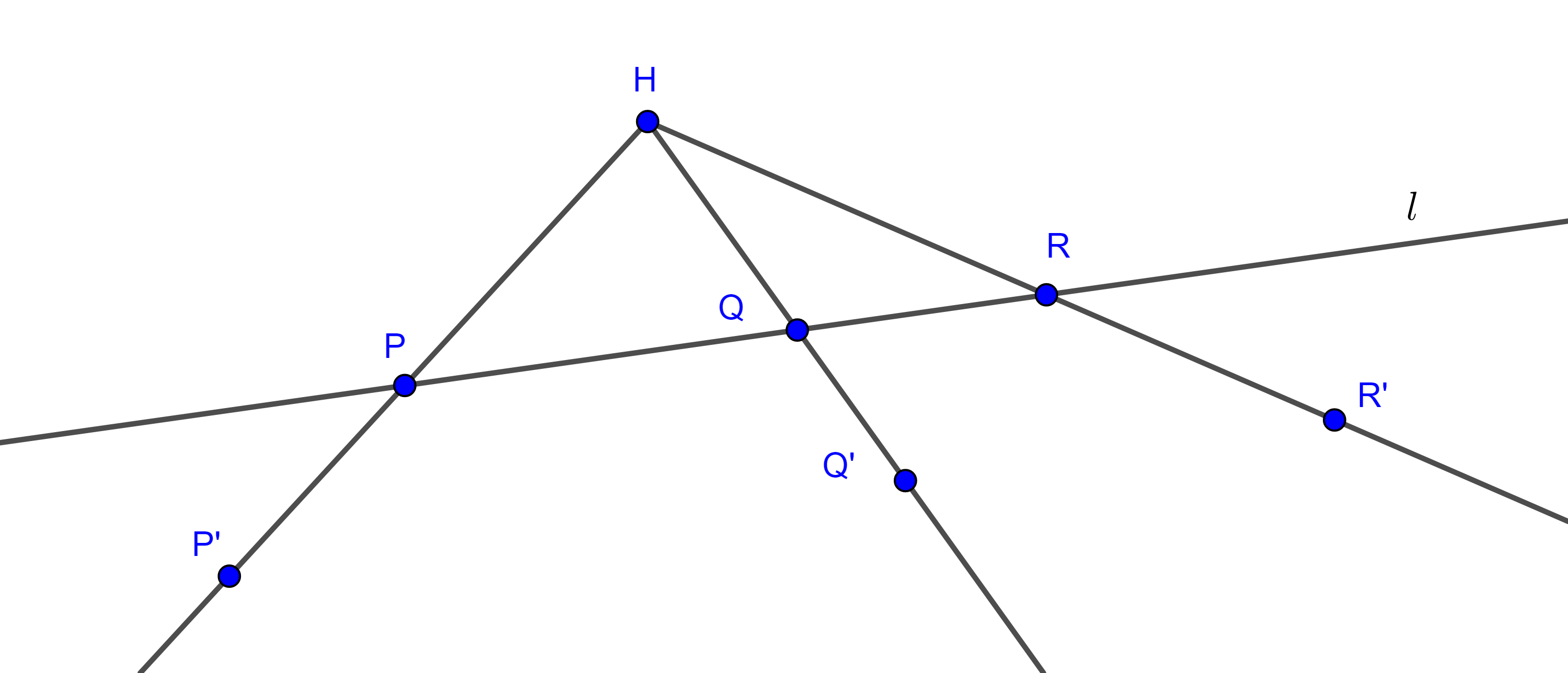
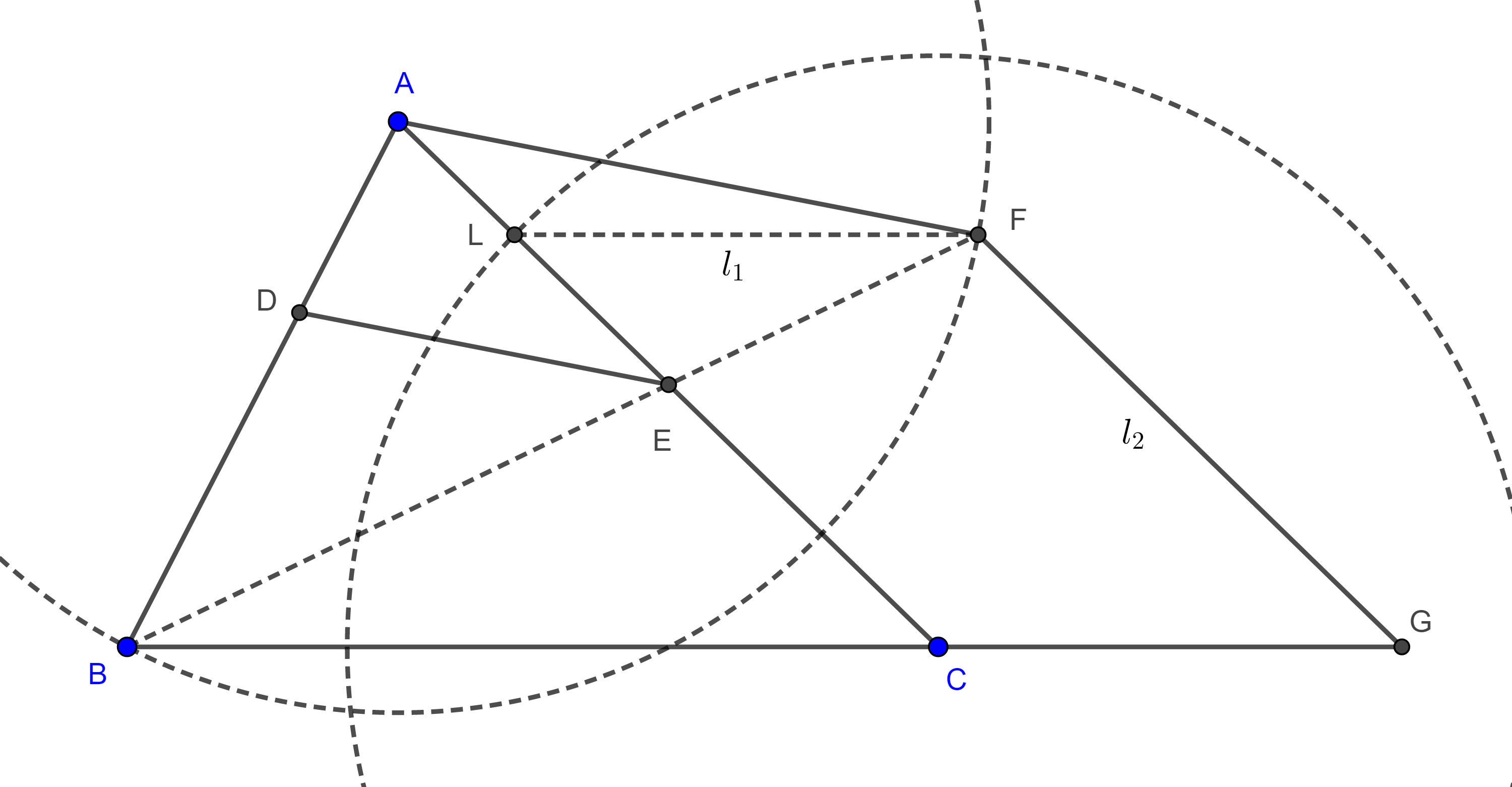
Teorema 3. Dadas dos circunferencias de centros o radios distintos, siempre es posible encontrar una homotecia entre las dos.

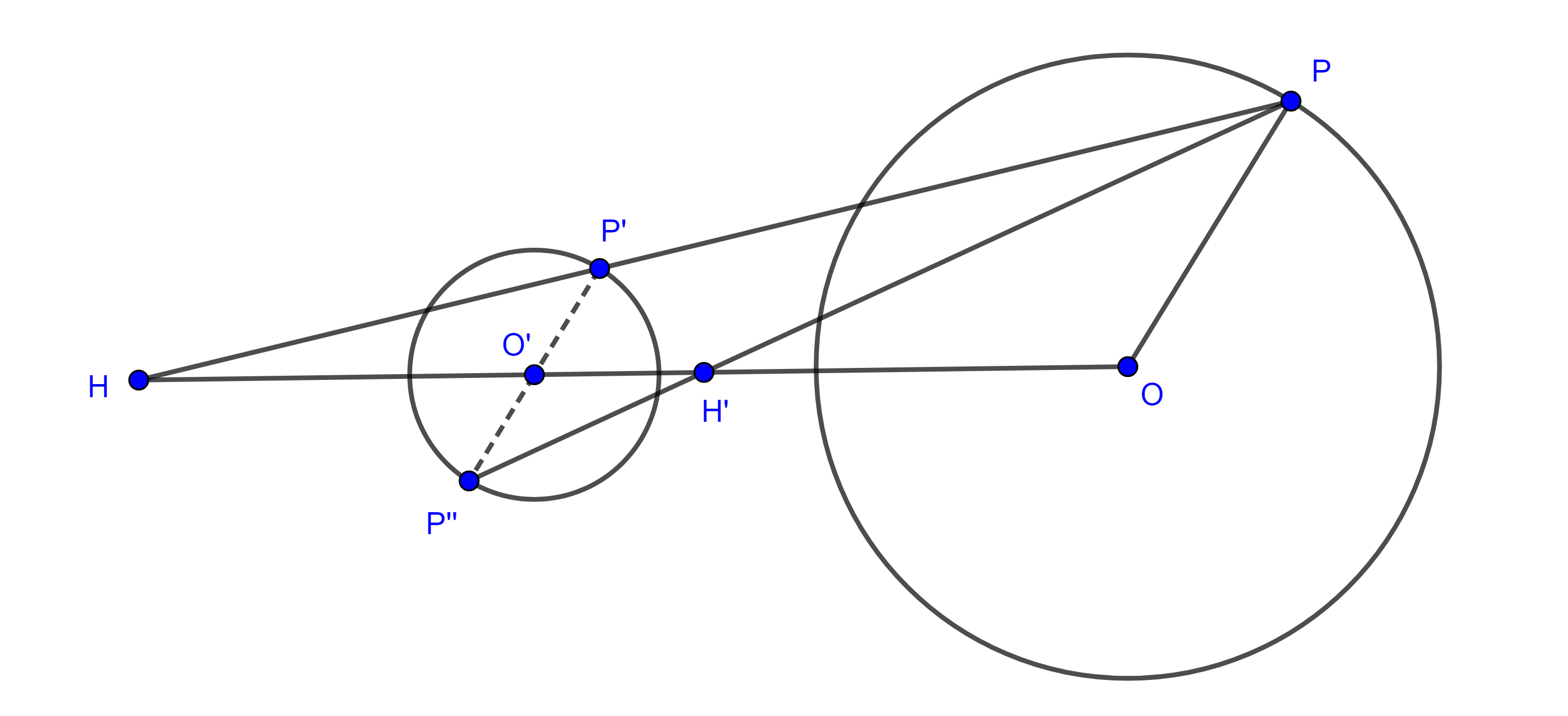
Demostración. Sean $(O, r)$ y $(O^{'}, r^{'})$ tal que $O \neq O^{'}$ y $r \neq r^{'}$ , tomemos $P \in (O, r)$ y tracemos por $O^{'}$ un radio $O^{'} P^{'}$ paralelo a $O P$ , sea $H = O O^{'} \cap P P^{'}$ .

Entonces $△ H O^{'} P^{'} \sim △ H O P$
$\Rightarrow \frac{H P^{'}}{H P} = \frac{H O^{'}}{H O} = \frac{O^{'} P^{'}}{O P} = \frac{r^{'}}{r}$ .

En consecuencia, la homotecia con centro en $H$ y razón $k = \frac{r^{'}}{r}$ lleva a $(O, r)$ en $(O^{'}, r^{'})$ .

Ahora consideremos $P^{″}$ el punto diametralmente opuesto a $P^{'}$ en $(O^{'}, r^{'})$ , sea $H^{'} = O O^{'} \cap P P^{″}$ , entonces $△ H^{'} O^{'} P^{″} \sim △ H^{'} O P$
$\Rightarrow \frac{H^{'} P^{″}}{H^{'} P} = \frac{H^{'} O^{'}}{H^{'} O} = \frac{O^{'} P^{″}}{O P} = \frac{r^{'}}{r} = k$ .

Así, hemos encontrado dos homotecias entre $(O, r)$ y $(O^{'}, r^{'})$ .

Observación. Si las circunferencias son concéntricas entonces solo hay una homotecia entre ellas, la que tiene como centro el centro de las circunferencias.

Si las circunferencias tienen el mismo radio entonces la única homotecia entre ellas es la que tiene como centro el punto medio del segmento que une los radios.

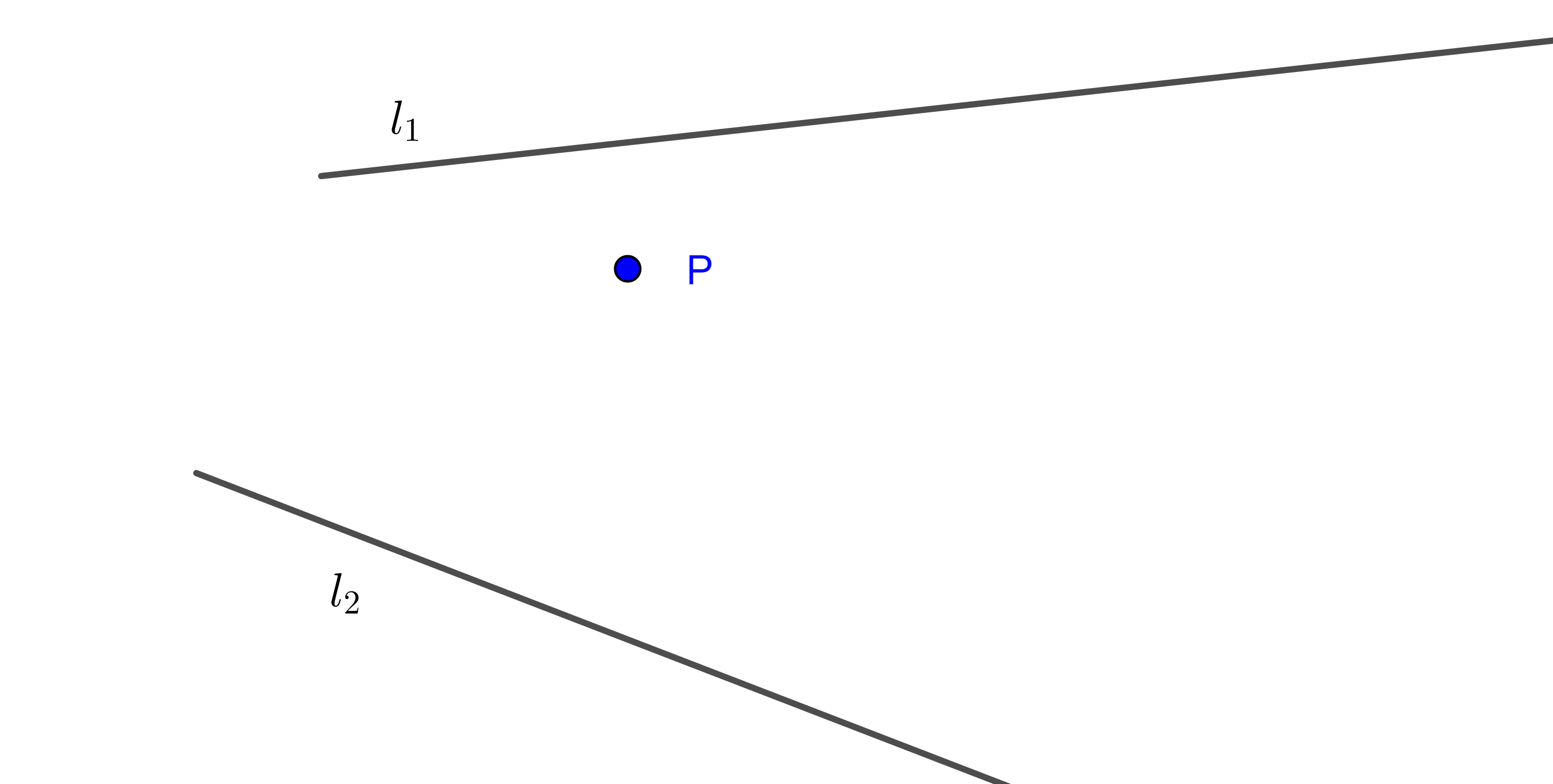
Corolario 1. Rectas tangentes comunes a dos circunferencias pasan por un centro de homotecia.

Demostración. Supongamos que $T T^{'}$ es una recta tangente exterior (es decir, la recta $T T^{'}$ corta al segmento $O O^{'}$ exteriormente) a dos circunferencias $(O, r)$ y $(O^{'}, r^{'})$ , donde $T \in (O, r)$ y $T^{'} \in (O^{'}, r^{'})$ .

Sea $H = O O^{'} \cap T T^{'}$ , como $O^{'} T^{'} ∥ O T$ entonces $△ H O^{'} T^{'} \sim △ H O T$
$\Rightarrow \frac{H T^{'}}{H T} = \frac{H O^{'}}{H O} = \frac{O^{'} T^{'}}{O T} = \frac{r^{'}}{r}$ .

Como el punto que divide externamente al segmento $O O^{'}$ en la razón $\frac{r^{'}}{r}$ es único, entonces $H$ es un centro de homotecia de $(O, r)$ y $(O^{'}, r^{'})$ .

Es análogo ver que las tangentes internas de dos circunferencias pasan por un centro de homotecia.

Incírculo y exírculo en homotecia

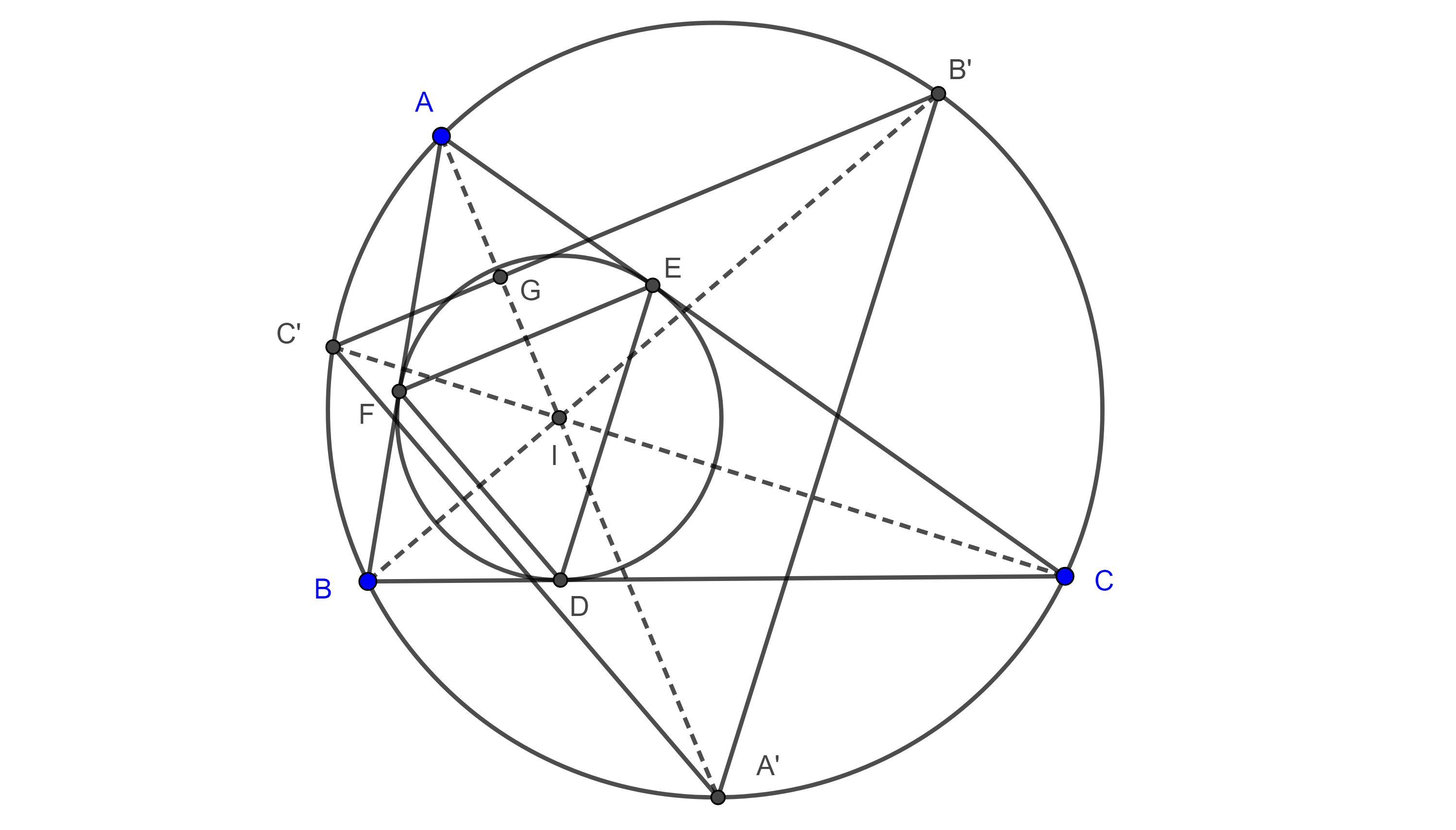
Teorema 3. Sea $△ A B C$ , considera $(I, r)$ y $(I_{b}, r_{b})$ su incírculo y $B$ -excírculo respectivamente, sean $D$ el punto de tangencia de $A C$ con $(I, r)$ y $D^{'}$ el punto diametralmente opuesto a $D$ en $(I, r)$ , sea $E = B D^{'} \cap A C$ , entonces $E$ es el punto de tangencia de $A C$ con $(I_{b}, r_{b})$ y el punto medio de $A C$ es el punto medio de $D E$ .

Demostración. Por el corolario 1, existe una homotecia con centro en $B$ y razón $\frac{r_{b}}{r}$ que lleva a $(I, r)$ en $(I_{b}, r_{b})$ , sea $X \in (I_{b}, r_{b})$ el punto correspondiente a $D^{'} \in (I, r)$ bajo esta transformación.

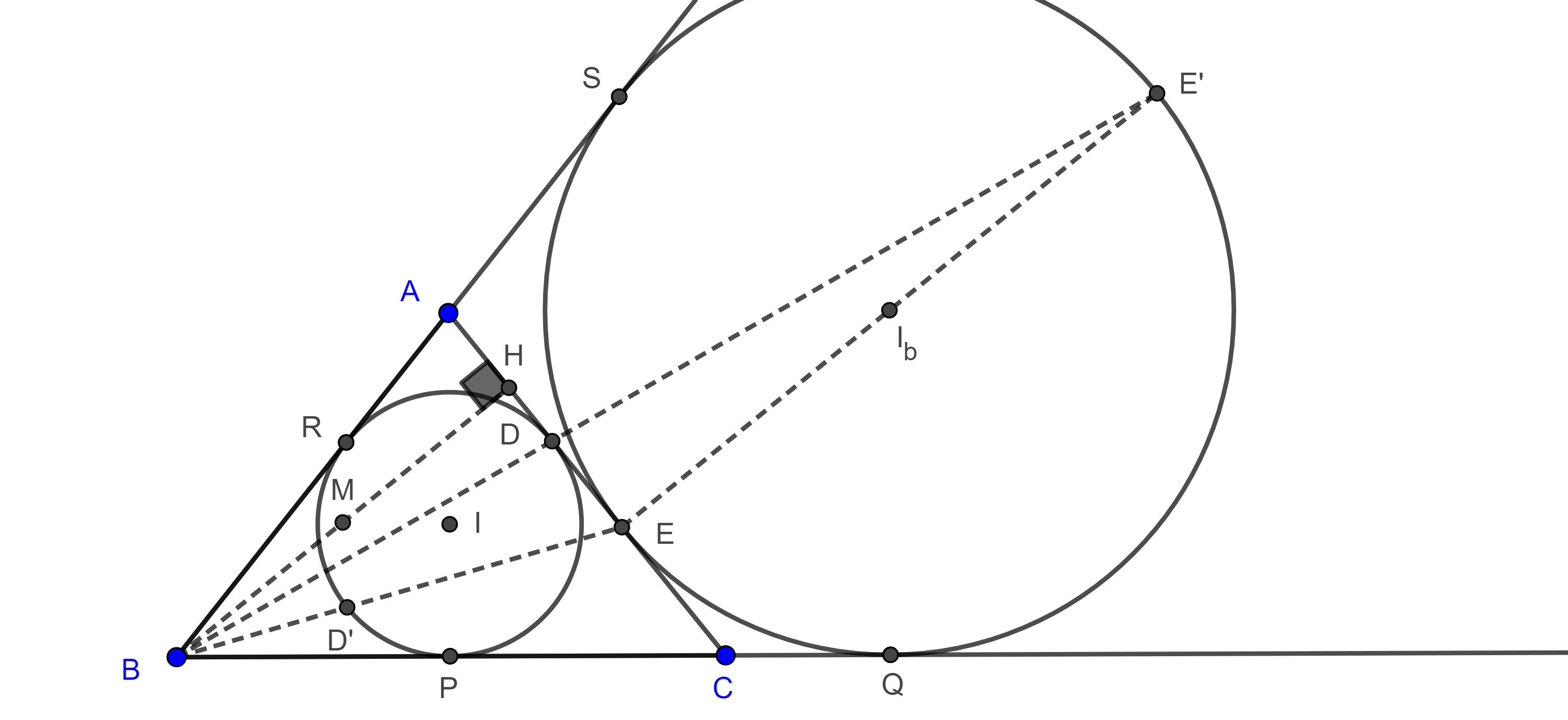
Entonces $I D^{'} ∥ I_{b} X$ , pero $I D^{'} ⊥ A C$ $\Rightarrow I_{b} X ⊥ A C$ y como $A C$ es tangente a $(I_{b}, r_{b})$ entonces $X \in A C$ .

Como $X \in A C$ y $X$ es colineal con $B$ y $D^{'}$ entonces $X = E$ , así, $A C$ es tangente a $(I_{b}, r_{b})$ en $E$ .

Por otro, lado sean $P$ , $Q$ los puntos de tangencia de $B C$ con $(I, r)$ y $(I_{b}, r_{b})$ respectivamente y sean $R$ , $S$ los puntos de tangencia de $A B$ con $(I, r)$ y $(I_{b}, r_{b})$ respectivamente.

Recordemos que las tangentes desde un punto externo a una circunferencia son iguales.

$B P + P C + C Q = B Q = B S = B R + R A + A S \Rightarrow P C + C Q = R A + A S$
$\Rightarrow C D + C E = A D + A E \Rightarrow 2 C E + D E = 2 A D + D E$
$\Rightarrow C E = A D$

Por lo tanto, el punto medio de $A C$ es el punto medio de $D E$ .

Concurrencia de rectas

Corolario 2. Con las mismas condiciones y notación del teorema anterior, sea $H \in A C$ el pie de la altura por $B$ , y sea $M$ el punto medio de $B H$ , entonces $E I$ y $I_{b} D$ concurren en $M$ (figura 6).

Demostración. Ya que $D^{'} D ∥ B H$ entonces $△ E B H \sim △ E D^{'} D$ ,
$\Rightarrow \frac{E B}{E D^{'}} = \frac{E H}{E D}$ .

Es decir, hay una homotecia con centro en $E$ que lleva a los puntos $D^{'}$ y $D$ a los puntos $B$ y $H$ respectivamente, esto implica que el punto medio de $D^{'} D$ es homólogo del punto medio de $B H$ .

Por lo tanto, $E$ , $I$ y $M$ son colineales.

Por otra parte, consideremos la homotecia con centro en $B$ que lleva a $(I, r)$ en $(I_{b}, r_{b})$ y sea $E^{'} \in (I_{b}, r_{b})$ el punto homólogo de $D \in (I, r)$ .

Como $(D, E^{'})$ y $(D^{'}, E)$ son pares de puntos homólogos bajo la misma homotecia, entonces $D D^{'} ∥ E^{'} E$ pero $D D^{'} ∥ H B$ $\Rightarrow E^{'} E ∥ H B$ .

Entonces $△ D E E^{'} \sim △ D H B$ .
$\Rightarrow \frac{D B}{D E^{'}} = \frac{D H}{D E}$ .

En consecuencia, existe una homotecia con centro en $D$ , y $(E, H)$ , $(E^{'}, B)$ son pares de puntos homólogos, de esto de sigue que el punto medio de $E E^{'}$ y el punto medio de $B H$ son puntos homólogos.

Ya que $E^{'} E ⊥ A C$ , entonces es diámetro de $(I_{b}, r_{b})$ , por lo que $I_{b}$ es el punto medio de $E^{'} E$ y así, $I_{b}$ , $D$ y $M$ son colineales.

Por lo tanto, $E I$ y $I_{b} D$ concurren en $M$ .

Más adelante…

En la siguiente entrada hablaremos sobre la potencia de un punto con respecto a una circunferencia, es una herramienta útil que relaciona cualesquiera dos secantes a una circunferencia desde un punto en el plano, incluyendo el caso cuando una secante se vuelve tangente.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Un triángulo variable tiene un vértice sobre un punto fijo, un vértice sobre una recta fija y el triangulo permanece semejante a un triángulo dado, muestra que el tercer vértice describe una línea recta.
Considera dos circunferencias que se intersecan, por uno de los puntos de intersección traza una recta que forme una cuerda en cada circunferencia y tal que la razón entre sus longitudes sea igual a una razón dada.
Construye un triángulo semejante a un triángulo dado, de tal forma que un vértice sea un punto dado y los otros dos vértices estén sobre dos circunferencias dadas.
Construye un triangulo $△ A B C$ dado su incentro, el punto medio del lado $B C$ y el pie de la altura por $A$ .
Lema de Arquímedes. Sea $Γ_{2}$ una circunferencia internamente tangente a una circunferencia $Γ_{1}$ en un punto $H$ , considera $A B$ , una cuerda de $Γ_{1}$ que es tangente a $Γ_{2}$ en $P$ , sea $Q$ el punto medio del arco $\overset{⌢}{A B}$ (figura 7), muestra que:
$i)$ $Q$ , $P$ y $H$ son colineales,
$i i)$ $Q P \times Q H = Q B^{2}$ .

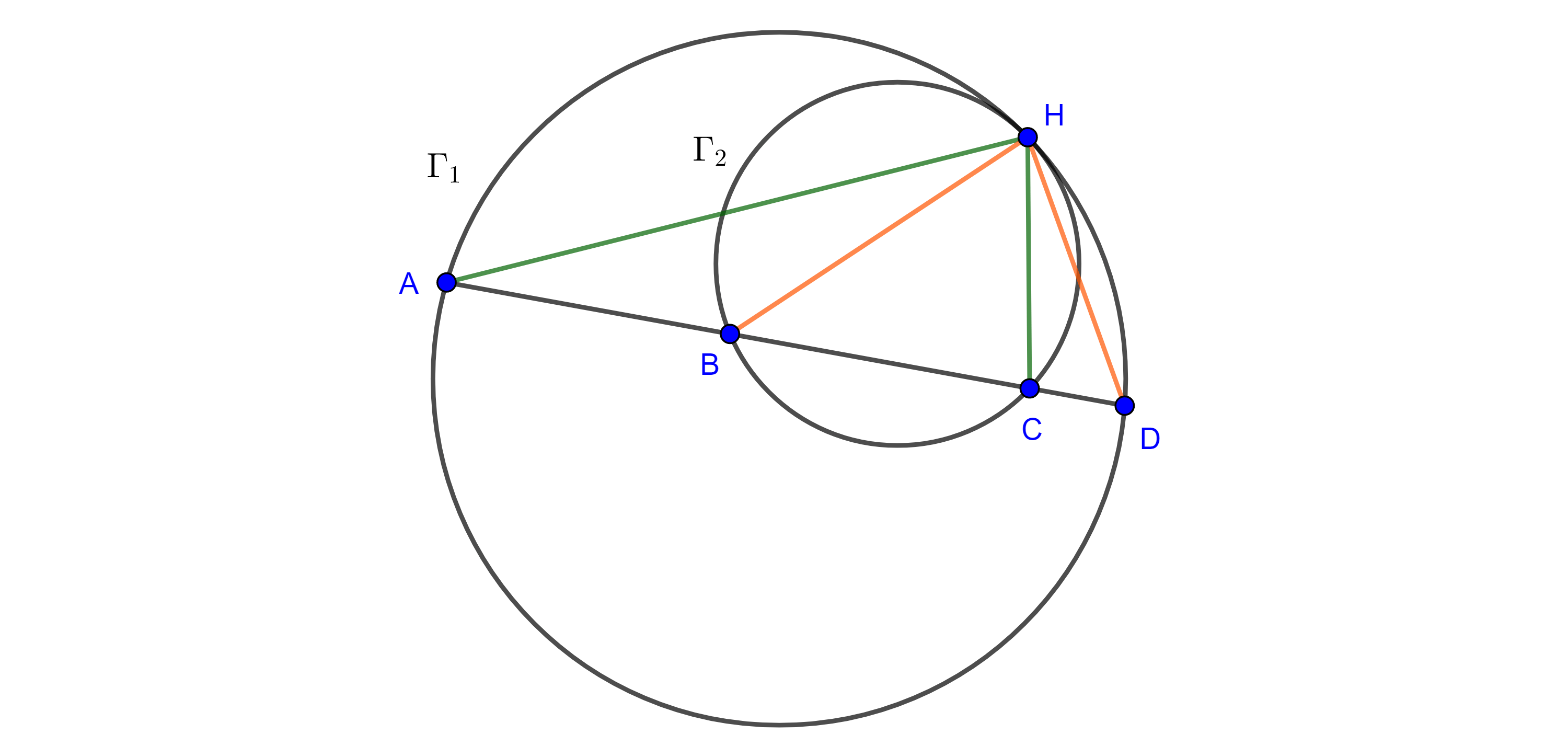
Sea $Γ_{2}$ una circunferencia internamente tangente a una circunferencia $Γ_{1}$ en un punto $H$ , considera una secante a ambas circunferencias en $A$ , $B$ , $C$ y $D$ (figura 8), prueba que $∠ A H C = ∠ B H D$ .

Entradas relacionadas

Ir a Geometría Moderna I.
Entrada anterior del curso: Homotecia.
Siguiente entrada del curso: Potencia de un punto.
Otros cursos.

Fuentes

Altshiller, N., College Geometry. New York: Dover, 2007, pp 46-51.
Andreescu, T., Korsky, S. y Pohoata, C., Lemmas in Olympiad Geometry. USA: XYZ Press, 2016, pp 199-208.
Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 109-114.

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Geometría Moderna I: Homotecia

Por Rubén Alexander Ocampo Arellano

Deja un comentario

Introducción

En esta entrada estudiamos el tema de homotecia, se trata de una transformación que lleva una figura del plano a otra semejante, con lados correspondientes paralelos y vértices correspondientes concurrentes, esto nos permite entre otras cosas, abordar algunos problemas de construcciones geométricas.

Definición 1. Considera un punto $H$ , un conjunto de puntos $F$ y $k$ un numero real, para cada $X \in F$ sea $X^{'}$ tal que $X^{'}$ , $X$ y $H$ son colineales y $\frac{H X^{'}}{H X} = k$ .

Sea $F^{'}$ el conjunto de puntos $X^{'}$ , diremos que los conjuntos $F$ y $F^{'}$ son figuras homotéticas y los puntos $X$ y $X^{'}$ son puntos homólogos.

$H$ se llama centro de homotecia, $k$ es la razón de homotecia y la relación entre $F$ y $F^{'}$ es una homotecia con centro en $H$ y razón $k$ . Por convención el centro de homotecia $H$ es su propio punto homólogo.

Si puntos homólogos de una homotecia están del mismo lado del centro de homotecia decimos que los conjuntos son directamente homotéticos y la razón de homotecia es positiva, si los puntos homólogos están en lados opuestos respecto del centro de homotecia decimos que las figuras son inversamente homotéticas y la razón de homotecia será negativa.

Homotecia de una recta

Teorema 1. La homotecia de una recta que no pasa por el centro de homotecia es una recta paralela.

Demostración. Sean $H$ y $k$ el centro y la razón de homotecia, y sea $l$ una recta que no pasa por $H$ . Tomemos tres puntos arbitrarios $P$ , $Q$ , $R \in l$ , sean $P^{'}$ , $Q^{'}$ y $R^{'}$ sus correspondientes puntos homólogos.

Como $\frac{H P^{'}}{H P} = k = \frac{H Q^{'}}{H Q}$ , por el reciproco del teorema de Tales, $P Q ∥ P^{'} Q^{'}$ .

Análogamente vemos que $Q R ∥ Q^{'} R^{'}$ y $P R ∥ P^{'} R^{'}$ .

Supongamos que $P^{'}$ , $Q^{'}$ y $R^{'}$ no son colineales, entonces $△ P^{'} Q^{'} R^{'}$ es un triángulo y así $△ P Q R$ es un triángulo con lados paralelos a los de $△ P^{'} Q^{'} R^{'}$ , lo cual es una contradicción, pues $P Q R$ es una recta.

Si fijamos $P$ y $Q$ , y tomamos $R$ como variable, entonces $P^{'}$ y $Q^{'}$ son fijos y $R^{'}$ es variable, así todos los puntos $R^{'}$ son colineales con $P^{'}$ y $Q^{'}$ .

Por lo tanto, la homotecia de una recta es una recta paralela a esta.

Definición 2. Decimos que dos polígonos $A B C D \dots$ y $A^{'} B^{'} C^{'} D^{'} \dots$ son semejantes si los correspondientes lados son proporcionales $\frac{A B}{A^{'} B^{'}} = \frac{B C}{B^{'} C^{'}} = \dots$ y los ángulos correspondientes son iguales $∠ A = ∠ A^{'}$ , $∠ B = ∠ B^{'}$ , $\dots$

Corolario. Dos polígonos homotéticos son semejantes.

Demostración. Sean $A$ , $B$ y $C$ vértices de un polígono $A B C D \dots$

Por el teorema anterior, los lados del triángulo $△ A^{'} B^{'} C^{'}$ , formado por los puntos homólogos de $A$ , $B$ y $C$ , son paralelos a los lados correspondientes de $△ A B C$ , por lo tanto, los triángulos son semejantes y así los ángulos correspondientes son iguales y los lados correspondientes son proporcionales.

Polígonos homotéticos

Teorema 2. Si los lados correspondientes de dos polígonos son proporcionales y paralelos entonces los polígonos son homotéticos.

Demostración. Sean $A B C D \dots$ y $A^{'} B^{'} C^{'} D^{'} \dots$ dos polígonos que cumplen las condiciones dadas, sea $H$ la intersección de las rectas $A A^{'}$ y $B B^{'}$ y supongamos que $C C^{'}$ no pasa por $H$ , entonces sea $H^{'} = C C^{'} \cap B B^{'}$ .

Como $A B ∥ A^{'} B^{'}$ y $B C ∥ B^{'} C^{'}$ entonces $△ H A B \sim △ H A^{'} B^{'}$ y $△ H^{'} B C \sim △ H^{'} B^{'} C^{'}$
$\Rightarrow \frac{A B}{A^{'} B^{'}} = \frac{H B}{H B^{'}}$ y $\frac{B C}{B^{'} C^{'}} = \frac{H^{'} B}{H^{'} B^{'}}$ .

Ya que los lados correspondientes de $A B C D \dots$ son proporcionales a los de $A^{'} B^{'} C^{'} D^{'} \dots$ , entonces
$\frac{H B}{H B^{'}} = \frac{A B}{A^{'} B^{'}} = \frac{B C}{B^{'} C^{'}} = \frac{H^{'} B}{H^{'} B^{'}}$
$\Rightarrow \frac{H B}{H B^{'}} - 1 = \frac{H^{'} B}{H^{'} B^{'}} - 1 \Rightarrow \frac{H B - H B^{'}}{H B^{'}} = \frac{H^{'} B - H^{'} B^{'}}{H^{'} B^{'}}$
$\Rightarrow \frac{B^{'} B}{H B^{'}} = \frac{B^{'} B}{H^{'} B^{'}} \Rightarrow H B^{'} = H^{'} B^{'}$ .

Por lo tanto, $H = H^{'}$ .

Así, $A A^{'}$ , $B B^{'}$ y $C C^{'}$ son concurrentes y $\frac{H A^{'}}{H A} = \frac{H B^{'}}{H B} = \frac{H C^{'}}{H C}$ , es análogo ver que las demás rectas que unen vértices correspondientes concurren en $H$ .

Por tanto, $A B C D \dots$ y $A^{'} B^{'} C^{'} D^{'} \dots$ se encuentran en homotecia desde $H$ y por el corolario 1, $A B C D \dots$ y $A^{'} B^{'} C^{'} D^{'} \dots$ , son semejantes, la razón de homotecia es la razón de semejanza, $\frac{H A^{'}}{H A} = \frac{A B}{A^{'} B^{'}} = \frac{B C}{B^{'} C^{'}} = \dots$

Observación 1. Si la razón de homotecia es 1, los lados correspondientes de las figuras $A B C D \dots$ y $A^{'} B^{'} C^{'} D^{'} \dots$ son congruentes y así $A A^{'} B^{'} B$ es un paralelogramo, es decir, $A A^{'}$ y $B B^{'}$ no pueden ser concurrentes.

Observación 2. En el caso particular cuando los polígonos son triángulos, solo es necesario pedir que los lados correspondientes sean paralelos, pues esto asegura la semejanza y por tanto la condición de proporcionalidad.

Rectas concurrentes

Proposición. Sea $△ A B C$ un triángulo y sean $D$ , $E$ y $F$ los puntos de tangencia del incírculo $(I, r)$ de $△ A B C$ , con los lados $B C$ , $A C$ y $A B$ respectivamente, sean $A^{'}$ , $B^{'}$ y $C^{'}$ la intersección de las rectas $A I$ , $B I$ y $C I$ con el circuncírculo del triángulo $△ A B C$ , entonces la rectas $A^{'} D$ , $B^{'} E$ y $C^{'} F$ son concurrentes.

Demostración. Notemos que $A F = A E$ , pues son las tangentes trazadas desde $A$ a $(I, r)$ , como $△ A E F$ es isósceles entonces la bisectriz de $A$ es perpendicular a $E F$ , $A I ⊥ E F$ .

Por otro lado, tenemos que $∠ C^{'} B^{'} B = ∠ C^{'} C B = \frac{∠ C}{2}$ pues abarcan el mismo arco; el ángulo $∠ B^{'} I A$ es un ángulo exterior del triángulo $△ A I B$ , entonces
$∠ B^{'} I A = ∠ B A I + ∠ I B A = \frac{∠ A + ∠ B}{2}$ .

Sea $G = A I \cap C^{'} B^{'}$ , en el triángulo $△ G I B^{'}$ tenemos que
$∠ I G B^{'} = π - (∠ C^{'} B^{'} B + ∠ B^{'} I A)$
$= π - \frac{∠ A + ∠ B + ∠ C}{2} = \frac{π}{2}$ .

Por lo tanto, $A I ⊥ B^{'} C^{'}$ $\Rightarrow E F ∥ B^{'} C^{'}$ , de manera análoga podemos ver que $E D ∥ B^{'} A^{'}$ y $D F ∥ A^{'} C^{'}$ .

De lo anterior se sigue que $△ D E F \sim △ A^{'} B^{'} C^{'}$ , y por el teorema 2, $A^{'} D$ , $B^{'} E$ y $C^{'} F$ concurren en algún punto $H$ que es el centro de homotecia de los triángulos $△ D E F$ y $△ A^{'} B^{'} C^{'}$ .

Inscribir un triángulo en otro triángulo dado

Problema. 1 En un triángulo dado inscribir un triángulo cuyos lados sean perpendiculares a los lados del triángulo dado.

Solución. Sea $△ A B C$ el triángulo dado, la idea es construir una homotecia desde uno de los vértices, tomemos $D \in B C$ , distinto de $B$ , $C$ y también diferente al pie de la altura por $A$ .

Por $D$ trazamos la perpendicular a $B C$ que interseca a $A C$ en $E$ , por $E$ trazamos la perpendicular a $A C$ que interseca a $A B$ en $F$ .

Por $F$ trazamos la perpendicular a $A B$ que interseca a $D E$ en $G$ .

Sea $G^{'} = B C \cap A G$ , por $G^{'}$ trazamos la paralela a $G E$ que interseca a $A C$ en $E^{'}$ , también trazamos la paralela a $G F$ por $G^{'}$ que interseca a $A B$ en $F^{'}$ .

Por construcción $E E^{'}$ , $F F^{'}$ y $G G^{'}$ concurren en $A$ , $G^{'} F^{'} ⊥ A B$ y $G^{'} E^{'} ⊥ A C$ .

Como $△ A F^{'} G^{'} \sim △ A F G$ y $△ A G^{'} E^{'} \sim △ A G E$
$\frac{A F^{'}}{A F} = \frac{A G^{'}}{A G} = \frac{A E^{'}}{A E}$ .

Por tanto, $E^{'}$ , $F^{'}$ y $G^{'}$ son puntos homólogos de $E$ , $F$ y $G$ respectivamente, con centro de homotecia en $A$ .

Por el teorema 1, $E^{'} F^{'} ∥ E F$ y así $E^{'} F^{'} ⊥ A C$ .

Observación. Notemos que construimos $D E ⊥ B C$ y tal que $E \in A C$ , pero pudimos haber construido $E \in A B$ de lo que resultaría un triangulo distinto $△ E^{'} F^{'} G^{'}$ y por lo tanto tenemos dos soluciones.

Inscribir un cuadrado en un triángulo dado

Problema 2. Dado un triángulo, inscribir un cuadrado en el triángulo dado.

Solución. Sea $△ A B C$ el triángulo dado, construimos un cuadrado exteriormente $B D E C$ sobre $B C$ , sean $D^{'} = A D \cap B C$ y $E^{'} = A E \cap B C$ .

Como $B C ∥ D E$ entonces $D^{'}$ y $E^{'}$ son puntos homólogos de $D$ y $E$ respectivamente con centro de homotecia en $A$ .

Por $D^{'}$ trazamos una paralela a $B D$ que interseca a $A B$ en $B^{'}$ y por $E^{'}$ trazamos una paralela a $C E$ que interseca a $A C$ en $C^{'}$ .

Como $B^{'} D^{'}$ es transversal a $A B$ y a $A D$ y es paralela a $B D$ entonces $\frac{A B^{'}}{A B} = \frac{A D^{'}}{A D}$ y por tanto, $B$ y $B^{'}$ son puntos homólogos, de manera similar podemos ver que $C$ y $C^{'}$ son puntos homólogos.

Como $B D E C$ y $B^{'} D^{'} E^{'} C^{'}$ son figuras homotéticas entonces, por el corolario, son semejantes, por lo tanto, $B^{'} D^{'} E^{'} C^{'}$ es un cuadrado.

Observación. Si alguno de los ángulos $∠ B$ o $∠ C$ es obtuso, entonces una de las rectas $A D$ o $A E$ intersecaría a $B C$ por fuera y no seria posible la construcción.

Así, si nuestro triángulo $△ A B C$ es obtusángulo tenemos que tomar como centro de homotecia el vértice del ángulo obtuso.

Si $△ A B C$ es acutángulo existen tres soluciones, una por cada vértice como centro de homotecia, y si es rectángulo hay dos soluciones.

Construir una secante a un triángulo dado

Problema 3. Dado un triángulo $△ A B C$ , construye $D \in A B$ y $E \in A C$ tal que $B D = D E = E C$ .

Solución. Supongamos que ya tenemos la figura requerida (figura 6). Por $A$ trazamos una paralela a $D E$ que interseca a $B E$ en $F$ , por $F$ trazamos una paralela a $A C$ que interseca a $B C$ en $G$ .

Como $A F ∥ D E$ y $F G ∥ E C$ , por el teorema de Tales, tenemos
$\frac{B A}{B D} = \frac{B F}{B E} = \frac{B G}{B C}$ .

Así que $(A, D)$ , $(F, E)$ y $(G, C)$ son pares de puntos homólogos, con centro en $B$ .

Inversamente, para construir el cuadrilátero auxiliar $B A F G$ hacemos lo siguiente (figura 7), trazamos una circunferencia con centro en $A$ y radio $A B$ , $(A, A B)$ , construimos $L \in A C$ tal que $L C = A B$ , trazamos una paralela $l_{1}$ a $B C$ por $L$ , sea $F = (A, A B) \cap l_{1}$ , trazamos una paralela $l_{2}$ a $A C$ por $F$ , sea $G = B C \cap l_{2}$ .

Como $L C G F$ es un paralelogramo entonces $F G = L C = A B = A F$ .

Finalmente, sean $E = A C \cap B F$ y $D$ la intersección de la paralela por $E$ a $A F$ con $A B$ .

Por construcción $B D E C$ y $B A F G$ son homotéticos, con centro de homotecia en $B$ , y tenemos que $\frac{B D}{B A} = \frac{D E}{A F} = \frac{E C}{F G}$ $\Rightarrow B D = D E = E C$ .

Más adelante…

Continuando con el tema de homotecia, en la próxima entrada veremos circunferencias homotéticas.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Sean $B$ , $B^{'}$ y $C$ , $C^{'}$ pares de puntos homólogos de dos figuras homotéticas $F$ y $F^{'}$ , considera $A \in F$ , por $B^{'}$ y $C^{'}$ tracemos paralelas a $A B$ y $A C$ respectivamente, sea $A^{'}$ la intersección de estas dos últimas rectas, prueba que $A$ y $A^{'}$ son puntos homólogos.
Si dos triángulos están en homotecia muestra que sus incentros, circuncentros, ortocentros y centroides son puntos homólogos, y que sus bisectrices, mediatrices, alturas y medianas son rectas homotéticas.
Dadas dos rectas $l_{1}$ y $l_{2}$ que se intersecan en un punto inaccesible, trazar una recta que pase por un punto dado $P$ y la intersección de las rectas dadas (figura 8).

En un triangulo dado inscribir un triangulo cuyos lados sean paralelos a las bisectrices internas del triangulo dado.
En un triangulo dado $△ A B C$ , construir un cuadrado tal que un vértice este en la extensión de $A B$ , otro en la exención de $A C$ y los otros dos vértices en $B C$ .
Construir un triangulo $△ A B C$ dados $∠ A$ , $A B + B C$ y $A C + B C$ .

Entradas relacionadas

Ir a Geometría Moderna I.
Entrada anterior del curso: Construcciones geométricas.
Siguiente entrada del curso: Circunferencias homotéticas.
Otros cursos.

Fuentes

Altshiller, N., College Geometry. New York: Dover, 2007, pp 38-45.
Andreescu, T., Korsky, S. y Pohoata, C., Lemmas in Olympiad Geometry. USA: XYZ Press, 2016, pp 199-200.
Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 110-111.
Cut the Knot

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

El blog de Leo

Aprendiendo, creando y compartiendo matemáticas

Archivo de la etiqueta: razón de homotecia

Geometría Moderna I: Circunferencias homotéticas

Introducción

Homotecia de una circunferencia

Un triangulo variable

Homotecia entre dos circunferencias dadas

Incírculo y exírculo en homotecia

Concurrencia de rectas

Más adelante…

Tarea moral

Entradas relacionadas

Fuentes

Agradecimientos

Geometría Moderna I: Homotecia

Introducción

Homotecia de una recta

Polígonos homotéticos

Rectas concurrentes

Inscribir un triángulo en otro triángulo dado

Inscribir un cuadrado en un triángulo dado

Construir una secante a un triángulo dado

Más adelante…

Tarea moral

Entradas relacionadas

Fuentes

Agradecimientos