Archivo de la etiqueta: composición

Geometría Analítica I: Recordatorio de funciones

Por Paola Berenice García Ramírez

Introducción

En la entrada anterior [Enlace entrada anterior] se introdujo la esencia del concepto de transformaciones y que estaremos viendo diversos tipos de transformaciones, pero para que no trabajemos en un espacio desconocido, en ésta entrada hablaremos de nociones básicas de funciones que debemos tener presentes para luego definir formalmente el concepto de qué es una transformación.

Funciones

Sean $E$ y $F$ dos conjuntos no vacíos, denominaremos función de un conjunto $E$ en un conjunto $F$ (o función definida en $E$ con valores en $F$ ) a una regla o ley $f$ que a todo elemento $x \in E$ le pone en correspondencia un determinado elemento $f (x) \in F$ .

Al conjunto de los elementos $x \in E$ les llamamos dominio o argumento de la función $f$ y normalmente su notación es $D o m (f)$ . Al conjunto de los elementos $f (x) \in F$ le llamamos rango o imagen y se denota por $I m (f)$ . Además se encuentra el conjunto $F$ del contradominio, el cual contiene al rango.

A una función la designamos por lo general con la letra $f$ o con el símbolo $f : E ⟶ F$ , que nos señala que $f$ aplica el conjunto $E$ en $F$ . También podemos emplear la notación $x \mapsto f (x)$ para indicarnos que al elemento $x$ le corresponde el elemento $f (x)$ . Cabe mencionar que en la mayoría de los casos las funciones se definen mediante igualdades, las cuales describen la ley de correspondencia.

Ejemplo 1. Podemos decir que la función $f$ está definida mediante la igualdad $f (x) = \sqrt{x^{2} + 1}$ , $x \in [a, b]$ . Si $y$ es la notación general de los elementos del conjunto $F$ , o sea $F = {y}$ , la aplicación $f : E ⟶ F$ se escribe en forma de la igualdad $y = f (x)$ , y decimos entonces que la función se encuentra dada en su forma explícita.

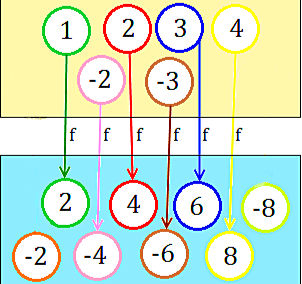
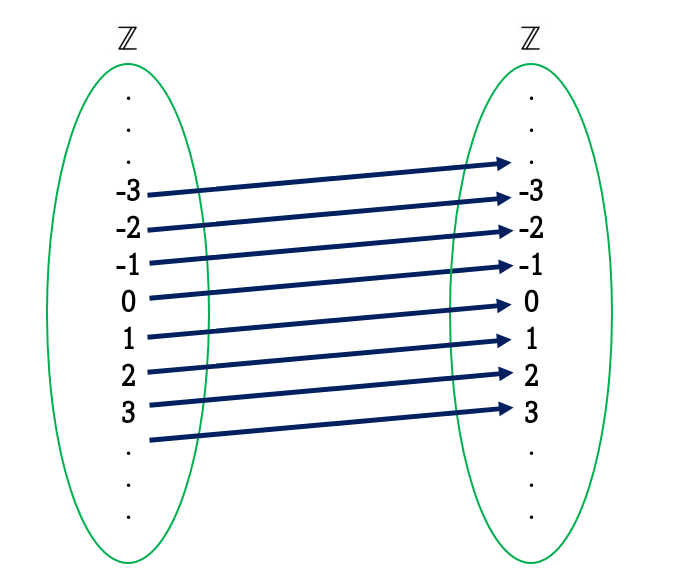
Ejemplo 2. Mediante la siguiente imagen vamos a obtener $D o m f$ , $I m f$ y el $C o d f$ .

Podemos ver que $D o m f$ es el conjunto formado por ${1, - 2, 2, - 3, 3, 4}$ . La $I m f$ es ${2, - 4, 4, - 6, 6, 8}$ y el $C o d f$ es ${- 2, 2, - 4, 4, - 6, 6, 8, - 8}$ . Podemos darnos cuenta que no necesariamente la $I m f$ debe coincidir siempre con el $C o d f$ .

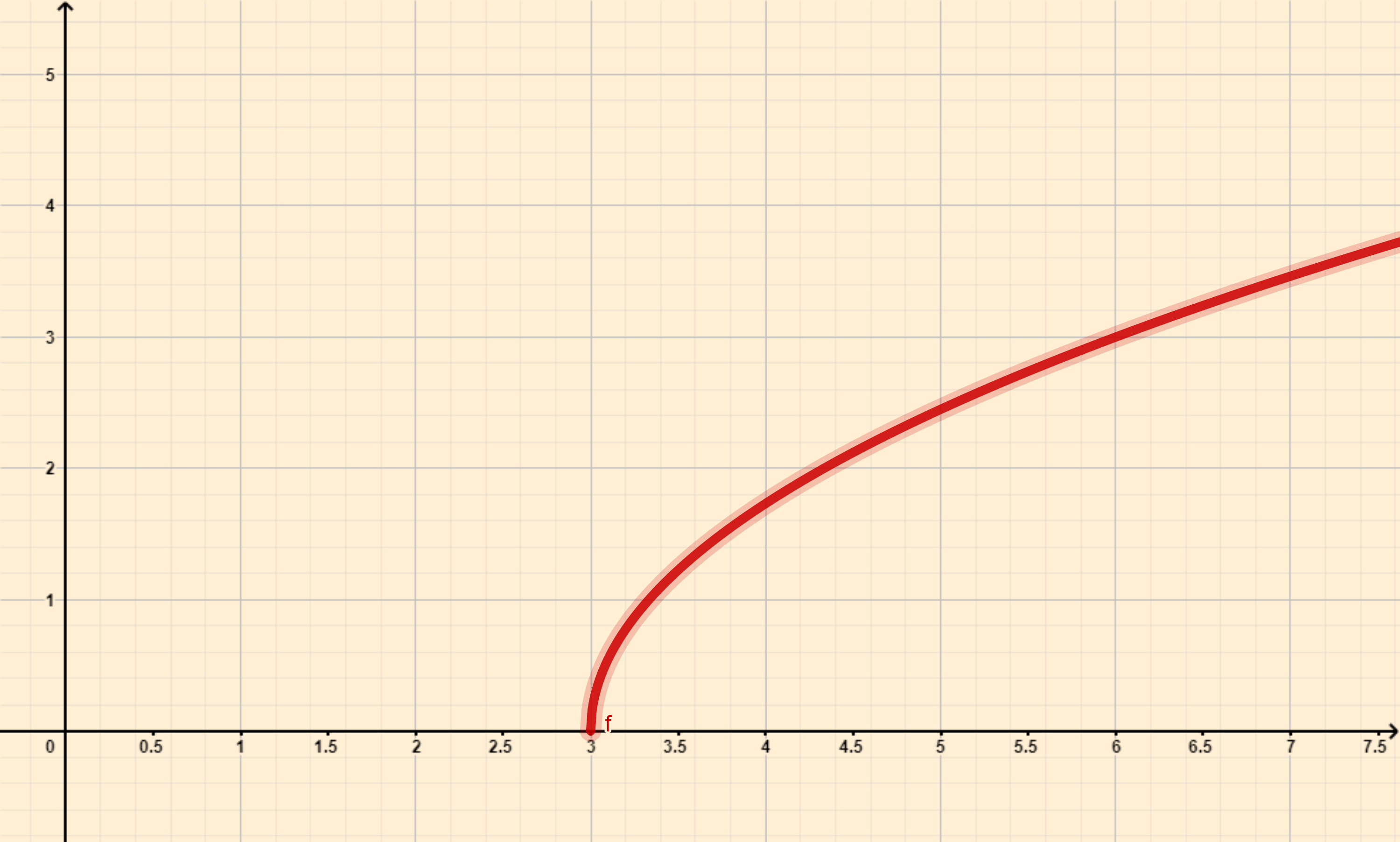
Ejemplo 3. Sea la función definida por la ecuación $y = \sqrt{3 - 9 x}$ . Debido a que la función es una raíz cuadrada, $y$ es función de $x$ sólo para $3 - 9 x \geq 0$ ; pues para cualquier $x$ que satisfaga esta desigualdad, se determina un valor único de $y$ . Procedemos a resolver la desigualdad:

$\begin{aligned} 3 - 9 x & \geq 0, \\ 3 & \geq 9 x, \\ \frac{3}{9} & \geq x, \\ \frac{1}{3} & \geq x . \end{aligned}$

Sin embargo si $x > \frac{1}{3}$ , obtenemos la raíz cuadrada de un número negativo y en consecuencia no existe un número real $y$ . Por tanto $x$ debe estar restringida a $\frac{1}{3} \geq x$ . Concluimos que el $D o m f$ es el intervalo $(- \infty, \frac{1}{3}]$ y la $I m f$ es $[0, + \infty) .$

Función inyectiva, sobreyectiva y biyectiva

Definición. Una función $f : E ⟶ F$ se denomina:

Inyectiva si $f (x) = f (x^{'})$ implica que $x = x^{'}$ . Otra forma de expresarlo es que no existen dos elementos de $E$ con una misma imagen ( $x \neq x$ implica que $f (x) \neq f (x^{'})$ ).
Suprayectiva o sobreyectiva si $\forall y \in F$ existe $x \in E$ tal que $f (x) = y$ . Es decir que todos los elementos del conjunto $F$ son imagen de algún elemento de $E$ .
Biyectiva si la función cumple ser inyectiva y suprayectiva.

Problema 1. Consideren la función $f : R ⟶ R$ definida por $f (x) = \frac{3 x - 1}{x + 3}$ y determinen su dominio y si es biyectiva.

Solución. Veamos el dominio de la función, para que la función racional $f (x) = \frac{3 x - 1}{x + 3}$ no se indetermine debe cumplirse que:

$\begin{aligned} x + 3 & \neq 0, \\ x & \neq - 3, \\ ∴ D o m f & = R - {- 3} . \end{aligned}$

Ahora veamos si $f$ es biyectiva. Sean $a, b \in R - {- 3}$ , para que $f$ sea inyectiva debe cumplir que $f (x) = f (x^{'})$ implica que $x = x^{'}$ , por ello:

$f (a) = f (b) ⟹ \frac{3 a - 1}{a + 3} = \frac{3 b - 1}{b + 3} .$

Resolviendo:

$\begin{aligned} (3 a - 1) (b + 3) & = (3 b - 1) (a + 3), \\ 3 a b + 9 a - b - 3 & = 3 a b + 9 b - a - 3, \\ 10 a & = 10 b, \\ a & = b . \end{aligned}$

Por tanto $f$ es inyectiva. Ahora veamos si $f$ es suprayectiva, sean $x, y \in E$ entonces:

$\begin{aligned} f (x) = f (y) & ⟹ y = \frac{3 x - 1}{x + 3}, \end{aligned}$

Resolviendo

$\begin{aligned} y (x + 3) & = 3 x - 1, \\ y x + 3 y & = 3 x - 1, \\ y x - 3 x & = - 3 y - 1, \\ x (y - 3) & = - 3 y - 1, \end{aligned}$

y despejando a $x$

$\begin{aligned} x & = \frac{- 3 y - 1}{y - 3}, \\ x & = \frac{3 y + 1}{3 - y}, \end{aligned}$

y como $3 - y \neq 0$ , entonces $y \neq 3$ . En consecuencia $y \in R - {3}$ . Pero al estar definida $f$ por $f : R ⟶ R$ , tenemos que $f$ no es suprayectiva.

$\begin{array}{r} ∴ f no es biyectiva . \end{array}$

Composición de funciones y funciones inversas.

Definición. Dadas las funciones $f : A ⟶ B$ y $g : B ⟶ C$ , donde la imagen de $f$ está contenida en el dominio de $g$ , se define la función composición $(g \circ f) : A ⟶ C$ como $(g \circ f) (x) = g (f (x)),$ para todos los elementos $x$ de $A$ .

La composición de funciones se realiza aplicando dichas funciones en orden de derecha a izquierda, de manera que en $(g \circ f) (x)$ primero actúa la función $f$ y luego la $g$ sobre $f (x)$ .

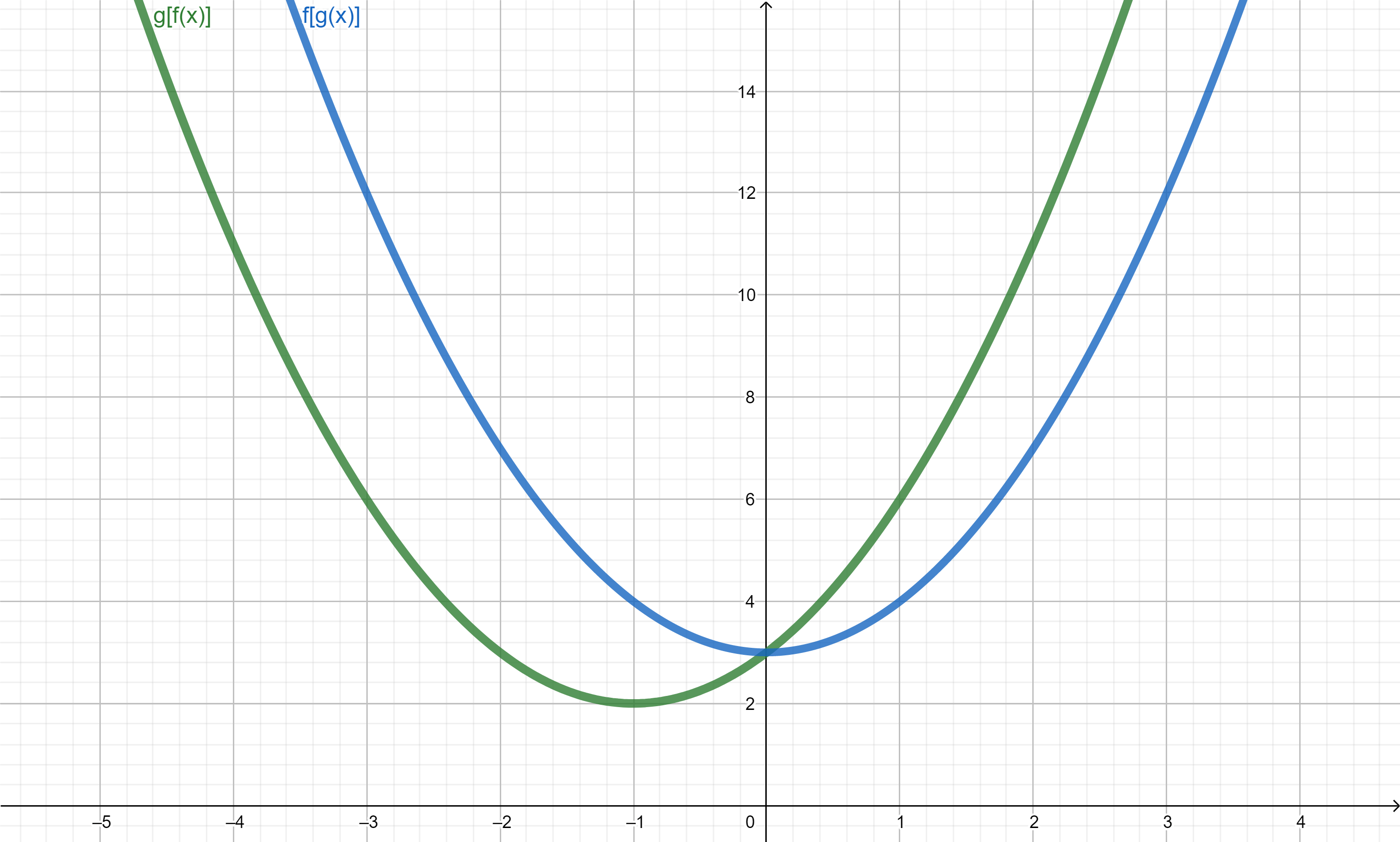
Ejemplo 4. Sean las funciones $f$ y $g$ tales que $f (x) = x + 1$ y $g (x) = x^{2} + 2$ , calcularemos las funciones composición $(g \circ f) (x)$ y $(f \circ g) (x)$ . Tenemos para $(g \circ f) (x)$

$\begin{aligned} (g \circ f) (x) = g [f (x)] & = g (x + 1), \\ = (x + 1)^{2} + 2, \\ = x^{2} + 2 x + 1 + 2, \\ = x^{2} + 2 x + 3. \end{aligned}$

Y para $(f \circ g) (x)$

$\begin{aligned} (f \circ g) (x) = f [g (x)] & = f (x^{2} + 2), \\ = (x^{2} + 2) + 1, \\ = x^{2} + 3. \end{aligned}$

Observemos que la composición no es conmutativa pues las funciones $(f \circ g)$ y $(g \circ f)$ no son iguales.

Definición. Llamaremos función inversa de $f$ a otra función $f^{- 1}$ que cumple que si $f (x) = y$ , entonces $f^{- 1} (y) = x$ .

Sólo es posible determinar la función inversa $f^{- 1} : B ⟶ A$ si y sólo si $f : A ⟶ B$ es biyectiva.

Notemos que la función inversa $f^{- 1} : B ⟶ A$ también es biyectiva y cumple:

$\begin{aligned} f^{- 1} (f (x)) & = x, \forall x \in A, \\ f (f^{- 1} (y)) & = y, \forall y \in B . \end{aligned}$

Dicho de otro modo,

$\begin{aligned} f^{- 1} \circ f & = i d_{A}, \\ f \circ f^{- 1} & = i d_{B}, \end{aligned}$

donde $i d_{A}$ e $i d_{B}$ son las funciones identidad de $A$ y $B$ respectivamente. Es decir, son las funciones $i d_{A} : A ⟶ A$ definida por $i d_{A} (x) = x$ e $i d_{B} : B ⟶ B$ definida por $i d_{B} (y) = y$ .

Concepto formal de transformación

Ahora hemos llegado a la definición de nuestro interés.

Definición. Una transformación en un plano A es una función biyectiva $f : A ⟶ A$ del plano en sí mismo.

Llamaremos transformación en el plano, a toda función que hace corresponder a cada punto del plano, otro punto del mismo.

Tarea moral

Vamos a realizar unos par de ejercicios para repasar y practicar los conceptos que vimos en esta entrada.

Ejercicio 1. Consideren la siguiente función $f : R ⟶ R$ definida por $f (x) = \frac{3 x - 1}{x + 3}$ y determinen su dominio, si ella es inyectiva, suprayectiva y la inversa de $f$ .

Ejercicio 2. Sean $f : X ⟶ Y$ y $g : Y ⟶ Z$ funciones, demuestren que

(1) Si $f$ y $g$ son inyectivas, entonces $g \circ f$ es inyectiva.

(2) Si $g \circ f$ es suprayectiva, entonces $g$ es suprayectiva.

Más adelante

En esta entrada vimos las nociones básicas de funciones que nos llevaron a definir formalmente el concepto de una transformación. Dicho concepto nos permitirá comenzar a trabajar en la siguiente entrada con unos primeros conjuntos cuyas propiedades hacen que tengan un nombre especial: los grupos de transformaciones.

Enlaces

Página principal del curso:
Entrada anterior del curso:
Siguiente entrada del curso:

Álgebra Superior I: Relaciones en conjuntos: dominio, codominio y composición

Por Guillermo Oswaldo Cota Martínez

2 respuestas

Introducción

Habiendo hablado del producto cartesiano, ya tenemos los ingredientes para irnos acercando a la definición de función, pero antes de hablar de ellas, tenemos que hablar de relaciones y de algunos de sus conceptos. En esta entrada introduciremos el concepto de relación, dominio, codominio y composición entre relaciones.

Relaciones

Cuando estamos hablando de el producto cartesiano, estamos juntando las parejas posibles de elementos entre dos conjuntos. Pero quizá no nos interesen todas las parejas posibles, quizá a veces solo nos interesaría hablar de algún subconjunto de estas parejas. Por ejemplo, si tenemos los conjuntos de zapatos izquierdos y derechos denotados por $I, D$ entonces no siempre nos interesan todas las parejas posibles de zapatos, quizá solo nos interese combinar cada zapato izquierda con su par correspondiente. Para dar un ejemplo, imagina que hay tres zapatos $A, B, C$ y los conjuntos $I$ y $D$ contienen tres zapatos de cada uno de los zapatos que hay:

$I = {I_{A}, I_{B}, I_{C}}$

$D = {D_{A}, D_{B}, D_{C}}$

Si quisieramos unir cada zapato con su par, nos podemos fijar en su producto cartesiano $I \times D$ , sin embargo hay elementos que sí nos van a interesar y otros que no. Por ejemplo, la pareja $(I_{A}, D_{A})$ sí nos interesa, pues es el zapato izquierdo y derecho del zapato $A$ . Por otro lado, la pareja $(I_{A}, D_{C})$ no nos interesa, pues estamos juntando dos zapatos pero de modelos distintos. En particular, el subconjunto de $I \times D$ que describe a los tres zapatos es: $R = {(I_{A}, D_{A}), (I_{B}, D_{B}), (I_{C}, D_{C})} .$ Este conjunto es una relación entre los conjuntos $I$ y $D$ . Como podrás notar, $R \subset I \times D$ , y para la definición de relación, basta con que el conjunto esté contenido en el producto cartesiano para que cumpla la definicón.

Definición. Sean $X$ y $Y$ dos conjuntos, una relación entre los conjuntos $X$ y $Y$ es un subconjunto $R$ del producto cartesiano $X \times Y$ : $R \subset X \times Y$

Definición. Si $R$ es una relación de $X$ en $Y$ , diremos que $x$ está relacionado con $y$ bajo la relación $R$ si la pareja $(x, y) \in X \times Y$ y $(x, y) \in R$ .

Con esta última definición, podemos notar que el zapato izquierdo $A$ ( $I_{A}$ ) está relacionado con el zapato derecho $A$ ( $D_{A}$ ) bajo la relación $R$ , pues la pareja $(I_{A}, D_{A})$ pertenece a la relación $R$ .

En nuestro ejemplo anterior, mostramos una relación entre $I$ y $D$ . Otros ejemplos de relaciones entre $I$ y $D$ son los siguientes:

${(I_{B}, D_{A}), (I_{C}, D_{B}), (I_{C}, D_{A})},$
${(I_{C}, D_{B})}$
${(I_{A}, D_{A}), (I_{C}, D_{B})}$
$\emptyset$
$I \times D$

Dominio y codominio de relaciones

Vamos ahora a trabajar con el conjunto de los números enteros $Z$ . Y trabajaremos con el producto cartesiano $Z \times Z$ . Llamemos a este producto cartesiano $Z^{2}$ que es la forma en que comúnmente se le denota al producto cartesiano entre el mismo conjunto (en este caso $Z$ ) en la literatura.

Ahora, consideremos la siguiente relación entre los conjuntos: $R = {(x, y) \in Z^{2} : (x es múltiplo de 3) \land (y = 2 x)}$

Y notemos que algunos ejemplos de elementos de esta relación son: ${(3, 6), (0, 0), (- 3, - 6), (3^{10}, 2 * 3^{10}), (- 300, - 600)} \subset R$ . Gráficamente, podemos ver la relación en la siguiente imagen:

Del lado izquierdo corresponden los elementos $x$ de las parejas $(x, y) \in R$ y del lado derecho los elementos $y$ . Notemos que del lado izquierdo (los elementos $x$ ), no consideramos todos los elementos. Por ejemplo, los números ${- 5, - 4, - 2, - 1, 1, 2, 4, 5}$ no forman ninguna pareja, pues en la definición de nuestro conjunto, solo estamos considerando los múltiplos de $3$ del lado izquierdo de la relación. A estos números que sí forman parejas del lado izquierdo, les llamamos dominio.

Definición. Sean $X, Y$ dos conjuntos y $R$ una relación de $X$ en $Y$ . El dominio de la relación $R$ es $D o m (R) = {x \in X : \exists y \in Y tal que (x, y) \in R}$

Notemos que siempre pasará que $D o m (R) \subset X$ , otra definición que no hay que confundir con la de dominio es la de contradominio, al que nos referimos como el conjunto $Y$ .

Definición. Sean $X, Y$ dos conjuntos y $R$ una relación de $X$ en $Y$ . El contradominio de $R$ es el conjunto $Y$ .

En nuestro ejemplo anterior, $D o m (R) = {x \in X : x es múltiplo de 3}$ .

Esto es cierto, pues las parejas de la relación $R$ son aquellas parejas de la forma $(3 n, 6 n)$ , pues pedimos que del lado izquierdo estén los múltiplos de $3$ (todo múltiplo de $3$ puede escribirse como algún número entero $n$ multiplicado por $3$ ), y del lado izquierdo el doble del número que escribimos del otro lado (si del lado izquierdo está $3 n$ entonces del derecho estará $2 * 3 n = 6 n$ ). Así que el dominio son aquellos números que forman alguna pareja, es decir, los múltiplos de $3$ .

Por otro lado, el contradominio es $Z$ . Ahora, podemos preguntarnos en un concepto análogo a la idea de los elementos $y$ para los cuales existe un elemento $x$ de forma que $(x, y)$ pertenezca a la relación, para eso, podemos observar que los únicos elementos de $Z$ que pertenecen a alguna pareja del lado derecho son ${\dots, - 12, - 6, 0, 6, 12, \dots}$ , es decir, los múltiplos de $6$ , de manera que podríamos hablar de que este conjunto es la imagen de la relación $R$ .

Definición. Sean $X, Y$ dos conjuntos y $R$ una relación de $X$ en $Y$ . La imagen de $R$ es: $I m (R) = {y \in Y : \exists x \in X tal que (x, y) \in R}$

Imagen Directa e Imagen Inversa

Ahora, tomemos a los conjuntos $A = {0, 2, 3, 5, 6, 7, 8, 9}$ y $B = {- 6, - 1, 2, 3, 4, 6, 7, 12, 21}$ veamos que $A \times B \subset Z^{2}$ pues ambos son subconjuntos de números enteros. El siguiente concepto que vamos a presentar, va a ser la imagen directa e inversa. Para esto, consideremos nuevamente nuestra relación $R$ de la sección anterior. Veamos que los elementos de $A$ que pertenecen al dominio de $R$ son ${0, 3, 6, 9}$ esto pues ${(0, 0), (3, 6), (6, 12), (9, 18)} \subset R$ . Definamos la imagen directa de $A$ como los elementos en la imagen de $R$ con la restricción de que únicamente consideremos elementos de $A$ del lado izquierdo.

Definición. Sean $X, Y$ dos conjuntos, $A \subset X$ y $R$ una relación de $X$ en $Y$ . La imagen directa de $A$ es el conjunto: $I m [A] = {y \in Y : \exists x \in A tal que (x, y) \in R}$

Compara esta definición con la definición de imagen, lo único que estamos cambiando es el conjunto al que pertencen las $x$ .

De manera similar, tenemos un concepto similar para $B$ , en donde restringiremos ahora el dominio. Para esto, nota que las parejas de $R$ que tienen su imagen en $B$ son ${(- 3, - 6), (3, 6), (6, 12)}$ . Y el concepto de imagen inversa, serán aquellos elementos del dominio de $R$ los cuales están relacionados con algún elemento de $B$ .

Definición. Sean $X, Y$ dos conjuntos, $B \subset Y$ y $R$ una relación de $X$ en $Y$ . La imagen inversa de $B$ es el conjunto: $I m^{- 1} [B] = {x \in X : \exists y \in B tal que (x, y) \in R}$

De esta, manera:

$I m [A] = {0, 6, 12, 18},$ $I m^{- 1} [B] = {- 3, 3, 6} .$

A continuación, vamos a introducir una última definición de esta entrada, que da la idea intuitiva de juntar distintas relaciones.

Composición de funciones

Ahora, veremos la siguiente relación entre el conjunto de zapatos izquierdos $I$ y conjunto de zapatos derechos $D$ :

$R = {(x, y) \in I \times D : x es del mismo color que y}$

Y la relación entre zapatos derechos y el conjunto $P$ de pantalones:

$T = {(x, y) \in D \times P : x es del mismo color que y}$

Estas relaciones solo nos están juntando colores de prendas, la primera nos junta zapatos del mismo color y la tercera relaciones el color de los zapatos derechos con el del pantalón.

Así que por si ejemplol tuvieramos los colores rojo, amarillo y azul entre zapatos izquierdos, derechos y pantalones, entonces la primera relación tendría al zapato izquierdo rojo $I_{R}$ , el zapato derecho rojo $D_{R}$ y el pantalón rojo $P_{R}$ , de manera que $(I_{R}, D_{R}) \in R \land (D_{R}, P_{R}) \in T$ . ¿Podemos establecer la conexión entre los zapatos izquierdos y los pantalones? Pues con esta pareja, resulta que de alguna manera el zapato $D_{R}$ une a los dos elementos mediante dos relaciones distintas. La primera relación tiene como contradominio el conjunto $D$ mientras que la segunda lo tiene como dominio.

De la misma manera, podemos conectar el zapato izquierdo azul $I_{A}$ con algún pantalón de la siguiente manera:

Notamos que $I_{A}$ está relacionado con el zapato derecho azul $D_{A}$ mediante la relación $R$ .
Observamos que a su vez el zapato $D_{A}$ está relacionado con el pantalón azul $P_{A}$ mediante $T$ .

De esta manera, podemos encontrar alguna conexión del zapato $I_{A}$ al pantalón $P_{A}$ viendo que hay una relación entre $I_{A}$ con $D_{A}$ y de $D_{A}$ con $P_{A}$ . Así que podríamos definir una relación entre los zapatos izquierdos y los pantalones a través de las relaciones $R$ y $T$ . Definamos esta relación como $R \circ T$ de la siguiente manera:

$T \circ R = {(x, y) \in I \times P : \exists z \in D tal que ((x, z) \in R \land (z, y) \in T)}$

Lo que queremos decir con esta expresión, es que los elementos de la relación $T \circ R$ son los elementos $(x, y)$ de tal forma que existe una forma de conectar $(x, y)$ mediante un elemento $z$ de tal forma que $x$ está relacionado con $y$ mediante la relación $T \circ R$ si existe un elemento $z$ que los conecta, es decir, si existe $z$ en $I m (R) \cap D o m (T)$ de tal forma que $(x, z) \in R$ y $(z, y) \in T$ .

Definición. Sean $X, Z, Y$ tres conjuntos, $R$ una relación de $X$ en $Z$ y $T$ una relación de $Z$ en $Y$ . La relación composición de $R$ con $T$ es la relación:
$T \circ R = {(x, y) \in X \times Y : \exists z \in Z ((x, z) \in R \land (z, y) \in T)$

Veamos ahora un ejemplo de nuevo con los número enteros. Considera la relación que ya habíamos visto anteriormente, dada por: $R = {(x, y) \in Z^{2} : (x es múltiplo de 3) \land (y = 2 x)}$ Nota ahora, que como dijimos anteriormente, estos son las parejas de la forma $(3 n, 6 n)$ de manera que otra forma de escribir el conjunto es $R = {(3 n, 6 n) : n \in Z}$ .

Ahora considera la siguiente relación $T$ : $T = {(x, y) \in Z^{2} : x = y + 1}$

Algunos elementos de esta relación son: ${(3, 2), (7, 6), (1, 0), (- 9, - 10)}$ . Gráficamente se ve de la siguiente manera:

Y si te das cuenta, únicamente son los números de la forma $(n + 1, n)$ . Por lo que podríamos escribir esta relación como $T = {(n + 1, n) : n \in Z}$ .

Ahora veamos cómo se ve la composición $T \circ R$ . Para ello, tomemos un elemento de la relación $R$ . Por ejemplo, $(3, 6) \in R$ . Ahora notemos que de igual forma, $(6, 5)$ pertenece a la relación $T$ . De manera que $(3, 5) \in T \circ R$ . En general, un elemento de la relación $R$ se escribe como $(3 n, 6 n)$ , y un elemento de la relación $T$ , como dijimos al principio del párrafo, es de la forma $(n + 1, n)$ o lo que es lo mismo, $(n, n - 1)$ . Y enseguida nota que si tomamos un número entero $n$ , entonces $(3 n, 6 n) \in R$ y $(6 n, 6 n - 1) \in T$ . De esta manera, podemos escribir a la composición de $R$ con $T$ como el conjunto: $T \circ R = {(3 n, 6 n - 1) : n \in Z}$

Más adelante…

En la siguiente entrada seguiremos hablando de las relaciones entre conjuntos y veremos algunos tipos de relaciones especiales que tendrán algunas propiedades interesantes. También hablaremos un poco más de relaciones de un conjunto en sí mismo, este tipo de relaciones ya las hemos visto, sin embargo, veremos más propiedades que pueden cumplir estas. Esto nos servirá para hablar después de órdenes entre conjuntos.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Sea $R = {(x, y) \in Z^{2} : x + y = 0}$ y la relación $T = {(x, y) \in Z^{2} : x - y = 0} .$ Encuentra:
- $D o m (R)$
- $I m (R)$
- Escribe todos los elementos de $T \circ R$
- Encuentra $I m [{1, 2, 3, 4, 5}]$ sobre la relación $R$
- Encuentra $I m^{- 1} [{- 1, - 2, - 3, - 4, - 5}]$ sobre la relación $T$
Demuestra que si $R = {(x, y) \in Z^{2} : (x es múltiplo de 3) \land (y = 2 x)}$ , entonces $R = {(3 n, 6 n) : n \in Z}$
La recta $L$ con pendiente $m$ e intersección $b$ con el eje $y$ en los números enteros es el conjunto: $L = {(x, y) \in Z^{2} : m x + b = y}$ Encuentra $L_{1} \cap L_{2}$ donde $L_{1}$ es la recta con $m = 1, b = 0$ y $L_{2}$ es la recta con $m = - 1, b = 2$ .

Entradas relacionadas

Ir a Álgebra Superior I
Entrada anterior del curso: Problemas de producto cartesiano
Siguiente entrada del curso: Tipos de relaciones en conjuntos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Álgebra Lineal I: Producto de matrices y composición de sus transformaciones

Por Julio Sampietro

4 respuestas

Introducción

En una entrada previa estudiamos el vínculo entre las matrices y las transformaciones lineales. Más precisamente vimos que existe una biyección entre ambos conjuntos, de manera que tener una matriz de $m \times n$ con entradas en algún campo $F$ es lo mismo que tener una transformación lineal $φ : F^{n} \to F^{m}$ . En esta entrada, estudiaremos cómo esta correspondencia se comporta respecto a las dos operaciones ‘naturales’ en ambos: el producto de matrices y la composición de funciones.

Veremos que multiplicar matrices se corresponde con componer sus transformaciones lineales y vice versa. Esto puede explicar algunos fenómenos de la multiplicación de matrices que pueden ser extraños al principio, como la falta de conmutatividad ( $A B \neq B A$ ) entre otros.

El producto de matrices

Sean $m, n, p$ números naturales positivos y sean $A \in M_{m, n} (F), B \in M_{n, p} (F)$ dos matrices. Es importante observar que el número de columnas de $A$ es el mismo que el de renglones de $B$ . Esto es fundamental para que el producto de matrices esté definida.

Por nuestra correspondencia previa, sabemos que tanto a $A$ como a $B$ les corresponden transformaciones lineales

$\begin{array}{r} φ_{A} : F^{n} \to F^{m} φ_{B} : F^{p} \to F^{n} \end{array}$

Recuerda que $φ_{A}$ es la transformación que manda a $X \in F^{n}$ en $A X \in F^{m}$ y $φ_{B}$ es la transformación que manda a $Y \in F^{p}$ en $B Y \in F^{n}$ .

Podemos entonces preguntarnos por la composición

$\begin{array}{r} φ_{A} \circ φ_{B} : F^{p} \to F^{m} (φ_{A} \circ φ_{B}) (X) = φ_{A} (φ_{B} (X)), \end{array}$

la cual primero manda a un $X$ de $F^{p}$ a $B X$ , y luego a este lo manda a $A (B X)$ .

Como $φ_{A}$ y $φ_{B}$ son lineales, podemos verificar que la composición también lo es. Para verificar esto, si $X, Y \in F^{p}$ son arbitrarios así como $α, β \in F$ , entonces

$\begin{aligned} (φ_{A} \circ φ_{B}) (α X + β Y) & = φ_{A} (φ_{B} (α X + β Y)) \\ = φ_{A} (α φ_{B} (X) + β φ_{B} (Y)) \\ = α φ_{A} (φ_{B} (X)) + β φ_{A} (φ_{B} (Y)) \\ = α \cdot (φ_{A} \circ φ_{B}) (X) + β \cdot (φ_{A} \circ φ_{B}) (Y) . \end{aligned}$

Aquí la segunda igualdad se debe a que $φ_{B}$ es lineal y la tercera porque $φ_{A}$ lo es. En el resto de las igualdades estamos usando la definición de la composición.

Como $φ_{A} \circ φ_{B}$ es una transformación lineal, por el teorema de correspondencia entre matrices y transformaciones lineales, debe existir una única matriz $C \in M_{m, p} (F)$ tal que

$\begin{array}{r} φ_{A} \circ φ_{B} = φ_{C} . \end{array}$

Esto motiva la siguiente (importante) definición:

Definición. El producto de dos matrices $A \in M_{m, n} (F)$ y $B \in M_{n, p} (F)$ (de nuevo, observamos que el número de renglones de $B$ y el número de columnas de $A$ deben coincidir) es la única matriz $A B \in M_{m, p} (F)$ tal que

$\begin{array}{r} A (B (X)) = (A B) (X) \end{array}$

Para todo $X \in F^{p}$ .

Un truco para acordarse de la condición de compatibilidad en renglones y columnas es pensar en términos de transformaciones lineales: Sabemos que dos funciones $f$ y $g$ se pueden componer solo si el codominio de una es el dominio de la otra.

Observación. Como mencionamos previamente, podemos identificar a $F^{n}$ con el espacio $M_{n, 1} (F)$ (esto es especialmente claro cuando escribimos un vector en columna: Tenemos $n$ renglones y una sola columna). Así, si a un vector $X \in F^{n}$ lo identificamos con su matriz $\tilde{X} \in M_{n, 1} (F)$ entonces podemos considerar el producto $A \tilde{X} \in M_{m, 1} (F)$ , que resulta (al identificar de vuelta con $F^{m}$ ) coincide con $A X$ . Es decir, pensar la aplicación $A X$ como una transformación o como un producto de matrices no afecta el resultado, aunque es recomendable (para nuestros propósitos) pensarlo como una transformación lineal.

Calculando el producto de matrices

Si bien la definición que dimos del producto tiene sentido desde una perspectiva un poco más abstracta, queremos poder calcular explícitamente el producto $A B$ sabiendo las entradas de $A$ y de $B$ .

Para esto, sean $A = [a_{i j}]$ y $B = [b_{i j}]$ con tamaños como en la definición. Sea $e_{1}, \dots, e_{p}$ la base canónica de $F^{p}$ . Entonces $(A B) e_{j}$ es la $j$ -ésima columna de $A B$ (por una observación que hicimos aquí). Denotaremos por $C_{1} (A), \dots, C_{n} (A)$ y $C_{1} (B), \dots, C_{p} (B)$ a las columnas de $A$ y las de $B$ respectivamente. Usando la misma observación, podemos escribir

$\begin{aligned} A (B e_{j}) & = A C_{j} (B) \\ = b_{1 j} C_{1} (A) + b_{2 j} C_{2} (A) + \dots + b_{n j} C_{n} (A) . \end{aligned}$

Para la segunda igualdad, estamos usando la segunda parte de la observación de esta entrada. Por definición del producto, tenemos que $A (B e_{j}) = (A B) e_{j} = C_{j} (A B)$ . Juntando esto con la igualdad anterior, tenemos

$\begin{array}{r} C_{j} (A B) = b_{1 j} C_{1} (A) + b_{2 j} C_{2} (A) + \dots + b_{n j} C_{n} (A) . \end{array}$

Estamos muy cerca de encontrar cualquier entrada $(i, j)$ del producto. Notamos que esta entrada está en la fila $i$ de $C_{j} (A B)$ . Haciendo las operaciones entrada a entrada, obtenemos entonces que

$\begin{array}{r} (A B)_{i j} = a_{i 1} b_{1 j} + a_{i 2} b_{2 j} + \dots + a_{i n} b_{n j} . \end{array}$

La discusión anterior prueba el siguiente resultado.

Teorema. (Regla del producto) Sean $A = [a_{i j}] \in M_{m, n} (F)$ y $B = [b_{i j}] \in M_{n, p} (F)$ . Entonces la $(i, j)$ -ésima entrada de $A B$ está dada por

$\begin{array}{r} (A B)_{i j} = \sum_{k = 1}^{n} a_{i k} b_{k j} . \end{array}$

Hubiéramos podido dar como definición de $A B$ a la matriz con las entradas que especifica el teorema, pero esto hubiera escondido la motivación detrás de la definición: A ojos del álgebra lineal, las matrices «son» transformaciones lineales y el producto, su composición.

Lo más importante a recuperar de lo que hemos platicado hasta ahora es que el producto $A B$ se puede pensar de cualquiera de las dos formas siguientes:

Como la transformación lineal que corresponde a la composición de las transformaciones de $A$ y $B$ .
Como la matriz cuyas entradas están dadas por la regla del producto.

Ambas formas de ver al producto tienen ventajas y desventajas. Usaremos una o la otra según nos convenga.

Ejemplos de producto de matrices

Ejemplo 1. Si $A = (\begin{matrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{matrix})$ y $B = (\begin{matrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{matrix})$ son matrices en $M_{2} (F)$ , entonces el producto existe y por el teorema tenemos que

$\begin{array}{r} A B = (\begin{array}{c} a_{11} b_{11} + a_{12} b_{21} & a_{11} b_{12} + a_{12} b_{22} \\ a_{21} b_{11} + a_{22} b_{21} & a_{21} b_{12} + a_{22} b_{22} \end{array}) . \end{array}$

Observa que si $C_{1}$ y $C_{2}$ son las dos columnas de $B$ , entonces las dos columnas de $A B$ son $A C_{1}$ y $A C_{2}$ . Esta es una buena forma de recordar cómo hacer el producto.

$△$

Ejemplo 2. Si $A = (\begin{matrix} a_{11} & a_{12} \\ a_{21} & a_{22} \\ a_{31} & a_{32} \end{matrix})$ y $B = (\begin{matrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{matrix})$ entonces el producto $A B$ es una matriz de tamaño $3 \times 2$ , y está dada por

$\begin{array}{r} A B = (\begin{array}{c} a_{11} b_{11} + a_{12} b_{21} & a_{11} b_{12} + a_{12} b_{22} \\ a_{21} b_{11} + a_{22} b_{21} & a_{21} b_{12} + a_{22} b_{22} \\ a_{31} b_{11} + a_{32} b_{21} & a_{31} b_{12} + a_{32} b_{22} \end{array}) . \end{array}$

$△$

Ejemplo 3. Tomando en cuenta el ejemplo anterior con las matrices $A = (\begin{matrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{matrix})$ y $B = (\begin{matrix} 1 & - 1 \\ 0 & 2 \end{matrix})$ entonces

$\begin{array}{r} A B = (\begin{array}{c} 1 & 3 \\ 3 & 5 \\ 5 & 7 \end{array}) . \end{array}$

$△$

Observa que no podemos hacer el producto $B A$ , pues la cantidad de columnas de $B$ es $2$ , la cantidad de filas de $A$ es $3$ , y estos números no coinciden.

Ejemplo 4. Si $A = (\begin{matrix} 1 & 0 \\ 0 & 0 \end{matrix})$ y $B = (\begin{matrix} 0 & 0 \\ 2 & 0 \end{matrix})$ entonces podemos calcular tanto $A B$ como $B A$ y obtenemos

$\begin{array}{r} A B = (\begin{array}{c} 0 & 0 \\ 0 & 0 \end{array}) = O_{2} y B A = (\begin{array}{c} 0 & 0 \\ 2 & 0 \end{array}) . \end{array}$

$△$

Propiedades básicas del producto

El último ejemplo de la sección pasada refleja dos cosas importantes del producto de matrices:

El producto no es conmutativo. Es decir, aunque existan ambos $A B$ y $B A$ , estos no tienen por qué coincidir.
Aunque $A$ y $B$ no sean cero, su producto si puede serlo. En el ejemplo $A$ y $B$ eran distintas de cero pero $A B = O_{2}$ .

Definición. Dos matrices $A, B \in M_{n} (F)$ conmutan si $A B = B A$ .

Entonces uno tiene que tener cuidado cuando realiza manipulaciones algebraicas con matrices, pues muchas propiedades a las que estamos acostumbrados en campos dejan de ser ciertas.

Ejemplo. En un campo, uno generalmente usa las reglas para desarrollar cuadrados:

$\begin{aligned} (a + b)^{2} & = a^{2} + 2 a b + b^{2}, \\ (a + b) (a - b) & = a^{2} - b^{2} . \end{aligned}$

Sin embargo, trabajando con matrices estas identidades dejan de ser ciertas, y son reemplazadas por una versión menos sencilla:

$\begin{aligned} (A + B)^{2} & = A^{2} + A B + B A + B^{2}, \\ (A + B) (A - B) & = A^{2} - A B + B A - B^{2} . \end{aligned}$

Estas coinciden con las correspondientes en el campo solo si $A$ y $B$ conmutan.

$△$

Sin embargo, hay buenas noticias. Aparte de la conmutatividad, muchas otras propiedades algebraicas deseables se preservan, y las resumimos en la siguiente proposición:

Proposición. La multiplicación de matrices satisface las siguientes:

Asociatividad: Se cumple que $(A B) C = A (B C)$ para cualesquiera matrices $A \in M_{m, n} (F), B \in M_{n, p} (F), C \in M_{p, q} (F)$ .
Compatibilidad con el producto por escalares: Se cumple que $α (A B) = (α A) B = A (α B)$ para cualesquiera $α \in F, A \in M_{m, n} (F), B \in M_{n, p} (F)$ .
Distributividad con respecto a la suma: Se cumplen

$\begin{aligned} (A + B) C & = A C + B C \\ D (A + B) & = D A + D B \end{aligned}$

para cualesquiera $A, B \in M_{m, n} (F)$ , $C \in M_{n, p} (F)$ y $D \in M_{p, m} (F) .$

Demostración: La demostración de estas propiedades se sigue directamente de la definición, o bien haciendo los cálculos a través de la regla del producto. Probaremos la asociatividad usando la definición, para mostrar las ventajas que tiene pensar al producto como la matriz correspondiente a la composición. Tras ver la demostración, piensa en lo tedioso que sería hacer la prueba usando la regla del producto.

Para verificar la asociatividad, basta ver que las transformaciones lineales de $(A B) C$ y $A (B C)$ son iguales (vimos en ésta entrada que si dos matrices tienen la misma transformación asociada, entonces son iguales). Es decir, que para todo $X \in F^{q}$ se cumple que

$\begin{array}{r} ((A B) C) X = (A (B C)) X . \end{array}$

Por definición del producto, tenemos que

$\begin{array}{r} ((A B) C) X = (A B) (C X) = A (B (C (X)), \end{array}$

y desarrollando análogamente $A (B C) X$ tenemos

$\begin{array}{r} A (B C) X = A ((B C) X) = A (B (C (X)) . \end{array}$

Comparando ambas expresiones se sigue el resultado. Como mencionamos, esto se pudo haber probado usando la regla del producto, comparando la $(i, j)$ -ésima entrada de $(A B) C$ y la de $A (B C)$ , verificando que ambas son iguales a

$\begin{array}{r} \sum_{k, l} a_{i k} b_{k l} c_{l j} . \end{array}$

Observación. Gracias a la asociatividad del producto, podemos escribir $A B C$ en lugar de $(A B) C$ o de $A (B C)$ , aligerando la notación. Esto es más útil con más factores, por ejemplo el poder escribir $A B C D$ en lugar de $(A (B C)) D$ o $A (B (C D))$ . Así mismo, tampoco tenemos ambigüedad al definir el producto de cualquier número de matrices. Usaremos la notación

$\begin{array}{r} A^{n} = A \cdot A \cdot ⋱ \cdot A, \end{array}$

donde el lado derecho tiene $n$ factores. Esta es la $n$ -ésima potencia de una matriz cuadrada $A$ . Por construcción

$\begin{array}{r} A^{n} = A \cdot A^{n - 1} . \end{array}$

Y tomaremos como convención que $A^{0} = I_{n}$ para cualquier $A \in M_{n} (F)$ . Dejamos como tarea moral el verificar que $I_{n}$ actúa como un neutro para la multiplicación, es decir que para cualquier matriz $A$ de tamaño $m \times n$ se tiene

$\begin{array}{r} A \cdot I_{n} = A y I_{m} \cdot A = A . \end{array}$

Acabamos esta sección con un problema para practicar los conceptos vistos.

Problema. Sea $A (x) \in M_{3} (R)$ la matriz definida por

$\begin{array}{r} A (x) = (\begin{array}{c} 1 & x & x^{2} \\ 0 & 1 & 2 x \\ 0 & 0 & 1 \end{array}) . \end{array}$

Demuestra que $A (x_{1}) A (x_{2}) = A (x_{1} + x_{2})$ para cualesquiera $x_{1}, x_{2} \in R$ .

Solución. En este problema es más conveniente usar la regla del producto, que pensar a la composición de transformaciones. En todo problema es recomendable pensar en cuál de las formas del producto conviene más usar.

Usando la regla del producto, tenemos que

$\begin{aligned} A (x_{1}) A (x_{2}) & = (\begin{array}{c} 1 & x_{1} & x_{1}^{2} \\ 0 & 1 & 2 x_{1} \\ 0 & 0 & 1 \end{array}) (\begin{array}{c} 1 & x_{2} & x_{2}^{2} \\ 0 & 1 & 2 x_{2} \\ 0 & 0 & 1 \end{array}) \\ = (\begin{array}{c} 1 & x_{2} + x_{1} & x_{2}^{2} + 2 x_{1} x_{2} + x_{1}^{2} \\ 0 & 1 & 2 x_{2} + 2 x_{1} \\ 0 & 0 & 1 \end{array}) \\ = (\begin{array}{c} 1 & x_{1} + x_{2} & (x_{1} + x_{2})^{2} \\ 0 & 1 & 2 (x_{1} + x_{2}) \\ 0 & 0 & 1 \end{array}) . \end{aligned}$

Y el lado derecho es simplemente $A (x_{1} + x_{2})$ .

Más adelante…

Si bien en esta entrada definimos el producto de matrices y estudiamos su relación con la composición de matrices, esto no es más que el primer paso de un estudio más grande: Ahora nos podemos hacer preguntas sobre transformaciones lineales (por ejemplo, ¿será biyectiva o invertible?) y estudiarlas en términos de matrices y su producto. Más adelante en el curso entrará el concepto de determinante que jugará un papel fundamental para responder muchas de estas preguntas.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Realiza la operación ${(\begin{matrix} 2 & 1 & 0 \\ 1 & 2 & 0 \\ 0 & - 1 & 0 \end{matrix})}^{4} .$
Toma al vector canónico $e_{i}$ de $F^{n}$ pensado como matriz en $M_{1 n} (F)$ y al vector canónico $e_{j}$ de $F^{n}$ pensado como matriz en $M_{n 1} (F)$ . ¿Quién es el producto de matrices $e_{i} e_{j}$ ? ¿Quién es el producto de matrices $e_{j} e_{i}$ ?
Verifica las propiedades de compatibilidad con el producto por escalares y distributividad con respecto a la suma del producto de matrices.
Verifica que las matrices identidad actúan como neutro para la multiplicación de matrices.
Recuerda (o investiga) los axiomas de un anillo con unidad y verifica que las matrices cuadradas de tamaño $n$ forman un anillo con unidad para cualquier $n$ .

Entradas relacionadas

Ir a Álgebra Lineal I
Entrada anterior del curso: Problemas de vectores, matrices y matrices como transformaciones lineales
Siguiente entrada del curso: Matrices invertibles

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104721 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM»

Álgebra Lineal I: Cambio de base de transformaciones lineales

Por Leonardo Ignacio Martínez Sandoval

1 respuesta

Introducción

En la entrada anterior definimos las matrices de cambio de base. Vimos algunas de sus propiedades básicas y mostramos cómo nos pueden ayudar para resolver el primero de los siguientes dos problemas.

Supongamos que tenemos dos bases $B_{1}$ y $B_{2}$ de un espacio vectorial $V$ y que tomamos un vector $v$ en $V$ . Si ya sabemos la combinación lineal de elementos de $B_{1}$ que da $v$ , ¿cómo podemos saber la combinación lineal de elementos de $B_{2}$ que da $v$ ? En otras palabras, ¿cómo podemos pasar a $v$ de su expresión en base $B_{1}$ a su expresión en base $B_{2}$ ?
Supongamos que tenemos una transformación lineal $T : V \to W$ entre dos espacios vectoriales $V$ y $W$ , dos bases $B_{1}$ y $B_{2}$ de $V$ y dos bases $C_{1}$ y $C_{2}$ de $W$ . Si ya sabemos qué le hace $T$ a los elementos de $V$ en términos de las bases $B_{1}$ y $C_{1}$ , ¿cómo podemos saber qué hace $T$ en términos de las bases $B_{2}$ y $C_{2}$ ?

El objetivo de esta entrada es ver cómo con las matrices de cambio de base también podemos resolver el segundo problema. Después de hacer esto, hablaremos de una noción fundamental en álgebra lineal: la de matrices similares.

Matrices de cambio de base y transformaciones lineales

Las matrices de cambios de base nos ayudan a entender a las matrices de transformaciones lineales en bases diferentes.

Teorema. Sea $T : V \to W$ una transformación lineal entre espacios de dimensión finita $V$ y $W$ . Sean $B_{1}$ y $B_{2}$ bases de $V$ , y $C_{1}$ y $C_{2}$ bases de $W$ . Entonces ${Mat}_{C_{2}, B_{2}} (T) = {Mat}_{C_{2}} (C_{1}) {Mat}_{C_{1}, B_{1}} (T) {Mat}_{B_{1}} (B_{2}) .$

Observa cómo la elección de orden en la notación está rindiendo fruto. En el lado derecho «van apareciendo las bases» en el «orden natural» $C_{2}$ , $C_{1}$ , $B_{1}$ , $B_{2}$ .

Demostración. Sean $P = {Mat}_{C_{1}} (C_{2})$ y $Q = {Mat}_{B_{1}} (B_{2})$ . Por un resultado de la entrada anterior, $P$ es la matriz que representa a la transformación identidad en $W$ con respecto a las bases $C_{1}$ y $C_{2}$ , es decir, $P = {Mat}_{C_{1}, C_{2}} ({id}_{W})$ .

Por cómo son las matrices de composiciones de transformaciones lineales, y usando que ${id}_{W} \circ T = T$ , tenemos que ${Mat}_{C_{1}, C_{2}} ({id}_{W}) {Mat}_{C_{2}, B_{2}} (T) = {Mat}_{C_{1}, B_{2}} (T) .$

De manera análoga, $Q$ es la matriz que representa a la transformación identidad en $V$ con respecto a las bases $B_{1}$ y $B_{2}$ , de donde tenemos que ${Mat}_{C_{1}, B_{1}} (T) {Mat}_{B_{1}, B_{2}} ({id}_{V}) = {Mat}_{C_{1}, B_{2}} (T) .$

De esta forma, $P {Mat}_{C_{2}, B_{2}} (T) = {Mat}_{C_{1}, B_{2}} (T) = {Mat}_{C_{1}, B_{1}} (T) Q .$ El resultado se obtiene multiplicando por la izquierda ambos lados de esta ecuación por $P^{- 1} = {Mat}_{C_{2}} (C_{1})$ .

En la siguiente entrada se verán varios ejemplos que involucran crear matrices para transformaciones lineales, matrices de cambios de base y multiplicarlas para entender una transformación lineal en distintas bases.

Por el momento, dejamos únicamente un corolario del teorema anterior, para el caso en el que tenemos una transformación lineal de un espacio vectorial a sí mismo expresado en términos de dos bases.

Corolario. Sea $T : V \to V$ una transformación lineal de un espacio vectorial $V$ de dimensión finita a sí mismo. Sean $B$ y $B^{'}$ bases de $V$ y $P$ la matriz de cambio de base de $B$ a $B^{'}$ . Entonces ${Mat}_{B^{'}} (T) = P^{- 1} {Mat}_{B} (T) P .$

Matrices similares

Definición. Decimos que dos matrices $A$ y $B$ en $M_{n} (F)$ son similares o conjugadas si existe una matriz invertible $P$ en $M_{n} (F)$ tal que $B = P^{- 1} A P$ .

En otras palabras, $A$ y $B$ son matrices similares si representan a una misma transformación lineal en diferentes bases.

Proposición. La relación «ser similares» es una relación de equivalencia en $M_{n} (F)$ .

Demostración. Toda matriz es similar a sí misma usando $P = I_{n}$ , la identidad. Si $A$ y $B$ son similares con matriz invertible $P$ , entonces $B$ y $A$ son similares con matriz invertible $P^{- 1}$ . Si $A$ y $B$ son similares con matriz invertible $P$ y $B$ y $C$ son similares con matriz invertible $Q$ , notemos que $A = P^{- 1} B P = P^{- 1} (Q^{- 1} C Q) P = (Q P)^{- 1} C (Q P)$ , de modo que $A$ y $C$ son similares con matriz invertible $Q P$ .

¿Por qué es importante saber si dos matrices son similares? Resulta que dos matrices similares comparten muchas propiedades, como su traza, su determinante, su rango, etc. Para algunas matrices es más sencillo calcular estas propiedades. Así que una buena estrategia en álgebra lineal es tomar una matriz $A$ «complicada» y de ahí encontrar una matriz similar $B$ «más simple», y usar $B$ para encontrar propiedades de $A$ .

Veamos un ejemplo de esto. Mediante un sencillo argumento inductivo se puede mostrar lo siguiente.

Proposición. Si $A$ y $B$ son matrices similares con $A = P^{- 1} B P$ , entonces $A^{n} = P^{- 1} B^{n} P$ .

Si $B$ fuera una matriz diagonal, entonces es fácil encontrar $B^{n}$ : basta con elevar cada una de las entradas de su diagonal a la $n$ (lo cual es mucho más fácil que hacer productos de matrices). Así, esto da una forma muy fácil de encontrar $A^{n}$ : basta con encontrar $B^{n}$ , y luego hacer dos multiplicaciones de matrices más, por $P^{- 1}$ a la izquierda y por $P$ a la derecha.

Más adelante…

En estas últimas dos entradas aprendimos a hacer «cambios de base», tanto para coordenadas, como para formas matriciales. También, introdujimos el concepto de similitud de matrices. Cuando $A$ es una matriz similar a una matriz diagonal, decimos que $A$ es diagonalizable. Que una matriz sea diagonalizable trae muchas ventajas. Como ya mencionamos, una de ellas es poder elevar la matriz a potencias de manera sencilla. Otra ventaja es que en las matrices diagonalizables es sencillo calcular rangos, determinantes y otras invariantes de álgebra lineal.

Una parte importante de lo que resta del curso consistirá en entender por qué las matrices simétricas con entradas reales son diagonalizables. El teorema principal del curso (el teorema espectral), consistirá en mostrar que toda matriz simétrica con entradas reales es diagonalizable mediante matrices ortogonales. Para poder demostrarlo, necesitaremos primero estudiar teoría geométrica de espacios vectoriales y teoría de determinantes.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Deduce el corolario del teorema principal de esta entrada.
Considera $R [x]_{2}$ de polinomios con coeficientes reales y grado a lo más dos. Sea $T : R [x]_{2}$ la transformación tal que $T (p) = p^{'}$ , el polinomio derivado. Encuentra la matriz que representa a la transformación en la base ${1 + x + x^{2}, 1 + 2 x, 1}$ y la matriz que representa a la transformación en la base ${1, x, x^{2}}$ . Encuentra también la matriz de cambio de base de la primera a la segunda. Verifica que se cumple la conclusión del corolario.
Sean $A$ y $B$ matrices similares. Muestra que $A$ es invertible si y sólo si $B$ lo es.
Sean $A$ y $B$ matrices similares. Muestra que $A$ y $B$ tienen la misma traza.
Completa el argumento inductivo para demostrar la última proposición.
Considera la matriz con entradas complejas $A = (\begin{matrix} 1 & 0 & 0 \\ 0 & i & 0 \\ 0 & 0 & - 1 \end{matrix})$ . Encuentra $A^{105}$ .

Entradas relacionadas

Ir a Álgebra Lineal I
Entrada anterior del curso: Matrices de cambio de base
Siguiente entrada del curso: Problemas de cambio de base

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104721 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM»

Álgebra Lineal I: Matrices de cambio de base

Por Leonardo Ignacio Martínez Sandoval

10 respuestas

Introducción

Anteriormente platicamos de cómo al elegir una base ordenada $B$ de un espacio vectorial $V$ de dimensión finita $n$ , podemos expresar a cada uno de sus vectores en términos de «coordenadas», que vienen de los coeficientes de la combinación lineal de elementos de $B$ que da el vector. Así mismo, vimos cómo podemos comenzar con una transformación lineal $T : V \to W$ entre espacios vectoriales $V$ y $W$ y de ahí obtener una «matriz que la represente». Para ello, necesitamos elegir bases ordenadas $B_{V}$ y $B_{W}$ de $V$ y $W$ respectivamente. Tanto las coordenadas, como las matrices que representan a transformaciones lineales, dependen fuertemente de las bases ordenadas elegidas. En esta entrada hablaremos de las matrices de cambio de base, pues nos ayudarán a pasar de unas coordenadas a otras.

Siento más concretos, es posible que en algunas aplicaciones de álgebra lineal tengamos una transformación $T : V \to W$ , y que los vectores de $V$ o los de $W$ los tengamos que entender en más de una base. Así, los dos siguientes problemas aparecen frecuentemente:

Supongamos que tenemos dos bases (ordenadas) $B_{1}$ y $B_{2}$ de un espacio vectorial $V$ y que tomamos un vector $v$ en $V$ . Si ya sabemos la combinación lineal de elementos de $B_{1}$ que da $v$ , ¿cómo podemos saber la combinación lineal de elementos de $B_{2}$ que da $v$ ? En otras palabras, ¿cómo podemos pasar a $v$ de su expresión en base $B_{1}$ a su expresión en base $B_{2}$ ?
Supongamos que tenemos una transformación lineal $T : V \to W$ entre dos espacios vectoriales $V$ y $W$ , dos bases (ordenadas) $B_{1}$ y $B_{2}$ de $V$ y dos bases (ordenadas) $C_{1}$ y $C_{2}$ de $W$ . Si ya sabemos qué le hace $T$ a los elementos de $V$ en términos de las bases $B_{1}$ y $C_{1}$ , ¿cómo podemos saber qué hace $T$ en términos de las bases $B_{2}$ y $C_{2}$ ?

La herramienta que necesitamos para responder ambos problemas se le conoce como matrices de cambio de base. El objetivo de esta entrada es definir estas matrices, ver algunas propiedades básicas que cumplen y ver cómo nos ayudan a resolver el primero de los problemas de aquí arriba. En una segunda entrada veremos cómo también sirven para resolver el segundo.

Matrices de cambio de base

Definición. Sea $V$ un espacio vectorial de dimensión $n$ sobre el campo $F$ . Sean $B = (v_{1}, \dots, v_{n})$ y $B^{'} = (v_{1}', \dots, v_{n}^{'})$ dos bases ordenadas de $V$ . La matriz de cambio de base de $B$ a $B^{'}$ es la matriz $P = [p_{i j}]$ en $M_{n} (F)$ cuya columna $j$ tiene como entradas a las coordenadas de $v_{j}^{'}$ escrito en términos de la base $B$ . En otras palabras, las entradas $p_{1 j}, \dots, p_{n j}$ de la $j$ -ésima columna de $P$ son los únicos elementos de $F$ para los cuales $v_{j}^{'} = p_{1 j} v_{1} + \dots + p_{n j} v_{n},$ para toda $j = 1, 2, \dots, n$ .

Ejemplo. Considera la base ordenada $B = (1, x, x^{2})$ de $R_{2} [x]$ , el espacio vectorial de polinomios de coeficientes reales grado a lo más $2$ . Veremos que $B^{'} = (3 x^{2}, 2 x, 1)$ es también una base de $R_{2} [x]$ . Encontraremos la matriz de cambio de base de $B$ a $B^{'}$ y la matriz de cambio de base de $B^{'}$ a $B$ .

La dimensión de $R_{2} [x]$ es $3$ y $B^{'}$ tiene $3$ elementos, así que basta ver que los elementos de $B^{'}$ son linealmente independientes para ver que $B^{'}$ es base. Una combinación lineal $a (3 x^{2}) + b (2 x) + c (1) = 0$ es equivalente a que $3 a x^{2} + 2 b x + c = 0$ , lo cual sucede si y sólo si $a = b = c = 0$ . Esto muestra que $B^{'}$ es base.

Para encontrar a la matriz de cambio de base de $B$ a $B^{'}$ lo que tenemos que hacer es escribir a los elementos de $B^{'}$ como combinación lineal de los elementos de $B$ . Esto lo hacemos de la siguiente manera (recuerda que el orden es importante):

$\begin{aligned} 3 x^{2} & = 0 \cdot 1 + 0 \cdot x + 3 \cdot x^{2} \\ 2 x & = 0 \cdot 1 + 2 \cdot x + 0 \cdot x^{2} \\ 1 & = 1 \cdot 1 + 0 \cdot x + 0 \cdot x^{2} . \end{aligned}$

Como los coeficientes de $3 x^{2}$ en la base ordenada $B$ son $0$ , $0$ y $3$ , entonces la primer columna de la matriz de cambio de base será $(\begin{matrix} 0 \\ 0 \\ 3 \end{matrix})$ . Argumentando de manera similar para $2 x$ y $1$ , tenemos que la matriz de cambio de base de $B$ a $B^{'}$ es $(\begin{matrix} 0 & 0 & 1 \\ 0 & 2 & 0 \\ 3 & 0 & 0 \end{matrix}) .$

Para encontrar a la matriz de cambio de base de $B^{'}$ a $B$ , expresamos a los elementos de $B$ en términos de la base $B^{'}$ como sigue:

$\begin{aligned} 1 & = 0 \cdot (3 x^{2}) + 0 \cdot (2 x) + 1 \cdot 1 \\ x & = 0 \cdot (3 x^{2}) + \frac{1}{2} \cdot (2 x) + 0 \cdot 1 \\ x^{2} & = \frac{1}{3} \cdot (3 x^{2}) + 0 \cdot (2 x) + 0 \cdot 1. \end{aligned}$

En este caso fue sencillo hacerlo, pero en otros problemas frecuentemente esto se hace resolviendo un sistema de ecuaciones.

De esta manera, tenemos que la matriz de cambio de base de $B^{'}$ a $B$ es $(\begin{matrix} 0 & 0 & \frac{1}{3} \\ 0 & \frac{1}{2} & 0 \\ 1 & 0 & 0 \end{matrix}) .$

$△$

Cambio de coordenadas usando matrices de cambio de base

Las matrices de cambio de base nos ayudan a responder la primer pregunta que planteamos al inicio de esta entrada. Si conocemos las coordenadas de un vector en una base, podemos usar la matriz de cambio de base para encontrar las coordenadas del vector en otra base.

Proposición. Sea $V$ un espacio vectorial de dimensión $n$ , $B = (v_{1}, \dots, v_{n})$ , $B^{'} = (v_{1}', \dots, v_{n}^{'})$ bases ordenadas de $V$ y $P$ la matriz de cambio de base de $B$ a $B^{'}$ . Supongamos que el vector $v$ de $V$ se escribe en base $B$ como $v = c_{1} v_{1} + c_{2} v_{2} + \dots + c_{n} v_{n}$ y en base $B^{'}$ como $v = c_{1}^{'} v_{1}^{'} + c_{2}^{'} v_{2}^{'} + \dots + c_{n}^{'} v_{n}^{'} .$ Entonces: $P (\begin{matrix} c_{1}' \\ ⋮ \\ c_{n}^{'} \end{matrix}) = (\begin{matrix} c_{1} \\ ⋮ \\ c_{n} \end{matrix}) .$

En otras palabras, la matriz $P$ de cambio de base de $B$ a $B^{'}$ manda las coordenadas de un vector en base $B^{'}$ a coordenadas en base $B$ al multiplicar por la izquierda. Ojo: para construir $P$ expresamos a $B^{'}$ en términos de $B$ , pero lo que hace $P$ es expresar a alguien de coordenadas en $B^{'}$ a coordenadas en $B$ .

Demostración. El vector de coordenadas de $v_{j}^{'}$ escrito en base $B^{'}$ es el vector canónico $e_{j}$ de $F^{n}$ . Además, $P e_{j}$ es la $j$ -ésima columna de $P$ , que por construcción es el vector de coordenadas de $v_{j}^{'}$ en la base $B$ . Así, el resultado es cierto para los vectores $v_{j}^{'}$ de la base $B^{'}$ . Para cualquier otro vector $v$ , basta expresarlo en términos de la base $B^{'}$ y usar la linealidad de asignar el vector de coordenadas y la linealidad de $P$ .

Problema. Escribe a los vectores $v_{1} = (4, 3, 5, 2)$ , $v_{2} = (2, 2, 2, 2)$ y $v_{3} (0, 0, 0, 1)$ de $R^{4}$ como combinación lineal de los elementos de la base $B$ de $R^{4}$ conformada por los vectores $(1, 0, 0, 0)$ , $(1, 1, 0, 0)$ , $(1, 1, 1, 0)$ y $(1, 1, 1, 1)$ .

Solución. Conocemos las coordenadas de $v_{1}, v_{2}, v_{3}$ en la base canónica $(1, 0, 0, 0)$ , $(0, 1, 0, 0)$ , $(0, 0, 1, 0)$ , $(0, 0, 0, 1)$ . De hecho, el vector de coordenadas de $v_{1}$ es exactamente $v_{1}$ (esto es algo que sucede pues estamos trabajando en $R^{4}$ ). Lo que nos estan pidiendo son las coordenadas de $v_{1}, v_{2}, v_{3}$ en la base $B$ . Nos gustaría usar la proposición anterior. Para ello, necesitamos encontrar la matriz de cambio de base de $B$ a la base canónica. Escribamos entonces a la base canónica en términos de los vectores de $B$ :

$\begin{aligned} (1, 0, 0, 0) & = 1 \cdot (1, 0, 0, 0) + 0 \cdot (1, 1, 0, 0) + 0 \cdot (1, 1, 1, 0) + 0 \cdot (1, 1, 1, 1) \\ (0, 1, 0, 0) & = - 1 \cdot (1, 0, 0, 0) + 1 \cdot (1, 1, 0, 0) + 0 \cdot (1, 1, 1, 0) + 0 \cdot (1, 1, 1, 1) \\ (0, 0, 1, 0) & = 0 \cdot (1, 0, 0, 0) - 1 \cdot (1, 1, 0, 0) + 1 \cdot (1, 1, 1, 0) + 0 \cdot (1, 1, 1, 1) \\ (0, 0, 0, 1) & = 0 \cdot (1, 0, 0, 0) + 0 \cdot (1, 1, 0, 0) - 1 \cdot (1, 1, 1, 0) + 1 \cdot (1, 1, 1, 1) \end{aligned}$

A estas coordenadas las ponemos como columnas para encontrar la matriz de cambio de base de $B$ a la base canónica:
$(\begin{matrix} 1 & - 1 & 0 & 0 \\ 0 & 1 & - 1 & 0 \\ 0 & 0 & 1 & - 1 \\ 0 & 0 & 0 & 1 \end{matrix}) .$

Para encontrar las coordenadas de $v_{1}, v_{2}, v_{3}$ en términos de la base $B$ , basta con multiplicar esta matriz a la izquierda para cada uno de ellos:

$(\begin{matrix} 1 & - 1 & 0 & 0 \\ 0 & 1 & - 1 & 0 \\ 0 & 0 & 1 & - 1 \\ 0 & 0 & 0 & 1 \end{matrix}) (\begin{matrix} 4 \\ 3 \\ 5 \\ 2 \end{matrix}) = (\begin{matrix} 1 \\ - 2 \\ 3 \\ 2 \end{matrix}),$

$(\begin{matrix} 1 & - 1 & 0 & 0 \\ 0 & 1 & - 1 & 0 \\ 0 & 0 & 1 & - 1 \\ 0 & 0 & 0 & 1 \end{matrix}) (\begin{matrix} 2 \\ 2 \\ 2 \\ 2 \end{matrix}) = (\begin{matrix} 0 \\ 0 \\ 0 \\ 2 \end{matrix})$ y

$(\begin{matrix} 1 & - 1 & 0 & 0 \\ 0 & 1 & - 1 & 0 \\ 0 & 0 & 1 & - 1 \\ 0 & 0 & 0 & 1 \end{matrix}) (\begin{matrix} 0 \\ 0 \\ 0 \\ 1 \end{matrix}) = (\begin{matrix} 0 \\ 0 \\ - 1 \\ 1 \end{matrix}) .$

En efecto, se puede verificar que estos nuevos vectores dan las combinaciones lineales de la base $B$ que hacen a $v_{1}$ , $v_{2}$ y $v_{3}$ , por ejemplo, para $v_{1}$ tenemos: $(4, 5, 3, 2) = (1, 0, 0, 0) - 2 (1, 1, 0, 0) + 3 (1, 1, 1, 0) + 2 (1, 1, 1, 1) .$

$△$

Matrices de cambio de base como la forma matricial de una transformación lineal

A la matriz de cambio de base de $B$ a $B^{'}$ la denotamos por ${Mat}_{B} (B^{'})$ .

Una observación crucial es que podemos pensar a las matrices de cambio de base en un espacio vectorial $V$ justo como formas matriciales correspondientes a una transformación lineal específica. De hecho, la transformación lineal que le corresponde es muy bonita: es la identidad ${id}_{V}$ que manda a cada vector de $V$ a sí mismo.

De manera más concreta, si $B$ y $B^{'}$ son bases de $V$ y ${Mat}_{B} (B^{'})$ es la matriz de cambio de base de $B$ a $B^{'}$ , entonces ${Mat}_{B} (B^{'}) = {Mat}_{B, B^{'}} ({id}_{V}) .$ A estas alturas tienes todas las herramientas necesarias para demostrar esto.

¿Qué sucede si ahora tenemos tres bases $B$ , $B^{'}$ y $B »$ de $V$ y componemos a la identidad consigo misma? Utilizando los argumentos de la entrada anterior, la matriz correspondiente a la composición es el producto de las matrices de cada transformación. Juntando esto con la observación anterior, tenemos la siguiente propiedad para matrices de cambio de base:

${Mat}_{B} (B ») = {Mat}_{B} (B^{'}) \cdot {Mat}_{B^{'}} (B ») .$

Finalmente, ¿qué sucede si en la igualdad anterior ponemos $B » = B$ ? Al lado izquierdo tenemos la matriz de cambio de base de $B$ a sí misma, que puedes verificar que es la identidad. Al lado derecho tenemos al producto de la matriz de cambio de base de $B$ a $B^{'}$ con la matriz de cambio de $B^{'}$ a $B$ . Esto muestra que las matrices de cambio de base son invertibles.

Resumimos todas estas observaciones en la siguiente proposición:

Proposición. Sean $B$ , $B^{'}$ y $B »$ bases del espacio vectorial de dimensión finita $V$ .

La matriz de cambio de base de $B$ a $B^{'}$ corresponde a la matriz de la transformación identidad de $V$ a $V$ , en donde el primer $V$ lo pensamos con la base $B^{'}$ y al segundo con la base $B$ .
El producto de matrices de cambio de base de $B$ a $B^{'}$ y de $B^{'}$ a $B »$ es la matriz de cambio de base de $B$ a $B »$ .
La matriz de cambio de base de $B$ a $B^{'}$ es invertible, y su inversa es la de cambio de base de $B^{'}$ a $B$ .

En la próxima entrada veremos cómo las matrices de cambio de base también nos ayudan a entender transformaciones lineales bajo distintas bases.

Más adelante…

En esta entrada ya vimos cómo cambian las coordenadas de un vector cuando cambiamos de base. Lo que haremos en la siguiente entrada es estudiar cómo cambia la forma matricial de una transformación lineal cuando cambiamos las bases de su espacio vectorial origen y su espacio vectorial destino.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero te servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

¿Qué sucede en el primer ejemplo si multiplicas ambas matrices de cambio de base que encontramos?
En el segundo ejemplo, encuentra la matriz de cambio de base de la base canónica a la matriz $B$
Considera las cuatro matrices de $2 \times 2$ que puedes formar colocando tres unos y un cero. Muestra que estas cuatro matrices forman una base $B$ de $M_{2, 2} (R)$ . Determina la matriz de cambio de base de $B$ a la base canónica de $M_{2, 2} (R)$ . Ojo: Una cosa son los elementos del espacio vectorial y otra cosa van a ser las matrices de cambio de base. Como $M_{2, 2} (R)$ es de dimensión $4$ , la matriz de cambio de base que tienes que determinar en realidad es de $4 \times 4$ .
Da una demostración de que, en efecto ${Mat}_{B} (B^{'}) = {Mat}_{B, B^{'}} ({id}_{V}) .$
Verifica que la matriz de cambio de base $B$ a sí misma es la identidad.

Entradas relacionadas

Ir a Álgebra Lineal I
Entrada anterior del curso: Problemas de transformaciones lineales, vectores independientes y forma matricial
Siguiente entrada del curso: Cambio de base de transformaciones lineales

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104721 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM»