Introducción
En esta nueva entrada demostraremos algunas de las propiedades del producto cartesiano. Discutiremos sobre si esta operación en conjuntos es conmutativa, además de ver el comportamiento del producto cartesiano con respecto a las operaciones que definimos antes: unión, intersección, diferencia y diferencia simétrica.
Producto cartesiano
Recordemos la definición de producto cartesiano.
Definición. Sean $A$ y $B$ conjuntos cualesquiera, definimos el producto cartesiano de $A$ y $B$, como:
$A\times B=\set{(a,b): a\in A\ y\ b\in B}$.
Ejemplo.
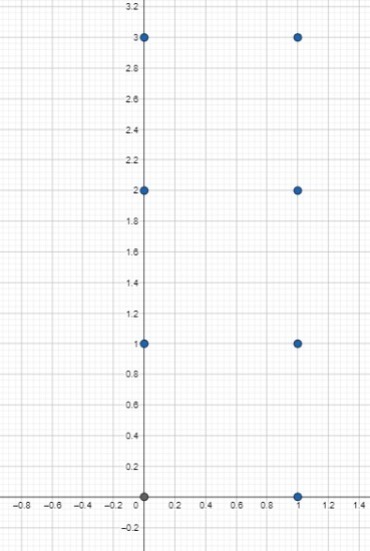
Consideremos los conjuntos $A=\set{0,1}$ y $B=\set{0,1,2,3}$. Tenemos que $A\times B=\set{(0,0),(0,1), (0,2), (0,3), (1,0), (1,1), (1,2), (1,3)}$. De hecho, podemos representar geométricamente a este conjunto como se muestra en la siguiente imagen:
Por supuesto, esta representación es un poco informal pues estamos usando la recta numérica con números reales (que no hemos dicho qué son) y estamos asumiendo cierto orden (del cuál no hemos hablado). Por el momento, piensa que esta representación es sólo para conectar la idea de producto cartesiano con conceptos que has visto en otros cursos.
$\square$
Conmutatividad del producto cartesiano
En general el producto cartesiano no es conmutativo, es decir, si $A$ y $B$ son conjuntos, no necesariamente es cierto que $A\times B=B\times A$.
Ejemplo.
Sean $A=\set{\emptyset}$ y $B=\set{\set{\emptyset}}$, tenemos que:
$A\times B=\set{(\emptyset, \set{\emptyset})}$.
Por otro lado,
$B\times A=\set{(\set{\emptyset},\emptyset)}$.
Dado que tanto $A\times B$ y $B\times A$ sólo tienen un elemento, para que pase que $A\times B=B\times A$, tendría que ocurrir que $(\emptyset,\set{\emptyset})=(\set{\emptyset}, \emptyset)$. Usando el teorema que vimos en la entrada pasada tendríamos que $\emptyset=\set{\emptyset}$ y $\set{\emptyset}=\emptyset$, lo cual no ocurre. Por lo tanto, $A\times B\not=B\times A$.
$\square$
Veamos ahora bajo qué condición el producto cartesiano sí conmuta.
Proposición. Sean $A$ y $B$ conjuntos. Entonces $A\times B=B\times A$ si y sólo si $A=B$ o $A=\emptyset$ o $B=\emptyset$.
Demostración.
$\rightarrow$] Supongamos que $A$ y $B$ son conjuntos tales que $A\times B=B\times A$.
Caso 1: Si $A=\emptyset$ se cumple la proposición.
Caso 2: Si $B=\emptyset$ se cumple la proposición.
Caso 3: Si $A$ y $B$ son conjuntos no vacíos. Sea $x\in A$. Como $B\not=\emptyset$, existe $y\in B$ y así la pareja $(x,y)\in A\times B$. Por hipótesis $A\times B=B\times A$, por lo que $(x,y)\in B\times A$, esto es $x\in B$ y $y\in A$. En particular, $x\in B$ y por lo tanto, $A\subseteq B$.
Para ver que $B\subseteq A$ seguimos un argumento análogo al anterior. Por lo tanto, $A=B$.
$\leftarrow$] Si $A=B$, tenemos que $A\times B=A\times A=B\times B= B\times A$. Si $A=\emptyset$, entonces por definición de producto cartesiano $A\times B=\emptyset\times B=\emptyset$ y $B\times A=B\times \emptyset= \emptyset$, por lo que $A\times B=B\times A$. Análogamente si $B=\emptyset$.
$\square$
Producto cartesiano y unión
Las siguientes dos proposiciones verifican que el producto cartesiano se distribuye sobre la unión.
Proposición. Para $A,B,C$ conjuntos se cumple que $(A\cup B)\times C=(A\times C)\cup (B\times C)$.
Demostración.
Se tiene que $(x,y)\in (A\cup B)\times C$
si y sólo si $x\in A\cup B$ y $y\in C$
si y sólo si $(x\in A$ o $x\in B)$ y $y\in C$
si y sólo si $(x\in A$ y $y\in C)$ o $(x\in B$ y $y\in C)$
si y sólo si $(x,y)\in A\times C$ o $(x,y)\in B\times C$
si y sólo si $(x, y)\in (A\times C)\cup (B\times C)$.
$\square$
Proposición. Para $A,B,C$ conjuntos se cumple que $A\times (B\cup C)=(A\times B)\cup (A\times C)$.
Demostración.
Se tiene que $(x,y)\in A\times (B\cup C)$
si y sólo si $x\in A$ y $y\in B\cup C$
si y sólo si $x\in A$ y $(y\in B$ o $y\in C)$
si y sólo si $(x\in A$ y $y\in B)$ o $(x\in A$ y $y\in C)$
si y sólo si $(x,y)\in A\times B$ o $(x,y)\in A\times C$
si y sólo si $(x, y)\in (A\times B)\cup (A\times C)$.
$\square$
Proposición. Para cualesquiera $A, B, C, D$ conjuntos no vacíos ocurre que $(A\times C)\cup (B\times D)\subseteq (A\cup B)\times (C\cup D)$.
Demostración.
Sean $A, B, C, D$ conjuntos no vacíos. Tomemos $(x,y)\in (A\times C)\cup (B\times D)$ arbitrario, entonces $(x,y)\in A\times C$ o $(x,y)\in B\times D$.
Si $(x, y)\in A\times C$, entonces $x\in A$ y $y\in C$. Luego, como $A\subseteq A\cup B$ y $C\subseteq C\cup D$ se sigue que $x\in A\cup B$ y $y\in C\cup D$. Así, $(x,y)\in (A\cup B)\times (C\cup D)$.
Si $(x, y)\in B\times D$, entonces $x\in B$ y $y\in D$. Luego, como $B\subseteq A\cup B$ y $D\subseteq C\cup D$ se sigue que $x\in A\cup B$ y $y\in C\cup D$. Así, $(x,y)\in (A\cup B)\times (C\cup D)$.
$\square$
Producto cartesiano e intersección
Con la siguientes dos demostraciones podremos ver que el producto cartesiano se distribuye sobre la intersección.
Proposición. Para $A,B,C$ conjuntos se cumple que $(A\cap B)\times C=(A\times C)\cap (B\times C)$.
Demostración.
Se tiene que $(x,y)\in (A\cap B)\times C$
si y sólo si $x\in A\cap B$ y $y\in C$
si y sólo si $(x\in A$ y $x\in B)$ y $y\in C$
si y sólo si $(x\in A$ y $y\in C)$ y $(x\in B$ y $y\in C)$
si y sólo si $(x,y)\in A\times C$ y $(x,y)\in B\times C$
si y sólo si $(x, y)\in (A\times C)\cap (B\times C)$.
$\square$
Proposición. Para $A,B,C$ conjuntos se cumple que $A\times (B\cap C)=(A\times B)\cap (A\times C)$.
Demostración.
Se tiene que $(x,y)\in A\times (B\cap C)$
si y sólo si $x\in A$ y $y\in B\cap C$
si y sólo si $x\in A$ y $(y\in B$ y $y\in C)$
si y sólo si $(x\in A$ y $y\in B)$ y $(x\in A$ y $y\in C)$
si y sólo si $(x,y)\in A\times B$ y $(x,y)\in A\times C$
si y sólo si $(x, y)\in (A\times B)\cap (A\times C)$.
$\square$
Proposición. Para cualesquiera $A, B, C, D$ conjuntos ocurre que $(A\times C)\cap (B\times D)= (A\cap B)\times (C\cap D)$.
Demostración.
Sean $A, B, C, D$ conjuntos. Tenemos que:
$(x,y)\in (A\times C)\cap (B\times D)$
si y sólo si $(x,y)\in A\times C$ y $(x,y)\in B\times D$
si y sólo si $(x\in A$ y $y\in C)$ y $(x\in B$ y $y\in D)$
si y sólo si $(x\in A$ y $x\in B)$ y $(y\in C$ y $y\in D)$
si y sólo si $x\in A\cap B$ y $y\in C\times D$
si y sólo si $(x,y)\in (A\cap B)\times (C\cap D)$.
$\square$
Producto cartesiano y diferencia
Con los siguientes resultados probamos que el producto cartesiano se distribuye sobre la diferencia.
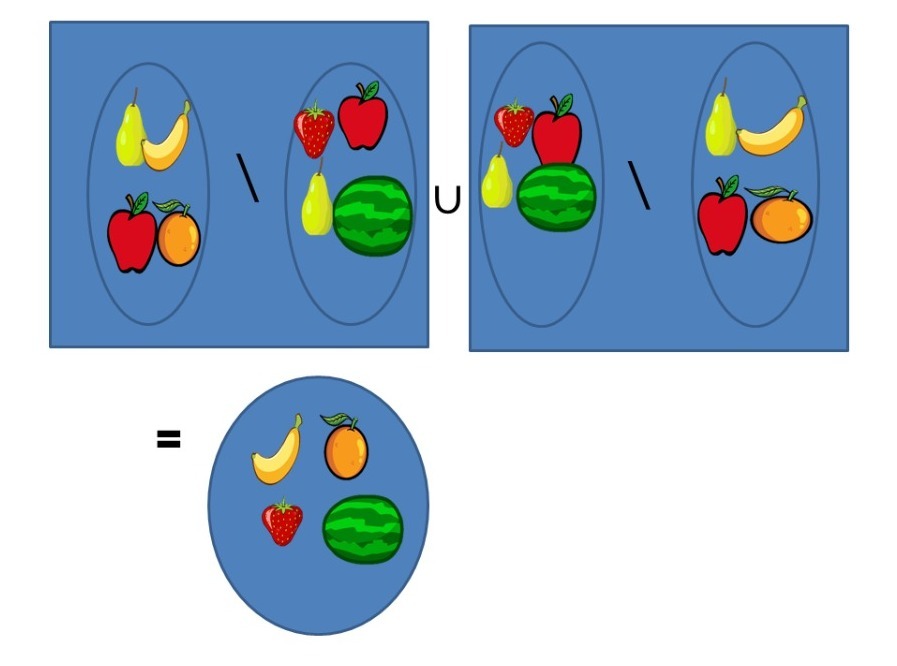
Proposición. Sean $A, B, C$ conjuntos. Se tiene que $A\times (B\setminus C)= (A\times B)\setminus (A\times C)$.
Demostración.
Se tiene que $(x,y)\in A\times (B\setminus C)$
si y sólo si $x\in A$ y $y\in B\setminus C$
si y sólo si $x\in A$ y ($y\in B$ y $y\notin C$)
si y sólo si $(x\in A$ y $y\in B)$ y $(x\in A$ y $y\notin C)$
si y sólo si $(x,y)\in A\times B$ y $(x,y)\notin A\times C$
si y sólo si $(x,y)\in (A\times B)\setminus (A\times C)$.
$\square$
Proposición. Para $A,B,C$ conjuntos se cumple que $(A\setminus B)\times C=(A\times C)\setminus (B\times C)$.
Demostración.
Se tiene que $(x,y)\in (A\setminus B)\times C$
si y sólo si $x\in A\setminus B$ y $y\in C$
si y sólo si $(x\in A$ y $x\notin B)$ y $y\in C$
si y sólo si $(x\in A$ y $y\in C)$ y $(x\notin B$ y $y\in C)$
si y sólo si $(x,y)\in A\times C$ y $(x,y)\notin B\times C$
si y sólo si $(x, y)\in (A\times C)\setminus (B\times C)$.
$\square$
Producto cartesiano y diferencia simétrica
La siguiente proposición demuestra que el producto cartesiano distribuye a la diferencia simétrica. Como ya demostramos propiedades de cómo interactúa el producto cartesiano con la unión, intersección y diferencia, podremos dar una demostración muy breve usando álgebra de conjuntos.
Proposición. Sean $A, B, C$ conjuntos. Se tiene que $A\times (B\triangle C)= (A\times B)\triangle (A\times C)$.
Demostración. Procedemos por álgebra de conjuntos:
\begin{align*}
A\times (B\triangle C) &= A\times ((B\cup C)\setminus (B\cap C))\\
&=(A\times (B\cup C))\setminus (A\times (B\cap C))\\
&=((A\times B)\cup (A\times C))\setminus (A\times (B\cap C))\\
&=((A\times B)\cup (A\times C) \setminus ((A\times B)\cap (A\times C))\\
&=(A\times B)\triangle (A\times C).
\end{align*}
$\square$
Tarea moral
- Demuestra que $A\times B=\emptyset$ si y sólo si $A=\emptyset$ o $B=\emptyset$.
- Muestra que si $C\times D\not=\emptyset$ entonces $C\times D\subseteq A\times B$ si y sólo si $C\subseteq A$ y $D\subseteq B$.
- Muestra que no siempre se da la igualdad $(A\times C)\cup (B\times D)= (A\cup B)\times (C\cup D)$.
- Demuestra que $(A\cup B)\times (C\cup D)=(A\times C)\cup (B\times D)\cup (A\times D)\cup (B\times C)$.
- Muestra que $(X\times Y)\setminus (B\times C)=((X\setminus B)\times Y)\cup(X\times (Y\setminus C))$.
- Demuestra que $(A\triangle B)\times C=(A\times C)\triangle (B\times C)$.
Más adelante…
En la siguiente entrada definiremos qué es una relación. Para ello utilizaremos el concepto de producto cartesiano y pareja ordenada. Resultará que una relación es un subconjunto de un producto cartesiano, por lo que es importante que comprendas bien el concepto de producto cartesiano que hemos visto en las últimas dos entradas.
Entradas relacionadas
- Ir a Teoría de los Conjuntos I
- Entrada anterior: Teoría de los Conjuntos I: Parejas ordenadas y producto cartesiano
- Siguiente entrada: Teoría de los Conjuntos I: Relaciones
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»