Introducción

Habiendo establecido los axiomas de la teoría de conjuntos, ahora vamos a empezar a trabajar con ellos. En particular en esta entrada nos intereseran tres operaciones: La intersección, la unión y el complemento de conjuntos.

Pensando en conjuntos

Para empezar a hablar de las operaciones que usaremos, pues primero debemos de ponernos de acuerdo a qué nos referiremos y qué queremos construir cuando hablamos de operaciones. Para estos fines, nos interesa qué podemos hacer con los conjuntos y cómo se relacionan los unos a los otros. Por ejemplo: ¿Habrá algunos elementos que pertenezcan a dos conjuntos a la vez? o ¿Qué pasa con el con elementos que sí están en unos conjuntos y en otros no? Pues veremos algunas operaciones, sin embargo hay que ver la idea intuitiva detrás de algunos de ellos.

Será bueno que de igual manera tengas los axiomas a la mano, pues serán útiles para la definición de algunas de estas operaciones:

Axioma 1	Existe un conjunto.
Axioma 2	Podemos hacer conjuntos a partir de proposiciones que cumplen o no cumplen elementos de algún conjunto.
Axioma 3	Si $X$ y $Y$ son conjuntos, entonces $\{X,Y\}$ es un conjunto.
Axioma 4	Dos conjuntos son iguales si todos sus elementos son iguales.
Axioma 5	Existe un conjunto que tiene como elementos a todos los elementos que pertenecen a algún elemento de $X$.
Axioma 6	Para cada conjunto $X$, existe su conjunto potencia $\mathcal P (X)$ cuyos elementos son los subconjuntos de $X$.

Intersección

Supongamos que tenemos dos conjuntos $X,Y$ de números enteros positivos del 1 al 20. $X$ es el conjunto de los números pares y $Y$ es el conjunto de los números primos. Entonces $X$ lo podemos ver como:

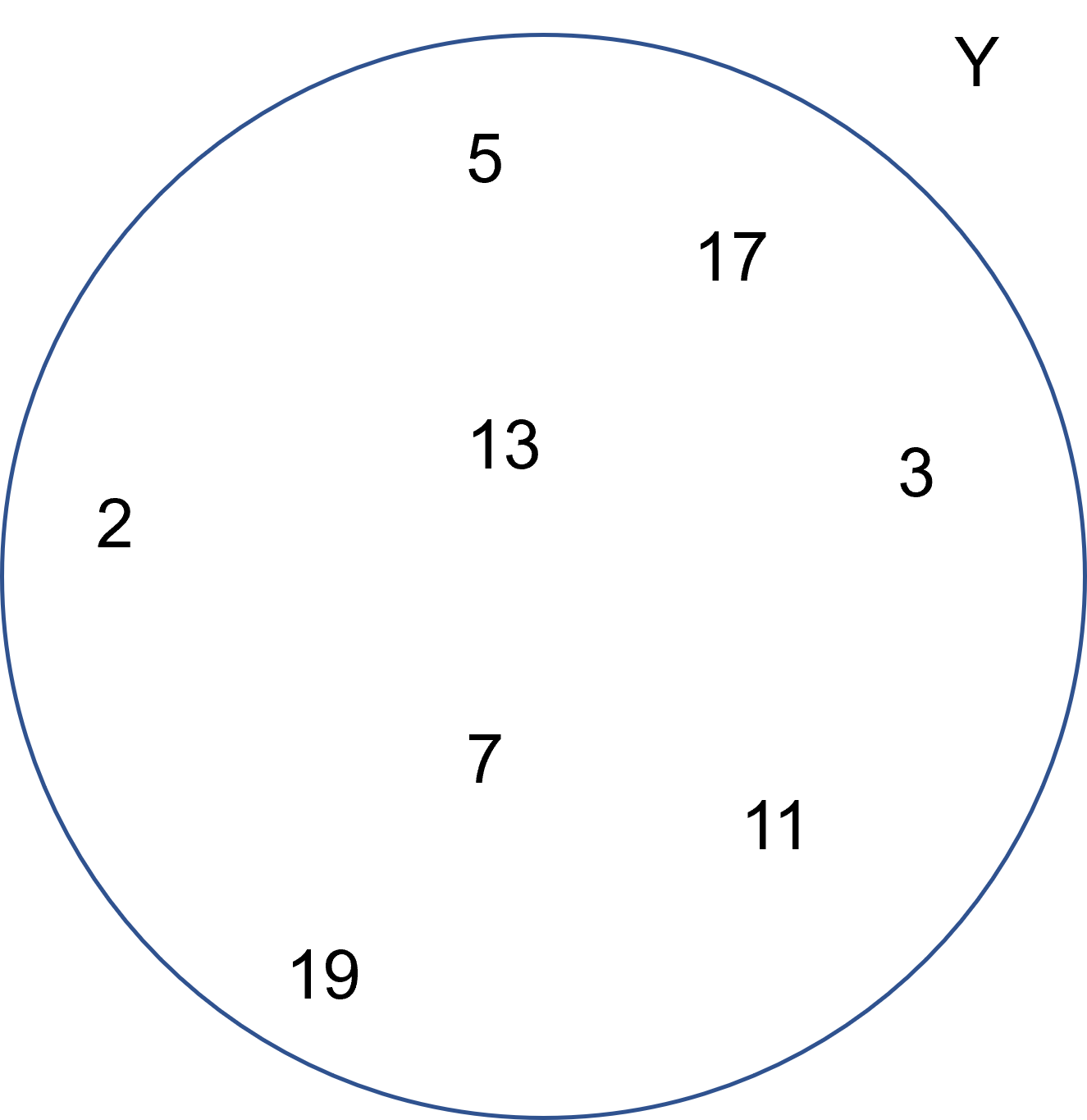
Mientras que $Y$ se podría ver como:

Nota que hay un elemento en común con ambos conjuntos, pues $2$ es el único par primo, es decir hay un punto de intersección que es el $2$:

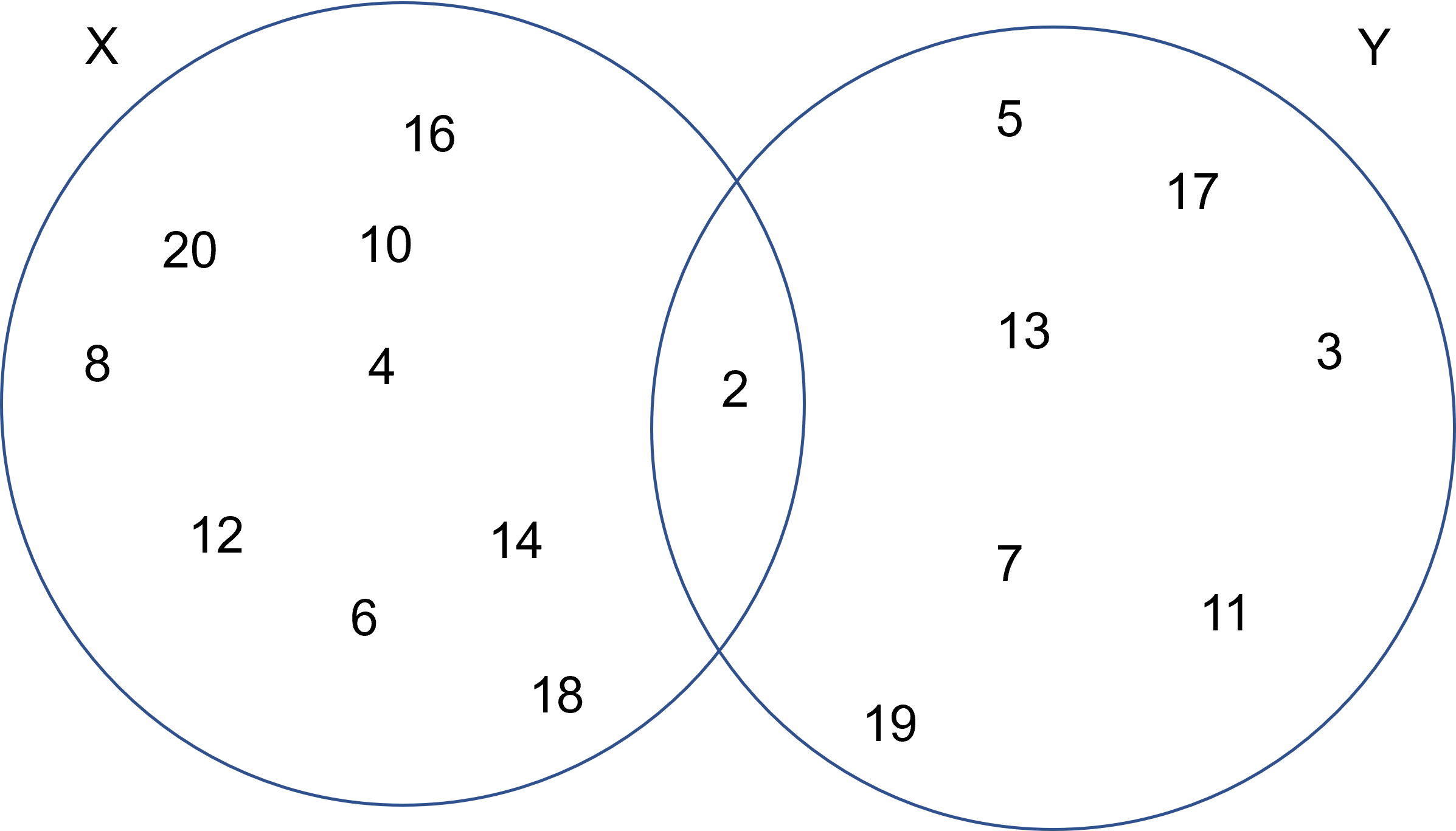
En este caso diremos que $2$ se encuentra en la intersección de $X$ con $Y$, pues está en ambos conjuntos. Con esto en mente definiremos la intersección:

Definición. Sean $X$ y $Y$ dos conjuntos, entonces el conjunto intersección de $X$ y $Y$, $X \cap Y$ es: $$X\cap Y = \{x \in X : x \in Y\} $$

En nuestro ejemplo anterior, $X=\{2,4,6,8,10,12,14,16,18,20\}, Y=\{2,3,5,7,11,13,17,19\}$, y $X \cap Y = \{2\}$ pues es el único par primo.

Como puedes ver, gráficamente el área que representa la intersección entre dos conjuntos es:

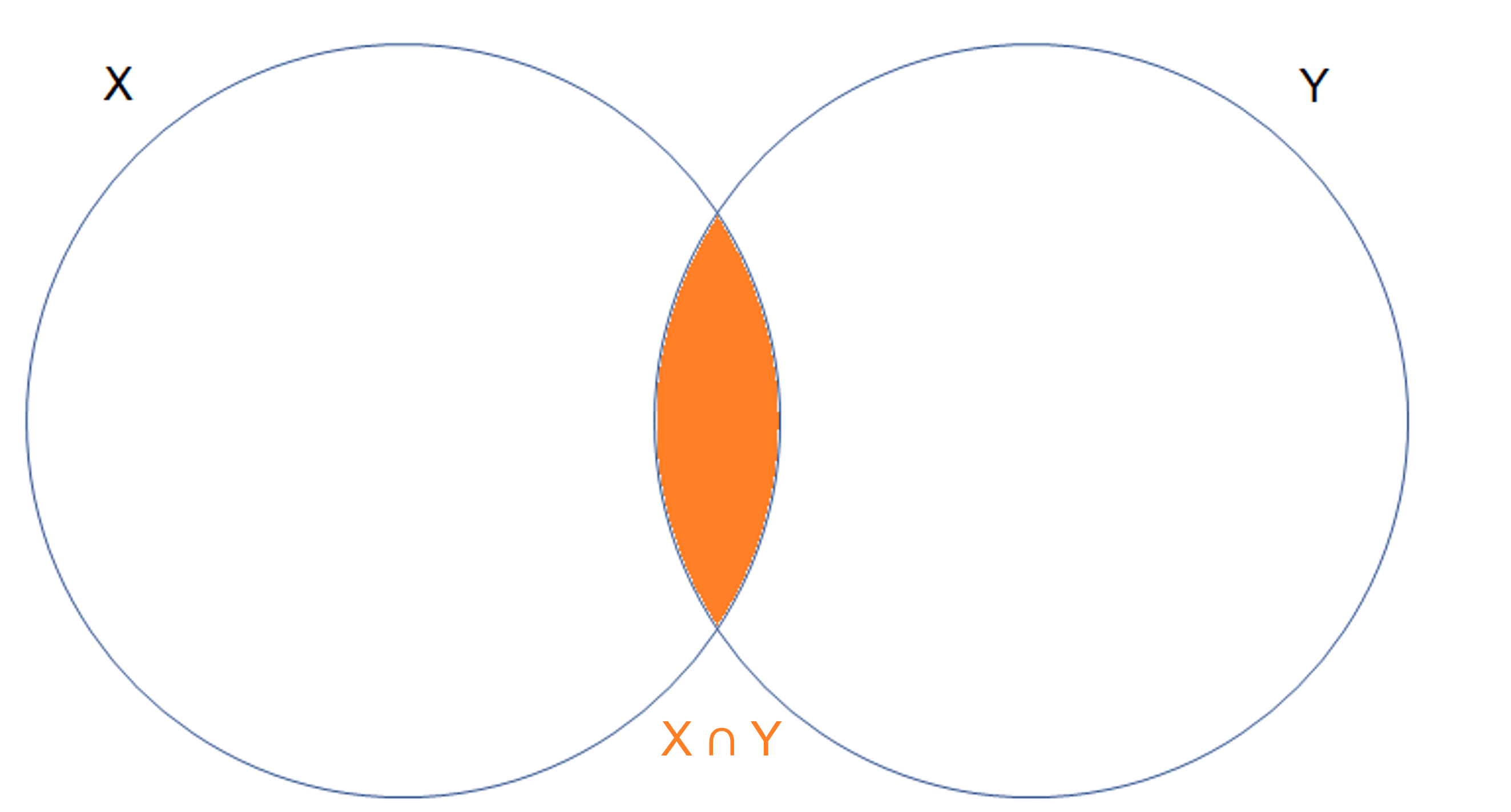
Ahora vamos a ver algunas propiedades como: la conmutatividad y la asociatividad .

Proposición. La intersección es conmutativa, es decir: $$X \cap Y = Y \cap X .$$

Demostración. Recuerda que por el axioma 4, tenemos que demostrar dos cosas: primero que $X \cap Y \subset Y \cap X$ y después que $Y \cap X \subset X \cap Y$. Vas a ver una similitud en demostrar este tipo de proposiciones de igualdad de conjuntos a las demostraciones que usan el «si y solo si», pues primero tendremos que demostrar la contención de «ida» y después la del «regreso». Y esto tiene sentido, pues demostrar la igualdad entre conjuntos es demostrar la doble implicación de que un elemento pertenezca a alguno de los dos conjuntos, pues habría que demostrar:

$$\forall x \big( x \in X \cap Y \Leftrightarrow x \in Y \cap X) .$$

Así que empezamos nuestra demostración probando una contención.

$\subset)$ Consideremos $x \in X\cap Y$. Para demostrar que $X \cap Y \subset Y \cap X$, habría que demostrar que cada elemento del primer conjunto se encuentra en el segundo, así que hay que demostrar que $ x \in Y \cap X$. Para ello, nota que $$X \cap Y = \{x \in X: x \in Y\} = \{x \in X: P(x)\}$$ son los elementos de $X$ que cumplen la proposición $P(x):x \in Y$. Entonces sabemos que $x \in Y$. Por otro lado, sabemos que la proposición $Q(x): x \in X$ se cumple, entonces $x$ pertenece al conjunto

$$x \in \{y \in Y: Q(y)\} = \{y \in Y: y \in X\} = Y \cap X$$

puesto que $x$ pertenece a $Y$ y cumple $Q(x)$. De esta forma $X \cap Y \subset Y \cap X$.

$\supset )$ Nota que para demostrar la otra contención, únicamente deberíamos copiar la demostración anterior cambiando de lugar $X$ con $Y$, es decir que nuestra demostración sería muy parecida a la primera contención que hicimos. Lo podríamos poner tal cual haciendo los cambios mencionados, sin embargo puede ser redundante. En este caso diremos que «La demostración de este caso es análoga a la anterior», que significa: para hacer esta demostración tendríamos un razonamiento muy parecido a la anterior sin ningún modificación interesante, pues seguiríamos los mismos pasos. Muchas veces verás este tipo de oraciones en demostraciones, siendo una herramienta para ahorrar palabras y no ser redundante, pues el razonamiento para hacer alguna demostración (en este caso la segunda contención), sigue un razonamiento casi idéntico a algo ya hecho (en este caso la primera contención).

De esta manera, al ser esta contención análoga a la anterior, $Y \cap X \subset X \cap Y$

$\square$

Proposición. La intersección es asociativa, es decir $$X \cap (Y \cap Z) = (X \cap Y) \cap Z$$.

Demostración. Podríamos hacer esta demostración como la anterior donde hicimos la conmutatividad, sin embargo emplearemos otro razonamiento en donde cada uno de los pasos es válido. Para ello nota que queremos demostrar que $$X \cap (Y \cap Z) = (X \cap Y) \cap Z$$ y que $$(X \cap Y) \cap Z = X \cap (Y \cap Z)$$. Y para esto debemos de demostrar que $$\big( x \in X \cap (Y \cap Z) \big) \Leftrightarrow \big(x \in (X \cap Y) \cap Z\big).$$

Ahora nota que

\begin{align*}
x \in X \cap (Y \cap Z)& \Leftrightarrow (x \in X) \land \big((x \in Y)\land(x \in Z) \big)\\
& \Leftrightarrow \big((x \in X) \land (x \in Y)\big) \land (x \in Z) \ \ \ (\text{Por la asociatividad de la disyunción}) \\
& \Leftrightarrow x \in (X \cap Y) \cap Z \\
\end{align*}

De esta manera hicimos una cadena de equivalencias lógicas válidas, empezamos con un elemento en el conjunto $X \cap (Y \cap Z)$ y demostramos que ese elemento estaba en $(X \cap Y) \cap Z$ y viceversa. Esto lo hicimos con el conocimiento que ya sabíamos, y como antes ya habíamos demostrado que la disyunción es asociativa, entonces cada paso lógico es válido y con esto demostramos la igualdad entre conjuntos.

$\square$

Unión

Ahora en vez de fijarnos en donde dos conjuntos se intersectan, pensemos en cuando dos conjuntos se unen. Para esto, considera el siguiente ejemplo. Digamos que $X = \{ 1,2,3,4,5\}$ y $Y = \{4, 5,6,7 \}$ son conjuntos de números enteros.

Los conjuntos $X,Y$ son los siguientes:

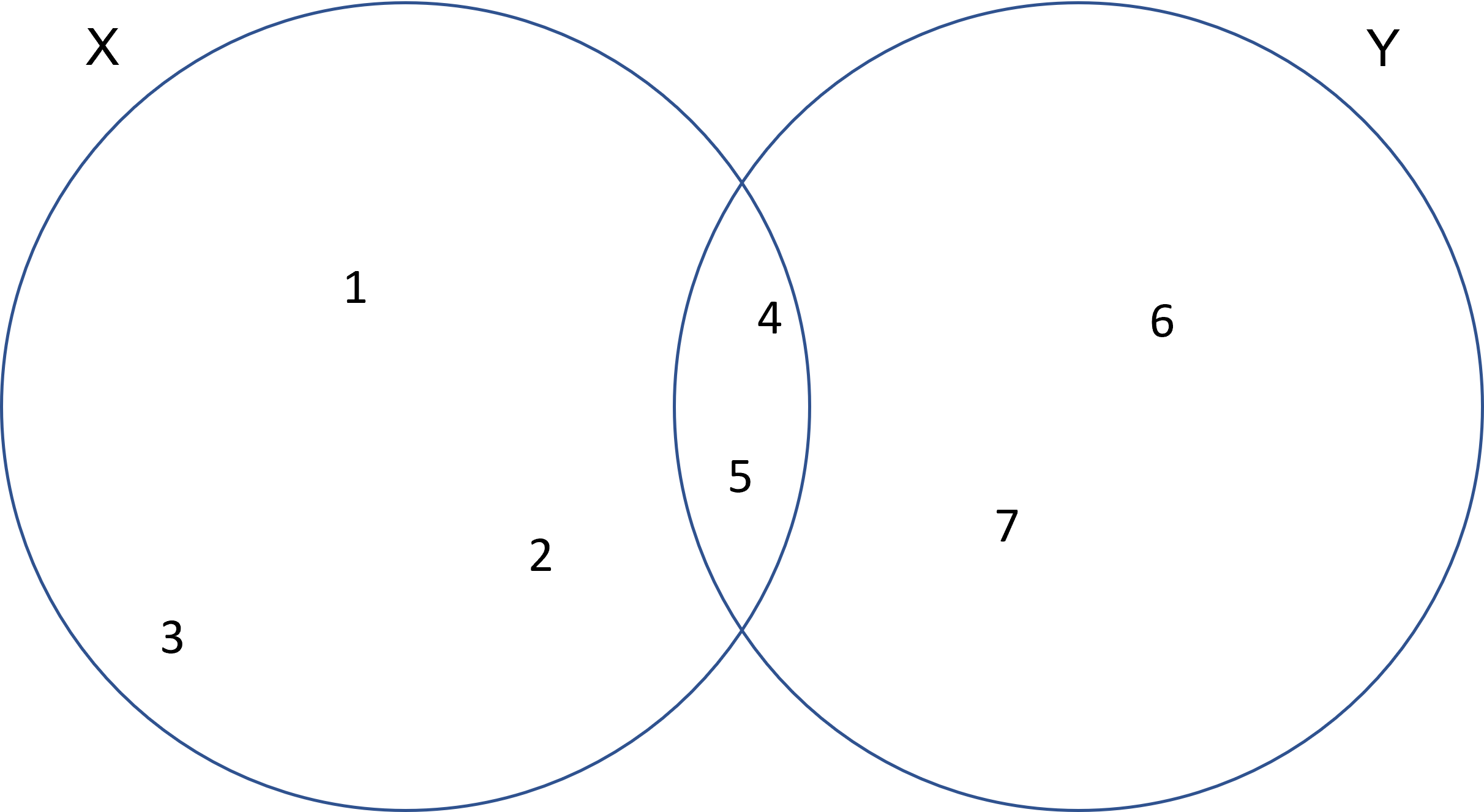
El siguiente paso es construir el conjunto que tiene como elementos a los elementos de ambos conjuntos ¿Recuerdas el axioma 4? Este nos hablaba de un conjunto que contiene a todos los elementos que son elementos del mismo conjunto. Suena confuso pero este axioma junto al axioma 3 justifican la existencia de este conjunto. Veamos como lo podemos construir:

Por el axioma 3, existe el conjunto $\{X,Y\}$, es decir que existe el conjunto $A = \{\{1,2,3,4,5\}\{4,5,6,7\}\}$.

Después, como existe este conjunto $A$, por el axioma 4, existe un conjunto cuyos elementos son elementos que pertenecen a elementos de $\{X,Y\}$, entonces para dicho conjunto que llamaremos $X \cup Y$, sus elementos son $$X \cup Y = \{x: x \in X \lor x \in Y\}$$.

Entonces el conjunto unión de $X$ y $Y$ $X \cup Y = \{1,2,3,4,5,6,7\}$, pues es el conjunto que contiene a todos los elementos de ambos conjuntos.

Definición. El conjunto unión de dos conjuntos $X,Y$ es el conjunto: $$X \cup Y = \{x: x \in X \lor x \in Y\} $$

De manera gráfica, podemos ver la unión como:

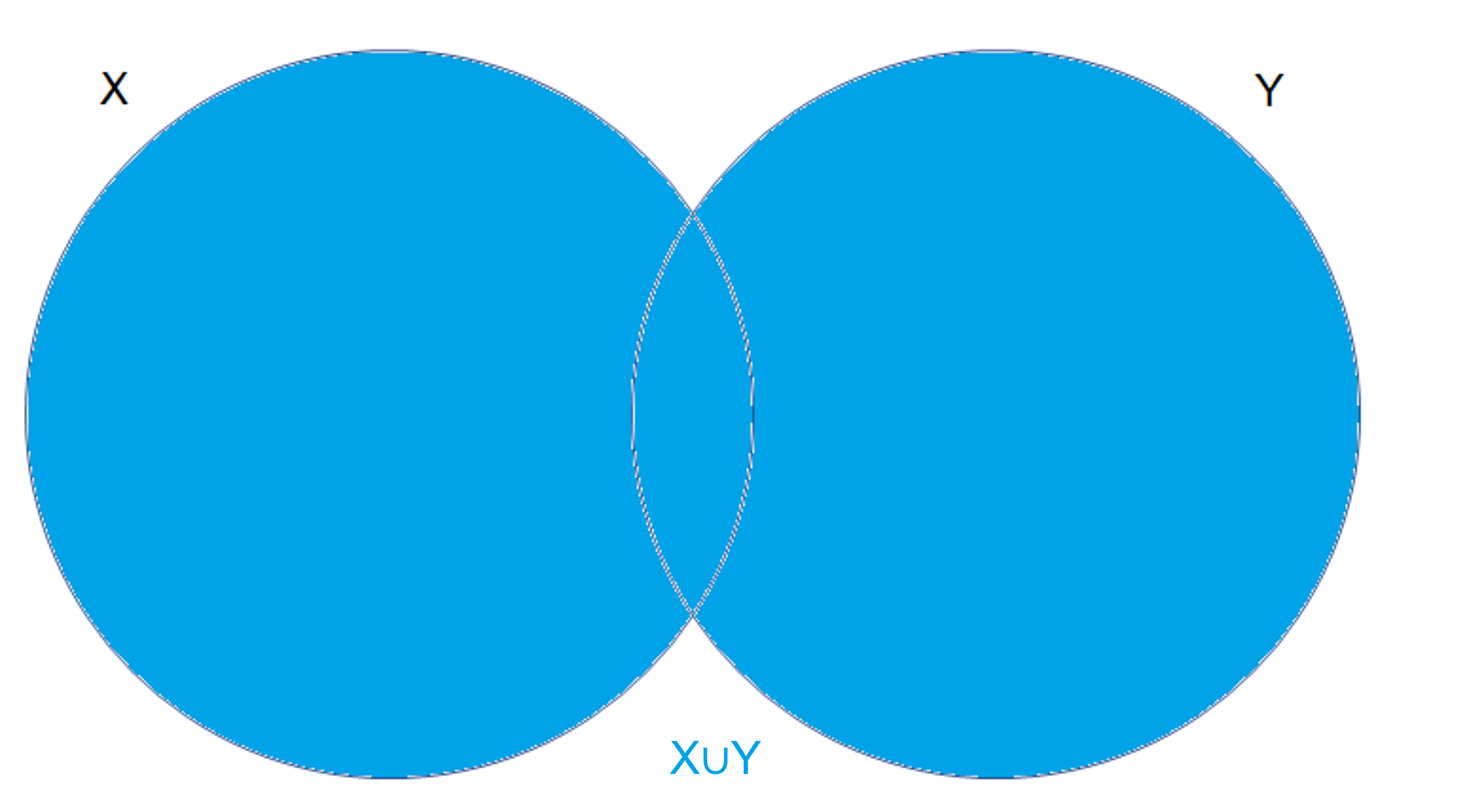
Ahora enunciaremos las proposiciones que demostramos para la intersección, pero ahora usando la unión:

Proposición. La unión es conmutativa.

Demostración. Considera a $X$ y $Y$ dos conjuntos, entonces

\begin{align*}
x \in X \cup Y & \Leftrightarrow (x \in X) \lor (x \in Y)\\
& \Leftrightarrow (x \in Y) \lor (x \in X) \ \ \ (\text{Por la conmutatividad de la conjunción}) \\
& \Leftrightarrow x \in Y \cup X
\end{align*}

$\square$

Proposición. La unión es asociativa.

Para esta última no daremos demostración, sin embargo es una demotración parecida a su contraparte de la intersección.

Una vez que hemos establecido estas dos operaciones, solo falta una más por revisar ahora. Si la intersección es la disyunción y la unión es la conjunción, la siguiente que definiremos es la negación.

Complemento de conjuntos

Cuando estemos hablando de conjuntos, muchas veces estaremos dentro de un contexto de conjuntos, o un Conjunto universal, dentro del cual siempre estaremos trabajando. Por ejemplo, si estamos en cálculo de una variable, todos los conjuntos o casi todos sobre los que estemos trabajando serán conjuntos de números reales. Nota ahora que cuando estuvimos dando los ejemplos de conjuntos paraexplicar la unión y la intersección, decíamos que $X,Y$ eran conjuntos de números enteros. Es decir, estábamos acordando que nuestro conjunto universal eran los números enteros $\mathbb{Z}$.

Muchas veces el contexto sobre el conjunto universal sobre el que estamos trabajando no será especificado y se puede inferir, pues si estamos trabajando por ejemplo con números reales, no es posible que un conjunto tenga números complejos, por ejemplo.

Ahora con esto acordado, vamos a ver que cualquier conjunto $X$ en un conjunto universal $U$ se puede escribir de la siguiente manera: $$ X = \{x \in U: x \in X\}.$$

Es decir, podemos escribir al conjunto $X$ como los elementos del conjunto universal que están en $X$. Así, definiremos el complemento de $X$ o $X^c$ como: $$X^c = \{x \in U:x \not \in X\}. $$

Definición. Sea $X$ un conjunto sobre el conjunto universal $U$, entonces definimos el complemento de $X$ como $$X^c = \{x \in U: x\not \in X\}^* $$

Por ejemplo, considera $X = \{2,4,6,8,10\}$ al conjunto de los números pares dentro del conjunto de los números enteros del 1 al 10. Entonces en este caso $U = \{1,2,3,4,5,6,7,8,9,10\}$ y su complemento es $X^c = \{1,3,5,7,9\}$.

Gráficamente, podemos ver al complemento como:

Algunas de las cosas que podemos decir del complemento son:

Proposición. Sea $X$ un conjuntos dentro del conjunto universal $U$. Entonces:

1. $X \cup X^c = U$
2. $U^c = \emptyset$

Demostración.

1. Esta proposición nos quiere decir que un conjunto junto al complemento «llenan» todo el espacio. Para esto, nota que
   \begin{align*}
   x \in X^c \cup X & \Leftrightarrow x \in X^c \lor x \in X \\
   & \Leftrightarrow x \in \{x \in U : x \in X \lor x \not \in X\}
   \end{align*}
   Ahora nota que $P(x): x \in X \lor x \not \in X$ es una tautología, es decir, cualquier elemento de $U$ cumple dicha definición, así,
   \begin{align*}
   x \in X^c \cup X & \Leftrightarrow x \in X^c \lor x \in X \\
   & \Leftrightarrow x \in \{x \in U : x \in X \lor x \not \in X\}\\
   & \Leftrightarrow x \in U
   \end{align*}
2. Nota primero que ya hemos dicho que $\emptyset$ es subconjunto de cualquier conjunto, así se tiene la contención $\emptyset \subset U$. Para la otra contención, supón que no sucede que $U \subset \emptyset$. Entonces se tiene que existe un elemento $x\in U$ que cumple:$$ x\in \{x \in U: x \not \in U\}. $$ Donde se tendría que $x \in U \land x \not \in U$, lo cual es imposible. Entonces $U \subset \emptyset$. De esta manera se tiene la igualdad entre conjuntos.
   

$\square$

Nota

*: En la literatura, también puedes encontrar escrito el complemento de un conjunto $A$ escrito como $\bar A$ en lugar de $A^c$

Más adelante…

Ahora ya hemos visto tres operaciones básicas en la teoría de conjuntos, junto a la definición del conjunto universal, que recuerda: no siempre verás implícitamente y puede ser un conjunto que dependa del contexto. En la siguiente entrada veremos dos operaciones más que se pueden definir en términos de las que vimos ahora, así como otras propiedades de las operaciones.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

1. Sea $N = \{1,2,3,4,6,9,10,15,20,30\}$ y $X = \{x \in \mathbb{Z}: x= 2n, n \in N \}$, encuentra:
   • $X \cap N$
   • $X \cup N$
2. Demuestra que la unión es asociativa.
3. Demuestra que la unión de subconjuntos de un conjunto $X$ siempre está contenida en $X$.
4. Demuestra que si $Y \subset X $ y $Z \subset X$ entonces $Y \cup Z \subset X$
5. Demuestra que si $X \subset Y$ son dos conjuntos, entonces:
   • $X \cap Y = X$
   • $X \cup Y = Y$
6. Demuestra que:
   • $X^c \cap X^c = \emptyset$
   • $\emptyset^c = U$

Entradas relacionadas

• Ir a Álgebra Superior I
• Entrada anterior del curso: Problemas de conjuntos y subconjuntos
• Siguiente entrada del curso: Leyes de De Morgan y diferencia simétrica de conjuntos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»