Archivo de la etiqueta: kernel

Álgebra Moderna I: Núcleo e Imagen de un Homomorfismo

Por Cecilia del Carmen Villatoro Ramos

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

Estamos trabajando con homomorfismos, que son funciones entre dos grupos que respetan sus operaciones. Entre las propiedades que vimos, está que el neutro del dominio siempre va al neutro del codominio. Es decir, al menos hay un elemento que, bajo el homomorfismo, cae en el neutro del codominio.

Para esta entrada consideraremos a la colección de todos los elementos del dominio que van al neutro del codominio. A este subconjunto, lo llamamos el núcleo de $φ$ . Por otro lado, podemos tomar todos los elementos del dominio, aplicarles $φ$ y tomar el subconjunto que resulta en el codominio, a esto le llamamos la imagen de $φ$ . Estos dos subconjuntos van a ser importantes en el estudio de los homomorfismos.

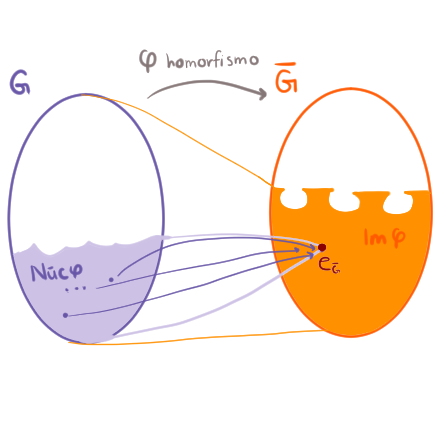
La imagen muestra que para $φ : G \to \bar{G}$ un homomorfismo, el núcleo $Núc φ \subseteq G$ y la imagen $Im φ \subseteq \bar{G}$ .

El núcleo y la imagen de un homomorfismo

Comencemos definiendo formalmente los subconjuntos.

Definición. Sean $G, \bar{G}$ grupos, $φ : G \to \bar{G}$ un homomorfismo. Definimos al núcleo de $φ$ como
$\begin{array}{r} Núc φ = {g \in G | φ (g) = e_{\bar{G}}} . \end{array}$

Es decir, es el conjunto de todos los elementos de $G$ que, bajo $φ$ van a dar al neutro de $\bar{G}$ .

Notación. Es común, por el nombre en alemán, denotar al $Núc φ$ como $Ker φ$ , es llamado el Kernel de $φ$ .

Definición. La imagen de $φ$ es
$\begin{array}{r} Im φ = {φ (g) | g \in G} . \end{array}$

Notemos que $Núc φ \subseteq G$ y $Im φ \subseteq \bar{G}$ .

Ejemplos.

Ejemplo 1. Tomemos el homomorfismo $φ : S_{n} \to {+ 1, - 1}$ con $φ (α) = s g n α$ para toda $α \in S_{n}$ . Veamos quién es el núcleo de $φ$ :
$\begin{aligned} Núc φ & = {α \in S_{n} | φ (α) = + 1} \\ = {α \in S_{n} | s g n \in α = + 1} = A_{n} . \end{aligned}$
Si tomamos el caso no trivial, con $n > 1$ ,
$\begin{array}{r} Im φ = {+ 1, - 1} . \end{array}$
Ya que $φ ((1)) = 1$ y $φ ((1 2)) = - 1$ .

Ejemplo 2. Sea $n \in Z^{+}$ . Consideremos el homomorfismo $φ : Z \to C^{*}$ con
$\begin{array}{r} φ (m) = {(e^{\frac{2 π i}{n}})}^{m} \forall m \in Z . \end{array}$
Buscamos describir su núcleo y su imagen.
$\begin{aligned} Núc φ & = {m \in Z | φ (m) = 1} \\ = {m \in Z | {(e^{\frac{2 π i}{n}})}^{m} = 1} = n Z . \end{aligned}$
La última igualdad se da porque ya sabemos que $e^{2 π i} = 1$ , más aún $e^{θ i} = 1$ si y sólo si $θ$ es un múltiplo de $2 π$ , entonces ${(e^{\frac{2 π i}{n}})}^{m} = 1$ si y sólo si $m$ es un múltiplo de $n$ .

Ahora la imagen:
$\begin{aligned} Im φ & = {φ (m) | m \in Z} \\ = {{(e^{\frac{2 π i}{n}})}^{m} | m \in Z} = ⟨ e^{\frac{2 π i}{n}} ⟩ . \end{aligned}$

El núcleo y la imagen son subgrupos

Ahora, probaremos que el núcleo y la imagen de un homomorfismo no son sólo subconjuntos del dominio y codominio respectivamente, si no que son subgrupos.

Teorema. Sean $G, \bar{G}$ grupos, $φ : G \to \bar{G}$ un homomorfismo.

$Núc φ ⊴ G$ .
$Im φ \leq \bar{G}$ .
$φ$ es un monomorfismo si y sólo si $Núc φ = {e_{G}}$ .

Demostración.
Sean $G, \bar{G}$ grupos, $φ : G \to \bar{G}$ un homomorfismo.

P.D. $Núc φ ⊴ G$ .
Primero probaremos que $Núc φ \leq G$ .

Como $φ$ es un homomorfismo, $φ (e_{G}) = e_{\bar{G}}$ . Entonces $e_{G} \in Núc φ$ .

Si $a, b \in Núc φ$ .
$\begin{aligned} φ (a b^{- 1}) & = φ (a) φ (b^{- 1}) & φ es un homomorfismo \\ = φ (a) (φ (b))^{- 1} & Proposición de homomorfismo \\ = e_{\bar{G}} e_{\bar{G}}^{- 1} = e_{\bar{G}} & a, b \in Núc φ \end{aligned}$
Entonces $a b^{- 1} \in Núc φ$ . Por lo tanto $Núc φ \leq G$ .

Además, si $a \in G$ y $n \in Núc φ$ :
$\begin{aligned} φ (a n a^{- 1}) & = φ (a) φ (n) φ (a^{- 1}) & φ es un homomorfismo \\ = φ (a) φ (n) (φ (a))^{- 1} & Proposición \\ = φ (a) e_{\bar{G}} (φ (a))^{- 1} & n \in Núc φ \\ = φ (a) (φ (a))^{- 1} = e_{\bar{G}} \end{aligned}$
Así, $a n a^{- 1} \in Núc φ$ . Esto nos dice que el núcleo de $φ$ es cerrado bajo conjugación. Por lo tanto $Núc φ ⊴ G$ .
P.D. $Im φ \leq \bar{G}$ .
Primero veamos que el neutro de $\bar{G}$ está en $Im φ$ . Esto pasa porque
$e_{\bar{G}} = φ (e_{G}) \in Im φ .$

Ahora, si $c, d \in Im φ$ , entonces $c = φ (a), d = φ (b)$ para algunos $a, b \in G$ .
$\begin{aligned} a d^{- 1} = φ (a) (φ (b))^{- 1} & = φ (a) φ (b^{- 1}) & Proposición \\ = φ (a b^{- 1}) \in Im φ & φ es un homomorfismo \end{aligned}$
Por lo tanto $Im φ \leq \bar{G}$ .
P.D. $φ$ es un monomorfismo si y sólo si $Núc φ = {e_{G}}$ .

$| \Rightarrow]$ Supongamos que $φ$ es un monomorfismo (un homomorfismo inyectivo).
Como $Núc φ \leq G$ , entonces ${e_{G}} \subseteq Núc φ$ .
Ahora, si $g \in Núc φ$ , por la proposición anterior,
$\begin{array}{r} φ (g) = e_{\bar{G}} = φ (e_{G}) . \end{array}$
Y como $φ$ es inyectiva, $g = e_{G}$ . Por lo tanto, $Núc φ = {e_{G}}$ .

$[\Leftarrow |$ Supongamos que $Núc φ = {e_{G}}$ .
Sean $a, b \in G$ tales que $φ (a) = φ (b)$ . Entonces
$\begin{aligned} e_{\bar{G}} & = φ (b) (φ (a))^{- 1} \\ = φ (b) φ (a^{- 1}) & Proposición \\ = φ (b a^{- 1}) & φ es un homomorfismo \end{aligned}$
Entonces $b a^{- 1} \in Núc φ = {e_{G}}$ , así $b a^{- 1} = e_{G}$ , esto implica que $b = a$ .
Por lo tanto $φ$ es un monomorfismo.

Observemos que el inciso 3 del teorema nos da una herramienta para determinar si un homomorfismo es inyectivo o no usando el núcleo.

Proyección Canónica

Ahora, tomando un grupo y un subgrupo normal, definiremos un epimorfismo de un grupo al grupo cociente.

Proposición. Sea $G$ un grupo, $N$ un subgrupo normal de $G$ . La función $π_{:} G \to G / N$ con $π (a) = a N$ para toda $a \in G$ , es un epimorfismo tal que $Núc π = N$ .

Esta función se conoce como la proyección canónica.

Demostración.
Sea $G$ un grupo, $N ⊴ G$ , $π : G \to G / N$ con $π (a) = a N$ para cualquier $a \in G$ .

Veamos que $π$ es un homomorfismo
Sean $a, b \in G$ , entonces
$\begin{array}{r} π (a b) = a b N = (a N) (b N) = π (a) π (b) . \end{array}$

Ahora veamos que es suprayectivo. Esto es debido a que dado $a N \in G / N$ , $a N = π (a) .$

Por lo tanto $π$ es un epimorfismo.

Finalmente,
$\begin{array}{r} Núc π = {a \in G | π (a) = e_{G / N}} = {a \in G | a N = N} = N . \end{array}$

Ahora veamos un corolario que se desprende directamente de lo que acabamos de ver.

Corolario. Todo subgrupo normal es el núcleo de un homomorfismo. De hecho, es el núcleo de un epimorfismo.

Ejemplos

Para terminar veamos unos ejemplos

Ejemplo 1. Tomemos $φ : (R, +) \to (C^{*}, \cdot)$ con $φ (x) = e^{x i}$ para toda $x \in R$ . Toma 2 min para pensar porqué es un homomorfismo.

Veamos el núcleo y la imágen de $φ$ :
$\begin{aligned} Núc φ & = {x \in R | φ (x) = 1} \\ = {x \in R | e^{x i} = 1} \\ = {2 π n | n \in Z} = ⟨ 2 π ⟩ . \\ Im φ & = {φ (x) | x \in R} \\ = {e^{x i} | x \in R} \\ = {z \in C | | z | = 1} = S^{1} . \end{aligned}$
¿Cómo es $R / ⟨ 2 π ⟩$ ?
Tomemos $a, b \in R$ .
$\begin{aligned} a + ⟨ 2 π ⟩ = b + ⟨ 2 π ⟩ & \Leftrightarrow a - b \in ⟨ 2 π ⟩ \\ \Leftrightarrow a - b = 2 π n, n \in Z . \end{aligned}$
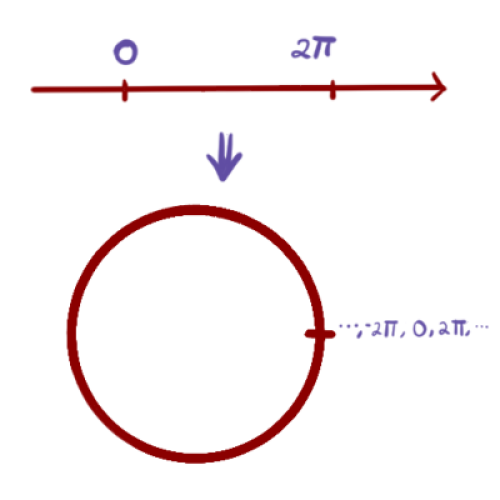
Si lo anterior nos dice que dos números $a, b$ están en la misma clase si y sólo si difieren por un múltiplo de $2 π$ . Si lo pensamos en la recta numérica, nos dice que el $0$ y $2 π$ quedan indentificados en la misma clase. Intuitivamente podríamos pensar que estamos doblando la recta numérica para obtener una circunferencia donde $0$ y $2 π$ están en el mismo punto.

Así, $R / ⟨ 2 π ⟩ = {a + ⟨ 2 π ⟩ | a \in [0, 2 π)}$ .

Ejemplo 2. Consideremos $φ : (R^{*}, \cdot) \to (R^{*}, \cdot)$ con $φ (x) = | x |$ para toda $x \in R^{*}$ (recuerda que $R^{*} = R ∖ {0}$ ).
$\begin{aligned} Núc φ & = {x \in R^{*} | φ (x) = 1} \\ = {x \in R^{*} | | x | = 1} = {+ 1, - 1} . \\ Im φ & = {φ (x) | x \in R^{*}} \\ = {| x | | x \in R^{*}} = R^{+} . \end{aligned}$
¿Cómo es $R^{*} / {+ 1, - 1}$ ?
Tomemos $a, b \in R^{*}$ .
$\begin{aligned} a {+ 1, - 1} = b {+ 1, - 1} & \Leftrightarrow a^{- 1} b \in {+ 1, - 1} \\ \Leftrightarrow a^{- 1} b = \pm 1 \Leftrightarrow b = \pm a . \end{aligned}$
Entonces, dos clases laterales van a ser iguales si y sólo si sus representantes difieren a lo más sólo por el signo.

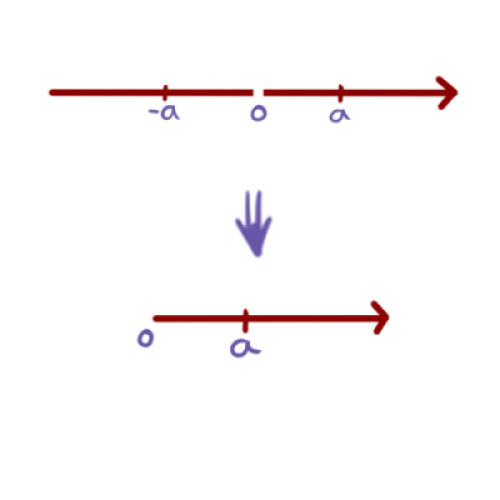
Lo que hicimos fue tomar a los reales sin el cero y estamos identificando a cada número real $a$ con su inverso aditivo. Entonces la imagen de $φ$ en realidad es como si dobláramos la recta por el 0 e identificamos a los reales negativos con su correspondiente positivo.

Así, $R^{*} / {+ 1, - 1} = {a {+ 1, - 1} | a \in R^{+}}$ .

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Sea $φ : G L (2, R) \to R^{*}$ el homomorfismo tal que $φ (A) = det A$ . Encuentra el núcleo y la imagen de $φ$ .
Sean $G, \bar{G}$ grupos y $φ : G \to \bar{G}$ un homomorfismo. ¿Es $Im φ$ normal en $\bar{G}$ ? Prueba o da un contraejemplo.
Sean $G, \bar{G}$ grupos y $φ : G \to \bar{G}$ un homomorfismo. Sean también, $H \leq G, \bar{H} \leq \bar{G}$ .
- ¿Qué puedes decir de $φ [H] = {φ (h) | h \in H}$ ?¿Y si $H ⊴ G$ ?
- ¿Qué puedes decir de $φ^{- 1} [\bar{H}] = {g \in G | φ (g) \in \bar{H}}$ ? ¿Y si $\bar{H} ⊴ \bar{G}$ ?
En cada inciso calcula $Núc φ, Im φ, G / Núc$ y analiza cómo se relacionan:
- $G$ grupo, $φ : G \to G$ , con $φ = {id}_{G}$ .
- $G$ grupo, $φ : G \to G$ , con $φ (g) = e_{G}$ para toda $g \in G$ .
- $φ : (C^{*}, \cdot) \to (R^{*}, \cdot)$ , con $φ (z) = | z |$ para toda $z \in C^{*}$ .
- $φ : Z \times Z \to Z \times Z$ , con $φ (x, y) = (x, 0)$ para toda $(x, y) \in Z \times Z$ .

Más adelante…

Ahora que ya tenemos muy claras las definiciones de núcleo e imagen de un homomorfismo, comenzaremos a ver teoremas que relacionan lo que vimos aquí con isomorfismos y grupo cociente.

Entradas relacionadas

Ir a Álgebra Moderna I.
Entrada anterior del curso: Propiedades de Homomorfismo.
Siguiente entrada del curso: Primer Teorema de Isomorfía y Diagrama de Retícula.
Resto de cursos: Cursos.

Álgebra Lineal I: Problemas de formas cuadráticas y producto interior

Por Blanca Radillo

2 respuestas

Introducción

En las últimas sesiones, hemos introducido el tema de formas bilineales y formas cuadráticas. Más adelante, hablamos de positividad de formas cuadráticas y de producto interior. Ahora veremos algunos problemas de formas cuadráticas y producto interior.

Problemas resueltos de formas cuadráticas

Sabemos que si $T : V \times V \to R$ es una transformación lineal, $T$ no necesariamente es una forma bilineal (durante la clase del viernes se discutió un ejemplo), entonces una pregunta interesante es ¿qué información tenemos sobre el núcleo de una forma cuadrática? Es fácil ver que una forma cuadrática no es una transformación lineal, pero está asociada a una forma bilineal. Interesadas en esta pregunta, analizaremos algunas propiedades del núcleo de una forma bilineal y de una forma cuadrática.

Problema 1. a) Si $q$ es una forma cuadrática en $R^{n}$ , ¿el conjunto ${x \in R^{n} : q (x) = 0}$ es un subespacio de $R^{n}$ ?
b) Describe $x \in R^{n} : q (x) = 0$ si:
1) $q (x, y) = x^{2} + y^{2}$ ,
2) $q (x, y, z) = x y + y z + z x$
3) $q (x, y, z) = (x - y)^{2} + (y - z)^{2} + (z - x)^{2}$ .

Solución. a) La respuesta es: no, el conjunto ${x \in R^{n} : q (x) = 0}$ no necesariamente es un subespacio, ya que no necesariamente es cerrado bajo la suma. Daremos un ejemplo.

Sea $q : R^{2} \to R$ definido como $q ((x, y)) = x^{2} - y^{2}$ . Sabemos que ésta es una forma cuadrática. Notemos que para todo $x, y \in R$ , si $v_{1} = (x, x), v_{2} = (y, - y)$ , entonces $q (v_{1}) = x^{2} - x^{2} = 0$ y $q (v_{2}) = y^{2} - (- y)^{2} = 0$ , entonces $v_{1}, v_{2} \in {x \in R^{n} : q (x) = 0}$ . Pero $v_{1} + v_{2} = (x + y, x - y)$ no pertenecen al núcleo de $q$ , ya que $q (v_{1} + v_{2}) = q ((x + y, x - y)) = (x + y)^{2} - (x - y)^{2} = 4 x y \neq 0$ si $x, y \neq 0$ .

b.1) Sea $(x, y) \in R^{2}$ tal que $q ((x, y)) = x^{2} + y^{2} = 0$ . Como $x, y \in R$ , sabemos que la única posibilidad en que la suma de dos cuadrados sea cero es que ambos sean cero, por lo tanto ${x \in R^{2} : q (x) = 0} = {(0, 0)}$ .

b.2) Sea $(x, y, z) \in R^{3}$ tal que $q ((x, y, z)) = x y + y z + z x = 0$ . Si $x = 0$ entonces $y z = 0$ , esto es posible sólo si $y = 0$ o $z = 0$ . Entonces el núcleo contiene a los ejes $(x, 0, 0)$ , $(0, y, 0)$ y $(0, 0, z)$ . Ahora, si $x = - y$ , entonces $x y + y z + z x = - x^{2} - x z + z x = - x^{2} = 0$ , por lo tanto $x = 0 = y$ , obteniendo nuevamente a los ejes. Ahora suponemos que $x + y \neq 0$ . Entonces $x y + y z + z x = x y + z (x + y) = 0$ , obteniendo que $z = - \frac{x y}{x + y}$ (el cono elíptico). Por lo tanto el núcleo de $q$ son los ejes y el cono elíptico.

b.3) Sea $(x, y, z) \in R^{3}$ tal que $q ((x, y, z)) = (x - y)^{2} + (y - z)^{2} + (z - x)^{2} = 0$ . Al igual que en el inciso (b.1), esto sólo es posible si $x - y = y - z = z - x = 0$ , entonces $x = y = z$ . Por lo tanto, ${x \in R^{n} : q (x) = 0} = {(x, x, x) : x \in R}$ .

$△$

Problema 2. Sea $V = P_{2} (R)$ el espacio de polinomios en $[- 1, 1]$ con coeficientes reales de grado a lo más 2 y considera el mapeo $b : V \times V \to R$ definido como

$b (f, g) = \int_{- 1}^{1} t f (t) g (t) d t .$

Prueba que $b$ es una forma bilineal simétrica de $V$ . Si $q$ es la forma cuadrática asociada, encuentra las $f$ en $V$ tales que $q (f) = 0$ .

Solución. Mostrar que $b$ es bilineal es sencillo, y queda como tarea moral. Es fácil ver que es simétrica, ya que

$\begin{aligned} b (f, g) & = \int_{- 1}^{1} t f (t) g (t) d t \\ = \int_{- 1}^{1} t g (t) f (t) d t = b (g, f) . \end{aligned}$

Ahora, queremos encontrar las funciones $f$ tales que $q (f) = b (f, f) = \int_{- 1}^{1} t f^{2} (t) d t = 0$ . Como $f$ es un polinomio de grado $2$ , es de la forma $f (x) = a x^{2} + b x + c$ para reales $a, b, c$ y entonces

$\begin{aligned} 0 & = q (f) \\ = \int_{- 1}^{1} t f^{2} (t) d t \\ = \int_{- 1}^{1} t (a t^{2} + b t + c)^{2} d t \\ = \int_{- 1}^{1} t (a^{2} t^{4} + 2 a b t^{3} + (b^{2} + 2 a c) t^{2} + 2 b c t + c^{2}) d t \\ = \int_{- 1}^{1} (a^{2} t^{5} + 2 a b t^{4} + (b^{2} + 2 a c) t^{3} + 2 b c t^{2} + c^{2} t) d t \\ = \frac{4 a b}{5} + \frac{4 b c}{3} = 0 \end{aligned}$

Esto implica que $4 b (3 a + 5 c) = 0$ , entonces $b = 0$ o $3 a + 5 c = 0$ . Por lo tanto ${f \in V : q (f) = 0} = {a x^{2} + c} \cup {a x^{2} + b x - \frac{3 a}{5}} .$

Problemas resueltos de producto interior

Ahora recordemos que en la clase de ayer, definimos formas bilineales y cuadráticas positivas y definidas positivas, y a partir de ello, definimos qué es un producto interior. Así, en los siguientes problemas, veremos algunos ejemplos de estas definiciones.

Problema 3. Determina cuáles de las siguientes formas cuadráticas son positivas. ¿Cuáles también son definidas positivas?

$q (x, y, z) = x y + y z + z x$ .
$q (x, y, z) = (x - y)^{2} + (y - z)^{2} + (z - x)^{2}$ .
$q (x, y, z) = x^{2} - y^{2} + z^{2} - x y + 2 y z - 3 z x$ .

Solución. Sea $v = (x, y, z) \in R^{3}$ , recordemos que para cada uno de los incisos $q$ es positiva si $q (v) \geq 0$ para toda $v$ y es definida positiva si es positiva y $q (v) = 0$ si y sólo si $v = 0$ .

1) Si escogemos a $v$ como $v = (1, - 2, 1)$ tenemos que
$\begin{aligned} q (v) & = q (1, - 2, 1) \\ = 1 (- 2) + (- 2) (1) + 1 (1) \\ = - 2 - 2 + 1 \\ = - 3. \end{aligned}$ Por lo tanto no es positiva ni definida positiva.

2) Dado que para todo $x, y, z$ , tenemos que $(x - y)^{2}, (y - z)^{2}, (z - x)^{2} \geq 0$ , entonces $q (v) \geq 0$ para todo $v \in R^{3}$ . Pero si $q (v) = 0$ , entonces $x = y = z$ , pero no necesariamente son iguales a cero. Por lo tanto, $q$ es positiva pero no es definida positiva.

3) Si tomamos $v = (3, 0, 3)$ , obtenemos que $\begin{aligned} q (v) & = (3)^{2} + (3)^{2} - 3 (3) (3) \\ = 9 + 9 - 27 \\ = - 9 \\ < 0. \end{aligned}$ Por lo tanto no es positiva ni definida positiva.

$△$

Problema 4. Sea $V = C ([a, b], R)$ . Prueba que el mapeo $⟨ \cdot, \cdot ⟩$ definido por $⟨ f, g ⟩ = \int_{a}^{b} f (x) g (x) d x$ es un producto interior en $V$ .

Solución. Por lo visto en la clase de ayer, tenemos que un producto interior es una forma bilineal simétrica y definida positiva.
Es fácil ver que es forma bilineal simétrica. Basta con probar que es una forma definida positiva. Entonces $⟨ f, f ⟩ = \int_{0}^{1} f^{2} (x) d x \geq 0$ ya que $f^{2} (x) \geq 0$ para toda $x$ . Por lo tanto $⟨ \cdot, \cdot ⟩$ es positiva. Como $f^{2}$ es continua y positiva, si $\int_{0}^{1} f^{2} (x) d x = 0$ , implica que $f^{2} = 0$ , entonces $f = 0$ . Por lo tanto, $⟨ \cdot, \cdot ⟩$ es definida positiva, y por ende, es un producto interior.

$△$

Para finalizar, el siguiente problema es un ejemplo que pareciera ser producto interior, pero resulta que no serlo.

Problema 5. Sea $C^{\infty} ([0, 1], R)$ es el espacio de funciones suaves (funciones continuas cuyas derivadas de cualquier orden existen y son continuas). Definimos el espacio $V = f \in C^{\infty} ([0, 1], R) : f (0) = f (1) = 0$ . Si definimos $⟨ f, g ⟩ := \int_{0}^{1} (f (x) g^{'} (x) + f^{'} (x) g (x)) d x,$ ¿es $⟨ \cdot, \cdot ⟩$ un producto interior en $V$ ?

Solución. Es claro ver que $⟨ \cdot, \cdot ⟩$ es bilineal y simétrica, entonces falta demostrar si es o no es una forma definida positiva. Para $f \in V$ , tenemos que $⟨ f, f ⟩ = \int_{0}^{1} 2 f (x) f^{'} (x) d x .$

Notemos que, por la regla de la cadena, $\frac{d}{d x} f^{2} (x) = 2 f (x) f^{'} (x)$ , entonces $\begin{aligned} ⟨ f, f ⟩ & = \int_{0}^{1} \frac{d}{d x} f^{2} (x) d x \\ = f^{2} (1) - f^{2} (0) \\ = 0. \end{aligned}$

Por lo tanto $⟨ f, f ⟩ = 0$ para toda $f$ . Esto implica que no es definida positiva, y como consecuencia, no es producto interior de $V$ .

$△$

Entradas relacionadas

Ir a Álgebra Lineal I
Entrada anterior del curso: Producto interior y desigualdad de Cauchy-Schwarz
Siguiente entrada del curso: Ángulos, norma, distancia y desigualdad de Minkowski

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104721 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM»

Álgebra Lineal I: Rango de transformaciones lineales y matrices

Por Leonardo Ignacio Martínez Sandoval

4 respuestas

Introducción

En entradas anteriores hablamos de transformaciones lineales, cómo actúan en conjuntos especiales de vectores y de cómo se pueden representar con matrices. Hablamos también de cómo cambiar de una base a otra y cómo usar esto para entender transformaciones en varias bases. Estamos listos para introducir un concepto fundamental de álgebra lineal, el de rango de una transformación lineal y de una matriz.

Antes de entrar en las definiciones formales, vale la pena hablar un poco de rango de manera intuitiva. Supongamos que $V$ es un espacio vectorial de dimensión $n$ y que $W$ es un espacio vectorial sobre el mismo campo que $V$ . Una transformación lineal $T : V \to W$ puede «guardar mucha independencia lineal» o «muy poquita». Si $T$ es inyectiva, ya vimos antes que $T$ manda linealmente independientes a linealmente independientes. Si $T$ es la transformación $0$ , entonces se «pierde toda la independencia».

El rango mide algo intermedio entre estos dos extremos. Mientras mayor sea el rango, más independencia lineal se preserva y viceversa. Si mantienes esta intuición en mente, varias de las proposiciones te resultarán más naturales.

Otro buen ejemplo para tener en mente es tomar una transformación lineal $T : R^{3} \to R^{3}$ . Si es la transformación identidad, la base canónica se preserva. Si es la proyección al plano $x y$ , entonces «perdemos» al vector $(0, 0, 1)$ , pues se va al $(0, 0, 0)$ . Si es la proyección al eje $x$ , «perdemos» al $(0, 1, 0)$ y al $(0, 0, 1)$ pues ambos se van a $(0, 0, 0)$ . Y si es la transformación $0$ , perdemos a todos. El rango precisamente va a medir esto, y para estos ejemplos tendremos rango $3$ , $2$ , $1$ y $0$ respectivamente.

Rango para transformaciones lineales

Como en otras ocasiones, cuando hablemos de transformaciones lineales entre espacios vectoriales, serán sobre un mismo campo $F$ .

Definición. Sean $V$ y $W$ espacios de dimensión finita. El rango de una transformación lineal $T : V \to W$ es la dimensión de la imagen de $T$ , es decir, $rank (T) = \dim Im T .$

Si $B$ es una base de $V$ , entonces genera a $V$ . La transformación $T$ es suprayectiva de $V$ a $Im T$ , de modo que $T (B)$ es generador de $Im T$ . De esta forma, para encontrar el rango de una transformación lineal $T : V \to W$ basta:

Tomar una base $B$ de $V$ .
Aplicar $T$ a cada elemento de $B$ .
Determinar un conjunto linealmente independiente máximo en $T (B)$ .

Para hacer este último paso, podemos poner a los vectores coordenada de $T (B)$ con respecto a una base de $W$ como los vectores fila de una matriz $A$ y usar reducción gaussiana. Las operaciones elementales no cambian el espacio generado por las filas, así que el rango de $T$ es el número de vectores fila no cero en la forma escalonada reducida $A_{red}$ de $A$ .

Ejemplo. Encuentra el rango de la transformación lineal $T : R^{3} \to M_{2} (R)$ que manda $(x, y, z)$ a $(\begin{matrix} x + y - z & 2 x \\ 2 y - 2 z & x + z - y \end{matrix}) .$

Solución. Tomemos $e_{1}, e_{2}, e_{3}$ la base canónica de $R^{3}$ . Tenemos que $T (e_{1}) = (\begin{matrix} 1 & 2 \\ 0 & 1 \end{matrix})$ , $T (e_{2}) = (\begin{matrix} 1 & 0 \\ 2 & - 1 \end{matrix})$ y $T (e_{3}) = (\begin{matrix} - 1 & 0 \\ - 2 & 1 \end{matrix})$ .

Tomando la base canónica $E_{11}, E_{12}, E_{21}, E_{22}$ de $M_{2} (R)$ , podemos entonces poner a las coordenadas de $T (e_{1}), T (e_{2}), T (e_{2})$ como vectores fila de una matriz $(\begin{matrix} 1 & 2 & 0 & 1 \\ 1 & 0 & 2 & - 1 \\ - 1 & 0 & - 2 & 1 \end{matrix}) .$ Sumando la segunda fila a la tercera, y después restando la primera a la segunda,obtenemos la matriz $(\begin{matrix} 1 & 2 & 0 & 1 \\ 0 & - 2 & 2 & - 2 \\ 0 & 0 & 0 & 0 \end{matrix}) .$ De aquí, sin necesidad de terminar la reducción gaussiana, podemos ver que habrá exactamente dos filas no cero. De este modo, el rango de la transformación es $2$ .

$△$

Propiedades del rango

Demostremos ahora algunas propiedades teóricas importantes acerca del rango de una transfromación lineal.

Proposición. Sean $U$ , $V$ y $W$ espacios de dimensión finita. Sean $S : U \to V$ , $T : V \to W$ , $T^{'} : V \to W$ transformaciones lineales. Entonces:

$rank (T) \leq \dim V$
$rank (T) \leq \dim W$
$rank (T \circ S) \leq rank (T)$
$rank (T \circ S) \leq rank (S)$
$rank (T + T^{'}) \leq rank (T) + rank (T^{'})$

Demostración. (1) Pensemos a $T$ como una transformación $T : V \to Im (T)$ . Haciendo esto, $T$ resulta ser suprayectiva, y por un resultado anterior tenemos que $\dim V \geq \dim Im T = rank (T)$ .

(2) Sabemos que $Im (T)$ es un subespacio de $W$ , así que $rank (T) = \dim Im T \leq \dim W$ .

(3) La imagen de $T$ contiene a la imagen de $T \circ S$ , pues cada vector de la forma $T (S (v))$ es de la forma $T (w)$ (para $w = S (v)$ ). Así, $\begin{aligned} rank (T) & = \dim Im T \geq \dim Im T \circ S \\ = rank (T \circ S) . \end{aligned}$

(4) La función $T \circ S$ coincide con la restricción $T_{Im S}$ de $T$ a $Im S$ . Por el inciso (1), $rank (T_{Im S}) \leq \dim Im S = rank (S)$ , así que $rank (T \circ S) \leq rank (S)$ .

(5) Tenemos que $Im (T + T^{'}) \subseteq Im T + Im T^{'}$ . Además, por un corolario de la fórmula de Grassman, sabemos que
$\begin{aligned} \dim (Im T + Im T^{'}) & \leq \dim Im T + \dim Im T^{'} \\ = rank (T) + rank (T^{'}) . \end{aligned}$

Así,
$\begin{aligned} rank (T + T^{'}) & \leq rank (Im T + Im T^{'}) \\ \leq rank (T) + rank (T^{'}) . \end{aligned}$

Proposición. Sean $R : U \to V$ , $T : V \to W$ y $S : W \to Z$ transformaciones lineales con $R$ suprayectiva y $S$ inyectiva. Entonces $rank (S \circ T \circ R) = rank (T) .$

Dicho de otra forma «composición por la izquierda con transformaciones inyectivas no cambia el rango» y «composición por la derecha con transformaciones suprayectivas no cambia el rango». Un corolario es «composición con transformaciones invertibles no cambia el rango».

Demostración. De la proposición anterior, tenemos que $rank (S \circ T) \leq rank (T)$ . La restricción $S_{Im T}$ de $S$ a la imagen de $T$ es una transformación lineal de $Im T$ a $Im (S \circ T)$ que es inyectiva, de modo que $\dim Im T \leq \dim Im (S \circ T)$ , que es justo $rank (T) \leq rank (S \circ T)$ , de modo que tenemos la igualdad $rank (S \circ T) = rank (T)$ .

Como $R$ es suprayectiva, $Im R = V$ , de modo que $Im (S \circ T \circ R) = Im (S \circ T)$ . Así, $\begin{aligned} rank (S \circ T \circ R) & = rank (S \circ T) \\ = rank (T) . \end{aligned}$

Teorema de rango-nulidad

Una transformación lineal $T : V \to W$ determina automáticamente dos subespacios de manera natural: el kernel $\ker T$ y la imagen $Im T$ . Resulta que las dimensiones de $\ker T$ , de $Im T$ y de $V$ están fuertemente relacionadas entre sí.

Teorema. Sean $V$ y $W$ espacios de dimensión finita. Sea $T : V \to W$ una transformación lineal. Entonces $\dim \ker T + rank (T) = \dim V .$

Demostración. Supongamos que $\dim V = n$ y $\dim \ker T = k$ . Queremos mostrar que $rank (T) = n - k$ . Para ello, tomemos una base $B$ de $\ker T$ y tomemos $B^{'} = {v_{1}, \dots, v_{n - k}}$ tal que $B \cup B^{'}$ sea base de $V$ . Basta mostrar que $T (B^{'}) = {T (v_{1}), \dots, T (v_{n - k})} \subset Im T$ es base de $Im T$ . Sea $U$ el generado por $B^{'}$ , de modo que $V = U \oplus \ker T$ .

Veamos que $T (B^{'})$ es generador de $Im T$ . Tomemos $T (v)$ en $Im T$ . Podemos escribir $v = z + u$ con $z \in \ker T$ y $u \in U$ . Así, $T (v) = T (z) + T (u) = T (u)$ , y este último está en el generado por $T (B^{'})$ .

Ahora veamos que $T (B^{'})$ es linealmente independiente. Si $α_{1} T (v_{1}) + \dots + α_{n - k} T (v_{n - k}) = 0,$ entonces $T (α_{1} v_{1} + \dots + α_{n - k} v_{n - k}) = 0$ , de modo que $α_{1} v_{1} + \dots + α_{n - k} v_{n - k}$ está en $U$ y en $\ker T$ , pero la intersección de estos espacios es ${0}$ . Como esta combinación lineal es $0$ y $B^{'}$ es linealmente independiente, $α_{1} = \dots = α_{n} = 0$ .

De esta forma, $T (B^{'})$ es linealmente independiente y genera a $Im T$ , de modo que $rank (T) = | B^{'} | = n - k$ .

Ejemplo. Consideremos de nuevo la transformación lineal $T : R^{3} \to M_{2} (R)$ que manda $(x, y, z)$ a $(\begin{matrix} x + y - z & 2 x \\ 2 y - 2 z & x + z - y \end{matrix}) .$ Muestra que $T$ no es inyectiva.

Solución. Ya determinamos previamente que esta transformación tiene rango $2$ . Por el teorema de rango-nulidad, su kernel tiene dimensión $1$ . Así, hay un vector $v \neq (0, 0, 0)$ en el kernel, para el cual $T (v) = 0 = T (0)$ , de modo que $T$ no es inyectiva.

Problema. Demuestra que para cualquier entero $n$ existe una terna $(a, b, c) \neq (0, 0, 0)$ con $a + b + c = 0$ y tal que $\int_{0}^{1} a t^{2 n} + b t^{n} + c d t = 0.$

Solución. Podríamos hacer la integral y plantear dos ecuaciones lineales. Sin embargo, daremos argumentos dimensionales para evitar la integral. Consideremos las transformaciones lineales $T : R^{3} \to R$ y $S : R^{3} \to R$ dadas por
$\begin{aligned} T (x, y, z) & = \int_{0}^{1} x t^{2 n} + y t^{n} + z d t \\ S (x, y, z) & = x + y + z . \end{aligned}$
Notemos que $T (0, 0, 1) = \int_{0}^{1} 1 d t = 1 = S (0, 0, 1)$ , de modo que ni $T$ ni $S$ son la transformación $0$ . Como su rango puede ser a lo más $\dim R = 1$ , entonces su rango es $1$ . Por el teorema de rango-nulidad, $\dim \ker S = \dim \ker T = 2$ . Como ambos son subespacios de $R^{3}$ , es imposible que $\ker S \cap \ker T = {0}$ , de modo que existe $(a, b, c)$ no cero tal que $T (a, b, c) = S (a, b, c) = 0$ . Esto es justo lo que buscábamos.

Rango para matrices

Definición. El rango de una matriz $A$ en $M_{m, n} (F)$ es el rango de la transformación lineal asociada de $F^{n}$ a $F^{m}$ dada por $X \mapsto A X$ . Lo denotamos por $rank (A)$ .

A partir de esta definición y de las propiedades de rango para transformaciones lineales obtenemos directamente las siguientes propiedades para rango de matrices.

Proposición. Sean $m$ , $n$ y $p$ enteros. Sea $B$ una matriz en $M_{n, p} (F)$ y $A$ , $A^{'}$ matrices en $M_{m, n} (F)$ . Sea $P$ una matriz en $M_{n, p} (F)$ cuya transformación lineal asociada es suprayectiva y $Q$ una matriz en $M_{r, m} (F)$ cuya transformación lineal asociada es inyectiva. Entonces:

$rank (A) \leq min (m, n)$
$rank (A B) \leq min (rank (A), rank (B))$
$rank (A + A^{'}) \leq rank (A) + rank (A^{'})$
$rank (Q A P) = rank (A)$

Como discutimos anteriormente, el rango de una transformación se puede obtener aplicando la transformación a una base y viendo cuál es el máximo subconjunto de imágenes de elementos de la base que sea linealmente independiente. Si tomamos una matriz $A$ en $M_{m, n} (F)$ , podemos aplicar esta idea con los vectores $e_{1}, \dots, e_{n}$ de la base canónica de $F^{n}$ . Como hemos visto con anterioridad, para cada $i = 1, \dots, n$ tenemos que el vector $A e_{i}$ es exactamente la $i$ -ésima columna de $A$ . Esto nos permite determinar el rango de una matriz en términos de sus vectores columna.

Proposición. El rango de una matriz en $M_{m, n} (F)$ es igual a la dimensión del subespacio de $F^{m}$ generado por sus vectores columna.

Problema. Determina el rango de la matriz $(\begin{matrix} 3 & 1 & 0 & 5 & 0 \\ 0 & 8 & 2 & - 9 & 0 \\ 0 & - 1 & 0 & 4 & - 2 \end{matrix}) .$

Solución. Como es una matriz con $3$ filas, el rango es a lo más $3$ . Notemos que entre las columnas están los vectores $(3, 0, 0)$ , $(0, 2, 0)$ y $(0, 0, - 2)$ , que son linealmente independientes. De esta forma, el rango de la matriz es $3$ .

$△$

A veces queremos ver que el rango de un producto de matrices es grande. Una herramienta que puede servir en estos casos es la desigualdad de Sylvester.

Problema (Desigualdad de Sylvester). Muestra que para todas las matrices $A$ , $B$ en $M_{n} (F)$ se tiene que $rank (A B) \geq rank (A) + rank (B) - n .$

Solución. Tomemos $T_{1} : F^{n} \to F^{n}$ y $T_{2} : F^{n} \to F^{n}$ tales que $T_{1} (X) = A X$ y $T_{2} (X) = B X$ . Lo que tenemos que probar es que $rank (T_{1} \circ T_{2}) \geq rank (T_{1}) + rank (T_{2}) - n .$

Consideremos $S_{1}$ como la restricción de $T_{1}$ a $Im T_{2}$ . Tenemos que $\ker S_{1} \subset \ker T_{1}$ , así que $\dim \ker S_{1} \leq \dim \ker T_{1}$ . Por el teorema de rango-nulidad en $S_{1}$ , tenemos que
$\begin{aligned} r a n k (T_{2}) & = \dim Im T_{2} \\ = \dim \ker S_{1} + rank (S_{1}) \\ = \dim \ker S_{1} + rank (T_{1} \circ T_{2}) \\ \leq \dim \ker T_{1} + rank (T_{1} \circ T_{2}), \end{aligned}$ así que $rank (T_{2}) \leq \dim \ker T_{1} + rank (T_{1} \circ T_{2}) .$

Por el teorema de rango-nulidad en $T_{1}$ tenemos que $\dim \ker T_{1} + rank (T_{1}) = n .$

Sumando la desigualdad anterior con esta igualdad obtenemos el resultado.

El teorema $P J Q$ (opcional)

El siguiente resultado no se encuentra en el temario usual de Álgebra Lineal I. Si bien no formará parte de la evaluación del curso, recomendamos fuertemente conocerlo y acostumbrarse a usarlo pues tiene amplias aplicaciones a través del álgebra lineal.

Teorema (Teorema PJQ). Sea $A$ una matriz en $M_{m, n} (F)$ y $r$ un entero en ${0, \dots, min (m, n)}$ . El rango de $A$ es igual a $r$ si y sólo si existen matrices invertibles $P \in M_{m} (F)$ y $Q \in M_{n} (F)$ tales que $A = P J_{r} Q$ , en donde $J_{r}$ es la matriz en $M_{m, n}$ cuyas primeras $r$ entradas de su diagonal principal son $1$ y todas las demás entradas son cero, es decir, en términos de matrices de bloque, $J_{r} = (\begin{matrix} I_{r} & 0 \\ 0 & 0 \end{matrix}) .$

No damos la demostración aquí. Se puede encontrar en el libro de Titu Andreescu, Teorema 5.68. Veamos algunas aplicaciones de este teorema.

Problema 1. Muestra que una matriz tiene el mismo rango que su transpuesta.

Solución. Llamemos $r$ al rango de $A$ . Escribimos $A = P J_{r} Q$ usando el teorema $P J Q$ , con $P$ y $Q$ matrices invertibles. Tenemos que $^{t} A =^{t} Q^{t} J_{r}^{t} P$ , con $^{t} Q$ y $^{t} P$ matrices invertibles. Además, $^{t} J_{r}$ es de nuevo de la forma de $J_{r}$ . Así, por el teorema $P J Q$ , tenemos que $^{t} A$ es de rango $r$ .

Combinando el problema anterior con el resultado del rango de una matriz en términos de sus vectores columna obtenemos lo siguiente.

Proposición. El rango de una matriz en $M_{m, n} (F)$ es igual a la dimensión del subespacio de $F^{n}$ generado por sus vectores renglón.

Terminamos esta entrada con una aplicación más del teorema $P J Q$ .

Problema 2. Muestra que una matriz $A$ de rango $r$ se puede escribir como suma de $r$ matrices de rango $1$ . Muestra que es imposible hacerlo con menos matrices.

Solución. Expresamos $A = P J_{r} Q$ usando el teorema $P J Q$ . Si definimos $A_{i} = P E_{i i} Q$ para $i = 1, \dots, r$ , donde $E_{i i}$ es la matriz cuya entrada $(i, i)$ es uno y las demás cero, claramente tenemos que $J_{r} = E_{11} + E_{22} + \dots + E_{r r}$ , por lo que $A = P J_{r} Q = A_{1} + A_{2} + \dots + A_{r} .$ Además, como $E_{i i}$ es de rango $1$ , por el teorema $P J Q$ cada matriz $A_{i}$ es de rango $1$ .

Veamos que es imposible con menos. Si $B_{1}, \dots, B_{s}$ son matrices de rango $1$ , como el rango es subaditivo tenemos que $rank (B_{1} + \dots + B_{s}) \leq s$ . Así, si sumamos menos de $r$ matrices, no podemos obtener a $A$ .

Más adelante…

Esta entrada es solamente una breve introducción al concepto de rango y a algunas propiedades que pueden ser de utilidad al momento de calcular el rango de una matriz o una transformación lineal. Más adelante, veremos que el rango de una matriz está también relacionado con las soluciones de su sistema lineal homogéneo asociado.

El teorema de rango-nulidad es fundamental para el álgebra lineal. Muchas veces necesitamos calcular el rango de la imagen de una transformación lineal, pero es mucho más fácil calcular la dimensión de su kernel. O viceversa. En estas situaciones es muy importante recordar la forma en la que dicho teorema las relaciona.

Con este tema termina la segunda unidad del curso. Ahora estudiaremos aspectos un poco más geométricos de espacios vectoriales. En la siguiente unidad, hablaremos de dualidad, ortogonalidad, formas bilineales y productos interiores.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Termina de hacer la reducción gaussiana del primer ejemplo.
Sea $T$ una transformación de un espacio vectorial $V$ de dimensión finita a si mismo. Usa el teorema de rango-nulidad para mostrar que si $T$ es inyectiva o suprayectiva, entonces es biyectiva.
Determina el rango de la matriz $(\begin{matrix} 0 & 0 & 0 & 8 & 3 \\ 7 & 8 & - 1 & - 2 & 0 \\ 3 & - 1 & 4 & 4 & - 9 \end{matrix}) .$
Demuestra que aplicar operaciones elementales a una matriz no cambia su rango.
Demuestra que matrices similares tienen el mismo rango.
Demuestra por inducción que para matrices $A_{1}, \dots, A_{n}$ del mismo tamaño tenemos que $rank (A_{1} + \dots + A_{n}) \leq \sum_{i = 1}^{n} rank (A_{i}) .$
Escribe la demostración de la última proposición de la sección del teorema $P J Q$
Revisa la demostración del teorema de descomposición $P J Q$ en el libro de Titu Andreescu.

Entradas relacionadas

Ir a Álgebra Lineal I
Entrada anterior del curso: Problemas de cambio de base
Siguiente entrada del curso: Problemas de rango de transformaciones y matrices

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104721 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM»

Álgebra Lineal I: Transformaciones lineales

Por Leonardo Ignacio Martínez Sandoval

14 respuestas

Introducción

En entradas pasadas ya platicamos de espacios vectoriales y de subespacios. También desarrollamos teoría de dimensión para espacios vectoriales de dimensión finita. Para ello, hablamos de conjuntos generadores, de independientes y de bases. Esto nos ayuda a entender a los espacios vectoriales «uno por uno». Lo que queremos entender ahora es cómo interactúan los espacios vectoriales entre sí. Para ello, hablaremos de transformaciones lineales entre espacios vectoriales.

Ya platicamos un poco de transformaciones lineales cuando estudiamos $F^{n}$ a detalle. En esa parte del curso, vimos cómo cualquier matriz en $M_{m, n} (F)$ se podía ver como una transformación lineal de $F^{n}$ a $F^{m}$ y viceversa. Retomaremos varias de estas ideas, pues son fundamentales para esta unidad y las siguientes.

La idea de esta entrada es:

Dar la intuición y definición de transformaciones lineales en general.
Probar propiedades básicas de las transformaciones lineales.
Dar varios ejemplos de transformaciones lineales.
Dar las definiciones de kernel (o núcleo) y de imagen para una transformación lineal.
Ver un ejemplo que abarque ambas definiciones.
Finalmente, probar que el kernel y la imagen son subespacios vectoriales.

A grandes rasgos, las transformaciones lineales se pueden pensar como «funciones bonitas» entre espacios vectoriales que «preservan las operaciones de suma y multiplicación por escalar».

Definición de transformaciones lineales

Definición. Para $V$ y $W$ espacios vectoriales sobre un campo $F$ , una transformación lineal entre $V$ y $W$ es una función $T : V \to W$ tal que:

Para todo $v_{1}$ y $v_{2}$ en $V$ se tiene que $T (v_{1} + v_{2}) = T (v_{1}) + T (v_{2})$ . Esto informalmente se le conoce como que « $T$ abre sumas».
Para todo $v$ en $V$ y $c$ en el campo $F$ se tiene que $T (c v) = c T (v)$ . A esto se le conoce como que « $T$ saca escalares».

En la primer condición la suma de la izquierda (dentro del paréntesis) es «la suma de $V$ » y la suma de la derecha es «la suma de $W$ ». De manera similar, en la segunda condición el producto por escalar de la izquierda (dentro del paréntesis) es el de $V$ y el de la derecha es el de $W$ .

En lo que resta de esta entrada, supondremos que los espacios vectoriales son sobre un mismo campo $F$ .

Ejemplos de tranformaciones lineales

Ejemplo 1. La función $T : R^{2} \to R$ dada por $T (x, y) = x + y + 1$ no es una transformación lineal. De hecho falla en ambas condiciones. Falla en abrir sumas pues, por ejemplo, $T (1, 1) = 3$ , $T (2, 2) = 5$ , pero $(1, 1) + (2, 2) = (3, 3)$ y $T (3, 3) = 7 \neq 5 = T (1, 1) + T (2, 2.)$ También falla en sacar escalares pues, por ejemplo $T (4, 2) = 7 \neq 8 = 2 T (2, 1) .$

$△$

Ejemplo 2. La función $T : R^{3} \to R^{3}$ dada por $T (x, y, z) = (2 x, 2 y, 2 z)$ es una transformación lineal.

Para convencernos de que esto es cierto, notemos que si $v = (x, y, z)$ entonces la transformación está dada por $T (v) = 2 v$ . Ahora, tomemos dos vectores $v_{1}$ y $v_{2}$ en $V$ , y un real $c$ . Tenemos por la asociatividad y conmutatividad de multiplicar por escalares en $R^{3}$ que: $\begin{aligned} T (v_{1} + v_{2}) & = 2 (v_{1} + v_{2}) \\ = 2 v_{1} + 2 v_{2} \\ = T (v_{1}) + T (v_{2}), \end{aligned}$ y que $T (c v_{1}) = 2 (c v_{1}) = c (2 v_{1}) = c T (v_{1}) .$ Esto muestra que $T$ es transformación lineal.

$△$

Ejemplo 3. De hecho, para cualquier espacio vectorial $V$ sobre el campo $F$ y $c$ un escalar de $F$ , la función $T : V \to V$ dada por $T (v) = c v$ es una transformación lineal. El argumento es similar.

$△$

Recuerda que $F_{n} [x]$ es el espacio vectorial de polinomios con coeficientes en $F$ y grado a lo más $n$ . Recuerda también que hemos visto muchos tipos de espacios vectoriales, los $F^{n}$ , los de polinomios, los de matrices, etc. Entre cualesquiera de ellos se pueden tener transformaciones lineales. La única condición es que sean espacios vectoriales sobre el mismo campo $F$ .

Ejemplo 4. La función $T : R^{2} \to R_{2} [x]$ que manda al vector $(a, b)$ al polinomio $x^{2} + (a - b) x + a b$ no es una transformación lineal. Esto lo podemos verificar viendo que falla la parte de sacar escalares. Por un lado $2 (T (1, 1)) = 2 (x^{2} + 1) = 2 x^{2} + 2,$ mientras que por otro lado $T (2, 2) = x^{2} + 4,$ así que $2 (T (1, 1)) \neq T (2, 2)$ , de modo que $T$ no saca escalares.

$△$

En cambio, si tomamos la función que manda al vector $(a, b)$ al polinomio $a x^{2} + (a - b) x + a + b$ , puedes verificar por tu cuenta que sí es una transformación lineal.

Ejemplo 5. La función $T : M_{2, 3} (R) \to R^{3}$ que manda a la matriz $M = (\begin{matrix} a & b & c \\ d & e & f \end{matrix})$ al vector $T (M) := (a - d, b - e, c - f)$ es una transfomación lineal.

Veamos que $T$ abre sumas. Tomemos dos matrices $M_{1} = (\begin{matrix} a_{1} & b_{1} & c_{1} \\ d_{1} & e_{1} & f_{1} \end{matrix})$ y $M_{2} = (\begin{matrix} a_{2} & b_{2} & c_{2} \\ d_{2} & e_{2} & f_{2} \end{matrix}) .$ Por un lado $\begin{aligned} T (M_{1}) & = (a_{1} - d_{1}, b_{1} - e_{1}, c_{1} - f_{1}) \\ T (M_{2}) & = (a_{2} - d_{2}, b_{2} - e_{2}, c_{2} - f_{2}), \end{aligned}$ de modo que sumando los vectores y reacomodando tenemos que $T (M_{1}) + T (M_{2}) = ((a_{1} + a_{2}) - (d_{1} + d_{2}), (b_{1} + b_{2}) - (e_{1} + e_{2}), (c_{1} + c_{2}) - (f_{1} + f_{2})) .$

Por otro lado, si primero sumamos las matrices, obtenemos la matriz $M_{1} + M_{2} = (\begin{matrix} a_{1} + a_{2} & b_{1} + b_{2} & c_{1} + c_{2} \\ d_{1} + d_{2} & e_{1} + e_{2} & f_{1} + f_{2} \end{matrix}) .$

Así, $T (M_{1} + M_{2}) = ((a_{1} + a_{2}) - (d_{1} + d_{2}), (b_{1} + b_{2}) - (e_{1} + e_{2}), (c_{1} + c_{2}) - (f_{1} + f_{2})) .$ Esto muestra que $T (M_{1} + M_{2}) = T (M_{1}) + T (M_{2})$ , es decir, que $T$ abre sumas. Con un argumento parecido se puede mostrar que saca escalares.

$△$

Ejemplo 6. La función $T : R^{2} \to R_{2} [x]$ que manda al vector $(a, b)$ al polinomio $T (a, b) = (a + b) x^{2} + (a - b) x + b$ es una transformación lineal.

$△$

Recuerda que $C [0, 1]$ es el espacio vectorial de funciones $f : [0, 1] \to R$ continuas.

Ejemplo 7. La función $T : C [0, 1] \to R$ que manda a la función $f$ al real $T (f) := \int_{0}^{1} f (x) d x$ es una transformación lineal. En efecto, para dos funciones $f$ y $g$ continuas en el $[0, 1]$ y un real $c$ se tiene por definición de suma de funciones, de multiplicación por escalar y de propiedades de la integral que $\begin{aligned} \int_{0}^{1} (f + g) (x) d x & = \int_{0}^{1} f (x) + g (x) d x \\ = \int_{0}^{1} f (x) d x + \int_{0}^{1} g (x) d x \end{aligned}$ y que $\begin{aligned} \int_{0}^{1} (c f) (x) d x & = \int_{0}^{1} c f (x) d x \\ = c \int_{0}^{1} f (x) d x . \end{aligned}$

En otras palabras, $T (f + g) = T (f) + T (g)$ y $T (c f) = c T (f)$ .

$△$

Propiedades básicas de transformaciones lineales

La definición de «transformación lineal» pide dos cosas por separado: abrir sumar y sacar escalares. Es bueno tenerlas por separado para referirnos a ellas individualmente. Sin embargo, la siguiente proposición nos ayuda a probar de manera más práctica que $T$ es una transformación lineal.

Proposición (verificación abreviada). Sean $V$ y $W$ espacios vectoriales sobre un mismo campo $F$ . $T : V \to W$ es una transformación lineal si y sólo si para todo $v_{1}, v_{2}$ en $V$ y $c$ en $F$ se tiene que $T (c v_{1} + v_{2}) = c T (v_{1}) + T (v_{2}) .$

Demostración. En efecto, si $T$ es transformación lineal, entonces $T (c v_{1}) = c T (v_{1})$ porque $T$ saca escalares y así $\begin{aligned} T (c v_{1} + v_{2}) & = T (c v_{1}) + T (v_{2}) \\ = c T (v_{1}) + T (v_{2}) . \end{aligned}$ Por otro lado, si se cumple $T (c v_{1} + v_{2}) = c T (v_{1}) + T (v_{2})$ para todos $v_{1}$ y $v_{2}$ vectores en $V$ y $c$ escalar en $F$ , entonces con $v_{2} = 0$ recuperamos que $T$ saca escalares y con $c = 1$ recuperamos que $T$ abre sumas.

Las transformaciones lineales mandan al cero de un espacio vectorial al cero del otro.

Proposición (cero va a cero). Sean $V$ y $W$ espacios vectoriales sobre un mismo campo. Si $T : V \to W$ es una transformación lineal, entonces $T (0) = 0$ .

Demostración. El truco es encontrar $T (0 + 0)$ de dos formas distintas. Por un lado, como $0 + 0 = 0$ , tenemos que $T (0 + 0) = T (0)$ . Por otro lado, como $T$ abre sumas, tenemos que $T (0 + 0) = T (0) + T (0)$ . Así, tenemos que $T (0) + T (0) = T (0) .$ Restando $T (0)$ de ambos lados obtenemos $T (0) = 0$ .

De hecho, hay otra forma de probar la proposición anterior usando que $T$ saca escalares: $T (0) = T (0 \cdot 0) = 0 T (0) = 0$ . Piensa en por qué cada una de estas igualdades se vale y por qué adentro del paréntesis que hay dos ceros, uno de ellos es vector y el otro escalar.

Las transformaciones lineales también «respetan» inversos aditivos.

Proposición (inversos aditivos van a inversos aditivos). Sean $V$ y $W$ espacios vectoriales sobre un mismo campo. Si $T : V \to W$ es una transformación lineal, entonces $T (- v) = - T (v)$ .

La demostración es sencilla y la puedes pensar por tu cuenta.

El haber enunciado estas proposiciones nos puede ayudar para decir, de golpe, que algunas funciones no son transformaciones lineales: si una función falla en tener alguna de las propiedades anteriores, entonces no es transformación lineal.

Ejemplo 1. Sea $V$ el espacio vectorial $R^{2}$ y $W$ el espacio vectorial de matrices de $2 \times 2$ con entradas complejas, pero visto como espacio vectorial sobre $R$ (sólo se permite usar reales para la multiplicación escalar).

La transformación $T : V \to W$ que manda al vector real $(a, b)$ a la matriz de entradas complejas $T (a, b) = (\begin{matrix} a + i b & a - i b \\ a - i b & 1 + a b i \end{matrix})$ no es una transformación lineal pues manda al $(0, 0)$ a la matriz $(\begin{matrix} 0 & 0 \\ 0 & 1 \end{matrix}),$ la cual no es la matriz $0$ .

$△$

Sin embargo, una pequeña advertencia. Es posible que $T$ sí mande el $0$ al $0$ , pero que de cualquier forma no sea una transformación lineal, debido a que falle por otras razones.

Ejemplo 2. La transformación $T : R^{3} \to R^{3}$ dada por $T (x, y, z) = (x + y + z, x y + y z + z x, x y z)$ cumple que $T (0, 0, 0) = (0, 0, 0)$ , pero no es una transformación lineal pues no saca escalares. Por ejemplo, $T (3, 3, 3) = (9, 27, 27) \neq 3 (3, 3, 1) = 3 T (1, 1, 1) .$

$△$

Kernel e imagen de una transformación lineal

Tomemos $T : V \to W$ una transformación lineal. Hay dos conjuntos muy importantes relacionados con $T$ .

El kernel (o núcleo) de $T$ es el conjunto de vectores en $V$ que se van al vector $0$ de $W$ cuando les aplicamos $T$ . En símbolos, $\ker (T) = {v \in V : T (v) = 0} .$

La imagen de $T$ son los vectores en $W$ que se pueden escribir de la forma $T (v)$ para algún $v$ en $V$ , es decir, es la imagen en el sentido clásico de teoría de conjuntos o de cálculo. En símbolos, $Im (T) = {T (v) : v \in V} .$

Haciendo énfasis de nuevo: $\ker (T)$ es un subconjunto de vectores de $V$ e $Im (T)$ es un subconjunto de vectores de $W$ . Veamos un ejemplo que nos ayudará a repasar varios de los conceptos clave de esta entrada.

Problema. Consideremos la transformación $T : M_{2} (R) \to M_{2, 3} (R)$ dada por $T (\begin{matrix} a & b \\ c & d \end{matrix}) = (\begin{matrix} a & b \\ c & d \end{matrix}) (\begin{matrix} 1 & 1 & 1 \\ 1 & 1 & 1 \end{matrix}) .$

Muestra que $T$ es una transformación lineal y determina $\ker (T)$ e $Im (T)$ .

Intenta resolver este problema por tu cuenta antes de seguir.

Solución. Sean $A$ y $B$ matrices de $2 \times 2$ con entradas reales y $r$ un real. Nombremos $C = (\begin{matrix} 1 & 1 & 1 \\ 1 & 1 & 1 \end{matrix})$ . Por propiedades de producto de matrices, tenemos que $\begin{aligned} T (r A + B) & = (r A + B) C \\ = r (A C) + B C \\ = r T (A) + T (B), \end{aligned}$ así que por la proposición de verificación abreviada, tenemos que $T$ es una transformación lineal.

Ahora, tomemos una matriz $A = (\begin{matrix} a & b \\ c & d \end{matrix})$ y notemos al hacer la multiplicación de manera explícita, obtenemos que $T (A)$ es la matriz $(\begin{matrix} a + b & a + b & a + b \\ c + d & c + d & c + d \end{matrix}) .$

Determinemos quién es $Im (T)$ . Para que una matriz $M := (\begin{matrix} e & f & g \\ h & i & j \end{matrix})$ esté en la imagen de $T$ , se tiene que cumplir que $e = f = g$ y que $h = i = j$ .

Y viceversa, si $e = f = g$ y $h = i = j$ , entonces $M$ está en la imagen de $T$ pues, por ejemplo $T (\begin{matrix} e & 0 \\ h & 0 \end{matrix}) = (\begin{matrix} e & e & e \\ h & h & h \end{matrix}) = M .$

Esto muestra que $Im (T) = {(\begin{matrix} e & e & e \\ h & h & h \end{matrix}) : e, h \in R} .$

Ahora determinemos quién es $\ker (T)$ . Para que $A$ esté en el kernel de $T$ , necesitamos que todas las entradas de $T (A)$ sean $0$ . Para esto es suficiente y necesario que $a + b = 0$ y que $c + d = 0$ , o dicho de otra forma, que $A$ sea de la forma $A = (\begin{matrix} a & - a \\ c & - c \end{matrix})$ . Así, concluimos que $\ker (T) = {(\begin{matrix} a & - a \\ c & - c \end{matrix}) : a, c \in R} .$

Con esto ya terminamos lo que pide el problema. Sin embargo, hagamos una observación clave. En el problema anterior, $\ker (T)$ e $Im (T)$ no solamente son subconjuntos de $M_{2} (R)$ y de $M_{2, 3} (R)$ respectivamente, sino que además son subespacios. Esto no es casualidad.

Los kernels e imágenes de transformaciones lineales son subespacios

Teorema. Sean $V$ y $W$ espacios vectoriales sobre un mismo campo. Si $T : V \to W$ es una transformación lineal, entonces $\ker (T)$ es un subespacio de $V$ e $Im (T)$ es un subespacio de $W$ .

Demostración. Demostraremos primero que $\ker (T)$ es un subespacio de $V$ . Para ello basta con tomar $v_{1}, v_{2}$ en $\ker (T)$ y $c$ en el campo $F$ y mostrar que $c v_{1} + v_{2}$ también está en $\ker (T)$ , es decir, que también sucede que $T (c v_{1} + v_{2}) = 0$ . Esto se debe a la siguiente cadena de igualdades, que justificamos abajo $\begin{aligned} T (c v_{1} + v_{2}) & = T (c v_{1}) + T (v_{2}) \\ = c T (v_{1}) + T (v_{2}) \\ = c \cdot 0 + 0 \\ = 0. \end{aligned}$

La primera igualdad se debe a que $T$ abre sumas. La segunda a que $T$ saca escalares. La tercera a que $v_{1}$ y $v_{2}$ están en el kernel de $T$ y por lo tanto sabemos que $T (v_{1}) = T (v_{2}) = 0$ . La última es simplemente hacer la operación. Con esto mostramos que $\ker (T)$ es un subespacio de $V$ .

Ahora, veremos que $Im (T)$ es un subespacio de $W$ . Tomemos $w_{1}$ y $w_{2}$ en $Im (T)$ , y un escalar $c$ en el campo $F$ . De nuevo, basta mostrar que $c w_{1} + w_{2}$ está en $Im (T)$ . Como $w_{1}$ y $w_{2}$ están en la imagen de $T$ , esto quiere decir que existen vectores $v_{1}$ y $v_{2}$ en $V$ tales que $T (v_{1}) = w_{1}$ y $T (v_{2}) = w_{2}$ . Notemos que entonces:
$\begin{aligned} c w_{1} + w_{2} & = c T (v_{1}) + T (v_{2}) \\ = T (c v_{1}) + T (v_{2}) \\ = T (c v_{1} + v_{2}) . \end{aligned}$

La segunda y tercera igualdad vienen de que $T$ saca escalares y abre sumas respectivamente. Esta cadena de igualdades muestra que podemos poner a $c w_{1} + w_{2}$ como imagen de alguien en $V$ bajo $T$ , es decir, que $c w_{1} + w_{2}$ pertenece a $Im (T)$ . Esto es lo que queríamos mostrar.

Más adelante…

En esta entrada definimos los conceptos de transformación lineal, de imagen y de kernel. También vimos que la imagen y kernel de transformaciones lineales son subespacios. Más adelante veremos que $\ker (T)$ e $Im (T)$ están de hecho relacionados más profundamente.

Por ahora, nota que en el ejemplo antes del teorema tenemos que $(\begin{matrix} 1 & 1 & 1 \\ 0 & 0 & 0 \end{matrix})$ y $(\begin{matrix} 0 & 0 & 0 \\ 1 & 1 & 1 \end{matrix})$ forman una base de $Im (T)$ pues son linealmente independientes y todo elemento en la imagen es combinación lineal de estas matrices. Además, nota que de manera similar $(\begin{matrix} 1 & - 1 \\ 0 & 0 \end{matrix})$ y $(\begin{matrix} 0 & 0 \\ 1 & - 1 \end{matrix})$ forman una base de $\ker (T)$ .

Esto nos dice que $\dim (Im (T)) = 2$ y que $\dim (\ker (T)) = 2$ . Si sumamos ambos, nos da la dimensión de $M_{2} (R)$ . ¿Será casualidad?

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero te servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

Verifica que las transformaciones lineales que se pusieron como ejemplo en efecto abren sumas y sacan escalares.
Asegúrate de entender los detalles de la prueba de la proposición de la verificación abreviada. Úsala para mostrar que la función que manda al vector $(a, b, c)$ a la matriz $(\begin{matrix} a & b & c \\ c & a & b \\ b & c & a \end{matrix})$ es una transformación lineal de $R^{3}$ a $M_{3} (R)$ .
Muestra la proposición de que inversos aditivos van a inversos aditivos.
Determina el kernel y la imagen de las transformaciones lineales $T : V \to W$ que se dieron como ejemplo.
Para cada kernel e imagen que encuentres, convéncete de que son subespacios. Determina si tienen dimensión finita y, en ese caso, determina la dimensión. Para estos casos, ¿cómo están relacionados $\dim (Im (T)), \dim (\ker (T)), \dim (V)$ ?

Entradas relacionadas

Ir a Álgebra Lineal I
Entrada anterior del curso: Problemas de bases y dimensión de espacios vectoriales
Siguiente entrada del curso: Proyecciones, simetrías y subespacios estables

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104721 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM»

El blog de Leo

Aprendiendo, creando y compartiendo matemáticas

Archivo de la etiqueta: kernel

Álgebra Moderna I: Núcleo e Imagen de un Homomorfismo

Introducción

El núcleo y la imagen de un homomorfismo

El núcleo y la imagen son subgrupos

Proyección Canónica

Ejemplos

Tarea moral

Más adelante…

Entradas relacionadas

Álgebra Lineal I: Problemas de formas cuadráticas y producto interior

Introducción

Problemas resueltos de formas cuadráticas

Problemas resueltos de producto interior

Entradas relacionadas

Agradecimientos

Álgebra Lineal I: Rango de transformaciones lineales y matrices

Introducción

Rango para transformaciones lineales

Propiedades del rango

Teorema de rango-nulidad

Rango para matrices

El teorema $P J Q$ (opcional)

Más adelante…

Tarea moral

Entradas relacionadas

Agradecimientos

Álgebra Lineal I: Transformaciones lineales

Introducción

Definición de transformaciones lineales

Ejemplos de tranformaciones lineales

Propiedades básicas de transformaciones lineales

Kernel e imagen de una transformación lineal

Los kernels e imágenes de transformaciones lineales son subespacios

Más adelante…

Tarea moral

Entradas relacionadas

Agradecimientos

Introducción

El núcleo y la imagen de un homomorfismo

El núcleo y la imagen son subgrupos

Proyección Canónica

Ejemplos

Tarea moral

Más adelante…

Entradas relacionadas

Introducción

Problemas resueltos de formas cuadráticas

Problemas resueltos de producto interior

Entradas relacionadas

Agradecimientos

Introducción

Rango para transformaciones lineales

Propiedades del rango

Teorema de rango-nulidad

Rango para matrices

El teorema PJQ (opcional)

Más adelante…

Tarea moral

Entradas relacionadas

Agradecimientos

Introducción

Definición de transformaciones lineales

Ejemplos de tranformaciones lineales

Propiedades básicas de transformaciones lineales

Kernel e imagen de una transformación lineal

Los kernels e imágenes de transformaciones lineales son subespacios

Más adelante…

Tarea moral

Entradas relacionadas

Agradecimientos

El teorema $P J Q$ (opcional)