Introducción
En la primera entrada de esta unidad [1a entrada] indicamos que serán muy importantes tanto las propiedades de los vectores como los lugares geométricos vistos en las primeras dos unidades, pues serán de vital apoyo para comprender los tipos de transformaciones que estaremos viendo.
En la entrada anterior [2a entrada] contemplamos los conceptos necesarios de las funciones que nos ayudaron a definir formalmente a una transformación. En ésta entrada vamos a comenzar por dos conjuntos: $\Delta_{2}$ y $\Delta_{3}$, las propiedades que cumplen y que nos ayudarán a comprender la definición de un grupo. Ambos conjuntos son los ejemplos más representativos de los grupos de transformaciones: los grupos simétricos de orden n. Pretendemos dar a conocer el tema en éste primer curso de Geometría Analítica de forma introductoria; pero puede profundizarse en asignaturas más avanzadas de la carrera universitaria, una de ellas es Álgebra Moderna en la Teoría de Grupos.
El conjunto $\Delta_{2}$
Antes que nada nos pondremos de acuerdo en la notación que vamos a usar: $x \mapsto y$ nos indicará que al elemento $x$ le corresponde el elemento $y$ bajo la función correspondiente.
El primero conjunto que conoceremos tiene dos elementos $\{ 0,1 \}$, a quien identificaremos por $\Delta_{2}$ y se lee «delta-dos». ¿Cuáles son las funciones de $\Delta_{2}$ en sí mismas? Primero tenemos a
\begin{align*}
0 & \xmapsto{id} 0\\
1 & \mapsto 1\\
\end{align*}
a quien llamaremos por $id$ (identidad de $\Delta_{2}$); porque al elemento $0$ le corresponde él mismo y al elemento $1$ le corresponde él mismo. La siguiente función es
\begin{align*}
0 & \xmapsto{\rho} 1\\
1 & \mapsto 0\\
\end{align*}
que denotamos por $\rho$. ¿Qué ocurre si recurrimos a la función composición $\rho \circ \rho$? Si comenzamos con $0$ sabemos bajo $\rho$ que $\rho (0) = 1$, por ello
\begin{align*}
(\rho \circ \rho)(0) &= \rho [\rho (0)]\\
& = \rho (1) = 0.\\
\end{align*}
Y si comenzamos con $\rho (1)$, en forma análoga obtendremos $(\rho \circ \rho)(1) = 1$. Podemos darnos cuenta que $\rho$ es su propio inverso, pues $(\rho \circ \rho = id)$.
Otra forma en que podemos trabajar la composición de funciones es siguiendo los elementos mediante una tablita. Vamos a ver que $\rho \circ \rho = id$ como sigue:
\begin{align*}
0 & \xmapsto{p} 1 \xmapsto{p} 0\\
1 & \mapsto 0 \mapsto 1\\
\end{align*}
donde colocamos la función correspondiente sobre cada flecha entre los elementos y nos damos cuenta que los elementos iniciales coinciden con las imágenes finales bajo la composición. Entonces concluimos que se cumple $\rho \circ \rho = id$.
Tenemos otras dos funciones:
\begin{align*}
0 & \xmapsto{C_{0}} 0 \hspace{0.2cm} & 0 \xmapsto{C_{1}} 1\\
1 & \mapsto 0 \hspace{0.18cm} &1 \mapsto 1\\
\end{align*}
e independientemente del elemento inicial, bajo $C_{0}$ corresponde el elemento $0$ y bajo $C_{1}$ corresponde el elemento $1$. Tanto $C_{0}$ como $C_{1}$ se consideran funciones constantes; mientras que las únicas transformaciones que contemplaremos de $\Delta_{2}$ son $ id $ y $ \rho $.
El conjunto $\Delta_{3}$
Ahora consideremos al conjunto $\Delta_{3} := \{ 0,1,2 \}$ e indicaremos las funciones de $\Delta_{3}$ en sí mismo bajo la notación
\begin{align*}
0 & \mapsto x\\
1 & \mapsto y\\
2 & \mapsto z
\end{align*}
donde $x, y, z \in \Delta_{3}$. Como $x, y, z \in \Delta_{3}$ son imágenes arbitrarias, habrán $3^3 = 27$ funciones, pero sólo 6 serán transformaciones. Vamos a explicar porqué sólo 6 transformaciones: puesto que queremos biyectividad, al elegir a $0$ y corresponderle su imagen, entonces al $1$ le podrán corresponder sólo $2$ opciones y a su vez, cuando llegamos al $2$, ya sólo le podrá corresponder $1$ opción. En resumen, en la primera posición hay $3$ opciones, en la segunda hay $2$ opciones y en la tercera sólo $1$ y el número de transformaciones será de $3 \times 2 \times 1 = 6$.
Las primeras 3 transformaciones que veremos son:
\begin{align*}
&0 \xmapsto{id} 0 &0 \xmapsto{\rho_{1}} 1& \hspace{0.2cm} &0 \xmapsto{\rho_{2}} 2\\
&1 \mapsto 1 &1 \mapsto 2 & \hspace{0.2cm} &1 \mapsto 0\\
&2 \mapsto 2 &2 \mapsto 0 & \hspace{0.2cm} &2 \mapsto 1
\end{align*}
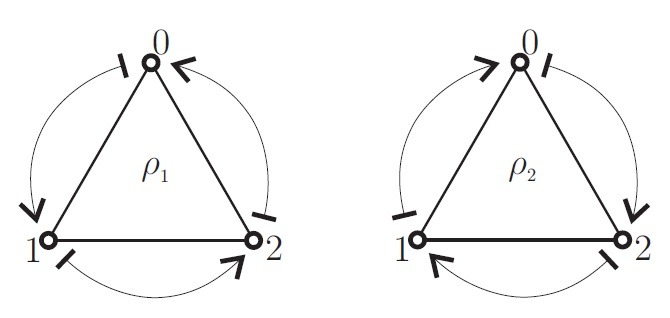
De hecho a las 6 transformaciones las visualizaremos como las «simetrías» de un triángulo equilátero. Las primeras 3 corresponden a rotaciones (la identidad es quien rota $0$ grados). Diremos que $\rho_{1}$ y $\rho_{2}$ son inversas, pues $\rho_{1} \circ \rho_{2} = \rho_{2} \circ \rho_{1} = id$ (vamos a dejar esta relación como ejercicio de la tarea moral, para practicar). Es decir, con cualquier elemento inicial, la imagen de la composición será el mismo elemento inicial. Esto quiere decir que una rotación rotará $120°$ en una dirección y al aplicar la segunda rotación rota $120°$ pero en dirección contraria. Los triángulos correspondientes son:
También se cumple que $\rho_{1} \circ \rho_{1} = \rho_{2}$, pues
\begin{align*}
0 & \xmapsto{\rho_{1}} 1 \xmapsto{\rho_{1}} 2\\
1 & \mapsto 2 \mapsto 0 \\
2 & \mapsto 0 \mapsto 1
\end{align*}
Entonces decimos que cumple la siguiente definición:
Definición. Sea $f$ cualquier transformación, decimos que
\begin{equation*}
f^{n} = f \circ f \circ \cdots \circ f,
\end{equation*}
es decir, $f^{n}$ es $f$ compuesta consigo misma n veces.
En nuestro ejemplo, escribiremos que se cumple entonces la relación $\rho_{1}^{2} = \rho_{2}$. Por otro lado, para $\Delta_{3}$ tenemos otras 3 transformaciones llamadas transposiciones que geométricamente las visualizamos como reflexiones y son:
\begin{align*}
&0 \xmapsto{\alpha} 0 & 0 \xmapsto{\beta} 2 & \hspace{0.2cm} & 0 \xmapsto{\gamma} 1\\
&1 \mapsto 2 &1 \mapsto 1 & \hspace{0.2cm} &1 \mapsto 0\\
&2 \mapsto 1 &2 \mapsto 0 & \hspace{0.2cm} &2 \mapsto 2
\end{align*}
El triángulo que representa a estas transformaciones es:
Las direcciones de la flecha dependerán de cada transformación. Ahora vamos a probar una relación que cumple $ \alpha, $ la cual es:
Demostrar que se cumple $\alpha^{2} = id$.
Demostración. En efecto, recordemos que $ \alpha^{2} = \alpha \circ \alpha$, así que desarrollaremos el seguimiento de elementos a través de la composición $\alpha \circ \alpha$ como sigue:
\begin{align*}
0 & \xmapsto{\alpha} 0 \xmapsto{\alpha} 0\\
1 & \mapsto 2 \mapsto 1 \\
2 & \mapsto 1 \mapsto 2
\end{align*}
y observemos que al final de la composición obtuvimos $\alpha^2 (0)=0$, $\alpha^2 (1)=1$, $\alpha^2 (2)=2$ y con ello vemos que $\alpha^{2}=id.$
$\square$
En la sección de tarea moral dejaremos unos ejercicios de práctica sobre más relaciones que cumplen $\alpha$, $\beta$ y $\gamma$; como son $\alpha^2 = \beta^2 = \gamma^2 = id$, $\alpha \circ \beta = \rho_{1}$ y que $\alpha \circ \beta \circ \alpha = \beta \circ \alpha \circ \beta = \gamma$.
A continuación vamos a definir a un conjunto de transformaciones que cumplen ciertas propiedades interesantes y para ejemplificar a dicho conjunto retomaremos uno de los conjuntos vistos en esta entrada.
Grupos de transformaciones
Definición. A un conjunto $G$ de transformaciones de un conjunto $A$ le llamaremos un grupo de transformaciones de $A$ si cumple:
- $id_{A} \in G$
- $f,g \in G \longrightarrow g \circ f \in G$
- $f \in G \longrightarrow f^{-1} \in G$
Como ejemplos, tomemos a $A$ como $A = \Delta_{3}$. Sabemos que tiene 6 elementos, pero un grupo de transformaciones es el de las rotaciones ya que contiene a la identidad $(1)$, es cerrado bajo la composición $(2)$ y es cerrado bajo inversas $(3)$.
Otro grupo de transformaciones de $A=\Delta_{3}$ es el de las transposiciones (o reflexiones) junto con la identidad.
Definición. Dado un conjunto cualquiera de transformaciones de $A$, el grupo que genera es el grupo de transformaciones obtenido de todas las posibles composiciones con elementos de él o sus inversos.
Como ejemplo de un grupo que genera tenemos a $\alpha$ y $\beta$ ya que generan todas las transformaciones de $\Delta_{3}$.
También $\rho_{1}$ genera el grupo de rotaciones de $\Delta_{3}$ ( porque $\rho^{3} = id$, $\rho_{1}$ y $\rho^{2} = \rho_{2}$).
Para terminar con esta entrada daremos un concepto adicional. Si te llamaron la atención los conjuntos $\Delta_{2}$ y $\Delta_{3}$ y quieres saber más de ellos o si hay más conjuntos similares, la respuesta es sí. Pertenecen a un conjunto de transformaciones, el cual definiremos a continuación:
Definición. Al conjunto de todas las transformaciones de un conjunto con $n$ elementos $\Delta_{n} := \{ 0, 1, \cdots, n-1 \}$ se le llama grupo simétrico de orden $n$ y se le denota $S_{n}$. Dicho grupo tiene $n! = n \times (n-1) \times (n-2 ) \cdots \times 2 \times 1$ ($n$ factorial) elementos a los cuales se le llaman permutaciones.
Tarea moral
- Considerando el conjunto $\Delta_{3}$ y sus transformaciones $id$, $\rho_{1}$ y $\rho_{2}$ que vimos en esta entrada, demostrar que $\rho_{1}$ y $\rho_{2}$ son inversas, es decir:
- $\rho_{1} \circ \rho_{2} = \rho_{2} \circ \rho_{1} = id$
- Considerando el conjunto $\Delta_{3}$ y sus transformaciones $id$, $\alpha$, $\beta$ y $\gamma$ que vimos en esta entrada, demostrar que se cumplen las relaciones siguientes:
- $\alpha^2 = \beta^2 = \gamma^2 = id$. [Sugerencia: Hacer cada composición por separado].
- $\alpha \circ \beta = \rho_{1}$
- $\alpha \circ \beta \circ \alpha = \beta \circ \alpha \circ \beta = \gamma$.
- Demuestren que $\rho_{1}$ genera el grupo de rotaciones de $\Delta_{3}$. [Sugerencia: Demuestren que se cumplen las relaciones $\rho^{3} = id$, y $\rho^{2} = \rho_{2}$), porque $\rho_{1}$ es un elemento de dicho grupo de rotaciones].
Más adelante
En esta entrada vimos que en el conjunto $\Delta_{3}$ hay dos posibles grupos de transformaciones: el de las rotaciones y el de las transposiciones junto con la identidad. Mediante triángulos pudimos visualizar el comportamiento que hay en los elementos iniciales y sus imágenes; con ello se comprende porque están en cada grupo.
En la siguiente entrada continuaremos con un primer grupo de transformaciones en los \mathbb{R}, que es de las transformaciones afines, que tiene una muy buena relación con un lugar geométrico que ya hemos visto: las rectas. La entrada [Rectas en forma paramétrica] de la Unidad 1 nos podrá ayudar como repaso si lo requerimos.
Enlaces
- Página principal del curso:
- Entrada anterior del curso:
- Siguiente entrada del curso: