Archivo de la etiqueta: circuncentro

Geometría Moderna I: Circunferencias tritangentes

Por Rubén Alexander Ocampo Arellano

Deja un comentario

Introducción

En esta ocasión estudiaremos algunas propiedades de las circunferencias tritangentes de un triángulo, esto nos permitirá entre otras cosas, derivar formulas para el área del triángulo.

Definición 1. El incírculo $(I, r)$ y los tres excírculos $(I_a, r_a)$, $(I_b, r_b)$ y $(I_c, r_c)$ de un triángulo a veces son referidos como las circunferencias tritangentes del triángulo, sus centros como centros tritangentes y sus radios, radios tritangentes.

Centros tritangentes

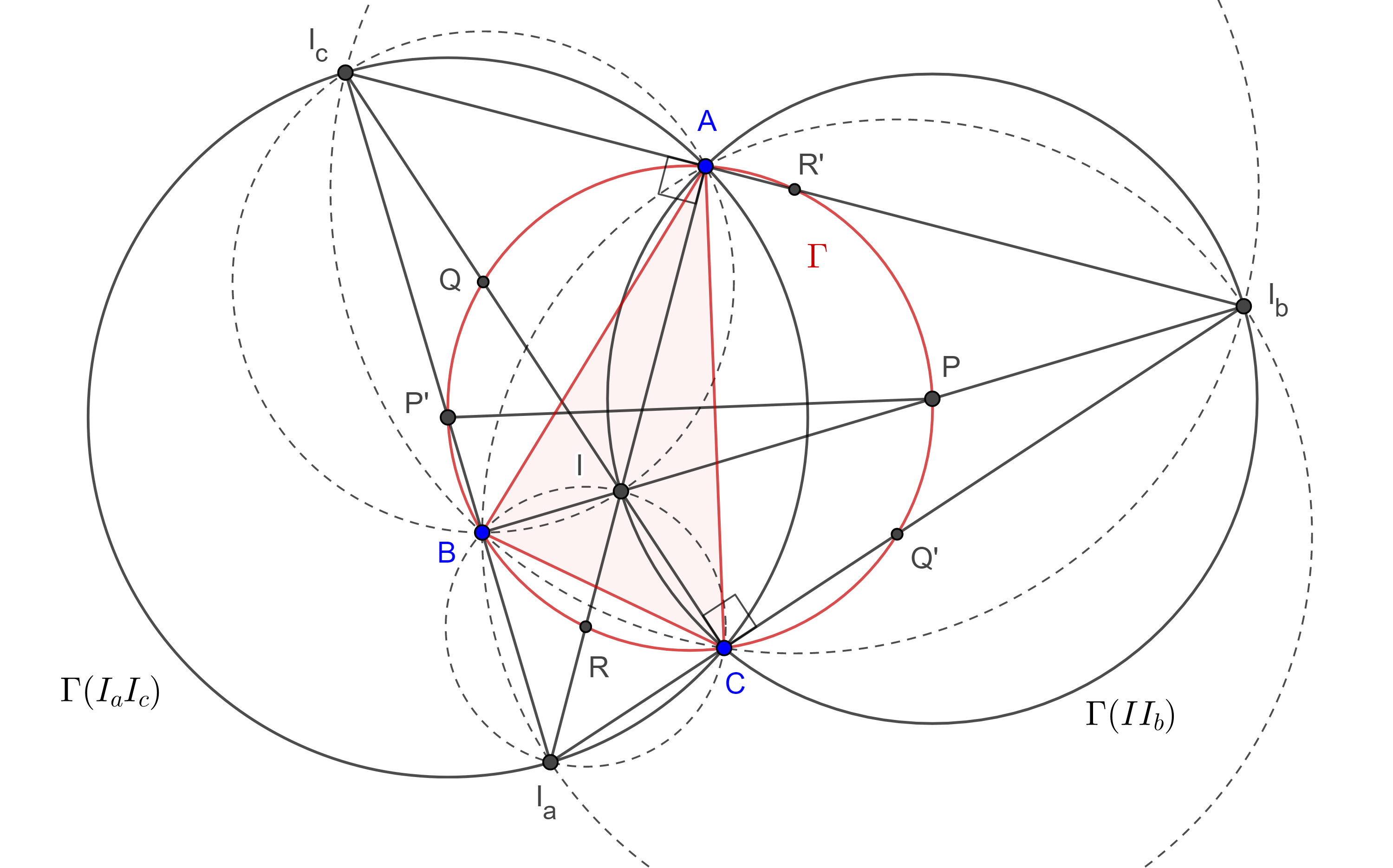
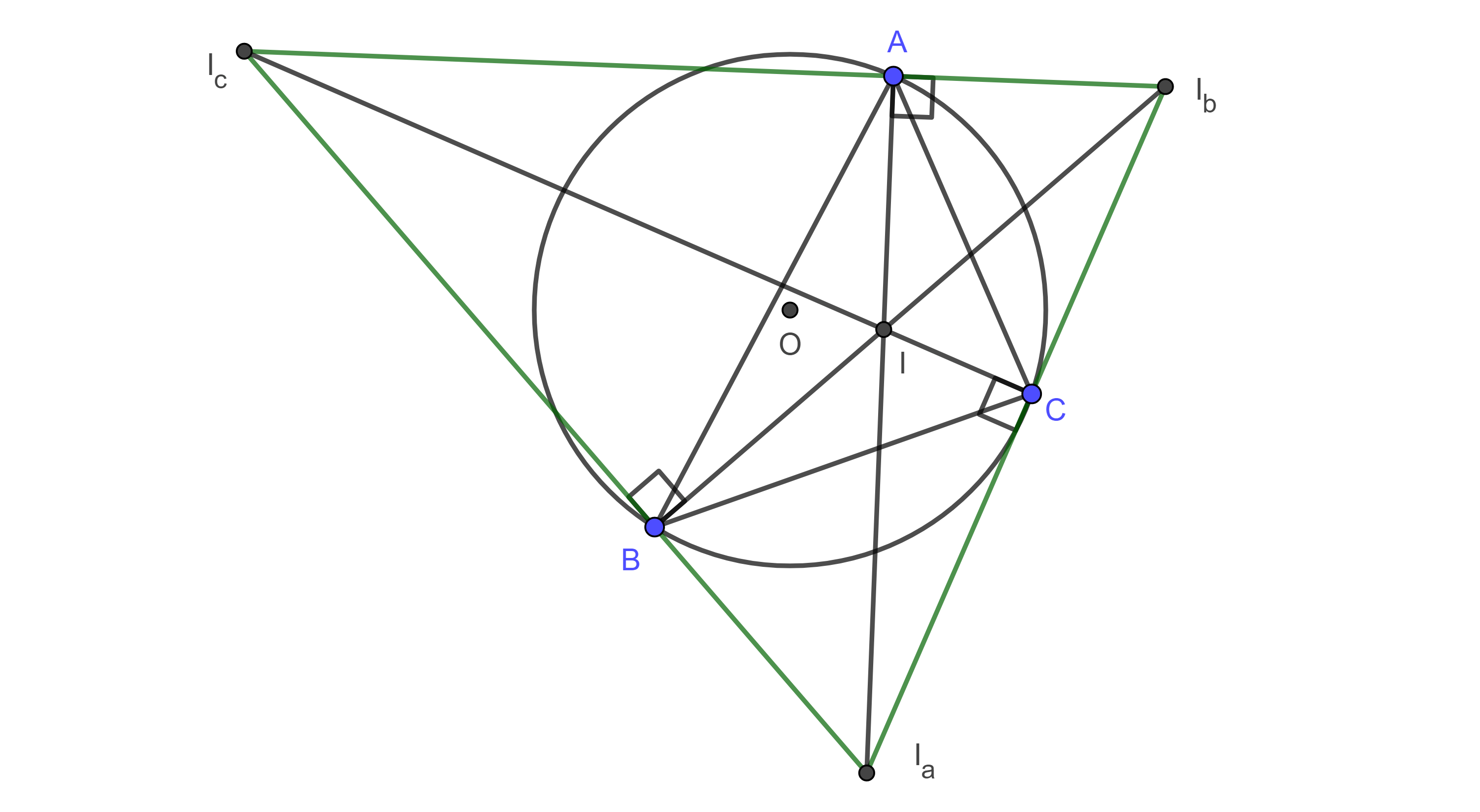
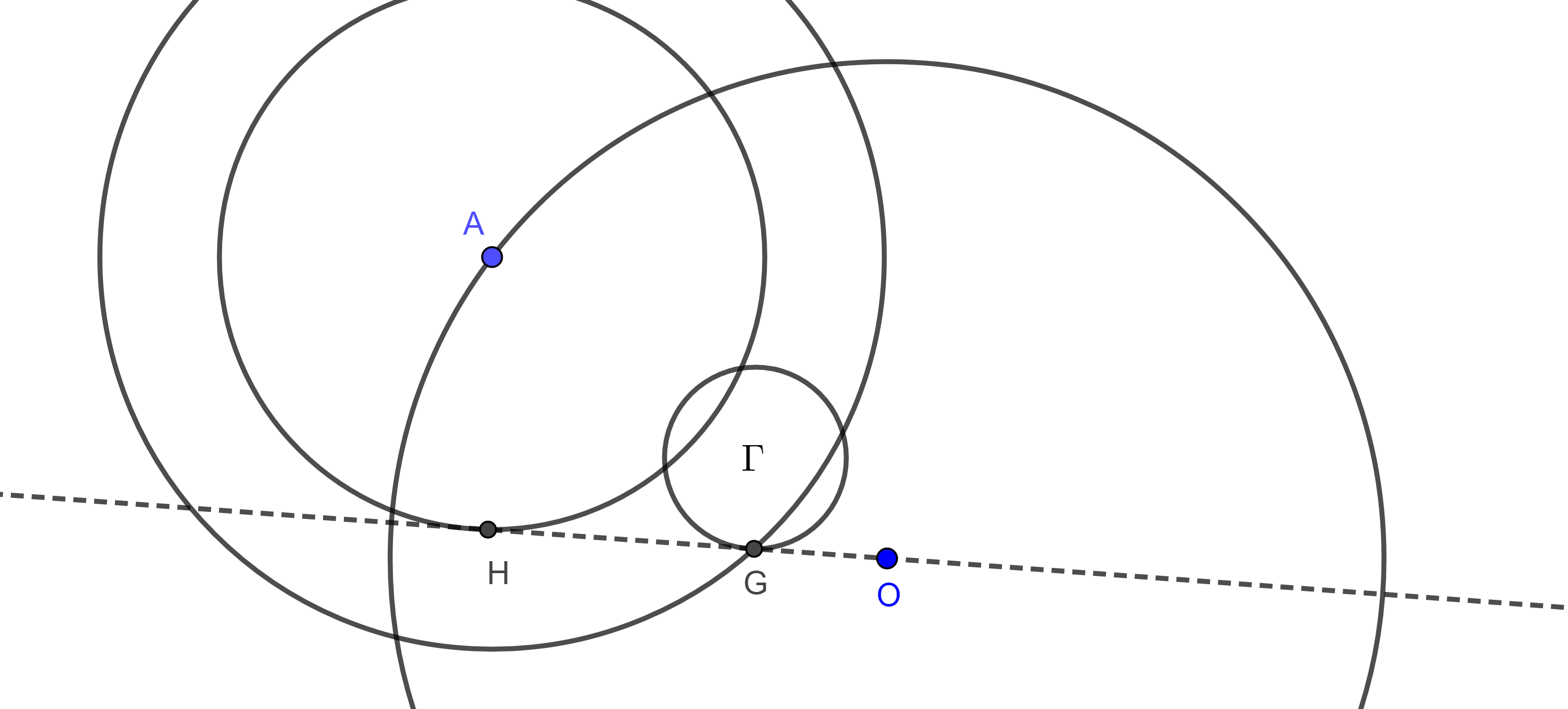
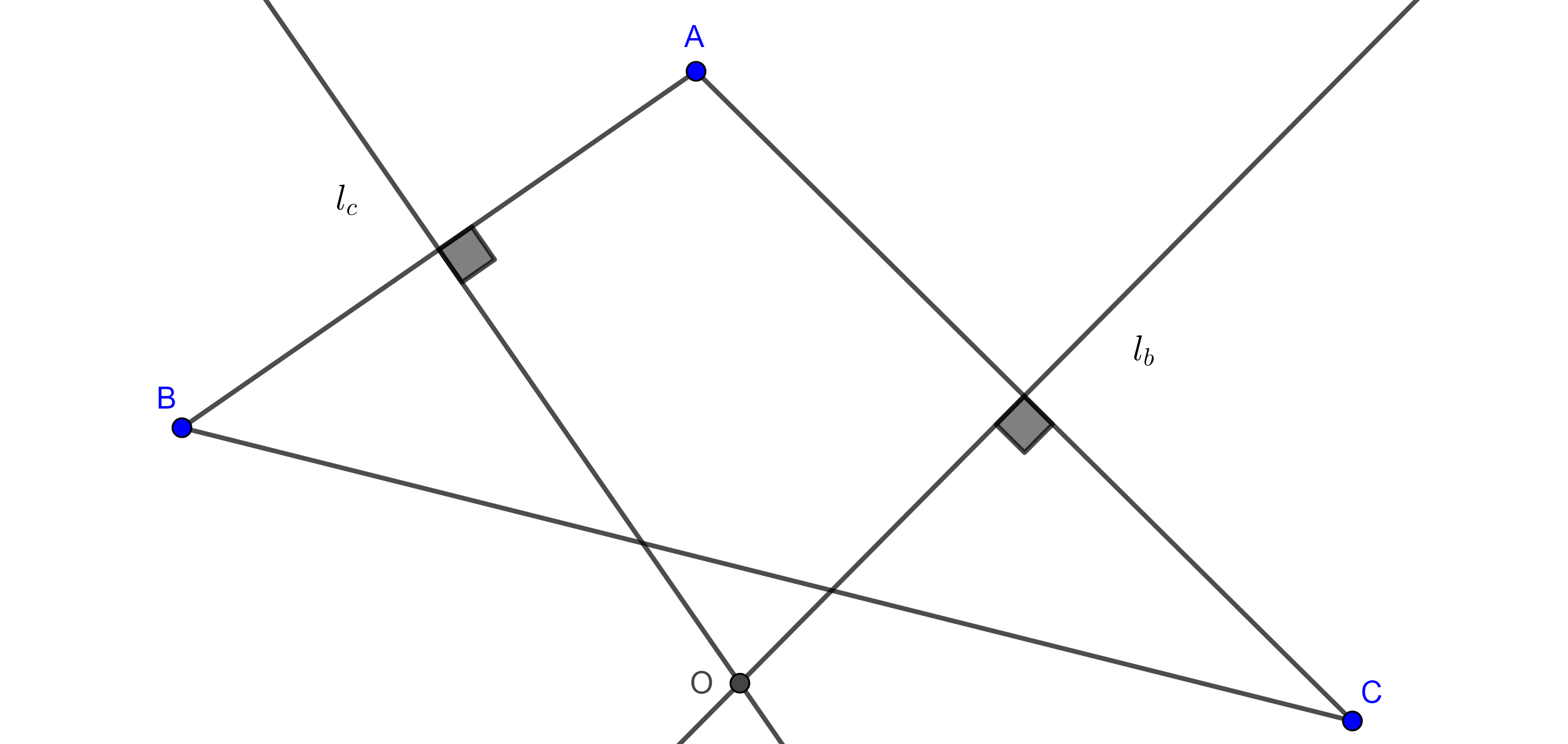
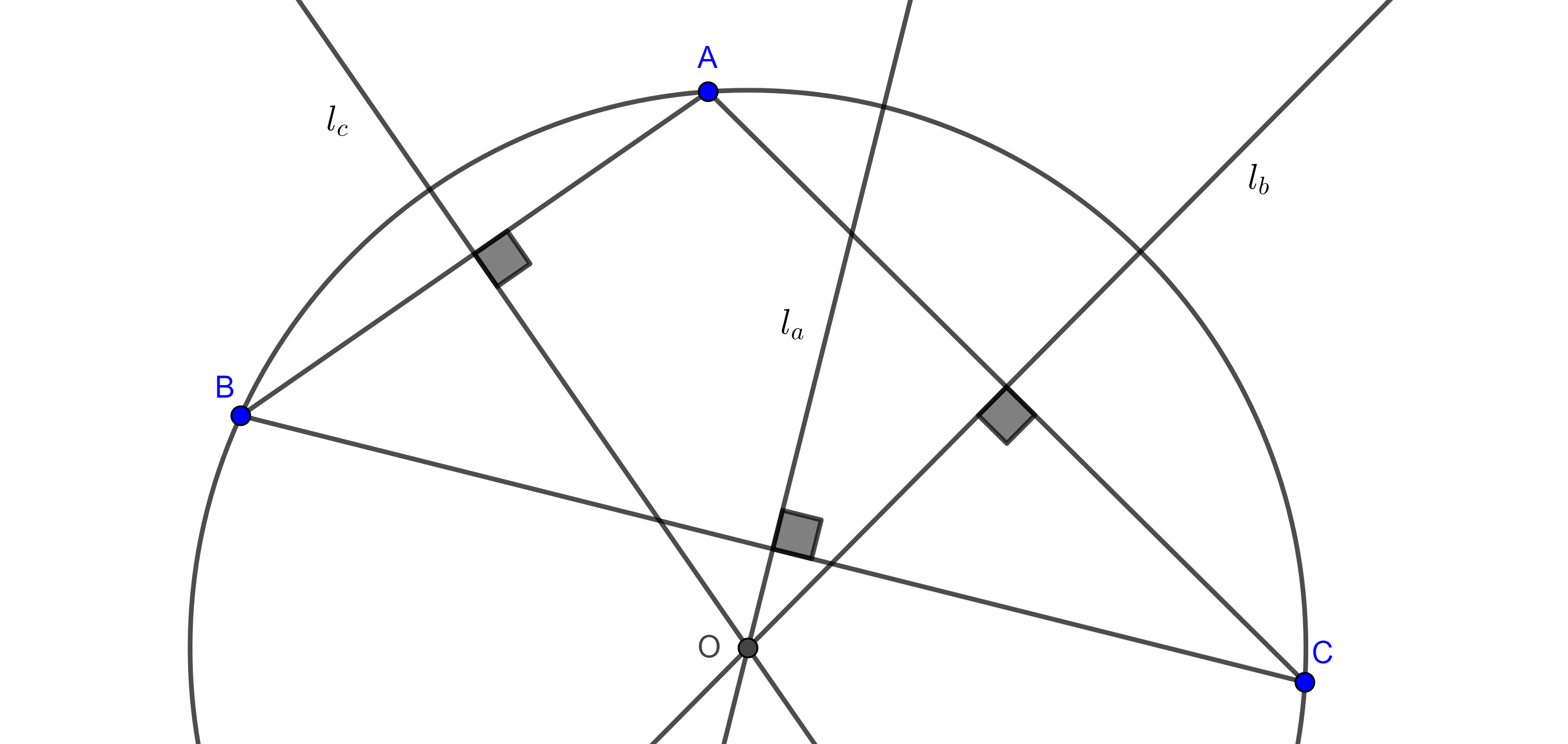
Teorema 1. El segmento que une dos centros tritangentes de un triángulo es el diámetro de una circunferencia que contiene dos de los vértices del triángulo, los cuales no son colineales con los centros tritangentes considerados.

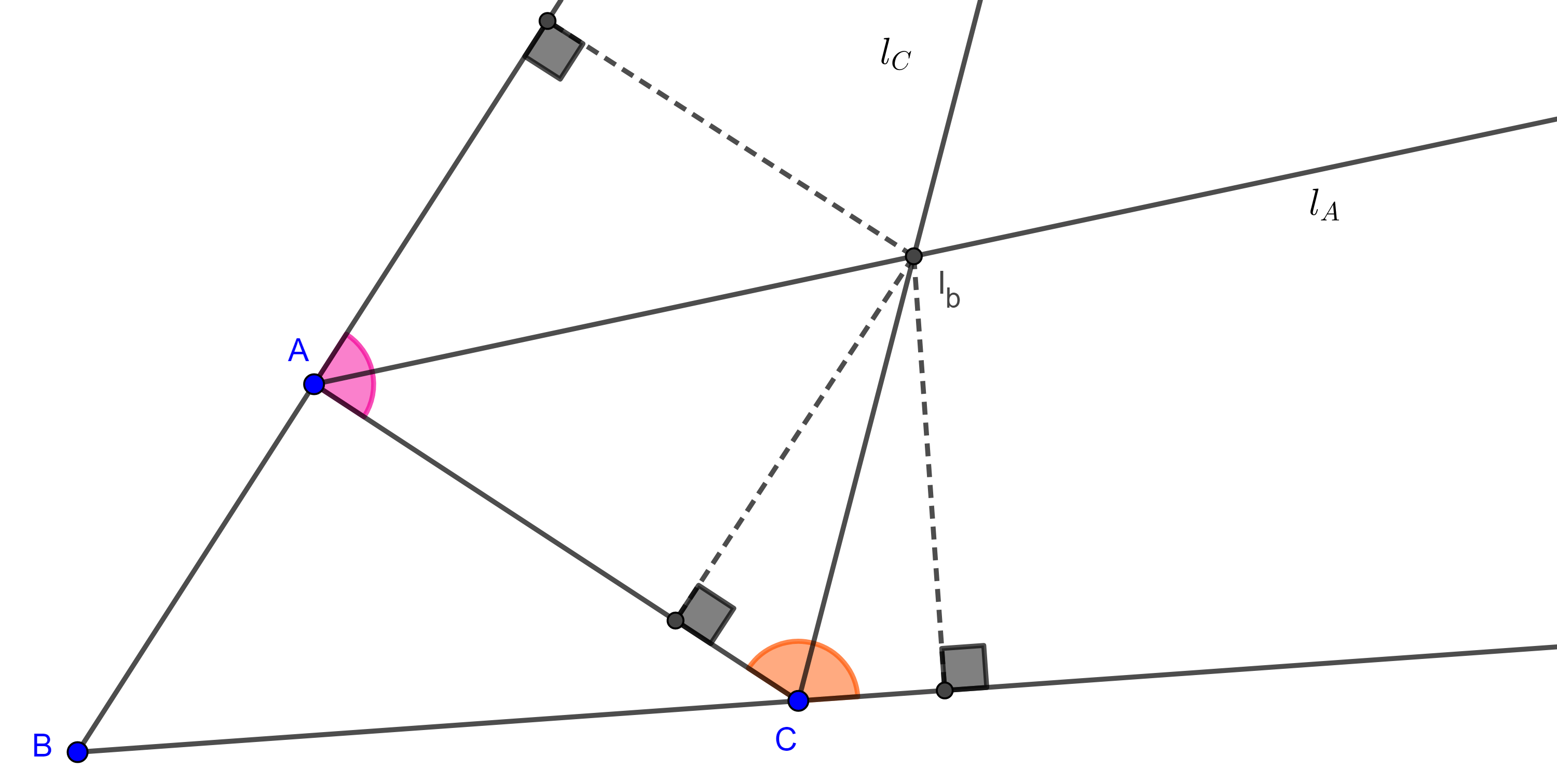
Demostración. Sean $\triangle ABC$, $\Gamma$ su circuncírculo, $I$, $I_a$, $I_b$ y $I_c$ sus centros tritangentes.

Consideremos la circunferencia $\Gamma(II_b)$ cuyo diámetro es $II_b$, como las bisectrices internas y externas de $\angle A$, $AI$ y $AI_b$ son perpendiculares entonces $A \in \Gamma(II_b)$, de manera análoga vemos que $C \in \Gamma(II_b)$.

Figura 1

Como $AC$ es cuerda de $\Gamma(II_b)$, entonces su mediatriz interseca a $II_b$ en el centro $P$ de $\Gamma(II_b)$. Ya que $AC$ es cuerda de $\Gamma$, entonces su mediatriz interseca al circuncírculo de $\triangle ABC$ en el punto medio del arco $\overset{\LARGE{\frown}}{CA}$ que no contiene a $B$.

Como $II_b$ es bisectriz de $\angle B$ entonces $II_b$ interseca al circuncírculo de $\triangle ABC$ en el punto medio del arco $\overset{\LARGE{\frown}}{CA}$ que no contiene a $B$.

Por lo tanto, el centro $P$ de $\Gamma(II_b)$ pertenece al circuncírculo de $\triangle ABC$.

Ahora consideremos la circunferencia $\Gamma(I_aI_c)$, cuyo diámetro es $I_aI_c$, como las bisectrices interna y externa de $\angle A$, son perpendiculares entonces $A \in \Gamma(I_aI_c)$, con un razonamiento análogo vemos que $C \in \Gamma(I_aI_c)$.

Considera el punto diametralmente opuesto a $P$, $P’$ en el circuncírculo de $\triangle ABC$ entonces $\angle PBP’$ es ángulo recto y como $BP$ es la bisectriz interna de $\angle B$ entonces $BP’$ es la bisectriz externa de $\angle B$.

Como $AC$ es cuerda de $\Gamma(I_aI_c)$ entonces su mediatriz $PP’$ interseca a $I_aI_c$ en su punto medio.

Por lo tanto, el punto medio, $P’$, del arco $\overset{\LARGE{\frown}}{AC}$, es el punto medio del diámetro, $I_aI_c$, de $\Gamma(I_aI_c)$.

Del mismo modo podemos ver que $\Gamma(II_c)$, $\Gamma(I_bI_a)$ pasan por los vértices $A$, $B$ y que $\Gamma(II_a)$, $\Gamma(I_bI_c)$ pasan por los vertices $C$, $B$.

$\blacksquare$

Puntos de contacto

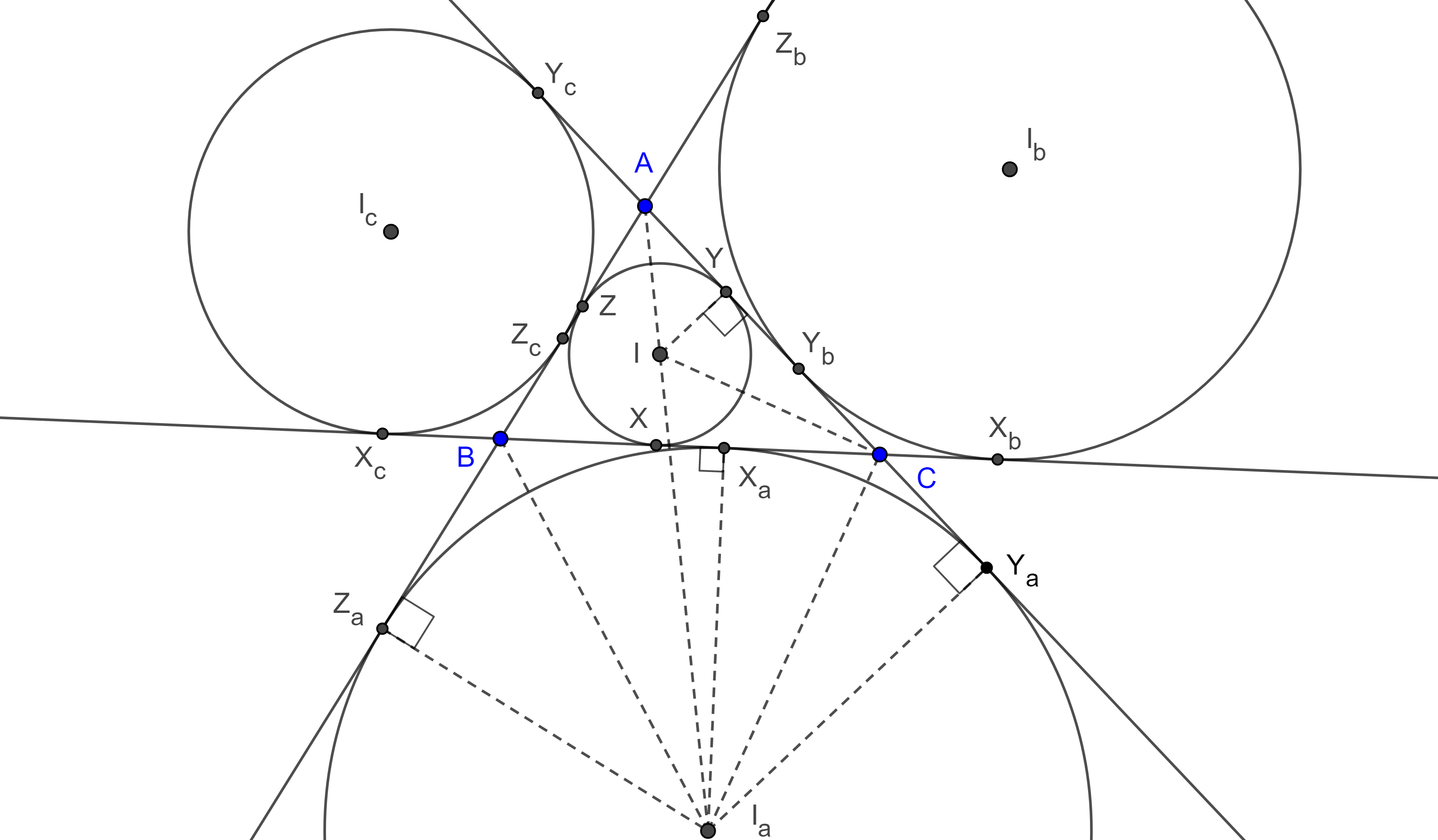
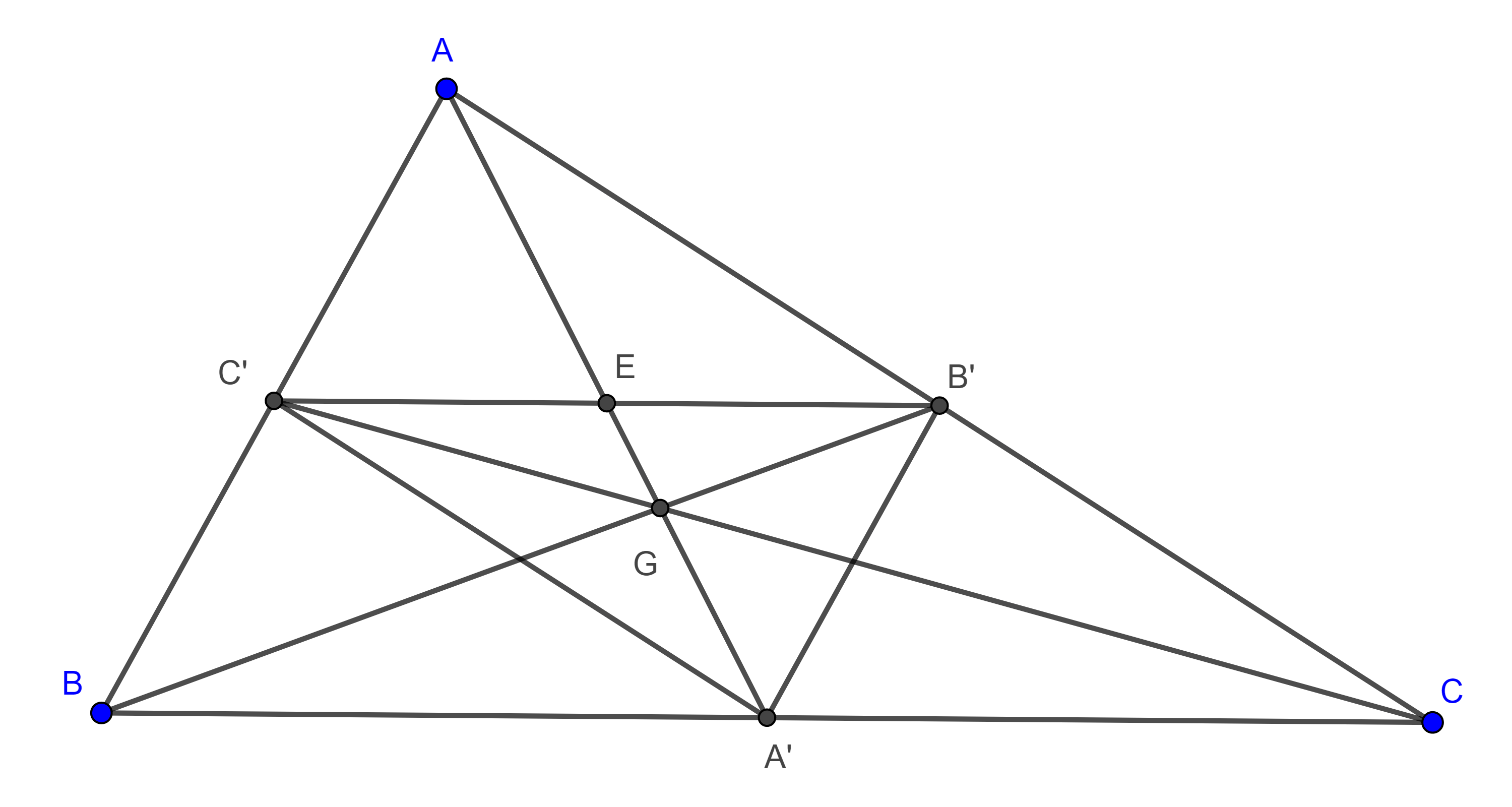
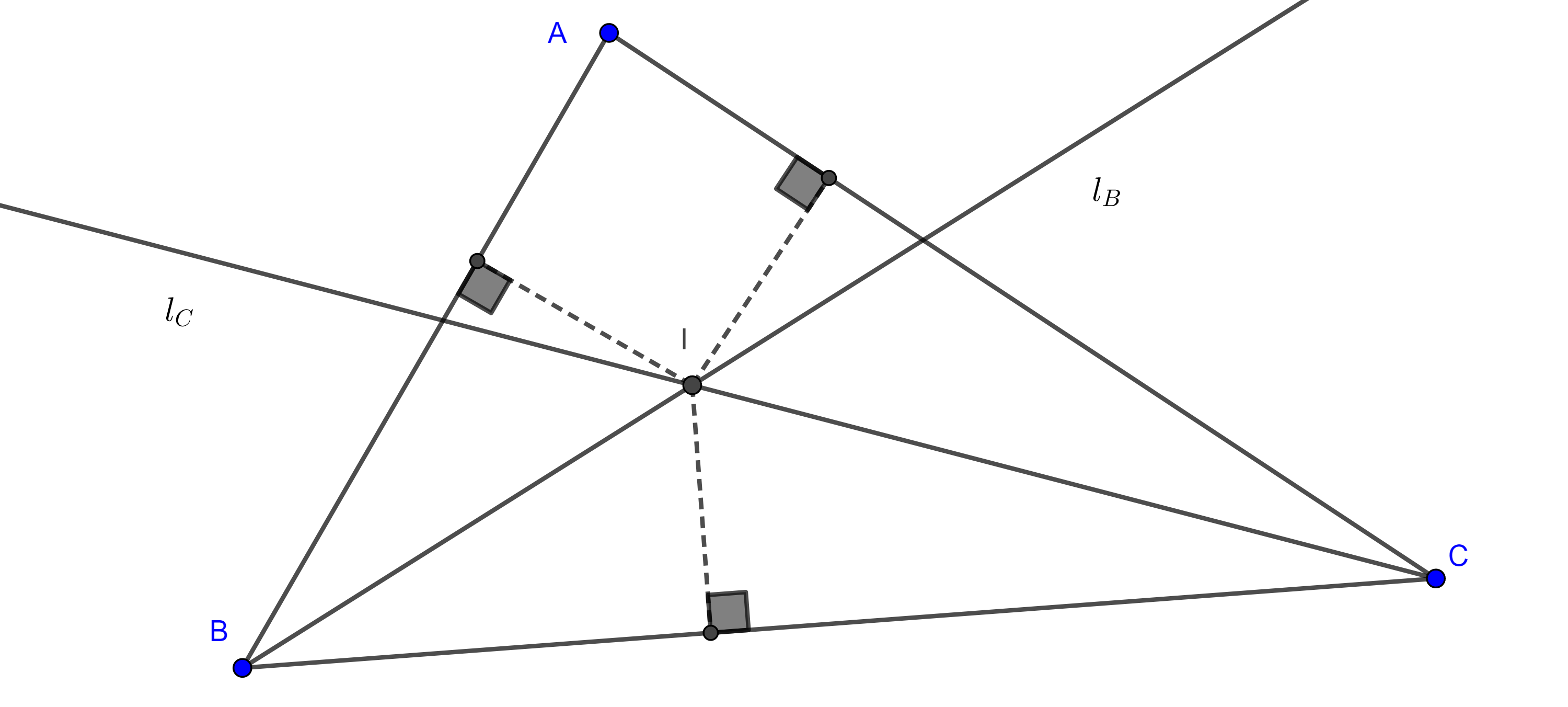
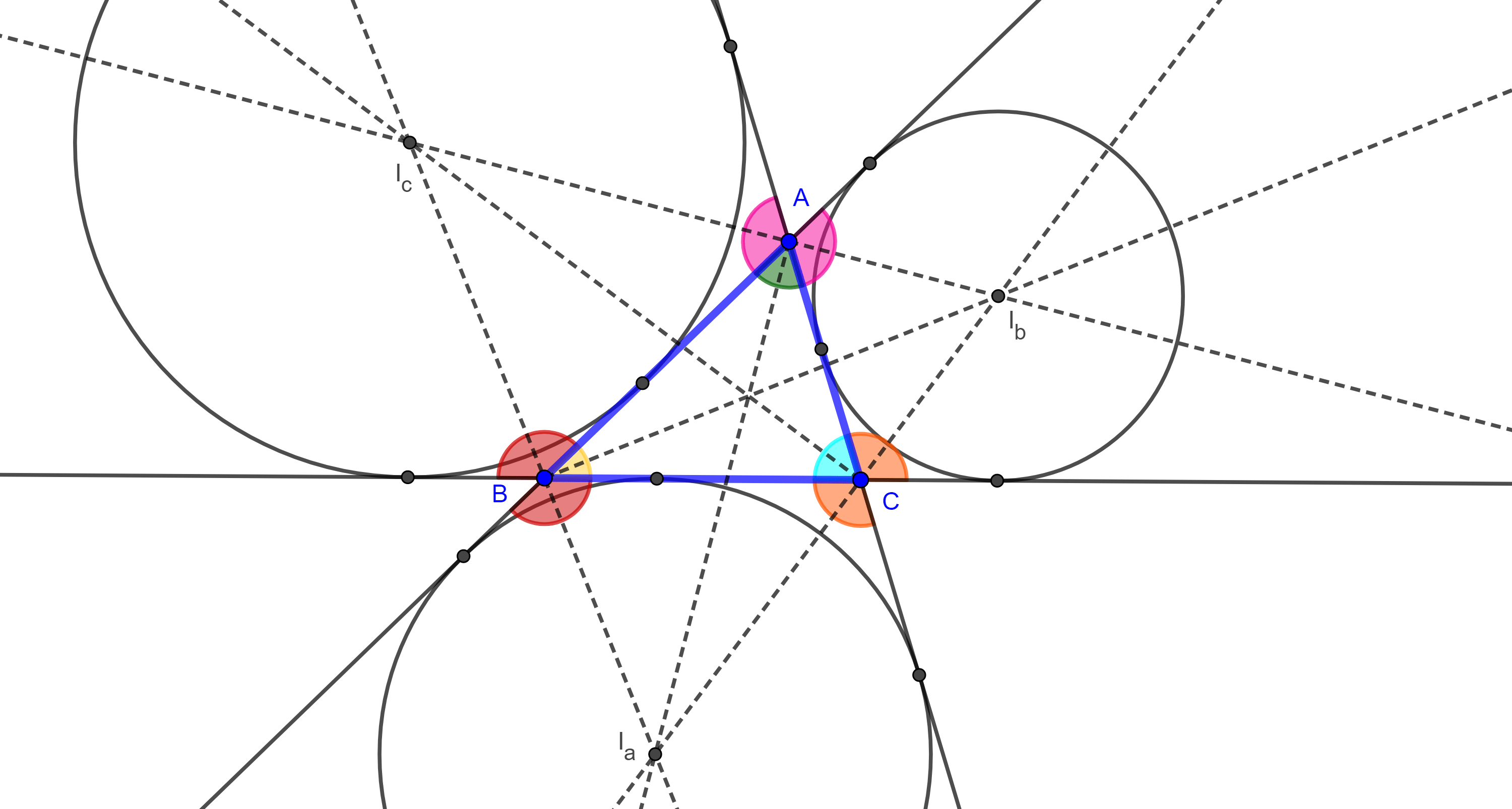
Notación. Nos referiremos a los puntos de tangencia de los círculos tritangentes $(I, r)$, $(I_a, r_a)$, $(I_b, r_b)$ y $(I_c, r_c)$ con el lado $BC$ de un triángulo $\triangle ABC$ como $X$, $X_a$, $X_b$ y $X_c$ respectivamente. Usaremos las letras $Y$ y $Z$ para los lados $AC$ y $AB$ respectivamente.

Emplearemos la letra $s$ para referirnos al semiperímetro $\dfrac{a + b + c}{2}$ de un triángulo $\triangle ABC$ donde $BC = a$, $AC = b$  y $AB = c$.

Proposición 1. La distancia desde el vértice de un triángulo al punto de tangencia de su circuncírculo en uno de sus lados adyacentes es igual al semiperímetro menos la longitud del lado opuesto.

Demostración. Sea $\triangle ABC$ y $(I, r)$ su circuncírculo. Como las tangentes desde un punto exterior a una circunferencia son iguales entonces $AZ = AY$, $BZ = BX$ y $CX = CY$.

Figura 2

Por otra parte, $AZ + BZ + BX + CX + CY +AY = c + a + b = 2s$.

Por lo tanto, $AZ + BX + CX = s$.

Y así, $AY = AZ = s – a$.

Similarmente, $BZ = BX = s – b$ y $CX = CY = s – c$.

$\blacksquare$

Proposición 2. La distancia desde el vértice de un triángulo al punto de tangencia del excírculo opuesto, a uno de los lados adyacentes al vértice considerado es igual al semiperímetro del triángulo.

Demostración. Sea $\triangle ABC$ y $(I_a, r_a)$, $(I_b, r_b)$ y $(I_c, r_c)$ sus excentros (figura 2). Como las tangentes desde un punto exterior a una circunferencia son iguales entonces
$AZ_a = AY_a$, $BX_b = BZ_b$ y $CX_c = CY_c$.

Por otro lado,
$AZ_a + AY_a = AB + BZ_a + AC + CY_a $
$= AB + AC + BX_a + CX_a = AB + AC + BC = 2s$.

Por lo tanto, $AZ_a = AY_a = s$.

Igualmente, $BX_b = BY_b = CX_c = CY_c = s$.

$\blacksquare$

Corolario 1. $AZ_c = AY_c = s – b$, y $AY_b = AZ_b = s – c$.

Demostración. En la figura 2 tenemos lo siguiente:
$AY_c = CY_c – AC = s – AC$,
$AZ_b = BZ_b – AB = s – AB$.

Similarmente,
$BZ_c = BX_c = s – a$, $BX_a = BZ_a = s – c$,
$CX_a = CY_a = s – b$, $CY_b = CX_b = s – a$.

$\blacksquare$

Puntos isotómicos

Definición 2. Si dos puntos en uno de los lados de un triángulo equidistan al punto medio del lado considerado decimos que son puntos isotómicos.

Proposición 3. El punto de tangencia del incírculo con uno de los lados de un triángulo y el punto de tangencia del excírculo relativo al lado considerado, son puntos isotómicos.

Demostración. Por la proposición 1 y el corolario 1, tenemos que $BX = s – b = CX_a$ (figura 2).

Esto implica que el punto medio de $XX_a$ es el punto medio de $BC$, por lo tanto, $X$ y $X_a$ son puntos isotómicos.

Análogamente vemos que $Z$, $Z_c$ e $Y$, $Y_b$ son pares de puntos isotómicos.

$\blacksquare$

Proposición 4. Los dos puntos de contacto de un lado de un triángulo con los dos excírculos opuestos a los vértices que pasan por ese lado son isotómicos, además la distancia entre estos dos puntos es igual a la suma de los otros dos lados.

Demostración. En la figura 2, tenemos lo siguiente:
$BX_c = CX_c – BC = s – a$, $CX_b = BX_b – BC = s – a$.

Por lo tanto, el punto medio de $X_cX_b$ coincide con el punto medio de $BC$.

Por otro lado, $X_cX_b = BX_c + a + CX_b = a + 2(s – a) = 2s – a = c + b$.

Igualmente, $Y_aY_c = a + c$, $Z_aZ_b = a + b$.

$\blacksquare$

Radios tritangentes y área del triangulo

Proposición 5. El área de un triángulo es igual al producto del semiperímetro por el inradio.

Demostración. De la figura 2,
$(\triangle ABC) = (\triangle AIB) + (\triangle BIC) + (\triangle AIC) = \dfrac{cr}{2} + \dfrac{ar}{2} + \dfrac{br}{2} = sr$.

$\blacksquare$

Proposición 6. El área de un triángulo es igual al producto de un exradio por la diferencia entre el semiperímetro y el lado relativo al excírculo considerado.

Demostración. En la figura 2,
$(\triangle ABC) = (\triangle AI_aB) + (\triangle AI_aC) – (\triangle BI_aC) $
$= \dfrac{cr_a}{2} + \dfrac{br_a}{2} – \dfrac{ar_a}{2} = \dfrac{r_a}{2}(2s – 2a) = r_a(s – a)$.

$\blacksquare$

Corolario 2. El reciproco del inradio es igual a la suma de los recíprocos de los exradios.

Demostración. De las proposiciones 5 y 6 se sigue que
$\dfrac{1}{r_a} + \dfrac{1}{r_b} + \dfrac{1}{r_c} = \dfrac{(s – a) + (s – b) + (s – c)}{( \triangle ABC)}
= \dfrac{s}{(\triangle ABC)} = \dfrac{1}{r}$.

$\blacksquare$

Proposición 7. El área de un triángulo es igual al producto de sus lados sobre cuatro veces su circunradio.

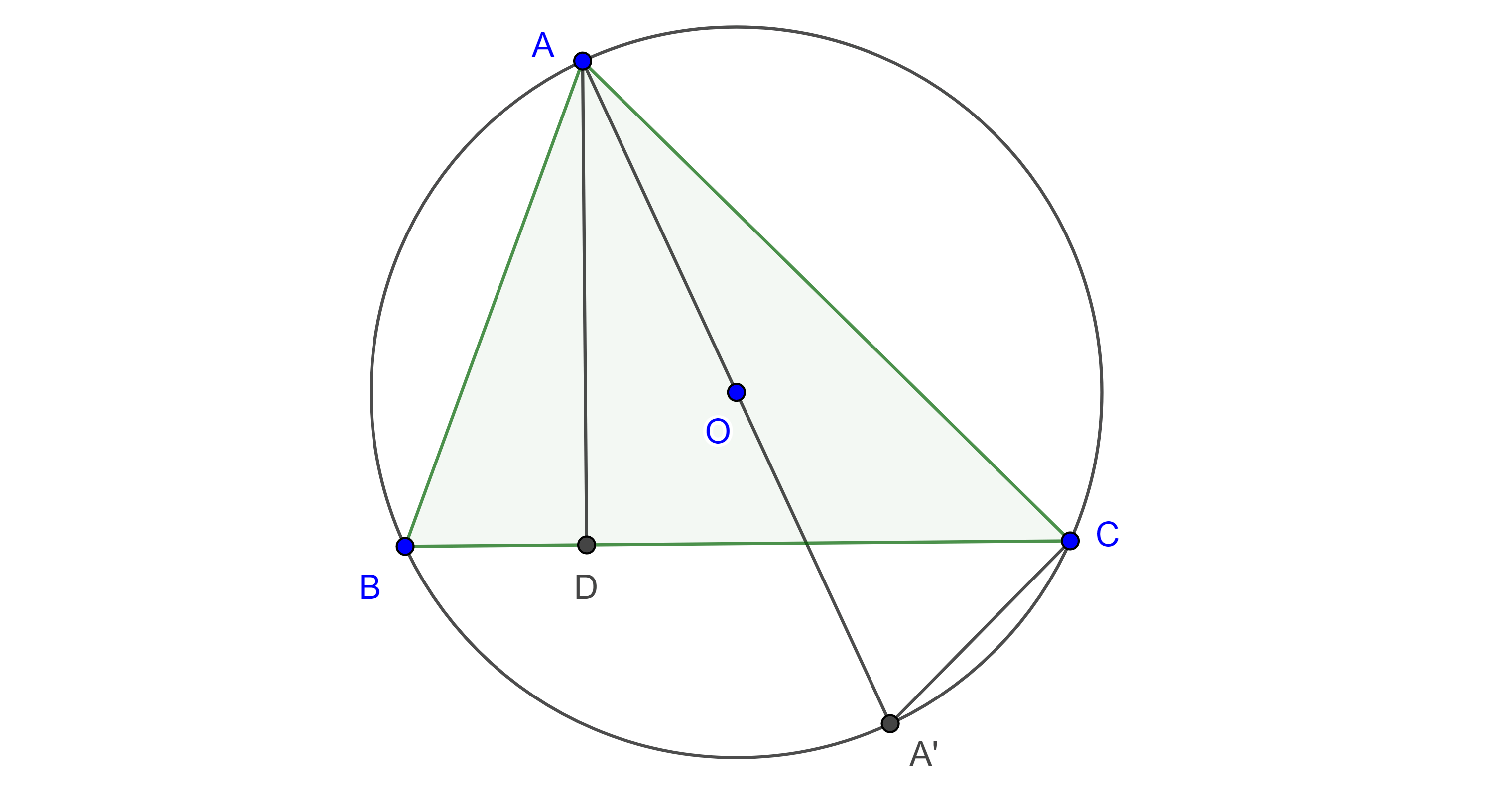
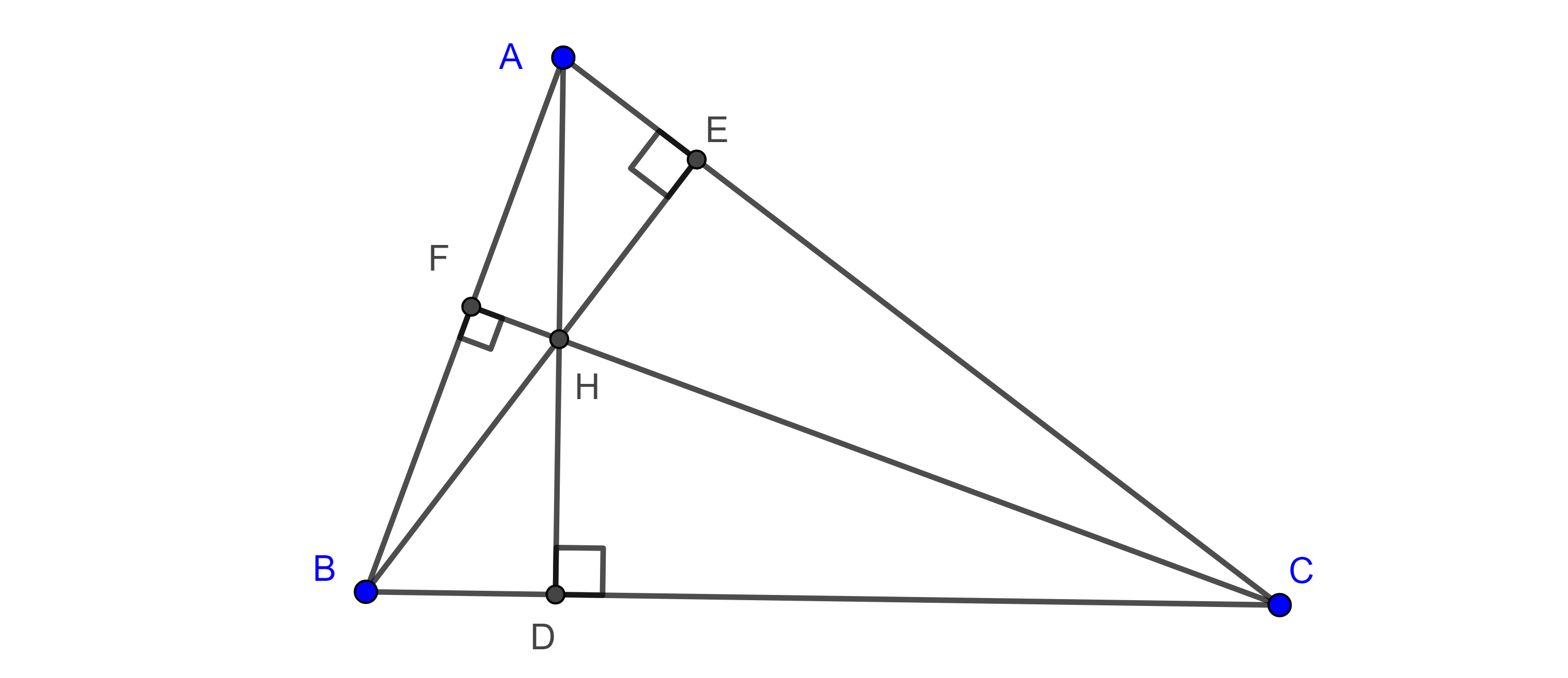
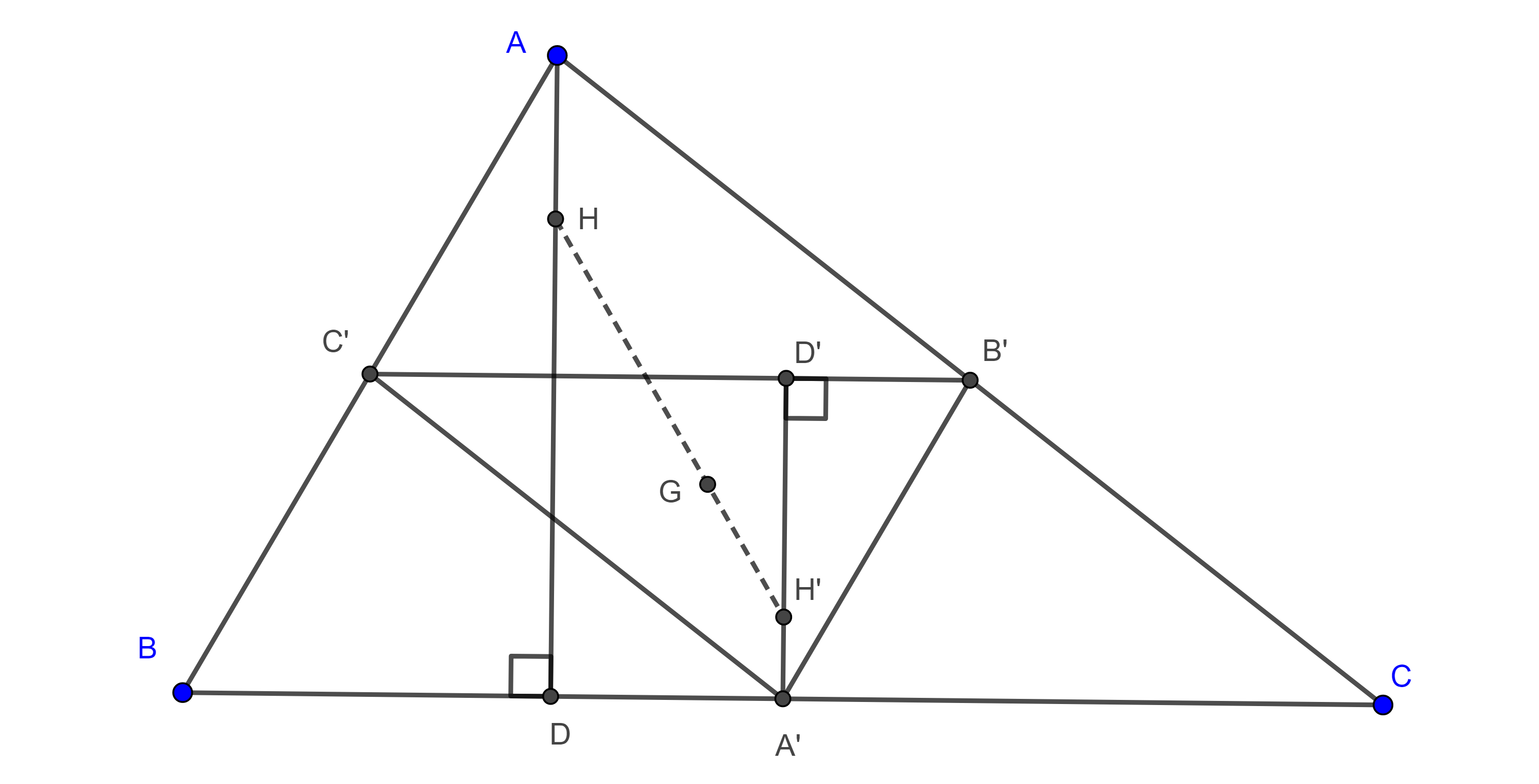
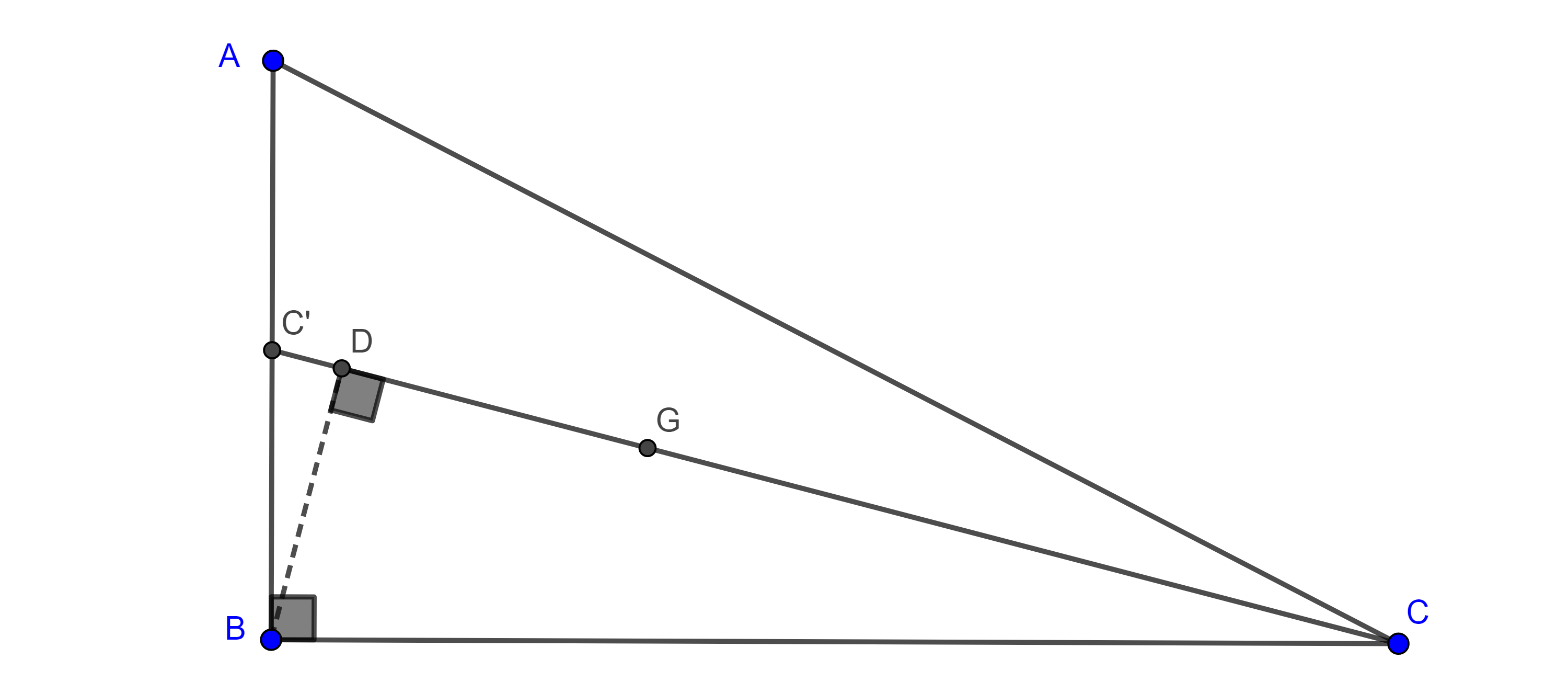
Demostración. Sean $\triangle ABC$, $(O, R)$ su circuncírculo, $D$ el pie de la altura por $A$, y $A’$ el punto diametralmente opuesto a $A$.

Figura 3

$\angle ABD = \angle AA’C$, pues abarcan el mismo arco y $\angle ACA’ = \dfrac{\pi}{2}$ es recto ya que $AA’$ es diámetro, así que $\triangle ABD \sim \triangle AA’C$, por criterio de semejanza AA.

Esto es, $\dfrac{AB}{AA’} = \dfrac{AD}{AC}$.

Se sigue que, $bc = 2RAD$ y $abc = a2RAD = 4R(\triangle ABC)$.

Por lo tanto, $\dfrac{abc}{4R} = (\triangle ABC)$.

$\blacksquare$

Formula de Herón y teorema de Carnot

Teorema 2, fórmula de Herón. Podemos calcular el área de un triángulo mediante la fórmula
$(\triangle ABC) = \sqrt{s(s – a)(s – b)(s – c)}$.

Demostración. Como $\angle YCI$ y $\angle I_ACY_a$ son suplementarios, por criterio de semejanza AAA $\triangle YCI \sim \triangle Y_aI_aC$,
por lo tanto, $\dfrac{Y_aI_a}{YC} = \dfrac{Y_aC}{YI}$,
es decir, $\dfrac{r_a}{s – c} = \dfrac{s – b}{r}$.

También $\triangle AYI \sim \triangle AY_aI_a$,
por lo tanto, $\dfrac{Y_aI_a}{YI} = \dfrac{AY_a}{AY}$,  
es decir, $\dfrac{r_a}{r} = \dfrac{s}{s – a}$,
entonces $\dfrac{rs}{s – a} = \dfrac{(s – b)(s – c)}{r}$. 

Por la proposición 5, $(\triangle ABC) = rs$,
por lo tanto, $(\triangle ABC) = \dfrac{(s – a)(s – b)(s – c)}{\dfrac{(\triangle ABC)}{s}}$,
así que $(\triangle ABC)^2 = s(s – a)(s – b)(s – c)$.

En conclusión, $(\triangle ABC) = \sqrt{s(s – a)(s – b)(s – c)}$.

$\blacksquare$

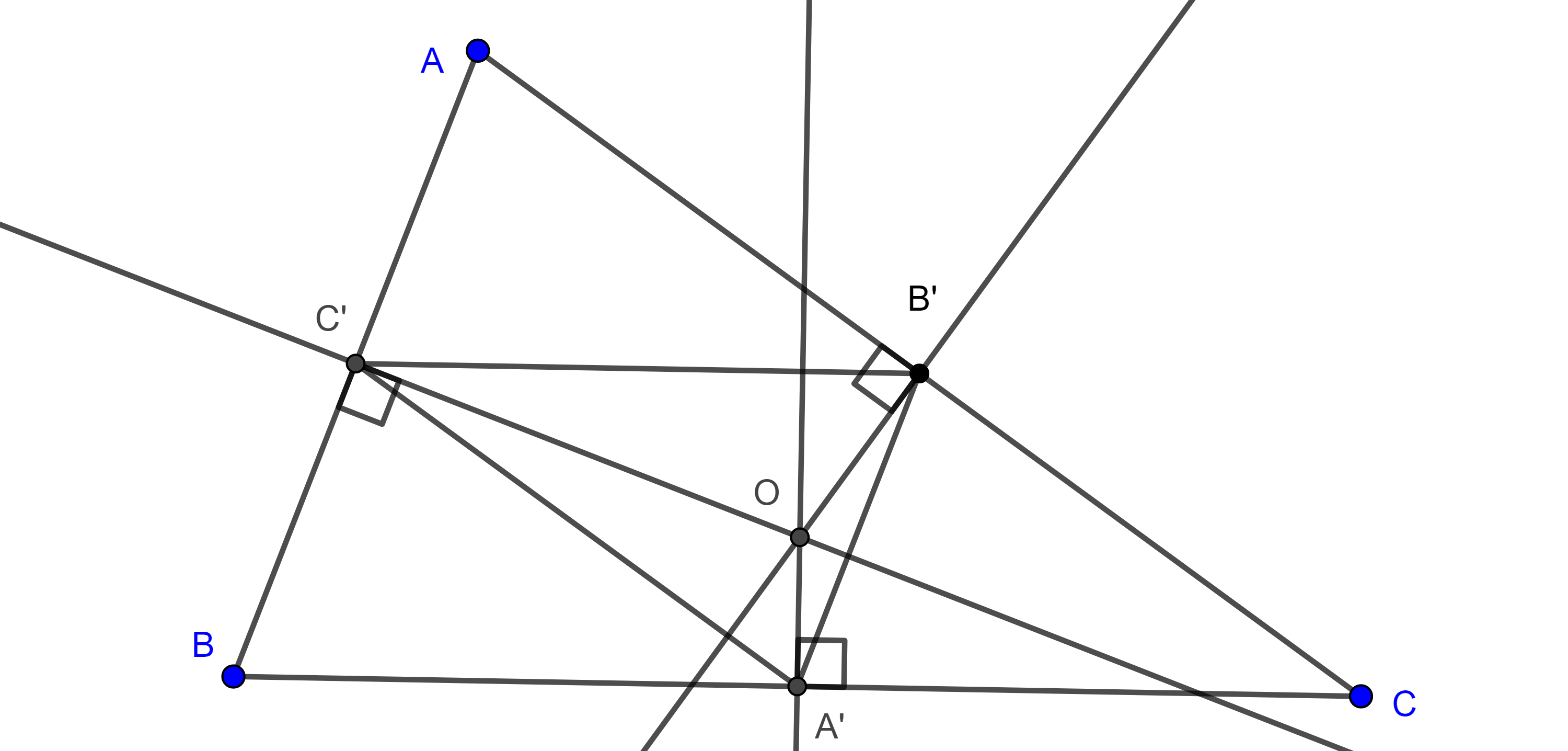
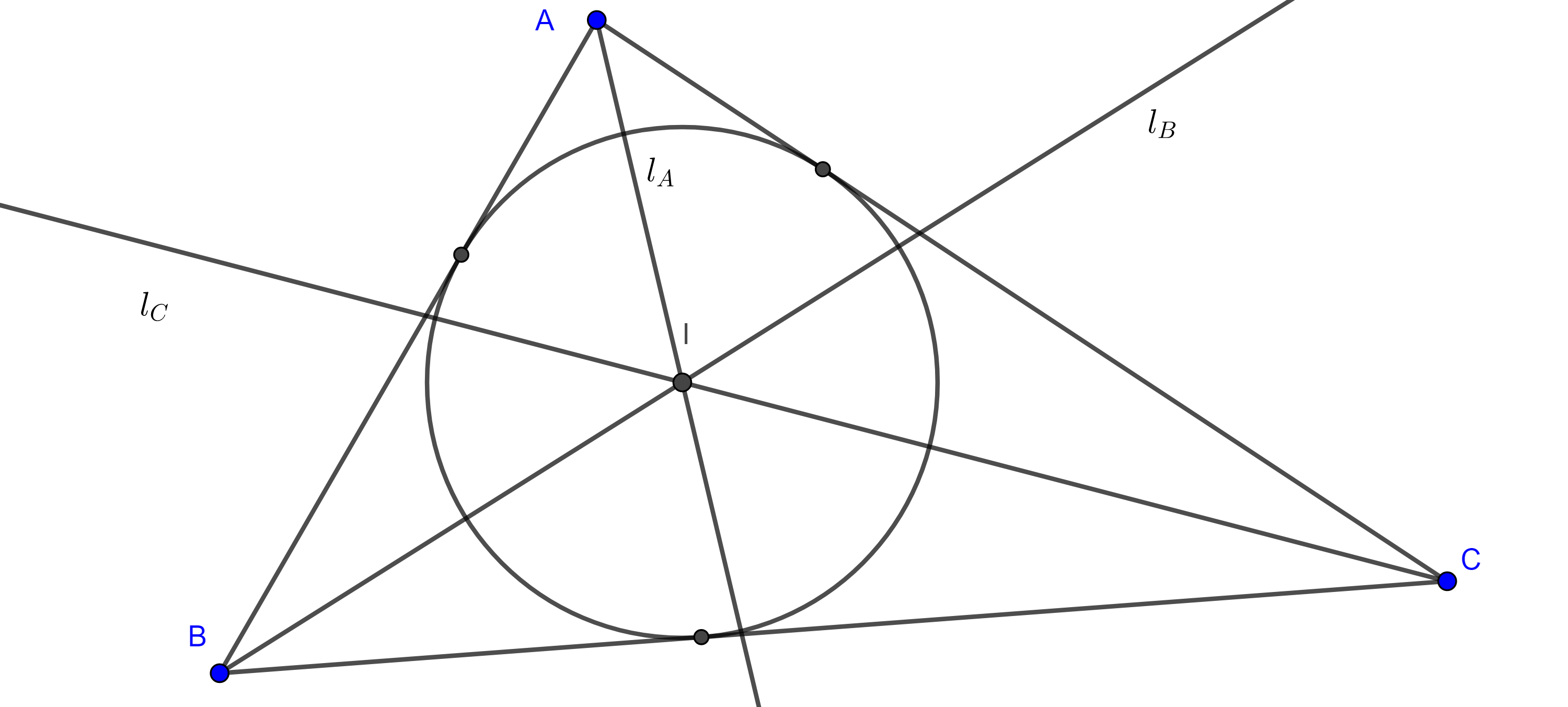
Teorema 3, de Carnot. La suma de las distancias desde el circuncentro a los lados del triángulo es igual a la suma del circunradio y el inradio.

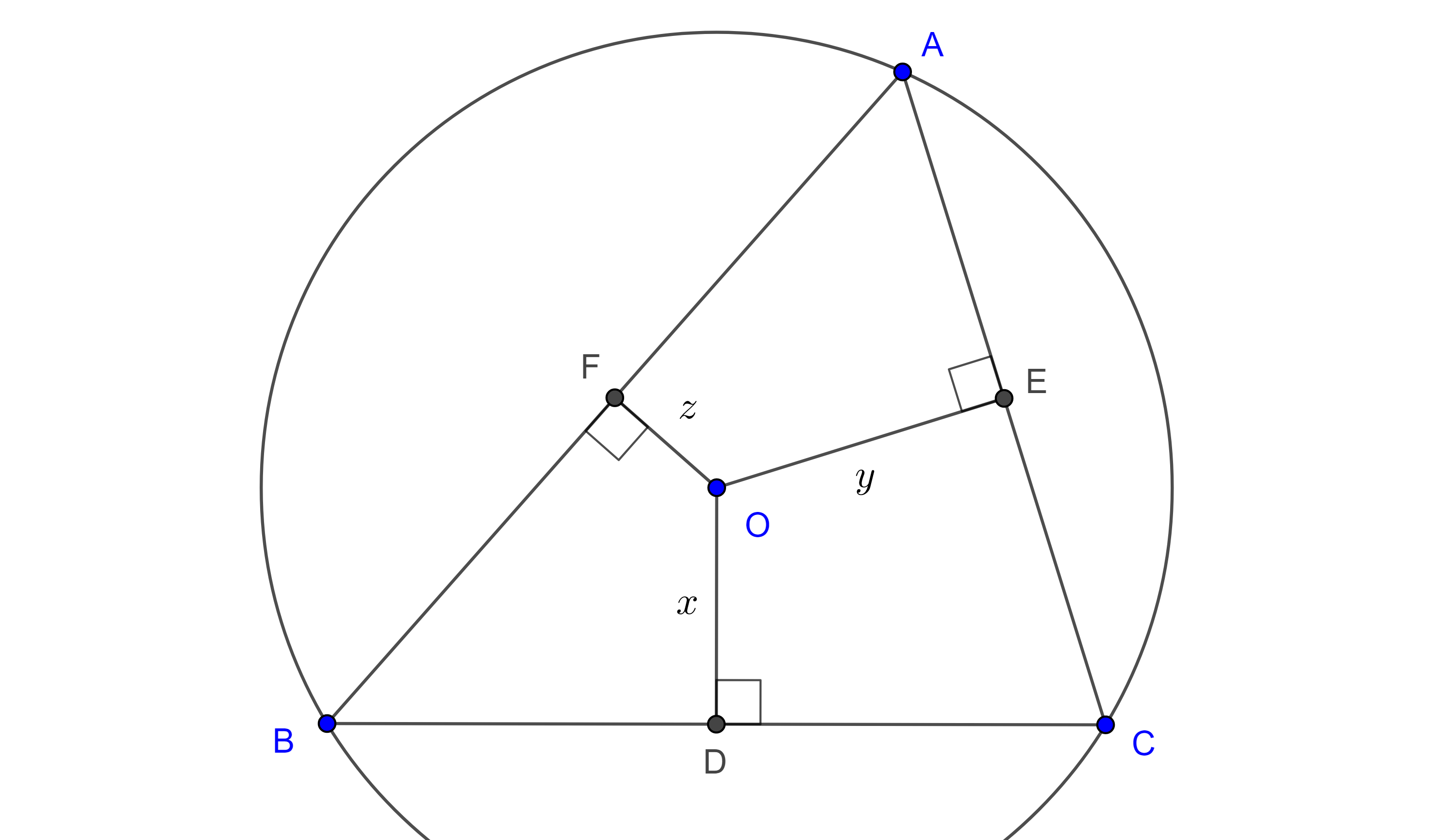
Demostración. Sea $\triangle ABC$ un triángulo acutángulo, $(O, R)$ su circuncírculo y $D$, $E$, $F$ las proyecciones de $O$ en $BC$, $AC$ y $AB$ respectivamente.

Figura 4

Aplicando el teorema de Ptolomeo a $\square AFOE$, $\square FBDO$ y $\square ODCE$ tenemos:
$AF \times OE + AE \times OF = OA \times EF$,
$BF \times OD + BD \times OF = OB \times DF$,
$CE \times OD + CD \times OE = OC \times DE$.

Por otra parte, como $O$ está en la mediatriz de $BC$, $AC$ y $AB$ entonces $D$, $E$ y $F$ son los respectivos puntos medios y podemos aplicar el teorema del segmento medio. Si nombramos $OD = x$, $OE = y$, $OF = z$, entonces:

$\dfrac{cy}{2} + \dfrac{bz}{2} = \dfrac{Ra}{2}$,
$\dfrac{cx}{2} + \dfrac{az}{2} = \dfrac{Rb}{2}$,
$\dfrac{bx}{2} + \dfrac{ay}{2} = \dfrac{Rc}{2}$.

Sumamos las tres expresiones,

$x(c + b) + y(a + c) + z(a + b) = R(a + b + c)$
$\Rightarrow x(2s – a) + y(2s – b) + z(2s – c) = R2s$
$\Rightarrow 2s(x + y + z) – (ax + by + cz) = R2s$
$ \Rightarrow 2s(x + y + z) – 2(\triangle ABC) = R2s$.

De la proposición 5 tenemos $(\triangle ABC) = rs$,
por lo tanto, $2s(x + y + z) – 2rs = R2s$.

Como resultado, $x + y + z = R + r$.

$\blacksquare$

Más adelante…

Con la ayuda de las formulas para el calculo del área de un triángulo vistas en esta entrada, en la próxima entrada mostraremos algunas desigualdades geométricas.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Muestra que:
    $i)$ la bisectriz interna del ángulo de un triángulo es perpendicular al segmento que une los puntos donde las otras bisectrices internas intersecan al circuncírculo del triangulo,
    $ii)$ la bisectriz externa del ángulo de un triángulo es paralela al segmento que une los puntos donde las bisectrices externas (internas) de los otros dos ángulos intersecan al circuncírculo del triángulo.
  2. Demuestra que: 
    $i)$ la suma de los catetos de un triángulo rectángulo menos la hipotenusa es igual al diámetro de su incírculo,
    $ii)$ el área de un triángulo rectángulo es igual al producto de los segmentos en los cuales la hipotenusa es dividida por el punto de tangencia de su incírculo.
  3. Muestra que en la figura 2 se tienen las siguientes igualdades:
    $i)$ $XX_a = b – c$, $YY_b = a – c$, $ZZ_c = a – b$,
    $ii)$ $ZZ_a = YY_a = a$, $XX_b = ZZ_b = b$, $YY_c = XX_c = c$,
    $iii)$ $Y_bY_c = Z_bZ_c = a$, $X_aX_c = Z_aZ_c = b$, $X_aX_b = Y_aY_b = c$.
  4. Prueba que:
    $i)$ el producto de los cuatro radios tritangentes de un triángulo es igual al cuadrado del área del triángulo $(\triangle ABC)^2 = rr_ar_br_c$
    $ii)$ el reciproco del inradio de un triángulo es igual a la suma de los recíprocos de las alturas del triangulo, $\dfrac{1}{r} = \dfrac{1}{h_a} + \dfrac{1}{h_b} + \dfrac{1}{h_c}$,
    $iii)$ en la figura 2, $\dfrac{AZ \times BX \times CY}{r} = (\triangle ABC)$.
  5. Demuestra que la razón entre el área de un triangulo y el area del triángulo formado por los puntos de contacto de su circuncírculo con sus lados es igual a la razón entre el inradio y el circundiámetro. En la figura 2, $\dfrac{(\triangle XYZ)}{(\triangle ABC)} = \dfrac{r}{2R}$.
  6. Muestra que en el teorema de Carnot, cuando $\angle A$ es obtuso (figura 4), entonces $y + z – x = R + r$.
  7. Sean $\triangle ABC$, $\alpha = \angle BAC$, $\beta = \angle CBA$, $\gamma = \angle ACB$, $R$ el circunradio y $r$ el inradio, muestra que:
    $i)$ $\sin \dfrac{\alpha}{2} = \sqrt{\dfrac{(s – b)(s – c)}{bc}}$, $\sin \dfrac{\beta}{2} = \sqrt{\dfrac{(s – a)(s – c)}{ac}}$, $\sin \dfrac{\gamma}{2} = \sqrt{\dfrac{(s – a)(s – b)}{ab}}$
    $ii)$ $\cos \alpha + \cos \beta + \cos \gamma = 1 + \dfrac{r}{R}$.

Entradas relacionadas

Fuentes

  • Altshiller, N., College Geometry. New York: Dover, 2007, pp 73-79, 87-91.
  • Coxeter, H. y Greitzer, L., Geometry Revisited. Washington: The Mathematical Association of America, 1967, pp 11-13.
  • Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 86-89, 97-98.
  • Quora
  • Cut the Knot

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Geometría Moderna I: Cuadrángulo ortocéntrico

Por Rubén Alexander Ocampo Arellano

Deja un comentario

Introducción

En esta entrada veremos que los cuatro triángulos que se forman con los vértices de un cuadrángulo ortocéntrico, tienen la misma circunferencia de los nueve puntos y derivaremos algunas otras propiedades.

Cuadrángulo ortocéntrico

Definición. Un cuadrángulo ortocéntrico es el conjunto de puntos formado por los vértices de un triángulo y su ortocentro.

Nos referiremos a los cuatro triángulos que se pueden formar con los cuatro puntos de un cuadrángulo ortocéntrico como grupo ortocéntrico de triángulos.

Teorema 1. Cualquier punto de un cuadrángulo ortocéntrico es el ortocentro del triángulo formado por los otros tres puntos y los triángulos de este grupo ortocéntrico tienen el mismo triangulo órtico.

Demostración. Sea $\triangle ABC$ y $H$ su ortocentro.

Figura 1

Notemos que el ortocentro de $\triangle BHC$ es $A$ pues $AB \perp HC$, $AH \perp BC$ y $AC \perp HB$.

De manera análoga podemos ver que $B$ es el ortocentro de $\triangle AHC$ y $C$ es el ortocentro de $\triangle AHB$.

Por otro lado, los pares de rectas perpendiculares $AH$, $BC$; $BH$, $AC$ y $CH$, $AB$, se intersecan en $D$, $E$ y $F$, respectivamente.

Por lo tanto, estos tres puntos son fijos, así el triángulo órtico es el mismo para los cuatro triángulos $\triangle ABC$, $\triangle HAB$, $\triangle HAC$ y $\triangle HBC$.

$\blacksquare$

Corolario 1. Las circunferencias de los nueve puntos de un grupo ortocéntrico de triángulos coinciden y sus circunradios son iguales.

Demostración. Como el circuncírculo del triángulo órtico de un triángulo dado es la circunferencia de los nueve puntos, por el teorema 1, los triángulos de un grupo ortocéntrico tienen la misma circunferencia de los nueve puntos.

En la entrada anterior vimos que el radio de la circunferencia de los nueve puntos es igual a la mitad del circunradio de su triángulo de referencia.

Por lo tanto, $\triangle ABC$, $\triangle HAB$, $\triangle HAC$ y $\triangle HBC$ tienen el mismo circunradio (figura 1).

$\blacksquare$

Circuncentros

Teorema 2. Los circuncentros de un grupo ortocéntrico de triángulos forman un cuadrángulo ortocéntrico.

Demostración. Por el teorema 2 de la entrada anterior, sabemos que el circuncentro de un triángulo es la reflexión de su ortocentro respecto de $N$, el centro de los nueve puntos.

Como los triángulos de un grupo ortocéntrico tienen el mismo centro de los nueve puntos, los circuncentros $O_a$, $O_b$, $O_c$ y $O$ de $\triangle HBC$, $\triangle HAC$, $\triangle HAB$ y $\triangle ABC$ son las reflexiones de $A$, $B$, $C$ y $H$ respectivamente respecto a $N$.

Figura 2

Dado que una reflexión es una homotecia de razón $-1$ entonces las figuras $ABCH$ y $O_aO_bO_cO$ son congruentes y por lo tanto $O_aO_bO_cO$ es un cuadrángulo ortocéntrico.

$\blacksquare$

Corolario 2. Un grupo ortocéntrico de triángulos y el grupo ortocéntrico de triángulos formado por sus circuncentros tienen la misma circunferencia de los nueve puntos.

Demostración. Como las figuras $ABCH$ y $O_aO_bO_cO$ son simétricas respecto a $N$ entonces también sus circunferencias de los nueve puntos son simétricas respecto a $N$.

Como $N$ es el centro de una de estas circunferencias, entonces coinciden.

Observación. Notemos que como $O_aO_bO_cO$ es un grupo ortocéntrico de triángulos, entonces la reflexión de sus ortocentros respecto al centro de los nueve puntos $N$ será el conjunto de sus circuncentros.

Entonces $A$, $B$, $C$ y $H$ son los circuncentros de $\triangle O_bO_cO$, $\triangle O_aO_cO$, $\triangle O_aO_bO$ y $\triangle O_aO_bO_c$ respectivamente.

$\blacksquare$

Problema. Construye un triángulo $\triangle ABC$ dados el centro de los nueve puntos $N$ y los circuncentros $O_b$ y $O_c$ de los triángulos $\triangle CAH$ y $\triangle ABH$ respectivamente donde $H$ es el ortocentro de $\triangle ABC$.

Solución. $O_b$ y $O_c$ son los ortocentros de $\triangle O_aO_cO$ y $\triangle O_aO_bO$ respectivamente y si los reflejamos respecto a $N$ obtendremos a los circuncentros de sus respectivos triángulos, estos son los vértices $B$ y $C$ del triángulo requerido.

Ahora tenemos dos vértices y el centro de los nueve puntos, este problema lo resolvimos en la entrada anterior.

$\blacksquare$

Centroices

Teorema 3. Los cuatro centroides de un grupo ortocéntrico de triángulos forman un cuadrángulo ortocéntrico.

Demostración. Sea $\triangle ABC$ y $H$ su ortocentro.

Sabemos que el centro de los nueve puntos $N$ de $\triangle ABC$ divide internamente al segmento $HG$ en razón $3:1$, donde $G$ es el centroide de $\triangle ABC$.

Figura 3

Como el grupo ortocéntrico de triángulos $\triangle ABC$, $\triangle HBC$, $\triangle HAC$, $\triangle HAB$ tienen el mismo centro de los nueve puntos $N$, entonces sus respectivos centroides $G$, $G_a$, $G_b$, $G_c$ están en homotecia con $H$, $A$, $B$, $C$ respectivamente desde $N$ y la razón de homotecia es $-3$.

Como dos figuras homotéticas son semejantes, entonces $GG_aG_bG_c$ es un cuadrángulo ortocéntrico.

$\blacksquare$

Corolario 3. La circunferencia de los nueve puntos de un grupo ortocéntrico de triángulos y la circunferencia de los nueve puntos del grupo ortocéntrico formado por sus centroides son concéntricas.

Demostración. Como las figuras $HABC$ y $GG_aG_bG_c$ están en homotecia desde el centro de los nueve puntos $N$ de $\triangle ABC$ entonces sus respetivas circunferencias de los nueve puntos también están en homotecia desde $N$.

Como $N$ es el centro de una de ellas, entonces son concéntricas.

$\blacksquare$

Corolario 4. Dado un cuadrángulo ortocéntrico, el cuadrángulo ortocéntrico formado por sus circuncentros y el cuadrángulo ortocéntrico formado por sus centroides tienen el mismo centro de los nueve puntos y además existe una homotecia entre ellos con centro en este punto.

Demostración. Por los corolarios 2 y 3, $OO_aO_bO_c$ y $GG_aG_bG_c$ tienen el mismo centro de los nueve puntos que $HABC$ y son homotéticos con este último precisamente desde $N$ en razón $-1$ y $-3$ respectivamente.

Figura 4

Por lo tanto, existe una homotecia con centro en $N$ y razón $3$ que lleva a $GG_aG_bG_c$ en $OO_aO_bO_c$.

$\blacksquare$

Incentro y excentros

Teorema 4. El incentro y los excentros de un triángulo dado forman un cuadrángulo ortocéntrico y el circuncírculo del triángulo dado es la circunferencia de los nueve puntos de este grupo ortocéntrico de triángulos.

Demostración. Como las bisectrices interna y externa de los ángulos de un triángulo $\triangle ABC$ son perpendiculares entre si entonces el incentro $I$ es el ortocentro del triángulo formado por los excentros $\triangle I_aI_bI_c$ y el triángulo $\triangle ABC$ es el triángulo órtico de $\triangle I_aI_bI_c$.

Figura 5

Entonces, por el teorema 1 y corolario 1, $I_aI_bI_cI$ es un grupo ortocéntrico de puntos y su circunferencia de los nueve puntos es el circuncírculo de $\triangle ABC$.

$\blacksquare$

Proposición. El segmento que une el ortocentro de un triángulo dado con el circuncentro del triángulo formado por los excentros del triángulo dado es bisecado por el incentro del triángulo medial del triángulo dado.

Demostración. Sea $\triangle ABC$ un triángulo, $I$, $I_a$, $I_b$, $I_c$, el incentro y sus respectivos excentros, $O$ y $O_e$ los circuncentros de $\triangle ABC$ y $\triangle I_aI_bI_c$ respectivamente.

Figura 6

Por el teorema anterior, $I$ y $O$ son el ortocentro y el centro de los nueve puntos respectivamente de $\triangle I_aI_bI_c$, por lo tanto, $O$ es el punto medio de $IO_e$.

Sean $H$ y $G$ el ortocentro y el centroide respectivamente de $\triangle ABC$, como $H$, $G$ y $O$ son colineales y $G$ triseca el segmento $OH$, entonces, $G$ es el centroide de $\triangle IO_eH$.

Por lo tanto, $IG$ biseca a $O_eH$ en $I’$ y $\dfrac{IG}{2} = GI’$.

Por otro lado, sabemos que existe una homotecia con centro en $G$ y razón $\dfrac{-1}{2}$, que lleva a $\triangle ABC$, a su triangulo medial $\triangle A’B’C’$, por lo que sus respectivos incentros $I$ y $I_m$ son puntos homólogos de esta homotecia, es decir $I$, $G$ y $I_m$ son colineales y $G$ triseca al segmento $II_m$.

Como $I’$ cumple con estas características entonces $I’ = I_m$.

$\blacksquare$

Más adelante…

En la próxima entrada estudiaremos otra recta notable del triángulo, la recta de Simson, veremos que la intersección de dos rectas de Simson se intersecan en la circunferencia de los nueve puntos y que cierto conjunto de rectas de Simson forman un cuadrángulo ortocéntrico.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Muestra que las rectas de Euler de los cuatro triángulos de un grupo ortocéntrico son concurrentes.
  2. Demuestra que el simétrico del circuncentro de un triángulo con respecto a uno de los lados del triángulo coincide con el simétrico del vértice opuesto al lado considerado respecto al centro de los nueve puntos del triángulo.
  3. Muestra que los vértices de un grupo ortocéntrico de triángulos pueden ser considerados como los centroides de otro grupo ortocéntrico de triángulos.
  4. Sea $\triangle ABC$ un triángulo rectángulo con $\angle A = \dfrac{\pi}{2}$, $D$ el pie de la altura por $A$, las bisectrices de $\angle BAD$ y $\angle DAC$ intersecan a $BC$ en $P$ y $P’$ respectivamente. Las bisectrices de $\angle DBA$ y $\angle ACD$ intersecan a $AD$ en $Q$ y $Q’$ respectivamente.
    $i)$ Muestra que $PP’QQ’$ es un cuadrángulo ortocéntrico,
    $ii)$ si $I$, $J$ y $K$ son los incentros de $\triangle ABC$, $\triangle ABD$ y $\triangle ADC$, muestra que $AIJK$ es un cuadrángulo ortocéntrico.
  5. Prueba que la suma de los cuadrados de dos segmentos no adyacentes que unen vértices de un cuadrángulo ortocéntrico es igual al cuadrado del circundiámetro de los triángulos de este grupo ortocéntrico.
  6.  Construye un triángulo $\triangle ABC$ dados su circuncentro $O$, y los circuncentros de los triángulos $\triangle II_bI_c$ y $\triangle II_aI_c$, donde $I$, $I_a$, $I_b$ y $I_c$ es el incentro y los excentros de $\triangle ABC$.

Entradas relacionadas

Fuentes

  • Altshiller, N., College Geometry. New York: Dover, 2007, pp 109-115.
  • Johnson, R., Advanced Euclidean Geometry. New York: Dover, 2007, pp 165-167.
  • Shively, L., Introducción a la Geómetra Moderna. México: Ed. Continental, 1961, pp 58.

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Geometría Moderna I: Triángulo medial y recta de Euler

Por Rubén Alexander Ocampo Arellano

2 respuestas

Introducción

Continuando con el estudio de las propiedades del centroide, en esta entrada veremos que es colineal con el ortocentro y el circuncentro, y que además triseca al segmento que une dichos puntos. Para establecer estos resultados, veremos primero algunos resultados del triángulo medial de un triángulo dado.

Triángulo medial

Definición 1. Al triángulo que tiene como vértices los puntos medios de un triángulo dado se le conoce como triángulo medial o triángulo complementario del triángulo dado.

Teorema 1. Un triángulo y su triángulo medial son homotéticos además comparten el mismo centroide.

Demostración. Sean $\triangle ABC$, $A’$, $B’$ y $C’$ los puntos medios de $BC$, $AC$ y $AB$ respectivamente.

Por el teorema del segmento medio, los lados del triángulo medial $\triangle A’B’C’$ son paralelos a los lados de $\triangle ABC$ y por lo tanto son homotéticos.

Ya que las rectas determinadas por dos puntos homólogos, $AA’$, $BB’$ y $CC’$ son las medianas de $\triangle ABC$, entonces el centroide $G$ es el centro de homotecia y sabemos que $AG = 2GA’$, por lo que la razón de homotecia es $\dfrac{-1}{2}$, donde el signo menos indica que dos puntos homólogos de esta homotecia se encuentran en lados opuestos respecto del centro de homotecia.

Figura 1

Como $BC$ y $B’C’$ son rectas homotéticas, entonces el punto homólogo de $A’ \in BC$ es $E = A’G \cap B’C’$, y como $A’$ es el punto medio de $BC$ entonces $E$ es el punto medio de $B’C’$, pues la homotecia preserva las proporciones.

Por lo tanto, $A’G$ es mediana de $\triangle A’B’C’$, de manera similar podemos ver que $B’G$ y $C’G$ son medianas de $\triangle A’B’C’$, por lo tanto, $G$ es el centroide de $\triangle A’B’C’$.

$\blacksquare$

Proposición 1. El circuncentro de un triángulo es el ortocentro de su triángulo medial.

Demostración. Se sigue del hecho de que las mediatrices de un triángulo son las alturas de su triángulo medial, esto es así porque los vértices del triángulo medial son, por definición, los puntos medios de un triángulo dado y los lados del triángulo medial son paralelos a los lados del triángulo dado.

$\blacksquare$

Figura 2

Triángulo anticomplementario

Definición 2. Dado un triángulo, al triángulo formado por las rectas paralelas a los lados del triángulo dado a través de los respectivos vértices opuestos, se le conoce como triángulo anticomplementario del triángulo dado.

Proposición 2. Un triángulo y su triángulo anticomplementario son homotéticos y tienen el mismo centroide.

Demostración. Consideremos $\triangle ABC$ y $\triangle A’’B’’C’’$ su triángulo anticomplementario.

Figura 3

Como $\square C’’BCA$ y $\square ABCB’’$ son paralelogramos entonces $C’’A = BC = AB’’$, por lo tanto, $A$ es el punto medio de $B’’C’’$. De manera análoga vemos que $B$ y $C$ son puntos medio de $A’’C’’$ y $A’’B’’$ respectivamente,

Por lo tanto, $\triangle ABC$ es el triángulo medial de $\triangle A’’B’’C’’$ y por el teorema 1 se tiene el resultado.

$\blacksquare$

Circunferencia de Droz Farny

Proposición 3. El producto de los segmentos en que el ortocentro divide a la altura de un triángulo es igual para las tres alturas del triángulo.

Demostración. Sean $\triangle ABC$ y $D$, $E$ y $F$ los pies de las alturas por $A$, $B$ y $C$ respectivamente y $H$ el ortocentro.

Figura 4

Notemos que $\triangle AFH \sim \triangle CDH$ y $\triangle AEH \sim \triangle BDH$ (son semejantes) pues son triángulos rectángulos y comparten un ángulo opuesto por el vértice, por lo tanto
$\dfrac{AH}{CH} = \dfrac{FH}{DH}$ $\Rightarrow AH \times DH = CH \times HF$,
$\dfrac{AH}{BH} = \dfrac{EH}{DH}$ $\Rightarrow AH \times DH = BH \times HE$.

De esto se sigue que
$CH \times HF = AH \times DH = BH \times HE$.

$\blacksquare$

Teorema 2. Si tomamos los vértices de un triángulo como centros de circunferencias del mismo radio, estas cortaran a los respectivos lados de su triángulo medial en tres pares de puntos que son equidistantes del ortocentro del triángulo.

Demostración. Sean $\triangle ABC$ y $\triangle A’B’C’$ su triángulo medial, tracemos tres circunferencias del mismo radio $(A, r)$, $(B, r)$ y $(C, r)$ las cuales intersecan a $B’C’$, $A’C’$ y $A’B’$ en $P$, $P’$; $Q$, $Q’$ y $R$, $R’$, respectivamente.

Sean $D \in BC$ el pie de la altura por $A$, y $M = AD \cap B’C’$, por el teorema de Pitágoras en $\triangle AMP$ y $\triangle HMP$ tenemos
$AP^2 – AM^2 = MP^2 = HP^2 – HM^2$
$\Rightarrow AP^2 – HP^2 = AM^2 – HM^2 = (AM + HM)(AM – HM)$.

Figura 5

Como $\triangle AC’B’ \cong \triangle C’BA’$ son congruentes por criterio LLL entonces sus alturas desde $A$ y $C’$, respectivamente, son iguales , por lo tanto $AM = MD$,
$\Rightarrow AP^2 – HP^2 = (MD + HM)AH = HD \times AH$.

Por otra parte, $\triangle PAP’$ es isósceles y como $AM$ es altura entonces $AM$ es mediatriz de $PP’$, por lo tanto $HP = HP’$$\Rightarrow$
$\begin{equation} HP’^2 = HP^2 = AP^2 – AH \times HD. \end{equation}$.

Si consideramos $E$ y $F$ los pies de las alturas por $B$ y $C$ respectivamente podemos encontrar fórmulas análogas
$\begin{equation} HQ’^2 = HQ^2 = BQ^2 – BH \times HE, \end{equation} $
$\begin{equation} HR’^2 = HR^2 = CR^2 – CH \times HF. \end{equation} $.

Como $(A, r)$, $(B, r)$ y $(C, r)$ tienen el mismo radio, entonces $AP = BQ = CR$ y por la proposición 3, $AH \times DH = BH \times HE = CH \times HF$.

Tomando lo anterior en cuenta y a las ecuaciones $(1)$, $(2)$ y $(3)$ se sigue que
$HP = HP’ = HQ = HQ’ = HR = HR’$.

$\blacksquare$

Recta de Euler

Teorema 3. El circuncentro, el centroide y el ortocentro de todo triangulo son colineales, con el centroide siempre en medio, a la recta determinada por estos tres puntos se le conoce como recta de Euler del triángulo, además $HG = 2GO$.

Demostración. Sean $\triangle ABC$ y $\triangle A’B’C’$ su triángulo medial, por el teorema 1, $\triangle ABC$ y $\triangle A’B’C’$ están en homotecia desde $G$, el centroide, que es el mismo para ambos triángulos, y la razón de homotecia es $\dfrac{-1}{2}$.

Consideremos la altura $AD$ de $\triangle ABC$, la homotecia de $AD$ es una recta paralela a ella y que pasa por el punto homólogo de $A$, $A’$, es decir la homotecia de una altura de $\triangle ABC$ es una altura de $\triangle A’B’C’$.

Figura 6

Como el ortocentro $H$ de $\triangle ABC$ es la intersección de sus alturas, entonces su punto homologo bajo la homotecia estará en la intersección de las alturas de $\triangle A’B’C’$, esto es, el ortocentro de $\triangle A’B’C’$, $H’$.

Con esto tenemos que el ortocentro de $\triangle A’B’C’$ es colineal con $G$ el centroide y el ortocentro de $\triangle ABC$ respectivamente, además, debido a la razón de homotecia, $HG = 2GH’$.

Por la proposición 1, el ortocentro del triángulo medial $\triangle A’B’C’$ es el circuncentro $O$ de $\triangle ABC$.

Así, $O$, $G$ y $H$ son colineales y $HG = 2GO$.

$\blacksquare$

Observación. Notemos que si el triángulo es equilátero el ortocentro, el centroide y el circuncentro son el mismo punto y por lo tanto la recta de Euler degenera en un punto.

Problema. Construye un triángulo $\triangle ABC$ dados el vértice $A$, el circuncentro $O$ y las distancias de $A$ al ortocentro $AH$, y al centroide $AG$.

Solución. El centroide $G$ se encuentra en la circunferencia con centro en $A$ y radio $AG$, $(A, AG)$, el ortocentro $H$ se encuentra en la circunferencia con centro en $A$ y radio $H$, $(A, AH)$.

Por el teorema 3 sabemos que $H$, $G$ y $O$ son colineales y que $HO = 3GO$, por lo que $H$ y $G$ se encuentran en homotecia desde $O$.

Entonces, a $(A, AH)$ le aplicamos una homotecia con centro en $O $ y razón $\dfrac{1}{3}$, esto será una circunferencia $\Gamma$ y $G$ resultara de la intersección de $\Gamma$ con $(A, AG)$.

Figura 7

Teniendo a $G$ construido, como tenemos el circuncírculo $(O, OA)$ y un vértice del triángulo, el problema se reduce a la solución del problema 2 de la entrada anterior.

$\blacksquare$

Distancia entre puntos notables

Teorema 4. Para un triángulo con lados $a$, $b$, $c$, ortocentro $H$, centroide $G$, y circuncírculo $(O, R)$ tenemos:
$OH^2 = 9R^2 – (a^2 + b^2 + c^2)$,
$HG^2 = 4R^2 – \dfrac{4}{9}( a^2 – b^2 + c^2)$.

Demostración. Por el teorema 3 sabemos que $OH = 3OG$ y $HG = 2GO$, además en la entrada anterior calculamos
$OG^2 = R^2 – (\dfrac{a^2 + b^2 + c^2}{9})$.

Por lo tanto,
$OH^2 = 9OG^2 = 9R^2 – (a^2 + b^2 + c^2)$,
$HG^2 = 4OG^2 = 4R^2 – \dfrac{4}{9}(a^2 + b^2 + c^2)$.

$\blacksquare$

Corolario. Podemos calcular la suma de los cuadrados de las distancias del ortocentro a los vértices del triángulo en función del circunradio y los lados del triángulo con la siguiente fórmula.
$HA^2 + HB^2 + HC^2 = 12R^2 + (a^2 + b^2 + c^2)$.

Demostración. Por el teorema 4, y usando las fórmulas encontradas en la entrada anterior
$HA^2 + HB^2 + HC^2 = GA^2 + GB^2 + GC^2 + 3HG^2$,
$GA^2 + GB^2 + GC^2 = \dfrac{a^2 + b^2 + c^2}{3}$ .

Esto implica que,
$HA^2 + HB^2 + HC^2 = \dfrac{a^2 + b^2 + c^2}{3} + 12R^2 – \dfrac{4}{3}(a^2 + b^2 + c^2)$
$= 12R^2 – (a^2 + b^2 + c^2)$.

$\blacksquare$

Más adelante…

En la siguiente entrada estudiaremos otro triángulo asociado a un triángulo dado, aquel cuyos vértices son los pies de las alturas del triángulo dado.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Muestra que el triángulo complementario y el triángulo anticomplementario de un triángulo dado son homotéticos, encuentra el centro y la razón de homotecia.
  2. Sea $\triangle ABC$ y $P$ un punto en el plano, considera $A’$, $B’$ y $C’$ los pies de las perpendiculares dese $P$ a $BC$, $AC$ y $AB$ respectivamente. Desde los puntos medios de $A’B’$, $A’C’$ y $B’C’$ traza perpendiculares a los lados de $AB$, $AC$ y $BC$ respectivamente, muestra que este último conjunto de perpendiculares son concurrentes.
  3. Sean $D$, $D’ \in BC$ de un triangulo $\triangle ABC$, tal que el punto medio de $BC$ es el punto medio de $DD’$, sea $E = AD \cap B’C’$, donde $B’$ y $C’$ son los puntos medios de $AC$ y $AB$ respectivamente, muestra que $ED’$ pasa por el centroide de $\triangle ABC$.
  4. Muestra que la recta de Euler de un triángulo pasa por uno de los vértices del triángulo si y solo si el triángulo es isósceles o rectángulo.
  5. Prueba que la recta que une el centroide de un triangulo con un punto $P$ en su circuncírculo biseca al segmento que une el punto diametralmente opuesto a $P$ con el ortocentro.
  6. Sean $H$, $G$, $(O, R)$ y $(I, r)$, el ortocentro, el centroide, el circuncírculo y el incírculo de un triángulo, muestra que:
    $i)$ $HI^2 + 2OI^2 = 3(IG^2 + 2OG^2)$,
    $ii)$ $3(IG^2 + \dfrac{HG^2}{2}) – IH^2 = 2R(R – 2r)$.

Entradas relacionadas

Fuentes

  • Altshiller, N., College Geometry. New York: Dover, 2007, pp 68-69, 94-96, 101-102.
  • Coxeter, H. y Greitzer, L., Geometry Revisited. Washington: The Mathematical Association of America, 1967, pp 18-19.
  • Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 65-68.

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Geometría Moderna I: Puntos notables del triángulo

Por Rubén Alexander Ocampo Arellano

Deja un comentario

Introducción

En esta entrada estudiamos la concurrencia de rectas importantes en el triangulo, a saber, las medianas, mediatrices, bisectrices y alturas. Mencionamos también consecuencias inmediatas de los puntos de concurrencia.

Centroide

Teorema 1. Las medianas de todo triángulo concurren en un punto que las triseca.

Demostración. Sean $\triangle ABC$, $B’$ y $C’$ los puntos medios de $AC$ y $AB$ respectivamente, por el teorema del segmento medio sabemos que $C’B’ = \dfrac{BC}{2}$ y $C’B’ \parallel BC$.

Figura 1

Sea $G$ la intersección de las medianas $BB’$ y $CC’$, en $\triangle GBC$ consideremos $M$ y $N$ los puntos medios de los lados $GB$ y $GC$ respectivamente, entonces
$MN = \dfrac{BC}{2}$ y $MN \parallel BC$.

Por transitividad $C’B’ = MN$ y $C’B’ \parallel MN$, esto implica que $\square C’MNB’$ es un paralelogramo y por lo tanto sus diagonales se bisecan, es decir,
$C’G = GN$ y $MG = GB’$.

Por construcción, $MG = BM$ y $GN = NC$
$\Rightarrow GB’= \dfrac{BB’}{3}$ y $C’G = \dfrac{CC’}{3}$,
esto es, la medianas $BB’$ y $CC’$ se trisecan

Si repetimos el mismo procedimiento pero ahora con las medianas $AA’$ y $BB’$ encontraremos un punto $G’$ en donde las medianas se trisecaran, $G’B’= \dfrac{BB’}{3}$ y $G’A’ = \dfrac{AA’}{3}$.

Como $GB’= \dfrac{BB’}{3} = G’B’$, concluimos que $G’ = G$.

Por lo tanto, las medianas de un triángulo concurren en un punto que las triseca.

$\blacksquare$

Definición 1. Decimos que el punto en que concurren las medianas de un triángulo es el gravicentro, baricentro o centroide del triángulo y lo denotamos con la letra $G$ mayúscula.

Figura 2

Circuncentro

Teorema 2. Las mediatrices de los lados de todo triángulo son concurrentes.

Demostración. Sea $\triangle ABC$, consideremos las mediatrices $l_c$ y $l_b$ de $AB$ y $AC$ respectivamente y $O = l_b \cap l_c$.

Figura 3

En la entrada desigualdad del triángulo y lugar geométrico mostramos que un punto está en la mediatriz de un segmento si y solo si equidista a los puntos extremos del segmento.

Ya que $O \in l_c$ y $O \in l_b$, entonces $OA = OB$ y $OA = OC$
$\Rightarrow OB = OC$.

Por el resultado mencionado anteriormente $OB = OC$ implica que $O \in l_a$, la mediatriz de $BC$.

Por lo tanto, las mediatrices de un triángulo son concurrentes.

$\blacksquare$

Corolario. Tres puntos distintos y no colineales se encuentran en una única circunferencia.

Demostración. Sea $\triangle ABC$, por el teorema anterior las mediatrices de los segmentos determinados por los vértices del triángulo concurren en un punto $O$ cuya distancia a cada uno de los vértices es la misma $R = OA = OB = OC$.

Por definición de circunferencia, $A$, $B$ y $C$ pertenecen a la circunferencia con centro en $O$ y radio $R$, $A$, $B$, $C \in (O, R) = \Gamma$.

Ahora supongamos que existe $\Gamma’ = (O’, R’)$ tal que $A$, $B$, $C \in \Gamma’$, entonces, por definición, $O’A = O’B = O’C = R’$.

Esto implica que $O’ \in l_a$, $O’ \in l_b$ y $O’ \in l_c$, las mediatices de $BC$, $AC$ y $AB$ respectivamente,
$\Rightarrow O \in l_a \cap l_b \cap l_c$.

Como ya probamos que las mediatrices son concurrentes entonces $O’ = O$ y $R’ = R$, así que $\Gamma$ es única.

$\blacksquare$

Definición 2. Al punto de concurrencia de las mediatrices de los lados de un triángulo le llamamos circuncentro y lo denotamos como $O$.

A la distancia constante de $O$ a los vértices del triángulo le llamamos circunradio denotado con la letra $R$ mayúscula.

A la circunferencia única $(O, R)$ determinada por los vértices del triángulo se le conoce como circuncírculo.

Figura 4

Incentro

Teorema 3. Las bisectrices interiores de todo triángulo son concurrentes.

Demostración. Sean $l_B$ y $l_C$ las bisectrices de los ángulos interiores en $\angle B$ y $\angle C$ respectivamente e $I = l_{B} \cap l_{C}$.

Figura 5

En la entrada desigualdad del triángulo y lugar geométrico mostramos que un punto está en la bisectriz de un ángulo si y solo si equidista a los lados que forman el ángulo. Recordemos que la distancia de un punto a una recta es la longitud del punto al pie de la perpendicular a la recta trazada desde el punto.

Denotamos la distancia de un punto $P$ a una recta $l$ como $(P, l)$.

Como $I \in l_{b}$ e $I \in l_{c}$, entonces $(I, AB) = (I, BC)$ y $(I, BC) = (I, AC)$,
$\Rightarrow (I, AB) = (I, AC)$.

Por el resultado citado anteriormente, $(I, AB) = (I, AC)$ implica que $I \in l_A$, la bisectriz interior de $\angle A$.

Por tanto, las bisectrices interiores de un triángulo son concurrentes.

$\blacksquare$

Si consideramos los pies de las perpendiculares a los lados del triángulo trazados desde el punto en que concurren las bisectrices, encontramos tres puntos distintos que equidistan a un punto fijo y por el corolario anterior estos determinan una única circunferencia, esto motiva la siguiente definición.

Definición 3. Al punto de concurrencia de las bisectrices interiores de un triángulo se le conoce como incentro del triángulo y lo denotamos con la letra $I$ mayúscula.

A la distancia de $I$ a los lados del triángulo le llamamos inradio y lo denotamos como $r = (I, AB) = (I, BC) = (I, AC)$.

La circunferencia con centro en $I$ y radio $r$, $(I, r)$, se llama incírculo.

Figura 6

Excentros

Teorema 4. En todo triángulo las bisectrices exteriores de dos ángulos y la bisectriz interior del tercer ángulo son concurrentes.

Demostración. Sea $\triangle ABC$, $l_A$ y $l_C$ las bisectrices exteriores de $\angle A$ y $\angle C$ respectivamente e $I_b = l_A \cap l_C$.

Figura 7

De manera análoga al caso de las bisectrices internas tenemos que
como $I_b \in l_A$ e $I_b \in l_C$, entonces $(I_b, AB) = (I_b, AC)$ y $(I_b, AC) = (I_b, BC)$,
$\Rightarrow (I_b, AB) = (I_b, BC)$.

Como $I_b$ está en la región acotada por el ángulo $\angle CBA$ entonces $I \in l_B$, la bisectriz interior de $\angle B$.

Por lo tanto, la bisectriz interna de $\angle B$ y las bisectrices externas de $A$ y $C$ son concurrentes.

De manera análoga probamos que las bisectrices externas de $\angle A$ y $\angle B$ concurren con la bisectriz interna de $\angle C$, y las bisectrices externas de $\angle B$ y $\angle C$ concurren con la bisectriz interna de $\angle A$.

$\blacksquare$

Similarmente a como lo hicimos con el incentro, notamos que, para cada uno de estos tres puntos de concurrencia, existen tres puntos distintos, uno en cada lado del triángulo que equidistan a un punto fijo y por lo tanto determinan una única circunferencia.

Definición 4. A los puntos en que concurren dos bisectrices externas y una bisectriz interna de un triángulo les llamamos excentros del triángulo y los denotamos como $I_a$, $I_b$ e $I_c$ de acuerdo a si se encuentran en la bisectriz interna de $\angle A$, $\angle B$ o $\angle C$ respectivamente y decimos que son opuestos a dichos vértices.

Las distancias de $I_a$, $I_b$ e $I_c$ a los lados del triángulo son los exradios y se les denota como $r_a$, $r_b$ y $r_c$ respectivamente.

A las circunferencias $(I_a, r_a)$, $(I_b, r_b)$ y $(I_c, r_c)$ se les conoce como excírculos del triángulo.

Figura 8

Ortocentro

Teorema 5. Las alturas de todo triángulo son concurrentes.

Demostración. Sea $\triangle ABC$, tracemos en cada vértice la paralela al lado opuesto.

Sean $A’$ la intersección de la paralela a $AB$ trazada en $C$ con la paralela a $AC$ trazada en $B$, de manera análoga definimos $B’$ y $C’$.

Figura 9

Por construcción, $\square ABCB’$ es un paralelogramo por lo que $AB’ = BC$, también $\square C’BCA$ es paralelogramo así que $C’A = BC$,
$\Rightarrow AB’ = BC = C’A \Rightarrow A$ es el punto medio de $C’B’$.

De manera similar podemos ver que $B$ es el punto medio de $C’A’$ y $C$ es el punto medio de $A’B’$.

En consecuencia, las alturas del triángulo $\triangle ABC$ son las mediatrices del triángulo $\triangle C’A’B’$ y ya probamos que las mediatrices de los lados de todo triangulo son concurrentes, por lo tanto, las alturas de $\triangle ABC$ son concurrentes.

$\blacksquare$

Definición 5. Al punto en común en que las tres alturas de un triángulo se intersecan le llamamos ortocentro y lo denotamos con la letra $H$ mayúscula.

Figura 10

Más adelante…

En la siguiente entrada demostraremos algunos teoremas que nos permitirán calcular la magnitud de ángulos relativos a una circunferencia.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. ¿Qué puntos notables vistos en esta entrada, caen siempre dentro del triangulo y cuales siempre fuera?
  2. Muestra que una recta paralela a un lado de un triangulo a través del centroide divide el área del triangulo en dos partes tal que la razón de esta áreas es $\dfrac{4}{5}$.
  3. Considera un triangulo rectángulo $\triangle ABC$ con $\angle B = \dfrac{\pi}{2}$, sean $CC’$ la mediana por $C$ y $D$ el pie de la perpendicular a $CC’$ trazada desde $B$ (figura 11), calcula la distancia de $D$ al centroide $G$ del triangulo en términos de los catetos.
Figura 11
  1. Un triángulo rectángulo tiene un ángulo interior de $\dfrac{\pi}{3}$, calcula la distancia del vértice donde se intersecan los catetos al incentro $I$ del triángulo en términos de la hipotenusa.
  2. Sea $\triangle ABC$ un triángulo tal que la mediana $AD$ es perpendicular a la mediana $BE$, encuentra $AB$ si $BC = a$ y $AC = b$.

Entradas relacionadas

Fuentes

  • Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 29-34.
  • Altshiller, N., College Geometry. New York: Dover, 2007, pp 65-94.
  • Geometría interactiva

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Geometría analítica I: Aplicaciones a geometría del triángulo

Por Elsa Fernanda Torres Feria

Deja un comentario

Introducción

En esta entrada usaremos la forma normal de la recta para demostrar dos teoremas conocidos como teoremas de concurrencia de líneas.

Medianas y baricentro

Cerremos la entrada con la enunciación y la demostración del siguiente teorema.

Teorema. Dado un triángulo PQR, sus tres medianas concurren en un punto que divide al segmento dentro del triángulo (de cada mediana) en proporción 1:2.

Demostración.

Para empezar la demostración, construimos un triángulo PQR.

Para construir las medianas, primero localizamos los puntos medios de cada segmento (A, B, C) cuyas coordenadas baricéntricas están dadas por

\begin{align*}
A&=\frac{1}{2}P + \frac{1}{2}Q \\
B&=\frac{1}{2}Q + \frac{1}{2}R \\
C&=\frac{1}{2}R + \frac{1}{2}P \\
\end{align*}

Ya que queremos que se encuentren justo en el punto medio de cada segmento.

Al trazar la mediana del segmento $PQ$ tenemos lo siguiente

La manera en la que procederemos a partir de ahora, es que localizaremos el punto en el segmento de cada mediana que lo divide en proporción 1:2 esperando llegar a que los tres puntos son el mismo.

Comencemos con el punto $G$ que divide al segmento $AR$ en proporción 1:2, esto es que $G$ sea:

$G=\frac{1}{3}R+\frac{2}{3}A $

AL sustituir el valor de $A$, tenemos como resultado
\begin{align*}
G&=\frac{1}{3}R+\frac{2}{3}\left( \frac{1}{2}P + \frac{1}{2}Q \right) \\
&= \frac{1}{3}R+\frac{1}{3}P+\frac{1}{3}Q \\
\end{align*}

Lo que puede ser replicado para cada segmento. Para el $BP$ se tiene

\begin{align*}
G’ &=\frac{1}{3}P+\frac{2}{3}B \\
&=\frac{1}{3}P+\frac{2}{3} \left( \frac{1}{2}Q + \frac{1}{2}R \right) \\
&= \frac{1}{3}P+\frac{1}{3}Q+\frac{1}{3}R \\
&= \frac{1}{3}R+\frac{1}{3}P+\frac{1}{3}Q \\
\end{align*}

Y para el $CQ$

\begin{align*}
G»&=\frac{1}{3}Q+\frac{2}{3}C \\
&=\frac{1}{3}Q+\frac{2}{3} \left( \frac{1}{2}R + \frac{1}{2}P \right) \\
&= \frac{1}{3}Q+\frac{1}{3}R+\frac{1}{3}P \\
&= \frac{1}{3}R+\frac{1}{3}P+\frac{1}{3}Q \\
\end{align*}

$\therefore$ $G=G’=G»$

Acabamos de demostrar que los puntos que dividen a cada mediana en una proporción 1:2 son el mismo para cada una, por lo que las tres medianas concurren en este punto.

$\square$

A este punto $G$ se le conoce como el baricentro del triángulo, y podrás imaginar después de que discutimos la idea física de estas coordenadas, que $G$ corresponde al centro de masa o punto de equilibrio del triángulo.

Utiliza el siguiente interactivo para asegurarte de que esto es válido con cualquier triángulo, puedes mover los puntos P,Q y R y aún existirá el punto $G$ de intersección de las 3 medianas. Si te da curiosidad, puedes usar la herramienta de distancia de GeoGebra para medir la longitud de cada segmento de la mediana y verificar que efectivamente, está en una relación 1:2 con respecto al punto $G$.

Teoremas de concurrencia

Para poder realizar las demostraciones, definiremos a la altura de un triángulo como la recta que pasa por uno de sus vértices y es ortogonal al lado opuesto. Ahora, enunciemos y demostremos el primer teorema.

Teorema 1. Las alturas de un triángulo son concurrentes.

Demostración

Comencemos esta demostración con un interactivo que ilustre un triángulo y sus alturas.

Las rectas verdes son las alturas del triángulo y en el interactivo es bastante evidente que concurren en un punto y que esto pasa para cualquier triángulo (para comprobarlo puedes mover con tu cursor los vértices para modificar el triángulo). Sin embargo en este curso de geometría analítica, queremos demostrarlo de manera algebraica.

Para esta demostración algebraica, notemos que los vértices del triángulo son $A$, $B$, y $C$ y las alturas asociadas a cada vértice son $a$, $b$ y $c$ respectivamente. Escribamos la forma normal de cada una de estas rectas (alturas). Para $a$ tenemos

$a$ : $(C-B) \cdot x = (C-B) \cdot A$

pues la recta $a$ es ortogonal al lado del triángulo que pasa por los vértices $C$ y $B$, por lo que este lado tiene dirección $(C-B)$ y pasa por el punto $A$. De manera análoga, sabemos que $b$ es perpendicular a la recta que pasa por $A$ y $C$ con dirección $A-C$ y pasa también por el punto $B$, así

$b$ : $(A-C) \cdot x = (A-C) \cdot B$

Y de la misma forma para $c$ tenemos

$c$ : $(B-A) \cdot x = (B-A) \cdot C$

Nota que si sumamos las dos primeras ecuaciones, obtendremos la ecuación negativa de $c$:

\begin{align*}
(C-B) \cdot x + (A-C) \cdot x &= (C-B) \cdot A + (A-C) \cdot B \\
(C-B + A-C) \cdot x & = C \cdot A – B \cdot A + A \cdot B – C \cdot B\\
(-B+A) \cdot x & = C \cdot A – A \cdot B + A \cdot B – C \cdot B\\
(-B+A) \cdot x & = C \cdot A – C \cdot B \\
(-B+A) \cdot x & =(A – B) \cdot C
\end{align*}

Esto es importante, pues si tomamos un elemento en la intersección de las alturas $a$ y $b$ ($x \in a \cap b$), entonces también está en la suma y está última nos da como resultado el negativo de la ecuación de la recta $c$, por lo tanto $x \in c$.

De manera análoga, si sumamos $b$ y $c$ obtenemos

$(B-C) \cdot x = (B- C) \cdot A$

que corresponde a la ecuación negativa de $a$, por lo que si $x \in b \cap c$, entonces $x$ está en la suma de las ecuaciones y por tanto está en $a$.

Para completar la demostración, deberíamos realizar el mismo procedimiento al sumar las ecuaciones de $c$ y $a$ y confirmar que un punto en su intersección está en $b$.

$\therefore$ si dos de las alturas se intersectan, entonces la tercera recta también y en el mismo punto.

$square$

Teorema 2.

Demuestra que las tres mediatrices de un triángulo son concurrentes.

Demostración

Para comenzar la demostración, recordemos que la mediatriz de un segmento es la recta que es ortogonal a este y pasa por su punto medio.

De nuevo, es claro que las tres mediatrices del triángulo con vértices $D$, $E$ y $F$ concurren en un punto. Denominamos a los puntos medios de cada lado como $a$, $b$ y $c$, que es por donde pasan las mediatrices.

Ahora, para comenzar la parte algebraica de la demostración, definamos en su forma normal la primera miediatriz $i$. Siguiendo la idea de la demostración pasada, $i$ es ortogonal a $(E-F)$ y pasa por el punto $a$ por lo que

$i$ : $(E-F) \cdot x = (E-F) \cdot a$

De la misma manera, $j$ es ortogonal a $(D-E)$ y pasa por $b$, así

$j$ : $(D-E) \cdot x = (D-E) \cdot b$

Y para $k$ tenemos

$k$ : $(F-D) \cdot x = (F-D) \cdot c

Sigamos la intuición de la demostración anterior y sumemos las expresiones de $i$ y $j$

\begin{align*}
(E-F) \cdot x + (D-E) \cdot x &= (E-F) \cdot a + (D-E) \cdot b \\
E \cdot x – F \cdot x + D \cdot x – E \cdot x &= E \cdot a – F \cdot a + D \cdot b – E \cdot b \\
D \cdot x- F \cdot x &=E \cdot a – F \cdot a + D \cdot b – E \cdot b
\end{align*}

Para seguir avanzando con nuestra demostración, debemos recordar que $a,$, $b$ y $c$ son los puntos medios de cada lado del triángulo, por lo que podemos expresarlos en términos de los vértices de la siguiente manera

$a=\frac{F+E}{2}$, $b=\frac{E+D}{2}$ Y $c=\frac{D+F}{2}$

Con esto en mente, podemos sustituir $a$ y $b$ en la ecuación anterior y desarrollar

$D \cdot x- F \cdot x = E \cdot \left( \frac{F+E}{2} \right) – F \cdot \left( \frac{F+E}{2} \right) + D \cdot \left( \frac{E+D}{2} \right) – E \cdot \left( \frac{E+D}{2} \right) $

Al realizar todo el desarrollo obtenemos que

$D \cdot x- F \cdot x = \frac{1}{2}( D \cdot D – F \cdot F)$

Ahora, en la demostración pasada queríamos llegar a algún múltiplo de $k$ para demostrar que las 3 rectas se intersectaban, siguiendo con esa lógica, desarrollemos el lado derecho de $k$ tomando en cuenta a $c$ como punto medio de un lado

\begin{align*}
(F-D) \cdot c &= (F-D) \cdot \frac{D+F}{2} \\
&= \frac{1}{2} (F-D) \cdot (D+F) \\
&= \frac{1}{2}(F \cdot D + F \¢dot F – D \cdot D – F \cdot D) \\
&= \frac{1}{2}(F \cdot F – D \cdot D)
\end{align*}

Que es justamente el negativo de lo que obtuvimos arriba, por lo que al sumar las expresiones de $i$ y $j$ obtenemos el negativo de la expresión de $k$. Así, si un punto $x$ está en $ i \cap j$, entonces está en la suma y por lo tanto está en $k$.

El procedimiento es análogo para cada uno de los casos faltantes.

$\square$

Para concluir esta entrada, denotaremos al punto en el que concurren las mediatrices como circuncentro.

Más adelante…

En las próximas entradas discutiremos la forma normal de un elemento geométrico en el espacio $\mathbb{R}^3$ que no será la recta y hablaremos de la norma de un vector, que de cierta manera apareció en nuestras demostraciones pero no lo hemos discutido con formalidad hasta ahora.

Tarea moral

  • Completa los casos faltantes en la demostración del primer teorema.
  • Completa los casos faltantes en la demostración del segundo teorema.
  • Encuentra el circuncentro del triángulo que tiene como vértices los puntos $(5,3)$, $(2,-1)$ y $(8,0)$.