Archivo de la categoría: Matemáticas

Posts de matemáticas, la ciencia más cercana a las artes.

Geometría Moderna I: Cuadrilátero circunscrito

Por Rubén Alexander Ocampo Arellano

Deja un comentario

Introducción

Decimos que un cuadrilátero convexo es circunscrito si sus lados son tangentes a una misma circunferencia dentro del cuadrilátero. Nos referimos a dicha circunferencia como el incírculo y a su radio como el inradio del cuadrilátero.

Sabemos que los lados de un triángulo siempre son tangentes a una misma circunferencia, el incírculo del triángulo, cuyo centro es el punto donde concurren las bisectrices internas, en esta entrada estudiaremos cuando un cuadrilátero es circunscrito y algunas propiedades.

Primera caracterización para el cuadrilátero circunscrito

Teorema 1. Un cuadrilátero es circunscrito si y solo si la suma de dos lados opuestos es igual a la suma de los otros dos lados opuestos.

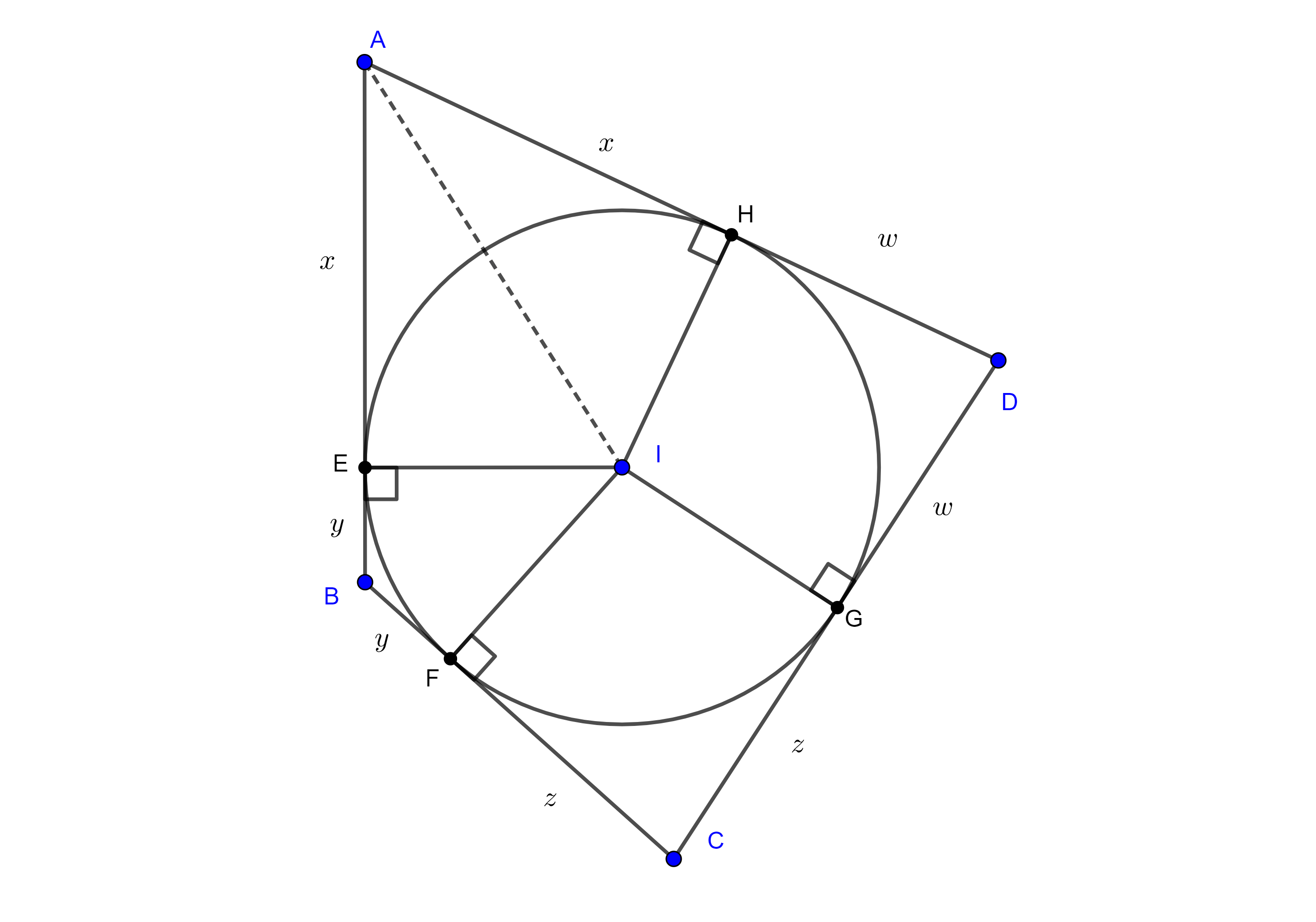
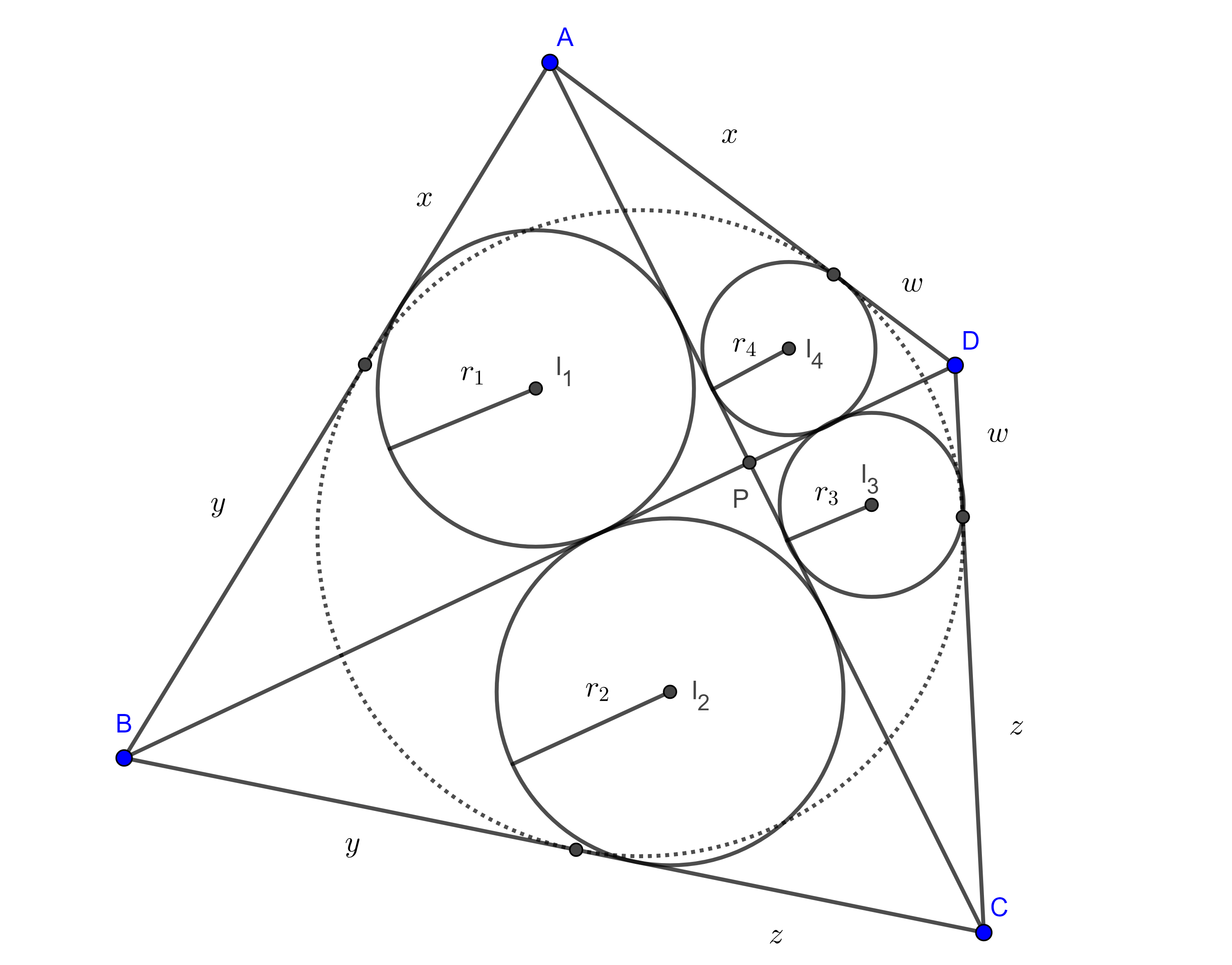
Demostración. Sean $\square ABCD$ un cuadrilátero circunscrito, $E$, $F$, $G$ y $H$ los puntos de tangencia de la circunferencia a los lados $AB$, $BC$, $CD$ y $AD$ respectivamente y consideremos $I$ el incentro de $\square ABCD$.

Figura 1

Recordemos que las tangentes a una circunferencia desde un punto externo a esta son iguales, por lo tanto, $AH = AE = x$, $BE = BF = y$, $CF = CG = z$, $DG = DH = w$.

Entonces $AB + CD = (x + y) + (z + w) = (x + w) + (y + z) = AD + BC$.

$\blacksquare$

Ahora supongamos que en $\square ABCD$ se tiene que $AB + CD = AD + BC$ y que tiene un par de lados adyacentes que no son iguales.

Sin pérdida de generalidad podemos suponer que $AB > BC$ entonces,
$\begin{equation} AD – CD = AB – BC > 0. \end{equation}$.

Figura 2

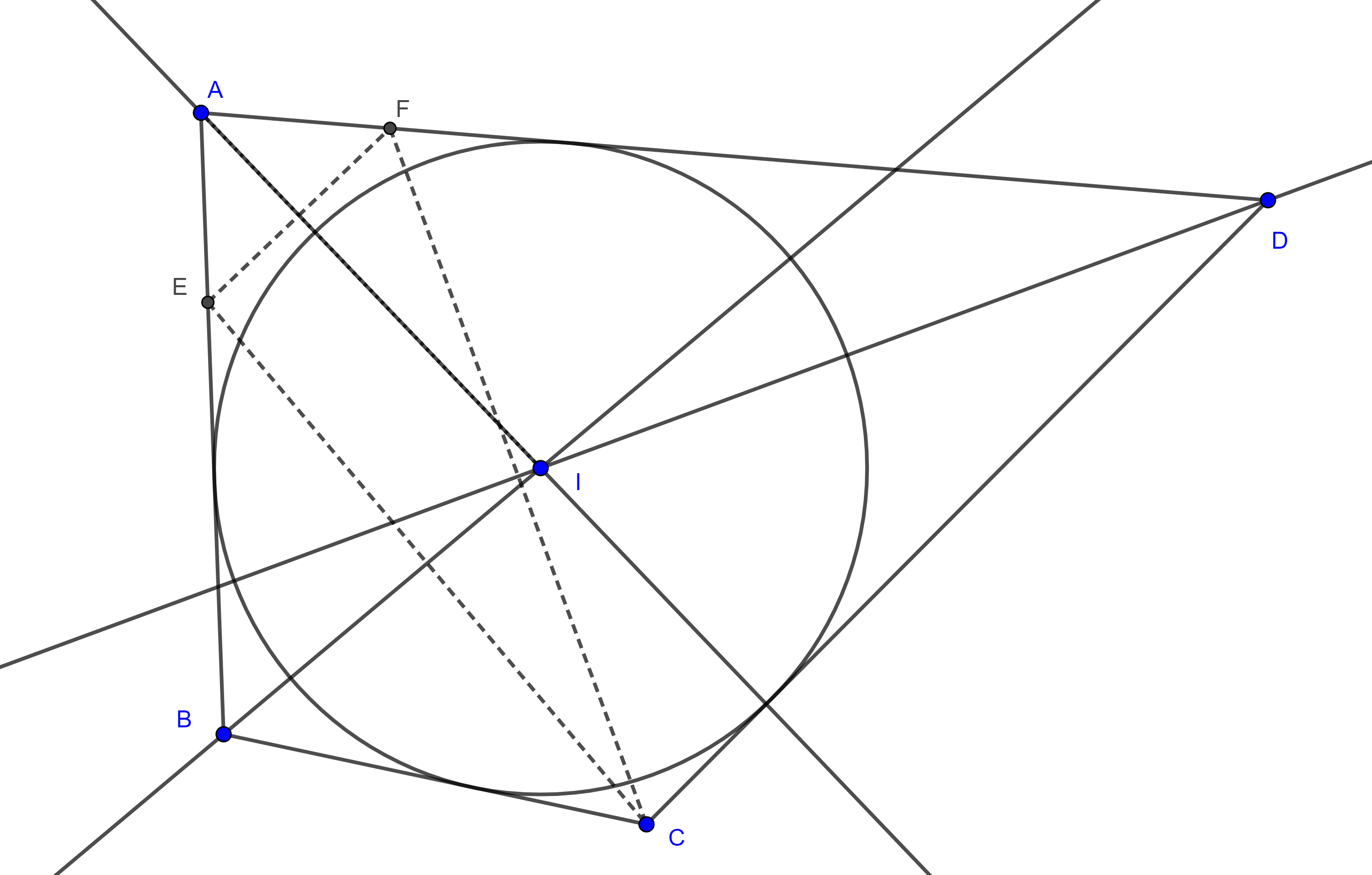
Sean $E \in AB$ y $F \in AD$ tales que $EB = BC$ y $FD = CD$ entonces por la ecuación $(1)$ $AE = AF$ y así $\triangle AEF$, $\triangle BCE$ y $\triangle DFC$ son isósceles.

Por lo tanto, las bisectrices internas de los ángulos $\angle EAF$, $\angle CBE$ y $\angle ADC$, son las mediatrices de $\triangle EFC$, por lo tanto, concurren en un punto $I$.

Como $I$ está en las bisectrices internas de los ángulos $\angle AEF$, $\angle BCE$ y $\angle DFC$, entonces, equidista a cado uno de los lados que forman dichos ángulos y de esta forma $I$ es el centro de una circunferencia tangente a los lados de $\square ABCD$.

La otra posibilidad es que todos los lados del cuadrilátero sean iguales es decir el cuadrilátero sea un rombo, este caso se queda como ejercicio.

$\blacksquare$

Teorema de Newton

Teorema 2, de Leon Anne. Sea $\square ABCD$ un cuadrilátero que no es un paralelogramo, el lugar geométrico de los puntos $P$ en el interior de $\square ABCD$ tal que $(\triangle APB) + (\triangle CPD) = (\triangle BPC) + (APD)$, es la recta de Newton de $\square ABCD$.

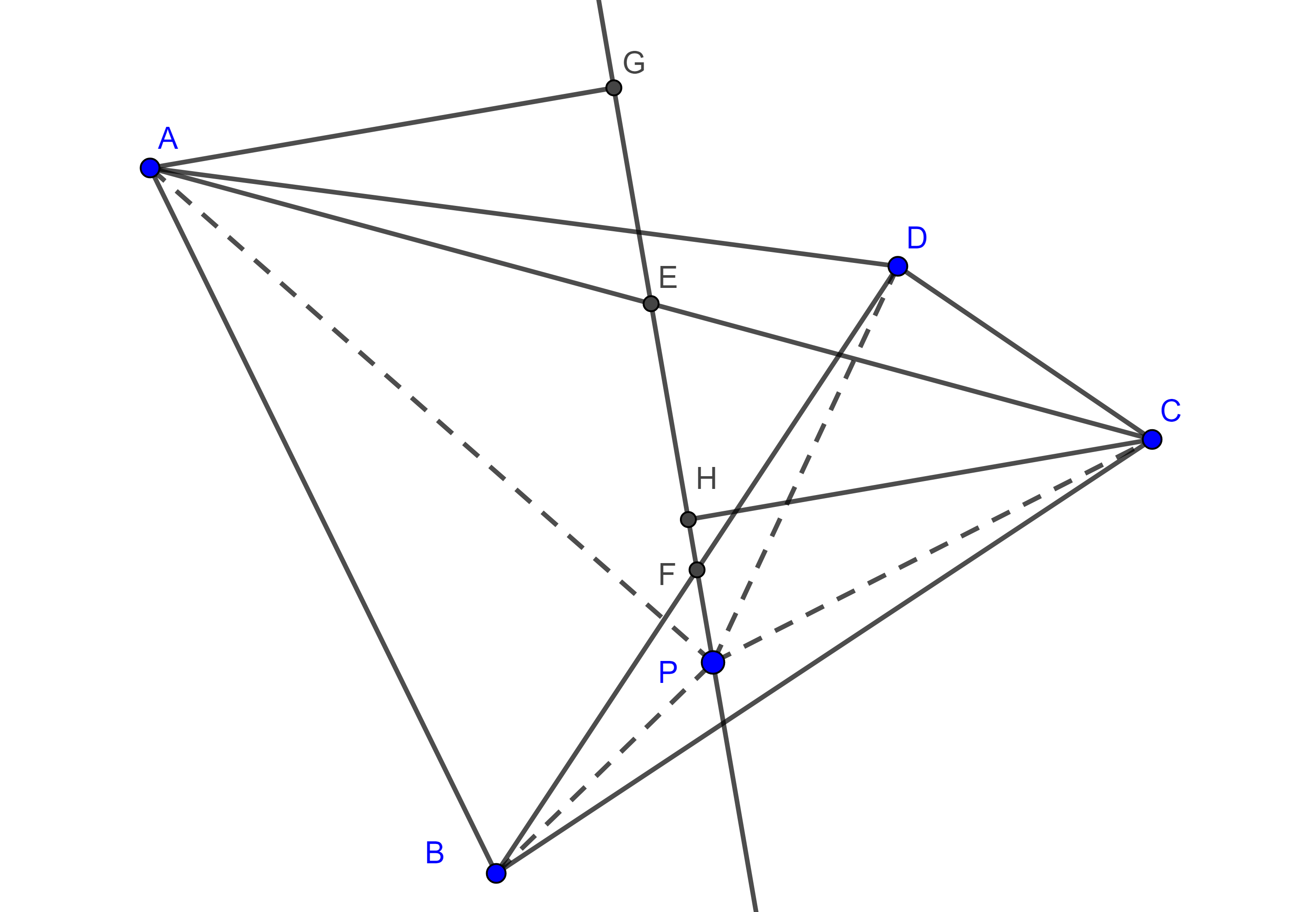
Demostración. Sean $P$ un punto en el interior de $\square ABCD$ tal que $(\triangle APB) + (\triangle CPD) = (\triangle BPC) + (APD)$ y $F$ el punto medio de $BD$.

Figura 3

Podemos ver el área de los triángulos considerados como suma y diferencia de otras áreas:

$(\triangle APB) = (\triangle AFB) + (\triangle BFP) – (\triangle AFP)$,
$ (\triangle CPD) = (\triangle CFD) + (\triangle CFP) – (\triangle DFP)$,
$(\triangle APD) = (\triangle AFD) + (\triangle AFP) + (\triangle DFP)$,
$ (\triangle BPC) = (\triangle BFC) – (\triangle BFP) – (\triangle CFP)$.

Entonces, por hipótesis:
$(\triangle AFB) + (\triangle BFP) – (\triangle AFP) + (\triangle CFD) + (\triangle CFP) – (\triangle DFP)$
$= (\triangle AFD) + (\triangle AFP) + (\triangle DFP) + (\triangle BFC) – (\triangle BFP) – (\triangle CFP)$.

$\Leftrightarrow$
$(\triangle AFB) + 2(\triangle BFP) + (\triangle CFD) + 2(\triangle CFP)$
$\begin{equation} = (\triangle AFD) + 2(\triangle AFP) + 2(\triangle DFP) + (\triangle BFC). \end{equation}$

Notemos que como $B$, $F$ y $D$ son colineales entonces $\triangle AFB$ y $\triangle AFD$ tienen la misma altura desde $A$, y ya que $FB = FD$ entonces $(\triangle AFB) = (\triangle AFD)$.

Igualmente podemos ver que
$(\triangle BFP) = (\triangle DFP)$ y $(\triangle CFD) = (\triangle BFC)$.

De la ecuación $(2)$ se sigue que $(\triangle CFP) = (\triangle AFP)$.

Como ambos triángulos tienen la misma base entonces las alturas trazadas desde $A$ y $C$ a la recta $FP$ son la mismas, digamos $AG = CH$.

Consideremos $E$ la intersección de $AC$ con $FP$, entonces $\triangle AEG$ y $\triangle CEH$ son congruentes, por criterio ángulo, lado, ángulo.

Por lo tanto $E$ es el punto medio de $AC$ y así $P$ está en la recta de Newton de $\square ABCD$.

La implicación reciproca se puede ver tomando en sentido contrario los argumentos anteriores.

$\blacksquare$

Teorema 3. De Newton. Si un cuadrilátero es circunscrito entonces su incentro esta en la recta de Newton del cuadrilátero.

Demostración. Sean $\square ABCD$ un cuadrilátero circunscrito $I$ y $r$ el centro y el radio de su incírculo respectivamente, entonces por el teorema 1 sabemos que:
$AB + CD = AD + BC$
$\Rightarrow \dfrac{r}{2}(AB + CD) = \dfrac{r}{2}(AD + BC)$
$\Rightarrow (\triangle AIB) + (\triangle CID) = (\triangle AID) + (\triangle BIC)$.

Por lo tanto, $I$ se encuentra en la recta de Newton de $\square ABCD$.

$\blacksquare$

Rectas concurrentes en el cuadrilátero circunscrito

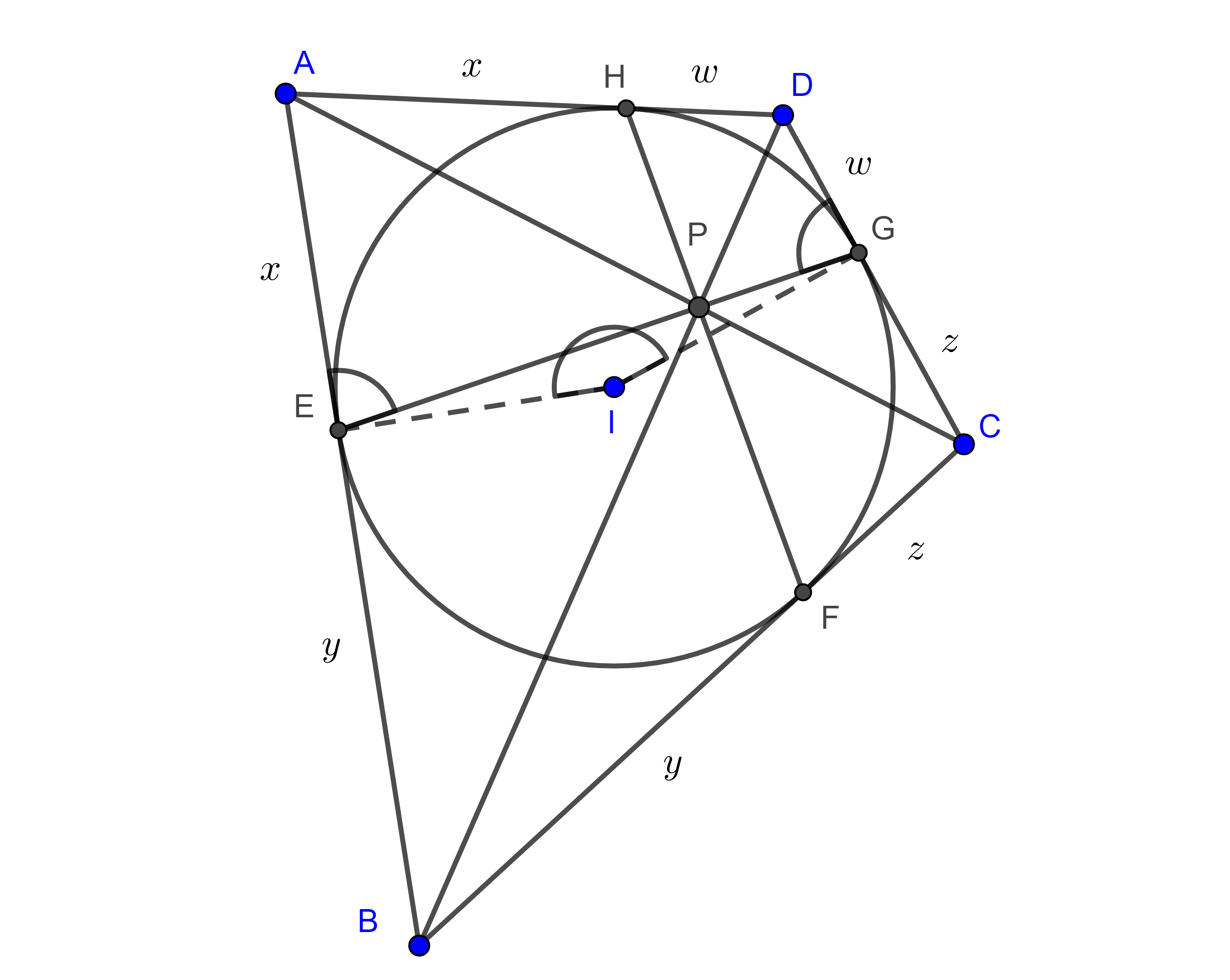
Teorema 4. Sea $\square ABCD$ un cuadrilátero circunscrito y sean $E$, $F$, $G$ y $H$ los puntos de tangencia del circuncírculo con los lados $AB$, $BC$, $CD$ y $AD$ respectivamente, entonces,
$i)$ las cuerdas $EG$, $FH$ y las diagonales $AC$, $BD$ son concurrentes
$ii)$ si $P$ es el punto de concurrencia, entonces,
$\dfrac{AP}{CP}  = \dfrac{x}{z}$ y $\dfrac{BP}{DP}  = \dfrac{y}{w}$.

Donde $AH = AE = x$, $BE = BF = y$, $CF = CG = z$, $DG = DH = w$.

Demostración. Sean $I$ el incentro de $\square ABCD$ y $P = AC \cap EG$.

Como $AB$ y $CD$ son tangentes al circuncírculo en $E$ y $G$ respectivamente, entonces $\angle GEA = \angle DGE$, pues ambos son ángulos semiinscritos que abarcan el mismo arco.

Figura 4

Por lo tanto,
$\sin \angle PEA = \sin \angle DGP = \sin (\pi – \angle DGP) = \sin \angle PGC$.

Por otro lado,
$2(\triangle AEP) = AP \times EP \sin \angle APE = AE \times EP \sin \angle PEA$,
$2(\triangle CGP) = PG \times CP \sin \angle CPG = CG \times GP \sin \angle PGC$.

$\Rightarrow \dfrac{(\triangle AEP) }{(\triangle CGP)} = \dfrac{AP \times EP}{PG \times CP} = \dfrac{AE \times EP}{CG \times GP}$
$\Rightarrow \dfrac{AP}{CP}  = \dfrac{AE}{CG}$.

Lo que significa que la cuerda $EG$ divide internamente a la diagonal $AC$ en la razón $\dfrac{AE}{CG} = \dfrac{x}{z}$.

Similarmente podemos mostrar que la cuerda $FH$ divide internamente a la diagonal $AC$ en la razón $\dfrac{x}{z}$, por lo tanto, $EG$, $FH$, se intersecan en $AC$.

Repitiendo este procedimiento, pero esta vez para la diagonal $BD$ podemos ver que $BD$, $EG$ y $FH$ concurren, y que $\dfrac{BP}{DP}  = \dfrac{y}{w}$.

Por lo tanto, las diagonales $AC$, $BD$ y las cuerdas $EG$, $FH$ son concurrentes.

$\blacksquare$

Corolario. Tenemos las siguientes igualdades (figura 4),
$\dfrac{(\triangle APB)}{xy} = \dfrac{(\triangle BPC)}{yz} = \dfrac{(\triangle CPD)}{zw} = \dfrac{(\triangle APD)}{xw}$.

Demostración. Notemos que los triángulos $\triangle APB$ y $\triangle BPC$ tienen la misma altura desde el vértice $B$, y ya que $A$, $P$ y $C$ son colineales, entonces usando la razón, encontrada en el teorema anterior, en la que $P$ divide a $AC$.

$\dfrac{(\triangle APB)}{(\triangle BPC)} = \dfrac{AP}{PC} = \dfrac{x}{z} \Leftrightarrow \dfrac{(\triangle APB)}{xy} = \dfrac{(\triangle BPC)}{zy}$.

Las otras igualdades se muestran de manera análoga.

$\blacksquare$

Una propiedad referente a inradios

Teorema 5. Sean $\square ABCD$ circunscrito, $P$ el punto de intersección de las diagonales, y consideremos los inradios $r_{1}$, $r_{2}$, $r_{3}$, $r_{4}$, de los triángulos $\triangle APB$, $\triangle BPC$, $\triangle CPD$ y $\triangle APD$ respectivamente, entonces
$\dfrac{1}{ r_{1}} + \dfrac{1}{ r_{3}} = \dfrac{1}{ r_{2}} + \dfrac{1}{ r_{4}}$.

Demostración. Por el corolario anterior, sea $\lambda = \dfrac{(\triangle APB)}{xy} = \dfrac{(\triangle BPC)}{yz} = \dfrac{(\triangle CPD)}{zw} = \dfrac{(\triangle APD)}{xw} \neq 0$.

Figura 5

Por el teorema 4, tenemos que $\dfrac{AP}{CP}  = \dfrac{x}{z}$ y $\dfrac{BP}{DP}  = \dfrac{y}{w}$.

Entonces sean $\eta = \dfrac{AP}{x}  = \dfrac{CP}{z}$ y $\mu = \dfrac{BP}{y}  = \dfrac{DP}{w}$.

Ahora calculamos el área de $\triangle APB$.

$(\triangle APB) = r_{1}s = \dfrac{r_{1}}{2}(AP + PB + AB)$
$\Leftrightarrow \dfrac{1}{r_{1}} = \dfrac{AP + PB + AB}{2(\triangle APB)} = \dfrac{AP + PB + AB}{2 \lambda xy}$
$\Leftrightarrow \dfrac{2 \lambda}{r_{1}} = \dfrac{AP + PB + AB}{xy} = \dfrac{x \eta + y \mu + (x + y)}{xy}$
$= \dfrac{x(\eta + 1) + y(\mu + 1))}{xy} = \dfrac{\eta + 1}{y} + \dfrac{\mu + 1}{x}$.

De manera análoga podemos ver que
$\dfrac{2 \lambda}{r_{3}} = \dfrac{\eta + 1}{w} + \dfrac{\mu + 1}{z}$.

Entonces,
$\dfrac{2 \lambda}{r_{1}} + \dfrac{2 \lambda}{r_{3}} = \dfrac{\eta + 1}{y} + \dfrac{\mu + 1}{x} + \dfrac{\eta + 1}{w} + \dfrac{\mu + 1}{z}$.

Podemos encontrar de la misma forma
$\dfrac{2 \lambda}{r_{2}} + \dfrac{2 \lambda}{r_{4}} = \dfrac{\eta + 1}{y} + \dfrac{\mu + 1}{z} + \dfrac{\mu + 1}{x} + \dfrac{\eta + 1}{w}$.

Por lo tanto,
$\dfrac{2 \lambda}{r_{1}} + \dfrac{2 \lambda}{r_{3}} = \dfrac{2 \lambda}{r_{1}} + \dfrac{2 \lambda}{r_{3}}$
$\Leftrightarrow \dfrac{1}{r_{1}} + \dfrac{1}{r_{3}} = \dfrac{1}{r_{2}} + \dfrac{1}{r_{4}}$.

$\blacksquare$

Puntos cíclicos en el cuadrilátero circunscrito

Lema. Sean $\triangle ABC$, $I$ y $r$ el incentro y el inradio de su circuncírculo entonces
$i)$ $AB + AC – BC = 2 r \cot \dfrac{\angle A}{2}$,
$ii)$ $AI = \dfrac{r}{\sin \dfrac{\angle A}{2}}$.

Demostración. Consideremos $D$, $E$ y $F$ los puntos de tangencia de $(I, r)$ con $AB$, $BC$ y $AD$ respectivamente entonces $AD = AF$, $BD = BE$ y $CE = CF$ además en el triángulo rectángulo $\triangle ADI$
$\tan\dfrac{\angle A}{2} = \dfrac{ID}{AD} \Leftrightarrow AD = r \cot \dfrac{\angle A}{2}$.

Figura 6

Por lo tanto, $AB + AC – BC = (AD + BD) + (AF + CF) – (BE + CE) = 2AD = 2 r \cot \dfrac{\angle A}{2}$.

Por otra parte en $\triangle ADI$,
$\sin \dfrac{\angle A}{2} = \dfrac{ID}{IA} \Leftrightarrow AI = \dfrac{r}{\sin \dfrac{\angle A}{2}}$.

$\blacksquare$

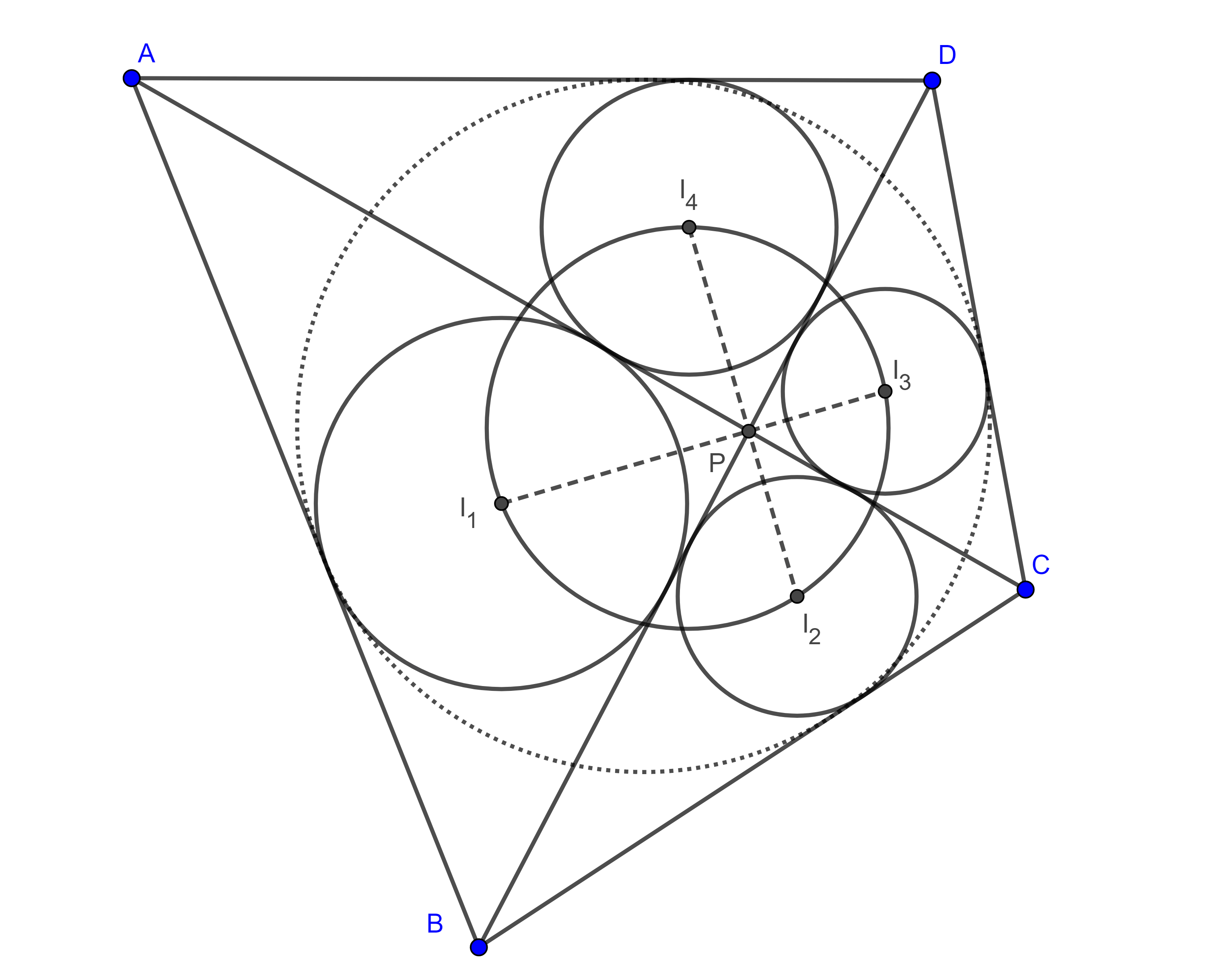
Teorema 6. Sean $\square ABCD$ circunscrito, $P$ la intersección de las diagonales, $I_{1}$, $I_{2}$, $I_{3}$ e $I_{4}$ los incentros de los triángulos $\triangle APB$, $\triangle BPC$, $\triangle CPD$ y $\triangle APD$ respectivamente entonces el cuadrilátero $\square I_{1}I_{2}I_{3} I_{4}$ es cíclico.

Demostración. Sean $r_{1}$, $r_{2}$, $r_{3}$ y $r_{4}$ los inradios de $\triangle APB$, $\triangle BPC$, $\triangle CPD$ y $\triangle APD$ respectivamente, notemos que $\angle APB = \angle CPD$ y $\angle BPC = \angle DPA$ pues son opuestos por el vértice, entonces
$2(\angle APB + \angle DPA) = 2\pi \Leftrightarrow \dfrac{\angle APB + \angle DPA}{2} = \dfrac{\pi}{2}$ por lo que
$\sin \dfrac{\angle APB}{2} = \cos \dfrac{\angle DPA}{2}$ y $\cos \dfrac{\angle APB}{2} = \sin \dfrac{\angle DPA}{2}$.

Figura 7

Aplicando el lema parte 1 a $\triangle APB$ y $\triangle CPD$ obtenemos
$(AP + BP – AB) + (CP + DP – CD)$
$= 2 r_{1} \cot \dfrac{\angle APB}{2} + 2 r_{3}  \cot \dfrac{\angle CPD}{2} = 2\cot \dfrac{\angle APB}{2}( r_{1} + r_{3})$.

Hacemos lo mismo con $\triangle BPC$ y $\triangle APD$,
$(BP + CP – BC) + (DP + AP – AD) = 2\cot \dfrac{\angle DPA}{2}( r_{2} + r_{4})$.

Como $\square ABCD$ es circunscrito por el teorema 1, $AB + CD = BC + AD$ por lo que
$(AP + BP – AB) + (CP + DP – CD) = (BP + CP – BC) + (DP + AP – AD)$.

Y por lo tanto,
$2\cot \dfrac{\angle APB}{2}( r_{1} + r_{3}) = 2\cot \dfrac{\angle DPA}{2}( r_{2} + r_{4})$

$\Rightarrow \dfrac{ r_{1} + r_{3}}{ r_{2} + r_{4}} = \dfrac{\cot \dfrac{\angle DPA}{2}}{\cot \dfrac{\angle APB}{2}}$
$= \dfrac{\dfrac{\cos \dfrac{\angle DPA}{2}}{\sin \dfrac{\angle DPA}{2}}}{\dfrac{\cos \dfrac{\angle APB}{2}}{\sin \dfrac{\angle APB}{2}}}
= \dfrac{\dfrac{\sin \dfrac{\angle APB}{2}}{\cos \dfrac{\angle APB}{2}}}{\dfrac{\cos \dfrac{\angle APB}{2}}{\sin \dfrac{\angle APB}{2}}}
= \dfrac{\sin^2 \dfrac{\angle APB}{2}}{\cos^2 \dfrac{\angle APB}{2}}$

$\begin{equation} = \tan^2 \dfrac{\angle APB}{2}. \end{equation}$

Por otra parte aplicamos el lema parte 2 a $\triangle APB$ y $\triangle CPD$
$PI_{1} \times PI_{3} = \dfrac{r_{1}}{\sin \dfrac{\angle APB}{2}} \dfrac{r_{3}}{\sin \dfrac{\angle CPD}{2}} = \dfrac{ r_{1} r_{3}}{\sin^2 \dfrac{\angle APB}{2}}$.

Hacemos lo mismo con $\triangle BPC$ y $\triangle APD$
$PI_{2} \times PI_{4} = \dfrac{r_{2}}{\sin \dfrac{\angle BPC}{2}} \dfrac{r_{4}}{\sin \dfrac{\angle DPA}{2}} = \dfrac{ r_{2} r_{4}}{\sin^2 \dfrac{\angle DPA}{2}}$.

Realizamos el cociente de las dos últimas expresiones encontradas
$\dfrac{PI_{2} \times PI_{4}}{PI_{1} \times PI_{3}} = \dfrac{r_{2} r_{4}}{\sin^2 \dfrac{\angle DPA}{2}} \dfrac{\sin^2 \dfrac{\angle APB}{2}}{r_{1} r_{3}} = \dfrac{r_{2} r_{4}}{r_{1} r_{3}} \dfrac{\sin^2 \dfrac{\angle APB}{2}}{\cos^2 \dfrac{\angle APB}{2}}$

$\begin{equation} = \dfrac{r_{2} r_{4}}{r_{1} r_{3}} \tan^2 \dfrac{\angle APB}{2}. \end{equation}$

Entonces podemos sustituir la ecuación $(3)$ en $(4)$
$\dfrac{PI_{2} \times PI_{4}}{PI_{1} \times PI_{3}} = (\dfrac{r_{2} r_{4}}{r_{1} r_{3}}) (\dfrac{r_{1} + r_{3}}{r_{2} + r_{4}}) = \dfrac{\dfrac{r_{1} + r_{3}}{r_{1} r_{3}}}{\dfrac{r_{2} + r_{4}}{r_{2} r_{4}}}
= \dfrac{\dfrac{1}{r_{1}} + \dfrac{1}{r_{3}}}{\dfrac{1}{r_{2}} + \dfrac{1}{r_{4}}}$.

Por el teorema 5, sabemos que
$\dfrac{1}{r_{1}} + \dfrac{1}{ r_{3}} = \dfrac{1}{r_{2}} + \dfrac{1}{ r_{4}}$.

Por lo tanto,
$\dfrac{PI_{2} \times PI_{4}}{ PI_{1} \times PI_{3}} = 1$
$\Leftrightarrow PI_{2} \times PI_{4} = PI_{1} \times PI_{3}$.

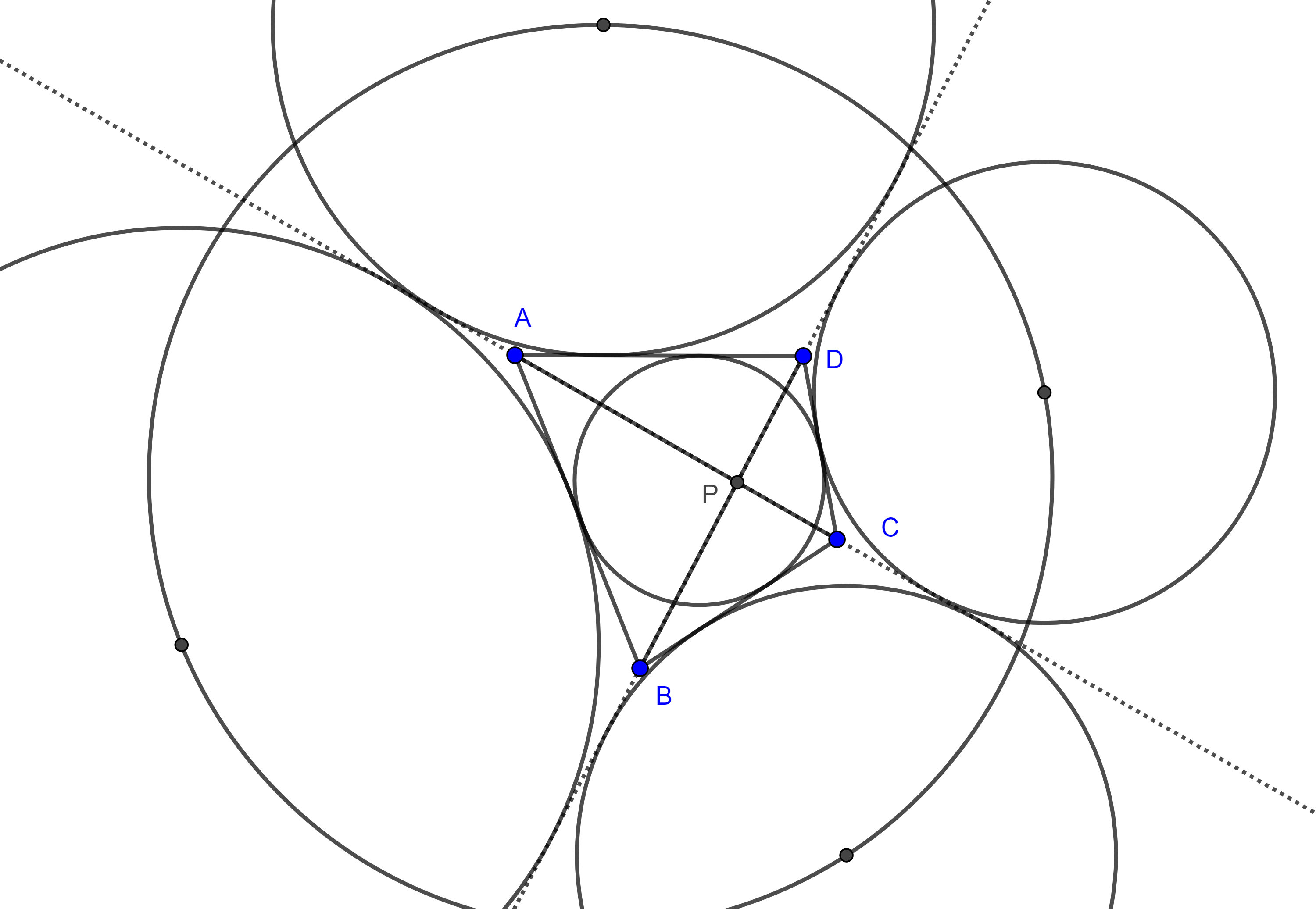
Como $P = I_1I_3 \cap I_2I_4$, pues estas rectas son las bisectrices interna y externa de $\angle APB$, por el teorema de las cuerdas, el cuadrilátero $\square I_1I_2I_3I_4$ es cíclico.

$\blacksquare$

Más adelante…

En la siguiente entrada estudiaremos características de los cuadriláteros que son tanto cíclicos como circunscritos.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. $i)$ Muestra que un cuadrilátero convexo es circunscrito si y solo si sus bisectrices internas son concurrentes.
    $ii)$ Prueba que todo rombo es circunscrito.
  2. Muestra que $\square ABCD$ convexo, es circunscrito si y solo si los incírculos de los triángulos $\triangle ABC$ y $\triangle ACD$ son tangentes entre si.
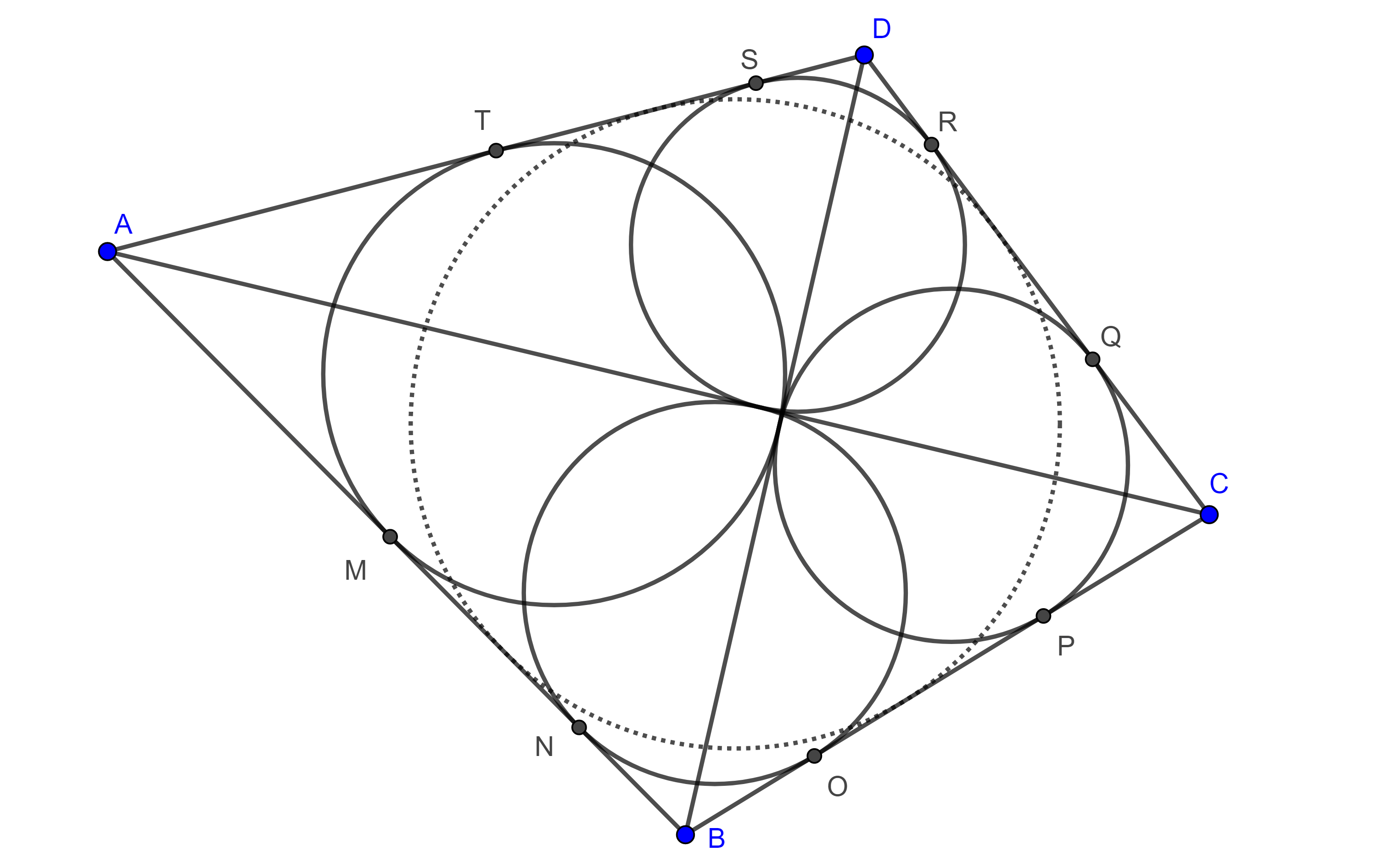
  3. Sea $\square ABCD$ convexo, consideremos los incirculos de los triángulos $\triangle ABD$, $\triangle ABC$, $\triangle BCD$ y $\triangle ADC$ que son tangentes a los lados del cuadrilátero en $M$, $T$, $N$, $O$, $P$, $Q$, y $R$, $S$ respectivamente, muestra que $\square ABCD$ es circunscrito si y solo si $MN + QR = OP + ST$.
  1. Si $\square ABCD$ es circunscrito, con lados $a$, $b$, $c$ y $d$ muestra que:
    $i)$ $(\square ABCD) = \sqrt{abcd} \sin \dfrac{\angle A + \angle C}{2} = \sqrt{abcd} \sin \dfrac{\angle B + \angle D}{2}$,
    $ii)$ $(\square ABCD) \leq \sqrt{abcd}$.
  2. Sean $\square ABCD$ circunscrito, $I$ el incentro del cuadrilátero y $P$ la intersección de las diagonales, muestra que los ortocentros de los triángulos $\triangle AIB$, $\triangle BIC$, $\triangle CID$, $\triangle AID$ y $P$ son colineales.
  1. Sean $\square ABCD$ circunscrito y $P$ la intersección de sus diagonales, muestra que los centros de los excírculos de los triángulos $\triangle APB$, $\triangle BPC$, $\triangle CPD$ y $\triangle APD$ opuestos a $P$ forman un cuadrilátero cíclico.

Entradas relacionadas

Fuentes

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Ecuaciones Diferenciales I – Videos: Ecuaciones lineales de segundo orden con coeficientes variables. Solución por series cerca de un punto singular regular

Por Eduardo Vera Rosales

Deja un comentario

Introducción

En la entrada anterior resolvimos la ecuación diferencial de Euler, cerca del punto singular $t_{0}=0$, como un caso particular de las ecuaciones que consideraremos en esta ocasión. Vimos que la forma que tenga la solución general depende de las raíces de la ecuación cuadrática $r^{2}+(\alpha -1)r+\beta=0$.

Es turno de revisar el caso cuando queremos encontrar una solución en forma de serie cerca de un punto singular ecuación diferencial $$a_{0}(t)\frac{d^{2}y}{dt^{2}}+a_{1}(t)\frac{dy}{dt}+a_{2}(t)y=0.$$ Clasificaremos a los puntos singulares en dos tipos: regulares e irregulares. Debido a la complejidad para encontrar soluciones alrededor de puntos singulares irregulares, nos enfocaremos exclusivamente en los puntos singulares regulares, y trataremos de generalizar el método utilizado para resolver la ecuación de Euler, el cual lleva el nombre de método de Frobenius, gracias al matemático Ferdinand Georg Frobenius.

Para facilitar el desarrollo de la teoría, en esta entrada siempre supondremos que el punto singular regular sobre el que trabajaremos es $t_{0}=0$. En la práctica, si tenemos un punto singular $t_{0}\neq 0$, basta con hacer el cambio de variable $z=t-t_{0}$.

Consideraciones generales. Solución cuando la ecuación indicial tiene dos raíces distintas que no difieren por un entero

En el primer video, damos las definiciones de punto singular regular e irregular y damos las consideraciones generales con las que trabajaremos a lo largo de toda la entrada. Además presentamos la ecuación indicial de la cual depende la forma de la solución general a la ecuación $$a_{0}(t)\frac{d^{2}y}{dt^{2}}+a_{1}(t)\frac{dy}{dt}+a_{2}(t)y=0$$ cerca del punto singular regular $t_{0}=0$. Finalmente resolvemos el primer caso del método de Frobenius cuando la ecuación indicial $r^{2}+(b_{0}-1)r+c_{0}=0$ tiene raíces distintas que no difieren por un entero.

Solución cuando la ecuación indicial tienen raíces repetidas

En el segundo video resolvemos el segundo caso del método de Frobenius, cuando la ecuación indicial tiene dos raíces repetidas.

Solución cuando al ecuación indicial tiene raíces que difieren por un entero

Finalizamos esta serie de videos con el último caso del método de Frobenius, cuando la ecuación indicial tiene dos raíces que difieren por un entero.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero te servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

  • Prueba que si $r_{1}$, $r_{2}$ son raíces complejas de la ecuación indicial $r^{2}+(b_{0}-1)r+c_{0}=0$, entonces $F(r_{1}+k)$ y $F(r_{2}+k)$ no se anulan para cualquier $k\geq1$. Por lo tanto la solución general a la ecuación diferencial tiene la misma forma que cuando consideramos raíces reales que no difieren por un entero, pero con valores complejos.
  • Encuentra una expresión para la solución general del ejercicio anterior pero con valores únicamente reales.
  • Muestra que las soluciones $y_{1}(t)$, $y_{2}(t)$ encontradas en el caso cuando la ecuación indicial tiene raíces repetidas, son linealmente independientes.
  • Encuentra los radios de convergencia para cada solución dada en forma de series en esta entrada. (Hint: Las demostraciones son análogas al caso de radios de convergencia para soluciones por series de potencias alrededor de puntos ordinarios).

Más adelante

Hemos concluido de desarrollar la teoría que involucra soluciones en series, tanto alrededor de un punto ordinario como cerca de un punto singular regular. Como te pudiste dar cuenta en esta entrada no resolvimos ejemplos, ya que en las siguientes entradas emplearemos esta teoría para resolver algunas ecuaciones especiales que se usan principalmente en la física. En la siguiente entrada en particular, estudiaremos las ecuaciones de Hermite y Laguerre.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Álgebra Superior I: Demostración de condicionales y dobles condicionales

Por Guillermo Oswaldo Cota Martínez

Deja un comentario

Introducción

Esta entrada es parte de una serie de notas introductorias sobre técnicas de demostración. En esta entrada se habla sobre demostraciones de condicionales y dobles condicionales. Cada entrada está ligeramente relacionada con las otras. Para entenderlas bien, usamos el siguiente diagrama que recopila cómo se comporta un mundo fantástico llamado Axios, en donde habitan creaturas llamadas Blorgs. Para leer más sobre ello, haz click aquí.

Para terminar nuestra sección de demostraciones (no significa que terminamos de demostrar, para nada, apenas es el comienzo), vamos a ver el caso en donde tengamos la doble implicación. Esto no va a ser difícil, pues hemos desarrollado suficientes estrategias para ello, y solo verás que la forma de demostrar estas proposiciones, es ver la doble implicación de otra manera.

La suficiencia y necesidad

Es común ver proposiciones matemáticas de la forma

$$\forall x (P(x) \Leftrightarrow Q(x)) $$

Como por ejemplo

Proposición. Un blorg come dos veces a la semana si y solo si tiene amigos amarillos y rojos.

Para este tipo de demostraciones, lo que haremos será demostrar dos cosas: la suficiencia y la necesidad. Recordemos que la doble implicación puede escribirse de la siguiente manera:

$$\forall x (P(x) \Leftrightarrow Q(x)) = \forall x ((P(x) \Rightarrow Q(x)) \land (Q(x) \Rightarrow P(x) )) $$

Es decir, para demostrar la condición, es necesario demostrar que si un blorg come dos veces a la semana entonces tiene amigos amarillos y rojos, y también será necesario mostrar que si un blorg tiene amigos amarillos y rojos come dos veces a la semana. Esto es, demostrar que las condiciones son equivalentes: un blorg solo tiene amigos amarillos y rojos si y solo si come dos veces por semana.

Demostración. Para esto, consideremos primero a un blorg $x$, para demostrar la doble implicación, es común dividir el problema en dos partes que podrás encontrar como «la ida» y «el regreso», esto hace referencia a que al demostrar la ida, demostraras que $P(x) \Rightarrow Q(x)$ y el regreso demuestra que $P(x) \Leftarrow Q(x)$. No dejes que te confunda la dirección de la flecha, simplemente es otra forma de demostrar que $Q(x) \Rightarrow P(x)$ (mira la dirección de la flecha).

Y comúnmente encontrarás en las demostraciones las notaciones de $\Rightarrow$ y $\Leftarrow$ haciendo referencia a si demostrarán la ida o el regreso, justo como lo haremos a continuación.

$\Rightarrow$

Primero demostraremos que si un $x$ come dos veces a la semana, entonces tiene amigos rojos y amarillos.

Como $x$ come dos veces a la semana, entonces es un blurg, pues es la única especie que come los Lunes y Viernes, mientras que los Blargs y Blergs comen solo los Lunes. Ahora, notemos que un blurg es amigo de los Blergs y los Blargs, cuyos respectivos colores son rojos y amarillos. Así hemos demostrado que si un $x$ come dos veces a la semana, entonces tiene amigos rojos y amarillos.

$\Leftarrow$

Ahora, para demostrar el regreso, supongamos que $x$ tiene amigos rojos y amarillos y lleguemos a la conclusión de que come dos veces a la semana.

Notemos a los amigos de cada especie de blorg. Los Blargs son amigos de los Blurgs y de los delfines, los cuales son azules, entonces no tienes amigos amarillos y rojos, por otro lado los Blergs son amigos de los Blurgs, que son azules, por lo que tampoco cumplen la condición. Mientras que los Blurgs son amigos de los Blergs y Blargs, que cumplen con ser rojos y amarillos. Entonces $x$ tiene que se un blurg. A continuación, notemos que los Blurgs comen los Lunes y Viernes, esto es, que comen dos veces por la semana, cumpliendo la proposición.

De esta forma hemos demostrado que un blorg come dos veces a la semana si y solo si tiene amigos amarillos y rojos.

Otro vistazo a la doble implicación

Para que te des una idea mejor sobre el poder de este tipo de proposiciones, recuerda lo siguiente: «La doble implicación es la forma de decir que dos cosas son equivalentes». Esto no es algo nuevo, pues ya hemos mencionado esto antes. La diferencia es que ahora ya tenemos aplicaciones prácticas de esto, ve el siguiente ejemplo:

Proposición. Un blorg come dos veces por semana si y solo si tiene un amigo de otra especie que puede comer fresas.

Demostración. Ahora, no solo vamos a usar la doble implicación para la demostración, sino que juntaremos proposiciones que hemos demostrado anteriormente. Primero que nada, notemos que la proposición se parece en parte a la pasada. Usaremos lo que sabemos de la proposición pasada. Como un blorg come dos veces por semana si y solo si tiene amigos amarillos y rojos. Ahora veamos cómo podemos usarla para demostrar esto.

Considera las proposiciones:

$$ P(x) = \text{ x come dos veces por semana},$$

$$ Q(x) = \text{ x tiene amigos rojos y amarillos},$$

$$ R(x) = \text{ x tiene un amigo de otra especie que puede comer fresas}.$$

Lo que nos pide demostrar la proposición es que

$$\forall x (P(x) \Leftrightarrow R(x)). $$

Pero sabemos que

$$\forall x (P(x) \Leftrightarrow Q(x)). $$

Y notemos que la siguiente regla de inferencia es válida

$$ \begin{array}{rl} & P \Leftrightarrow Q \\ & P \Leftrightarrow R \\ \hline \therefore & Q \Leftrightarrow R\end{array}.$$

Entonces podemos reducir esta proposición a demostrar «Un blorg tiene amigos amarillos y rojos si y solo si uno de sus amigos de otra especie puede comer fresas». Entonces demostremos esto.

Afirmación. Un blorg tiene amigos amarillos y rojos si y solo si uno de sus amigos de otra especie puede comer fresas.

Demostración de la afirmación.

$\Rightarrow$

Sea $y$ un blorg con amigos amarillos y rojos. Basta exhibir a algún amigo que pueda comer fresas, así que ingeniosamente decimos: sea $x$ un amigo rojo de $y$ (esto lo podemos hacer, ya que suponemos que el blorg tiene amigos amarillos y rojos). Como $x$ es rojo, entonces es un blerg. Además, sabemos por una proposición de la entrada anterior que existe una única raza de Blorgs que pueden comer fresas, y son precesiamente los Blergs. De esta manera $x$ puede comer fresas.

Por lo tanto $y$ tiene un amigo que puede comer fresas. Como además tiene amigos de dos colores, y la única especie que puede tener amigos amarillos y rojos son los Blurgs, entonces $y$ es un blurg. Así, $y$ tiene un amigo de otra especie que puede comer fresas.

$\Leftarrow$

Ahora supongamos que $y$ es un blorg y tiene un amigo $x$ de otra especie que puede comer fresas. Como la única especie vegetariana son los Blergs, entonces $x$ es un Blerg (supongamos que esto es cierto por ahora, más adelante lo demostrarás). De esta manera, $y$ es un blarg o blurg (pues recordemos que $x$ y $y$ son de diferentes especies). Veamos que si $y$ fuera un blarg, tendría únicamente amigos Blurgs y delfines, y no de Blergs, mientras que los Blurgs sí son amigos de los Blergs, por lo tanto $y$ es blurg.

Finalmente, nota que los Blurgs tienen amigos Blargs y Blergs, los cuales son amarillos y rojos.

De esta manera, hemos demostrado que un blorg tiene amigos amarillos y rojos si y solo si uno de sus amigos de otra especie puede comer fresas.

$\square$

Habiendo demostrado la afirmación, y sabiendo que $$ \begin{array}{rl} & P \Leftrightarrow Q \\ & P \Leftrightarrow R \\ \hline \therefore & Q \Leftrightarrow R\end{array}.$$ Entonces se cumple que Un blorg come dos veces por semana si y solo si tiene un amigo de otra especie que puede comer fresas.

$\square$

Más adelante…

El mundo de los Blorgs nos ayudó a poner un paso dentro del pensamiento matemático. Nos acompañarán solo un poco más, pero ya no estaremos enfocados en las demostraciones. Daremos pasos hacia un camino que puede resultar un poco distinto, pero verás que se parece mucho a la lógica proposicional. Algunos dicen que no puede haber una sin otra. Y este tema es la teoría de conjuntos. Si pudiéramos poner las matemáticas como un edificio, algunos dirían que la estructura estaría hecha de lógica y conjuntos. Así que exploraremos este otro «ingrediente» de las matemáticas.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Prueba que la siguiente regla de inferencia es válida: $$ \begin{array}{rl} & P \Leftrightarrow Q \\ & P \Leftrightarrow R \\ \hline \therefore & Q \Leftrightarrow R\end{array}.$$
  2. Demuestra que un blorg es vegetariano si y solo si es un blerg.
  3. Usando la última proposición de la entrada, demuestra que Un blorg come dos veces por semana si y solo si tiene un amigo que puede comer alimentos con semillas.
  4. Demuestra que un blorg no es amigo de los Blergs si y solo si come los mismos días que los Blergs y es amigo de un animal marino.

Entradas relacionadas

  • Ir a Álgebra Superior I
  • Entrada anterior del curso: Problemas de demostraciones con conectores y cuantificadores
  • Siguiente entrada del curso: Problemas de demostraciones de condicionales y dobles condicionales.

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Álgebra Superior I: Demostración de proposiciones con cuantificadores

Por Guillermo Oswaldo Cota Martínez

Deja un comentario

Introducción

Esta entrada es parte de una serie de notas introductorias sobre técnicas de demostración. En esta entrada se habla sobre demostraciones de proposiciones con cuantificadores. Cada entrada está ligeramente relacionada con las otras. Para entenderlas bien, usamos el siguiente diagrama que recopila cómo se comporta un mundo fantástico llamado Axios, en donde habitan creaturas llamadas Blorgs. Para leer más sobre ello, haz click aquí.

En esta entrada revisaremos más a fondo cómo es que los cuantificadores que repasamos antes se usan dentro de las proposiciones y cómo demostrar estas. Veremos ejemplos con cuantificadores universales y existenciales, y algunos ejemplos famosos de proposiciones que los usan.

Los cuantificadores en las demostraciones

Ya hemos trabajado antes con los cuantificadores, aunque quizás no lo hayas notado. Por ejemplo, cuando hicimos la demostración de «Los Blorgs verdes comen peces», lo que hicimos fue considerar cualquier Blorg verde e hicimos una serie de pasos lógicos para demostrarlo. En ningún lugar dice que sólo algunos Blorgs verdes comen peces, en general dice que los Blorgs verdes comen peces, es decir todos los Blorgs verdes cumplen la condición de comer peces. ¿La palabra resaltada te recuerda algo? Seguramente a lo que vimos en la entrada de cuantificadores.

Como recordatorio, para usar cuantificadores necesitamos un universo de discurso y un predicado $P(x)$, que podíamos pensar como una proposición en donde aún no decidimos quién es $x$ de entre los objetos de nuestro universo de discurso. Considerando como universo de discurso a los Blorgs, podemos tomar el predicado $P(x) = \text{$x$ come los viernes}$. Sería falso entonces afirmar que

$$\forall x: P(x),$$

pues los únicos que comen los viernes son los Blurgs. En cambio existe al menos una especie que sí come esos días, así que sería verdadero decir:

$$\exists x: P(x), $$

ya que al tomar un Blurg $x$, tendríamos que $P(x)$ es verdadero y por lo tanto la proposición cuantificada $\exists x: P(x)$ también.

Así que podríamos demostrar la siguiente afirmación:

Proposición. Existen Blorgs que comen los viernes.

Demostración. Para ello, notemos que un Blorg puede ser Blarg, Blerg y Blurgs. A continuación vamos a considerar a $x$ un Blorg que es Blurg. Y como sabemos, todos los Blurgs comen los lunes y viernes. En particular, comen los viernes, por lo que hemos demostrado la proposición.

$\square$

Diferencias entre cuantificadores

Vamos a detenernos y analizar cómo se diferenció la última demostración con lo que hemos estado haciendo antes. Analiza la demostración anterior con la siguiente:

Proposición. Los Blorgs comen un día antes de los Martes.

Demostración. Consideremos $x$ un blorg. Como es un blorg puede que sea un blarg, blerg o blurg.

Caso 1. $x$ es un Blarg.

Como $x$ es Blarg, entonces come los Lunes, que resulta ser un día antes de los Martes.

Caso 2. $x$ es un Blerg.

Igual que en el caso anterior, si $x$ es Blerg, entonces come los días antes de los Martes.

Caso 3. $x$ es un Blurg.

Sabemos que los Blurgs comen los Lunes y los Viernes. Si $x$ es un Blurg, entonces en particular come los lunes, y así, come los días antes de los Martes.

En cualquiera de los casos, $x$ cumple la proposición.

$\square$

Esta es una demostración que bien pudimos haber escrito como «Todos los Blorgs comen los días antes de los Martes». Sin embargo, en la práctica no es muy común ver escrito explícitamente la palabra «todos/todas», pues al hablar de «Los Blorgs», se infiere que hablamos de todos los Blorgs. Así podemos hacer notar las siguientes diferencias entre las dos demostraciones, la primera en donde usamos el cuantificador existe y en la que usamos todos.

Existen Blorgs que comen los viernes.(todos) Los Blorgs comen un día antes de los Martes.
Se puede reescribir como
$$\exists x P(x) $$		Se puede reescribir como
$$\forall x P(x) $$
Consideramos un blorg «mañoso». Es decir, dentro del «conjunto» de los Blorgs, consideramos a uno estratégicamente que nos ayudara a demostrar que al menos un blorg cumplía la condición, en este caso un blurg. Consideramos un blorg arbitrario (tuvimos que considerar distintos casos en los que el blorg fuera blarg, blerg o blurg)
Exhibimos el ejemplo de un blorg, que comía los viernes. Y con eso demostramso que la proposición se cumplía.Llegamos a la conclusión de que sin importar cómo fuera el blorg, comía un dia antes de los Martes.

Esto nos quiere decir que cuando estemos hablando del cuantificador $\exists$, no necesitamos generalizar el caso, solo necesitamos exhibir un ejemplo donde la proposición se cumpla. Mientras que cuando hablamos de $\forall$, tenemos que generalizar, es decir, tenemos que considerar todos los casos posibles para probar que una afirmación sea verdadera o no.

Tratando con la unicidad.

Vamos a ver ahora un pequeño mapa de cómo viven los Blorgs en el mundo Blorg:

Este mapa muestra cómo se dividen los Blorgs, así que cuando estuvimos haciendo la demostración de existencia de los Blorgs que comen los Viernes, elegimos alguno de estos:

Mientras que cuando hablamos de $\forall$, tuvimos que comprobar que se cumplía para cualquiera de los Blorgs, ya fueran Blergs, Blargs o Blurgs. Pero aún falta otro cuantificador, que es el $\exists !$.

Ahora lee la siguiente proposición:

Proposición. Existe una única raza de Blorgs que dentro de su dieta puede haber fresas.

Nota que ahora no estamos hablando de los Blorgs como criaturas, sino de sus especies, y solo existen tres especies de blorg: Blargs, Blergs y Blurgs. Es decir, nos piden demostrar que entre estas tres, solo existe una que come fresas.

Nuestra proposición no nos habla de los Blorgs como criaturas individuales, sino que ahora nos habla de las especies de los Blorgs. Nota que ahora la flecha señala a las especies (círculos).

Entonces para demostrar que se cumple la proposición, tendremos que primero exhibir una especie que coma fresas y después demostrar que es única.

Demostración. Solo existen tres especies de Blorgs, notemos que dentro de estas, se encuentran los Blergs que comen frutos, por lo que son los Blergs quienes pueden incluir fresas en sus dietas.

(Hasta aquí hemos probado que existe una especie que puede comer fresas)

Ahora, para demostrar que es única, veamos que las otras dos razas solo comen peces, los cuales evidentemente no pueden incluir las fresas, por tanto esta especie es única.

(Así demostramos la unicidad)

$\square$

Esta es una proposición que se puede escribir como

$$\exists ! x P(x) $$

Entonces para demostrar el cuantificador $\exists ! x P(x)$, primero debemos demostrar $\exists x P(x)$ y después que es única. Nota que demostrar la unicidad, equivale a demostrar lo siguiente:

$$\exists! x P(x) = \exists x (P(x) \land \forall y \neq x (\neg P(y))) $$

Es decir «Existe $x$ que cumple $P(x)$ y todo elemento $y$ distinto a $x$, no cumple $P(y)$»

En nuestra demostración la primera parte antes del primer paréntesis, demostramos que existe $x$ (Blergs) que cumple $P(x)$. Mientras que en la segunda parte mostramos que todo elemento $y$ distinto a $x$(Blargs y Blurgs) , no cumple $P(y)$. Para la segunda parte, vimos que si $y$ no eran los Blergs, entonces no podían comer fresas.

Nos saltamos un conector, que es el $\nexists$, para demostrar estos casos, es suficiente notar que

$$\nexists x P(x) = \forall x (\neg P(x)) $$

Por ejemplo, para demostrar que «No existen especies de Blorgs que coman los miércoles», solo basta demostrar que todas las especies de Blorgs no comen los miércoles.

Algunos ejemplos de demostraciones con los cuantificadores que utilizan

A continuación mostramos algunos ejemplos de proposiciones y de qué cuantificador hablan ayudados de su escritura como lógica proposicional. No es necesario que entiendas a qué se refiere cada uno, pero nota cómo traducimos el enunciado a lógica proposicional.

ProposiciónProposición en lógica proposicional
Para todo $a$ número real, $a \leq |a|$ y $-a \leq |a|$Sea $P(a)$ = $a \leq |a|$ y $-a \leq |a|$:
$$\forall a \text{ número real } P(a)$$
El neutro aditivo es único en los números reales.Sea $P(x)$ = $x$ es neutro aditivo:
$$\exists ! x \text{ número real } P(x)$$
Para todo binomio con coeficientes reales (es de la forma $ax^2+b^x+c$ donde $a,b,c$ son números reales), existe solución compleja. *Sea $P(p,x)$ = $p$ tiene solución compleja $x$:
$$\forall p \text{ binomio con coeficientes reales } \exists x (P(p,x)) $$

Notas

*: Esta es una consecuencia de algo que se conoce como el «Teorema fundamental del álgebra», que se usa en un segundo curso de álgebra superior (la continuación de este curso). Sólo se utiliza, más no se demuestra. La herramienta necesaria para su demostración, normalmente se puede ver en un curso de Variable Compleja I, el cual corresponde hasta el tercer año de una licenciatura en matemáticas.

Más adelante…

Antes de terminar de estudiar estas «formas» de demostrar, vamos a terminar viendo el último conector que intencionalmente nos saltamos, este es la «doble implicación», y hay un motivo para ello, pues comúnmente te vas a encontrar este tipo de demostraciones y verás la técnica que se empleará.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Demuestra que existen Blorgs que no viven dentro del agua.
  2. Demuestra que todos los Blorgs comen al menos una vez a la semana.
  3. Demuestra que existe una única especie de Blorgs que habla con animales con aletas.
  4. Demuestra que no existe una especie de Blorgs que coman los miércoles.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Álgebra Superior I: Demostración de proposiciones con conectores

Por Guillermo Oswaldo Cota Martínez

Deja un comentario

Introducción

Esta entrada es parte de una serie de notas introductorias sobre técnicas de demostración. En esta entrada se habla sobre demostraciones de proposiciones con conectores. Cada entrada está ligeramente relacionada con las otras. Para entenderlas bien, usamos el siguiente diagrama que recopila cómo se comporta un mundo fantástico llamado Axios, en donde habitan creaturas llamadas Blorgs. Para leer más sobre ello, haz click aquí.

Hasta ahora hemos visto varias estrategias para demostrar: demostaciones directas, demostraciones indirectas y por contradicción. Ahora pensaremos en cómo realizar demostraciones de ciertas afirmaciones cuando hay conectores tanto en nuestras premisas, como en las conclusiones que queremos obtener. Veremos cómo es que se piensa al hacer estas demostraciones y algunas consideraciones que debemos tomar en cuenta.

Recordando conectores

Como breve recordatorio, tenemos los siguientes conectores lógicos:

  • Conjunción $P\land Q$, que es cierta si ambos $P$ y $Q$ lo son.
  • Disyunción $P\lor Q$, que es cierta si alguno de $P$ o $Q$ lo son.
  • Implicación $P\Rightarrow Q$, que es cierta si bien $P$ es falsa, o si $P$ y $Q$ son verdaderas simultáneamente.
  • Doble implicación $P\Leftrightarrow Q$, que es cierta si $P$ y $Q$ tienen el mismo valor de verdad.

En esta entrada veremos qué hacer con las demostraciones que tienen conjunciones y disyunciones. Más adelante hablaremos de las implicaciones y las dobles implicaciones. Los conectores lógicos pueden aparecer como las hipóteis, o como la conclusión de algo que queremos demostrar. Para realizar estas demostraciones, tomaremos en cuenta lo siguente.

  • Si una conjunción $P\land Q$ aparece como hipótesis, entonces podemos suponer tanto que $P$ como $Q$ son verdad.
  • Si una conjunción $P\land Q$ aparece como conclusión, entonces debemos mostrar, quizás por separado, que cada una de $P$ y $Q$ se siguen de las premisas.
  • Si una disyunción $P\lor Q$ aparece como hipótesis, sólo sabemos que $P\lor Q$ es cierta, no tenemos la garantía de que ninguna de ellas en específico sea cierta, solo que alguna lo es. Por ello, debemos separar en casos nuestra demostración, y argumentar por qué la conclusion se sigue tanto cuando $P$ es cierta, como cuando $Q$ es cierta. Esto típicamente llevará a dos o más subdemostraciones.
  • Si una disyunción $P\lor Q$ aparece como conclusión, entonces basta probar a partir de las hipótesis alguna de $P$ o $Q$, la que nos parezca más fácil, para concluir la demostración.

Ejemplos de demostraciones con conjunciones y disyunciones

Veamos algunos ejemplos.

Proposición: Si un Blorg es un Blarg o es un Blurg, entonces come peces.

Demostración: Aquí la disyunción está en la hipótesis. Un Blorg $x$ que cumple la hipótesis cumple que «$x$ es Blarg o $x$ es Blurg». Como no tenemos certeza de cuál de las proposiciones es cierta, debemos hacer casos.

  • Si $x$ es Blarg, entonces uno de los axiomas nos dice que $x$ come peces.
  • Si $x$ es Blurg, entonces otro de los axiomas nos dice que $x$ come peces.

En cualquier caso, concluimos que $x$ come peces.

$\square$

Veamos un ejemplo de la conjunción en la hipótesis.

Proposición. Si un Blorg que come en peces y es amigo de los delfines, entonces es un Blarg.

Demostración. Tomemos $x$ un Blorg que come peces y es amigo de los delfines. Entonces podemos usar la información de ambas proposiciones en la demostración. Como $x$ come peces, entonces $x$ es Blarg o $x$ es Blurg. Como tenemos una disyunción, hay dos posibilidades: que $x$ es Blarg o que $x$ es Blurg. Veremos que $x$ es Blarg. Para ello, procedemos por contradicción, y suponemos que $x$ no es Blarg. Como «$x$ es Blarg o $x$ es Blurg», entonces $x$ es Blurg. Pero entonces $x$ es Blurg y es amigo de los defines. Pero uno de los axiomas es que los Blurg son amigos sólo de los Blergs y los Blargs. ¡Esto es una contradicción! Así, el problema fue suponer que $x$ no es Blarg. Por lo tanto $x$ es Blarg.

$\square$

Veamos un ejemplo más, con una mezcla de conectores.

Proposición. Si un Blorg es Blerg o es Blarg, entonces come los lunes y es amigo de los Blurgs.

Demostración. Otra vez, en la hipótesis tenemos una disyunción. Tomemos un Blorg $x$ que cumple la hipótesis. Entonces «$x$ es Blerg o $x$ es Blarg». Se tienen que hacer casos.

  • Si $x$ es Blerg, entonces como axioma tenemos que $x$ come los lunes. También como axioma tenemos que $x$ es amigo de los Blurgs. Así, tenemos que «$x$ come los lunes y es amigo de los Blurgs.»
  • Si $x$ es Blarg, entonces como axioma tenemos que $x$ come los lunes. También como axioma tenemos que $x$ es amigo de los Blurgs. Así, tenemos que «$x$ come los lunes y es amigo de los Blurgs.»

En cualquier caso, ya mostramos las dos partes que conforman la conjunción de la conclusión. Por lo tanto, en cualquier caso $x$ come los lunes y es amigo de los Blurgs, como queríamos.

$\square$

Hagamos una demostración más.

Proposición: Los Blargs comen animales marinos y comen entre semana.

Demostración: Para probar la proposición, será necesario probar dos cosas: Que los Blargs comen animales marinos, y que los Blargs comen entre semana, es decir que no comen el fin de semana.

Ahora notemos que todos los Blargs comen peces, y estos son animales marinos, entonces se cumple la afirmación de que los Blargs comen animales marinos.

Como es una conjunción, ahora tenemos también que demostrar que comen entre semana. Para esto, recuerda que cada Blarg come los lunes, y como podrás imaginar, esto significa que comen entre semana, por lo que ya demostramos que «Los Blargs comen animales marinos y comen entre semana».

$\square$

Conectando conectores

Ahora podemos ir más allá y hacer otras combinaciones de conectores. Aunque al inicio parezca que se tienen enunciados complicados, basta con pensar la proposición en cada uno de sus componentes para pensar qué hacer.

Proposición: Si un Blorg no es verde, entonces come algún día entre jueves y domingo, o tiene amigos de color azul.

Antes de continuar con la demostración, vamos a desmenuzar la oración en sus partes escribiéndola con lógica proposicional. Si consideramos:

$ P(x): x$ no es verde,

$ Q(x): x$ come algún día entre jueves y domingo,

$ R(x): x$ tiene amigos de color azul,

entonces la proposición es de la forma

$\forall x (P(x) \Rightarrow (Q(x) \lor R(x))).$

De esta forma ya tenemos un poco más claro qué queremos demostrar. Empezaremos con un Blorg $x$ para el cual la proposición $P(x)$ sea válida y demostraremos que sucede $Q(x)$ o sucede $R(x)$.

Demostración: Sea $x$ un Blorg que no es verde. Esto significa que no es un Blarg, entonces tenemos dos casos:

Caso 1: $x$ es un Blerg.

Si $x$ es un Blerg, entonces es amigo de los Blurgs. Y como recordarás, los Blurgs son azules, de esta manera se cumple la proposición.

Caso 2: $x$ es un Blurg.

Si nuestro Blorg es un Blurg, entonces come los viernes, que resulta que son un día entre jueves y domingo. De esta manera la proposición también se cumple.

En cualquiera de los casos, la proposición es válida.

$\square$

Más adelante…

Ya hemos recorrido algunas de las formas de demostraciones que te encontrarás a lo largo de tu viaje matemático. Sin embargo aún hay algunas cosas que conviene que platiquemos. ¿Cómo demostramos proposiciones en las que están involucrados condicionales y cuantificadores? En la siguiente entrada comenzaremos con el caso de los cuantificadores y posteriormente hablaremos sobre los condicionales.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Prueba que «Para cualquier Blorg $x$, si $x$ no es rojo y $x$ no es amigo de los delfines, entonces $x$ come los viernes».
  2. Prueba que «Para cualquier Blorg $x$, o bien $x$ es verde, o bien $x$ es amarillo, o bien $x$ es azul».
  3. Prueba que «Para cualquier Blorg $x$, o bien $x$ es amigo de los animales marinos, o bien $x$ come los viernes, o bien $x$ es rojo».
  4. Escribe con lógica proposicional la proposición: «Si un Blorg come los viernes entonces en su hábitat hay árboles y come animales marinos».
  5. Demuestra que «Si un Blorg come los viernes entonces en su hábitat hay árboles y come animales marinos».

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»