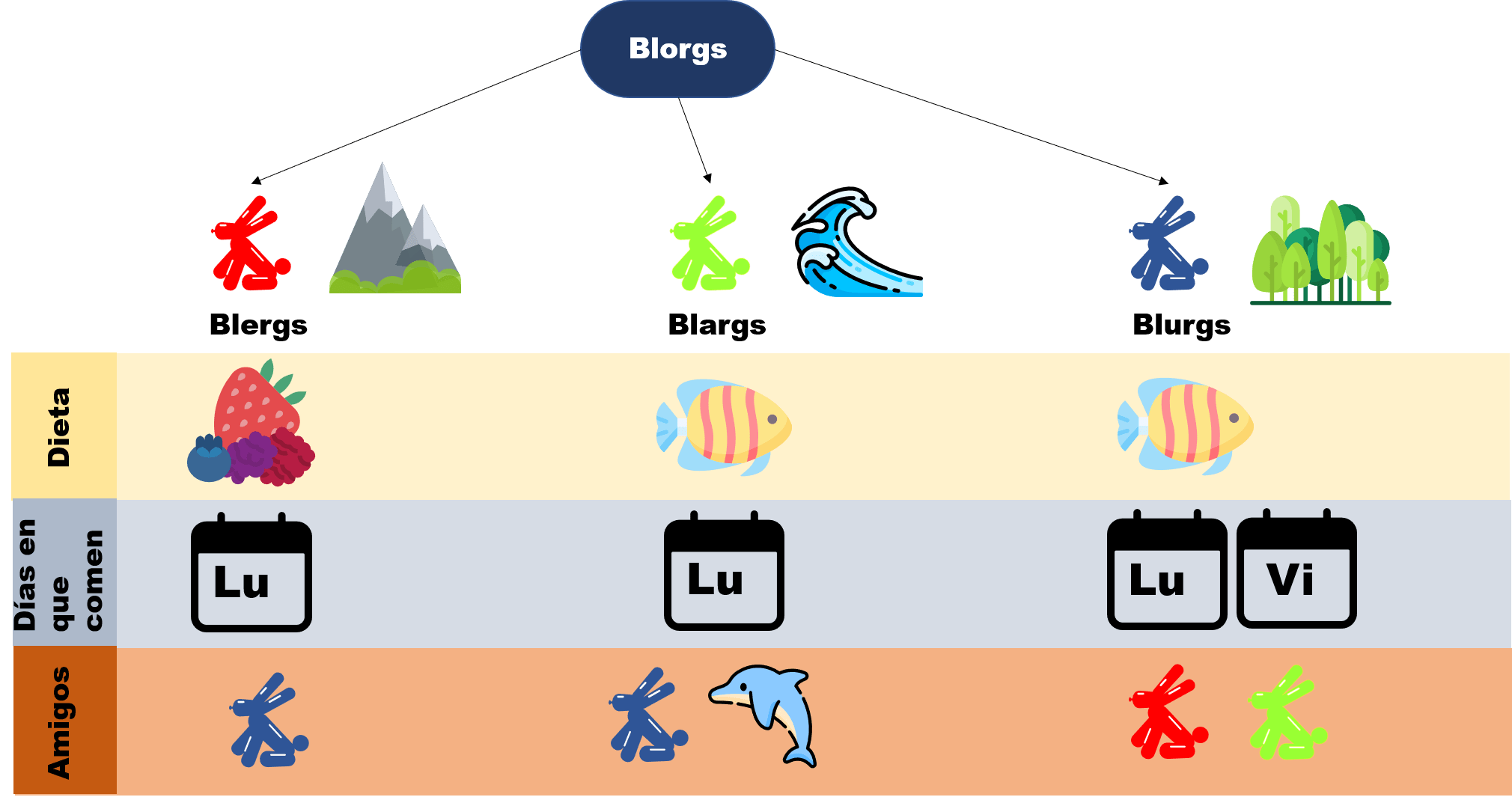
Esta entrada es parte de una serie de notas introductorias sobre técnicas de demostración. Cada una es independiente de la otra, y para su explicación, se usa el siguiente diagrama de un mundo imaginario llamado el mundo de los Blorgs. Para leer más sobre ello, haz click aquí.
Introducción
Hasta ahora hemos visto estrategias directas e indirectas para demostrar proposiciones, pero ahora vamos a pensar qué pasan con aquellas proposiciones que tienen conectores, cómo es que se piensan y las consideraciones que deberemos de tener al momento de hacer alguna de estas.
Pensando en conectores
Hasta ahora hemos pensado en las proposiciones que son del estilo $P \Rightarrow Q$ en donde empezamos con una hipótesis $P$ y mediante una sucesión de deducciones lógicas, llegamos hasta $Q$. Sin embargo en la tarea matemática, no se limita el trabajo a solo proposiciones de este estilo. En esta entrada veremos otros ejemplos de proposiciones a demostrar con otros conectores lógicos.
Recordando conectores
Antes de comenzar, vamos a recordar brevemente los conectores lógicos que hemos visto para entender cómo podríamos demostrar proposiciones que contengan estos. Para empezar, recordemos que la conjunción $P \lor Q$ se cumple siempre que alguna de las dos sean verdaderas.
Por ejemplo,
Proposición: Los blorgs comen frutas o peces.
Demostración: Como dijimos anteriormente, bastará con que cualquier blorg que consideres, coma peces o coma frutas. Pero para esto tenemos que recordar que hay tres tipos de Blorgs: Blargs, Blergs y Blurgs. Entonces tenemos que ver que en cada caso, la afirmación es correcta. Para ello consideremos a un Blorg $x$.
En primer lugar, si $x$ es Blerg, entonces come frutas, por lo que la afirmación se cumple.
Enseguida, si $x$ es un Blarg, también es cierta, pues come peces.
Finalmente, si $x$ es Blurg, también come peces, por lo que la afirmación es correcta.
En cualquiera de los casos, la proposición se cumple.
$\square$
De forma similar, podemos demostrar las proposiciones con una conjunción $P \land Q$ demostrando que se cumplen las dos al mismo tiempo. Por ejemplo,
Proposición: Los Blargs comen animales marinos y comen entre semana.
Demostración: Para probar la proposición, será necesario probar dos cosas: Que los Blargs comen animales marinos, y que los Blargs comen entre semana, es decir que no comen el fin de semana.
Ahora notemos que todos los Blargs comen peces, y estos son animales marinos, entonces se cumple la afirmación de que los Blargs comen animales marinos.
Como es una conjunción, ahora tenemos que demostrar que igual comen entre semana. Para esto, recuerda que cada Blarg come los lunes, y como podrás imaginar, esto significa que comen entre semana, por lo que ya demostramos que «Los Blargs comen animales marinos y comen entre semana».
$\square$
Conectando conectores
Ahora, podemos ir más allá y hacer combinaciones con los conectores, aunque en las proposiciones a veces parezcan un poco complicadas, será necesario analizar detenidamente qué dice la proposición para poder demostrarla. Por ejemplo, piensa en la siguiente proposición:
Proposición: Si un blorg no es amarillo, entonces come los días antes del sábado o tiene amigos de color azul.
Antes de continuar con la demostración, vamos a desmenuzar la oración en sus partes escribiéndola con lógica proposicional. Si consideramos:
$ P(x): x$ no es amarillo,
$ Q(x): x$ no come los días antes del sábado,
$ R(x): x$ tiene amigos de color azul,
entonces la proposición es de la forma
$\forall x (P(x) \Rightarrow (Q(x) \lor R(x))).$
De esta forma ya tenemos un poco más claro qué queremos demostrar. Empezaremos con un Blorg $x$ para el cual la proposición $P(x)$ sea válida y demostraremos que sucede $Q(x)$ o sucede $R(x)$.
Demostración: Sea $x$ un Blorg que no es amarillo. Esto significa que no es un Blarg, entonces tenemos dos casos:
Caso 1: $x$ es un Blerg.
Si $x$ es un Blerg, entonces es amigo de los Blurgs. Y como recordarás, los Blurgs son azules, de esta manera se cumple la proposición.
Caso 2: $x$ es un Blurg.
Si nuestro Blorg es un Blurg, entonces come los viernes, que resulta que son los días antes del sábado. De esta manera la proposición también se cumple.
En cualquiera de los casos, la proposición es válida.
$\square$
Más adelante…
Ya hemos recorrido algunas de las formas de demostraciones que te encontrarás a lo largo de tu viaje matemático, sin embargo aún hay algunas cosas que tendrás que saber antes, como el caso específico de las dobles condicionales y cómo afectan los cuantificadores. Esta última es la que revisaremos en la siguiente entrada. ¿Qué pasa cuando usamos los cuantificadores «existe» o «para todo» dentro de una proposición que queramos demostrar? Esto revisaremos en la siguiente entrada.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Prueba que «Los Blergs no comen los jueves o comen frutas».
- Prueba que «Los Blorgs es amarillo, rojo o azul».
- Prueba que «Los Blorgs comen los lunes y comen animales marinos o son vegetarianos». Para esto, recuerda que una dieta vegetariana solo excluye alimentos de origen animal.
- Escribe con lógica proposicional la proposición: «Si un Blorg come los viernes entonces en su hábitat hay árboles y come animales marinos».
- Demuestra que «Si un Blorg come los viernes entonces en su hábitat hay árboles y come animales marinos».
Entradas relacionadas
- Ir a Álgebra Superior I
- Entrada anterior del curso: Problemas introductorios a demostraciones
- Siguiente entrada del curso: Demostración de proposiciones con cuantificadores
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»
