Introducción

Decimos que un cuadrilátero convexo es circunscrito si sus lados son tangentes a una misma circunferencia dentro del cuadrilátero. Nos referimos a dicha circunferencia como el incírculo y a su radio como el inradio del cuadrilátero.

Sabemos que los lados de un triángulo siempre son tangentes a una misma circunferencia, el incírculo del triángulo, cuyo centro es el punto donde concurren las bisectrices internas, en esta entrada estudiaremos cuando un cuadrilátero es circunscrito y algunas propiedades.

Primera caracterización para el cuadrilátero circunscrito

Teorema 1. Un cuadrilátero es circunscrito si y solo si la suma de dos lados opuestos es igual a la suma de los otros dos lados opuestos.

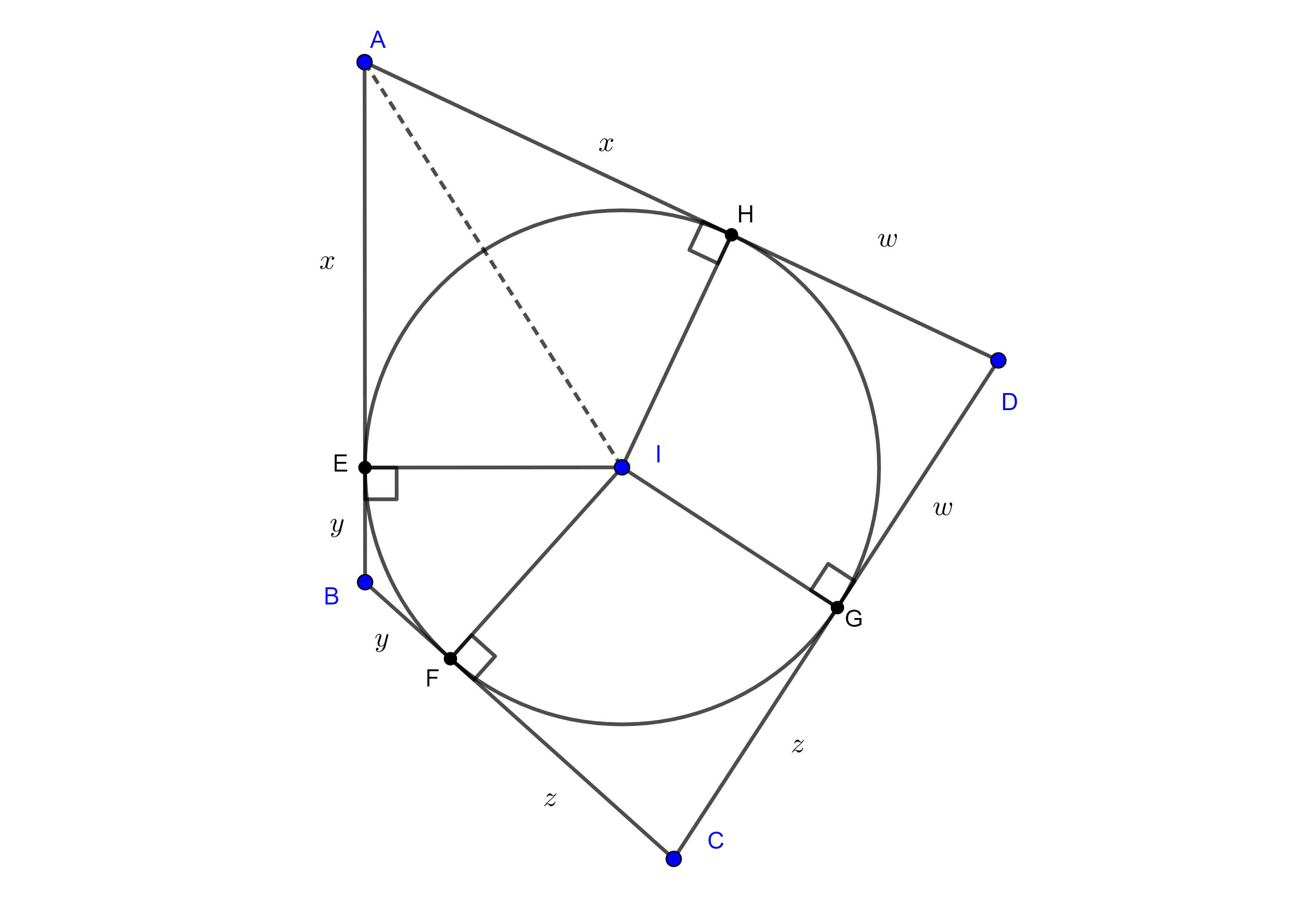
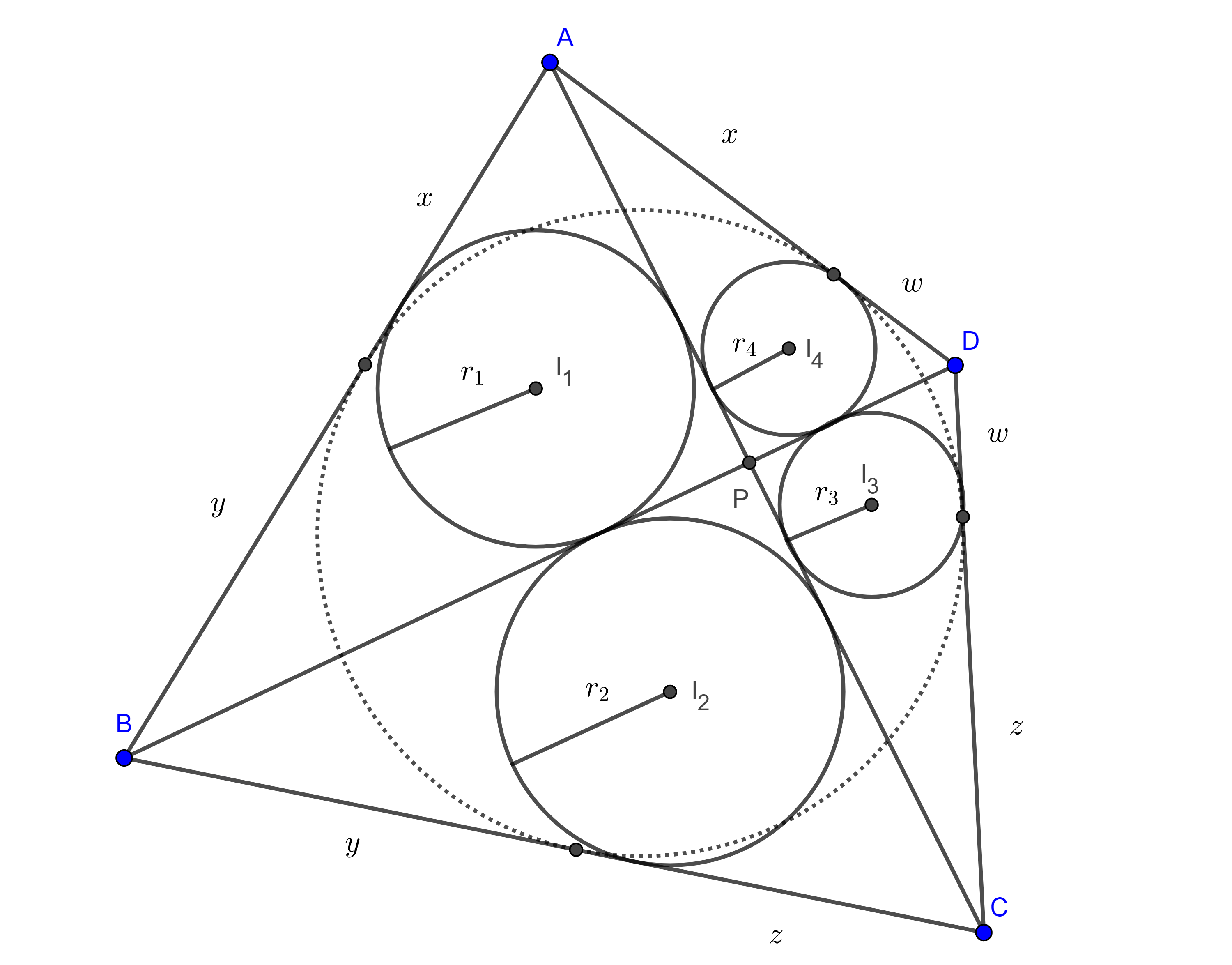
Demostración. Sean $\square ABCD$ un cuadrilátero circunscrito, $E$, $F$, $G$ y $H$ los puntos de tangencia de la circunferencia a los lados $AB$, $BC$, $CD$ y $AD$ respectivamente y consideremos $I$ el incentro de $\square ABCD$.

Recordemos que las tangentes a una circunferencia desde un punto externo a esta son iguales, por lo tanto, $AH = AE = x$, $BE = BF = y$, $CF = CG = z$, $DG = DH = w$.

Entonces $AB + CD = (x + y) + (z + w) = (x + w) + (y + z) = AD + BC$.

$\blacksquare$

Ahora supongamos que en $\square ABCD$ se tiene que $AB + CD = AD + BC$ y que tiene un par de lados adyacentes que no son iguales.

Sin pérdida de generalidad podemos suponer que $AB > BC$ entonces,
$\begin{equation} AD – CD = AB – BC > 0. \end{equation}$.

Sean $E \in AB$ y $F \in AD$ tales que $EB = BC$ y $FD = CD$ entonces por la ecuación $(1)$ $AE = AF$ y así $\triangle AEF$, $\triangle BCE$ y $\triangle DFC$ son isósceles.

Por lo tanto, las bisectrices internas de los ángulos $\angle EAF$, $\angle CBE$ y $\angle ADC$, son las mediatrices de $\triangle EFC$, por lo tanto, concurren en un punto $I$.

Como $I$ está en las bisectrices internas de los ángulos $\angle AEF$, $\angle BCE$ y $\angle DFC$, entonces, equidista a cado uno de los lados que forman dichos ángulos y de esta forma $I$ es el centro de una circunferencia tangente a los lados de $\square ABCD$.

La otra posibilidad es que todos los lados del cuadrilátero sean iguales es decir el cuadrilátero sea un rombo, este caso se queda como ejercicio.

$\blacksquare$

Teorema de Newton

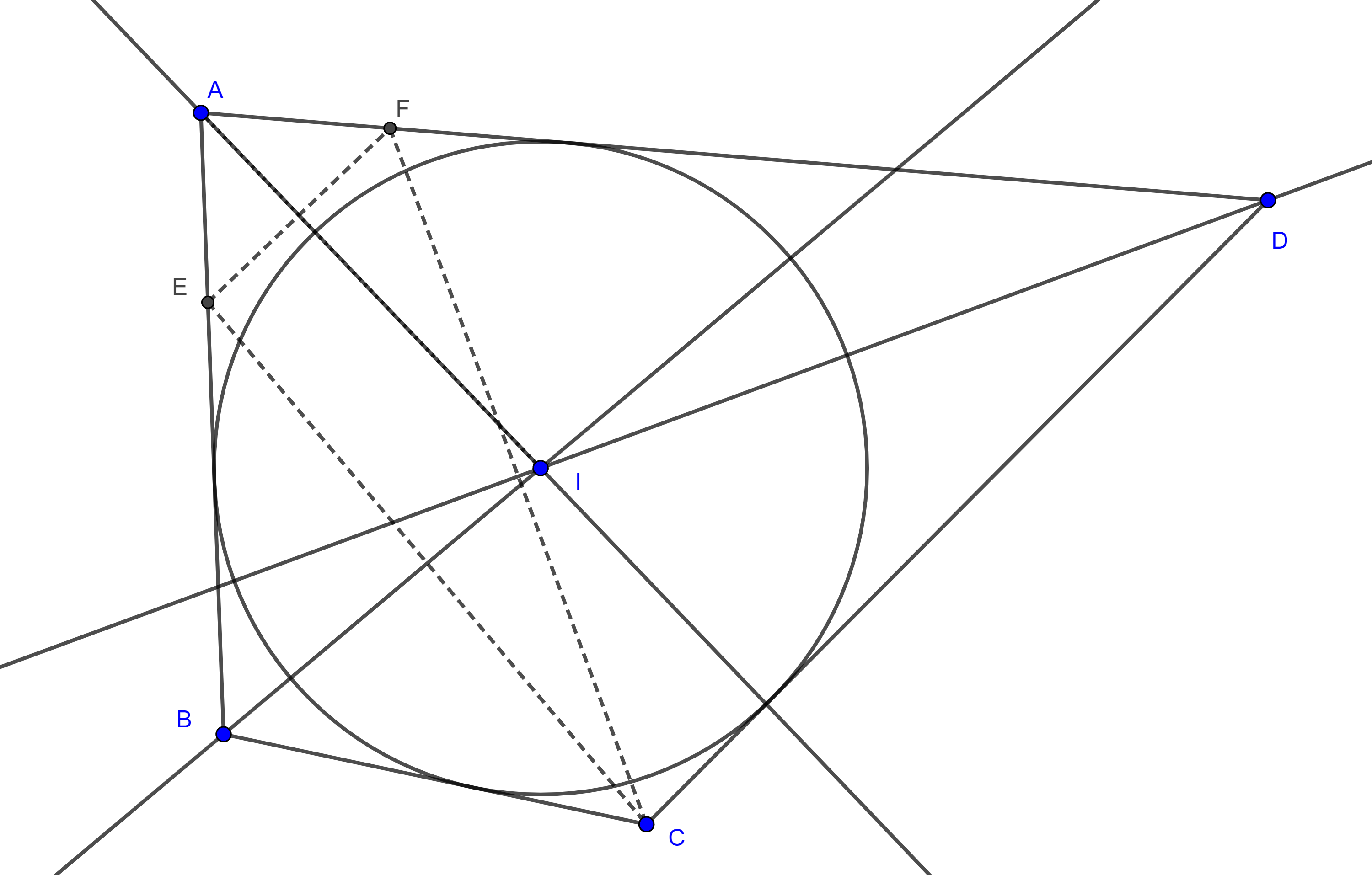
Teorema 2, de Leon Anne. Sea $\square ABCD$ un cuadrilátero que no es un paralelogramo, el lugar geométrico de los puntos $P$ en el interior de $\square ABCD$ tal que $(\triangle APB) + (\triangle CPD) = (\triangle BPC) + (APD)$, es la recta de Newton de $\square ABCD$.

Demostración. Sean $P$ un punto en el interior de $\square ABCD$ tal que $(\triangle APB) + (\triangle CPD) = (\triangle BPC) + (APD)$ y $F$ el punto medio de $BD$.

Podemos ver el área de los triángulos considerados como suma y diferencia de otras áreas:

$(\triangle APB) = (\triangle AFB) + (\triangle BFP) – (\triangle AFP)$,
$ (\triangle CPD) = (\triangle CFD) + (\triangle CFP) – (\triangle DFP)$,
$(\triangle APD) = (\triangle AFD) + (\triangle AFP) + (\triangle DFP)$,
$ (\triangle BPC) = (\triangle BFC) – (\triangle BFP) – (\triangle CFP)$.

Entonces, por hipótesis:
$(\triangle AFB) + (\triangle BFP) – (\triangle AFP) + (\triangle CFD) + (\triangle CFP) – (\triangle DFP)$
$= (\triangle AFD) + (\triangle AFP) + (\triangle DFP) + (\triangle BFC) – (\triangle BFP) – (\triangle CFP)$.

$\Leftrightarrow$
$(\triangle AFB) + 2(\triangle BFP) + (\triangle CFD) + 2(\triangle CFP)$
$\begin{equation} = (\triangle AFD) + 2(\triangle AFP) + 2(\triangle DFP) + (\triangle BFC). \end{equation}$

Notemos que como $B$, $F$ y $D$ son colineales entonces $\triangle AFB$ y $\triangle AFD$ tienen la misma altura desde $A$, y ya que $FB = FD$ entonces $(\triangle AFB) = (\triangle AFD)$.

Igualmente podemos ver que
$(\triangle BFP) = (\triangle DFP)$ y $(\triangle CFD) = (\triangle BFC)$.

De la ecuación $(2)$ se sigue que $(\triangle CFP) = (\triangle AFP)$.

Como ambos triángulos tienen la misma base entonces las alturas trazadas desde $A$ y $C$ a la recta $FP$ son la mismas, digamos $AG = CH$.

Consideremos $E$ la intersección de $AC$ con $FP$, entonces $\triangle AEG$ y $\triangle CEH$ son congruentes, por criterio ángulo, lado, ángulo.

Por lo tanto $E$ es el punto medio de $AC$ y así $P$ está en la recta de Newton de $\square ABCD$.

La implicación reciproca se puede ver tomando en sentido contrario los argumentos anteriores.

$\blacksquare$

Teorema 3. De Newton. Si un cuadrilátero es circunscrito entonces su incentro esta en la recta de Newton del cuadrilátero.

Demostración. Sean $\square ABCD$ un cuadrilátero circunscrito $I$ y $r$ el centro y el radio de su incírculo respectivamente, entonces por el teorema 1 sabemos que:
$AB + CD = AD + BC$
$\Rightarrow \dfrac{r}{2}(AB + CD) = \dfrac{r}{2}(AD + BC)$
$\Rightarrow (\triangle AIB) + (\triangle CID) = (\triangle AID) + (\triangle BIC)$.

Por lo tanto, $I$ se encuentra en la recta de Newton de $\square ABCD$.

$\blacksquare$

Rectas concurrentes en el cuadrilátero circunscrito

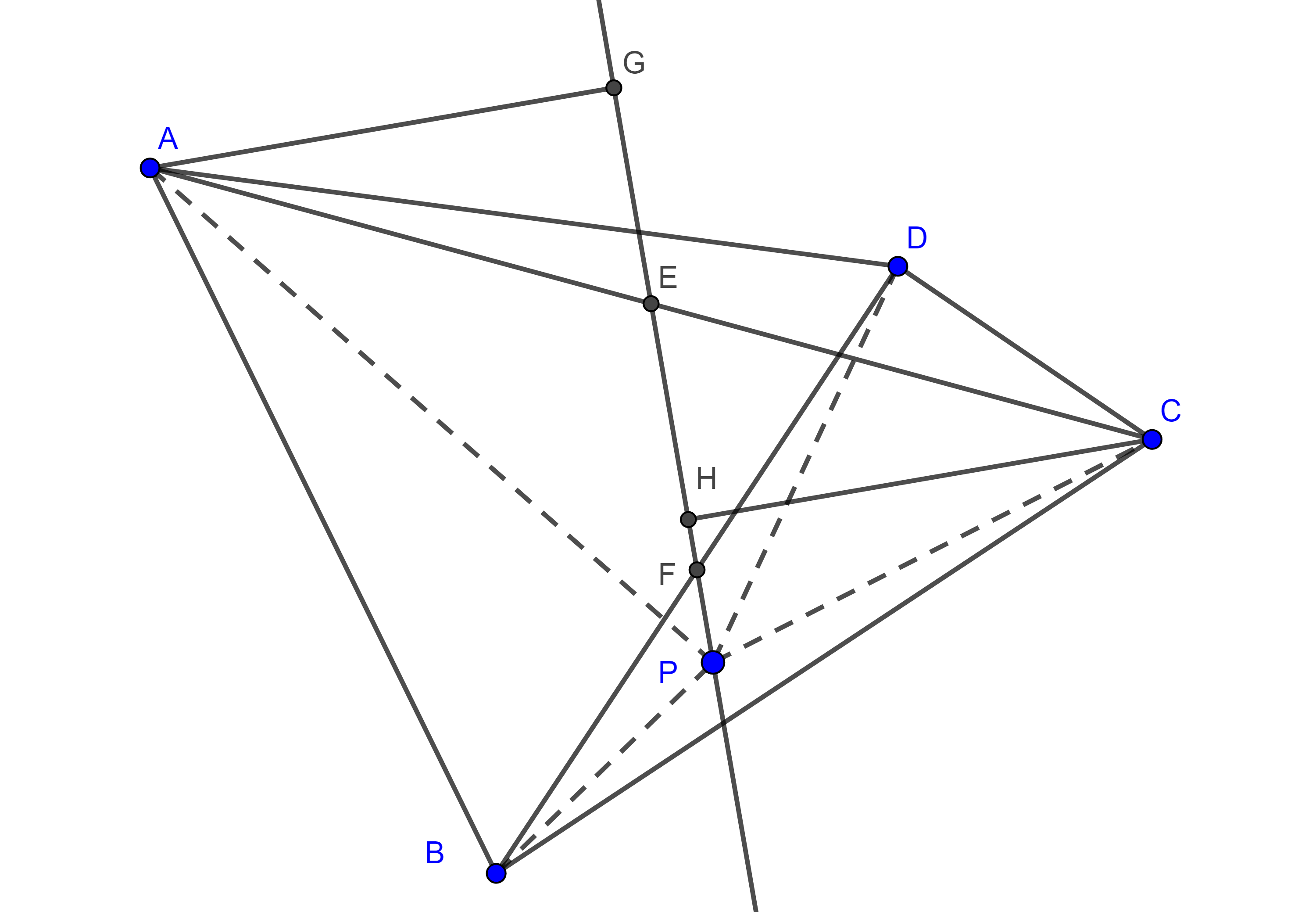
Teorema 4. Sea $\square ABCD$ un cuadrilátero circunscrito y sean $E$, $F$, $G$ y $H$ los puntos de tangencia del circuncírculo con los lados $AB$, $BC$, $CD$ y $AD$ respectivamente, entonces,
$i)$ las cuerdas $EG$, $FH$ y las diagonales $AC$, $BD$ son concurrentes
$ii)$ si $P$ es el punto de concurrencia, entonces,
$\dfrac{AP}{CP}  = \dfrac{x}{z}$ y $\dfrac{BP}{DP}  = \dfrac{y}{w}$.

Donde $AH = AE = x$, $BE = BF = y$, $CF = CG = z$, $DG = DH = w$.

Demostración. Sean $I$ el incentro de $\square ABCD$ y $P = AC \cap EG$.

Como $AB$ y $CD$ son tangentes al circuncírculo en $E$ y $G$ respectivamente, entonces $\angle GEA = \angle DGE$, pues ambos son ángulos semiinscritos que abarcan el mismo arco.

Por lo tanto,
$\sin \angle PEA = \sin \angle DGP = \sin (\pi – \angle DGP) = \sin \angle PGC$.

Por otro lado,
$2(\triangle AEP) = AP \times EP \sin \angle APE = AE \times EP \sin \angle PEA$,
$2(\triangle CGP) = PG \times CP \sin \angle CPG = CG \times GP \sin \angle PGC$.

$\Rightarrow \dfrac{(\triangle AEP) }{(\triangle CGP)} = \dfrac{AP \times EP}{PG \times CP} = \dfrac{AE \times EP}{CG \times GP}$
$\Rightarrow \dfrac{AP}{CP}  = \dfrac{AE}{CG}$.

Lo que significa que la cuerda $EG$ divide internamente a la diagonal $AC$ en la razón $\dfrac{AE}{CG} = \dfrac{x}{z}$.

Similarmente podemos mostrar que la cuerda $FH$ divide internamente a la diagonal $AC$ en la razón $\dfrac{x}{z}$, por lo tanto, $EG$, $FH$, se intersecan en $AC$.

Repitiendo este procedimiento, pero esta vez para la diagonal $BD$ podemos ver que $BD$, $EG$ y $FH$ concurren, y que $\dfrac{BP}{DP}  = \dfrac{y}{w}$.

Por lo tanto, las diagonales $AC$, $BD$ y las cuerdas $EG$, $FH$ son concurrentes.

$\blacksquare$

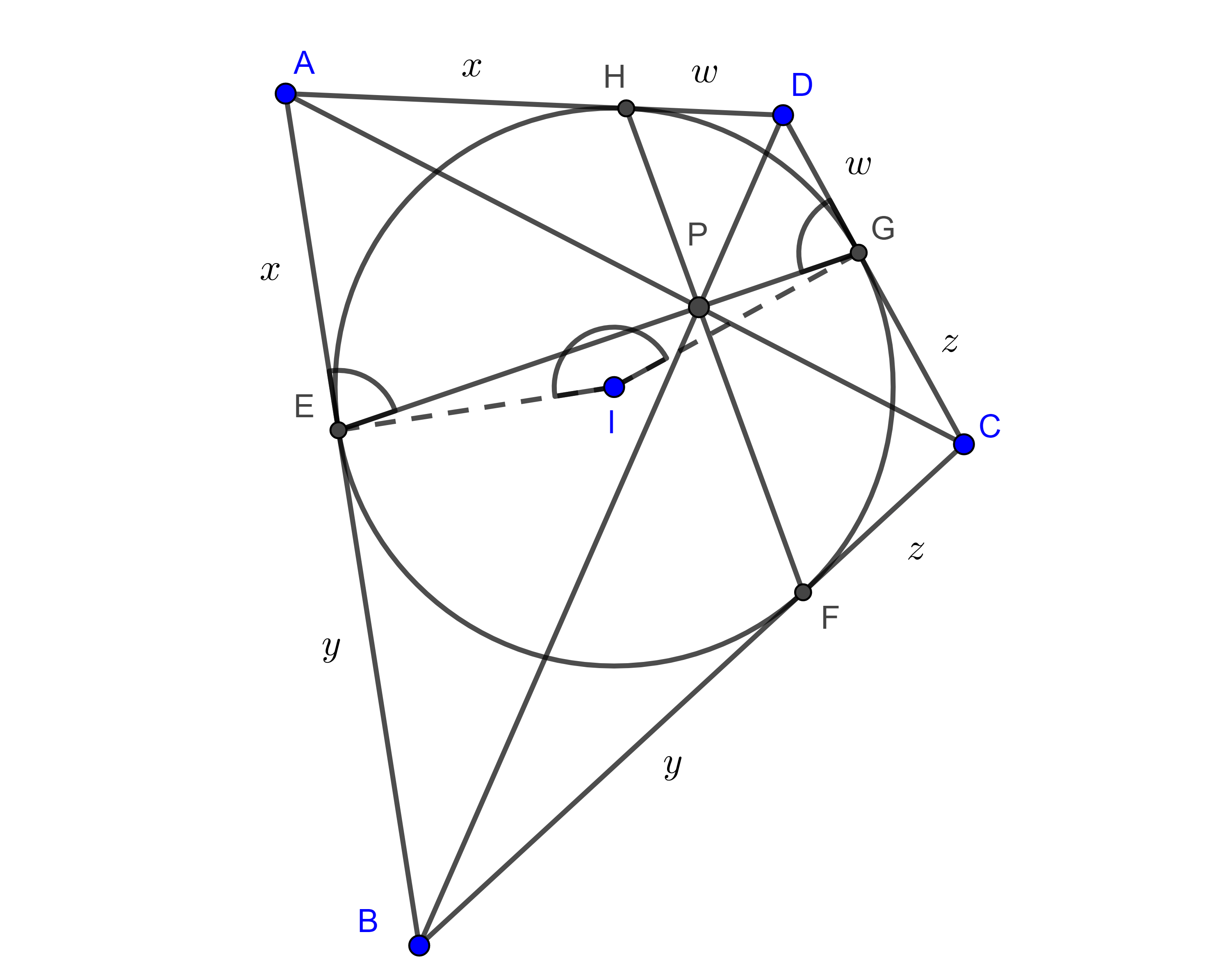
Corolario. Tenemos las siguientes igualdades (figura 4),
$\dfrac{(\triangle APB)}{xy} = \dfrac{(\triangle BPC)}{yz} = \dfrac{(\triangle CPD)}{zw} = \dfrac{(\triangle APD)}{xw}$.

Demostración. Notemos que los triángulos $\triangle APB$ y $\triangle BPC$ tienen la misma altura desde el vértice $B$, y ya que $A$, $P$ y $C$ son colineales, entonces usando la razón, encontrada en el teorema anterior, en la que $P$ divide a $AC$.

$\dfrac{(\triangle APB)}{(\triangle BPC)} = \dfrac{AP}{PC} = \dfrac{x}{z} \Leftrightarrow \dfrac{(\triangle APB)}{xy} = \dfrac{(\triangle BPC)}{zy}$.

Las otras igualdades se muestran de manera análoga.

$\blacksquare$

Una propiedad referente a inradios

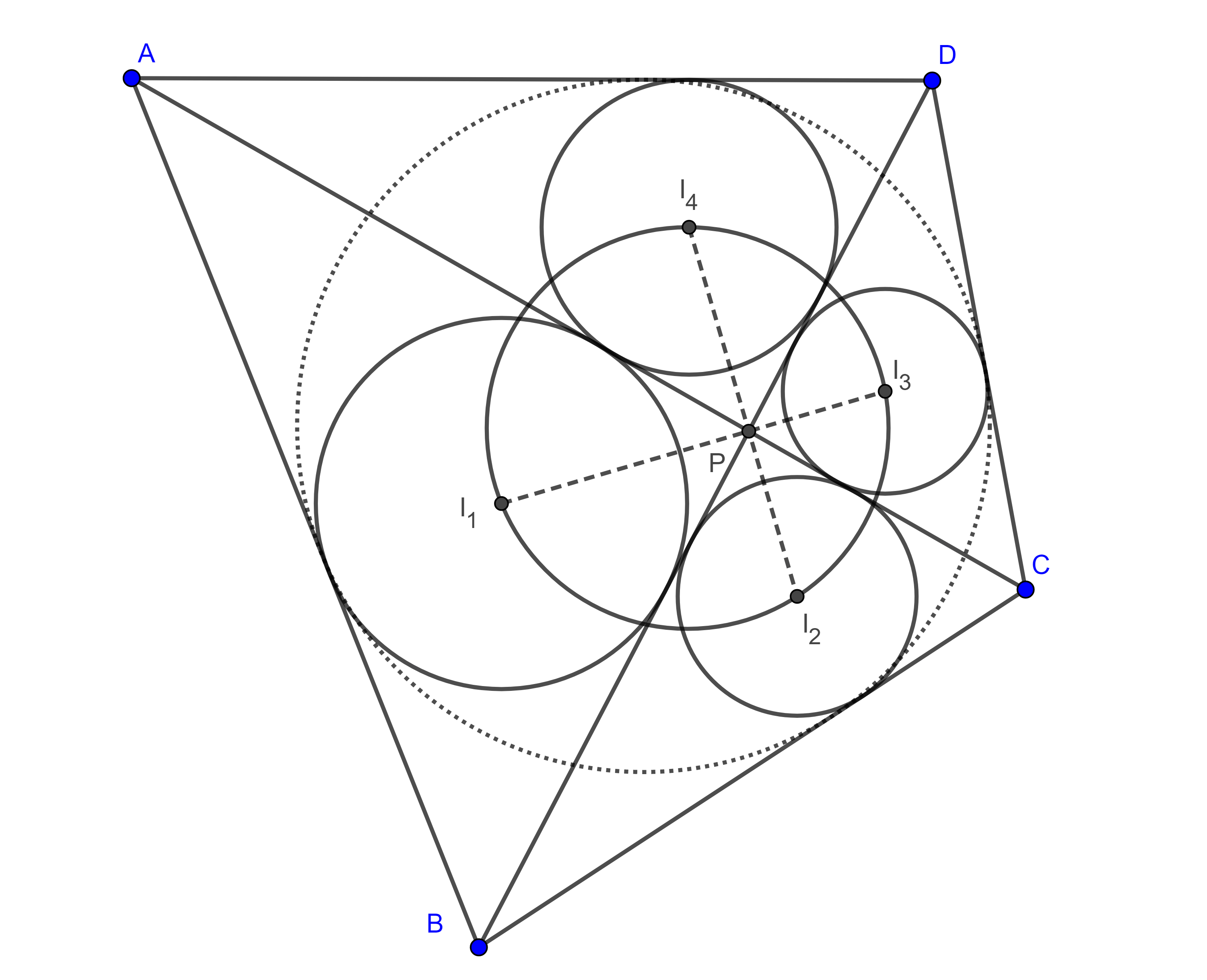
Teorema 5. Sean $\square ABCD$ circunscrito, $P$ el punto de intersección de las diagonales, y consideremos los inradios $r_{1}$, $r_{2}$, $r_{3}$, $r_{4}$, de los triángulos $\triangle APB$, $\triangle BPC$, $\triangle CPD$ y $\triangle APD$ respectivamente, entonces
$\dfrac{1}{ r_{1}} + \dfrac{1}{ r_{3}} = \dfrac{1}{ r_{2}} + \dfrac{1}{ r_{4}}$.

Demostración. Por el corolario anterior, sea $\lambda = \dfrac{(\triangle APB)}{xy} = \dfrac{(\triangle BPC)}{yz} = \dfrac{(\triangle CPD)}{zw} = \dfrac{(\triangle APD)}{xw} \neq 0$.

Por el teorema 4, tenemos que $\dfrac{AP}{CP}  = \dfrac{x}{z}$ y $\dfrac{BP}{DP}  = \dfrac{y}{w}$.

Entonces sean $\eta = \dfrac{AP}{x}  = \dfrac{CP}{z}$ y $\mu = \dfrac{BP}{y}  = \dfrac{DP}{w}$.

Ahora calculamos el área de $\triangle APB$.

$(\triangle APB) = r_{1}s = \dfrac{r_{1}}{2}(AP + PB + AB)$
$\Leftrightarrow \dfrac{1}{r_{1}} = \dfrac{AP + PB + AB}{2(\triangle APB)} = \dfrac{AP + PB + AB}{2 \lambda xy}$
$\Leftrightarrow \dfrac{2 \lambda}{r_{1}} = \dfrac{AP + PB + AB}{xy} = \dfrac{x \eta + y \mu + (x + y)}{xy}$
$= \dfrac{x(\eta + 1) + y(\mu + 1))}{xy} = \dfrac{\eta + 1}{y} + \dfrac{\mu + 1}{x}$.

De manera análoga podemos ver que
$\dfrac{2 \lambda}{r_{3}} = \dfrac{\eta + 1}{w} + \dfrac{\mu + 1}{z}$.

Entonces,
$\dfrac{2 \lambda}{r_{1}} + \dfrac{2 \lambda}{r_{3}} = \dfrac{\eta + 1}{y} + \dfrac{\mu + 1}{x} + \dfrac{\eta + 1}{w} + \dfrac{\mu + 1}{z}$.

Podemos encontrar de la misma forma
$\dfrac{2 \lambda}{r_{2}} + \dfrac{2 \lambda}{r_{4}} = \dfrac{\eta + 1}{y} + \dfrac{\mu + 1}{z} + \dfrac{\mu + 1}{x} + \dfrac{\eta + 1}{w}$.

Por lo tanto,
$\dfrac{2 \lambda}{r_{1}} + \dfrac{2 \lambda}{r_{3}} = \dfrac{2 \lambda}{r_{1}} + \dfrac{2 \lambda}{r_{3}}$
$\Leftrightarrow \dfrac{1}{r_{1}} + \dfrac{1}{r_{3}} = \dfrac{1}{r_{2}} + \dfrac{1}{r_{4}}$.

$\blacksquare$

Puntos cíclicos en el cuadrilátero circunscrito

Lema. Sean $\triangle ABC$, $I$ y $r$ el incentro y el inradio de su circuncírculo entonces
$i)$ $AB + AC – BC = 2 r \cot \dfrac{\angle A}{2}$,
$ii)$ $AI = \dfrac{r}{\sin \dfrac{\angle A}{2}}$.

Demostración. Consideremos $D$, $E$ y $F$ los puntos de tangencia de $(I, r)$ con $AB$, $BC$ y $AD$ respectivamente entonces $AD = AF$, $BD = BE$ y $CE = CF$ además en el triángulo rectángulo $\triangle ADI$
$\tan\dfrac{\angle A}{2} = \dfrac{ID}{AD} \Leftrightarrow AD = r \cot \dfrac{\angle A}{2}$.

Por lo tanto, $AB + AC – BC = (AD + BD) + (AF + CF) – (BE + CE) = 2AD = 2 r \cot \dfrac{\angle A}{2}$.

Por otra parte en $\triangle ADI$,
$\sin \dfrac{\angle A}{2} = \dfrac{ID}{IA} \Leftrightarrow AI = \dfrac{r}{\sin \dfrac{\angle A}{2}}$.

$\blacksquare$

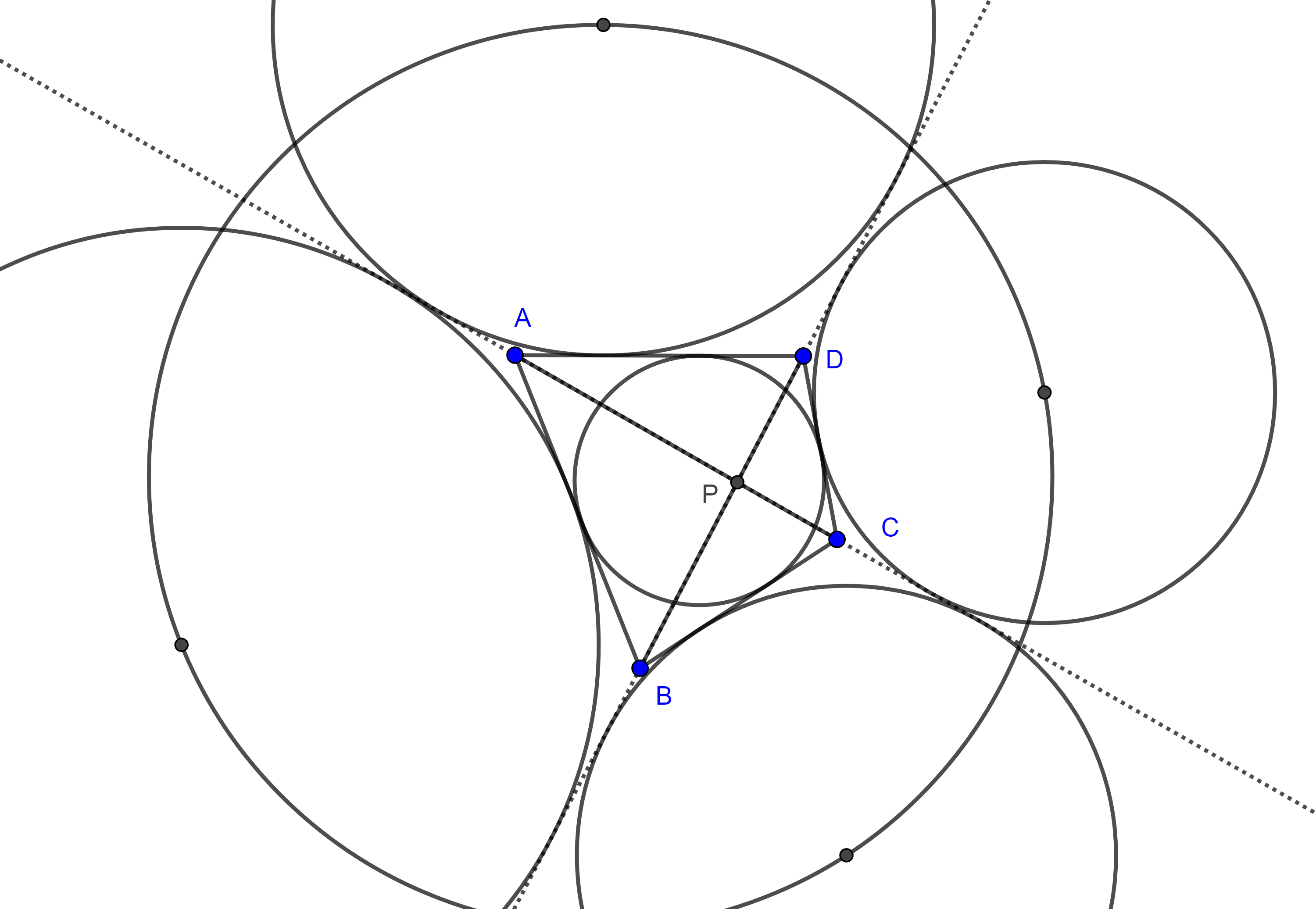
Teorema 6. Sean $\square ABCD$ circunscrito, $P$ la intersección de las diagonales, $I_{1}$, $I_{2}$, $I_{3}$ e $I_{4}$ los incentros de los triángulos $\triangle APB$, $\triangle BPC$, $\triangle CPD$ y $\triangle APD$ respectivamente entonces el cuadrilátero $\square I_{1}I_{2}I_{3} I_{4}$ es cíclico.

Demostración. Sean $r_{1}$, $r_{2}$, $r_{3}$ y $r_{4}$ los inradios de $\triangle APB$, $\triangle BPC$, $\triangle CPD$ y $\triangle APD$ respectivamente, notemos que $\angle APB = \angle CPD$ y $\angle BPC = \angle DPA$ pues son opuestos por el vértice, entonces
$2(\angle APB + \angle DPA) = 2\pi \Leftrightarrow \dfrac{\angle APB + \angle DPA}{2} = \dfrac{\pi}{2}$ por lo que
$\sin \dfrac{\angle APB}{2} = \cos \dfrac{\angle DPA}{2}$ y $\cos \dfrac{\angle APB}{2} = \sin \dfrac{\angle DPA}{2}$.

Aplicando el lema parte 1 a $\triangle APB$ y $\triangle CPD$ obtenemos
$(AP + BP – AB) + (CP + DP – CD)$
$= 2 r_{1} \cot \dfrac{\angle APB}{2} + 2 r_{3}  \cot \dfrac{\angle CPD}{2} = 2\cot \dfrac{\angle APB}{2}( r_{1} + r_{3})$.

Hacemos lo mismo con $\triangle BPC$ y $\triangle APD$,
$(BP + CP – BC) + (DP + AP – AD) = 2\cot \dfrac{\angle DPA}{2}( r_{2} + r_{4})$.

Como $\square ABCD$ es circunscrito por el teorema 1, $AB + CD = BC + AD$ por lo que
$(AP + BP – AB) + (CP + DP – CD) = (BP + CP – BC) + (DP + AP – AD)$.

Y por lo tanto,
$2\cot \dfrac{\angle APB}{2}( r_{1} + r_{3}) = 2\cot \dfrac{\angle DPA}{2}( r_{2} + r_{4})$

$\Rightarrow \dfrac{ r_{1} + r_{3}}{ r_{2} + r_{4}} = \dfrac{\cot \dfrac{\angle DPA}{2}}{\cot \dfrac{\angle APB}{2}}$
$= \dfrac{\dfrac{\cos \dfrac{\angle DPA}{2}}{\sin \dfrac{\angle DPA}{2}}}{\dfrac{\cos \dfrac{\angle APB}{2}}{\sin \dfrac{\angle APB}{2}}}
= \dfrac{\dfrac{\sin \dfrac{\angle APB}{2}}{\cos \dfrac{\angle APB}{2}}}{\dfrac{\cos \dfrac{\angle APB}{2}}{\sin \dfrac{\angle APB}{2}}}
= \dfrac{\sin^2 \dfrac{\angle APB}{2}}{\cos^2 \dfrac{\angle APB}{2}}$

$\begin{equation} = \tan^2 \dfrac{\angle APB}{2}. \end{equation}$

Por otra parte aplicamos el lema parte 2 a $\triangle APB$ y $\triangle CPD$
$PI_{1} \times PI_{3} = \dfrac{r_{1}}{\sin \dfrac{\angle APB}{2}} \dfrac{r_{3}}{\sin \dfrac{\angle CPD}{2}} = \dfrac{ r_{1} r_{3}}{\sin^2 \dfrac{\angle APB}{2}}$.

Hacemos lo mismo con $\triangle BPC$ y $\triangle APD$
$PI_{2} \times PI_{4} = \dfrac{r_{2}}{\sin \dfrac{\angle BPC}{2}} \dfrac{r_{4}}{\sin \dfrac{\angle DPA}{2}} = \dfrac{ r_{2} r_{4}}{\sin^2 \dfrac{\angle DPA}{2}}$.

Realizamos el cociente de las dos últimas expresiones encontradas
$\dfrac{PI_{2} \times PI_{4}}{PI_{1} \times PI_{3}} = \dfrac{r_{2} r_{4}}{\sin^2 \dfrac{\angle DPA}{2}} \dfrac{\sin^2 \dfrac{\angle APB}{2}}{r_{1} r_{3}} = \dfrac{r_{2} r_{4}}{r_{1} r_{3}} \dfrac{\sin^2 \dfrac{\angle APB}{2}}{\cos^2 \dfrac{\angle APB}{2}}$

$\begin{equation} = \dfrac{r_{2} r_{4}}{r_{1} r_{3}} \tan^2 \dfrac{\angle APB}{2}. \end{equation}$

Entonces podemos sustituir la ecuación $(3)$ en $(4)$
$\dfrac{PI_{2} \times PI_{4}}{PI_{1} \times PI_{3}} = (\dfrac{r_{2} r_{4}}{r_{1} r_{3}}) (\dfrac{r_{1} + r_{3}}{r_{2} + r_{4}}) = \dfrac{\dfrac{r_{1} + r_{3}}{r_{1} r_{3}}}{\dfrac{r_{2} + r_{4}}{r_{2} r_{4}}}
= \dfrac{\dfrac{1}{r_{1}} + \dfrac{1}{r_{3}}}{\dfrac{1}{r_{2}} + \dfrac{1}{r_{4}}}$.

Por el teorema 5, sabemos que
$\dfrac{1}{r_{1}} + \dfrac{1}{ r_{3}} = \dfrac{1}{r_{2}} + \dfrac{1}{ r_{4}}$.

Por lo tanto,
$\dfrac{PI_{2} \times PI_{4}}{ PI_{1} \times PI_{3}} = 1$
$\Leftrightarrow PI_{2} \times PI_{4} = PI_{1} \times PI_{3}$.

Como $P = I_1I_3 \cap I_2I_4$, pues estas rectas son las bisectrices interna y externa de $\angle APB$, por el teorema de las cuerdas, el cuadrilátero $\square I_1I_2I_3I_4$ es cíclico.

$\blacksquare$

Más adelante…

En la siguiente entrada estudiaremos características de los cuadriláteros que son tanto cíclicos como circunscritos.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

1. $i)$ Muestra que un cuadrilátero convexo es circunscrito si y solo si sus bisectrices internas son concurrentes.
   $ii)$ Prueba que todo rombo es circunscrito.
2. Muestra que $\square ABCD$ convexo, es circunscrito si y solo si los incírculos de los triángulos $\triangle ABC$ y $\triangle ACD$ son tangentes entre si.
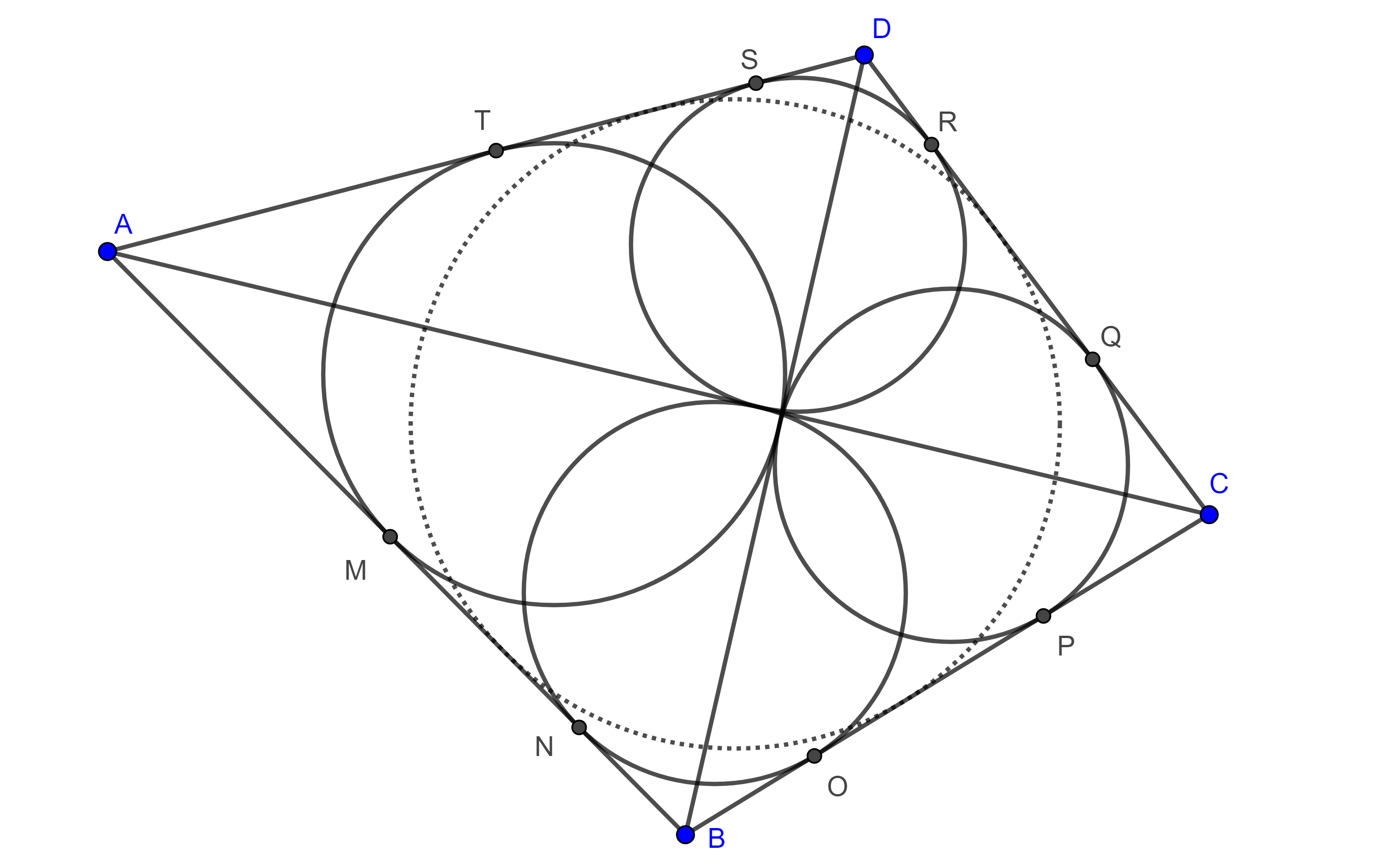
3. Sea $\square ABCD$ convexo, consideremos los incirculos de los triángulos $\triangle ABD$, $\triangle ABC$, $\triangle BCD$ y $\triangle ADC$ que son tangentes a los lados del cuadrilátero en $M$, $T$, $N$, $O$, $P$, $Q$, y $R$, $S$ respectivamente, muestra que $\square ABCD$ es circunscrito si y solo si $MN + QR = OP + ST$.

4. Si $\square ABCD$ es circunscrito, con lados $a$, $b$, $c$ y $d$ muestra que:
   $i)$ $(\square ABCD) = \sqrt{abcd} \sin \dfrac{\angle A + \angle C}{2} = \sqrt{abcd} \sin \dfrac{\angle B + \angle D}{2}$,
   $ii)$ $(\square ABCD) \leq \sqrt{abcd}$.
5. Sean $\square ABCD$ circunscrito, $I$ el incentro del cuadrilátero y $P$ la intersección de las diagonales, muestra que los ortocentros de los triángulos $\triangle AIB$, $\triangle BIC$, $\triangle CID$, $\triangle AID$ y $P$ son colineales.

6. Sean $\square ABCD$ circunscrito y $P$ la intersección de sus diagonales, muestra que los centros de los excírculos de los triángulos $\triangle APB$, $\triangle BPC$, $\triangle CPD$ y $\triangle APD$ opuestos a $P$ forman un cuadrilátero cíclico.

Entradas relacionadas

• Ir a Geometría Moderna I.
• Entrada anterior del curso: Cuadrilátero ortodiagonal.
• Siguiente entrada del curso: Cuadrilátero bicéntrico.
• Otros cursos.

Fuentes

• Altshiller, N., College Geometry. New York: Dover, 2007, pp 135-136.
• Santos, J., Tesis Geometría del Cuadrilátero. 2010, pp 34-38.
• Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 147-148.
• Grinberg, Darij, Circumscribed quadrilaterals revisited, 2008
• Cut the Knot
• Wikipedia

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»