Archivo de la etiqueta: vectores

Investigación de Operaciones: Soluciones básicas, factibles y no degeneradas (10)

Por Aldo Romero

Deja un comentario

Introducción

Ya hablamos de lo que es la forma canónica y la forma estándar de un problema lineal. Como platicamos, esto nos permitirá darle solución a los problemas siguiendo métodos que requieren tener el problema en alguna de estas dos formas. Lo que haremos ahora es reflexionar a qué nos referimos con resolver un problema de programación lineal. Para ello, recordemos los distintos tipos de soluciones que los problemas lineales pueden tener.

Tipos de soluciones y región de factibilidad

Recordemos los conceptos de soluciones factibles, soluciones básicas factibles (degeneradas y no degeneradas) y de región de factibilidad.

Supongamos que tenemos un problema de programación lineal en su forma canónica:

\begin{align*}
Max \quad z &= cx\\
s.a&\\
Ax &\leq b\\
x &\geq \bar 0\\
\end{align*}

donde usamos la misma notación que en la entrada anterior. Recordemos que $c$ es un vector fila en $\mathbb{R}^n$, $x$ es un vector columna en $\mathbb{R}^n$, $b$ es vector columna en $\mathbb{R}^m$ y $A$ es una matriz de $m\times n$. Recuerda que en la expresión anterior entendemos $\bar 0$ como un vector en $\mathbb{R}^n$ con entradas todas iguales a cero.

También recordemos la forma estándar de un problema de programación lineal:

\begin{align*}
Max \quad z &= cx\\
s.a&\\
Ax &=b\\
x &\geq \bar 0\\
\end{align*}

en donde $c$ es un vector fila en $\mathbb{R}^n$, $x$ es un vector columna en $\mathbb{R}^{n}$, $b$ es un vector columna en $\mathbb{R}^{m}$ y $A$ es una matriz de valores reales de $m \times n$.

Como recordatorio, tenemos las siguientes definiciones para los tipos de soluciones del problema lineal.

Definición. Una solución factible es aquella que satisface las restricciones de un problema de programación lineal.

Definición. La región de factibilidad es el conjunto de todas las soluciones factibles de un problema de programación lineal.

Definición. Una solución básica es una solución $x = (x_1,x_2, \ldots, x_n)$ correspondiente al problema en forma estándar ($Ax = b$) que tiene al menos $n-m$ entradas iguales a cero y las columnas de las $m$ variables restantes son linealmente independientes.

Definición. Una solución básica factible es una solución básica cuyas variables son todas no negativas.

Definición. Una solución básica factible no degenerada es una solución básica $x$ correspondiente a una solución $x$ del problema en forma estándar con exactamente $m$ componentes positivas. En otras palabras, $x$ tiene exactamente $n-m$ entradas iguales a cero.

Definición. Una solución básica factible degenerada es una solución básica correspondiente a una solución $x$ del problema en forma estándar con menos de $m$ componentes positivas. En otras palabras, $x$ tiene más de $n-m$ entradas iguales a cero.

Las soluciones básicas factibles no degeneradas son las que más nos interesan ya que el óptimo se encuentra entre estas soluciones. También se puede demostrar que toda solución básica factible es un punto extremo de la región factible.

A continuación explicaremos algunos de estos puntos con un ejemplo detallado, que te ayudará a entender la intuición detrás de estas definiciones y de su importancia.

Ejemplos de región de factibilidad y tipos de solución

Consideremos el siguiente problema de programación lineal en su forma canónica:

\begin{align*}
Max. \quad z &= 2x_1 + 3x_2\\
s.a.&\\
&\begin{matrix}2x_1 &+ x_2 &\leq & 4\\
x_1 &+ 2x_2 &\leq &5\end{matrix}\\
&x_1, x_2 \geq 0.
\end{align*}

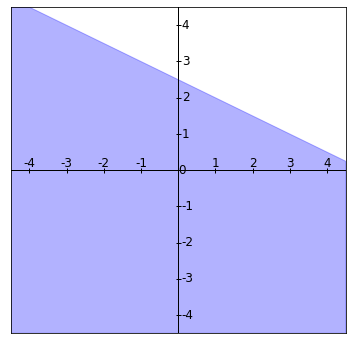
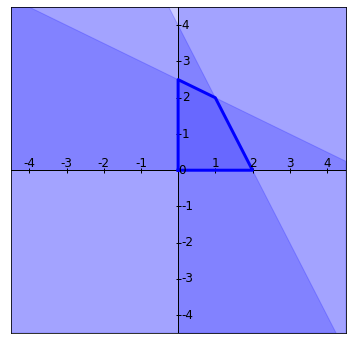
La región de factibilidad es el conjunto de todos los $(x_1,x_2)$ (en el plano $\mathbb{R}^2$) que cumplen las restricciones del problema, es decir, $2x_1 + x_2 \leq 4$, $x_1 + 2x_2 \leq 5$ y $x_1,x_2 \geq 0$. Para entender esto mejor, vamos a ilustrar cada restricción en $\mathbb{R}^2$ a continuación :

Región 1: La región $x_1\geq 0$, que son todos los elementos de $\mathbb{R}^2$ que se encuentran a la derecha del eje $Y$ incluyéndolo:

Región 2: La región $x_2\geq 0$, que son todos los elementos de $\mathbb{R}^2$ que se encuentran arriba del eje $X$ incluyéndolo:

Región 3: La región $2x_1 + x_2 \leq 4$, que son los elementos en $\mathbb{R}^2$ que están debajo de la recta $2x_1+x_2=4$ incluyéndola:

Región 4: La región $x_1+2x_2\leq 5$, que son los elementos en $\mathbb{R}^2$ que están debajo de la recta $x_1+2x_2=5$ incluyéndola:

Como queremos que se cumplan todas las restricciones al mismo tiempo, los puntos $(x_1,x_2) \in \mathbb{R}^2$ de la región de factibilidad que se encuentren en todas las regiones al mismo tiempo, es decir, los puntos que estén en la intersección. Al sobreponer las regiones que acabamos de ilustrar, obtenemos la región encerrada en la siguiente figura:

También puedes explorar el interactivo de Geogebra en donde se han coloreado los complementos de las regiones para más claridad. Puedes usar el cursor para mover la figura y las herramientas de lupa para hacer acercamientos y alejamientos.

Como hemos mencionado, el óptimo de un problema de programación lineal es una solución básica factible no degenerada y toda solución básica factible no degenerada se encuentra en algún vértice de la región de factibilidad. Entonces, el valor máximo de la función $2x_1+3x_2$ se alcanza en alguno de los vértices del polígono que es la región factible. Veamos dónde el álgebra nos dice esto.

Para ello, pensemos al problema en su forma estándar, tomando variables de holgura $s_1$ y $s_2$. Las restricciones que tienen las cuatro variables en conjunto son las siguientes.

\begin{align*}
2x_1 + x_2 + s_1 &= 4\\
x_1 + 2x_2 + s_2 &= 5\\
x_1, x_2, s_1, s_2 &\geq 0.
\end{align*}

La matriz $A’$ es $\begin{pmatrix}2 & 1 & 1 & 0 \\ 1 & 2 & 0 & 1 \end{pmatrix}$, tiene rango $2$ (recordemos que el rengo de una matriz es el número de filas o columnas linealmente independientes que posee). Las soluciones básicas y no degeneradas corresponden a tener en ese sistema de ecuaciones exactamente $m=2$ variables positivas, de manera que necesitamos hacer exactamente $n-m=4-2=2$ de estas variables iguales a cero. Al hacer esto, podemos resolver para las $m=2$ variables restantes. Por ejemplo, si establecemos $x_1 = 0$ y $x_2 = 0$, las ecuaciones se convierten en:

\begin{align*}
s_1 = 4\\
s_2 = 5\\
x_1, x_2, s_1, s_2 \geq 0,
\end{align*}

que tiene solución única $(x_1,x_2,s_1,s_2)=(0,0,4,5)$. Así, la solución básica del problema en forma canónica es $(x_1,x_2)=(0,0)$. Hay que recordar la solución básica sólo para las variables originales, es decir, las del problema en forma canónica.

Esta solución corresponde al punto $A$ del interactivo de GeoGebra. Se puede determinar otra solución básica fijando $s_1 = 0$ y $s_2 = 0$, donde el sistema sería ahora

\begin{align*}
2x_1 + x_2 = 4\\
x_1 + 2x_2 = 5\\
x_1, x_2, s_1, s_2 \geq 0,
\end{align*}

Resolvamos este sistema de ecuaciones de forma rápida. Si multiplicamos la segunda ecuación por un $-2$ y sumamos ambas ecuaciones, la variable $x_1$ se eliminará y tendremos solo una ecuación: $-3x_2 = -6$ lo que es equivalente a $x_2 = 2$. Si sustituimos ahora este valor para $x_2$ en cualquiera de las ecuaciones, tras unos simples despejes tendremos que $x_1 = 1$.

Así, la solución básica que se obtiene es $(x_1,x_2)=(1,2)$, que es el punto $D$ del interactivo de GeoGebra.

Si seguimos considerando todas las posibilidades en las que dos variables son cero y resolvemos los ssistemas de ecuaciones resultantes, eso nos dará todas soluciones básicas no degeneradas. La solución óptima es la solución básica factible (punto extremo) con el mejor valor objetivo.

En este ejemplo tenemos $\binom{4}{2} = \frac{4!}{2!2!} = 6$ formas de volver dos de las $n$ variables iguales a cero. Ya para las variables $x_1$ y $x_2$, los puntos que obtenemos son los puntos $A$, $B$, $C$, $D$ que son puntos extremos de la región de factibilidad. Los puntos $E$ y $F$ del interactivo también son puntos básicos y no degenerados (son las otras dos intersecciones de las rectas que dibujamos), pero como no satisfacen la condición de factibilidad del problema, entonces no los podemos considerar y por lo tanto no son candidatos a dar el valor óptimo.

La siguiente tabla muestra todas las soluciones básicas factibles y no factibles de este problema:

Variables no básicas (cero)Variables básicasSolución para $(x_1,x_2)$Punto de extremo asociado¿Factible?Valor objetivo z
$(x_1, x_2) = (0,0)$$(s_1, s_2) = (4,5)$$(0, 0)$ASí0
$(x_1, s_1) = (0,0)$$(x_2, s_2) = (4,-3)$$(0, 4)$ENo ya que $s_2 < 0$12 (No factible)
$(x_1, s_2) = (0,0)$$(x_2, s_1) = (2.5,1.5) $$(0, 2.5)$BSí7.5
$(x_2, s_1) = (0,0)$$(x_1, s_2) = (2,3)$$(2, 0)$CSí4
$(x_2, s_2) = (0,0)$$(x_1, s_1) = (5, -6)$$(5, 0)$FNo ya que
$s_1 < 0$		10 (No factible)
$(s_1, s_2) = (0,0)$$(x_1, x_2) = (1,2)$$(1, 2)$DSí8 (óptimo)

Más adelante…

Notemos que a medida que el tamaño del problema se incrementa, enumerar todos los puntos esquina se volverá una tarea que tomaría mucho tiempo. Por ejemplo, si tuviéramos $20$ variables (ya con las de holgura) y $10$ restricciones, es necesario resolver considerar $\binom{20}{10}=184756$ formas de crear ecuaciones de $10\times 10$, y resolver cada una de ellas. Aunque esto es finito, son demasiadas operaciones. Y este en la práctica incluso es un ejemplo pequeño, ya que en la vida real hay problemas lineales que pueden incluir miles de variables y restricciones.

Por ello, se vuelve cruciar encontrar un método que atenúe esta carga computacional en forma drástica, que permita investigar sólo un subconjunto de todas las posibles soluciones factibles básicas no degeneradas (vértices de la región de factibilidad), pero que garantice encontrar el óptimo. Una idea intuitiva que debería servir es comenzar en un vértice y «avanzar en una dirección que mejore la función objetivo». Esto precisamente es la intuición detrás del método simplex, que repasaremos a continuación.

Tarea moral

  1. Considera el siguiente problema lineal en su forma canónica:

\begin{align*}
Min \quad z &= 2x_1 + 3x_2 \\
s.a.&\\
&\begin{matrix}x_1 &+ 3x_2 &\geq&6\\
3x_1 &+ 2x_2 &\geq &6\end{matrix}\\
&x_1, x_2 \geq 0.
\end{align*}

Usa el procedimiento descrito arriba para encontrar todas sus soluciones básicas no degeneradas y encontrar el óptimo del problema.

  1. Considera un problema de programación lineal en dos variables $x$ y $y$, en forma canónica y con $m$ restricciones (desigualdades), además de las restricciones $x\geq 0$ y $y\geq 0$. Explica con tus propias palabras por qué la región de factibilidad siempre es un polígono con a lo más $m+2$ lados, y por qué entonces basta evaluar la función objetivo en a lo más $m+2$ puntos para encontrar su máximo.
  2. Explica con tus palabras cómo se vería la región de factibilidad de un problema de programación lineal de maximización que no tenga máximo. ¿Qué cambios se le tendrían que hacer a las restricciones del primer ejemplo para que se volviera un problema de maximización sin máximo?

Respuestas

1.- Primero vamos a cambiar este problema a su forma estándar.

Definamos variables de holgura no negativas $s_1$ y $s_2$ tales que $x_1 + 3x_2 – s_1 = 6$ y $3x_1 +2x_2 – s_2 = 6$.

Entonces la forma estandar del problema sería de la siguiente manera:

\begin{align*}
Min \quad z &= 2x_1 + 3x_2 \\
s.a.&\\
&\begin{matrix}x_1 &+ 3x_2 &- s_1 = &6\\
3x_1 &+ 2x_2 &- s_2 = &6\end{matrix}\\
&x_1, x_2, s_1, s_2 \geq 0.
\end{align*}

Su matriz A asociado a las restricciones $\begin{pmatrix}1 & 3 & -1 & 0 \\ 3 & 2 & 0 & -1 \end{pmatrix}$ en una matriz de $2 \times 4$. Las soluciones básicas no degeneradas $x’$ en $\mathbb{R}^4$ tienen $4-2 = 2$ entradas iguales a 0.

Variables no básicas (cero)Variables básicasSolución para $(x_1,x_2)$Punto de extremo asociado¿Factible?Valor objetivo z
$(x_1, x_2) = (0,0)$$(s_1, s_2) = (-6,-6)$$(0, 0)$ANo ya que $s_1,s_2 < 0$0
$(x_1, s_1) = (0,0)$$(x_2, s_2) = (2,-2)$$(0, 2)$BNo ya que $s_2 < 0$6 (No factible)
$(x_1, s_2) = (0,0)$$(x_2, s_1) = (3,3)$$(0, 3)$CSí9
$(x_2, s_1) = (0,0)$$(x_1, s_2) = (6, 12) $$(6, 0)$DSí12
$(x_2, s_2) = (0,0)$$(x_1, s_1) = (2,-4)$$(2, 0)$ENo ya que
$s_1 < 0$		4 (No factible)
$(s_1, s_2) = (0,0)$$(x_1, x_2) = (6/7,12/7)$$(6/7,12/7)$FSí48/7 = 6 + 6/7 (óptimo)

Por lo que el óptimo se encuentra en el punto F = (6/7, 12/7).

En el siguiente interactivo de GeoGebra, verifica uno por uno los puntos extremos que se encontraron.

2.- Se podría argumentar tal vez que cada restricción de un problema de programación lineal representa un lado del polígono que forma la región factible. Y como tenemos m restricciones en el problema y las condiciones de no negatividad son 2 restricciones más, el polígono tendrá a lo más m+2 lados.

3.- La región de factibilidad se vería como una región no acotada en el primer cuadrante del plano. En esta región, dada un punto x dentro de ella, existe otro punto x’ tal que $z(x) < z(x’)$.

El que se tendría que hacer en el primer problema sería simplemente invertir las desigualdades de las restricciones:

\begin{align*}
Max. \quad z &= 2x_1 + 3x_2\\
s.a.&\\
&\begin{matrix}2x_1 &+ x_2 &\geq & 4\\
x_1 &+ 2x_2 &\geq &5\end{matrix}\\
&x_1, x_2 \geq 0.
\end{align*}

Se puede verificar haciendo los cambios en el primer interactivo que estos cambios nos cambiaran la región factible a una región no acotada.

Referencias bibliográficas

  • Wayne L. Winston, Operations Research, Belmont, CA, USA: Thomson Learning, 2004.
  • David G. Luenberger, Linear and Nonlinear Programming, Stanford, CA, USA: Springer, 2008.
  • Frederick S. Hillier, Gerald J. Lieberman, Introducción a la investigación de operaciones, Stanford, CA, USA: McGRAW-HILL, 2010.

Entradas relacionadas

2.1. TRANSFORMACIÓN LINEAL: definición y ejemplos

Por Jennyfer Paulina Bennetts Castillo

Deja un comentario

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

INTRODUCCIÓN

¿Por qué el uso de la palabra «transformación»?
Como veremos, una transformación lineal es una función que va de un espacio lineal a otro espacio lineal. Y toda función, básica e informalmente, transforma un elemento del dominio en uno del rango.

Al igual que en una máquina se introducen los ingredientes o materiales y son transformados para obtener un resultado final, en una función se introduce un elemento del dominio y se transforma mediante la regla de correspondencia en uno del rango

Ahora bien, no es una función «cualquiera». Y aunque sólo son dos condiciones las que se piden, estas transformaciones de un espacio vectorial en sí mismo o en otro espacio vectorial tienen un comportamiento que permite aplicaciones muy útiles tanto en matemáticas, como en física, ingenierías e incluso arte digital. Sus propiedades gracias a esas dos condiciones hacen de este tipo de funciones sea un punto esencial del Álgebra lineal.

TRANSFORMACIÓN LINEAL

Definición: Sean $V$ y $W$ $K$ – espacios vectoriales. Una función $T:V\longrightarrow W$ es una transformación lineal de $V$ en $W$ si:
$1)$ $\forall u,v\in V(T(u+v)=T(u)+T(v))$
$2)$ $\forall \lambda\in K(\forall v\in V(T(\lambda v)=\lambda T(v)))$

Nota: Al conjunto de las transformaciones lineales de $V$ a $W$ se le denota como $\mathcal{L}(V,W)$. Cuando una función cumple la condición $1)$ diremos que abre sumas, y si cumple la condición $2)$ diremos que saca escalares.

Observación: Si $T$ abre sumas, entonces manda al neutro de $V$ en el neutro de $W$, pues $\theta_W+T(\theta_V)=T(\theta_V)=T(\theta_V+\theta_V)=T(\theta_V)+T(\theta_V)$
$\Rightarrow\theta_W+T(\theta_V)=T(\theta_V)+T(\theta_V)$
$\Rightarrow\theta_W=T(\theta_V)$
En otras palabras, las transformaciones lineales envían el neutro del dominio en el neutro del codominio.

Ejemplos

  • Sea $V$ un $K$ – espacio vectorial.
    $T:V\longrightarrow V$ donde $\forall v\in V(T(v)=\theta_V)$ es una transformación lineal de $V$ en $V$

Justificación. Sean $\lambda\in K$ y $u,v\in V$.

Entonces:
$T(u+v)=\theta_V=\theta_V+\theta_V=T(u)+T(v)$
$\lambda T(v)=\lambda\theta_V=\theta_V=T(\lambda v)$

  • Sea $K$ un campo. $T:K[x]\longrightarrow K[x]$ donde $\forall p(x)\in K[x](T(p(x))=p'(x))$ es una transformación lineal de $K[x]$ en $K[x]$

Justificación. Sean $\lambda\in K$ y $p(x),q(x)\in K[x]$.

Entonces:
$T(p(x)+q(x))=(p(x)+q(x))’=p'(x)+q'(x)=T(p(x))+T(q(x))$
$T(\lambda p(x))=(\lambda p(x))’=\lambda p'(x)=\lambda T(p(x))$

Proposición (2.1.1.): Sean $V,W$ $K$ – espacios vectoriales, $T:V\longrightarrow W$.
$T$ es lineal si y sólo si $\forall\lambda\in K , \forall u,v\in V$ $(T(\lambda u+v)=\lambda T(u)+T(v))$

Demostración: $\Longrightarrow )$ Sean $T:V\longrightarrow W$ lineal, $\lambda\in K$, $u,v\in V$.

$\begin{align*}
T(\lambda u+v)&=T(\lambda u)+T(v)\tag{$1$}\\
&=\lambda T(u)+T(v)\tag{$2$}\\
\therefore T(\lambda u+v)&=\lambda T(u)+T(v)
\end{align*}$

$\Longleftarrow )$ Sea $T$ tal que $\forall\lambda\in K$ $\forall u,v\in V$ $(T(\lambda u+v)=\lambda T(u)+T(v))$. Sean $\lambda\in K$ y $u,v\in V$.

$\begin{align*}
T(u+v)&=T(1_K u+v)\tag{}\\
&=1_KT(u)+T(v)\tag{hip}\\
&=T(u)+T(v)\tag{}\\
\therefore T(u+v)&=T(u)+T(v)
\end{align*}$

$\begin{align*}
T(\lambda u)&=T(\lambda u+\theta_V)\tag{}\\
&=\lambda T(u)+T(\theta_V)\tag{hip}\\
&=\lambda T(u)+\theta_W\tag{Observación}\\
&=\lambda T(u)\tag{}\\
\therefore T(\lambda u)&=\lambda T(u)
\end{align*}$

$\therefore T$ es lineal

Ejemplos

  • $T:\mathbb{R}^3\longrightarrow\mathbb{R}^2$ donde $\forall (x,y,z)\in\mathbb{R}^3(T(x,y,z)=(x+y+z,2x-7y))$ es una transformación lineal de $\mathbb{R}^3$ en $\mathbb{R}^3$.

Justificación. Sean $(x,y,z),(u,v,w)\in\mathbb{R}^3$ y $\lambda\in\mathbb{R}$.

$T(\lambda(x,y,z)+(u,v,w))=T((\lambda x,\lambda y,\lambda z)+(u,v,w))$$=T(\lambda x + u,\lambda y + v,\lambda z + w)$$=(\lambda x + u+\lambda y + v+\lambda z + w,2(\lambda x + u)-7(\lambda y + v))$$=(\lambda(x+y+z)+u+v+w,2\lambda x-7\lambda y+2u-7v)$$=\lambda (x+y+z,2x-7y)+(u+v+w,2u-7v)$$=\lambda T(x,y,z)+T(u,v,w)$

  • Sea $K$ un campo.
    Si $A\in\mathcal{M}_{m\times n}(K)$, entonces $T:K^n\longrightarrow K^m$ donde $\forall X\in K^n(T(X)=AX)$ es una transformación lineal de $K^n$ en $K^m$.

Justificación. Sean $X,Y\in K^n,\lambda\in K$.

$T(\lambda X+Y)=A(\lambda X+Y)=\lambda AX + AY=\lambda T(X)+T(Y)$.

Tarea Moral

  1. Sean $V$ y $W$ espacios vectoriales sobre un campo $F$.
    Sea $T: V \longrightarrow W$ una transformación lineal. Demuestra que para todo $v_1,v_2,…,v_n\in V$ y para todo $\lambda_1, \lambda_2,…,\lambda_n\in F$ con $n\in\mathbb{N}^{+}$ se tiene que $T(\lambda_1 v_1 + \lambda_2 v_2 + … + \lambda_n v_n) = \lambda_1 T(v_1) + \lambda_2 T(v_2) + … + \lambda_n T(v_n)$.
  2. Sea $T:\mathbb{R}^2 \longrightarrow \mathbb{R}^2$ una transformación lineal tal que $T(1,0)=(2,4)$ y $T(1,1)=(8,5)$. Determina si es posible hallar la regla de correspondencia de $T$, es decir, $T(x,y)$ para todo $(x,y)\in\mathbb{R}^2$. Si no es posible argumenta por qué y si es posible encuéntrala.
  3. ¿Existe una transformación lineal $T:\mathbb{R}^3\longrightarrow \mathbb{R}^2$ tal que $T(1,2,4)=(1,2)$ y $T(-2,-4,-8)=(-2,1)$?

Más adelante…

Veremos ahora cuatro elementos que surgen de una transformación lineal:
Núcleo e imagen, que son dos conjuntos relevantes para dominio y codominio.
Nulidad y rango, que son dos números que nos revelan dimensiones. Comenzaremos por definir el núcleo y la imagen de una transformación lineal y probando que son subespacios vectoriales.

Entradas relacionadas

Álgebra Superior I: El espacio vectorial $\mathbb{R}^n$

Por Eduardo García Caballero

1 respuesta

Introducción

En la entrada anterior introdujimos conceptos relacionados a los espacios vectoriales $\mathbb{R}^2$ y $\mathbb{R}^3$. Hablamos de vectores, combinaciones lineales, espacio generado, independencia lineal y bases. Ahora haremos lo análogo en dimensiones más altas, para lo cual hablaremos de $\mathbb{R}^n$.

La idea es sencilla, queremos extender lo que ya hicimos para vectores con $5$ o $100$ entradas. Sin embargo, visualizar estos espacios y entender su geometría ya no será tan sencillo. Es por esta razón que principalmente nos enfocaremos a generalizar las propiedades algebraicas que hemos discutido. Esta resultará una manera muy poderosa de estudiar los espacios vectoriales, pues nos permitirá generalizar sin mucha dificultad los conceptos aprendidos en la entrada anterior al espacio $\mathbb{R}^n$ para cualquier número natural $n$.

Definición del espacio vectorial $\mathbb{R}^n$

En la entrada anterior vimos cuáles son propiedades que debe cumplir una colección de objetos, en conjunto con una operación de suma y otra de producto escalar, para poder considerarse un espacio vectorial. Como ya vimos, tanto $\mathbb{R}^2$ y $\mathbb{R}^3$ son espacios vectoriales. Podemos definir a $\mathbb{R}^n$ y a sus operaciones como sigue.

Definición. El conjunto $\mathbb{R}^n$ consiste de todas las $n$-adas ordenadas $u=(u_1,u_2,\ldots,u_n)$ en donde cada $u_i$ es un número real, para $i=1,\ldots,n$. A $u_i$ le llamamos la $i$-ésima entrada de $u$. Para dos elementos de $\mathbb{R}^n$, digamos

\begin{align*}
u&=(u_1,u_2,\ldots,u_n)\\
v&=(v_1,v_2,\ldots,v_n),
\end{align*}

definimos la suma $u+v$ como la $n$-áda cuya $i$-ésima entrada es $u_i+v_i$ (decimos que sumamos entrada a entrada). En símbolos, $$u+v=(u_1+v_1,u_2+v_2,\ldots,u_n+v_n).$$

Además, si tomamos un real $r$, definimos el producto escalar de $r$ con $u$ como la $n$-ada cuya $i$-ésima entrada es $r u_i$, es decir, $ru=(ru_1,ru_2,\ldots,ru_n).$

El conjunto $\mathbb{R}^n$ con esta suma y producto escalar cumple ser un espacio vectorial. A continuación probaremos sólo algunas de las propiedades, ¿puedes completar el resto?

1. La suma es asociativa:
\begin{align*}
(u+v)+w
&= ((u_1,u_2,\ldots,u_n) + (v_1,v_2,\ldots,v_n)) + (w_1,w_2,\ldots,w_n) \\
&= (u_1+v_1,u_2+v_2,\ldots,u_n+v_n) + (w_1,w_2,\ldots,w_n) \\
&= ((u_1+v_1)+w_1,(u_2+v_2)+w_2,\ldots,(u_n+v_n)+w_n) \\
&= (u_1+(v_1+w_1),u_2+(v_2+w_2),\ldots,u_n+(v_n+w_n)) \\
&= (u_1,u_2,\ldots,u_n) + (v_1+w_1,v_2+w_2,\ldots,v_n+w_n) \\
&= (u_1,u_2,\ldots,u_n) + ((v_1,v_2,\ldots,v_n) + (w_1,w_2,\ldots,w_n)) \\
&= u + (v+w).
\end{align*}

La cuarta igualdad usa el paso clave de que en $\mathbb{R}$ sí sabemos que la suma es asociativa.

2. La suma es conmutativa:
\[
u+v = v+w.
\]

¡Intenta demostrarlo!

3. Existe un elemento neutro para la suma, que es el elemento de $\mathbb{R}^n$ en donde todas las entradas son iguales al neutro aditivo $0$ de $\mathbb{R}$:
\begin{align*}
u+0
&= (u_1,u_2,\ldots,u_n) + (0,0,\ldots,0) \\
&= (u_1+0,u_2+0,\ldots,u_n+0) \\
&= (u_1,u_2,\ldots,u_n) \\
&= u.
\end{align*}

Para demostrar esta propiedad, necesitaras usar que en $\mathbb{R}$ cada $u_i$ tiene inverso aditivo.

4. Para cada $n$-tupla existe un elemento inverso:
\[
u + (-u) = 0.
\]

5. La suma escalar se distribuye bajo el producto escalar:
\begin{align*}
(r+s)u
&= (r+s)(u_1,u_2,\ldots,u_n) \\
&= ((r+s)u_1,(r+s)u_2,\ldots,(r+s)u_n) \\
&= (ru_1 + su_1, ru_2 + su_2, \ldots, r_n + su_n) \\
&= (ru_1,ru_2,\ldots,ru_n) + (su_1,su_2,\ldots,su_n) \\
&= r(u_1,u_2,\ldots,u_n) + s(u_1,u_2,\ldots,u_n) \\
&= ru + su.
\end{align*}

Una vez más, se está usando una propiedad de $\mathbb{R}$ para concluir una propiedad análoga en $\mathbb{R}^n$. En este caso, se está usando fuertemente que hay una propiedad de distributividad en $\mathbb{R}$.

6. La suma de $n$-tuplas de distribuye bajo el producto de escalares:
\[
r(u+v) = ru + rv.
\]

7. El producto escalar es compatible con el producto de $\mathbb{R}$:
\begin{align*}
(rs)u
&= (rs)(u_1,u_2,\ldots,u_n) \\
&= ((rs)u_1,(rs)u_2,\ldots,(rs)u_n) \\
&= (r(su_1),r(su_2),\ldots,r(su_n)) \\
&= r(su_1, su_2, \ldots, su_n) \\
&= r(s(u_1,u_2,\ldots,u_n)) \\
&= r(su).
\end{align*}

8. El neutro multiplicativo $1$ de $\mathbb{R}$ funciona como neutro para el producto escalar:
\[
1u = u.
\]

De este modo, podemos trabajar con el espacio vectorial $\mathbb{R}^n$ para explorar sus propiedades. La gran ventaja es que lo que demostremos para $\mathbb{R}^n$ en general lo podremos usar para cualquier valor particular de $n$. y poder emplearlas cuando trabajemos con algún número $n$ en particular.

Combinaciones lineales y espacio generado

Al igual que hicimos con $\mathbb{R}^2$ y $\mathbb{R}^3$ podemos definir los conceptos de combinación lineal y espacio generado para el espacio vectorial $\mathbb{R}^n$.

Definición. En $\mathbb{R}^n$, diremos que un vector $u$ es combinación lineal de los vectores $v_1,\ldots,v_k$ si y sólo si existen números reales $r_1,\ldots,r_n$ en $\mathbb{R}$ tales que
\[
u = r_1v_1 + r_2v_2 + \cdots + r_kv_k.
\]

Ejemplo. En $\mathbb{R}^5$, el vector $(3,4,-2,5,5)$ es combinación lineal de los vectores $(2,1,2,0,3)$, $(0,1,-1,3,0)$ y $(1,-1,5,-2,1)$, pues
\[
(3,4,-2,5,5) = 2(2,1,2,0,3) + 1(0,1,-1,3,0) + -1(1,-1,5,-2,1).
\]

$\triangle$

La noción de combinación lineal nos permite hablar de todas las posibles combinaciones lineales, así como en $\mathbb{R}^2$ y $\mathbb{R}^3$.

Definición. Dado un conjunto de vectores $v_1,\ldots,v_n$ en $\mathbb{R}^n$, podemos definir el espacio generado por estos vectores como el conjunto de todas las posibles combinaciones lineales de $v_1,\ldots,v_n$ en $\mathbb{R}^n$.

Es este caso, ya no podremos visualizar geométricamente el espacio generado (aunque con un poco de imaginación, quizás puedas generalizar lo que ya hicimos en dimensiones anteriores: ¿cómo se vería un plano en $\mathbb{R}^4$?, ¿cómo se vería un sub-$\mathbb{R}^3$ de $\mathbb{R}^4$?). De cualquier manera, sí podemos seguir respondiendo preguntas del espacio generado a través de sistemas de ecuaciones.

Ejemplo. ¿El espacio generado por los vectores $(1,1,1,0)$, $(0,3,1,2)$, $(2,3,1,0)$ y $(1,0,2,1)$ es $\mathbb{R}^4$?

Para ver si $\mathbb{R}^4$ es el espacio generado por los vectores propuestos, debemos asegurarnos de que cada vector en $\mathbb{R}^4$ se pueda expresar como combinación lineal de estos. Entonces, seleccionamos un vector $(a,b,c,d)$ arbitrario en $\mathbb{R}^4$, y debemos ver si existen escalares $q$, $r$, $s$ y $t$ tales que
\[
q(1,1,1,0) + r(0,3,1,2) + s(2,3,1,0) + t(1,0,2,1) = (a,b,c,d);
\]
esto es,
\[
(q,q,q,0) + (0,3r,r,2r) + (2s,3s,s,0) + (t,0,2t,t) = (a,b,c,d),
\]
que equivale a
\[
(q+2s+t, q+3r+3s, q+r+s+2t, 2r+t)=(a,b,c,d),
\]
lo cual a su vez equivale al sistema de ecuaciones
\[
\left\{
\begin{alignedat}{4}
q & +{} & & +{} & 2s & +{} & t & = a \\
q & +{} & 3r & +{} & 3s & & & = b \\
q & +{} & r & +{} & s & +{} & 2t & = c \\
& & 2r & & & +{} & t & = d,
\end{alignedat}
\right.
\]
el cual podemos representar como
\[
\begin{pmatrix}
1 & 0 & 2 & 1 \\
1 & 3 & 3 & 0 \\
1 & 1 & 1 & 2 \\
0 & 2 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
q \\ r \\ s \\ t
\end{pmatrix}
=
\begin{pmatrix}
a \\ b \\ c \\ d
\end{pmatrix}.
\]
Además, podemos observar que la matriz en el lado izquierdo tiene determinante distinto de $0$ (para verificar esto, tendrás que calcularlo), lo que nos indica que es invertible, y la igualdad anterior equivale a
\[
\begin{pmatrix}
q \\ r \\ s \\ t
\end{pmatrix}
=
\begin{pmatrix}
1 & 0 & 2 & 1 \\
1 & 3 & 3 & 0 \\
1 & 1 & 1 & 2 \\
0 & 2 & 0 & 1
\end{pmatrix}^{-1}
\begin{pmatrix}
a \\ b \\ c \\ d
\end{pmatrix},
\]
o bien,
\[
\begin{pmatrix}
q \\ r \\ s \\ t
\end{pmatrix}
=
\begin{pmatrix}
-3 & 1 & 3 & -3 \\
-1/2 & 1/4 & 1/4 & 0 \\
3/2 & -1/4 & -5/4 & 1 \\
1 & -1/2 & -1/2 & 1
\end{pmatrix}
\begin{pmatrix}
a \\ b \\ c \\ d
\end{pmatrix},
\]
de donde tenemos la solución para $q,r,s,t$ siguiente:
\[
\left\{
\begin{alignedat}{4}
q & = & -3a & +{} & b & +{} & 3c & -{} & 3d \\
r & = & -\tfrac{1}{2}a & +{} & \tfrac{1}{4}b & +{} & \tfrac{1}{4}c & & \\
s & = & \tfrac{3}{2}a & -{} & \tfrac{1}{4}b & -{} & \tfrac{5}{4}c & +{} & d \\
t & = & a & -{} & \tfrac{1}{2}b & -{} & \tfrac{1}{2}c & +{} & d.
\end{alignedat}
\right.
\]
Este sistema nos da una fórmula para los escalares $q$, $r$, $s$ y $t$ en función del valor de las entradas del vector $(a,b,c,d)$, y estos escalares satisfacen
\[
q(1,1,1,0) + r(0,3,1,2) + s(2,3,1,0) + t(1,0,2,1) = (a,b,c,d).
\]
Como esto se cumple para un vector arbitrario $(a,b,c,d)$ en $\mathbb{R}^4$, entonces se cumple para todos los vectores de $\mathbb{R}^4$; es decir, ¡$\mathbb{R}^4$ es el espacio generado por los vectores $(1,1,1,0)$, $(0,3,1,2)$, $(2,3,1,0)$, $(1,0,2,1)$!

$\triangle$

Nuestra técnica de resolver sistemas de ecuaciones mediante la inversa de la matriz asociada ha resultado muy útil. Hemos tenido un poco de suerte en que la matriz sea invertible. Si no lo fuera, no podríamos haber hecho el procedimiento descrito en el ejemplo. ¿Será que si la matriz no es invertible, entonces el sistema no se podrá resolver? La respuesta es compleja: a veces sí, a veces no. En ese caso hay que entender el sistema de ecuaciones con otro método, como reducción gaussiana.

Independencia lineal

Cuando exploramos las propiedades de $\mathbb{R}^2$ y $\mathbb{R}^3$, observamos que hay ocasiones en las que el espacio generado por un conjunto de vectores es «más chico» de lo que se esperaría de la cantidad de vectores: por ejemplo, dos vectores en $\mathbb{R}^2$ generan una línea (y no todo $\mathbb{R}^2$) cuando estos dos se encuentran alineados con el origen. Cuando tres vectores en $\mathbb{R}^3$ no están alineados, pero se encuentran sobre el mismo plano por el origen, su espacio generado es dicho plano (y no todo $\mathbb{R}^3$).

Aunque el el espacio vectorial $\mathbb{R}^n$ no podamos visualizarlo de manera inmediata, podemos mantener la intuición de que un conjunto de vectores «genera todo lo que puede generar» o «genera algo más chico». Para identificar en qué situación nos encontramos, recurrimos a la siguiente definición.

Definición. Dado un conjunto de $k$ vectores $v_1, v_2, \ldots, v_k$ en $\mathbb{R}^n$ distintos de 0, diremos son linealmente independientes si la única forma de escribir al vector 0 como combinación lineal de ellos es cuando todos los coeficientes de la combinación lineal son igual al escalar 0; es decir, si tenemos que
\[
r_1v_1 + r_2v_2 + \cdots + r_kv_k = 0,
\]
entonces forzosamente $r_1 = r_2 = \cdots = r_n = 0$.

Teniendo esta definición en consideración, se puede mostrar que si un conjunto de vectores es linealmente independiente, entonces ninguno de los vectores se puede escribir como combinación lineal de los otros. De hecho, es únicamente en este caso cuando cuando el espacio generado por los vectores es «todo lo que se puede generar».

La justificación de por qué sucede esto es similar a la que vimos en la entrada anterior: como el primer vector es no genera una línea. Como el segundo vector no se puede escribir como combinación lineal del primero, entonces queda fuera de esta línea y ambos generan un plano. Como el tercer vector no se puede escribir como combinación lineal de los primeros dos, entonces queda fuera del plano, y entre los tres generan un espacio «más grande» («de dimensión $3$»). A partir de este punto, quizá no podamos visualizar inmediatamente la forma geométrica del espacio generado, pero como sabemos que los vectores son linealmente independientes, entonces el cuarto vector no se puede escribir como combinación lineal de los primeros tres. Por ello, queda fuera del espacio generado por los primeros tres, y el espacio generado por los cuatro es aún «más grande» («de dimensión $4$»); y así sucesivamente, para tantos vectores linealmente independientes como tengamos.

Una herramienta que podemos emplear para determinar cuándo un conjunto de vectores es linealmente independiente son nuevamente los sistemas de ecuaciones. Para esto veamos el siguiente ejemplo.

Ejemplo. ¿Son los vectores $(1,5,1,-2)$, $(3,-3,0,-1)$, $(-2,0,4,1)$ y $(0,1,-1,0)$ linealmente independientes en $\mathbb{R}^4$?

Supongamos que para ciertos escalares $a$, $b$, $c$ y $d$, se cumple que
\[
a(1,5,1,-2) + b(3,-3,0,-1) + c(-2,0,4,1) + d(0,1,-1,0) = (0,0,0,0).
\]
Esto es equivalente a decir que
\[
(a,5a,a,-2a) + (3b,-3b,0,-b) + (-2c,0,4c,c) + (0,d,-d,0) = (0,0,0,0)
\]
que equivale a
\[
(a+3b-2c, 5a-3b+d,a+4c-d,-2a-b+c) = (0,0,0,0),
\]
y a su vez equivale al sistema de ecuaciones
\[
\left\{
\begin{alignedat}{4}
a & +{} & 3b & -{} & 2c & & & = 0 \\
5a & -{} & 3b & & & +{} & d & = 0 \\
a & & & +{} & 4c & -{} & d & = 0 \\
-2a & -{} & b & +{} & c & & & = 0
\end{alignedat}
\right.
\]
el cual podemos representar de la forma
\[
\begin{pmatrix}
1 & 3 & -2 & 0 \\
5 & -3 & 0 & 1 \\
1 & 0 & 4 & -1 \\
-2 & 1 & 1 & 0
\end{pmatrix}
\begin{pmatrix}
a \\ b \\ c \\ d
\end{pmatrix}
=
\begin{pmatrix}
0 \\ 0 \\ 0 \\ 0
\end{pmatrix},
\]
y, como notamos que la matriz del lado izquierdo de la ecuación tiene determinante distinto de 0 (¿puedes verificarlo?), entonces es invertible, de modo que
\[
\begin{pmatrix}
a \\ b \\ c \\ d
\end{pmatrix}
=
\begin{pmatrix}
1 & 3 & -2 & 0 \\
5 & -3 & 0 & 1 \\
1 & 0 & 4 & -1 \\
-2 & 1 & 1 & 0
\end{pmatrix}^{-1}
\begin{pmatrix}
0 \\ 0 \\ 0 \\ 0
\end{pmatrix}
=
\begin{pmatrix}
0 \\ 0 \\ 0 \\ 0
\end{pmatrix},
\]
es decir,
\[
a = b = c = d = 0,
\]
lo que nos indica, basándonos en la definición, que los vectores anteriores son linealmente independientes.

$\triangle$

El ejemplo anterior nos da una idea de lo que debe cumplir un conjunto linealmente independiente de $n$ vectores en $\mathbb{R}^n$. En general, podemos mostrar que un conjunto de $n$ vectores $v_1 = (v_{11}, v_{12}, \ldots, v_{1n})$, $v_2 = (v_{21}, v_{22}, \ldots, v_{2n})$, $\ldots$, $v_n = (v_{n1}, v_{n2}, \ldots, v_{nn})$ es linealmente independiente si y sólo si la matriz
\[
\begin{pmatrix}
v_{11} & v_{21} & \cdots & v_{n1} \\
v_{12} & v_{22} & \cdots & v_{n2} \\
\vdots & \vdots & \ddots & \vdots \\
v_{1n} & v_{2n} & \cdots & v_{nn}
\end{pmatrix},
\]
formada por los vectores escritos como columna, es invertible. Esto ya platicamos que está relacionado con que su determinante sea distinto de 0. Pero no en todas las situaciones tendremos tantos vectores como entradas y entonces tendremos que estudiar el sistema de ecuaciones lineales con otras técnicas, como reducción gaussiana.

Ejemplo. ¿Serán los vectores $(1,2,3,4,5)$, $(6,7,8,9,10)$ y $(11,12,13,14,15)$ de $\mathbb{R}^5$ linealmente independientes? Tal y como lo hemos hecho arriba, podemos preguntarnos si hay reales $a,b,c$ tales que $$a(1,2,3,4,5)+b(6,7,8,9,10)+c(11,12,13,14,15)=(0,0,0,0,0),$$ y que no sean todos ellos cero. Tras plantear el sistema como sistema de ecuaciones y luego en forma matricial, lo que se busca es ver si el sistema $\begin{pmatrix} 1 & 6 & 11 \\ 2 & 7 & 12 \\ 3 & 8 & 13 \\ 4 & 9 & 14 \\ 5 & 10 & 15 \end{pmatrix} \begin{pmatrix} a \\ b \\ c \end{pmatrix}=\begin{pmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{pmatrix} $ tiene alguna solución no trivial. Esto puede entenderse aplicando reducción gaussiana a $A$, que muestra que toda solución al sistema anterior es solución al sistema $\begin{pmatrix} 1 & 0 & -1\\0 & 1 & 2\\0 & 0 & 0\\0 & 0 & 0\\0 & 0 & 0\end{pmatrix} \begin{pmatrix} a \\ b \\ c \end{pmatrix}=\begin{pmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{pmatrix},$ lo cual nos lleva a que el sistema original es equivalente al sistema $$\left\{ \begin{array} \,a – c &= 0\\ b + 2c &= 0\end{array}.\right.$$

De aquí, podemos tomar a $c$ como cualquier valor, digamos $1$, de donde $a=1$ y $b=-2$ es solución. En resumen, hemos detectado que $$(1,2,3,4,5)-2(6,7,8,9,10)+(11,12,13,14,15)=(0,0,0,0,0),$$ que es una combinación lineal de los vectores donde no todos los coeficientes son cero. Por ello, no son linealmente intependientes.

Puedes intentar «imaginar» esto como que son vectores en $\mathbb{R}^5$ (un espacio de «dimensión $5$»), pero no generan dentro de él algo de dimensión $3$, sino algo de dimensión menor. Como $(1,2,3,4,5)$ y $(6,7,8,9,10)$ sí son linealmente independientes (¡demuéstralo!), entonces los tres vectores en realidad generan sólo un plano mediante sus combinaciones lineales.

$\square$

Bases

De manera similar a lo que observamos en la entrada anterior, hay ocasiones en las que un conjunto de vectores no tiene como espacio generado a todo $\mathbb{R}^n$. Por otra parte, hay ocasiones en las que el conjunto de vectores sí genera a todo $\mathbb{R}^n$, pero lo hace de manera «redundante», en el sentido de que, aunque su espacio generado sí es todo $\mathbb{R}^n$, podríamos quitar a algún vector del conjunto y el espacio generado sería el mismo. La siguiente definición se enfoca en los conjuntos en los que no pasa mal ninguna de estas cosas. Es decir, los vectores generan exactamente al espacio: cada vector se genera por una y sólo una combinación lineal de ellos.

Definición. Diremos que un conjunto de vectores $v_1, v_2, \ldots, v_k$ es base del esapacio vectorial $\mathbb{R}^n$ si el conjunto de vectores es linealmente independiente y el espacio generado por estos es exactamente $\mathbb{R}^n$.

Ejemplo. Al igual que en $\mathbb{R}^2$ y $\mathbb{R}^3$, la «base canónica» es el primer ejemplo que seguramente se nos viene a la mente. La base canónica en $\mathbb{R}^n$ consiste en los $n$ vectores $\mathrm{e}_1 = (1,0,0,\cdots,0)$, $\mathrm{e}_2 = (0,1,0,\cdots,0)$, $\mathrm{e}_3 = (0,0,1,\ldots,0)$, $\ldots$, $\mathrm{e}_n = (0,0,0,\cdots,1)$. Es claro que cualquier vector $u = (u_1,u_2,\cdots,u_n)$ es combinación lineal de $\mathrm{e}_1,\ldots,\mathrm{e}_n$ pues podemos expresarlo como
\begin{align*}
u
&= (u_1,u_2,\cdots,u_n) \\
&= (u_1,0,\cdots,0) + (0,u_2,\cdots,0) + \cdots (0,0,\cdots,u_n) \\
&= u_1(1,0,\cdots,0) + u_2(0,1,\cdots,0) + \cdots + u_n(0,0,\cdots,1) \\
&= u_1\mathrm{e}_1 + u_2\mathrm{e}_2 + \cdots + u_n\mathrm{e}_n.
\end{align*}
Además, los vectores $\mathrm{e}_1,\ldots,\mathrm{e}_n$ son linealmente independientes (¿puedes ver por qué?). De este modo, verificamos que la «base canónica» es, en efecto, una base.

$\triangle$

Ejemplo. Más arriba verificamos que los vectores $(1,5,1,-2)$, $(3,-3,0,-1)$, $(-2,0,4,1)$ y $(0,1,-1,0)$ son linealmente independientes. Además, vimos que la matriz formada por estos es invertible. De este modo, verificamos que estos vectores forman una base para $\mathbb{R}^4$.

$\triangle$

Más adelante…

A lo largo de esta unidad nos hemos enfocado en estudiar a vectores, matrices, ecuaciones lineales y espacios vectroriales. En las últimas entradas, vimos que hay ocho condiciones que se deben cumplir para que un conjunto de objetos matemáticos (junto con una operación de suma y una de producto escalar) sean considerados espacio vectorial. Todos los ejemplos de espacio vectorial que vimos son de la forma $\mathbb{R}^n$, sin embargo, puede surgir la pregunta, ¿existen espacios vectoriales que no sean de esta forma?

De hecho, si has estado prestando atención en la formalidad de los resultados, hay muchos resultados que han quedado pendientes:

  • ¿Por qué el determinante no depende de la fila o columna en la que se expanda?
  • Si tenemos matrices de $n\times n$, ¿por qué son invertibles si y sólo si el determinate es cero?
  • En matrices de $n\times n$, ¿por qué el determinante es multiplicativo?
  • ¿Cómo se formaliza el proceso de reducción gaussiana y para qué más sirve?
  • ¿Será que podemos tener muchos vectores linealmente independientes en $\mathbb{R}^n$? ¿Será posible tener un conjunto generador de menos de $n$ vectores para $\mathbb{R}^n$? ¿Por qué?

Estas dudas no se resuelven en el curso de Álgebra Superior 2, que sigue a este. Sin embargo, en el curso de Álgebra Lineal I sí se resuelven varias de estas dudas.

Además, podrás ver que hay otros tipos de objetos matemáticos distintos a las listas ordenadas y que también forman un espacio vectorial; algunos con los cuales ya hemos trabajado, como lo son las matrices, y otros que se comportan de manera muy poco usual, como son los espacios con dimensión infinita. Asimismo, con las herramientas que hemos desarrollado hasta ahora, podremos aprender nuevos conceptos como transformaciones lineales, eigenvectores y eigenvalores; estos nos permitirán comprender de manera más íntima los espacios vectoriales, y podremos relacionarlos unos con otros.

Tarea moral

  1. Verifica lo siguiente:
    • $(1,1,1,1)$, $(2,2,2,2)$, $(1,1,2,2)$, $(2,2,1,1)$ no es un conjunto linealmente independiente de $\mathbb{R}^4$.
    • $(1,2,3,4)$, $(2,3,4,1)$, $(3,4,1,2)$, $(4,1,2,3)$ es un conjunto generador de $\mathbb{R}^4$.
    • $(1,1,1,1,1),(1,1,1,1,0),(1,1,1,0,0),(1,1,0,0,0),(1,0,0,0,0)$ es una base de $\mathbb{R}^5$.
  2. Demuestra las siguientes dos cosas:
    • Sea $S$ un conjunto generador de $\mathbb{R}^n$ y $T\supseteq S$. Entonces $T$ es conjunto generador de $\mathbb{R}^n$.
    • Sea $T$ un conjunto linealmente independiente de $\mathbb{R}^n$ y $S\subseteq T$. Entonces $S$ es un conjunto linealmente independiente de $\mathbb{R}^n$.
  3. Sean $v_1,v_2,v_3,\ldots,v_k$ vectores linealmente independientes de $\mathbb{R}^n$. Demuestra que $v_1, v_1+v_2, v_1+v_2+v_3,\ldots,v_1+v_2+v_3+\ldots+v_k$ son también vectores linealmente independientes de $\mathbb{R}^n$. ¿Es esto un si y sólo si?
  4. En vista de lo que hemos platicado para matrices de $2\times 2$, $3\times 3$, $\mathbb{R}^2$ y $\mathbb{R}^3$, ¿cómo definirías el producto matriz-vector $AX$ donde $A$ es una matriz de $m\times n$ y $X$ un vector en $\mathbb{R}^n$?
  5. Demuestra que la definición de base tal y como está en la entrada en efecto permite no sólo escribir a cada vector $v$ del espacio como combinación lineal de los elementos de una base $v_1,\ldots,v_n$, sino que también implica que dicha expresión será única.

Entradas relacionadas

Álgebra Superior I: Reducción de Gauss-Jordan

Por Eduardo García Caballero

Deja un comentario

Introducción

En la entrada anterior vimos que los sistemas de ecuaciones se encuentran íntimamente relacionados con los vectores y las matrices. Teniendo esto en cuenta, en esta entrada abordaremos una estrategia que nos permitirá encontrar soluciones de los sistemas de ecuaciones lineales.

Operaciones elementales por filas

Antes de pasar a describir el algoritmo con el cual podremos resolver un sistema de ecuaciones lineales, deberemos definir algunas operaciones y conceptos que nos ayudaran a efectuarlo. Empecemos con una lista de operaciones que se pueden aplicar a las matrices, las cuales son con conocidas como operaciones elementales por filas.

Para esto, consideremos una matriz
\[
A=
\begin{pmatrix}
5 & \pi & 3 \\
\sqrt{2} & -1 & 2 \\
-1/3 & 4 & 0 \\
9 & -3 & 2/3
\end{pmatrix},
\]
y veamos cómo la afecta cada una de estas operaciones.

La primera de estas operaciones es el reescalamiento. Esta operación consiste en seleccionar una fila de una matriz, y multiplicar cada una de las entradas de esta fila por un mismo número real distinto de cero. Por ejemplo, si reescalamos la tercera fila de $A$ por el número $-3$, obtendremos la matriz
\[
\begin{pmatrix}
5 & \pi & 3 \\
\sqrt{2} & -1 & 2 \\
(-3)(-1/3) & (-3)(4) & (-3)(0) \\
9 & -3 & 2/3
\end{pmatrix}
=
\begin{pmatrix}
5 & \pi & 3 \\
\sqrt{2} & -1 & 2 \\
1& -12 & 0 \\
9 & -3 & 2/3
\end{pmatrix}.
\]

Otra operación que podemos aplicar a las matrices es la trasposición, la cual consiste en intercambiar el contenido de dos filas distintas. Por ejemplo, si transponemos las filas 2 y 4 de $A$, el resultado será la matriz
\[
\begin{pmatrix}
5 & \pi & 3 \\
9 & -3 & 2/3 \\
-1/3 & 4 & 0 \\
\sqrt{2} & -1 & 2
\end{pmatrix}.
\]

La última de las operaciones que nos interesa es la transvección. Esta consiste en sumar el múltiplo de una fila (el resultado de multiplicar cada entrada de una fila por un mismo escalar) a otra fila (la suma se realiza entrada por entrada). Por ejemplo, si en $A$ realizamos la transvección que corresponde a “sumar 3/2 de la cuarta fila a la primera fila”, obtendremos la matriz
\[
\begin{pmatrix}
5 + (3/2)(9) & \pi+(3/2)(-3) & 3+(3/2)(2/3) \\
\sqrt{2} & -1 & 2 \\
-1/3 & 4 & 0 \\
9 & -3 & 2/3
\end{pmatrix}
=
\begin{pmatrix}
37/2 & -9/2+\pi & 4 \\
\sqrt{2} & -1 & 2 \\
-1/3 & 4 & 0 \\
9 & -3 & 2/3
\end{pmatrix}.
\]

Si recuerdas, todos los sistemas de ecuaciones se pueden escribir como $Ax=b$. Las operaciones elementales son muy importantes por las siguientes dos razones:

  • Si aplicamos la misma operación elemental a $A$ y $b$ para obtener la matriz $A’$ y el vector $b’$, entonces $Ax=b$ y $A’x=b’$ tienen exactamente el mismo conjunto solución. Decimos que «las operaciones elementales no cambian las soluciones del sistema».
  • Usando operaciones elementales se puede llevar el sistema $Ax=b$ a un sistema mucho más sencillo $A_{red}x=b_{red}$ (que discutiremos más abajo). Entonces «las operaciones ayudan a simplificar un sistema de ecuaciones».

Juntando ambas observaciones, con operaciones elementales podemos llevar cualquier sistema de ecuaciones a uno mucho más sencillo y con el mismo conjunto solución.

Puedes intentar convencerte de la primera afirmación pensando en lo siguiente. En un reescalamiento de filas corresponde a multiplicar por una constante no nula ambos lados de una ecuación; la transposición corresponde a cambiar el orden en el que aparecen dos ecuaciones diferentes; mientras que la transvección corresponde a sumar un múltiplo de una ecuación a otra ecuación, y el sistema tiene las mismas soluciones pues, si un conjunto de valores es solución para dos ecuaciones, entonces es solución para cualquier combinación lineal de estas. En un curso de Álgebra Lineal I puedes encontrar las justificaciones con mucho más detalle.

En las siguientes secciones hablamos un poco más de la segunda afirmación.

Forma escalonada y escalonada reducida para una matriz

Además de las operaciones elementales por filas, es importante definir algunos conceptos.

Comencemos con el concepto de pivote: diremos que una entrada de una matriz es un pivote si es el primer elemento distinto de cero en una fila.

Diremos que una matriz se encuentra en forma escalonada si se cumple: 1. Todas las filas nulas se encuentran hasta abajo; 2. Todos los pivotes de filas no-nulas tienen valor 1; 3. El pivote de cada fila se encuentra la derecha del pivote de una fila superior. Es fácil identificar las matrices en forma escalonada porque parecen “estar en escalerita”. Por ejemplo, la matriz
\[
\begin{pmatrix}
1 & 9 & 1 & 1 \\
0 & 1 & 2 & 3 \\
0 & 0 & 1 & 1
\end{pmatrix}
\]
se encuentra en forma escalonada, mientras que las matrices
\[
\begin{pmatrix}
1 & 0 & 2 & 4 \\
0 & 0 & 9 & 2 \\
0 & 3 & 0 & 0
\end{pmatrix}
\qquad
\text{y}
\qquad
\begin{pmatrix}
0 & 6 & 8 & -5 \\
0 & 0 & 0 & 0 \\
0 & 0 & 9 & 2
\end{pmatrix}
\]
no lo están. ¿Puedes justificar por qué?

Por su parte, diremos que una matriz se encuentra en forma escalonada reducida si está en forma escalonada y, además, si hay un pivote en alguna fila, todas las entradas que no sean pivote en la misma columna del pivote son iguales a $0$ (Ojo. Siempre hablamos de pivotes de renglones).

Por ejemplo, la matriz
\[
\begin{pmatrix}
1 & 0 & -1 & 0 \\
0 & 1 & 3 & 0 \\
0 & 0 & 0 & 1
\end{pmatrix}
\]
está en forma escalonada reducida.

Como recordarás de la entrada anterior, un sistema de ecuaciones lineales
\[
\begin{cases}
a_{11}x_1 + a_{12}x_2 + \cdots + a_{1n}x_n & = b_1 \\
a_{21}x_1 + a_{22}x_2 + \cdots + a_{2n}x_n & = b_2 \\
& \vdotswithin{\mspace{15mu}} \\
a_{m1}x_1 + a_{m2}x_2 + \cdots + a_{mn}x_n &= b_m
\end{cases}
\]
se puede codificar como
\[
\begin{pmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m1} & a_{m2} & \cdots & a_{mn}
\end{pmatrix}
\begin{pmatrix}
x_1 \\
x_2 \\
\vdots \\
x_n
\end{pmatrix}
=
\begin{pmatrix}
b_1 \\
b_2 \\
\vdots \\
b_m
\end{pmatrix}.
\]

Como podemos cambiar el nombre de las variables, pero el vector de soluciones sigue siendo el mismo, es común codificar el sistema como una única matriz aumentada
\[
\left(
\begin{matrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m1} & a_{m2} & \cdots & a_{mn}
\end{matrix}
\
\middle|
\
\begin{matrix}
b_1 \\
b_2 \\
\vdots \\
b_m
\end{matrix}
\right).
\]

Aquí pusimos una línea vertical, pero sólo es por ayuda visual. Esa matriz la puedes tratar como cualquier matriz que hemos platicado.

Teniendo esto en cuenta, las matrices en forma escalonada reducida nos son de gran utilidad al resolver sistemas de ecuaciones lineales. Por ejemplo, consideremos el sistema
\[
\begin{cases}
x + 3y + 2w &= 8 \\
z + w &= 9,
\end{cases}
\]
el cual tiene como matriz aumentada a
\[
\left(
\begin{matrix}
1 & 3 & 0 & 2 \\
0 & 0 & 1 & 1
\end{matrix}
\
\middle|
\
\begin{matrix}
8 \\
9
\end{matrix}
\right),
\]
la cual se encuentra en forma escalonada.

Gracias a que la matriz está en forma escalonada, podemos elegir en orden inverso $w$, $z$, $y$, $x$ a las variables libres y pivote como en la entrada anterior. En este caso, podemos elegir como queramos el valor de $w$ ($w$ es variable libre). Usando la segunda ecuación, podemos despejar $z$ en términos de $w$ ($z$ es variable pivote). Estos dos valores los sustituimos en la primera ecuación y notamos que $y$ puede ser lo que queramos ($y$ es variable libre). Finalmente, $x$ queda totalmente determinado por las demás variables ($x$ es pivote). Las variables pivote justo corresponden a columnas de la matriz que tengan pivote de alguna fila.

La ventaja de la forma escalonada es que podremos ir obteniendo fácilmente el valor de cada variable “de abajo hacia arriba”. En el caso de un sistema cuya matriz se encuentre en forma escalonada reducida, será aún más sencillo pues ya no tendremos que sustituir valores y obtenemos el despeje directamente.

Teorema de reducción de Gauss-Jordan

El siguiente teorema relaciona las operaciones elementales por filas con la forma escalonada reducida de una matriz.

Teorema (de reducción de Gauss-Jordan o reducción gaussiana). Cualquier matriz con entradas reales se puede a una forma escalonada reducida aplicando una cantidad finita de pasos.

A continuación presentamos un algoritmo con el cual podemos pasar de una matriz arbitraria a una matriz en su forma escalonada reducida. Para hacer más sencilla su aplicación, nos enfocaremos en comprender la estrategia que sigue el algoritmo. La descripción formal del algoritmo y demostración de que en efecto funciona como esperamos es un tema que abordarás en el curso de Álgebra Lineal I (puedes echarle un ojo a esta entrada).

Primeramente, describiremos los pasos del algoritmo, al que se le conoce como reducción de Gauss-Jordan o reducción gaussiana.

Estrategia: Iremos arreglando la matriz de izquierda a derecha. Para ello, haremos los siguientes pasos repetidamente.

  1. Buscamos la primera columna de la matriz (de izquierda a derecha) que no tenga puros ceros.
  2. Una vez encontrada dicha columna, buscamos la primera entrada (de arriba hacia abajo) que no sea cero.
  3. Pasamos la fila que contiene a dicha entrada hasta arriba mediante la operación de transposición.
  4. Multiplicamos cada entrada de la fila que acabamos de mover hasta arriba por el inverso multiplicativo de su primera entrada (aquí usamos la operación de reescalamiento). La primera entrada de esta fila ahora será 1.
  5. Mediante la operación de transvección, sustraemos múltiplos de la primera fila al resto de renglones de la matriz, de modo que el resto de los valores en la columna correspondiente a la primera entrada de la fila en la que estamos trabajando pasen a ser 0 (como puedes observar, la entrada primera entrada no-nula de la fila en la que estamos trabajando ahora será un pivote).
  6. Ignorando la primera fila, buscamos la primera columna (de izquierda a derecha) que no tenga puros ceros.
  7. Repetimos los pasos anteriores (2 a 6), pero ahora, en vez de mover la fila con la que estamos trabajando “hasta arriba”, la moveremos inmediatamente después de la última fila con la que trabajamos.
  8. Hacemos esto hasta haber arreglado todas las columnas.

Ejemplo de reducción de Gauss-Jordan

Ahora, como ejemplo, veamos cómo podemos implementar este algoritmo en la matriz
\[
\begin{pmatrix}
0 & 1 & 2 & 3 & 4 \\
-1 & 0 & 1 & 2 & 3 \\
3 & 1 & -1 & 0 & 2 \\
0 & 1 & 1 & 1 & 1
\end{pmatrix},
\]
la cual, si la consideramos como la matriz aumentada
\[
\left(
\begin{matrix}
0 & 1 & 2 & 3 \\
-1 & 0 & 1 & 2 \\
3 & 1 & -1 & 0 \\
0 & 1 & 1 & 1
\end{matrix}
\
\middle|
\
\begin{matrix}
4 \\
3 \\
2 \\
1
\end{matrix}
\right),
\]
corresponde al sistema de ecuaciones
\[
\begin{cases}
y + 2z + 3w &= 4 \\
-x + z + 2w &= 2 \\
3x + y -z &= 0 \\
y + z + w &= 1.
\end{cases}
\]

Buscamos la primera la primera columna no nula, la cual resulta ser la primera columna de la matriz. En esta columna, vemos que la segunda entrada es la primera entrada distinta de cero. Entonces, mediante trasposicón, intercambiamos las filas 1 y 2 (“movemos la segunda columna hasta arriba”):
\[
\begin{pmatrix}
-1 & 0 & 1 & 2 & 3 \\
0 & 1 & 2 & 3& 4 \\
3 & 1 & -1 & 0 & 2 \\
0 & 1 & 1 & 1 & 1
\end{pmatrix}.
\]

Ahora, nos fijamos en la primera entrada no nula de la primera fila, que es $-1$, y reescalamos la fila por su inverso multiplicativo, que es $-1$:
\[
\begin{pmatrix}
(-1)(-1) & (-1)(0) & (-1)(1) & (-1)(2) & (-1)(3) \\
0 & 1 & 2 & 3 & 4 \\
3 & 1 & -1 & 0 & 2 \\
0 & 1 & 1 & 1 & 1
\end{pmatrix}
=
\begin{pmatrix}
1 & 0 & -1 & -2 & -3 \\
0 & 1 & 2 & 3 & 4 \\
3 & 1 & -1 & 0 & 2 \\
0 & 1 & 1 & 1 & 1
\end{pmatrix}.
\]

Ahora, observamos el valor de la primera entrada de la tercera fila, el cual es $3$. Entonces, mediante transvección, sumamos $-3$ veces la fila 1 a la fila 3:
\[
\begin{pmatrix}
1 & 0 & -1 & -2 & -3 \\
0 & 1 & 2 & 3 & 4 \\
3+(-3)(1) & 1+(-3)(0) & -1+(-3)(-1) & 0+(-3)(-2) & 2+(-3)(-3) \\
0 & 1 & 1 & 1 & 1
\end{pmatrix}
=
\begin{pmatrix}
1 & 0 & -1 & -2 & -3 \\
0 & 1 & 2 & 3 & 4 \\
0 & 1 & 2 & 6 & 11 \\
0 & 1 & 1 & 1 & 1
\end{pmatrix},
\]
y realizamos lo mismo, pero ahora considerando la fila 4.
\[
\begin{pmatrix}
1 & 0 & -1 & -2 & -3 \\
0 & 1 & 2 & 3 & 4 \\
0 & 1 & 2 & 6 & 11 \\
0+(0)(1) & 1+(0)(0) & 1+(0)(-1) & 1+(0)(-2) & 1+(0)(-3)
\end{pmatrix}
=
\begin{pmatrix}
1 & 0 & -1 & -2 & -3 \\
0 & 1 & 2 & 3 & 4 \\
0 & 1 & 2 & 6 & 11 \\
0 & 1 & 1 & 1 & 1
\end{pmatrix}
\]
Como puedes observar, ninguna de las transvecciones influye en la otra, de manera que las podemos enlistar en un único paso. Además, al hacer una transvección con escalar $0$ no cambia nada de la fila, así que estas no se necesita hacerlas.

Ahora, ignorando la última fila con la que trabajamos (que es la primera), buscamos la primera columna no-nula, que en este caso será la segunda, posteriormente buscamos el primer elemento no nulo de la columna, el cual se encuentra en la segunda fila, y la “movemos enseguida de la última fila con la que trabajamos” (en este caso no tendríamos que realizar ninguna transposición, o bien, la transposición sería la de la segunda fila consigo misma, ya que ya se encuentra en seguida de la última fila con la que trabajamos). Después, reescalamos por el inverso multiplicativo del primer elemento no nulo de la fila, que es $1$:
\[
\begin{pmatrix}
1 & 0 & -1 & -2 & -3 \\
(1)(0) & (1)(1) & (1)(2) & (1)(3) & (1)(4) \\
0 & 1 & 2 & 6 & 11 \\
0 & 1 & 1 & 1 & 1
\end{pmatrix}
=
\begin{pmatrix}
1 & 0 & -1 & -2 & -3 \\
0 & 1 & 2 & 3 & 4 \\
0 & 1 & 2 & 6 & 11 \\
0 & 1 & 1 & 1 & 1
\end{pmatrix}
\]
(observa que reescalar por $1$ deja todas las entradas iguales) y posteriormente realizamos las transvecciones necesarias para que el resto de entradas de la segunda columna sean cero.
\[
\begin{pmatrix}
1 & 0+(0)(1) & -1+(0)(2) & -2+(0)(3) & -3+(0)(4) \\
0 & 1 & 2 & 3 & 4 \\
0 & 1+(-1)(1) & 2+(-1)(2) & 6+(-1)(3) & 11+(-1)(4) \\
0 & 1+(-1)(1) & 1+(-1)(2) & 1+(-1)(3) & 1+(-1)(4)
\end{pmatrix}
=
\begin{pmatrix}
1 & 0 & -1 & -2 & -3 \\
0 & 1 & 2 & 3 & 4 \\
0 & 0 & 0 & 3 & 7 \\
0 & 0 & -1 & -2 & -3
\end{pmatrix}
\]

De manera similar, ignorando ahora las primeras dos filas, buscamos la primera columna no-nula, la cual corresponde ahora a la tercera, y buscamos el primer elemento no-nulo de esta columna, el cual se encuentra en la cuarta fila. Entonces, transponemos las filas 3 y 4 para que el primer elemento no-nulo quede inmediatamente después de la última fila con la que trabajamos:
\[
\begin{pmatrix}
1 & 0 & -1 & -2 & -3 \\
0 & 1 & 2 & 3 & 4 \\
0 & 0 & -1 & -2 & -3 \\
0 & 0 & 0 & 3 & 7
\end{pmatrix}.
\]

Seguidamente, reescalamos la tercera fila,
\[
\begin{pmatrix}
1 & 0 & -1 & -2 & -3 \\
0 & 1 & 2 & 3 & 4 \\
(-1)(0) & (-1)(0) & (-1)(-1) & (-1)(-2) & (-1)(-3) \\
0 & 0 & 0 & 3 & 7
\end{pmatrix}
=
\begin{pmatrix}
1 & 0 & -1 & -2 & -3 \\
0 & 1 & 2 & 3 & 4 \\
0 & 0 & 1 & 2 & 3 \\
0 & 0 & 0 & 3 & 7
\end{pmatrix}
\]
y relizamos las transvecciones necesarias:
\[
\begin{pmatrix}
1+(1)(0) & 0+(1)(0) & -1+(1)(1) & -2+(1)(2) & -3+(1)(3) \\
0+(-2)(0) & 1+(-2)(0) & 2+(-2)(1) & 3+(-2)(2) & 4+(-2)(3) \\
0 & 0 & 1 & 2 & 3 \\
0 & 0 & 0 & 3 & 7
\end{pmatrix}
=
\begin{pmatrix}
1 & 0 & 0 & 0 & 0 \\
0 & 1 & 0 & -1 & -2 \\
0 & 0 & 1 & 2 & 3 \\
0 & 0 & 0 & 3 & 7
\end{pmatrix}.
\]

Finalmente, como nuestra última columna no cero es la cuarta y la primera fila no cero (ignorando las filas que ya tienen pivote) tiene un $3$, reescalamos de la siguiente manera:
\[
\begin{pmatrix}
1 & 0 & 0 & 0 & 0 \\
0 & 1 & 0 & -1 & -2 \\
0 & 0 & 1 & 2 & 3 \\
(1/3)(0) & (1/3)(0) & (1/3)(0) & (1/3)(3) & (1/3)(7)
\end{pmatrix}
=
\begin{pmatrix}
1 & 0 & 0 & 0 & 0 \\
0 & 1 & 0 & -1 & -2 \\
0 & 0 & 1 & 2 & 3 \\
0 & 0 & 0 & 1 & 7/3
\end{pmatrix},
\]

Y hacemos las transvecciones necesarias:
\[
\begin{pmatrix}
1 & 0 & 0 & 0 & 0 \\
0+(1)(0) & 1+(1)(0) & 0+(1)(0) & -1+(1)(1) & -2+(1)(7/3) \\
0+(-2)(0) & 0+(-2)(0) & 1+(-2)(0) & 2+(-2)(1) & 3+(-2)(7/3) \\
0 & 0 & 0 & 1 & 7/3
\end{pmatrix}
=
\begin{pmatrix}
1 & 0 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 & 1/3 \\
0 & 0 & 1 & 0 & -5/3 \\
0 & 0 & 0 & 1 & 7/3
\end{pmatrix}.
\]

Notemos que si consideramos esta matriz como la matriz aumentada
\[
\left(
\begin{matrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{matrix}
\
\middle|
\
\begin{matrix}
0 \\
1/3 \\
-5/3 \\
7/3
\end{matrix}
\right),
\]
este corresponde al sistema
\[
\begin{cases}
x = 0 \\
y = 1/3 \\
z = -5/3 \\
w = 7/3,
\end{cases}
\]
del cual sabemos inmediatamente su solución. Como mencionamos anteriormente, los sistemas de ecuaciones asociados a la matriz original y la matriz escalonada reducida resultante de aplicar operaciones elementales por filas, consideradas como matrices aumentadas, tienen las mismas soluciones. Entonces, ¡este último sistema es la solución para nuestro sistema de ecuaciones original!

Como podemos ver, los sistemas de ecuaciones asociados a una matriz en su forma escalonada reducida son fáciles de resolver por que vamos escogiendo valores arbitrarios para las variables en posición que no es pivote, mientras que podemos obtener el valor de las variables que son pivote mediante despejes sencillos.

Recuerda que este algoritmo funciona para cualquier matriz con entradas reales. ¿Podrías proponer otro sistema de ecuaciones e implementar la misma estrategia para resolverlo?

Más adelante…

Ahora vimos una estrategia para resolver sistemas de ecuaciones lineales de distintos tamaños. En las siguientes entradas conoceremos más propiedades sobre las matrices. Estas nuevas propiedades también juegan un rol fundamental en poder determinar de manera más rápida cuándo un sistema de ecuaciones lineales tiene solución, y tener otras alternativas para resolverlo bajo ciertas condiciones.

Tarea moral

  1. Aplica reducción gaussiana a las siguientes matrices:
    $$\begin{pmatrix} 5 & 2 \\ 13 & 5 \end{pmatrix},\quad \begin{pmatrix} 1 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 1 \end{pmatrix}.$$
  2. Resuelve el siguiente sistema de ecuaciones llevándolo a forma escalonada reducida, y luego aplicando a técnica de variables libres y pivote:
    $$\begin{cases} a + b + c + d + e &= -5\\2a+2b-3c-3d+e&=5 \\ a – b + c – d + e &= 0. \end{cases}$$
  3. Sea $I$ la matriz identidad de $n\times n$ y $A$ otra matriz de $n\times n$. Sea $E$ la matriz obtenida de aplicar una transvección a $I$. Sea $B$ la matriz de aplicar esa misma transvección a $A$. Demuestra que $EA=B$.
  4. Demuestra que una matriz $A$ de $2\times 2$ es invertible si y sólo si al aplicar reducción de Gauss-Jordan al final se obtiene la matriz identidad $I$. ¿Puedes hacerlo para matrices de $3\times 3$? ¿De $n\times n$?
  5. Sea $A$ una matriz de $2\times 2$ invertible. A $A$ le «pegamos» una identidad del mismo tamaño a la derecha para llegar a $(A|I)$, por ejemplo $\begin{pmatrix} a & b \\ c & d \end{pmatrix}$ se convertiría en $\begin{pmatrix} a & b & 1 & 0 \\ c & d & 0 & 1 \end{pmatrix}$. Muestra que si aplicamos reducción de Gauss-Jordan a $(A|I)$, se llega a $(I|A^{-1})$. Intenta extender tu demostración a matrices de $3\times 3$ ó $n\times n$.

Entradas relacionadas

Álgebra Superior I: Sistemas de ecuaciones lineales

Por Eduardo García Caballero

1 respuesta

Introducción

Una de las aplicaciones más importantes de los vectores y matrices tiene que ver con un tema que conociste desde la secundaria y preparatoria: los sistemas de ecuaciones.

Más específicamente, los vectores y matrices nos serán de gran utilidad para resolver sistemas de ecuaciones lineales, determinar cuándo un sistema sí tiene soluciones, y cuáles son todas sus soluciones.

Pero antes, repasemos un poco los conceptos de sistemas de ecuaciones lineales.

Sistemas de ecuaciones lineales

Recordemos que una ecuación es una expresión en la que hay variables o valores que no conocemos. En el caso de una ecuación lineal, se trata de ecuaciones en las que todas sus variables se encuentran elevadas a la primera potencia y acompañadas únicamente por coeficientes constantes. Por ejemplo, podemos ver que las expresiones
\[
2x + 9y – z = 3,
\qquad
4w + 3000a = y + \tfrac{1}{2}x
\]
son ecuaciones lineales, mientras que las expresiones
\[
ax^2 + bx + c = 0,
\qquad
2xz = 9y
\]
no lo son, pues contienen al menos una variable elevada a exponentes distintos de $1$, o bien hay variables multiplicándose entre sí.

De manera más formal, una ecuación de lineal es una ecuación que se puede escribir de la forma
\[
a_1x_2 + a_2x_2 + \cdots + a_nx_n = b,
\]
donde $x_1, \ldots, x_n$ son variables y $a_1, \ldots, a_n, b$ son coeficientes, todos del mismo tipo (en este curso trabajaremos con coeficientes reales, pero en otros cursos podrás encontrar coeficientes de otros tipos, como son números enteros, racionales, y complejos, entre otros).

Por su parte, un sistema de ecuaciones lineales es un conjunto de ecuaciones lineales. Por ejemplo, los siguientes son sistemas de ecuaciones lineales:
\[
\begin{cases}
2x -\tfrac{3}{2}y + 8z = 1 \\
9z + 2w + 5y = 3,
\end{cases}
\qquad
\begin{cases}
2 + 9a = 46b -5c \\
2d + 8x = \sqrt{3} \\
x + y + z = a + b + c \\
x = -y
\end{cases}
\]
Bajo esta definición, una única ecuación se puede considerar un sistema de ecuaciones lineales (con una ecuación).

Notemos que no es necesario que todas las ecuaciones compartan variables, sin embargo, generalmente esto sí sucederá. De hecho, podemos pensar que todas las variables aparecen en todas las ecuaciones. En caso de que esto no suceda, podemos considerar que las variables que no aparecen en una ecuación tienen coeficiente cero. Además, siempre podemos reordenar las variables en las ecuaciones para que en todas ellas aparezcan en el mimo orden. Por ejemplo, a continuación el sistema de ecuaciones a la izquierda lo podemos escribir como el de la derecha, sin alterarlo.

\[
\begin{cases}
2x -\tfrac{3}{2}z + 8y = 11 \\
9z + 2w + 5k = -3,
\end{cases}
\qquad
\begin{cases}
0k+0w+2x + 8y – \tfrac{3}{2}z = 11 \\
5k+2w+0x+0y+9z = -3.
\end{cases}
\]

¿Qué quiere decir resolver un sistema de ecuaciones lineales?

Como recordarás, encontrar una solución de una ecuación corresponde a encontrar valores que, al sustituirlos en las variables, hagan que la expresión sea verdadera. Por ejemplo, si tenemos la ecuación $2x-3y=0$, una solución está dada por $x=3$ y $y=2$, ya que al sustituir en efecto tenemos $(2)(3)-(3)(2)=0$. En ocasiones, una ecuación puede tener más de una solución. Por ejemplo, en este caso otra posible solución es $x=6$ y $y=4$, ya que al sustituir en efecto tenemos $(2)(6)-(3)(4)=0$. Para esta ecuación hemos encontrado entonces dos posibles soluciones. Pero aún no la hemos resuelto. Como veremos un poco más abajo, para resolverla tenemos que alcanzar una meta más grande.

Para el caso de sistemas de ecuaciones lineales, encontrar una solución consiste en dar una asignación de valores a las variables que hagan que todas las ecuaciones sean ciertas simultáneamente. Por ejemplo, podemos verificar que los valores
\[
x = 3 \quad y =5 \quad z = -2
\]
hacen que cada una de las ecuaciones en el sistema
\[
\begin{cases}
x + 2y – z = 15 \\
4x – y + z = 5
\end{cases}
\]
se cumplan simultáneamente. Otra posible solución está dada por la asignación
\[
x = 1 \quad y =15 \quad z = 16.
\]

Cuando hablamos de resolver una ecuación o un sistema de ecuaciones no nos bastará encontrar unas cuantas soluciones que funcionen. Queremos encontrar todas las posibles soluciones.

Como ejemplo más sencillo, tratemos de encontrar todas las soluciones del sigueinte sistema con una única ecuación
\[
\begin{cases}
2x + 3y – z = 5.
\end{cases}
\]

Si despejamos $x$ en la ecuación, obtenemos
\[
x = \frac{-3y+z+5}{2}.
\]
Esto nos indica que podemos escoger valores arbitrarios de $y$ y $z$, y el valor de $x$ quedará determinado por estos valores.

Entonces, la solución de la ecuación son todas las $(x,y,z)$ tales que $x = \frac{-3y+z+5}{2}$; es decir, todas las soluciones del sistema de ecuaciones son de la forma
\[
\left( \frac{-3y+z+5}{2}, y, z \right).
\]

Otra manera de decir esto es que el conjunto de soluciones para el sistema de ecuaciones es el siguiente:

$$S:=\left\{\left( \frac{-3y+z+5}{2}, y, z \right):y,z\in \mathbb{R}\right\}.$$

Esto ahora sí resuelve el sistema, pues hemos encontrado una descripción para todas las posibles soluciones del sistema. Si tomas los valores que quieras para $y$ y $z$, podrás dar una solución. Por ejemplo, al tomar $y=1,z=2$ obtenemos la solución $(2,1,2)$, la cual puedes verificar que es una solución al sistema de ecuaciones de una ecuación con el que comenzamos. Toda posible solución está en $S$. Como $y$ y $z$ pueden valer lo que sea, las llamamos variables libres. A $x$, que queda totalmente determinada una vez fijas las variables libres, la llamamos variable pivote.

¿Qué sucede si tenemos más ecuaciones? Tratemos de encontrar todas las soluciones para el sistema de ecuaciones siguiente
\[
\begin{cases}
y+z =1 \\
3x+2y+5z&=1.
\end{cases}
\]

Podemos intentar lo mismo que arriba y fijar algún valor e intentar poner al resto en términos de ese. Pero hay que ser cuidadosos. Por ejemplo, al fijar el valor de $x$, no podremos despejar a $y$ (ni a $z$) en términos únicamente de $x$. Sin embargo, fijamos el valor de $z$, sí podemos determinar todo completamente.

Al fijar $z$, entonces $y$ queda determinado como $y = -z + 1$. Sustituyendo este valor de $y$ en la segunda ecuación, obtendremos $3x + 2(-z+1) + 5z = 1$, que equivale a $3x +3z = -1$, de donde tenemos que $x = -z -1/3 $. Entonces, podemos pensar a $z$ como la variable libre y como $y$ y $x$ dependen completamente de $z$, las pensamos como variables pivote. La descripción de las soluciones quedaría entonces como

$$R=\{(-z-1/3,-z+1,z):z\in \mathbb{R}\}.$$

Aunque ahora hemos tenido éxito con describir totalmente las soluciones de dos sistemas de ecuaciones y en ambos casos hemos tenido una infinidad de soluciones, lo cierto es que existen sistemas de ecuaciones sin solución. Por ejemplo, consideremos el sistema
\[
\begin{cases}
12x + 9y = 7 \\
4x + 3y = 8.
\end{cases}
\]
Podemos ver que cada una de las ecuaciones, de manera individual, tienen soluciones, y hasta podríamos encontrar todas las posibles soluciones (¿puedes dar un par de ejemplos de cada una?). Sin embargo, no existen valores de $x$ y $y$ que resuelvan ambas ecuaciones al mismo tiempo. Esto lo podemos observar porque, si multiplicamos la segunda ecuación por $3$, obtendremos el sistema
\[
\begin{cases}
12x + 9y = 7 \\
12x + 9y = 24.
\end{cases}
\]
Si hubiera alguna solución, podríamos igualar ambas ecuaciones y llegar a que $7=24$, una contradicción.

Interpretación geométrica

El primer conjunto solución que encontramos arriba se puede reescribir en términos de cada variable $y$ y $z$ usando la suma y producto escalar que estudiamos en entradas anteriores de la siguiente manera:

\begin{align*}
S&=\left\{\left( \frac{-3y+z+5}{2}, y, z \right):y,z\in \mathbb{R}\right\}\\
&=\left\{y(-3/2,1,0) + z(1/2,0,1) + (5/2,0,0):y,z\in \mathbb{R}\right\}.
\end{align*}

Posiblemente hayas visto expresiones en algún curso de geometría analítica. Lo anterior es un plano en $\mathbb{R}^3$ que pasa por el punto $(5/2,0,0)$ y generado a partir de ese punto por los vectores $(-3/2,1,0)$ y $(1/2,0,1)$.

Del mismo modo, en el segundo ejemplo que vimos arriba el sistema de ecuaciones puede reescribirse como:

\begin{align*}
R&=\{(-z-1/3,-z+1,z):z\in \mathbb{R}\}\\
&=\{(-1/3,1,0)+z(-1,-1,1):z\in \mathbb{R}\},
\end{align*}

que posiblemente identifiques como la recta en $\mathbb{R}^3$ que parte del punto $(-1/3,1,0)$ y tiene dirección $(-1,-1,1)$.

Forma matricial de un sistema de ecuaciones

Como vimos en una entrada previa, dos vectores del mismo tamaño son iguales si y sólo si sus respectivas entradas son iguales. Una consecuencia de esta definición es que el sistema de ecuaciones
\[
\begin{cases}
a_{11}x_1 + a_{12}x_2 + \cdots + a_{1n}x_n & = b_1 \\
a_{21}x_1 + a_{22}x_2 + \cdots + a_{2n}x_n & = b_2 \\
& \vdotswithin{\mspace{15mu}} \\
a_{m1}x_1 + a_{m2}x_2 + \cdots + a_{mn}x_n &= b_m
\end{cases}
\]
se cumple si y sólo si
\[
\begin{pmatrix}
a_{11}x_1 + a_{12}x_2 + \cdots a_{1n}x_n \\
a_{21}x_1 + a_{22}x_2 + \cdots a_{2n}x_n \\
\vdots \\
a_{m1}x_1 + a_{m2}x_2 + \cdots a_{mn}x_n
\end{pmatrix}
=
\begin{pmatrix}
b_1 \\
b_2 \\
\vdots \\
b_m
\end{pmatrix}.
\]

Más aún, observemos que el lado izquierdo de esta igualdad lo podemos reescribir como un producto de matriz con vector de la siguiente manera
\[
\begin{pmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m1} & a_{m2} & \cdots & a_{mn}
\end{pmatrix}
\begin{pmatrix}
x_1 \\
x_2 \\
\vdots \\
x_n
\end{pmatrix}
=
\begin{pmatrix}
b_1 \\
b_2 \\
\vdots \\
b_m
\end{pmatrix},
\]
lo cual podemos denotar como
\[
Ax = b.
\]

Entonces, podemos decir que nuestro sistema tiene solución si existe un vector $x = \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix}$ tal que $Ax = b$, donde
\[
A
=
\begin{pmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m1} & a_{m2} & \cdots & a_{mn}
\end{pmatrix}
\quad
\text{y}
\quad
b
=
\begin{pmatrix}
b_1 \\
b_2 \\
\vdots \\
b_m
\end{pmatrix}.
\]

A la expresión $Ax=b$ le llamamos la forma matricial del sistema de ecuaciones.

Ejemplo de la utilidad de la forma matricial

La forma matricial de un sistema de ecuaciones es sumamente útil, como veremos en las siguientes entradas. Pero veamos un pequeño ejemplo de una de sus aplicaciones. Supongamos que sabemos que la matriz $A$ es invertible con inversa $A^{-1}$. Recordemos que entonces se cumple que$A^{-1}A = \mathcal{I}$. Gracias a esto, podemos comenzar con la forma matricial del sistema de ecuaciones y deducir lo siguiente:
\begin{align*}
&Ax = b \\
\Rightarrow & A^{-1}Ax = A^{-1}b \\
\Rightarrow &x = A^{-1}b.
\end{align*}

Es decir, si conocemos la matriz inversa de $A$, ¡podemos obtener de manera única el vector que resuelve el sistema de ecuaciones mediante una multiplicación de matriz por vector!

Aún cuando no hemos visto el método general para saber si una matriz tiene inversa, ya vimos previamente qué sucede con una matriz de $2\times 2$
\[
\begin{pmatrix}
a & b \\
c & d
\end{pmatrix}
\]

Así, verifiquemos mediante un ejemplo que el método que mostramos sirve para encontrar soluciones de sistemas de ecuaciones. Consideremos el sistema de ecuaciones
\[
\begin{cases}
2x + 8y &= 9 \\
-3x + 4y &= 2.
\end{cases}
\]

Este sistema puede ser representado en forma matricial como
\[
\begin{pmatrix}
2 & 8 \\
-3 & 4
\end{pmatrix}
\begin{pmatrix}
x \\
y
\end{pmatrix}
=
\begin{pmatrix}
9 \\
2
\end{pmatrix}.
\]

Como recordarás de entradas pasadas, la matriz inversa de $\begin{pmatrix} 2 & 8 \\ -3 & 4 \end{pmatrix}$ es
\[
\begin{pmatrix}
2 & 8 \\
-3 & 4
\end{pmatrix}^{-1}
=
\frac{1}{2\cdot4 – 8\cdot(-3)}
\begin{pmatrix}
4 & -8 \\
3 & 2
\end{pmatrix}
=
\frac{1}{32}
\begin{pmatrix}
4 & -8 \\
3 & 2
\end{pmatrix}
=
\begin{pmatrix}
1/8 & -1/4 \\
3/32 & 1/16
\end{pmatrix}.
\]

Entonces si multiplicamos esta por matriz por la izquierda a ambos lados de la ecuación
\[
\begin{pmatrix}
2 & 8 \\
-3 & 4
\end{pmatrix}
\begin{pmatrix}
x \\
y
\end{pmatrix}
=
\begin{pmatrix}
9 \\
2
\end{pmatrix},
\]
obtendremos
\begin{align*}
\begin{pmatrix}
2 & 8 \\
-3 & 4
\end{pmatrix}
\begin{pmatrix}
x \\
y
\end{pmatrix}
&=
\begin{pmatrix}
9 \\
2
\end{pmatrix}
\\[5pt]
\begin{pmatrix}
1/8 & -1/4 \\
3/32 & 1/16
\end{pmatrix}
\begin{pmatrix}
2 & 8 \\
-3 & 4
\end{pmatrix}
\begin{pmatrix}
x \\
y
\end{pmatrix}
&=
\begin{pmatrix}
1/8 & -1/4 \\
3/32 & 1/16
\end{pmatrix}
\begin{pmatrix}
9 \\
2
\end{pmatrix}
\\[5pt]
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix}
\begin{pmatrix}
x \\
y
\end{pmatrix}
&=
\begin{pmatrix}
5/8 \\
31/32
\end{pmatrix},
\end{align*}
lo que equivale a $x = 5/8$, $y = 31/32$; la solución del sistema. ¡Verifica que es solución!

Más adelante…

En esta entrada repasamos los conceptos y definiciones sobre sistemas de ecuaciones lineales, y nos adentramos a ver cómo existe una relación directa entre los sistemas de ecuaciones lineales y el producto de una matriz por un vector, así como que las matrices invertibles guardan relación con la solución del sistema.

Que la matriz asociada a un sistema de ecuaciones sea invertible en realidad no pasa tanto, y se tienen que desarrollar métodos más generales para resolver sistemas de ecuaciones. En la siguiente entrada conoceremos un algoritmo que nos permitirá resolver sistemas de ecuaciones con una cantidad arbitraria de variables y ecuaciones, y determinar exactamente cómo se ven todas las soluciones.

Tarea moral

  1. Usa el método de las variables libres y las variables pivote para describir al conjunto solución del siguiente sistema de ecuaciones y descríbelo geométricamente. Tendrás que elegir apropiadamente el orden en el que vas fijando las variables.
    \begin{cases}
    w+2x + 8y + 3z&= 0 \\
    -3x + 4y + z&= -1\\
    x+z&=2.\\
    \end{cases}
  2. Usa el método de la inversa para resolver los siguientes tres sistemas de ecuaciones:
    \[
    \begin{cases}
    2x + 8y &= 4 \\
    -3x + 4y &= 1,
    \end{cases} \quad \begin{cases}
    2x + 8y &= 3 \\
    -3x + 4y &= -2,
    \end{cases} \quad \begin{cases}
    2x + 8y &= 1 \\
    -3x + 4y &= -1.
    \end{cases}
    \]
  3. Intenta usar el método de las variables libres y pivote en el siguiente sistema de ecuaciones y explica qué dificultad tiene intentar usarlo directamente:
    \[
    \begin{cases}
    x + y &= 4 \\
    y+z &= 1\\
    z+x&=2.
    \end{cases}
    \]
    ¿Cómo describirías a un sistema de ecuaciones en el cuál se puede hacer el método de variables libres y pivote cómodamente?
  4. Considera un sistema de ecuaciones en forma matricial $Ax=b$. Demuestra que si $x$ y $x’$ son soluciones a este sistema, entonces $\frac{x+x’}{2}$ también lo es. Explica cómo puedes usar esto para a partir de dos soluciones $x$ y $x’$ distintas conseguir una infinidad de soluciones. Concluye que cualquier sistema de ecuaciones lineales o bien no tiene solución, o bien tiene una única solución, o bien tiene una infinidad de soluciones.
  5. Encuentra una matriz no invertible $A$ y un vector $b$ tales que el sistema de ecuaciones $Ax=b$ sí tenga solución. En ese sistema que diste, ¿la solución es única o puedes encontrar otra?

Entradas relacionadas