Archivo de la etiqueta: secante

Geometría Moderna II: Potencia de un punto

Por Armando Arzola Pérez

Deja un comentario

Introducción

En esta primera unidad abordaremos varios los temas relacionados con las circunferencias coaxiales. Para ello, iniciaremos hablando de la potencia de un punto con respecto a una circunferencia. A grandes rasgos, esto trata de lo siguiente.

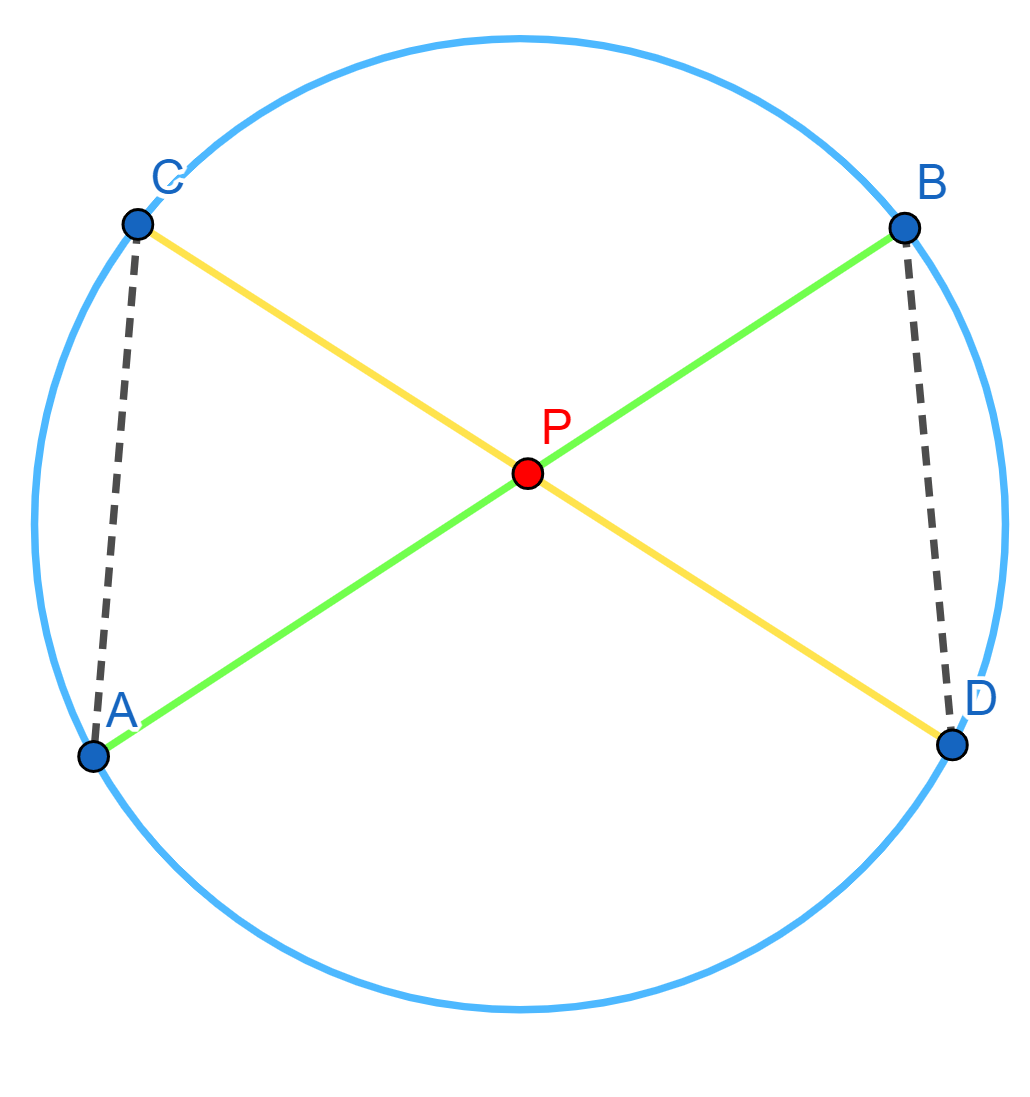
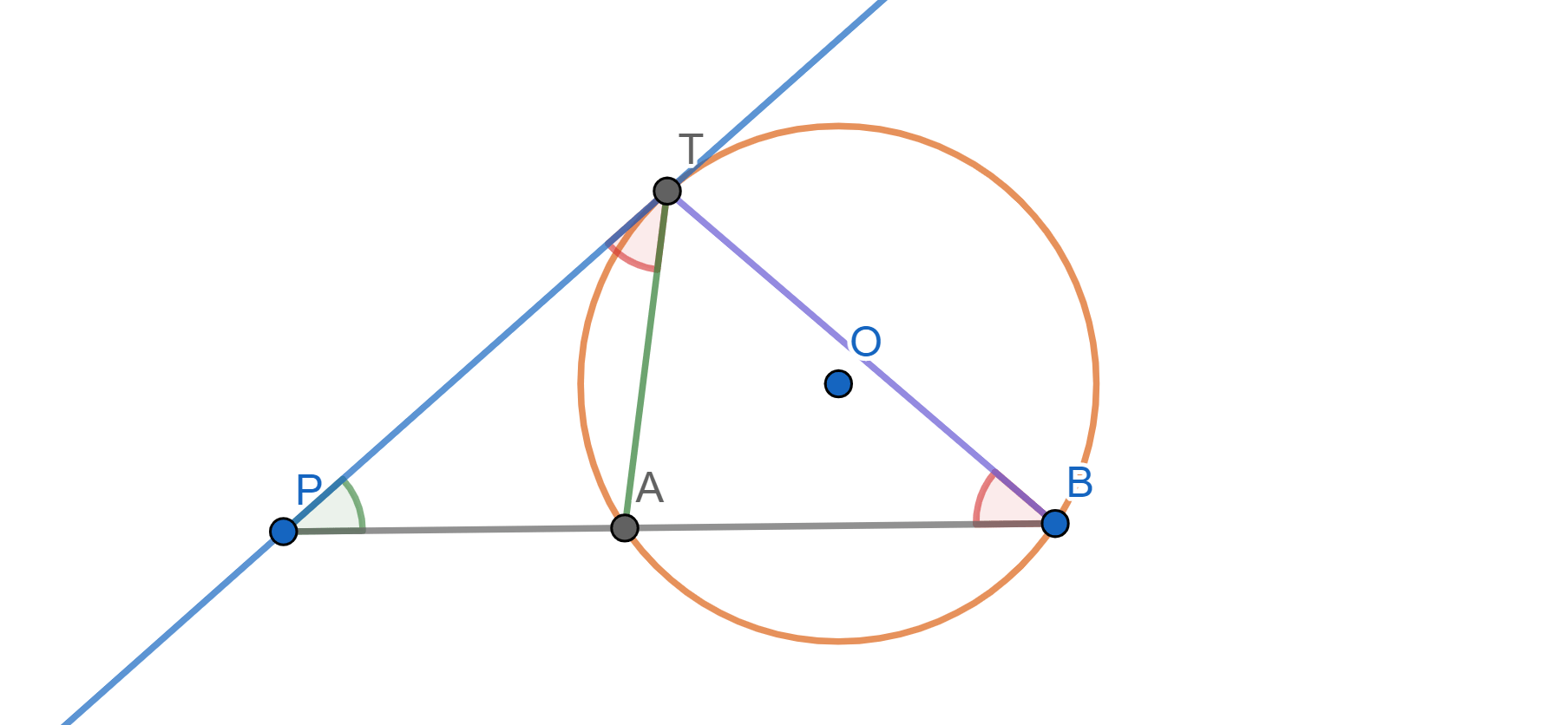
Tomemos una circunferencia $\mathcal{C}$. Tomemos $P$ un punto cualquiera. Tomemos una recta $l$ por $P$ y llamemos $A$ y $B$ los puntos de intersección de $l$ con $\mathcal{C}$. Bajo estas elecciones, la potencia de $P$ será $PA\cdot PB$. Lo que veremos en esta entrada es que dicho producto es constante sin importar la elección de $l$. Para mostrar esto, introduciremos algunas definiciones y posteriormente haremos una demostración por casos.

Definición de potencia de un punto

Comenzaremos dando una primer definición de potencia, que dependerá de cierto punto, circunferencia y recta que elijamos.

Definición. Sea $\mathcal{C}$ una circunferencia, $P$ un punto y $l$ una recta que intersecta a $\mathcal{C}$. Sean $A$ y $B$ los puntos de intersección de $l$ y $\mathcal{C}$ ($A=B$ si $l$ es tangente a $\mathcal{C}$). La potencia de $P$ con respecto a $\mathcal{C}$ en la recta $l$ es la cantidad $PA\cdot PB$. Usaremos la siguiente notación: $$\text{Pot}(P,\mathcal{C},l):=PA\cdot PB.$$

En esta definición y de aquí en adelante, a menos que se diga lo contrario, se estará trabajando con segmentos dirigidos. Es decir, estamos pensando que cada segmento tiene una dirección del primer punto al segundo. Así, por ejemplo, el valor de $PA$ dependerá de la longitud del segmento y su signo dependerá de una dirección (usualmente implícita) que se le asigne a la recta por $A$ y $P$. De este modo, tendremos, por ejemplo, que $PA=-AP$.

La definición de potencia de un punto puede simplificarse notablemente en vista de la siguiente proposición.

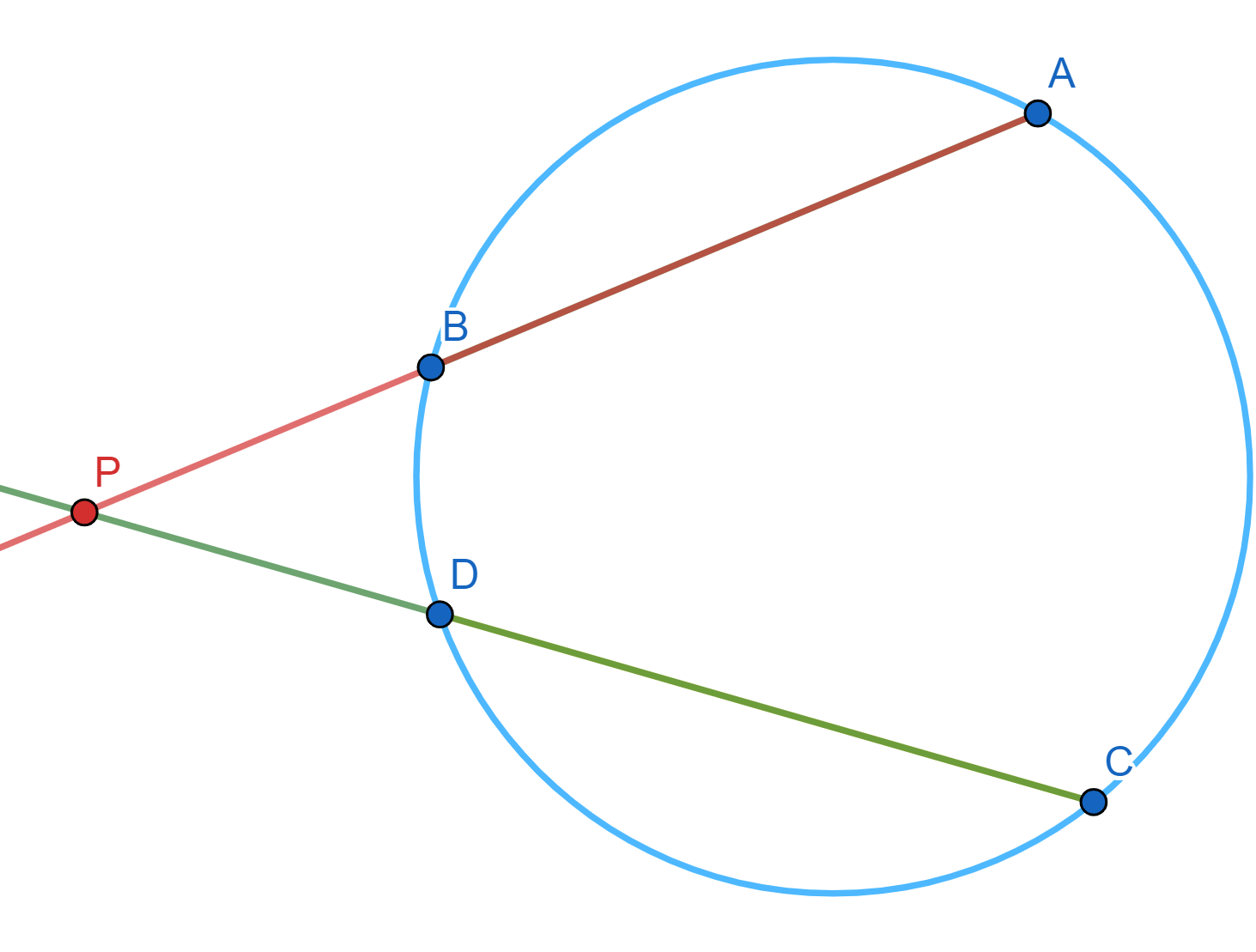
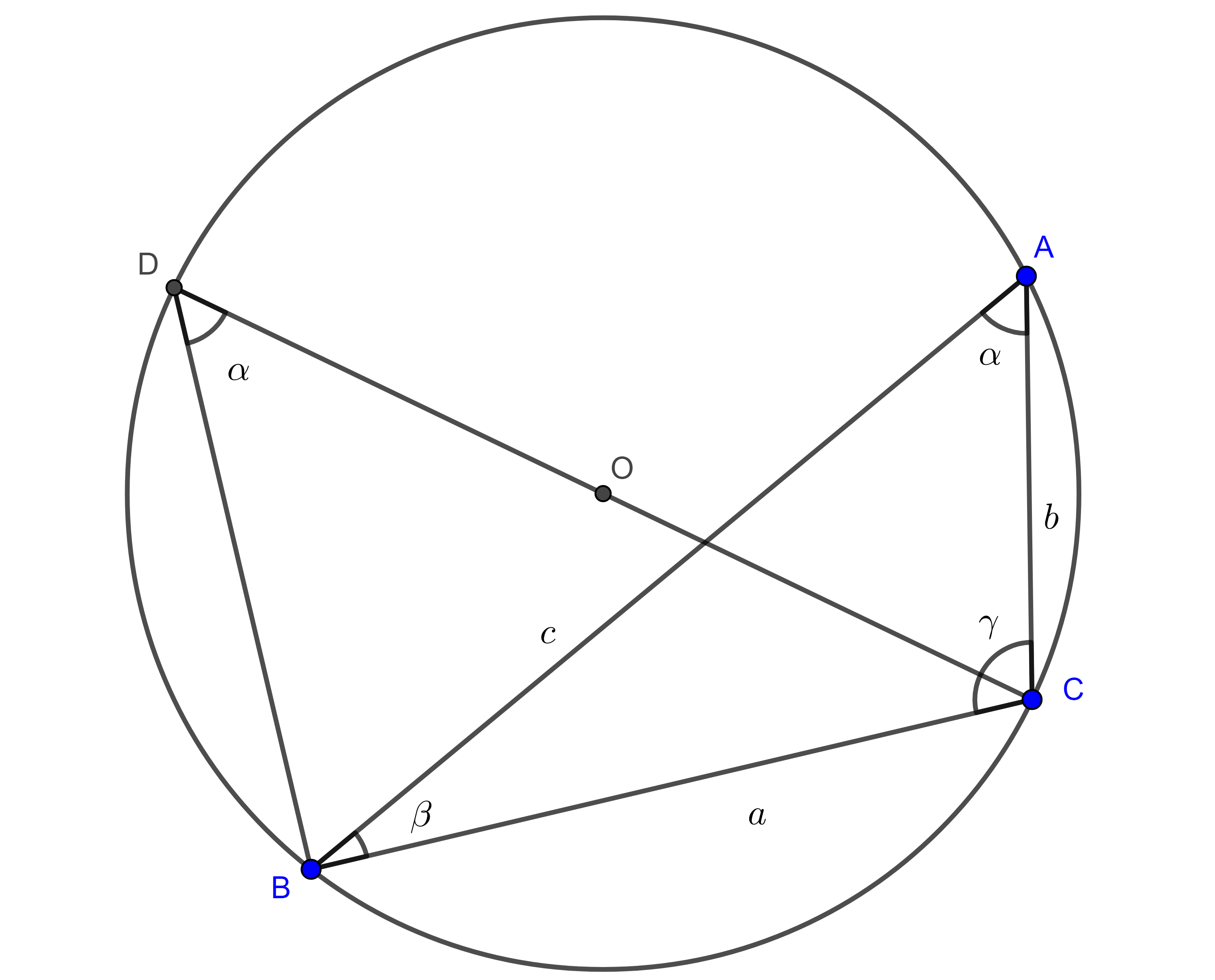
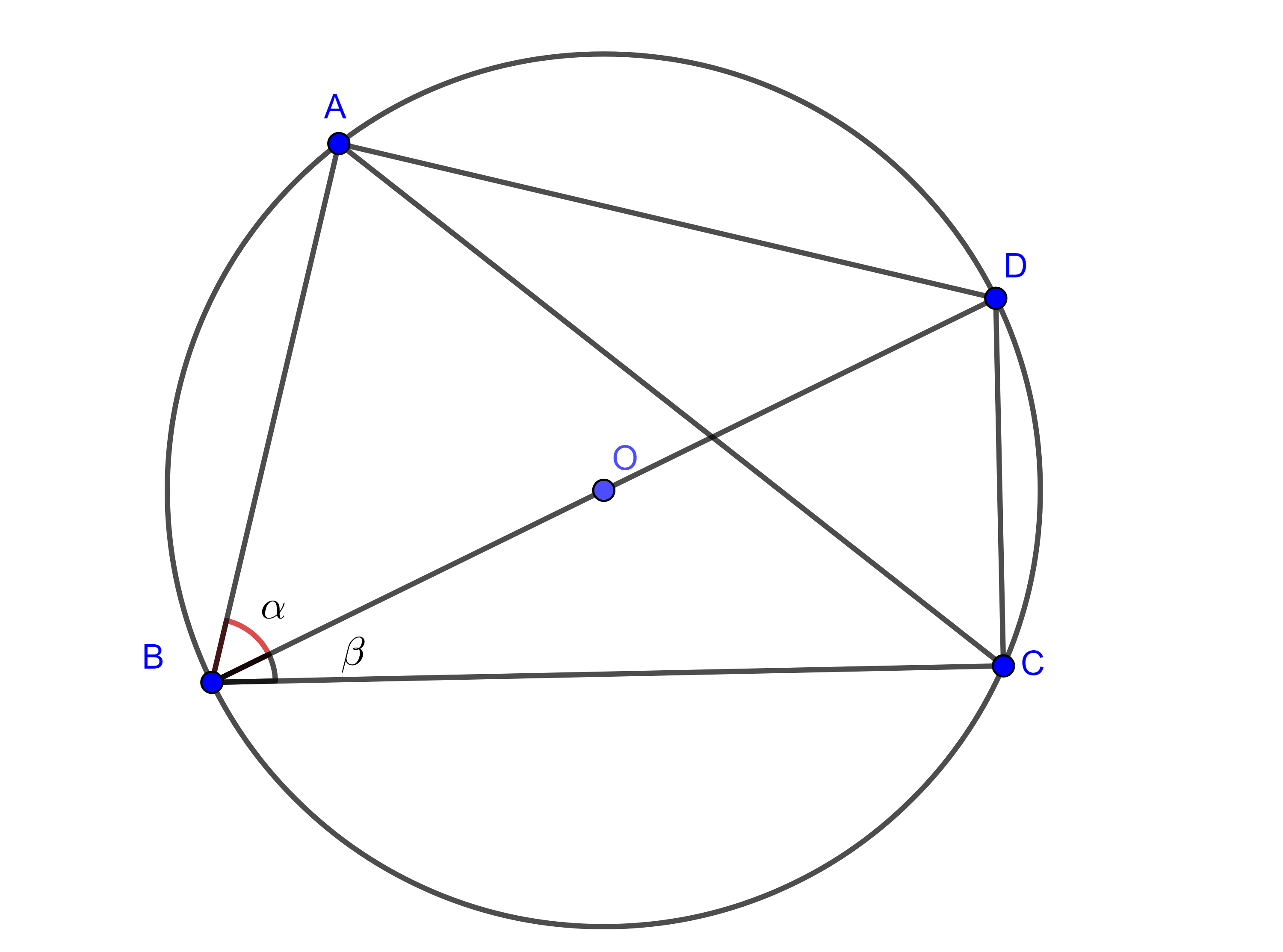
Proposición. La potencia de un punto con respecto a una circunferencia no depende de la recta elegida. Es decir, tomemos $\mathcal{C}$ una circunferencia, $P$ un punto y $l,m$ rectas. Supongamos que los puntos de intersección de $l$ con $\mathcal{C}$ son $A$ y $B$; y que los puntos de intersección de $m$ con $\mathcal{C}$ son $C$ y $D$ (en caso de tangencias, repetimos los puntos). Entonces: $$PA\cdot PB = PC\cdot PD.$$

Demostración. Haremos la demostración por casos de acuerdo a cuando $P$ está dentro o fuera de la circunferencia, o sobre ella.

Dentro de la circunferencia:

Tomemos las cuerdas $AB$ y $CD$ en la circunferencia, las cuales se cortan en $P$. Los triángulos $\triangle APC$ y $\triangle DPB$ son semejantes ya que:

Geometría Moderna II: Potencia de un punto proposición 1 cuando el punto está dentro de la circunferencia.
  1. $\angle PAC = \angle PDB $ por abrir el mismo arco $\overline{BC}$.
  2. $\angle APC = \angle BPD $ por ser opuestos al vértice.
  3. $\angle PCA = \angle PBD $ por abrir mismo arco $\overline{AD}$.

Entonces de la semejanza $\triangle APC \cong \triangle DPB $ tenemos que

$\frac{PA}{PD}=\frac{PC}{PB},$

de donde obtenemos la igualdad $PA\cdot PB =PC \cdot PD$ deseada.

Fuera de la circunferencia:

Ahora, $AB$ y $CD$ son dos secantes que se intersecan en $P$, pero con $P$ exterior a $\mathcal{C}$. Tenemos que $\triangle APC $ y $\triangle DPB $ son semejantes, ya que:

Geometría Moderna II: Potencia de un punto proposición 1 cuando el punto está fuera de la circunferencia.
  1. El cuadrilátero $\square ABDC$ es cíclico, entonces: $\angle ACD + \angle ABD = 180^\circ$ y $\angle ABD + \angle DBP = 180^\circ $, de donde $\angle DBP = \angle ACD$.
  2. $\angle BPD$ y $\angle CPA$ son los mismos ángulos.

Entonces $\frac{PA}{PC}=\frac{PD}{PB},$ de donde se obtiene la igualdad buscada $PA\cdot PB=PC\cdot PD.$

Sobre la circunferencia:

Este caso es sencillo pues sin importar las secantes tomadas, en cada una hay un punto igual a $P$ y por lo tanto una distancia igual a cero. De este modo, $PA\cdot PB=0=PC\cdot PD$.

$\square$

Nota que las demostraciones anteriores sirven aunque $l$ ó $m$ sean tangentes, sólo que hay que hacer ligeras adaptaciones sobre los ángulos usados y los motivos por los que son iguales. Enunciaremos el caso de la tangencia un poco más abajo.

En vista de la proposición anterior, podemos simplificar nuestra definición notablemente.

Definición. Sea $\mathcal{C}$ una circunferencia y $P$ un punto. Tomemos $l$ una recta que intersecta a $\mathcal{C}$. Sean $A$ y $B$ los puntos de intersección de $l$ y $\mathcal{C}$ ($A=B$ si $l$ es tangente a $\mathcal{C}$). La potencia de $P$ con respecto a $\mathcal{C}$ es la cantidad $PA\cdot PB$. Usaremos la siguiente notación: $$\text{Pot}(P,\mathcal{C}):=PA\cdot PB.$$

La potencia queda bien definida sin importar la recta $l$, debido a la proposición anterior.

El signo de la potencia

En esta definición estamos usando segmentos dirigidos, y eso nos lleva a que la potencia de un punto puede tener distintos signos. El comportamiento queda determinado por el siguiente resultado.

Proposición. La potencia de un punto $P$ con respecto a una circunferencia $\mathcal{C}$ es positiva, negativa o cero, de acuerdo a si el punto $P$ está fuera de $\mathcal{C}$, dentro de ella, o sobre ella, respectivamente.

Demostración. Veamos esto caso por caso.

  • Sea $P$ un punto externo a $\mathcal{C}$. Entonces $PA$ y $PB$ tienen la misma orientación y por lo tanto el mismo signo. Además, como $P$ no está sobre $\mathcal{C}$, ninguno de ellos es cero. Así, $\text{Pot}(P,\mathcal{C})> 0$.
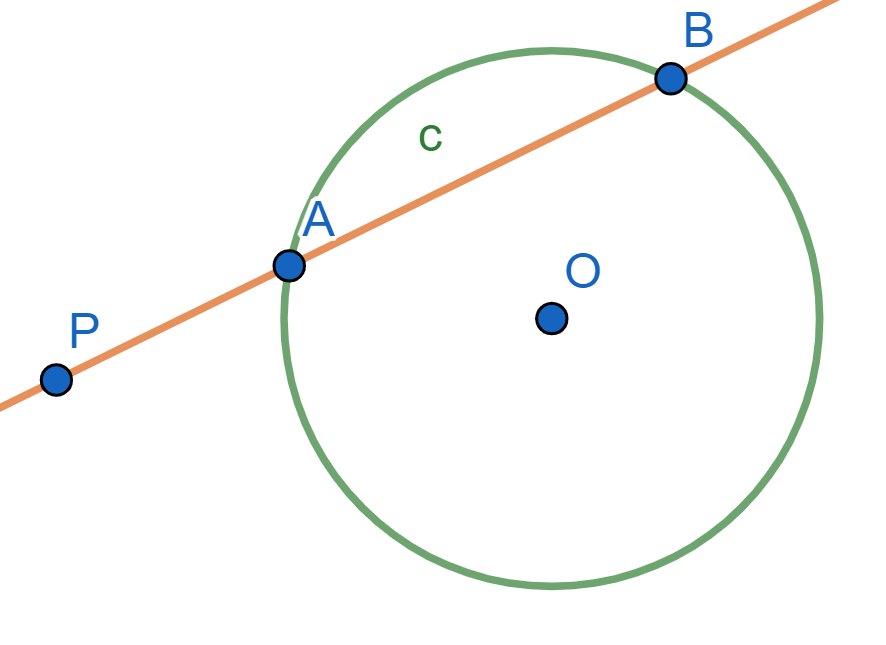
Geometría Moderna II: Potencia de un punto respecto a un punto externo.
  • Sea $P$ un punto interno a $\mathcal{C}$. Entonces $PA$ está dirigido hacia un lado y $PB$ está dirigido hacia el otro, de modo que tienen signo contrario. Además, ninguno de ellos es cero. Así, $\text{Pot}(P,\mathcal{C})<0$.
Geometría Moderna II: Potencia de un punto respecto a un punto interno de la circunferencia.
  • Finalmente, sea $P$ un punto sobre $\mathcal{C}$. Esto quiere decir que alguno de los puntos $A$ o $B$ es $P$ (quizás ambos, si $l$ es tangente). Así, $PA=0$ ó $PB=0$. De este modo $\text{Pot}(P,\mathcal{C})=0$.
Geometría Moderna II: Potencia de un punto que está sobre la circunferencia.

$\square$

Otras fórmulas para la potencia

La potencia es invariante sin importar la recta elegida. De este modo, podemos elegir a una recta tangente y obtener una fórmula para la potencia en términos de la longitud de dicha tangente.

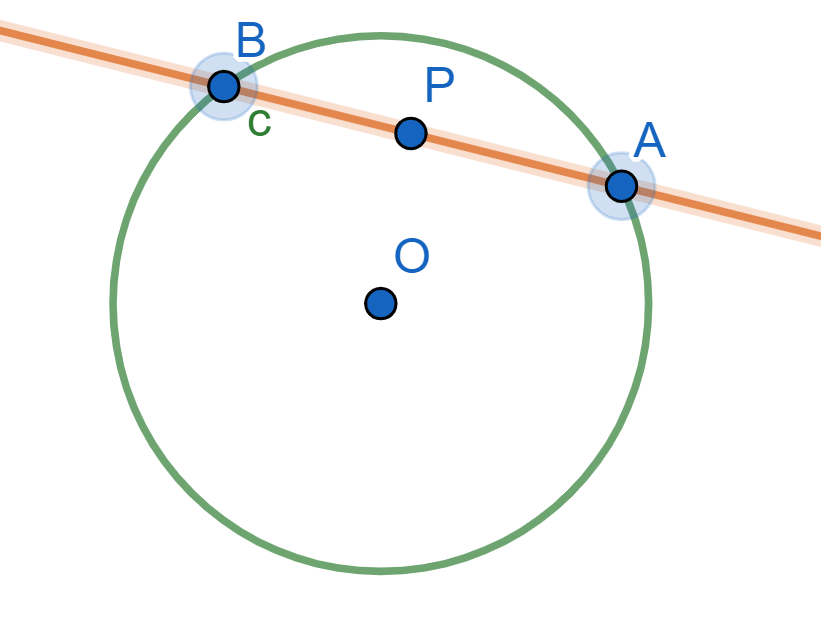
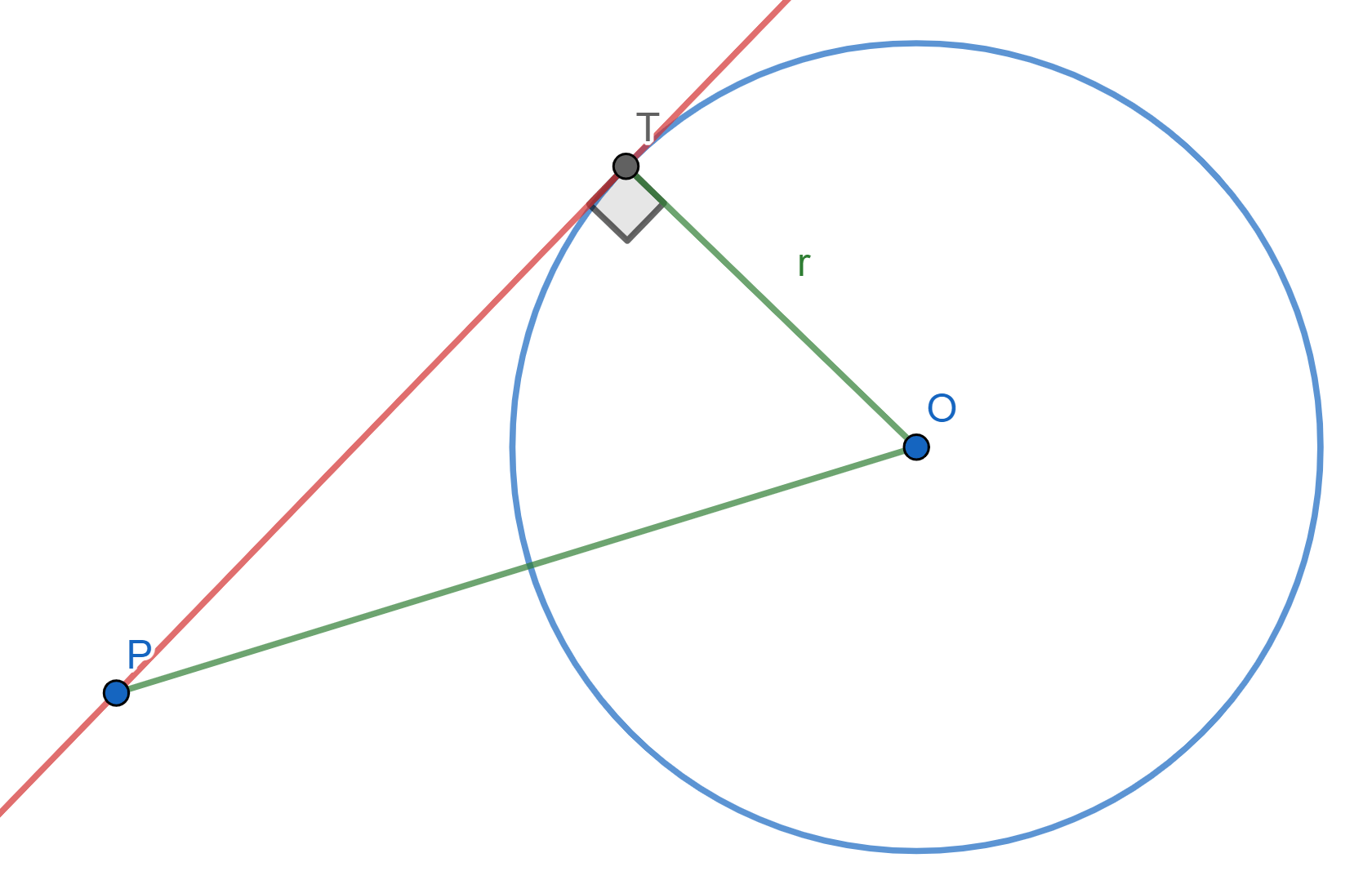
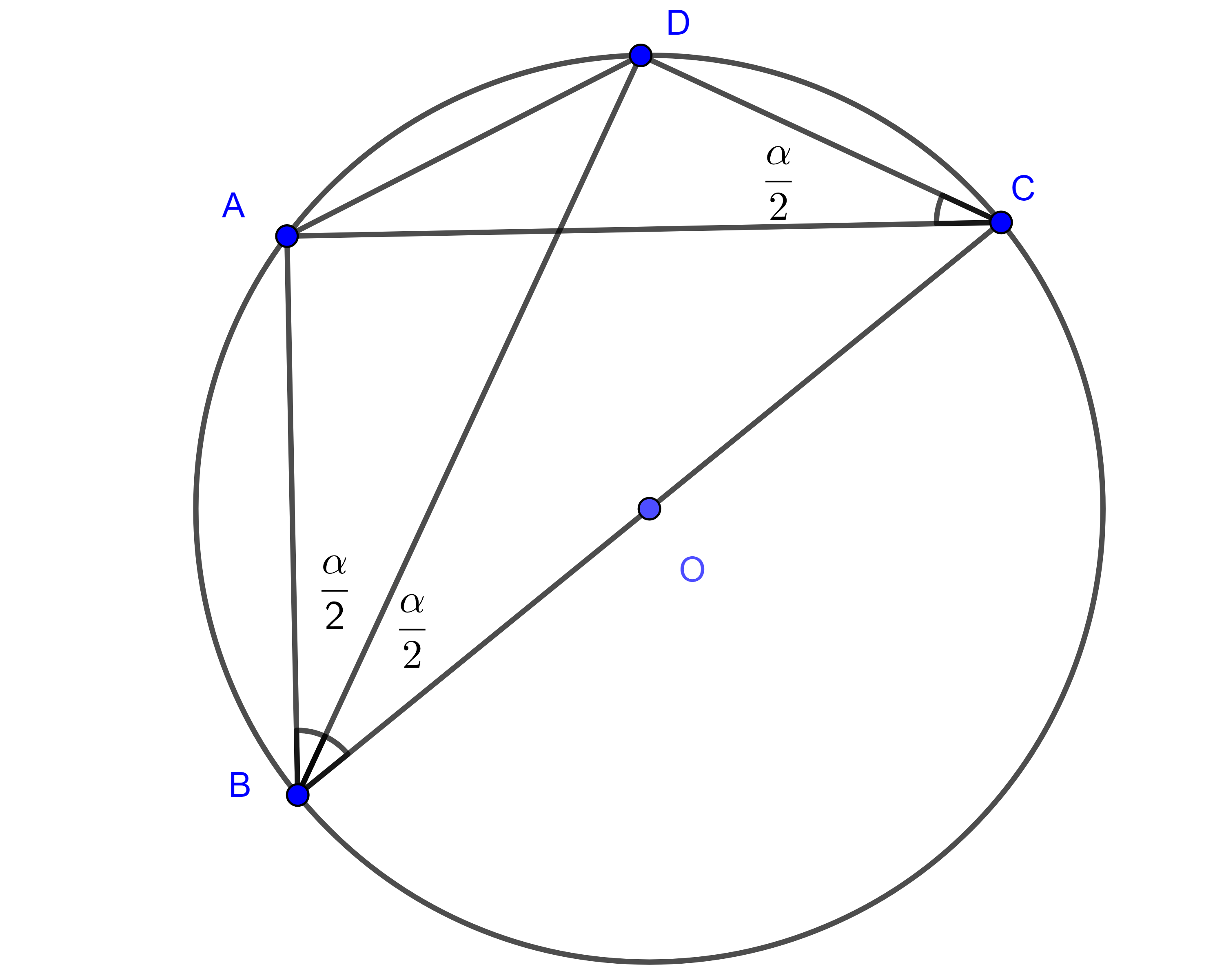
Proposición. Sea $\mathcal{C}$ una circunferencia. Para un punto $P$ fuera de $\mathcal{C}$, su potencia es igual al cuadrado de la longitud de una tangente de él a la circunferencia.

Es decir, sea $T$ un punto sobre la circunferencia tal que $PT$ sea tangente a $\mathcal{C}$. Entonces, $\text{Pot}(P,\mathcal{C})=PT^2$.

Imagen representativa de la Proposición 2.

El resultado se sigue de llevar al límite lo que ya probamos en la proposición de invarianza de la potencia. Pero a continuación damos un argumento alternativo.

Demostración. Tracemos otra recta por $P$ que no sea tangente a $\mathcal{C}$ y cuyos puntos de intersección con $\mathcal{C}$ son $A$ y $B$ como en la figura. Tenemos que mostrar que $PA\cdot PB =PT^2$.

El ángulo $\angle PTA$ es semi-inscrito y es igual al ángulo inscrito $ \angle TBA$, pues ambos tienen el mismo arco $\overline{AT}$.

Entonces los triángulos $\triangle APT$ y $\triangle TPB$ comparten el ángulo con vértice en $P$ y $\angle PTA=\angle TBA$. Por ello, se tiene que $\triangle APT \cong \triangle TPB $ son semejantes y sus lados son proporcionales: $\frac{PA}{PT} = \frac{PT}{PB}$. De aquí, $$PT^2=PT\cdot PT=PA\cdot PB=\text{Pot}(P,\mathcal{C}).$$

$\square$

También es posible conocer la potencia de un punto hacia una circunferencia si conocemos el radio de la circunferencia y la distancia del punto al centro.

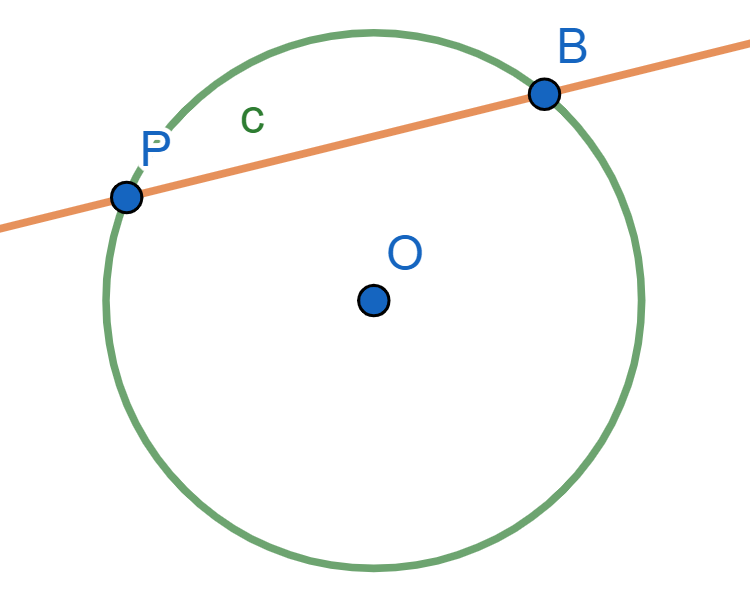
Proposición. Sea $\mathcal{C}$ una circunferencia de centro $O$ y radio $r$. Sea $P$ un punto en cualquier posición. La potencia de $P$ con respecto a $\mathcal{C}$ es $$\text{Pot}(P,\mathcal{C}) = OP^2 – r^2.$$

Demostración. Haremos la demostración por casos

Dentro de la circunferencia:

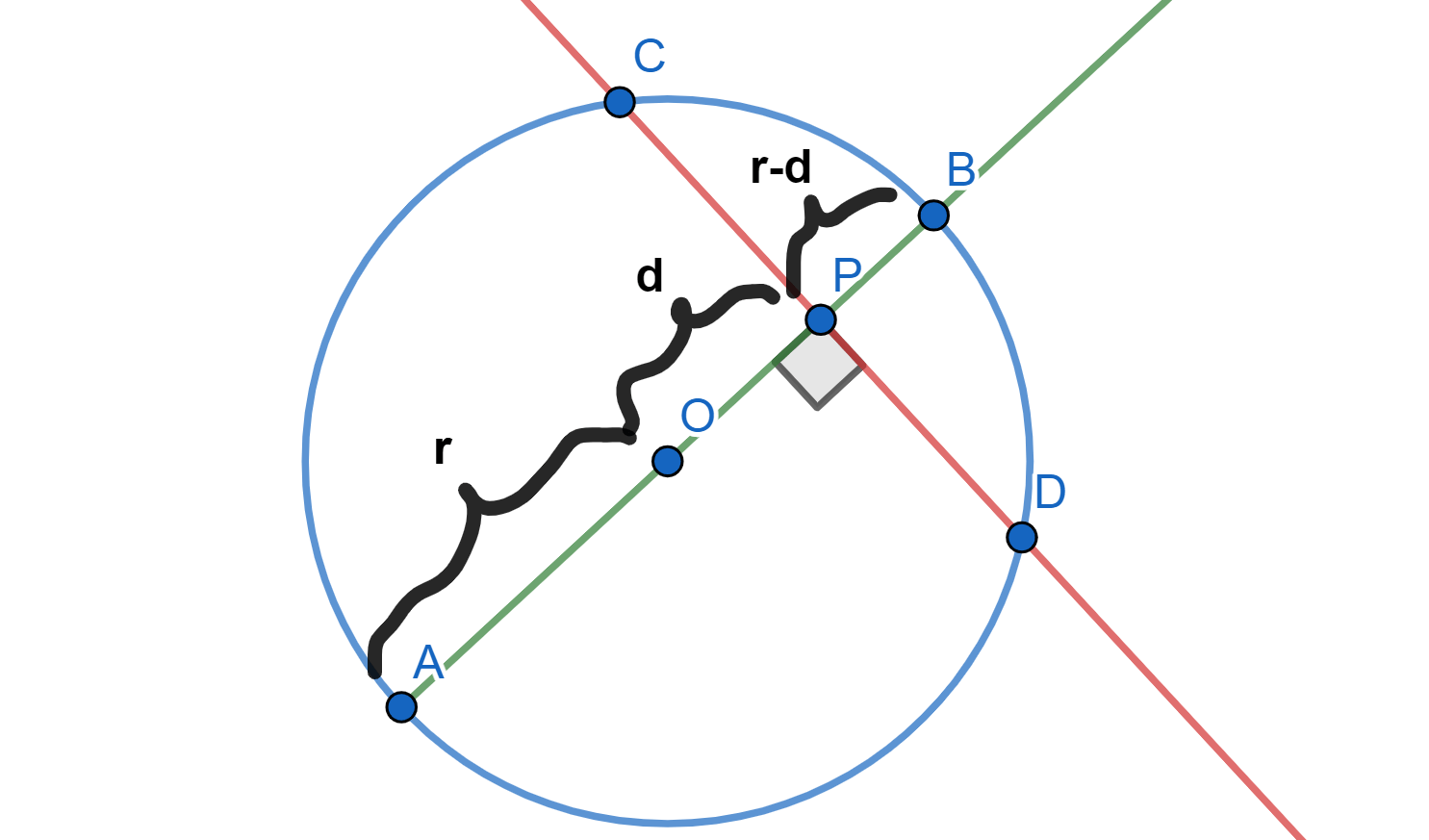
Sea $AB$ la cuerda que pasa por el centro $O$ y $P$ (si $O=P$, tomamos cualquier cuerda $AB$ por el centro). Supongamos sin pérdida de generalidad que la recta está dirigida de $A$ a $B$. Tenemos que $AO=r>0$ y llamemos $d=OP>0$. De aquí, $PB=r-d>0$. La siguiente figura resume estas igualdades.

Potencia de un punto imagen de Proposición 3 cuando un punto está dentro de la circunferencia.

La potencia desde $P$ sería entonces, cuidando los signos:

\begin{align*}
PA\cdot PB &= (PO+OA)(PB)\\
&=(-d-r)(r-d)\\
&=-(d+r)(r-d)\\
&=-(r^2-d^2)\\
&=d^2-r^2\\
&=OP^2-r^2.
\end{align*}

Así, $\text{Pot}(P,\mathcal{C})=OP^2-r^2$.

Fuera de la circunferencia:

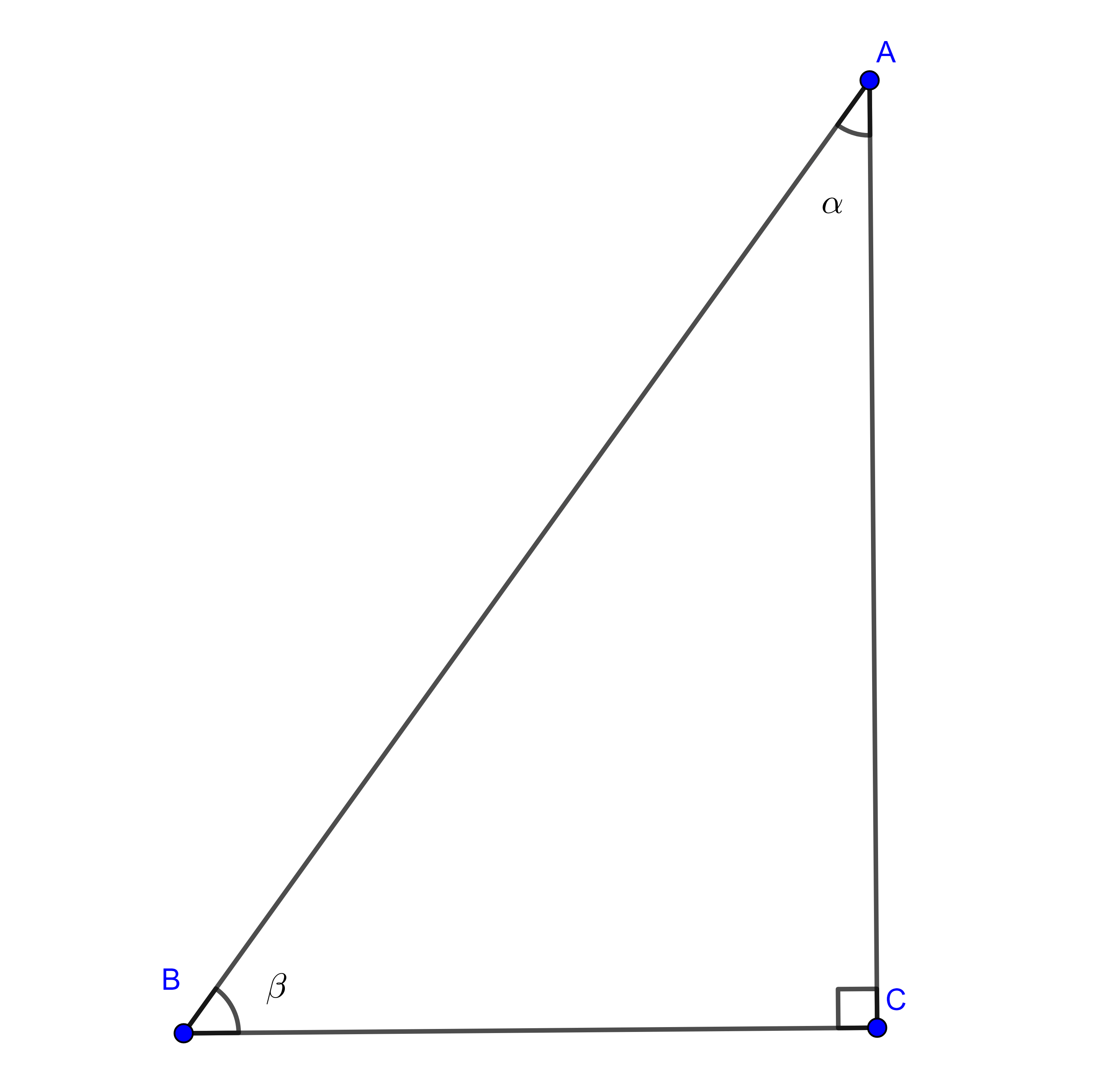
Ahora desde $P$ tracemos una tangente $PT$ a $\mathcal{C}$ con $T$ sobre $\mathcal{C}$. Como $\angle PTO =90^o$, entonces $\triangle POT$ es un triángulo rectángulo.

Potencia de un punto imagen de Proposición 3 cuando un punto está fuera de la circunferencia.

Por el teorema de Pitágoras y la expresión de potencia en términos de la tangente: $$OP^2=r^2+PT^2=r^2+\text{Pot}(P,\mathcal{C}).$$ Despejando, obtenemos la expresión deseada: $$\text{Pot}(P,\mathcal{C})=OP^2-r^2.$$

Sobre la circunferencia:

Este caso es sencillo, pues sabemos que la potencia de $P$ debe ser cero. Pero además, como $P$ está en la circunferencia, entonces $OP=r$, de modo que $OP^2-r^2=0$, y entonces la expresión también es lo que queremos.

$\square$

Más adelante…

Seguiremos abordando el tema de potencia de un punto y veremos cómo a partir de él se define el eje radical de dos circunferencias.

Entradas relacionadas

Cálculo Diferencial e Integral I: Funciones trigonométricas (Parte 2)

Por Karen González Cárdenas

Deja un comentario

Introducción


Ahora que hemos comenzado a revisar las funciones trigonométricas de seno y coseno, en esta entrada veremos las funciones tangente, cotangente, secante y cosecante. De igual manera, revisaremos las funciones inversas y su representación gráfica.

Hablemos de la tangente y la cotangente

Recordemos de la entrada anterior las definiciones:

\begin{align*}
tan(\theta)&=\frac{sen(\theta)}{cos(\theta)} & cot(\theta)&=\frac{cos(\theta)}{sen(\theta)}
\end{align*}

Para la función tangente tenemos que su gráfica se vería como:

Observación: La tangente presenta asíntotas en los valores $x=\frac{k \pi}{2}$ con $k \in \mathbb{Z}$.

Y su rama principal la consideramos definida en el dominio:
$$tan: \left(-\frac{\pi}{2}, \frac{\pi}{2} \right) \rightarrow \r$$

Y para la función cotangente su gráfica sería:

Observación: La cotangente presenta asíntotas en los valores $x=k \pi$ con $k \in \mathbb{Z}$.

Para esta función consideraremos como su rama principal en el siguiente dominio:
$$cot: (0,\pi) \rightarrow \r$$.

Ahora la secante y la cosecante

Ya vimos que están definidas como:
\begin{align*}
sec(\theta)&= \frac{1}{cos(\theta)} & csc(\theta)&= \frac{1}{sen(\theta)}.
\end{align*}

Comencemos con la gráfica para la función secante:

Observación: La secante presenta asíntotas en los valores $x=\frac{k \pi}{2}$ con $k \in \mathbb{Z}$.

Notemos que esta función se encuentra definida sobre cada cresta y por debajo de cada valle de la función $cos(\theta)$:

Tomaremos como domino donde la función es invertible a:
$$D= \left[0, \frac{\pi}{2} \right) \cup \left(\frac{\pi}{2},\pi \right].$$

Para la función cosecante vemos que se encuentra definida sobre cada cresta y por debajo de cada valle de la función $sen(\theta)$:

Observación: La cosecante presenta asíntotas en los valores $x=k \pi$ con $k \in \mathbb{Z}$.

Para esta función consideraremos al dominio donde es invertible a:
$$D= \left[-\frac{\pi}{2}, 0 \right) \cup \left(0, \frac{\pi}{2} \right].$$

¿Quiénes son las funciones inversas?

Para poder visualizar las gráficas de cada una de las funciones trigonométricas utilizaremos el método descrito previamente de reflejar la gráfica de la función respecto de la función identidad en el dominio donde es biyectiva o invertible.

Comenzaremos con la inversa de la función $f(x)=sen(x)$ en el dominio $D_{f}=\left[ -\frac{\pi}{2}, \frac{\pi}{2} \right]$:

A $f^{-1}(x)$ la llamaremos arcoseno de $x$:
$$f^{-1}(x)=arcsen(x),$$
geométricamente esta función nos da el arco cuyo seno es $x$ valor.

Procederemos de la misma manera con $g(x)=cos(x)$ en el dominio $D_{g}=[0,\pi]$:

Ahora a $g^{-1}$ la llamaremos arcocoseno de $x$:
$$g^{-1}(x)=arccos(x)$$
y su interpretación geométrica sería el arco cuyo coseno es el valor $x$.

Dejaremos como ejercicio de Tarea moral realizar la gráfica para la función inversa de $h(x)= tan(x)$ en el dominio $D_{h}= \left(-\frac{\pi}{2}, \frac{\pi}{2} \right)$:
$$h^{-1}(x)= arctan(x),$$
la función arcotangente nos da el arco cuya tangente es el valor $x$.

Más adelante

En la siguiente entrada veremos al conjunto de funciones exponenciales y logarítmicas, sus representaciones gráficas, la relación que existe entre ellas y algunos resultados que cumplen, como las leyes de los exponentes y las leyes de los logaritmos.

Tarea moral

  • Obtener la gráfica de las siguientes funciones:
    • $f(x)=-tan(x)$
    • $f(x)=-2sec(x)+1$
    • $f(x)=arctan(x)$
    • $f(x)=3-csc(x)$

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Geometría Moderna I: Trigonometría

Por Rubén Alexander Ocampo Arellano

Deja un comentario

Introducción

En esta entrada presentaremos las razones trigonométricas respecto de un ángulo agudo en un triángulo rectángulo, estas pueden ser vistas como funciones si consideramos el ángulo como una variable, veremos como extender estas funciones a ángulos de cualquier magnitud y algunas identidades trigonométricas.

Razones trigonométricas

Definiciones. Consideremos un triángulo rectángulo $\triangle ABC$ donde $AB$ es la hipotenusa y sea $\alpha =  \angle BAC$, decimos que $BC$ es el cateto opuesto a $\alpha$ y $AC$ es el cateto adyacente a $\alpha$.

Definimos las razones trigonométricas respecto del ángulo $\alpha$ como sigue:

El seno del ángulo $\alpha$ como $\dfrac{c.opuesto}{hipotenusa}$ y lo denotamos como $\sin \alpha = \dfrac{BC}{AB}$.
El coseno del ángulo $\alpha$ como $\dfrac{c.adyacente}{hipotenusa}$ y lo denotamos como $\cos \alpha = \dfrac{AC}{AB}$.
La tangente del ángulo $\alpha$ como $\dfrac{c.opuesto}{c.adyacente}$ y lo denotamos como $\tan \alpha = \dfrac{BC}{AC}$.
La cosecante del ángulo $\alpha$ como como $\dfrac{hipotenusa}{c.opuesto}$ y lo denotamos como $\csc \alpha = \dfrac{AB}{BC}$.
La secante del ángulo $\alpha$ como $\dfrac{hipotenusa}{c.adyacente}$  y lo denotamos como $\sec \alpha = \dfrac{AB}{AC}$.
La cotangente del ángulo $\alpha$ como $\dfrac{c.adyacente}{c.opuesto}$ y lo denotamos como $\cot \alpha = \dfrac{AC}{BC}$.

Figura 1

Si consideramos el ángulo complementario a $\alpha$, $\beta = \angle CBA$, entonces de las definiciones se siguen las siguientes relaciones:

$\sin \alpha = \cos \beta$, $\cos \alpha = \sin \beta$, $\tan \alpha = \dfrac{\sin \alpha}{\cos \alpha}$, $\tan \alpha \tan \beta = 1$.

$\csc \alpha = \sec \beta$, $\sec \alpha = \csc \beta$, $\cot \alpha = \dfrac{\cos \alpha}{\sin \alpha}$, $\cot \alpha \cot \beta = 1$.

Círculo trigonométrico

Consideremos $(O, 1)$ un círculo con centro en $O$ de radio $1$, por $O$ trazamos dos rectas perpendiculares $x$ e $y$, tomamos un punto $P \in (O, 1)$ en el cuadrante formado por el rayo derecho $Ox$ y el rayo superior $Oy$ y trazamos las proyecciones $X$, $Y$ de $O$ a las rectas $x$, $y$ respectivamente.

El triángulo $\triangle OPX$ es rectángulo y su hipotenusa $OP = 1$, si consideramos el ángulo $\angle XOP = \gamma$ entonces
$\sin \gamma = PX$ y
$\cos \gamma = OX$.

Figura 2

Tracemos la tangente a $(O, 1)$ por $Q$, la intersección entre $x$ y $(O, 1)$, tomemos $R$ como la intersección entre la tangente y $OP$ entonces $RQ \parallel PX$ y los triángulos $\triangle OPX$ y $\triangle ORQ$ son semejantes por lo tanto
$\tan \gamma = \dfrac{PX}{OX} = \dfrac{RQ}{OQ} = RQ$ y
$\sec \gamma = \dfrac{OP}{OX} = \dfrac{OR}{OQ} = OR$.

Ahora trazamos la tangente a $(O, 1)$ por $S$, la intersección de $y$ con $(O, 1)$, tomamos $T$ como la intersección de la tangente con $OP$ entonces $ST \parallel x$, por lo tanto $\gamma = \angle STO$ y así $\triangle OPX$ y $\triangle TOS$ son semejantes, por lo tanto,
$\csc \gamma = \dfrac{OP}{PX} = \dfrac{OT}{OS} = OT$ y 
$\cot \alpha = \dfrac{OX}{PX} = \dfrac{ST}{OS} = ST$.

Con esta construcción podemos extender las definiciones de función trigonométrica para ángulos agudos a ángulos de cualquier magnitud trasladando el punto $P$ alrededor de la circunferencia $(O, 1)$ y tomando las proyecciones de $P$, $X$ e $Y$ a las rectas $x$ e $y$ respectivamente que tomaremos como positivas si se encuentran en los rayos derecho y superior o negativas si se encuentran en los rayos izquierdos e inferior de las rectas $x$, $y$ respectivamente.

De esta manera todas las razones trigonométricas quedan determinadas por el valor de $\sin \gamma = PX$ y $\cos \gamma = OX$.

Teorema 1, identidad pitagórica. Sea $0 \leq \gamma < 2\pi$ entonces, $\sin^2 \gamma + \cos^2 \gamma = 1$.

Demostración. Aplicamos el teorema de Pitágoras al triángulo rectángulo $\triangle OPX$, (figura 2).

$1 = PX^2 + OX^2 = \sin^2 \gamma + \cos^2 \gamma$.

$\blacksquare$

Ley extendida de senos

Teorema 2, ley extendida de los senos. Sean $\triangle ABC$ y $(O, R)$ su circuncírculo, etiquetemos $\angle BAC = \alpha$, $\angle CBA = \beta$, $\angle ACB = \gamma$ y $a = BC$, $b = AC$, $c = AB$ las longitudes de sus lados, entonces
$\dfrac{\sin \alpha}{a} = \dfrac{\sin \beta}{b} = \dfrac{\sin \gamma}{c} = \dfrac{1}{2R}$.

Demostración. Tracemos $D$ el punto diametralmente opuesto a $C$, entonces $\angle BDC = \alpha$, pues subtienden el mismo arco.

$\angle CBD$ es un ángulo recto, pues $CD$ es diámetro, por lo tanto $\sin \alpha = \sin \angle BDC = \dfrac{a}{CD}$.

Por lo tanto, $\dfrac{\sin \alpha}{a} = \dfrac{1}{2R}$.

Figura 3

De manera análoga podemos ver que
$\sin \beta = \dfrac{b}{2R}$ y
$\sin \gamma = \dfrac{c}{2R}$.

Por lo tanto, $\dfrac{\sin \alpha}{a} = \dfrac{\sin \beta}{b} = \dfrac{\sin \gamma}{c} = \dfrac{1}{2R}$.

$\blacksquare$

Corolario. El seno de un ángulo inscrito en una circunferencia de diámetro $1$ es igual a la cuerda que abarca dicho ángulo.

Demostración. Se sigue de sustituir $2R = 1$ en el teorema anterior.

$\blacksquare$

Ley de cosenos

Teorema 3, ley de cosenos. Sean $\triangle ABC$, $\angle BAC = \alpha$, $\angle CBA = \beta$, $\angle ACB = \gamma$ y $a = BC$, $b = AC$, $c = AB$ las longitudes de sus lados, entonces se da la siguiente igualdad:
$c^2 = a^2 + b^2 – 2ab \cos \gamma$.

Demostración. Trazamos $D$ el pie de la perpendicular a $BC$ desde $A$ y aplicamos el teorema de Pitágoras a $\triangle ABD$ y $\triangle ADC,$ de donde obtenemos

$\begin{equation} c^2 = AD^2 + (a – DC)^2 = AD^2 + a^2 – 2a(DC) + DC^2, \end{equation}$
$b^2 = AD^2 + DC^2$
$\Leftrightarrow$ $\begin{equation} AD^2 = b^2 – DC^2. \end{equation}$

Figura 4

Sustituimos $(2)$ en $(1)$ y obtenemos $c^2 = b^2 + a^2 – 2a(DC)$.

Por otro lado $\cos \gamma = \dfrac{DC}{b}$ $\Leftrightarrow$ $b \cos \gamma = DC$.

Así que $c^2 = a^2 + b^2 – 2ab \cos \gamma$.

De manera similar se puede ver que
$a^2 = b^2 + c^2 – 2bc \cos \alpha$ y
$b^2 = a^2 + c^2 – 2ac \cos \beta$.

$\blacksquare$

El seno de la suma

Teorema 4, el seno de la suma de dos ángulos. Sean $\alpha$ y $\beta$ ángulos agudos entonces $\sin (\alpha + \beta) = \sin \alpha \cos \beta + \sin \beta \cos \alpha$.

Demostración. Sea $\square ABCD$ cíclico tal que $BD = 1$ es diámetro del circuncírculo, $\angle DBA = \alpha$ y $\angle CBD =\beta$.

Figura 5

Como consecuencia del corolario tenemos que $AC = \sin (\alpha + \beta)$, ademas $\triangle BAD$ y $\triangle DCB$ son triángulos rectángulos pues $DB$ es diámetro.

Se sigue que
$AB = \cos \alpha$,
$CD = \sin \beta$,
$AD = \sin \alpha$ y
$BC = \cos \beta$.

El teorema de Ptolomeo nos dice que
$\begin{equation} AC \times BD = AB \times CD + BC \times AD. \end{equation}$

Por lo tanto, $\sin (\alpha + \beta) = \cos \alpha \sin \beta +\sin \alpha \cos \beta$.

$\blacksquare$

El coseno de la suma

Teorema 5, el coseno de la suma de dos ángulos. Sean $\alpha \ne 0$ y $\beta$ ángulos agudos tales que $\alpha + \beta < \dfrac{\pi}{2}$ entonces $\cos (\alpha + \beta) = \cos \alpha \cos \beta – \sin \alpha \sin \beta$.

Demostración. Sea $\square ABCD$ cíclico tal que $BC = 1$ es diámetro del circuncírculo, $\angle CBD = \alpha$ y $\angle DBA = \beta$.

Figura 6

Como $\triangle BAC$ y $\triangle BDC$ son triángulos rectángulos y $BC = 1$ tenemos que
$AC = \sin (\alpha + \beta) = \sin \alpha \cos \beta + \sin \beta \cos \alpha$ (teorema 4),
$BD = \cos \alpha$,
$AB = \cos (\alpha + \beta)$,
$CD = \sin \alpha$,
$AD = \sin \angle DCA = \sin \beta$ (corolario).

Por el teorema de Ptolomeo $(3)$, aplicado a $\square ABCD$ obtenemos:
$\cos (\alpha + \beta) \sin \alpha + \sin \beta$
$= (\sin \alpha \cos \beta + \sin \beta \cos \alpha) \cos \alpha$
$= \sin \alpha \cos \beta \cos \alpha + \sin \beta \cos^2 \alpha$
$ = \sin \alpha \cos \beta \cos \alpha + (\sin \beta)(1 – \sin^2 \alpha)$ (teorema 1)
$= \sin \alpha \cos \beta \cos \alpha – \sin \beta \sin^2 \alpha + \sin \beta$.

$\Leftrightarrow$$\cos (\alpha + \beta) \sin \alpha = \sin \alpha \cos \beta \cos \alpha – \sin \beta \sin^2 \alpha$.

Por lo tanto, $\cos (\alpha + \beta) = \cos \beta \cos \alpha -\sin \beta \sin \alpha$.

$\blacksquare$

Seno y coseno del ángulo medio

Teorema 6, el seno y el coseno del ángulo medio. Sea $\alpha \ne 0$ un ángulo agudo entonces
$\sin \dfrac{\alpha}{2} = \sqrt{\dfrac{1 – \cos \alpha}{2}}$ y $\cos \dfrac{\alpha}{2} = \sqrt{\dfrac{1 + \cos \alpha}{2}}$.

Demostración. Sea $\square ABCD$ cíclico tal que $BC = 1$ es diámetro y $\angle CBD = \angle DBA = \dfrac{\alpha}{2}$.

Figura 7

Ya que $\triangle BAC$ y $\triangle BDC$ son triángulos rectángulos podemos ver que
$AC = \sin \alpha$,
$BD = \cos \dfrac{\alpha}{2}$,
$AB = \cos \alpha$,
$CD = \sin \dfrac{\alpha}{2}$,
$AD = \sin \angle DCA = \sin \dfrac{\alpha}{2}$ (corolario).

Aplicando Ptolomeo $(3)$ y el teorema 4 obtenemos:
$\cos \alpha \sin \dfrac{\alpha}{2} + \sin \dfrac{\alpha}{2} = \sin \alpha \cos \dfrac{\alpha}{2} $
$= \sin (\dfrac{\alpha}{2} +\dfrac{\alpha}{2}) \cos \dfrac{\alpha}{2} = 2 \sin \dfrac{\alpha}{2} \cos^2 \dfrac{\alpha}{2}$.

Por lo tanto, $2 \sin \dfrac{\alpha}{2} \cos^2 \dfrac{\alpha}{2} = \sin \dfrac{\alpha}{2} (\cos \alpha + 1)$ $\Rightarrow$  
$\begin{equation} \cos^2 \dfrac{\alpha}{2} = \dfrac{\cos \alpha + 1}{2}. \end{equation}$

De donde se sigue que $\cos \dfrac{\alpha}{2} = \sqrt{\dfrac{\cos \alpha + 1}{2}}$.

Ahora sustituimos la identidad pitagórica en la ecuación $(4)$ y obtenemos:
$1 – \sin^2 \dfrac{\alpha}{2} = \dfrac{\cos \alpha + 1}{2}$
$\Leftrightarrow$
$\sin \dfrac{\alpha}{2} = \sqrt{\dfrac{1 – \cos \alpha}{2}}$.

$\blacksquare$

Más adelante…

En la siguiente entrada estudiaremos algunas propiedades relacionadas con el incírculo y los excÍrculos de un triángulo, así como también sobre sus centros y radios.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. $i)$ A partir de un triangulo equilátero deriva los valores de las seis razones trigonométricas para los ángulos $\dfrac{\pi}{3}$ y $\dfrac{\pi}{6}$,
    $ii)$ A partir de un triángulo rectángulo isósceles deduce los valores de las seis razones trigonométricas para el ángulo $\dfrac{\pi}{4}$.
  2. Recordemos que consideramos la magnitud de un ángulo central como positiva, si recorremos el arco de circunferencia que subtiende dicho ángulo en el sentido contrario al de las manecillas del reloj y negativa en caso contraio, muestra que para cualquier valor de $\alpha$ se cumple que:
    $i)$ $\sin (-\alpha) = -\sin \alpha$,
    $ii)$ $\cos (-\alpha) = \cos \alpha$,
    $iii)$ $\sin (\pi – \alpha) = \sin \alpha$,
    $iv)$ $\cos (\pi – \alpha) = -\cos \alpha$,
    $v)$ $\sec^2 \alpha = 1 + \tan^2 \alpha$.
  3. Sean $\alpha$ y $\beta$ ángulos agudos tales que $\alpha \geq \beta$, muestra geométricamente:
    $i)$ el seno de la diferencia de dos ángulos, $\sin (\alpha – \beta) = \sin \alpha \cos \beta – \sin \beta \cos \alpha$,
    $ii)$ el coseno de la diferencia de dos ángulos, $\cos (\alpha – \beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta$.
  4.  Sean $\alpha$ y $\beta$ ángulos agudos prueba que:
    $i)$ $\sin \alpha \cos \beta = \dfrac{\sin (\alpha + \beta) + \sin (\alpha – \beta)}{2}$,
    $ii)$ $\cos \alpha \sin \beta = \dfrac{\sin (\alpha + \beta) – \sin (\alpha – \beta)}{2}$.
  5. Sea $\triangle ABC$, por $A$ traza cualquier recta que corte a $BC$ en $L$, muestra que $\dfrac{BL}{LC} = \dfrac{AB \sin \angle BAL}{AC \sin \angle LAC}$.
Figura 8
  1. Demuestra que si $\dfrac{\sin \alpha}{\sin \beta} = \dfrac{\sin \delta}{\sin \gamma}$ y $\alpha + \beta = \delta + \gamma < \pi$ entonces $\alpha = \delta$ y $\beta = \gamma$.
  2. Sea $\triangle ABC$ con $a = BC$, $b = AC$, $c = AB$, $\alpha = \angle BAC$, $\beta = \angle CBA$, $\gamma = \angle ACB$, demuestra las siguientes formulas para calcular el área de $\triangle ABC$:
    $i)$ $(\triangle ABC) = \dfrac{ac \sin \beta}{2} = \dfrac{ab \sin \gamma}{2} = \dfrac{bc \sin \alpha}{2}$,
    $ii)$ $(\triangle ABC) = \dfrac{a^2 \sin \beta \sin \gamma}{2 \sin (\beta + \gamma)} = \dfrac{b^2 \sin \alpha \sin \gamma}{2 \sin (\alpha + \gamma)} = \dfrac{c^2 \sin \alpha \sin \beta}{2 \sin (\alpha + \beta)}$.

Entradas relacionadas

Fuentes

  • Santos, J., Tesis Geometría del Cuadrilátero. 2010, pp 69-78.
  • Cárdenas, S., Notas de Geometría. México: Ed. Prensas de Ciencias, 2013, pp 55-62.
  • Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 89-95.

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»