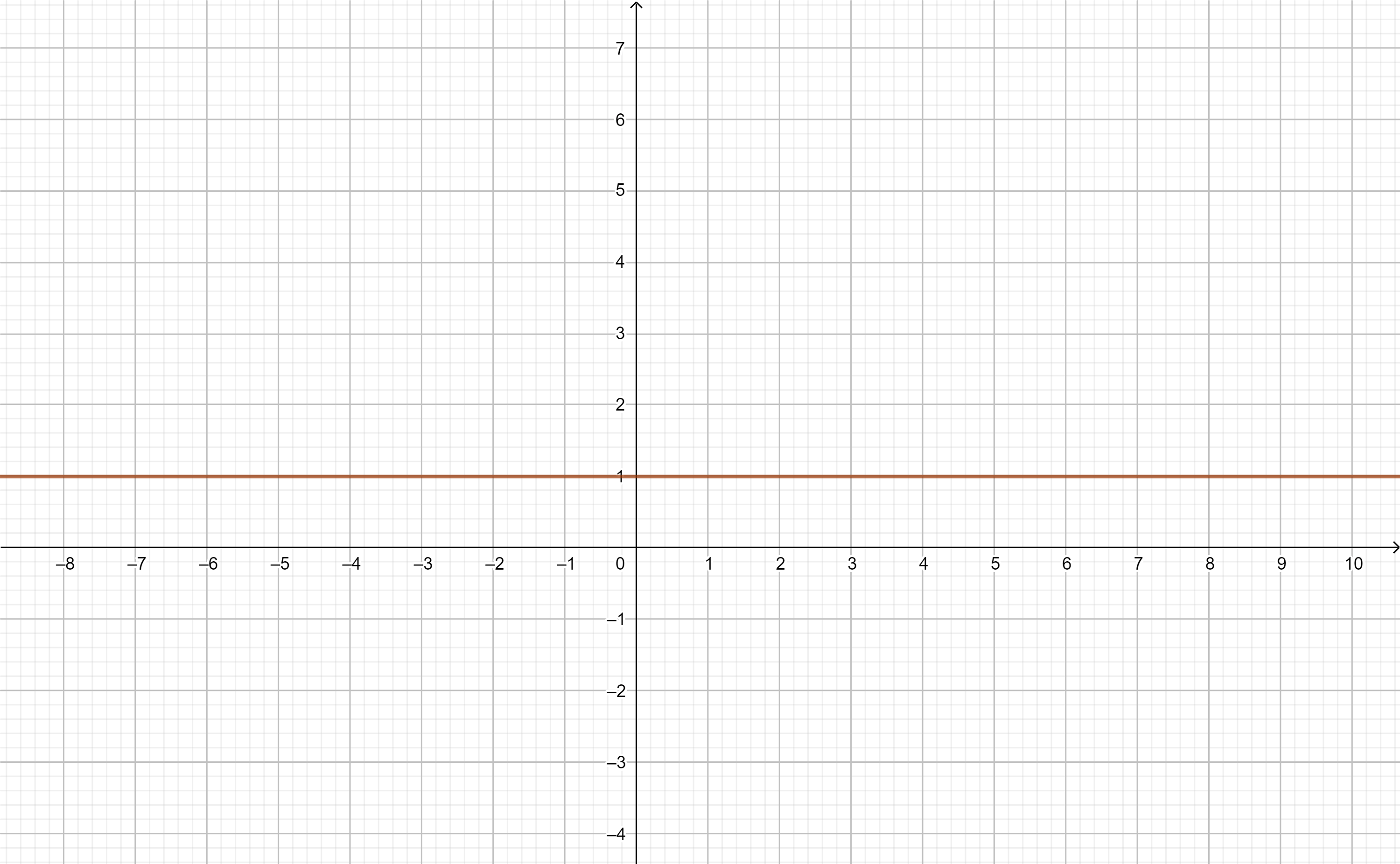Introducción

En esta entrada veremos un par de tipos de funciones muy particulares: las exponenciales y las logarítmicas. Probablemente en alguno de tus cursos anteriores te encontraste con funciones del tipo:
$$\begin{array}{rlrl}f(x)& =3^x& g(x)& =ln(x)\end{array}$$

Aquí veremos su representación gráfica, ejercicios relacionados y algunos resultados importantes, como las leyes de los exponentes y de los logaritmos. Se profundizará más en este conjunto de funciones en el curso de Cálculo Diferencial e Integral II.

Funciones exponenciales

Definición (función exponencial): Sea $f$ una función. Decimos que $f$ es una función exponencial si está definida como:
$$f:\mathbb{R}\to (0,\mathrm{\infty })$$
$$f(x)=a^x$$
con $a\in \mathbb{R}$ y $a>0$.
En este tipo de funciones tenemos que la variable $x$ está como exponente.
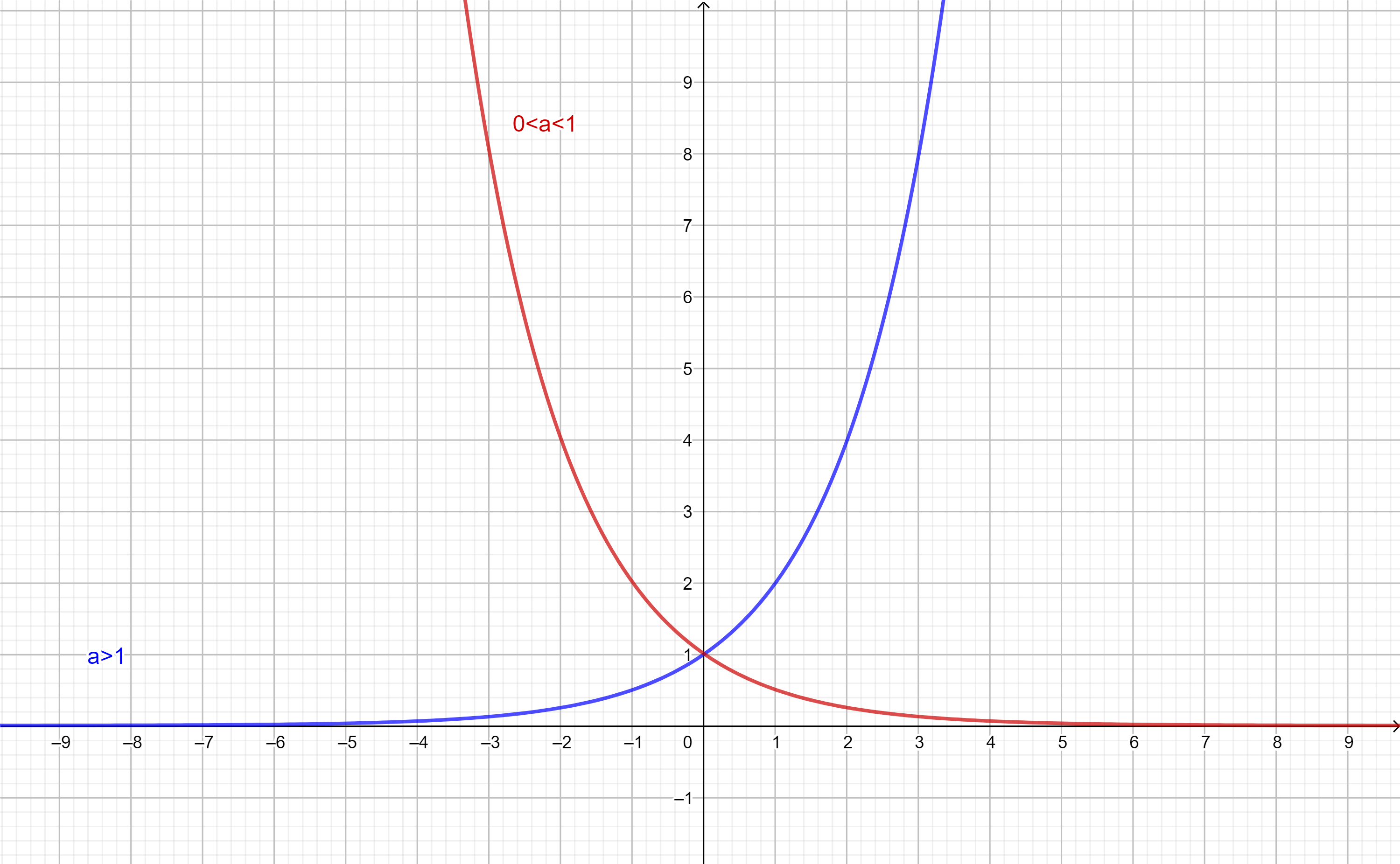
Observemos que tenemos los siguientes casos:

Veamos que al tomar $a=1$ tenemos que su gráfica se vería:
$$f(x)=1^x$$

Leyes de los exponentes

Teorema (Leyes de los exponentes): Consideremos a $a,m,n\in \mathbb{R}$ y $a>0$. Vemos que se cumplen las siguientes propiedades:

1. $a^m{a}^n=a^{m+n}$
2. $(a^n{)}^m=a^{(n\cdot m)}$
3. $a^0=1$
4. $a^{-1}=\frac{1}{a}$
5. $a^{-n}=\frac{1}{a^n}$
6. $a^{n-m}=\frac{a^n}{a^m}$
7. $a^{\frac{1}{q}}=\sqrt[q]{a}$
8. $a^{\frac{p}{q}}=\sqrt[q]{a^p}$

Por el momento no daremos las pruebas pertinentes, ya que las herramientas necesarias se verán durante el próximo curso de cálculo. Así pasaremos a revisar otros resultados relacionados a las funciones exponenciales.

Otros resultados sobre funciones exponenciales

Proposición: Consideremos $a>0$ y $r=\frac{p}{q}\in \mathbb{Q}$.

1. Si $a>1$ y $r>0$ entonces $a^r>1$
2. Si $0<a<1$ y $r>0$ entonces $a^r<1$
3. Si $a>1$ y $r<0$ entonces $a^r<1$
4. Si $0<a<1$ y $r<0$ entonces $a^r>1$

Demostración:

1. Como $a>1$ se sigue que:
   $$\begin{array}{rl}a>1& \Rightarrow \sqrt[q]{a}>\sqrt[q]{1}\\ & \Rightarrow (\sqrt[q]{a}{)}^p>(\sqrt[q]{1}{)}^p\\ & \Rightarrow a^{\frac{p}{q}}>1\\ & \Rightarrow a^r>1\end{array}$$
2. Ahora tenemos que $0<a<1$:
   $$\begin{array}{rl}& \Rightarrow \sqrt[q]{a}<\sqrt[q]{1}\\ & \Rightarrow (\sqrt[q]{a}{)}^p<(\sqrt[q]{1}{)}^p\\ & \Rightarrow a^r<1\end{array}$$
3. Tarea moral
4. Ya que $0<a<1$ observamos que:
   $$1<\frac{1}{a}$$
   Adicionalmente como $r<0$ se sigue:
   $$\begin{array}{rl}& \Rightarrow {\left(\frac{1}{a}\right)}^r<1\\ & \Rightarrow (a^{-1}{)}^r<1\\ & \Rightarrow a^{-r}<1\\ & \Rightarrow \frac{1}{a^r}<1\\ & \Rightarrow 1<a^r\end{array}$$

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Teorema: Sea $f:A\subseteq \mathbb{R}\to \mathbb{R}$.

1. Si $f$ es una función creciente $\Rightarrow f$ es inyectiva.
2. Si $f$ es una función decreciente $\Rightarrow f$ es inyectiva.

Demostración de 1:
Tomemos $x_1,x_2\in A$ tales que $x_1\ne x_2$ por lo que tenemos los siguientes casos:
Caso 1: Si $x_1>x_2$ entonces al aplicar la función $f$ tenemos
$$f(x_1)>f(x_2).$$
Por lo que:
$$f(x_1)\ne f(x_2).$$

Caso 2: Ahora si $x_1<x_2$ y aplicamos la función $f$
$$f(x_1)<f(x_2).$$
Así:
$$f(x_1)\ne f(x_2).$$
De los casos anteriores concluimos que $f$ es inyectiva.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Afirmación: Si tenemos $a>0$ y $f:\mathbb{R}\to {\mathbb{R}}^{+}$
$$f(x)=a^x$$

1. Si $a>1$ entonces $f$ es creciente.
2. Si $0<a<1$ entonces $f$ es decreciente.

Demostración:

1. Si $a>1$ y tomamos $x<y$ entonces $y-x>0$
   $$\begin{array}{rl}& \Rightarrow a^{y-x}>1\\ & \Rightarrow \frac{a^y}{a^x}>1\\ & \Rightarrow a^y>a^x\end{array}$$
2. En cambio si $0<a<1$ y ahora consideramos $x<y$. Queremos probar que:
   $f(x)>f(y)$
   $$\begin{array}{rl}x<y& \Rightarrow y-x>0\\ & \Rightarrow a^{y-x}<1\\ & \Rightarrow \frac{a^y}{a^x}<1\\ & \Rightarrow a^y<a^x\\ & \Rightarrow f(y)<f(x)\end{array}$$

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Observación: Si $a>0$ y $a\ne 1$ entonces $f(x)=a^x$ es inyectiva.
Observación: $f(x)=a^x$ es sobreyectiva.

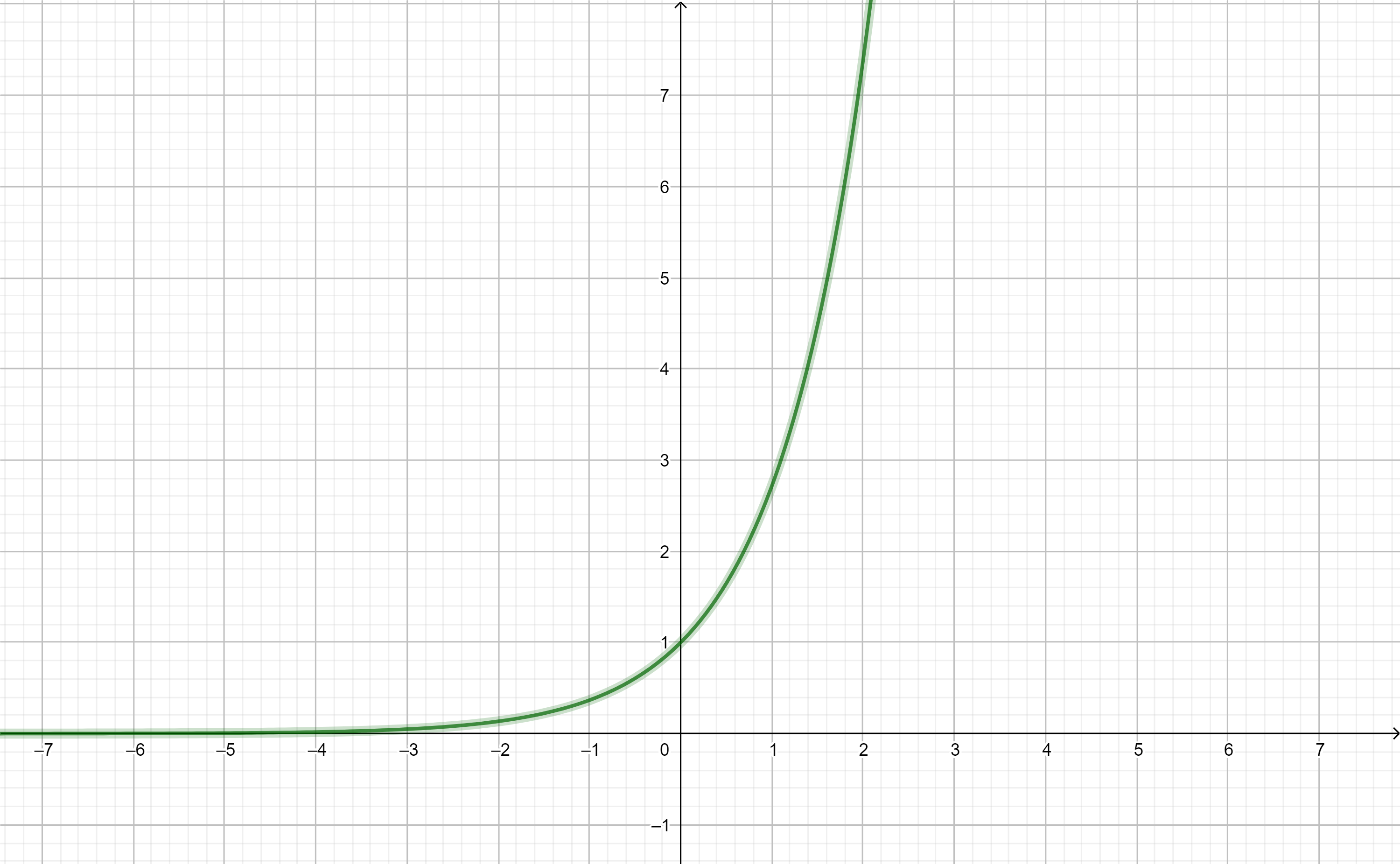
Ahora hablemos del número $e$

Si consideramos $a=e$ donde:
$$e=2.718282\dots$$
que es llamado el número de Euler.
Obtenemos la función:
$$f(x)=e^x,$$
llamada función exponencial, ésta es quizá las más conocida de este tipo de funciones.

Su gráfica se ve del siguiente modo:

¿Y su función inversa?

Si tomas la función $f(x)=a^x$, la función identidad y reflejamos su gráfica, obtenemos que $f^{-1}$ se ve como:

Observamos que $f^{-1}$ esta definida como:
$$f^{-1}:(0,\mathrm{\infty })\to \mathbb{R}$$
que vemos también cumple ser inyectiva.
A $f^{-1}(x)$ la denotaremos por:
$$f^{-1}(x)=lo{g}_a(x).$$

Funciones logarítmicas

Definición (función logarítmica): Sea $g$ una función en los reales. Decimos que $g$ es una función logarítmica si:
$$g:(0,\mathrm{\infty })\to \mathbb{R}$$
$$g(x)=lo{g}_a(x)$$
donde $lo{g}_a(x)$ se lee como logaritmo base $a$ de $x$.
Notación:

• Si tomamos $a=e$:
  $$lo{g}_e(x):=ln(x)$$
  llamado logaritmo natural de $x$.
• Si tomamos $a=10$ escribiremos:
  $$lo{g}_{10}(x):=log(x)$$

Leyes de los logaritmos

Teorema (Leyes de los logaritmos): Sean $a\in (0,\mathrm{\infty })$ con $a\ne 1$, $x,y\in (0,\mathrm{\infty })$ y $r\in \mathbb{R}$. Tenemos que se cumplen las siguientes igualdades:

1. $lo{g}_a(x\cdot y)=lo{g}_a(x)+lo{g}_b(y)$
2. $rlo{g}_a(x)=lo{g}_a(x^r)$
3. $lo{g}_a(\frac{x}{y})=lo{g}_a(x)-lo{g}_a(y)$

Demostración:
Tomemos $lo{g}_a(x)=z$ y $lo{g}_a(y)=w$ y notemos que:
$$\begin{array}{rlrl}{a}^z& =x& a^w& =y\end{array}$$

1. Para este punto consideremos el producto de $x$ con $y$:
   $$\begin{array}{rl}x\cdot y& =a^z\cdot a^w\\ & =a^{z+w}\end{array}$$
   Así sustituyendo al logaritmo del producto tenemos:
   $$\begin{array}{rl}lo{g}_a(x\cdot y)& =lo{g}_a(a^{z+w})\\ & =z+w\\ & =lo{g}_a(x)+lo{g}_a(y)\end{array}$$
2. Ahora si elevamos $a^z=x$ a la $r$ obtenemos:
   $$(a^z{)}^r=x^r\Rightarrow a^{rz}=x^r$$
   Tomando el $lo{g}_a(x^r)$ se sigue:
   $$\begin{array}{rl}lo{g}_a(x^r)& =lo{g}_a(a^{rz})\\ & =rz\\ & =rlo{g}_a(x)\end{array}$$
3. Por último veamos que:
   $$x=\frac{x}{y}\cdot y$$
   Tomando lo anterior y aplicando logaritmo:
   $$\begin{array}{rl}lo{g}_a(x)& =lo{g}_a(\frac{x}{y}\cdot y)\\ & =lo{g}_a\left(\frac{x}{y}\right)+lo{g}_a(y)\end{array}$$
   Reacomodando obtenemos:
   $$lo{g}_a\left(\frac{x}{y}\right)=lo{g}_a(x)-lo{g}_a(y)$$

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Cambio de base de logaritmos

Proposición (Cambio de base): Consideremos $a,b\in (0,\mathrm{\infty })$ donde $a\ne 1,b\ne 1$, $x\in \mathbb{R}$ y $y>0$. Se cumplen las siguientes propiedades:

1. $a^x=b^{xlo{g}_b(a)}$
2. $lo{g}_a(y)=\frac{lo{g}_b(y)}{lo{g}_b(a)}$

Demostración:

1. Si aplicamos la segunda ley de los logaritmos en la siguiente igualdad y simplificamos tenemos:
   $$\begin{array}{rl}{b}^{xlo{g}_b(a)}& =b^{lo{g}_b(a^x)}\\ & =a^x.\end{array}$$
2. Como $y>0$ entonces podemos considerar $x=lo{g}_a(y)$. Así sustituyendo en el punto 1:
   $$\begin{array}{rl}{a}^{lo{g}_a(y)}& =b^{lo{g}_a(y)lo{g}_b(a)}.\end{array}$$
   De lo anterior tenemos:
   $$y=b^{lo{g}_a(y)lo{g}_b(a)}.$$
   Tomando el logaritmo base $b$ en ambos lados de la igualdad:
   $$\begin{array}{rl}lo{g}_b(y)& =lo{g}_b(b^{lo{g}_a(y)lo{g}_b(a)})\\ & =lo{g}_a(y)\cdot lo{g}_b(a)\end{array}$$
   $$\therefore lo{g}_a(y)=\frac{lo{g}_b(y)}{lo{g}_b(a)}.$$

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Ejercicio

Resuelve la ecuación:
$$lo{g}_4(lo{g}_3(lo{g}_2(x)))=0.$$
Solución:
Comenzaremos realizando un cambio de variable considerando:
$$\beta =lo{g}_3(lo{g}_2(x)).$$
Por lo que tendríamos:
$$lo{g}_4(\beta )=0.$$
Lo anterior implica que:
$$4^{lo{g}_4(\beta )}=4^0=1.$$
$$\therefore \beta =1$$
$$\therefore lo{g}_3(lo{g}_2(x))=1$$
Procedemos con un razonamiento similar para $lo{g}_3(lo{g}_2(x))=1$:
$$3^{lo{g}_3(lo{g}_2(x))}=3^1=3.$$
Por lo que concluimos:
$$lo{g}_2(x)=3.$$
Finalmente, de $lo{g}_2(x)=3$ obtenemos:
$$2^{lo{g}_2(x)}=2^3=8.$$
Así tenemos que el valor para $x$ sería:
$$x=8.$$

Realizando la comprobación vemos que se cumple:
$$\begin{array}{rl}lo{g}_4(lo{g}_3(lo{g}_2(x)))& =lo{g}_4(lo{g}_3(lo{g}_2(8)))\\ & =lo{g}_4(lo{g}_3(3))\\ & =lo{g}_4(1)\\ & =0\end{array}$$
$$\therefore lo{g}_4(lo{g}_3(lo{g}_2(x)))=0.$$

Más adelante

Ahora que hemos terminado la unidad de funciones, en la próxima entrada comenzaremos con la unidad dedicada al estudio de un tipo especial de funciones: las sucesiones de números reales. Encontrarás una introducción intuitiva sobre el concepto de sucesión para luego pasar a su definición formal y una serie de ejemplos.

Tarea moral

• Demuestra el punto 3 de la Proposición.
• Grafica las siguientes funciones:
  • $f(x)=ln(x-2)$
  • $f(x)=1-e^x$
• Demuestra que dado $a\in (0,\mathrm{\infty })-\left\{1\right\}$:
  $$lo{g}_{\frac{1}{a}}(x)=-lo{g}_a(x)$$
• Resuelve los siguientes ejercicios:
  • $lo{g}_2(lo{g}_3(lo{g}_2(x)))=1$
  • $lo{g}_{16}(x)+lo{g}_4(x)+lo{g}_2(x)=7$

Entradas relacionadas

• Ir a: Cálculo Diferencial e Integral I
• Entrada anterior del curso: Cálculo Diferencial e Integral I: Funciones trigonométricas (Parte 2)
• Entrada siguiente del curso: Cálculo Diferencial e Integral I: Sucesiones de números reales.
• Resto de cursos: Cursos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»