Archivo de la etiqueta: naturales

Álgebra Superior II: Principio de inducción y teoremas de recursión

Por Roberto Manríquez Castillo

Deja un comentario

Introducción

Inducción y recursión son dos conceptos similares con los que seguramente te has topado en tu formación matemática, e incluso tal vez antes. Muchas veces se llegan a confundir ambos conceptos, ya que ambos tienen una fuerte relación con el 5° axioma de Peano.

Aunque lo detallaremos a lo largo de la entrada, el principio de Inducción es una propiedad de los números naturales, que nos sirve para demostrar que todos los naturales satisfacen una propiedad. Es decir, es una estrategia de demostración. En contraste, la recursión es un resultado que justifica el hecho de poder dar una definición para todos los naturales, basándonos en la definición de su antecesor. En otras palabras, es una estrategia de definición.

Al final de la entrada demostraremos el teorema de recursión débil, en cuya prueba, podremos apreciar cómo es que depende directamente del Principio de inducción.

Pruebas por inducción

Recordemos el 5° axioma de Peano, el cual probamos en la entrada pasada que se satisface en nuestro modelo:

Si $S\subset \mathbb{N}$ satisface que

  • $0\in S$ y
  • si $n\in S$, implica que $\sigma(s)\in S$,

entonces $S=\mathbb{N}$.

Como hemos mencionado en entradas anteriores, esta proposición es muy similar al principio de Inducción que probablemente hayas ocupado desde el curso de Álgebra Superior I. Más aún, en la entrada pasada, seguimos la misma estrategia que en otros cursos, a la hora de ocupar el 5° axioma. Efectivamente, la equivalencia entre ambos resultados es casi inmediata, y como ejemplo ilustrativo, probaremos el Principio de Inducción a partir del 5° axioma de Peano.

Proposición (Principio de Inducción): Sea $P(n)$ una propiedad, es decir, una proposición matemática que depende de un entero $n$. Si se tiene que:

  1. $P(0)$ es verdadera y
  2. cada vez que $P(n)$ es cierto, también lo es $P(n+1)$,

entonces P(n) es cierta para todos los números naturales.

Demostración. Sea $P(n)$ una propiedad que satisface 1. y 2. y consideremos el conjunto $S:=\{n\in\mathbb{N}: P(n)\text{es verdadera}\}$.

Como $P(0)$ es verdadera, entonces $0\in S$.

Tomemos $n\in S$, entonces $P(n)$ es verdadera, y por 2., tenemos que $P(n+1)$ es verdadera; es decir, $n+1\in S$. Por el 5° Axioma de Peano, se tiene que $S=\mathbb{N}$, por lo que por la definición de $S$, se tiene que $P(n)$ es cierta para cada $n\in \mathbb{N}$

$\square$

Definiciones por recursión

Una de nuestras primeras ideas para poder construir a $\mathbb{N}$, fue intentar construir a mano cada elemento. Para esto, dimos una definición de lo que significaba el $0$ y el sucesor de un número. Después empezamos a iterar una y otra vez la función sucesor para obtener el sucesor del último número encontrado. Discutimos por qué es que esta idea no sería el mejor camino (sólo nos permite llegar hasta una cantidad finita de naturales), por lo tuvimos que introducir el Axioma del Infinito para resolver el problema. Veamos la analogía entre esta idea y el siguiente ejemplo intuitivo.

Ejemplo: Definamos la función factorial de un número natural, como:

  • $0!=1$
  • $(n+1)!=(n!)(n+1)$

Entonces, $3!:=(2!)(3)=(1!)(2)(3)=(0!)(1)(2)(3)=(1)(1)(2)(3)=6$.

Recordemos que al definir a los naturales, necesitábamos conocer un número para poder definir su sucesor. Aquí sucede lo mismo: en la definición de factorial necesitamos conocer quién es el factorial de un número para poder definir el factorial de su sucesor. A este tipo de definiciones se les conoce como definiciones recursivas, ya que para definir algo para un número, necesitamos tener conocimiento del valor de la función en los números anteriores.

Queda una pregunta muy importante. Si a los naturales no los pudimos definir de manera recursiva, ¿por qué podemos afirmar que la función factorial sí existe? A continuación enunciaremos algunos teoremas que nos garantizarán que sí podemos hacer este tipo de definiciones recursivas en nuestro modelo. Daremos una versión fuerte y una versión débil. Demostraremos la versión débil, pues basta para mucho de lo que queremos definir en los naturales (sumas, productos, potencias).

Las siguientes secciones son un poquito técnicas. Si las puedes seguir por completo, es fantástico. Pero incluso si no es así, basta con que en el fondo te quedes con la idea importante detrás: sí se vale definir de manera recursiva. Más adelante podrás regresar a este tema y entenderlo por completo.

Los teoremas de la recursión

Antes de la demostración principal de esta entrada, enunciaremos los teoremas que nos importan y hablaremos de manera intuitiva de lo que dicen. Hay dos versiones que veremos: una fuerte y una débil. Aunque parece que dicen cosas diferentes, en realidad son equivalentes. Será muy claro que la versión fuerte «implica» a la débil. Pero luego, en los problemas de tarea moral, se esbozará cómo ver que la versión débil se puede utilizar para demostrar la fuerte.

Teorema (Recursión Fuerte): Sea $X$ un conjunto y $x_{0}\in X$. Supongamos que tenemos varias funciones (una por cada natural $i$)

$$\{f_i:X\to X\}_{i\in\mathbb{N}\setminus \{0\}}.$$

Entonces existe una única función $g:\mathbb{N}\to X$ tal que:

  • $g(0)=x_{0}$
  • $g(\sigma(n))=f_{\sigma(n)}(g(n))$.

¿Qué es lo que quiere decir este teorema? Para responder esta pregunta veamos el siguiente diagrama:

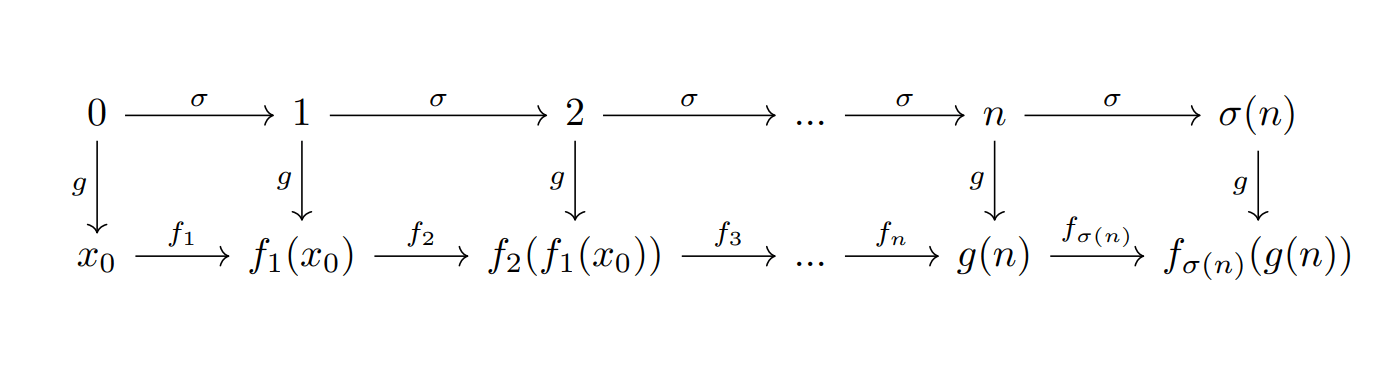
Nuestro diagrama empieza en $0$, el cual queremos que sea mandado a algún $x_{0}\in X$, para la definición de los demás números, ocupamos la segunda característica que esperamos que $g$ satisfaga. Por ejemplo $g(1)=g(\sigma(0))=f_{1}(g(0))=f_{1}(x_{0})$. Este análisis coincide con lo que nos presenta el primer cuadro de flechas del diagrama anterior, que nos presenta los dos caminos que debe satisfacer $g$, para que sea la función que queremos. Como da lo mismo si «primero aplicamos $\sigma$ y luego $g$», a que si «primero aplicamos $g$ y luego $f_1$», decimos que el primer cuadrado del diagrama conmuta.

Análogamente, ya que conocemos la definición de $g(1)$ podemos fijarnos en el segundo cuadro, para poder definir $g(2)$ (de nuevo, conmuta) y seguir «recursivamente» para cualquier número natural.

Ejemplo: ¿Qué conjunto, y qué funciones necesitamos para definir el factorial?

Consideremos $X=\mathbb{N}$, definiremos intuitivamente (ya que aún no lo hemos definido formalmente), $f_{i}:\mathbb{N}\longrightarrow \mathbb{N}$, como $f_{i}(n)=i\cdot n$, es decir, el producto por $i$.

El teorema de Recursión Fuerte, nos dice que existe una única función $g$ tal que

  • $g(0)=1$
  • $g(\sigma(n))=f_{\sigma(n)}(g(n))=\sigma(n)\cdot g(n)$

Denotemos $n!:=g(n)$. Entonces tenemos que $\sigma(n)!=n!\cdot \sigma(n)$, justo como queremos.

$\triangle$

El teorema de Recursión Débil y su demostración

El teorema de Recursión Débil tiene un enunciado parecido al teorema de recursión fuerte y puede ser visto como una consecuencia directa del teorema anterior pues se obtiene de la versión fuerte tomando $f_{1}=f_{2}=\ldots=f_{n}=\ldots$

Teorema (Recursión Débil): Sea $X$ un conjunto y $x_{0}\in X$. Supongamos que tenemos una función $f:X\to X$. Entonces existe una única función $g:\mathbb{N}\to X$ tal que:

  • $g(0)=x_{0}$
  • $g(\sigma(n))=f(g(n))$.

Para concluir con esta entrada, probaremos el teorema de Recursión Débil. Antes de hacer esto introducimos un concepto auxiliar y una propiedad de los naturales.

Recordemos que como conjunto, $m=\{0,1,…,m-1\}$, lo que sugiere la siguiente definición.

Definición: Si $n,m\in \mathbb{N}$, decimos que $n<m$ si $n\in m$.

Puede probarse que esta relación en $\mathbb{N}$ es un orden total, y que sastisface la siguiente propiedad.

Teorema (Principio el Buen Orden): Sea $S\subset\mathbb{N}$ un conjunto no vacío, es decir $S\neq \emptyset$. Entonces $S$ tiene un elemento mínimo. Es decir, existe $n\in S$ tal que $n<m$ para todo $m\in S\setminus\{n\}$.

La prueba del Principio del Buen Orden y más propiedades de $<$ serán estudiadas con mayor detalle en entradas posteriores. Con esto en mente demostramos el teorema de Recursión Débil.

Demostración. Recordemos que por definición, toda función con dominio $A$ y codominio $B$, es un subconjunto de $A\times B$, por lo que una buena idea es analizar el conjunto $\wp(\mathbb{N}\times X)$, definamos

\[\Re:=\{R\in\wp(\mathbb{N}\times X)\mid (0,x_{0})\in R \text{ y si }(n,x)\in R\text{, entonces }(\sigma(n),f(x))\in R\}\]

Esta definición se ve terriblemente complicada. Pero la intuición es clara: $\Re$ tiene a todas las posibles colecciones de parejas de $\mathbb{N}\times X$ que cumplen lo que queremos. El problema es que muchas de ellas no son funciones y tenemos que «arreglar esto».

Probablemente, notarás alguna similitud entre el conjunto $\Re$ y el conjunto de los subconjuntos inductivos (que se menciona en La construcción de los naturales). Siguiendo esta analogía, definiremos $g:=\bigcap \Re$ (podemos hacer esta intersección ya que $\Re$ no es vacío pues $\mathbb{N}\times X$ está en $\Re$).

  • Demostremos que $g\in \Re$:

Por las propiedades de la intersección, tenemos que $g\subset\mathbb{N}\times X$, por lo que $g\in \wp(\mathbb{N}\times X)$. Veamos que $(0,x_{0})\in g$. Sea $R\in\Re$ arbitrario, entonces $(0,x_{0})\in R$, por lo que $(0,x_{0})\in\bigcap \Re=g$. Por último, si $(n,x)\in g$, demostremos que $(\sigma(n),f(x))\in g$, para esto, sea $R\in \Re$ arbitrario, como $(n,x)\in g$, entonces $(n,x)\in R$, por lo que $(\sigma(n),f(x))\in R$. Es decir, $(\sigma(n), f(x))\in\bigcap \Re=g$. Por todo lo anterior, $g\in\Re$.

  • Veamos ahora que $Dom(g)=\mathbb{N}$:

Usemos el quinto axioma de Peano, como $(0,x_{0})\in g$, entonces $0\in Dom(g)$. Supongamos ahora que $n\in Dom(g)$ y demostremos que $\sigma(n)\in Dom(g)$, por la hipótesis de inducción, existe $x\in X$ tal que $(n,x)\in g$, y como $g\in\Re$, tenemos que $(\sigma(n),f(x))\in g$, pero esto quiere decir que $\sigma(n)\in Dom(g)$. Entonces $Dom(g)$ es inductivo, entonces $Dom(g)=\mathbb{N}$.

  • Demostremos ahora que $g$ sí es función. Para esto, tenemos ver que «cada natural se va a un sólo elemento», en símbolos, si $(n,x),(n,y)\in g$ entonces $n=m$.

Aquí es donde ocuparemos el Principio del Buen Orden. Consideremos $S:=\{n\in\mathbb{N}\mid (n,x),(n,y)\in g \text{ y } x\neq y \}$. Procedamos por contradicción, supongamos que $S\neq\emptyset$, entonces, $S$ tiene un elemento mínimo, denotémoslo por $n$.

Si $n=0$, entonces existe $x\in X$ tal que $(0,x)\in X$ y $x\neq x_{0}$. Entonces consideremos $g’=g\setminus\{(0,x)\}$. Notemos que $g’\in\Re$, ya que $(0,x_{0})\in g’$, ya que $(0,x_{0})\neq (0,x)$. Además si $(k,a)\in g’$, entonces $(k,a)\in g$, por lo que $(\sigma(k),f(a))\in g$, y como $0$ nunca es el sucesor de otro número, tenemos que $(\sigma(k),f(a))\neq(0,x)$, por lo tanto $(\sigma(k),f(a))\in g’$, es decir, $g’\in \Re$, lo que implica que $g=\bigcap \Re\subset g’=g\setminus\{(0,x)\}$ lo cual es absurdo, por lo que $n\neq 0$.

Como $n\neq 0$, debemos tener que existe $m$ tal que $\sigma(m)=n$ ¿Por qué?. Y como $n$ es el mínimo en $S$, tenemos que $m\not\in S$, es decir, existe un único $x\in X$ tal que $(m,x)\in g$, esto implica que $(\sigma(m),f(x))=(n,f(x))\in g$, y como $n\in S$, debe existir $y\in X$, $y\neq f(x)$ tal que $(n,y)\in g$. Análogamente a como lo hicimos antes, consideremos $g’=g\setminus (n,y)$ y veamos que $g’\in \Re$. Como $(n,y)\neq(0,x_{0})$, tenemos que $(0,x_{0})\in g’$. Más aún, si $(k,a)\in g’$, demostremos que $(\sigma(k),f(a))\in g’$, para esto supongamos que no.

Como $(k,a)\in g’$, tenemos que $(k,a)\in g$, por lo que $(\sigma(k),f(a))\in g$, esto implica que $(\sigma(k),f(a))=(n,y)$ ya que este es el único elemento de $g$ que no está en $g’$. Como $\sigma(k)=n=\sigma(m)$, concluimos, por la inyectividad de $\sigma$, que $k=m$. Esto quiere decir que $(k,a)=(m,a)\in g$, pero recordando que $x$ es el único elemento relacionado con $m$, concluimos que $x=a$, en síntesis, $(k,a)=(m,x)$, por lo que $(\sigma(k),f(a))=(\sigma(m),f(x))=(n,f(x))\neq(n,y)$. Esto implica que $(\sigma(k), f(a))\in g’$, contradiciendo nuestra suposición de que no lo estaba.

Entonces hemos probado que $(0,x_{0})\in g’$ y que cada vez que $(k,a)\in g’$, también lo está $(\sigma(k), f(a))$. Esto quiere decir que $g’\in\Re$, y como lo hicimos anteriormente, tendremos que $g=\bigcap \Re\subset g’=g\setminus\{(n,y)\}$, lo cual es una contradicción. Esto quiere decir, que suponer que $S$ tiene un elemento mínimo, es absurdo, por lo que $S=\emptyset$. Lo que traducido quiere decir que para todo $n\in\mathbb{N}$, existe un único $x\in X$ tal que $(n,x)\in g$. Es decir, que $g$ sí es una función.

  • Demostremos que $g$ satisface las dos propiedades del Teorema.

Ya vimos que $g\in \Re$, por lo que $g(0)=x_{0}$. Sea ahora $n\in \mathbb{N}$ y $x=g(n)$, de nuevo, como $g\in\Re$, tenemos que $g(\sigma(n))=f(x)=f(g(n))$.

  • Por último, demostremos la unicidad de $g$.

Si $h:\mathbb{N}\longrightarrow X$ es otra función que satisface las características del Teorema, consideremos $A=\{n\in\mathbb{N}\mid h(n)=g(n)\}$, como $h(0)=x_{0}=g(0)$. Tenemos que $0\in A$. Supongamos que $n\in A$. Tendríamos entonces que $h(\sigma(n))=f(h(n))=f(g(n))=g(\sigma(n))$, es decir que $\sigma(n)\in A$, por lo que $A$ es inductivo, y por consiguiente, $A=\mathbb{N}$. En resumen, $h$ y $g$, coinciden en dominio, codominio y regla de correspondencia, entonces $h=g$, como debíamos probar.

$\square$

La demostración del teorema de Recursión Fuerte requiere de algunos detalles adicionales, pero puede deducirse del teorema de Recursión Débil. Dejamos esto como uno de los problemas de la tarea moral.

Más adelante…

El teorema de Recursión será la mayor herramienta que tendremos para poder darle una forma más familiar a los números naturales, ya que las operaciones de suma y multiplicación, que veremos en la siguiente entrada, tendrán una definición recursiva.

Y así como el teorema de la Recursión nos permitirá definir, usaremos continuamente el principio de Inducción para poder demostrar las numerosas propiedades que estas operaciones tienen.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Demuestra el 5° Axioma de Peano a partir del Principio de Inducción.
  2. Demuestra que si $n\neq 0$ entonces existe $m$ tal que $\sigma(m)=n$.
  3. ¿Qué función $g$, satisface que $g(0)=1$ y $g(\sigma(n))=2\cdot g(n)$? ¿Qué función $f$ estamos ocupando?
  4. ¿Qué conjunto y que función nos permitiría definir la sucesión de Fibonacci $a_{n+2}=a_{n+1}+a_{n}$ usando el Teorema de Recursión?
  5. Demuestra el Teorema de Recursión Fuerte, usando el Débil. Sugerencia: Considera, $F(n,x):\mathbb{N}\times X\longrightarrow \mathbb{N}\times X$, como $F(n,x)=(\sigma(n),f_{\sigma(n)}(x))$.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Álgebra Superior II: La construcción de los naturales

Por Roberto Manríquez Castillo

Deja un comentario

Introducción

En la entrada pasada presentamos los axiomas de Peano como una formalización de por qué los naturales se comportan como nuestra intuición nos indica. Sin embargo, también vimos que, por si mismos, los axiomas de Peano no nos dicen cómo hacer una construcción de los naturales a partir de conceptos previos. Para intentar lograr esto, introdujimos la definición del sucesor de un conjunto arbitrario y empezamos a iterarla en el conjunto vacío para generar una lista de conjuntos, que relacionamos con los números naturales que conocemos.

Por último, notamos que ocupar esta idea, al menos de forma directa, tiene el problema de dar «pasitos muy chicos», que no nos permitirían acabar nunca de definir a todos los números naturales y, en consecuencia, que no nos dejaría definir en sí el conjunto de los naturales.  Es por eso que en esta entrada acabaremos, de una vez por todas, con el problema de definir con precisión el conjunto de números naturales. Veremos que, en efecto, esta construcción que haremos se apega no sólo a nuestra intuición, sino también a los axiomas de Peano.

Conjuntos inductivos

Antes de empezar con la tarea de definir a los números naturales, recordamos la definición del sucesor de un conjunto.

Definición. Si $A$ es un conjunto, definimos el sucesor de $A$, como $\sigma(A):=A\cup \{A\}$.

El conjunto que queremos definir es el conjunto $\mathbb{N}$ de números naturales. Como mencionamos en las entrada pasada, buscamos de manera formal lograr que \[\mathbb{N}=\{\emptyset,\sigma(\emptyset),\sigma(\sigma(\emptyset)),…\},\] por lo que $\mathbb{N}$ satisfaría dos propiedades que englobamos en la siguiente definición.

Definición. Diremos que un conjunto $S$ es inductivo si cumple que:

  1. $\emptyset\in S$ y
  2. si $X\in S$, entonces $\sigma(X)\in S$.

Notemos que estas dos propiedades son muy similares a los dos primeros axiomas de Peano.

Hay que remarcar que aunque no sabemos que exista un conjunto tal que sus elementos son $\emptyset,\sigma(\emptyset),\sigma(\sigma(\emptyset)),…$, en caso de que sí existiera, sería un hecho que tal conjunto sería inductivo.

Otro posible ejemplo de un conjunto inductivo podría verse como \[\{…\sigma(\sigma(\{\{\emptyset\}\})), \sigma(\{\{\emptyset\}\}), \{\{\emptyset\}\},\emptyset,\sigma(\emptyset),\sigma(\sigma(\emptyset)),…\}.\]

Intuitivamente podemos notar que si $S$ es un conjunto inductivo, entonces, $\mathbb{N}\subset S$, por lo que uno podría aventurarse y definir a los naturales como $$\{x:  x \text{ está en todo conjunto inductivo}\}.$$

Sin embargo, los axiomas que de teoría de conjuntos que tenemos hasta ahora no nos permiten saber si se puede construir un conjunto así.

¿Qué es lo que sí nos permiten hacer los axiomas de teoría de conjuntos? Si tenemos una colección de conjuntos, podemos hacer la intersección de todos ellos. Esto motiva la siguiente proposición acerca de la intersección de conjuntos inductivos.

Proposición. Si $B\neq\emptyset$ es un conjunto tal que todos sus elementos son conjuntos inductivos, entonces $\bigcap {B}$ es también un conjunto inductivo.

Demostración. Como $B\neq\emptyset$, sabemos que la intersección sí es un conjunto. Veamos que este conjunto es inductivo. Antes de hacer esto recordemos que, por definición, los elementos de $\bigcap{B}$ son precisamente, todos los $x$ tales que $x\in Y$ para todo $Y\in B$.

Para ver que $\bigcap B$ es inductivo, necesitamos verificar que cumpla las dos características de la definición:

  1. Veamos primero que $\emptyset\in\bigcap B$.
    Sea $Y\in B$ arbitrario. Como los elementos de $B$ son inductivos, $\emptyset\in Y$, y como $Y$ es arbitrario, podemos concluir que $\emptyset$ está en todos los elementos de $B$. Esta es justo la definición de que $\emptyset\in \bigcap B$.
  2. Veamos ahora que $x\in \bigcap B \Rightarrow \sigma(x)\in \bigcap B$.
    Sea $x\in \bigcap B$ y sea $Y\in B$. Como $x\in\bigcap B$, entonces $x\in Y$ y como $Y$ es inductivo, $\sigma(x)\in Y$. De nuevo, como $Y$ fue arbitrario, se sigue que $\sigma(x)$ está en todos los elementos de B, por lo que $\sigma(x)\in\bigcap B$.

Con esto demostramos que $\bigcap B$ es inductivo.

$\square$

En otras palabras, «la intersección arbitraria de conjuntos inductivos es un conjunto inductivo».

El axioma del infinito y la construcción de los naturales

Por todo lo escrito anteriormente, y meditando el hecho de que si partimos de los primeros axiomas de la teoría de conjuntos, sólo podemos crear conjuntos con una cantidad finita de elementos, parece ser que la existencia de un conjunto como los naturales no puede ser deducida con las herramientas que tenemos. Esto en efecto es así. Por ello, debemos introducir un nuevo axioma de la teoría de conjuntos.

Axioma (del infinito). Existe un conjunto inductivo.

El axioma del infinito no nos garantiza inmediatamente la existencia de $\mathbb{N}$, ya que como se vio en un ejemplo más arriba, $\mathbb{N}$ no es el único conjunto inductivo. Sin embargo, esta es la última pieza que necesitamos para poder dar la construcción de los naturales. Hacemos esto a continuación.

Sea $A$ algún conjunto inductivo (que nos garantiza el axioma del infinito), y consideremos $B=\{X\subset A \mid X \text{ es inductivo}\}$ (¿por qué $B$ es un conjunto?). Notemos que $A\in B$ por lo que $B$ es no vacío, por lo tanto, podemos pensar en su intersección, $\bigcap B$. Como los elementos de $B$ son conjuntos inductivos, por la proposición anterior concluimos que $\bigcap B$ es inductivo. A esta intersección la denotaremos como $\mathbb{N}_{A}$. ¡Ya apareció por primera vez el símbolo de números naturales! Pero tiene algo adicional: usamos un subíndice $A$ ya que, a primera vista, su construcción depende del conjunto inductivo $A$ con el que empezamos. Sin embargo, justamente, el paso siguiente será ver que $\mathbb{N}_{A}$ no depende de $A$.

Para ello, primero hacemos la observación de que si $Y\subset A$ es inductivo, entonces $\mathbb{N}_{A}\subset Y$, la cual te dejamos corroborar usando las propiedades de la intersección. Dicho esto, probamos lo siguiente.

Proposición. Si $C$ es otro conjunto inductivo, entonces $\mathbb{N}_{A}= \mathbb{N}_{C} $.

Demostración. Consideremos $\mathbb{N}_{A} \cap \mathbb{N}_{C} $, el cual sabemos que es un conjunto inductivo. Como $\mathbb{N}_{A} \cap \mathbb{N}_{C} \subset A$, por la observación anterior, concluimos que $\mathbb{N}_{A} \subset \mathbb{N}_{A} \cap \mathbb{N}_{C} $. Como la intersección está contenida en cada intersecando, $\mathbb{N}_{A} \subset \mathbb{N}_{A} \cap \mathbb{N}_{C}\subset\mathbb{N}_{A} $, por lo que $\mathbb{N}_{A} = \mathbb{N}_{A} \cap \mathbb{N}_{C} $. Haciendo las mismas observaciones para $\mathbb{N}_{C}$, concluimos que $\mathbb{N}_{A} = \mathbb{N}_{A} \cap \mathbb{N}_{C}= \mathbb{N}_{C} $, con lo que concluimos la prueba.

$\square$

Como sabemos ahora que el conjunto $\mathbb{N}_{A}$ no depende del conjunto $A$ inductivo con el que empecemos, finalmente podemos definir al conjunto de números naturales.

Definición. Si $A$ es algún conjunto inductivo, definimos al conjunto de los números naturales $\mathbb{N}$ como $\mathbb{N}:=\mathbb{N}_{A}$. Definimos al cero como $0:=\emptyset$ y la función sucesor para los naturales como $\sigma:\mathbb{N}\to \mathbb{N}$ tal que $\sigma(n)=n\cup \{n\}$.

Nuestra construcción de los naturales cumple los axiomas de Peano

Para concluir esta entrada veremos que la construcción de los naturales que dimos en efecto da un modelo para los axiomas de Peano. En realidad, la construcción de la función sucesor, la noción de conjunto inductivo y la forma en la que creamos $\mathbb{N}$ fueron todas ellas siempre motivadas por estas ideas, por lo que no deberá ser difícil probar que en verdad todo funciona como queremos.

Teorema. El conjunto $\mathbb{N}$ junto con el $0$ y la función $\sigma$ que definimos satisfacen los cinco axiomas de Peano.

Demostración. Veamos que se verifican los cinco axiomas de Peano.

Axioma 1. $0\in\mathbb{N}$.

Como $\mathbb{N}$ es inductivo, $0=\emptyset\in\mathbb{N}$.

Axioma 2. Si $n\in \mathbb{N}$, entonces $\sigma(n)\in\mathbb{N}$.

Si $n\in\mathbb{N}$, como $\mathbb{N}$ es inductivo, se sigue que $\sigma(n)\in\mathbb{N}$.

Axioma 3. Para toda $n\in\mathbb{N}$ se tiene que $\sigma(n)\neq 0$.

Como $\sigma(n)=n\cup\{n\}$, tenemos que $n\in\sigma(n)$ por lo que $\sigma(n)\neq\emptyset=0$.

Axioma 4. Si $\sigma(n)=\sigma(m)$, entonces $n=m$.

Como $\sigma(n)=\sigma(m)$ y $n\in\sigma(n)$, entonces $n\in\sigma(m)= m\cup\{m\}$. Como $n$ está en una unión, hay dos opciones: $n\in\{m\}$ o $n\in m$. Si $n\in \{m\}$, entonces $n=m$ y concluimos.

En otro caso, $n\in m$. Veamos que podemos decir de $m$. Procediendo análogamente, podemos notar que $m=n$ o $m\in n$. En el primer caso, llegamos a lo que queremos. El segundo caso es imposible, pues tendríamos $n\in m\in n$ lo cual contradice el axioma de regularidad de teoría de conjuntos.

Axioma 5. Si $S\subset\mathbb{N}$ tal que $0\in S$ y $n\in S \Rightarrow \sigma(n)\in S$, entonces $S=\mathbb{N}$.

Notemos que las hipótesis de $S$ implican que éste es un conjunto inductivo. Por ello, $\mathbb{N}=\mathbb{N}_{S}\subset S\subset \mathbb{N}$. Esta cadena de contenciones implica la igualdad $\mathbb{N}=S$.

$\square$

Notemos que todos los axiomas salieron de forma casi inmediata de la definición de $\mathbb{N}$ o de la definición de $\sigma$, justo como esperábamos.

Más adelante…

Ya dimos la construcción de los naturales. También vimos que en verdad funcionan como esperábamos. nuestro siguiente objetivo será definir una suma, un producto y un orden en $\mathbb{N}$. Así como lo hicimos con los axiomas de Peano, veremos que nuestras definiciones coincidirán con las propiedades que conocemos.

Para hacer esto seguiremos pensando simultáneamente tanto en la definición conjuntista que hemos dado de los naturales, como en los axiomas de Peano. Especialemente usaremos el quinto axioma de manera repetida. Veremos cómo este axioma es básicamente el principio de inducción que conocimos en Álgebra Superior I. También veremos cómo nos ayuda a demostrar el teorema de recursión, el cual a su vez la herramienta que necesitaremos para definir con toda formalidad la suma y producto en los naturales.

Tarea moral

  1. Completa los detalles faltantes de la construcción de los naturales. En particular, sobre por qué el conjunto $B$, de los conjuntos inductivos de $A$, sí existe. Necesitarás usar un axioma muy específico de la teoría de conjuntos.
  2. Demuestra que si $x\subset y\subset\sigma(x) $, entonces $y=x$ o $y=\sigma(x)$.
  3. Si aún no estás tan acostumbrado a las intersecciones arbitrarias, considera un conjunto inductivo $A$ y la siguiente definición: $$\mathbb{N}’:=\{x\in A:  x \text{ está en todo conjunto inductivo}\}.$$ ¿Cómo se relaciona el axioma del infinito, con el hecho de que esto sí sea un conjunto?
  4. Esboza una demostración de que $\mathbb{N}’=\mathbb{N}$.
  5. Usa el quinto axioma de Peano para demostrar que para cualquier natural $n$ se cumple que $$\sigma(n)=\{0, 1, 2, …, n\}.$$
    Sugerencia. Considera el conjunto $S\subseteq \mathbb{N}$ de enteros $n$ para los cuales la afirmación anterior es cierta. Demuestra que $S$ es inductivo y usa el quinto axioma para concluir que $S=\mathbb{N}$.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Álgebra Superior II: Introducción al curso y a los números naturales

Por Roberto Manríquez Castillo

Deja un comentario

Introducción

El curso de Álgebra Superior I tuvo como principal objetivo darte las herramientas necesarias para poder entender, a grandes rasgos, la teoría que sustenta las primeras asignaturas con las que te encuentras a nivel universitario en tu trayectoria matemática. Por esta razón, en el temario se incluyeron los temas de lógica, demostraciones, teoría de conjuntos, números naturales, inducción matemática, conteo y espacios vectoriales.

Sin embargo, quedaron abiertas algunas preguntas. Por ejemplo: ¿cómo sabemos que los conjuntos con los que trabajamos existen?, ¿qué es en el fondo el conjunto de números reales que usamos en los espacios vectoriales? o ¿por qué funciona el principio de inducción?

En este sentido, el curso de Álgebra Superior II es la continuación de Álgebra Superior I. El objetivo de este curso será responder estas preguntas que en el curso anterior quedaron sin responder. Con esto en mente, usaremos las herramientas de la teoría de conjuntos que desarrollamos con anterioridad para estudiar qué son los números naturales, los enteros y hasta los complejos. Haremos una escala en cada tema para poder entender a profundidad las propiedades con las que hemos estado familiarizados desde educación básicas y para conocer otras propiedades que te servirán a lo largo de tu formación matemática.

En la parte final del curso, introduciremos otra estructura con la que seguramente ya estarás familiarizado gracias al curso de Cálculo Diferencial e Integral I: el anillo de polinomios con coeficientes reales (o complejos). Como en el caso de los temas anteriores, nos detendremos a estudiar las propiedades que caracterizan a este conjunto y las similitudes que podemos encontrar con algunos de los sistemas numéricos, como los números enteros.

La intuición detrás de formalizar a los números naturales

Desde la educación básica se aprende a contar. Con el pasar del tiempo, la idea de los números naturales y las características que se necesitan para contar “de uno en uno” seguramente se han hecho muy familiares en tu mente. A grandes rasgos, cuando contamos tenemos mente a los números $$0,1,2,3,4,5,6,7,\ldots.$$ De hecho, las propiedades de estos números probablemente son tan familiares que ya no reparas en ello a la hora de contar. Al cero le sigue el uno. Al uno le sigue el dos. Y así sucesivamente. Esto resulta práctico a la hora de contar, pero algo impráctico a la hora de establecer los fundamentos matemáticos de los números naturales. Por esta razón, tomémonos un momento para pensar en las propiedades que satisface este sistema numérico.

La primera característica en la que podemos pensar es que los números naturales cuentan con un elemento especial de entre todos los demás números, el primero de todos ellos. Dependiendo del contexto, el $0$ (y no el $1$) es considerado como el primer número natural y coincide con la intuición de que podemos «tener cero cosas», es decir, ninguna. Es importante que sepas que en cierto contextos (por ejemplo, otros cursos o áreas de las matemáticas) podría no serlo. La recomendación es que siempre uses la convención del área o comunidad con la que estés trabajando. En este curso el número $0$ siempre será un número natural.

Otra característica con la que seguramente estamos muy familiarizados es que si bien los números naturales tienen un comienzo (en nuestro caso, el $0$), por otra parte nunca terminan. No importa hasta qué número podamos haber contado, siempre podemos dar un paso más y avanzar al siguiente número. Cuando tenemos un natural, decimos entonces que siempre tiene un sucesor. Sabemos que sólo hay un sucesor para cada número.

Otra característica clave de los números naturales es que, a la hora de contar, nunca regresamos a un número por el cual ya pasamos; es decir, bajo ninguna circunstancia contamos $107, 108, 109, 37, ‘ldots$. Para enunciar esto formalmente, lo diremos en dos partes. Primero, el $0$ no es el sucesor de ningún número y segundo, en ninguna circunstancia, un mismo número es el sucesor de dos números diferentes.

Existe una quinta propiedad, tal vez más sutil que las anteriores, y es que si empezamos a contar desde el cero y vamos contando de uno en uno, entonces podremos alcanzar cualquier número natural, siempre que el tiempo lo permita.

Resulta que estas propiedades intuitivas son suficientes para definir muchas otras operaciones en los números naturales y para obtener una gran cantidad de propiedades. Es por esta razón que conviene incluirlas en nuestra formalización de los naturales, como discutimos a continuación.

Los axiomas de Peano para los números naturales

A finales del siglo XIX, los matemáticos empezaron a notar que a partir de algunas propiedades tan elementales como las que discutimos arriba, se podían probar las leyes de la aritmética que conocemos. En 1889, Giuseppe Peano, basado en las propiedades que acabamos de enunciar, dio un conjunto de axiomas que usó para estudiar sistemáticamente a los números naturales. Estos axiomas son:

  1. $0$ es un número natural.
  2. Si $n$ es un número natural, entonces existe un único natural, denotado $\sigma(n)$ al que llamamos su sucesor.
  3. Para todo número natural, $\sigma(n)\neq0$.
  4. Si $n,m$ son números naturales, tales que $\sigma(n)=\sigma(m)$, entonces $n=m$.
  5. Si $S$ es un subconjunto de números naturales tal que: $0$ está en $S$, y para todo $n$ en $S$, se cumple que $\sigma(n)$ está también en $S$, entonces $S$ es el conjunto de todos los naturales.

Nota que cada una de las cinco propiedades coinciden con una de las propiedades intuitivas que mencionamos antes.

Encontrando los primeros números naturales

El logro de Peano fue muy importante, ya que permitió reducir la teoría de los números naturales a solo cinco axiomas; sin embargo, aún quedan abiertas las preguntas ¿qué son los números naturales? y ¿cómo sabemos que existen? Aunque se hayan mencionado las propiedades de un objeto, no necesariamente tiene que existir tal objeto. Este fue el gran problema al que se enfrentaron los matemáticos cuando intentaron definir a un conjunto al que pertenecen todos los conjuntos.

Es por esta razón que debemos fundamentar la construcción de los números naturales en teoría que ya tengamos desarrollada. Por esta razón, a partir de este punto se aparece la teoría de los conjuntos, la cual nos permitirá definir formalmente lo que significan los símbolos que diariamente ocupamos (como el $0$), para después ver que en efecto estos conjuntos satisfacen los axiomas de Peano.

Definición: Definimos al cero como $0:=\emptyset$.

Cuando ponemos $:=$, quiere decir que estamos definiendo algo, típicamente un símbolo. Cuando veas algo así aparecer, puedes pensar que significa «esta es la primera vez que usamos el símbolo $0$, y lo que querrá decir es el conjunto vacío». Podemos pensar en esta definición como una simple ocurrencia de notación; sin embargo, es curioso notar que, pensando intuitivamente, $\emptyset$ tiene en efecto cero elementos. Más adelante veremos que los demás números naturales también satisfacen esta intuitiva coincidencia.

Definición: Dado un conjunto $A$ arbitrario, definimos el sucesor de $A$ como $\sigma(A):=A\cup\{A\}$.

Notemos que en realidad $\sigma$ no es en el sentido estricto una función ¿por qué? Más bien, lo que estamos haciendo es explicar a qué nos referimos con el símbolo $\sigma(A)$.

Considerando que hemos construido el primer número natural (el $0$) y hemos dado una forma de construir sucesores, parece una buena idea considerar \[\sigma(0)=\sigma(\emptyset)=\emptyset\cup\{\emptyset\}=\{\emptyset\}.\]

Y definir $1:= \{\emptyset\}$. Análogamente podemos pensar que \[2:=\sigma(1)=\sigma(\{\emptyset\})=\{\emptyset\}\cup\{\{\emptyset\}\}=\{\emptyset,\{\emptyset\}\}.\]

Podríamos continuar así sucesivamente. Observa que, efectivamente, los conjuntos $1$ y $2$ coinciden con la intuición de tener respectivamente $1$ y $2$ elementos.

Los «disfraces» de los números naturales

Actualmente usamos el sistema de numeración arábigo y sabemos exactamente qué quieren decir los «dibujos» $1$, $2$, $3$, $4$, etc. Si fueramos romanos, estaríamos usando los «dibujos» $I$, $II$, $III$, $IV$, etc. De manera estricta, los «dibujos» no son lo mismo que «el concepto que representan». Es decir, en el fondo, $2$ y $II$ son «disfraces distintos para el mismo concepto». Pero ninguno de esos «dibujos» es el concepto mismo, ni vive de manera formal en la teoría que estamos construyendo.

Lo que sí vive en la teoría que construimos es el $\{\emptyset,\{\emptyset\}\}$, pues a partir de los axiomas se puede garantizar su existencia. Por supuesto, en el curso usaremos los «disfraces» habituales de estos conceptos, de modo que casi siempre escribiremos $2$, $7$, $51$, etc. Sin embargo, es crucial que en todo momento tengas en cuenta que cuando escribimos esos «dibujos», en el fondo están las construcciones formales que realizaremos.

Más adelante…

Hemos empezado a definir a los números naturales a partir del $0$ (el conjunto vacío) y la función sucesor $\sigma$; sin embargo, la realidad es que el proceso que hemos descrito debe ser refinado, ya que si continuamos así, jamás acabaremos de definir la infinidad de números naturales que queremos que existan.

Incluso asumiendo que los podemos definir a todos, un segundo problema que se origina es el intentar unirlos en un solo «conjunto de los números naturales». Uno podría intentar ocupar el principio de inducción para resolver el problema. Sin embargo, recordemos que por el momento sólo contamos con los axiomas de la teoría de conjuntos, y aún no sabemos que el principio de inducción (visto como en el curso de Álgebra Superior I, o a partir de los axiomas de Peano) sea válido. Entonces, necesitaremos pensar cómo resolver el problema desde otra perspectiva.

Además, queda el problema de ver que los números naturales que definamos sí satisfagan los axiomas de Peano. También haremos esto pronto, para que a partir de ello podamos comenzar a introducir otras propiedades aritméticas y de orden.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Prueba a partir de sólo los axiomas de Peano, que $n\neq \sigma (n) $ para todo $n\in\mathbb{N}$.
  2. ¿Qué axiomas de Peano satisface el conjunto $\sigma(\mathbb{N})$, es decir, el conjunto de los números a partir del $1$?
  3. ¿Cómo será un conjunto y una función que satisfagan los axiomas 1), 2), 4) y 5) de Peano, pero que no satisfaga el 3)? ¿Puedes construir formalmente un conjunto y una función así?
  4. A partir de la definición de $\sigma(n)$ que dimos, demuestra que para todo número natural $n$ se satisface que $n\in\sigma(n)$ y que $n\subset\sigma(n)$.
  5. Demuestra que si $A$ es un conjunto, entonces $\sigma(A)$ es un conjunto. Para ello, tendrás que recordar los axiomas de teoría de conjuntos.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Álgebra Superior II: Esbozo de construcción de los números racionales y reales

Por Leonardo Ignacio Martínez Sandoval

2 respuestas

Introducción

En la unidad pasada vimos la construcción de los números enteros a partir de los números naturales. Lo que hicimos fue considerar parejas de números naturales $(a,b)$ para las que dimos la relación $\sim$ definida por $(a,b)\sim (c,d)$ si y sólo si $a+d=b+c$, vimos que esta relación es de equivalencia. Dijimos que, aunque era incorrecto formalmente, convenía pensar a la pareja $(a,b)$ como $a-b$ (es incorrecto ya que no siempre se puede restar en $\mathbb{N}$).

La relación $\sim$, así definida, genera las clases de equivalencia $$\overline{(a, b)}=\lbrace (c, d)\in \mathbb{N}\times\mathbb{N} : a+d=b+c\rbrace$$ en $\mathbb{N}\times\mathbb{N}$. El conjunto $\mathbb{Z}$ lo construimos como el conjunto de todas estas clases de equivalencia. En él definimos las operaciones:

  • Suma: $\overline{(a,b)}+\overline{(c,d)}=\overline{(a+c,b+d)}$.
  • Producto: $ \overline{(a,b)}\overline{(c,d)}=\overline{(ac+bd,ad+bc)}$.

Vimos que estas operaciones están bien definidas. La suma es bastante natural. El producto parece algo artificial, pero se vuelve natural si pensamos en «multiplicar $a-b$ con $c-d$», pues $(a-b)(c-d)=(ac+bd)-(ad+bc)$. Recordemos que es una justificación informal, pero ayuda a entender la intuición.

Después, nos dedicamos a probar que con estas operaciones, suma y producto, el conjunto $\mathbb{Z}$ es un anillo conmutativo con $1$ en donde se vale cancelar. A partir de ahí empezamos a ver a $\mathbb{Z}$ desde el punto de vista de la teoría de números. Estudiamos el máximo común divisor, la relación de divisibilidad, el anillo de enteros módulo $n$, congruencias, ecuaciones en congruencias, teorema chino del residuo y mencionamos un poco de ecuaciones diofantinas.

Con eso terminamos la unidad de enteros, correspondiente al segundo segundo parcial del curso.

Las siguientes dos unidades contempladas por el temario oficial son:

  • Números complejos.
  • Anillo de polinomios.

Vale la pena hacer una observación. Típicamente tenemos la siguiente cadena de contenciones entre sistemas numéricos $$\mathbb{N}\subset \mathbb{Z}\subset \mathbb{Q} \subset \mathbb{R}\subset \mathbb{C}.$$

En las primeras dos unidades del curso hablamos de $\mathbb{N}$ y de $\mathbb{Z}$. De acuerdo a las contenciones anteriores, lo siguiente sería tratar a detalle los racionales $\mathbb{Q}$ y los reales $\mathbb{R}$. Sin embargo el temario oficial «se los salta». Esto es un poco raro, pero podría estar justificado en que estos sistemas numéricos se estudian en otros cursos del plan de estudios. Por ejemplo, $\mathbb{R}$ se estudia con algo de profundidad en los cursos de cálculo.

De cualquier forma nos va a ser muy útil mencionar, por lo menos por «encima», cómo hacer la construcción de $\mathbb{Q}$ y $\mathbb{R}$. La construcción de los números racionales ayuda a repasar la construcción de los enteros. En la construcción de los números reales nos encontraremos con propiedades útiles que usaremos, de manera continua, cuando hablemos de la construcción de los números complejos $\mathbb{C}$. Por estas razones, aunque no vayamos a evaluar, las construcciones de $\mathbb{Q}$ y $\mathbb{R}$, en el curso, las ponemos aquí para que las conozcas o las repases.

Motivación de construcción de los racionales

Los naturales no son suficientes para resolver todas las ecuaciones de la forma $$x+a=b,$$ pues si $a>b$ la ecuación no tiene solución en $\mathbb{N}$ y esta fue nuestra motivación para construir los números enteros. En $\mathbb{Z}$ todas estas ecuaciones tienen solución. Sin embargo, en $\mathbb{Z}$ la ecuación $$ax=b$$ tiene solución si y sólo si $a$ divide a $b$ (por definición se tiene que $a$ divide a $b$ si y sólo si $b$ es un múltiplo de $a$), pero no siempre sucede esto. Por ejemplo, $3x=7$ no tiene solución en $\mathbb{Z}$.

Construcción de los racionales

Para la construcción de los racionales consideremos el conjunto $\mathbb{Z}\times \mathbb{Z}\setminus\{0\}$ y sobre él la relación $\sim$ definida por $(a,b)\sim (c,d)$ si y sólo si $ad=bc$. Resulta que $\sim$ es relación de equivalencia, así que, para cada pareja $(a,b)$ denotaremos como $\overline{(a,b)}$ a su clase de equivalencia. En este caso $$\overline{(a, b)}=\lbrace (m, n)\in \mathbb{Z}\times\mathbb{Z}\setminus\{0\} : an=bm\rbrace.$$

Observa que esta construcción se parece mucho a la que hicimos para $\mathbb{Z}$, aunque ahora nos basamos en el producto en $\mathbb{Z}$ (antes era la suma en $\mathbb{N}$). De nuevo, una forma de pensar bastante intuitiva (aunque formalmente incorrecta), es pensar a cada clase $\overline{(a,b)}$ «como $\frac{a}{b}$». Nota que estamos considerando sólo aquellas parejas $(a,b)$ tales que $b\neq 0$.

De esta forma $\mathbb{Q}$ es el conjunto de clases de equivalencia de las parejas $(a,b)$ tales que $b\neq 0$, en símbolos, $$\mathbb{Q}:=\{\overline{(a,b)}: a\in \mathbb{Z}, b\in \mathbb{Z}\setminus\{0\}\}.$$

Operaciones y orden en los racionales

Vamos a definir las operaciones en $\mathbb{Q}$. Ahora el producto es «intuitivo» y la suma no tanto.

  • Suma: $\overline{(a,b)} + \overline{(c,d)} = \overline{(ad+bc,bd)}$.
  • Producto: $\overline{(a,b)}\overline{(c,d)}=\overline{(ac,bd)}$.

La suma se vuelve mucho más intuitiva si primero pensamos en nuestra interpretación (informal) de $\overline{(a,b)}$ como $\frac{a}{b}$ y luego, por lo que aprendimos en educación primaria sobre la suma de fracciones, vemos que $$\frac{a}{b}+\frac{c}{d}=\frac{ad+bc}{bd}.$$

Ahora, para definir el orden en $\mathbb{Q}$, tomemos la pareja $(a,b)\in \mathbb{Z}\times\mathbb{Z}\setminus\{0\}$. Tenemos que la clase $\overline{(a,b)}$ es

  • Cero si $a=0$,
  • Positiva si ambos ($a$ y $b$) son negativos o ninguno es negativo con el orden definido en $\mathbb{Z}$ y
  • Negativa si exactamente alguno ($a$ o $b$) es negativo con el orden definido en $\mathbb{Z}$.

Diremos que $\overline{(a,b)}>\overline{(c,d)}$ si $\overline{(a,b)}-\overline{(c,d)}$ es positiva.

Se puede probar que estas operaciones suma y producto, así como el orden están bien definidas (es decir que no dependen del representante que se tome).

Antes, de continuar, consideremos lo siguiente: un campo se puede pensar como un conjunto en el que están definidas la «suma» y la «multiplicación» tales que:

  • La suma es asociativa, conmutativa, tiene un neutro (el $0$) e inversos aditivos.
  • La multiplicación es asociativa, conmutativa, tiene un neutro (el $1$) y todo elemento distinto de $0$ tiene un inverso multiplicativo.
  • Se tiene la distributividad del producto sobre la suma $a(b+c)=ab+bc$.

En vista de lo anterior queremos mencionar que se puede probar lo siguiente:

Teorema. El conjunto $\mathbb{Q}$ con sus operaciones de suma y producto es un campo ordenado.

Retomando lo que hablamos del neutro para la multiplicación, en un campo, veamos un ejemplo.

Ejemplo. La clase $\overline{(c,c)}$ es el neutro multiplicativo en $\mathbb{Q}$, veamos:

Se tiene que $$\overline{(a, b)(c, c)} = \overline{(ac,bc)}=\lbrace (m, n)\in\mathbb{Z}\times\mathbb{Z}\setminus\{0\}: acn=bcm\rbrace$$

y $\lbrace (m, n)\in\mathbb{Z}\times\mathbb{Z}\setminus\{0\}: acn=bcm\rbrace=\lbrace (m, n)\in \mathbb{Z}\times\mathbb{Z}\setminus\{0\}: anc=bmc\rbrace$, pero $\lbrace (m, n)\in\mathbb{Z}\times\mathbb{Z}\setminus\{0\}: anc=bmc\rbrace=\lbrace (m, n)\in\mathbb{Z}\times\mathbb{Z}\setminus\{0\}: an=bm\rbrace=\overline{(a, b)}$. Por lo tanto $\overline{(a, b)(c, c)}=\overline{(a, b)}$. Nota que aquí estamos usando que el producto en $\mathbb{Z}$ es asociativo, conmutativo y que se pueden cancelar factores distintos de cero.

En $\mathbb{Q}$, el inverso multiplicativo de la clase $\overline{(a,b)}$ es $\overline{(b,a)}$, veamos:

Su producto es $$\overline{(ab,ba)}=\lbrace (m, n)\in \mathbb{Z}\times\mathbb{Z}\setminus\{0\}: abn=bam\rbrace$$ y $\lbrace (m, n)\in \mathbb{Z}\times\mathbb{Z}\setminus\{0\}: abn=bam\rbrace=\lbrace (m, n)\in \mathbb{Z}\times\mathbb{Z}\setminus\{0\}: m=n\rbrace=\overline{(c, c)}$.

$\triangle$

Notación simple de racionales y ecuaciones aún sin solución

Vamos a denotar la clase de equivalencia $\overline{(a,b)}$ por $\frac{a}{b}$, a partir de lo cual nuestra interpretación de pensarlo así ya se vuelve formal. Se puede mostrar que todo lo que aprendimos de esta notación en la primaria se deduce de las propiedades de $\mathbb{Q}$.

La ecuación $$ax=b$$ tiene solución casi siempre, el único problema es si $a=0$. Pero si $a\neq 0$, la solución es única y es $x=\frac{b}{a}$.

El conjunto $\mathbb{Q}$ es bastante bueno algebraicamente, pero le falta todavía más para ser bueno para análisis y cálculo. Todavía tiene «bastantes hoyos»: en él no podemos probar, por ejemplo, el teorema del valor intermedio para funciones continuas. Así mismo, hay varias ecuaciones que todavía no tienen solución en $\mathbb{Q}$.

Ejercicio. La ecuación $x^2=3$ no tiene una solución en $\mathbb{Q}$.

Una forma de enunciar el resultado anterior es decir «$\sqrt{3}$ es irracional». Pero nota que es incorrecto enunciarlo así, pues para ponerle un nombre a $\sqrt{3}$, es necesario saber quién es, y justo el punto del ejercicio es que, tan sólo con $\mathbb{Q}$, no podemos definirlo.

Solución. Vamos a proceder por contradicción. Supongamos que la ecuación $x^2=3$ tiene una solución $p/q$ en los racionales. De esta forma,$(p/q)^2=3$. Multiplicando por $q^2$ en ambos lados, $p^2=3q^2$.

La factorización en primos del lado izquierdo tiene una cantidad par de $3$’s. La factorización en primos del lado derecho tiene una cantidad impar de $3$’s. Esto es una contradicción al teorema fundamental de la aritmética, por lo tanto, no existe $p/q$ solución racional de $x^2=3$.

$\triangle$

Reales y hoyos en los racionales

Para la construcción de los reales, ya no podemos proceder como le hemos estado haciendo, considerando simplemente parejas de números del sistema anterior y construyendo una relación de equivalencia sobre ellas. Lo que buscamos cuando damos el paso entre $\mathbb{Q}$ y $\mathbb{R}$ ya no es sólo que los números tengan «inversos aditivos» o «inversos multiplicativos», sino que «todos los conjuntos acotados por abajo tengan un mejor mínimo». Esto es lo que garantiza que se «llenen los hoyos» que tienen los racionales.

Entendamos el concepto de «hoyo»:

Definición. Sea $X$ un orden total $\le$ y $S$ un subconjunto de $X$, un ínfimo de $S$, en $X$, es un $r\in X$ tal que

  • $r\leq s$ para todo $s\in S$ y
  • si $t\leq s$ para todo $t\in S$, entonces $t\leq s$.

Definición. Un conjunto $X$ con un orden total $\le$ es completo si todo subconjunto $S$ de $X$, acotado inferiormente, tiene un ínfimo.

Ejemplo. El conjunto $\mathbb{Q}$ no es completo, pues el subconjunto $$S=\{x\in \mathbb{Q}: x^2\geq 3\}$$ está acotado inferiormente, pero no tiene un ínfimo en $\mathbb{Q}$ (su ínfimo es $\sqrt{3}$ y $\sqrt{3}$ no pertenece a $\mathbb{Q}$).

$\triangle$

Sucesiones de Cauchy y construcción de los reales

Hay varias formas de construir un sistema numérico que extienda a $\mathbb{Q}$ y que no tenga hoyos. Se puede hacer mediante cortaduras de Dedekind, mediante expansiones decimales o mediante sucesiones de Cauchy de números racionales. Todas estas construcciones son equivalentes. Daremos las ideas generales de la última.

Definición. Una sucesión $$\{x_n\}=\{x_1,x_2,x_3,\ldots\}$$ es de Cauchy si para todo $N$ existe un $M$ tal que si $m\geq M$ y $n\geq M$, entonces $|x_m-x_n|<\frac{1}{N}$. Denotaremos con $C(\mathbb{Q})$ al conjunto de todas las sucesiones de Cauchy de números racionales.

Construiremos una relación de equivalencia $\sim$ en $C(\mathbb{Q})$. Si tenemos dos de estas sucesiones:
\begin{align*}
\{x_n\}&=\{x_1,x_2,x_3,\ldots\} \quad \text{y}\\
\{y_n\}&=\{y_1,y_2,y_3,\ldots\},
\end{align*}

diremos que $\{x_n\}\sim \{y_n\}$ si para todo natural $N$ existe un natural $M$ tal que para $n\geq M$ tenemos que $$|x_n-y_n|<\frac{1}{N}.$$

Se puede probar que $\sim$ es una relación de equivalencia. Para cada sucesión $\{x_n\}$ de Cauchy usamos $\overline{\{x_n\}}$ para denotar a la clase de equivalencia de $\{x_n\}$. Por definición, el conjunto $\mathbb{R}$ es el conjunto de clases de equivalencia de $\sim$, en símbolos: $$\mathbb{R}:=\{\overline{\{x_n\}}: \{x_n\} \in C(\mathbb{Q})\}.$$

Operaciones y orden en los reales

En $\mathbb{R}$ podemos definir las siguientes operaciones:

  • Suma: $\overline{\{x_n\}} + \overline{\{y_n\}}= \overline{\{x_n + y_n\}}$ .
  • Producto: $\overline{\{x_n\}} \overline{\{y_n\}}= \overline{\{x_ny_n\}}$.

También podemos definir el orden en $\mathbb{R}$. Decimos que $\overline{\{x_n\}}$ es positivo si para $n$ suficientemente grande tenemos $x_n>0$. Decimos que $\overline{\{x_n\}}>\overline{\{y_n\}}$ si $\overline{\{x_n\}}- \overline{\{y_n\}}$ es positivo.

Se puede ver que las operaciones de suma y producto, así como el orden, están bien definidos. Más aún, se puede probar el siguiente resultado.

Teorema. El conjunto $\mathbb{R}$ con sus operaciones de suma y producto es un campo ordenado y completo.

Como antes, una vez que se prueba este teorema, se abandona la notación de sucesiones y de clases de equivalencia. En realidad se oculta, pues la construcción siempre está detrás, como un esqueleto que respalda las propiedades que encontramos.

El teorema nos dice que $\mathbb{R}$ ya no tiene hoyos, y esto es precisamente lo que necesitamos para resolver algunas ecuaciones como $x^2=3$. Un esbozo de por qué es el siguiente. Gracias a la existencia de ínfimos se puede probar el teorema del valor intermedio en $\mathbb{R}$. Se puede probar que la función $x^2$ es continua, que en $x=0$ vale $0$ y que en $x=2$ vale $4$, de modo que por el teorema del valor intermedio debe haber un real $x$ tal que $x^2=3$.

Más adelante…

Las muchas otras importantes consecuencias de que $\mathbb{R}$ sea un campo ordenado y completo se discuten a detalle en cursos de cálculo. Si bien este es un logro enorme, aún tenemos un pequeño problema: ¡todavía no podemos resolver todas las ecuaciones polinomiales! Consideremos la ecuación $$x^2+1=0.$$ Podemos mostrar que para cualquier real $x$ tenemos que $x^2\geq 0$, de modo que $x^2+1\geq 1>0$. ¡Esta ecuación no tiene solución en los números reales!

Para encontrar una solución vamos a construir los números complejos. Con ellos podremos, finalmente, resolver todas las ecuaciones polinomiales, es decir, aquellas de la forma

$$a_nx^n+a_{n-1}x^{n-1}+\ldots+a_1x+a_0=0.$$

Hablaremos de esto en el transcurso de las siguientes dos unidades: números complejos y polinomios.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. ¿Cuál de las clases de equivalencia sería el neutro aditivo en $\mathbb{Q}$?
  2. ¿Por qué la definición de orden en $\mathbb{Q}$ no depende del representante elegido?
  3. ¿Cómo construirías el inverso multiplicativo de la sucesión de Cauchy $\{x_n\}$? Ten cuidado, pues algunos de sus racionales pueden ser $0$.
  4. Aprovecha esta entrada de transición entre unidades para repasar las construcciones de $\mathbb{N}$ y de $\mathbb{Z}$.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Álgebra Superior II: Ecuaciones diofantinas

Por Leonardo Ignacio Martínez Sandoval

2 respuestas

Introducción

En entradas anteriores platicamos de congruencias y teoremas que nos sirven para trabajar con aritmética modular. Así mismo, aprendimos a resolver ecuaciones lineales y sistemas de ecuaciones lineales en congruencias en una variable.

Regresemos a $\mathbb{Z}$. Se usa el término ecuación diofantina para referirse a una ecuación en la cual las variables deben tomar soluciones enteras. Existe una gran variedad de formas que puede tomar una ecuación diofantina. «Resolver una ecuación diofantina» se refiere a encontrar, con demostración, una descripción del conjunto de todas sus soluciones en «términos sencillos».

Ejemplo 1. Encuentra todas las soluciones enteras $x$ a la ecuación $13x=91$.

Ejemplo 2. Encuentra todas las soluciones enteras $x,y$ a la ecuación $7x+5y=3$.

Los ejemplos $1$ y $2$ son ecuaciones diofantinas lineales en una y dos variables respectivamente. El objetivo de esta entrada es explicar cómo resolver estas ecuaciones. Continuamos la discusión de más ejemplos para abrir el panorama del tipo de problemas que aparecen en el área, y de las técnicas que se pueden usar.

Ejemplo 3. Encuentra todas las soluciones con enteros $x,y,z$ a la ecuación $x^2+y^2=z^2$.

Al Ejemplo 3 se le conoce como la ecuación pitagórica. Esa es posible resolverla con todo lo que hemos visto hasta ahora, pero no es tan sencillo. Requiere de un análisis cuidadoso de casos.

Ejemplo 4. Encuentra todas las soluciones enteras positivas $x,y$ a la igualdad $x^y=y^x$.

El Ejemplo $4$ es curioso. Si consideramos a la función real $f(x)=x^{\frac{1}{x}}$, el problema pide encontrar a aquellas parejas de enteros $x$ y $y$ tales que $f(x)=f(y)$. Una forma de resolver la ecuación es utilizando herramientas de cálculo diferencial en $f(x)$ para mostrar que para $x>5$ la función ya es estrictamente creciente. Esto reduce el análisis de casos de enteros que tenemos que intentar, y muestra que $(2,4)$, $(4,2)$ y $(n,n)$ son las únicas parejas de enteros válidas. La moraleja de este ejemplo es que a veces se tienen que usar herramientas de otras áreas de las matemáticas para resolver una ecuación, aunque esta sólo requiera de soluciones enteras.

Ejemplo 5. Encuentra todas las soluciones con enteros $x,y,z$ a la ecuación $x^3+y^3=z^3$.

El Ejemplo $5$, o bien cualquier ecuación del estilo $x^n+y^n=z^n$ se le llama una ecuación de tipo Fermat, pues Pierre Fermat conjeturó que no existen soluciones para cuando $n\geq 3$ y $x,y,z$ son todos distintos de cero. Esta conjetura fue demostrada en $1995$ por Andrew Wiles. Una demostración de esta conjetura queda muy lejos de la teoría que hemos desarrollado hasta ahora, pero vale la pena decir que esta ecuación motivó fuertemente el desarrollo de varias herramientas de teoría de números, sobre unas llamadas curvas elípticas.

Ejemplo 6. Encuentra todas las soluciones enteras positivas $x,y$ a la igualdad $|2^x-3^y|=1$.

El Ejemplo $6$ se puede resolver también con herramientas que ya hemos visto en el curso, pero requiere de un análisis detallado. Este problema pide, en otras palabras, determinar cuándo «una potencia de $3$ está junto a una potencia de $2$». Un ejemplo de esto son $2^3=8$ y $3^2=9$. Otra pregunta clásica del área es la conjetura de Catalán, la cual afirma que estas son las únicas dos potencias no triviales que son consecutivas. Fue demostrada en $2002$ por Mihăilescu. Las técnicas también están muy lejos del alcance de este curso. Se usan técnicas en campos ciclotómicos y módulos de Galois.

En realidad, uno podría tomar cualquier ecuación en reales y hacerse la pregunta de si existirán soluciones en enteros y, de ser así, determinar cuántas o cuáles son. Ha existido (y existe) mucha investigación en el área. El interés de una ecuación diofantina en particular está relacionado con su aplicación a otros problemas y con la teoría que ayuda a desarrollar.

Ecuaciones diofantinas lineales

La ecuación diofantina del Ejemplo 1 se puede preguntar en general. Dados enteros $a$ y $b$, ¿cuáles son las soluciones enteras $x$ a la ecuación $ax=b$?

  • Si $a=0$, la ecuación tiene solución si y sólo si $b=0$, y en este caso, cualquier valor entero de $x$ es solución.
  • Si $a\neq 0$, esta ecuación tiene solución en enteros si y sólo si $a$ divide a $b$, y en este caso $x=b/a$ es la única solución entera.

Estudiemos ahora la generalización del Ejemplo 2.

Problema. Sean $a$ y $b$ enteros distintos de $0$ y $c$ un entero. Determina todas las soluciones enteras a la ecuación $$ax+by=c.$$

Primero, determinemos condiciones necesarias y suficientes en $a$, $b$ y $c$ para que la ecuación tenga soluciones enteras $x$ y $y$. Lo que nos está pidiendo la ecuación es que escribamos a $c$ como combinación lineal entera de $a$ y $b$. Recordemos que $$a\mathbb{Z}+b\mathbb{Z} = \text{MCD}(a,b) \mathbb{Z},$$ de modo que la ecuación tiene solución si y sólo si $\text{MCD}(a,b)$ divide a $c$. ¿Cuáles son todas las soluciones? Esto lo determinaremos mediante las siguientes proposiciones.

Proposición. Sean $a$ y $b$ enteros distintos de $0$ y $c$ un entero divisible entre $M:=\text{MCD}(a,b)$. Sean $a’=a/M$, $b’=b/M$, $c’=c/M$. Las soluciones enteras a la ecuación $ax+by=c$ son las mismas que para la ecuación $a’x+b’y=c’$.

Demostración. Se sigue de manera directa usando que $M\neq 0$, ya que de la original podemos pasar a la nueva dividiendo entre $M$, y de la nueva a la anterior multiplicando por $M$.

$\square$

Ejemplo 1. $x=2$ y $y=7$ son soluciones a la ecuación $6x-4y=-16$, y también son soluciones a la ecuación $3x-2y=-8$.

$\triangle$

Al dividir ambos lados de la ecuación entre el máximo común divisor de $a$ y $b$ obtenemos una ecuación en la que los coeficientes de las variables ahora son primos relativos. Este fenómeno ya lo habíamos visto cuando hablamos de ecuaciones en congruencias. Estudiemos este tipo de ecuaciones en enteros. Comenzaremos con unas un poco más sencillas: aquellas en las que $c=0$. A estas les llamamos ecuaciones homogéneas.

Proposición. Sean $a$ y $b$ enteros distintos de $0$ y primos relativos. Las soluciones de la ecuación diofantina $ax+by=0$ son exactamente de la forma $x=-kb$, $y=ka$ para $k$ en los enteros.

Demostración. De la ecuación obtenemos $-ax=by$, por lo que $a$ divide a $by$. Como $a$ y $b$ son primos relativos, tenemos que $a$ divide a $y$. Así, existe un $k$ entero tal que $y=ka$. Entonces, $-ax=bka$. Como $a\neq 0$, podemos cancelar y despejar $x=-kb$.

En efecto, todas estas parejas son soluciones pues $a(-kb)+b(ka)=0$.

$\square$

Ejemplo 2. Determina todas las soluciones a la ecuación diofantina $9x+5y=0$.

Solución. Tenemos que $9$ y $5$ son primos relativos y que la ecuación es homogénea. Por el resultado anterior, las soluciones son de la forma $x=-5k$ y $y=9k$.

$\triangle$

Ejemplo 3. Determina todas las soluciones a la ecuación diofrantina $9x-6y=0$.

Solución. Aquí hay que tener cuidado. Si bien la ecuación es homogénea, los coeficientes de las variables no son primos relativos. Si sólo consideramos las soluciones de la forma $x=6k$ y $y=9k$, en efecto todas estas son soluciones, pero nos faltará la solución $x=2$, $y=3$ que no es de esta forma.

Antes de poder usar la proposición, necesitamos dividir entre el máximo común divisor de $9$ y $6$, que es $3$, para obtener primero la ecuación diofantina equivalente $3x-2y=0$. Ahora sí, todas las soluciones enteras de esta ecuación (y por lo tanto de la original) son de la forma $x=2k$ y $y=3k$.

$\triangle$

Pasemos ahora al caso en el que los coeficientes de las variables son primos relativos, pero la ecuación ya no es homogénea.

Proposición. Sean $a$ y $b$ enteros distintos de $0$ y primos relativos. Sea $c$ un entero divisible entre $\text{MCD}(a,b)$. Se puede obtener una solución $x_0, y_0$ a la ecuación diofantina $ax+by=c$ usando el algoritmo de Euclides. El resto de las soluciones son exactamente de la forma $x=x_0-kb$, $y=y_0+ka$ en donde $k$ es cualquier entero positivo.

Demostración. Notemos que en efecto las soluciones propuestas satisfacen la ecuación diofantina pues
\begin{align*}
ax+by&=a(x_0-kb)+b(y_0+ka)\\
&=ax_0+by_0 + (-kab+kab)\\
&=ax_0+by_0\\
&=c.
\end{align*}

Aquí usamos que $x_0,y_0$ es una solución de $ax+by=c$. Veamos que estas soluciones son las únicas.

Si $x_1,y_1$ es una solución, entonces tenemos $$ax_1+by_1=c=ax_0+by_0,$$ y entonces $$a(x_1-x_0)+b(y_1-y_0)=c-c=0,$$ de modo que $(x_1-x_0)$, $(y_1-y_0)$ es una solución de la ecuación homogénea $ax+by=0$, y por la proposición anterior, debe suceder que $x_1-x_0=-ka$ y $y_1-y_0=kb$ con $k$ un entero. Así, $x_1=x_0-ka$ y $y_1=y_0+kb$, como queríamos.

$\square$

Ejemplo 4. Determina todas las soluciones a la ecuación diofantina $12x+13y=1$.

Solución. Por inspección, una solución es $x=-1$, $y=1$. Los coeficientes de las variables son primos relativos. Por la proposición anterior, todas las soluciones son de la forma $-13k-1$, $12k+1$ donde $k$ es un entero arbitrario.

$\triangle$

Resumimos todo lo obtenido en el siguiente resultado.

Teorema. Sean $a$ y $b$ enteros distintos de $0$ y $c$ un entero. Consideremos la ecuación diofantina $ax+by=c$. Si $M:=\text{MCD}(a,b)$ no divide a $c$, entonces la ecuación no tiene solución. Si sí, podemos usar el algoritmo de Euclides para encontrar una solución $x_0,y_0$. El resto de las soluciones son de la forma $x_0-ka’$, $y_0+kb’$, en donde $a’=a/M$, $b’=b/M$ y $k$ es cualquier entero.

Veamos un ejemplo en el que juntamos todo lo que ya sabemos.

Ejemplo 5. Determina todas las soluciones a la ecuación diofantina $21x-35y=14$.

Solución. Los coeficientes de las variables no son primos relativos, pues su máximo común divisor es $7$. Tenemos que $7$ divide a $14$, así que la ecuación sí tiene soluciones y son las mismas que las de la ecuación $3x-5y=2$. Por inspección, una solución es $x=-1, y=-1$. Así, todas las soluciones a esta ecuación (y por lo tanto a la original), son de la forma $x=5k-1, y=3k-1$.

$\triangle$

Más adelante…

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Resuelve el Ejemplo 2.
  2. En todos los ejemplos, verifica que las soluciones obtenidas en efecto son soluciones del sistema original.
  3. ¿Para cuántos enteros $c$ entre $1$ y $100$ se tiene que la ecuación lineal $21x+18y=c$ tiene solución $x,y$ en enteros?
  4. Sólo hemos visto ecuaciones diofantinas lineales en dos variables. Sin embargo, con lo visto hasta ahora puedes argumentar por qué la ecuación diofantina $91x+14y-70z=100$ no tiene soluciones en enteros. ¿Por qué?
  5. Investiga acerca de la ecuación pitagórica $x^2+y^2=z^2$.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»