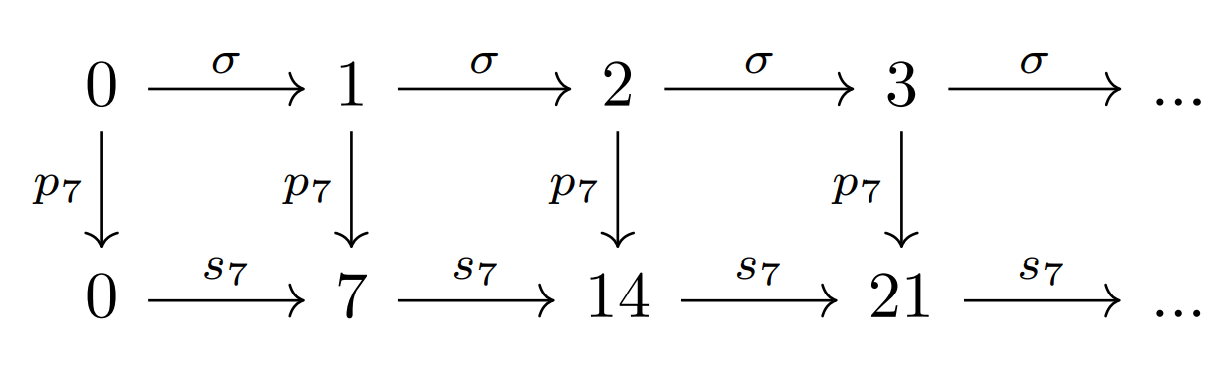Archivo de la etiqueta: naturales

Álgebra Superior II: El tamaño de los naturales y de cada natural

Por Roberto Manríquez Castillo

Deja un comentario

Introducción

En la entrada pasada, demostramos que todo número natural es el conjunto formado por los elementos $\{0,1,…,n-1\}$. Esto nos dice intuitivamente que cada número natural $n$, tiene exactamente $n$ elementos. Pero, de modo formal, ¿qué quiere decir que un conjunto tenga $n$ elementos? Esto lo precisaremos en esta entrada. Más aun, siguiendo esta idea, definiremos que quiere decir que un conjunto sea infinito. Después, veremos las propiedades que los conjuntos finitos e infinitos tienen.

El tamaño de los conjuntos

A la hora de pensar en determinar el tamaño de un conjunto, uno podría aventurarse y empezar a contar los elementos de este uno por uno. Esta forma de aproximar el problema no sólo parece muy laboriosa, sino que también presenta el problema de que no todos los conjuntos tienen la propiedad de que se pueda enlistar a sus elementos (aunque no lo definimos aún, seguramente has escuchado que el conjunto $\mathbb{R}$ de números reales no cumple esta propiedad).

De entrada, parecería que el problema de catalogar a los conjuntos por su tamaño es más complicado de lo que parece. Sin embargo, hay una idea famosa que viene a salvar la situación.

Imagina que eres el acomodador de una sala de cine con una cantidad desconocida de asientos (incluso posiblemente infinita) y que quieres sentar en ellos a un cierto conjunto de espectadores (cuya cantidad también se desconoce). Como dijimos anteriormente, la labor de contar todos los asientos de la sala podría ser demasiado complicada. ¿Cómo podríamos cerciorarnos de que cada espectador podrá tener un asiento?

La respuesta es inusualmente sencilla. La mejor forma de cerciorarse de que todos puedan sentarse, es pidiéndoles que se sienten. Si logran hacerlo de modo que a cada asistente le toque exactamente un asiento y no sobren asientos, podremos decir que hay el mismo número de personas que de lugares.

Notemos que de esta forma no necesitamos saber de forma explícita cuántas sillas hay, ni cuantas personas asistieron a la función, para saber que hay la misma cantidad de personas que de sillas. Formalmente hablando, hemos dado una relación entre el conjunto de personas y el de asientos.

Recordemos que a una relación entre conjuntos se le llama función si a cada elemento de nuestro dominio le corresponde uno y solo un elemento del codominio. Más aún, si a todo elemento del codominio, está relacionado con uno del dominio, la función se llamará suprayectiva. Si una función satisface que los elementos del codominio se relacionan con a lo más un elemento del dominio, se le llama función inyectiva. Cuando ambas condiciones se satisfacen, diremos que la función es biyectiva.

Nota que en el ejemplo de la sala de cine, si logramos hacer que todos los asistentes se sienten sin que sobre alguna silla, entonces la función que damos es una función biyectiva. Con estas observaciones, introducimos la siguiente definición.

Definición. Diremos que dos conjuntos $A$ y $B$ tienen la misma cantidad de elementos, o la misma cardinalidad, si existe una función biyectiva entre ellos. En este caso escribimos $\vert A\vert=\vert B \vert$.

El tamaño del conjunto $\mathbb{N}$

Aunque los conjuntos finitos parecen ser más cercanos a nuestra realidad, será más interesante definir primero qué son los conjuntos infinitos. Para ello usaremos una de las propiedades «raras» que estos tienen.

Definición. Diremos que un conjunto $X$ es infinito si existe un subconjunto propio $Y$ de $X$ y una función $f:X\to Y$ biyectiva entre ambos conjuntos.

Recuerda que un subconjunto propio es cualquier subconjunto que no sea el conjunto original. En otras palabras, un conjunto es infinito si tiene el mismo tamaño que alguno de sus subconjuntos propios.

Definición. Diremos que un conjunto es finito si no es infinito.

La propiedad que usamos para caracterizar a los conjuntos infinitos fue muy novedosa cuando se enunció por primera vez. Incluso con los años fue el origen de aparentes paradojas al sentido común. Si el tema te parece interesante, puedes leer o ver algún vídeo sobre el famoso Hotel de Hilbert.

Con nuestra definición lista, empezaremos a catalogar los conjuntos que ya conocemos en finitos e infinitos.

Teorema. El conjunto $\mathbb{N}$ de números naturales es infinito.

Demostración. Para demostrar esto, consideraremos el conjunto $\mathbb{N}\setminus\{0\}$. Este es un subconjunto propio de $\mathbb{N}$. Tomemos la función $\sigma:\mathbb{N}\to \mathbb{N}\setminus\{0\}$. De acuerdo con la definición de conjunto infinito hay que demostrar que $\sigma$ es biyectiva, es decir, que es inyectiva y suprayectiva.

El hecho de que el codominio esté bien definido y que $\sigma$ sea inyectiva, fue demostrado en la entrada La construcción de los naturales, a la hora de probar los axiomas de Peano. La prueba de la suprayectividad se dejó como un ejercicio moral en la entrada de Principio de inducción y teoremas de recursión, ya que se usó para la prueba del teorema de Recursión débil. De cualquier forma, a continuación damos esa prueba.

Demostraremos que $\{0\}\cup \sigma(\mathbb{N})$ es inductivo. Evidentemente $0\in\mathbb{N}$ , y si $n\in \{0\}\cup\sigma(\mathbb{N})$, entonces es trivial que $\sigma(n)\in\sigma(\mathbb{N})$. Entonces $\{0\}\cup \sigma(\mathbb{N})=\mathbb{N}$, por lo que $\sigma(n)$ sí es suprayectiva y por lo tanto biyectiva. Con esto se concluye la prueba.

$\square$

La idea de determinar si dos conjuntos tienen la misma cantidad de elementos usando funciones se puede extender un poco más. La usaremos a continuación para definir cuándo un conjunto tiene al menos tantos elementos como otro.

Definición. Decimos que un conjunto $A$ tiene a lo más tantos elementos como un conjunto $B$ si existe una función inyectiva $f:A\to B$. En este caso, escribimos $\vert A\vert\leq \vert B \vert$.

Todo número natural es finito

Como hemos visto, los conjuntos infinitos se comportan de forma inesperada. Sin embargo los conjuntos finitos sí se comportarán de una forma más intuitiva. El teorema siguiente ejemplifica esto.

Teorema. Si $A$ es un conjunto finito, y $f:A\to A$, entonces son equivalentes las siguientes tres afirmaciones:

  1. $f$ es biyectiva
  2. $f$ es inyectiva
  3. $f$ es suprayectiva

Demostración. Evidentemente, $1)\Rightarrow 2)$ y $1)\Rightarrow 3)$. Si logramos demostrar la equivalencia entre $2)$ y $3)$ terminaremos, pues al tener uno, tendríamos el otro y por lo tanto tendríamos ambas partes de la definición de biyectividad.

$2)\Rightarrow 3)$ Supongamos que $f$ es inyectiva y supongamos que $f$ no es suprayectiva. Entonces $f:A\to f(A)$ es una biyección de $A$ con un subconjunto propio, lo cual diría que $A$ es infinito. Esto es una contradicción, así que $f$ debe ser suprayectiva.

$3)\Rightarrow 2)$ Si $f$ es suprayectiva, entonces tiene inversa derecha, es decir, existe $g:A\to A$ tal que $f\circ g=Id_A$. A partir de esta igualdad se puede probar que $g$ es inyectiva. En efecto, si $g(a)=g(b)$, entonces $f(g(a))=f(g(b))$, pero entonces $a=b$. Por la implicación del párrafo anterior, $g$, también es suprayectiva. Pero con esto se puede mostrar que $f$ es inyectiva. Si tenemos $a$ y $b$ tales que $f(a)=f(b)$, tomemos $c$ y $d$ tales que $g(c)=a$ y $g(d)=b$. De aquí, $c=f(g(c))=f(g(d))=d$ y por lo tanto $a=g(c)=g(d)=b$.

$\square$

Sigamos estudiando propiedades de los conjuntos infinitos. El siguiente resultado es bastante intuitivo: si le quitamos un elemento a un conjunto infinito, sigue siendo infinito. La demostración es algo elaborada pues debemos hacerla a partir de nuestras definiciones.

Lema 1. Si $X$ es un conjunto infinito y $x\in X$, entonces $X\setminus \{x\}$ también es un conjunto infinito.

Demostración. Sea $f:X\to A $ una biyección de $X$ a un subconjunto propio $A$. Tenemos que considerar dos casos: que $x\notin A$ o que $x\in A$. Comencemos con el caso $x\notin A$.

Para mostrar que $X\setminus \{x\}$ es infinito, utilizaremos como subconjunto a $A\setminus\{f(x)\}$ y como función a la restricción de $f$ a $X\setminus\{x\}$. Debemos demostrar que $A\setminus\{f(x)\}$ es un subconjunto propio de $X\setminus \{x\}$ y que dicha restricción es una biyección.

Lo primero sucede ya que $$A\setminus\{f(x)\}\subsetneq A\subseteq X\setminus \{x\}.$$ El hecho de que $f:X\setminus \{x\}\to A\setminus\{f(x)\}$ sea una biyección es consecuencia directa de que originalmente $f:X\to A $ era una biyección. Los detalles quedan como tarea moral.

Si por el contrario $x\in A$, como $A\subsetneq X$ debe existir $x’\in X\setminus A$. Consideremos la función

\begin{align*}
&g: & &X & &\longrightarrow & (A\cup \{x’&\})\setminus \{x\}& \\
& & &y & &\mapsto & f(&y) &\text{ si } y\neq f^{-1}(x) \\
& & f^{-1}&(x) & &\mapsto & &x’ &
\end{align*}

Veamos que $g$ es una biyección entre $X$ y $(A\cup \{x’\})\setminus \{x\}$. Lo primero que notamos es que el codominio está bien definido ya que para todo $y\in X$ se tiene que $g(y)\neq x$ (¿por qué?).

Además es inyectiva, ya que si $g(y)=g(z)$, con $y\neq f^{-1}(x)\neq z$, entonces se tiene que $f(y)=g(y)=g(z)=f(z)$, y por la inyectividad de $f$ se tiene que $y=z$. Mientras que si $y=f^{-1}(x)$, tenemos que $g(y)=x’=g(z)$ si $z\neq f^{-1}(x)$, tendríamos que $x’=f(z)$, por lo que $x’\in A$ lo cual es absurdo, entonces $z=f^{-1}(x)=y$, así $g$ es efectivamente inyectiva.

Para probar que es suprayectiva, consideremos $z\in(A\cup \{x’\})\setminus \{x\}$. Si $z=x’$, entonces $g(f^{-1}(x))=x’$, mientras que si $z\in A\setminus \{x\}$, por la suprayectvidad de $f$, debe de existir $y$ tal que $f(y)=z$. Además $y\neq f^{-1}(x)$ ya que si lo fuera $f(f^{-1}(x))=x=z$, lo cual sería absurdo. Se tiene entonces que $g(y)=f(y)=z$.

Con esto probamos que $g$ es una biyección de $X$ a un subconjunto propio al que no pertenece $x$. Para concluir, aplicamos el primer caso.

$\square$

Usando el lema anterior es fácil dar un corolario importante sobre conjuntos finitos, cuya prueba queda como un ejercicio.

Corolario. Si $X$ es un conjunto finito, y $x$ es un conjunto arbitrario, entonces $X\cup \{x\}$ es también un conjunto finito.

Armados con este corolario, podemos dar uno de los teoremas importantes de esta entrada.

Teorema. Si $n$ es un natural, entonces $n$ es un conjunto finito.

Demostración. Procedamos por inducción. Si $n=0$, entonces $n=\emptyset$, entonces $n$ no tiene subconjuntos propios con los que pueda biyectarse, ya que no tiene subconjuntos propios. Entonces por vacuidad el vacío es finito.

Supongamos que $n$ es un natural finito. Debemos demostrar que $\sigma(n) $ es también finito. Pero como $\sigma(n)=n\cup\{n\}$, el paso inductivo es consecuencia del corolario anterior. Con esto concluimos la inducción.

$\square$

Caracterizando los conjuntos finito e infinitos

Ya probamos que cada número natural es finito y que el conjunto de todos los naturales es infinito. Lo siguiente que haremos es ver que estos conjuntos nos sirven para catalogar a todos los demás conjuntos en finitos o infinitos. Comenzamos con un lema bastante intuitivo: si con conjunto tiene un subconjunto infinito, entonces es infinito.

Lema 2. Si $X$ es infinito y $X\subset Y$ entonces $Y$ también es infinito.

Demostración. Como $X$ es infinito, existe una biyección $f$ entre $X$ y uno de sus subconjuntos propios $A$. Consideremos entonces $(Y\setminus X)\cup A\subsetneq Y$, y demos una biyección entre $Y$ y este conjunto dada por

\begin{align*}
&g: & &Y & &\longrightarrow &(Y\setminus &X)\cup A & \\
& & &y & &\mapsto & &y &\text{ si } y\notin Y\setminus X\\
& & &x & &\mapsto & f(&x) &\text{ si } x\in X
\end{align*}

Probaremos que esta función es una biyección. Primero, veamos que es inyectiva. Esto se debe a que si $g(x)=g(y)$ y $x\in X$, entonces $g(y)=g(x)=f(x)\in A\subset X$, entonces $g(y)$ está en $X$, y como $Y\setminus X$ es enviado en si mismo, debe pasar que $y$ también está en $X$, por lo que $f(y)=g(y)=f(x)$ y por la inyectividad de $f$, tenemos que $y=x$. Por el contrario, si $x\notin X$, se tiene que $g(x)=x=g(y)$ entonces $g(y)\notin X$, por lo que $y$ tampoco puede estar en $X$, así, $g(y)=y=x$.

Veamos ahora que la función es suprayectiva. Si $z\in(Y\setminus X)\cup A$, consideremos dos casos: $z\in Y\setminus X$ en cuyo caso $g(z)=z$, o $z\in A$, por lo que por la suprayectividad de $f$, debemos tener que existe $x\in X$ tal que $z=f(x)=g(x)$. Así, $g$ es suprayectiva y por lo tanto es una biyección..

$\square$

Ahora sí, pasamos a demostrar los teoremas con los que concluiremos la entrada.

Teorema. El conjunto de números naturales es el conjunto infinito más pequeño, es decir, que si $X$ es un conjunto infinito, entonces $\vert\mathbb{N}\vert\leq\vert X\vert$.

Demostración. Como $X$ es infinito, debe ser distinto del vacío. Así, existe $x_0\in X$. Consideremos el conjunto $X\setminus \{x_0\}$, por el lema 1 que demostramos, este es de nuevo infinito. Una vez más, no es vacío, entonces existe $x_1\in X\setminus \{x_0\}$, y el conjunto $X\setminus\{x_0,x_1\}=(X\setminus \{x_0\})\setminus\{x_1\}$ será de nuevo infinito. Procediendo de manera recursiva, podemos dar una función

\begin{align*}
h: &\mathbb{N} \to X \\
& n \mapsto x_n
\end{align*}

tal que todos los $x_n$ son distintos entre sí (esto se puede demostrar inductivamente). Pero entonces $h$ es una función inyectiva de $\mathbb{N}$ al conjunto $X$, que es precisamente nuestra definición de que $\vert\mathbb{N}\vert\leq \vert X\vert $.

$\square$

El regreso del teorema anterior es evidentemente cierto, es decir que si un conjunto $X$ cumple que $\vert\mathbb{N}\vert\leq \vert X\vert $, entonces $X$ es infinito. Queda como ejercicio demostrarlo.

Para finalizar la entrada, damos un resultado análogo al anterior, para conjuntos finitos.

Teorema. Si $X$ es un conjunto finito, entonces existe $n\in\mathbb{N}$ tal que $\vert X\vert =\vert n\vert$.

Demostración. Si $X=\emptyset$, entonces $\vert\emptyset\vert= \vert X\vert $. Si $X$ no es vacío, entonces existe $x_0\in X$. Consideremos entonces $X\setminus \{x_0\}$. Si este conjunto es vacío, significa que $X=\{x_0\}$ y claramente podríamos biyectarlo con el conjunto $\sigma(0)=\{0\}$. Si por el contrario, $X\setminus \{x_0\}\neq \emptyset$, podemos elegir $x_1\in X\setminus \{x_0\}$ y verificar la misma condición.

Necesariamente debemos de terminar en algún momento pues, de otro modo, podremos usar el teorema de recursión para construir una función inyectiva de $\mathbb{N}$ a $X$. Esto diría que $X$ sería infinito, lo cual sería absurdo.

Entonces debe ocurrir que existe una $n$ tal que $X\setminus\{x_0,x_1,…,x_n\}$ es vacío, por lo que $X=\{x_0,x_1,…,x_n\}$, y por lo tanto podemos biyectarlo con $\sigma(n)$.

$\square$

Más adelante…

Así como los conjuntos transitivos, la teoría que se desarrolla al estudiar las cardinalidades de los conjuntos es un área de estudio importante en la teoría de conjuntos. Aunque no lo veremos a profundidad, la teoría que acabamos de desarrollar es suficiente para comparar la cardinalidad de la mayoría de los conjuntos que veamos con total precisión. Esto será cierto para, conjuntos como $\mathbb{Z}$ (el de los números enteros) o $\mathbb{Q}$ (el de los números racionales). No será sino hasta que definamos el conjunto de números reales que tendremos un conjunto con una cardinalidad estrictamente mayor que la de $\mathbb{N}$.

En la siguiente entrada definiremos el orden de los naturales, para lo cual de nuevo pensaremos a los números naturales como conjuntos. Más aún, las propiedades que estudiamos en la entrada pasada, serán de suma importancia a la hora de definir el buen orden de un conjunto. Esta es una propiedad que usamos anteriormente sin prueba, cuando demostramos el teorema de Recursión.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Supón que diriges un hotel con tantas habitaciones como números naturales. Supón que todas tus habitaciones se encuentran ocupadas, y de repente llega una persona solicitando un cuarto. ¿Cómo puedes hospedarlo sin desalojar a ningún cliente? Supón ahora que después llega un camión con tantas personas como números naturales, todas buscando un cuarto. ¿De qué forma puedes acomodarlos a ellos y a todos los clientes ya hospedados?
  2. Completa los detalles de la prueba del lema 1.
  3. Demuestra el corolario de la entrada: Si $X$ es un conjunto finito, y $x$ es un conjunto arbitrario, entonces $X\cup \{x\}$ es también un conjunto finito.
  4. Demuestra que si $X$ es tal que $\vert\mathbb{N}\vert\leq \vert X\vert $, entonces $X$ es infinito.
  5. Demuestra por inducción que si $X$ es infinito y $A$ es un subconjunto con $k$ elementos, entonces $X\setminus A$ es infinito. Si $A$ tiene tantos elementos como naturales, ¿el resultado sigue siendo cierto?

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Álgebra Superior II: Conjuntos transitivos

Por Roberto Manríquez Castillo

Deja un comentario

Introducción

En las últimas cuatro entradas hemos visto al conjunto de números naturales como elementos del conjunto $\mathbb{N}$. Sin embargo, no debemos olvidar que los números naturales son también conjuntos. Y al ser conjuntos, cada uno de los naturales tiene unos ciertos elementos que los caracterizan de forma unívoca.

Pensando en esto, recordemos el ejercicio 5 de la Tarea moral de las notas sobre la Construcción de los naturales:

Problema. Muestra que si $n\neq 0$, entonces $n=\{0,1,2,…,n-1\}$.

En otras palabras, como conjunto, cada natural consiste exactamente de los números naturales anteriores. Antes de empezar a leer esta entrada, y si aún no lo has hecho, te invitamos a intentar este problema. Aunque comenzaremos la siguiente sección dando una prueba, es bueno que intentes familiarizarte por tu cuenta con lo que será necesario hacer pues dicho resultado será importante para la teoría que veremos en esta entrada.

Dos propiedades de los números naturales

Para empezar, y por la importancia de la aseveración, probamos justo el ejercicio comentado en la introducción. Primero, notemos que como en la hipótesis se pide que $n\neq0$, entonces tiene sentido hablar del número $n-1$. Aunque no hemos definido a la resta en los números naturales, podemos definir a esta expresión como el único número $m$ tal que $\sigma(m)=n$

Teorema. Si $n\neq 0$, entonces $n=\{0,1,2,…,n-1\}$.

Demostración. Procedamos por inducción sobre $n$. Como el resultado es a partir de $1$, la base inductiva corresponde al caso $n=1$. Este caso es claro, ya que por definición,
\begin{align*}
1&=\sigma(0)\\&=\sigma(\emptyset)\\&=\emptyset\cup\{\emptyset\}\\&=\{0\}.
\end{align*}

Supongamos que para alguna $n$, se tiene que $n=\{0,1,…,n-1\}$, y probemos que el resultado también es cierto para $\sigma(n)$. Para ello, se usa la siguiente cadena de igualdades, en la cual te invitamos a pensar por qué se da cada igualdad: $$\sigma(n)=n\cup\{n\}=\{0,1,…,n-1\}\cup\{n\}=\{0,1,…,n-1,n\}.$$

Esto termina el paso inductivo y por lo tanto la demostración.

$\square$

Consideremos un número natural y ocupemos este resultado para examinarlo como conjunto. Para no hacer la notación muy larga, veamos como ejemplo al $4$. Por el teorema anterior, tenemos que
\begin{align*}
4&=\{0,1,2,3\}\\&=\{\emptyset,\{0\},\{0,1\},\{0,1,2\}\}.
\end{align*}

Analizando cada elemento del conjunto $4$, podemos ver que cada uno de los elementos (ya expandidos) de nuestro conjunto, es a su vez un subconjunto del $4$. Por ejemplo, uno de los elementos de $4$ es el conjunto $2=\{0,1\}$, que claramente es un subconjunto de $4$. Pensando de forma similar, no debe ser difícil convencerse, al menos de forma intuitiva, que esta propiedad será satisfecha de manera más general en los naturales.

Motivados por lo anterior, enunciamos el teorema siguiente, y damos una prueba formal usando el principio de Inducción.

Teorema. Si $n$ es un número natural y se tiene que $y\in n$, entonces $y\subseteq n$.

En este punto es muy importante recordar que $y\in n$ significa que $y$ es un elemento de $n$, mientras que $y\subseteq n$ significa que $y$ es un subconjunto de $n$, es decir, que todo elemento de $y$ también es elemento de $n$. Pasemos a la demostración.

Demostración. De nuevo procedamos por inducción. Si $n=0$, la proposición $y\in0$ es falsa, ya que $0=\emptyset$. Como el antecedente es falso, la proposición $y\in0\Rightarrow y\subseteq0$, es verdadera, y así probamos el caso base (como $y=\emptyset$, a esto también se le conoce como una prueba por vacuidad).

Supongamos que el resultado es cierto para alguna $n$, es decir que si $y\in n$, entonces $y\subseteq n$. Probemos que también es cierta la afirmación al substituir $n$ por $\sigma(n)$.

Sea $y\in \sigma(n)=n\cup\{n\}$. Por la definición de la unión hay dos casos: o bien $y\in n$, o bien $y\in \{n\}$.

Tratemos el primer caso. Si $y\in n$, entonces por la hipótesis de inducción, tenemos que $y\subseteq n$, pero por definición de $\sigma(n)$ tenemos que $n\subseteq \sigma(n)$. Como la contención de conjuntos es transitiva, concluimos que $y\subseteq \sigma(n)$.

El caso restante es $y\in\{n\}$. En este caso, el único elemento en el conjunto del lado derecho es $n$, así que debe suceder que $y=n$. De aquí es inmediata la contención buscada, pues $y=n\subseteq \sigma(n)$. En cualquier caso, obtenemos lo que que queremos. Así la inducción y la prueba concluyen.

$\square$

Conjuntos transitivos y un ejemplo

Nota que la propiedad de un conjunto $X$ si $y\in X$ entonces $y\subseteq X$, es equivalente a la propiedad de que si $z\in y\in X$ entonces $z\in X$. En general, esta propiedad no se satisface para cualquier conjunto. Es así que motivamos la siguiente definición.

Definición. Se dice que un conjunto $X$ es transitivo, si $Z\in Y\in X$ implica que $Z\in X$.

Los conjuntos transitivos son de suma importancia en la teoría de conjuntos, y probablemente conocerás más de ellos si llevas algún curso de esa materia. Un estudio profundo de estos conjuntos se sale de los fines de nuestro curso, pero podemos decir unas pocas cosas más. Con esta nueva definición podemos reformular el teorema de la sección anterior como sigue.

Teorema. Cada uno de los números naturales es un conjunto transitivo.

Como mencionamos, los conjuntos transitivos parecen ser una clase muy particular de conjuntos. Sin embargo, podemos mencionar otro conjunto transitivo de suma importancia: el conjunto $\mathbb{N}$. Esperamos que así como hicimos con los números naturales, puedas formarte una intuición de por qué esta afirmación es cierta, usando el teorema inicial.

Antes de dar la prueba, consideramos pertinente hacer mención de los límites del principio de inducción. En el teorema anterior, probamos que cada número natural es transitivo, nunca se probó que $\mathbb{N}$, fuese transitivo. De la misma forma, si en algún momento pruebas que una afirmación es cierta para cualquier número natural, esa misma afirmación podría dejar de ser cierta al considerar el caso de todo el conjunto $\mathbb{N}$. Encontraremos ejemplos de esto en entradas posteriores. Ahora sí, enunciamos el teorema.

Teorema: El conjunto $\mathbb{N}$ de números naturales es transitivo.

Demostración. Debemos probar que si $n\in \mathbb{N}$, entonces $n\subseteq \mathbb{N}$. Es decir, que todo número natural es un subconjunto de $\mathbb{N}$. Para esto, usaremos inducción sobre $n$.

Evidentemente la base es cierta ya que $0=\emptyset$ es un subconjunto de todo conjunto, en particular del de los naturales.

Supongamos que para un natural fijo $n$ sucede que $n\subseteq\mathbb{N}$ y a partir de ello probemos que $\sigma(n)$ también es un subconjunto de los naturales.

Para ver que esto es cierto, usamos que $\sigma(n)=n\cup \{n\}$. Esta es una unión de conjuntos, así que basta ver que cada uno está contenido en $\mathbb{N}$. Por un lado, $\{n\}$ está contenido en los naturales, ya que su único elemento es el número $n$, que está en $\mathbb{N}$. Por otro lado, por hipótesis de inducción, $n\subseteq\mathbb{N}$. Concluimos entonces, como queríamos, que $\sigma(n)\subseteq \mathbb{N}$.

$\square$

Nota que el teorema inicial de la sección es un refinamiento de este teorema. No sólo nos dice que los números naturales están contenidos en $\mathbb{N}$. Además, también especifica quiénes son los elementos de $n$.

Más adelante…

El teorema que demostramos al inicio de la entrada tendrá de nuevo mucha importancia en el siguiente tema. Aunque demostramos que cada número $n$ es el conjunto de los $n$ elementos menores que el, necesitamos definir qué significa que un conjunto tenga $n$ elementos. Motivados por esta idea, y por las características de los números naturales, definiremos también la idea de que un conjunto tenga una cantidad infinita de elementos. Veremos que, como podrás intuir, el conjunto $\mathbb{N}$ de todos los números naturales es en verdad un conjunto infinito y que en cierto sentido formal es el «más pequeño» de todos estos conjuntos.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Demuestra que $\{2,3\} $ no es un conjunto transitivo ¿Quién es el mínimo conjunto transitivo que lo contiene?
  2. Prueba que si $X$ y $Y$ son transitivos, entonces $X\cap Y$ es transitivo.
  3. Demuestra que si $X$ es transitivo, entonces $\bigcup X$ también es un conjunto transitivo.
  4. Prueba que en general que si $X$ es transitivo, entonces $\sigma (X)$ también es transitivo.
  5. Demuestra que un conjunto es transitivo si y solo si $\bigcup X\subset X$.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Álgebra Superior II: Otras definiciones recursivas en los naturales (exponenciación y factorial)

Por Roberto Manríquez Castillo

Deja un comentario

Introducción

En las entradas pasadas hemos dado la definición recursiva de la suma y del producto usando el teorema de la recursión débil y probamos las propiedades elementales de estas operaciones usando el principio de inducción.

Continuando con esta línea de pensamiento, en esta entrada definiremos las funciones exponenciales usando las funciones producto; sin embargo, para definir estas funciones, también ocuparemos el teorema de recursión débil. Para ver que no enunciamos en vano la versión fuerte de este teorema, daremos como aplicación la definición de la función factorial, y de la misma forma a como lo hicimos antes, probaremos algunas de sus propiedades haciendo uso del principio de Inducción. Sin embargo, dejaremos algunas de las propiedades como ejercicio para que puedas practicar este tipo de pruebas una vez más.

Exponenciación en los naturales

Desde la educación elemental nos enseñan que «multiplicar es sumar repetidas veces» y que «exponenciar es multiplicar repetidas veces». Formalicemos esta intuición mediante el teorema de recursión.

Definición: Sea $m\in \mathbb{N}$. Definimos $\eta_{m}:\mathbb{N}\longrightarrow\mathbb(N),$ como la función que satisface las siguientes propiedades:

  1. $\eta_{m}(0)=1$
  2. $\eta_m(\sigma(n))=p_{m}(\eta_{m}(n)) $

Así como lo hemos hecho con la definición de producto y de suma, introduciremos la «notación usual» para hablar de esta función. En este caso, definimos $m^n:=\eta_m(n)$.

De este modo, en términos de las notaciones usuales, podemos suplir la propiedad (2) de la definición anterior como $m^{n+1}=m\cdot m^n$.

Las potencias de $0$ y de $1$

Así como lo hicimos con la suma y el producto, analizaremos de forma especial a las funciones $\eta_{0}$ y $\eta_{1}$.

Teorema: Tenemos que $\eta_{0}(0)=1$ y si $n\neq 0$, entonces $\eta_{0}(n)=0$.

La demostración queda como un ejercicio moral. La buena noticia es que hemos trabajado lo suficiente como para no tener que realizar una prueba por inducción. Cuando intentes demostrar esto por tu cuenta, recuerda qué sucede cuando multiplicamos por $0$.

Notemos que así como lo definimos, $0^0$ es $1$ en los números naturales. Sin embargo, como veremos más adelante y como posiblemente lo sabrás ya, la expresión $0^0$ no estará definida en otros sistemas numéricos como los números reales. Al igual que «$0$ es un natural», la definición de $0^0$ frecuentemente varía dependiendo del contexto.

Teorema: Tenemos que $\eta_{1}(n) =1$ para todo $n$ en los naturales.

Demostración. Para este resultado sí procederemos por inducción sobre $n$. Por la parte (1) de la definición de $\eta_{1}$, tenemos que $\eta_{1}(0)=1$. Esta es nuestra base de inducción.

Supongamos que $\eta_{1}(n)=1$. Queda demostrar que $\eta_{1}(\sigma(n))=1.$ Sin embargo esto se sigue ya que por definición, $\eta_{1}(\sigma(n))=1\cdot\eta_{1}(n)=1\cdot 1=1$. Te invitamos a identificar los argumentos que se ocuparon en cada paso.

$\square$

La exponencial no conmuta ni asocia

Como la notación que ocupamos para las funciones $\eta_{m}$ no es tan simétrica como la que ocupamos para el producto o para la suma, uno puede esperar que esta operación no sea en general conmutativa. En efecto esto es cierto, solo basta notar que

$0^1\neq1^0$

Así mismo la exponenciación no es en general asociativa, es decir que existen casos en que

$(n^m)^l\neq n^{(m^l)}$

Encontrar un contraejemplo queda como un ejercicio moral.

Le exponenciación y otras operaciones

Cuando estudiamos el producto de números naturales, vimos que esta operación se distribuye sobre la suma, entonces una buena pregunta es preguntarnos qué pasa cuando mezclamos la exponenciación con el producto y la suma. Quedará como ejercicio dar contraejemplos a todas las siguientes proposiciones:

  1. $n^{(l\cdot m)}=n^l\cdot n^l$
  2. $(l+m)^n=l^n+m^n$
  3. $n^{l+m}=n^l+n^m$

Sin embargo, probaremos dos teoremas conocidos usualmente como las leyes de los exponentes. El primero de ellos dice que por la izquierda, la exponenciación sí se distribuye sobre el producto.

Teorema: Si $a,b,n\in\mathbb{N}$, entonces $(a\cdot b)^n=a^n\cdot b^n$.

Demostración. Procedamos por inducción sobre $n$. De la definición de exponencial, tenemos que $(a\cdot b)^0=1=1\cdot 1= a^0\cdot b^0$, por lo que la base de inducción es cierta.

Supongamos que para algún $n$ se tiene que $(a\cdot b)^n=a^n\cdot b^n$ y probemos que $(a\cdot b)^{\sigma(n)}=a^{\sigma(n)}\cdot b^{\sigma(n)}$. Esto es cierto ya que

\begin{align*}
(a\cdot b)^{\sigma(n)}&=(a\cdot b)\cdot (a\cdot b)^n\\
&=(a\cdot b)\cdot (a^n\cdot b^n)\\
&=(a\cdot a^n)\cdot (b\cdot b^n)\\
&=a^{\sigma(n)}\cdot b^{\sigma(n)}
\end{align*}

A diferencia de las entradas anteriores ya ocupamos sin mención las propiedades ya demostradas o la hipótesis de inducción; sin embargo, sería bueno que detallaras las pruebas.

$\square$

Aunque vimos que en general no podemos hablar de que la exponencial se distribuya, sí hay importantes relaciones que notaremos en los siguientes dos teoremas.

Teorema: Si $a,b,n\in\mathbb{N}$, entonces $a^{b+n}=a^b\cdot a^n$.

Demostración. De nuevo procederemos por inducción sobre $n$. Si $n=0$, entonces $a^{b+0}=a^b =a ^b \cdot 1=a^b \cdot a^0$, con lo que probamos la base de inducción.

Supongamos entonces que para algún $n$ se tiene que $a^{b+n}=a^b\cdot a^n$, y demostremos el caso para $\sigma(n)$. Sabemos que

\begin{align*}
a^{b+ \sigma(n)}=&a^{\sigma(b+n)}\\
=&a\cdot a^{b+n}\\
=&a\cdot (a^b\cdot a^n)\\
=&a^b\cdot (a \cdot a^n)\\
=&a^b\cdot a^{\sigma(n)}
\end{align*}

Con esto termina la prueba.

$\square$

El siguiente teorema queda como ejercicio de la tarea moral, para que puedas practicar.

Teorema: Si $a,b,n\in\mathbb{N}$, entoces $(a^b)^n=a^{b\cdot n}$.

El factorial

Hasta ahora, sólo hemos ocupado el teorema de recursión débil a la hora de definir las operaciones. A pesar de que antes demostramos que ambas versiones del teorema son equivalentes, la siguiente definición mostrará la naturalidad que tiene el ocupar el teorema de Recursión Fuerte para algunas cosas.

Definición: Se define la función factorial, $f:\mathbb{N}\to \mathbb{N}$, como la única función dada por el teorema de recursión fuerte que cumple que

  • $f(0)=1$
  • $f(\sigma(n))=p_{\sigma(n)}(f(n))$

Usaremos la notación $n!:=f(n)$. Así, la primer parte de la definición dice que $0!=1$ y la segunda dice que $(n+1)!=(n+1)\cdot n!$.

Notemos que en la definición anterior es necesario ocupar el teorema de Recursión Fuerte ya que en cada paso damos una función distinta. En concreto, para dar la definición en $\sigma(n)$ usamos a la función $p_{\sigma(n)}$.

El factorial es una función que jugará un papel importante en varios temas que verás en la facultad. Tiene una fuerte relación con contar cosas, el cual es un tema que posiblemente hayas estudiado en Álgebra Superior II. Aparece al contar las permutaciones de objetos, pero también como parte de la fórmula para los coeficientes binomiales $\binom{n}{k}$. También, lo encontraremos en este curso a la hora de enunciar el teorema de Wilson de teoría de números, pero necesitamos definir más cosas antes de llegar ahí.

Sin embargo, algo que sí podemos hacer ahora es demostrar una propiedad interesante que satisface el factorial.

Proposición: Para todo $n\in \mathbb{N}$, se tiene que $0\cdot 0!+1\cdot 1!+2\cdot 2!+…+n\cdot n!+1=(n+1)!$

Demostración. Procederemos por inducción, el caso base es claro ya que $0\cdot 0!+1= 0+1=1!.$

Supongamos que el resultado es cierto para alguna $n$ y con esta suposición probemos que

$0\cdot 0!+1\cdot 1!+2\cdot 2!+…+n\cdot n!+(n+1)\cdot(n+1)!+1=(n+2)!$.

Sabemos por nuestra hipótesis de inducción que

\begin{align*}
&0\cdot 0!+1\cdot 1!+2\cdot 2!+…+n\cdot n!+(n+1)\cdot(n+1)!+1\\
=&(0\cdot 0!+1\cdot 1!+2\cdot 2!+…+n\cdot n!+1)+(n+1)\cdot(n+1)! \\
=&(n+1)!+ (n+1)\cdot(n+1)!\\
=&(n+1)!(1+n+1)\\
=&(n+1)!(n+2)\\
=&(n+2)!
\end{align*}

En la primer igualdad estamos usando la conmutatividad y asociatividad de la suma. En la segunda igualdad, la hipótesis de inducción. Para la tercer igualdad estamos factorizando el término $(n+1)!$. El resto de igualdades se siguen de las definiciones.

$\square$

Resumen de las propiedades de los exponentes

Para finalizar con la entrada, hacemos un repaso de las propiedades que demostramos, posiblemente las conozcas como las leyes de los exponentes

  • Para todo $n$ número natural, se tiene que $n^0=1$
  • Si $n\neq 0$,entonces $0^n=0$
  • Para todo $n$ número natural, se tiene que $n^1=n$
  • Para todo $n$ número natural, se tiene que $1^n=1$
  • Para $l,m,n$ naturales, se tiene que $(l\cdot m)^n=l\n\cdot m^n$
  • Para $l,m,n$ naturales, se tiene que $n^{l+m}=n^l\cdot n^m$
  • Para $l,m,n$ naturales, se tiene que $n^{l\cdot m}=(n^l)^m$

Más adelante…

Con esta entrada, acabamos con las definiciones de operaciones a través de los teoremas de Recursión; sin embargo, no podemos decir que no ocuparemos este teorema en futuras ocasiones, al menos de forma implícita, mucho menos nos olvidaremos del principio de Inducción, el cuál irá siempre adherido al concepto de número natural.

En las siguientes entradas, estudiaremos otro tipo de propiedades de los naturales, relacionadas con el orden y el tamaño que estos tienen. Sin embargo, aún ocuparemos las operaciones que definimos y las relacionaremos; por ejemplo, con el orden que les daremos.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Encuentra los contraejemplos que faltaron en la entrada
  2. Da la demostración de que $0^n=0$, para toda $n$
  3. Prueba que para todos los naturales $a,b,n$, se tiene que $(a^b)^n=a^{b\cdot n}$
  4. El factorial consiste en «multiplicar los primeros enteros». ¿Qué pasa si queremos hacer algo análogo para sumar los primeros enteros? Da una definición recursiva de una función $S(n)=0+1+2+…+n$, ¿por qué en realidad no es necesario dar una definición recursiva de esta función?
  5. Demuestra que si $n,m$ son naturales tales que existe $k\in\mathbb{N}$ tal que $n\cdot k=n^k=m$, entonces $n^m=m^n$. El regreso de esta afirmación es también verdadero, pero para verlo formalmente, necesitamos desarrollar más teoría.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Álgebra Superior II: Definición del producto y sus propiedades básicas

Por Roberto Manríquez Castillo

Deja un comentario

Introducción

En la entrada anterior, nos dedicamos a buscar una definición apropiada para la suma de números naturales, y después nos dedicamos a probar las propiedades más elementales que esta operación satisface.

Ahora es el turno de la multiplicación o producto, que se definirá de forma similar a la suma, ya que ocuparemos el teorema de Recursión Débil, y para probar sus propiedades ocuparemos el principio de Inducción.

Te motivamos a releer la entrada anterior y pensar unos momentos en el ejercicio 5 de la entrada anterior.

Definición del producto

Así como con la suma, recurriremos a una definición recursiva, la cual existe en virtud del teorema de Recursión.

Definición. Sea $m\in\mathbb{N}$, defnimos la función $p_{m}:\mathbb{N}\longrightarrow\mathbb{N}$, como la función que satisface las propiedades siguientes:

  1. $p_{m}(0)=0$.
  2. $p_{m}(\sigma(n))=s_{m}((p_{m}(n))$.

Denotaremos a $p_{m}(n)$ como $m\cdot n$, o simplemente como $mn$

Ejemplo. Para aclarar la definición anterior, consideremos $p_{7}$ y realicemos el diagrama conmutativo correspondiente a su definición recursiva.

Recordemos que las flechas indican a donde es mandado cada elemento bajo cada función, entonces las flechas verticales, justamente son las que nos indican los valores de $p_{7}$ en cada número natural, observemos que estos valores coinciden con la conocida tabla del $7$.

$\triangle$

Aprendiendo a multiplicar por uno

En este momento, demostraremos las propiedades más importantes del producto. Tenemos la fortuna de que contamos con una buena cantidad de propiedades de las funciones $s_{n}$, las cuales ya podremos usar sin ningún problema, más aún, para simplificar la notación haremos uso de la notación $m+n$, en vez de la notación $s_{m}(n)$, cada vez que se pueda.

Siguiendo la idea anterior, mencionamos la siguiente identidad, que es solo una reformulación del punto (2) de la definición del producto, pero que nos servirá para esclarecer la mayor parte de las pruebas.

Observación. $a\cdot\sigma(n)=a+(a\cdot n)$.

Para referir a esta observación en una demostración ocuparemos el símbolo $\overset{*}{=}$.

Proposición. Para toda $n\in\mathbb{N}$, se tiene que $p_{1}(n)=n$, es decir, $1\cdot n=n$

Demostración. Como se esperaba, la prueba es por inducción sobre $n$.

Base inductiva: Por la definición de $p_{1}$, tenemos que $p_{1}(0)=0$.

Hipótesis de inducción: Supongamos que para algún $n$, se tiene que $p_{1}(n)=n$

Paso inductivo: Debemos demostrar que $p_{1}(\sigma(n))=\sigma(n)$, esto se sigue por las siguientes igualdades

\begin{align*}
p_{1}(\sigma(n))&\overset{*}{=}1+(p_{1}(n))\\ &\overset{\text{H.I.}}{=}1+n=\sigma(n).
\end{align*}

Donde la última igualdad se da recordando que en la entrada anterior probamos que $s_{1}(n)=\sigma(n)$.

$\square$

Con esto hemos aprendido a multiplicar por $1$.

Aprendiendo a multiplicar por cero

Proposición. Para toda $n\in\mathbb{N}$, se tiene que $p_{0}(n)=0$.

Demostración. Procedamos por inducción sobre $n$, la base inductiva es directa de la definición, ya que $p_{0}(0)=0$.

Nuestra hipótesis de inducción consiste en suponer que para alguna $n$ se tiene que $p_{0}(n)=0$. Entonces queda demostrar que $p_{0}(\sigma(n))=0$. Esto se sigue de las siguientes igualdades.

\begin{align*}
p_{0}(\sigma(n))&\overset{*}{=}0+p_{0}(n)\\ &\overset{\text{H.I.}}{=}0+0=0
\end{align*}

$\square$

La propiedad distributiva izquierda

La siguiente propiedad es una de las más famosas, ya que nos permitirá relacionar la suma y el producto, además jugará un papel importante en la demostración de las siguientes propiedades.

Proposición (propiedad distributiva izquierda). Si $a,b,n$ son números naturales, entonces $p_{s_{a}(b)}(n)=s_{p_{a}(n)}(p_{b}(n))$, u ocupando la notación familiar $(a+b)\cdot n=(a\cdot n)+(b\cdot n)$.

Demostración. Procedamos por inducción, como podrás notar con todas estas demostraciones, la inducción será sobre la variable que aparezca más a la derecha de nuestras expresiones, es decir, la inducción será sobre $n$.

Base inductiva: Por la definición del producto tenemos que, $(a+b)\cdot 0=0$, y por las propiedades que demostramos para la suma, concluimos que $0=0+0$, sin embargo; de nuevo por la definición del producto, $0=(a\cdot n)$ y $0=(b\cdot n)$, uniendo todas estas igualdades concluimos que $(a+b)\cdot 0=(a\cdot n)+(b\cdot n)$, justo como queremos.

Hipótesis de inducción: Supongamos que para algún $n$ se tiene que $(a+b)\cdot n=(a\cdot n)+(b\cdot n)$.

Paso inductivo: Debemos probar que $(a+b)\cdot\sigma(n)=(a\cdot\sigma(n))+(b\cdot\sigma(n))$. Por la observación que hicimos, tenemos

\begin{align*}
(a+b)\cdot\sigma(n)&\overset{*}{=}(a+b)+((a+b)\cdot n)\\ &\overset{\text{H.I.}}{=}(a+b)+((a\cdot n)+(b\cdot n))
\end{align*}

A partir de aquí, el resultado se seguirá usando la asociatividad y la conmutatividad de la suma, en la siguiente cadena de igualades detallamos la demostración paso a paso ¿Puedes identificar cómo ocupamos las propiedades de la suma?.

\begin{align*}
(a+b)+((a\cdot n)+(b\cdot n))&=a+(b+((a\cdot n)+(b\cdot n)))\\
&=a+((b+(a\cdot n))+(b\cdot n))\\
&=a+(((a\cdot n)+b)+(b\cdot n))\\
&=a+((a\cdot n)+(b+(b\cdot n)))\\
&=(a+(a\cdot n))+(b+(b\cdot n))\\
&\overset{*}{=}(a\cdot \sigma (n))+(b\cdot \sigma (n))
\end{align*}

$\square$

Aunque la prueba anterior fue un poco más confusa que las anteriores, las consecuencias que tendrá esta proposición serán sumamente importantes.

El producto es conmutativo

Como mencionamos, la asociatividad y la conmutatividad, serán una consecuencia de las propiedades distributivas, por el momento veamos que en efecto el producto conmuta.

Proposición (conmutatividad). Si $m,n\in \mathbb{N}$, entonces $m\cdot n=n\cdot m$.

Demostración. Una vez más hagamos la prueba por inducción sobre $n$

Base inductiva: Por definición tenemos que $m\cdot 0 =0$, además $p_{0}(m)=0$ por lo demostrado antes, es decir que $m\cdot 0=0=0\cdot m$

Hipótesis de inducción: Supongamos que para alguna $n$, se tiene que $m\cdot n=n\cdot m$.

Paso inductivo: Debemos probar que $m\cdot\sigma(n)=\sigma(n)\cdot m$. Esto se sigue ya que

\begin{align*}
m\cdot\sigma(n)&\overset{*}{=}m+(m\cdot n)\\
&\overset{\text{H.I.}}{=}m+(n\cdot m)
\end{align*}

Pero ya demostramos que $m=1\cdot m$, usando esto y la propiedad ditributiva, podemos concluir que

\begin{align*}
m+(n\cdot m)&=(1\cdot m )+(n\cdot m)\\
&=(1+n)\cdot m=\sigma(n)\cdot m
\end{align*}

$\square$

Con la conmutatividad, podemos probar de manera inmediata el siguiente resultado

Corolario (propiedad distributiva derecha). Si $a,b,n$ son números naturales, entonces $a\cdot(b+ n)=(a\cdot b)+(a\cdot n)$.

La prueba queda como un ejercicio moral, en parte porque su prueba no requiere Inducción. Con este resultado, podemos probar la propiedad asociativa del producto.

El producto es asociativo

Con la propiedad distributiva derecha , podemos dar la demostración de la propiedad asociativa del producto.

Proposición (asociatividad). Si $a,b,n$ son números naturales, se tiene que $a\cdot(b\cdot n)=(a\cdot b)\cdot n$.

Demostración. De nuevo procedamos por inducción sobre $n$

Base inductiva: Notemos que por definición, para cualquier número natural $m$ se tiene que $0=p_{m}(0)=m\cdot 0$. Con esto en mente tenemos que, $(a\cdot b)\cdot(0)=0=a\cdot 0=a\cdot(b\cdot 0)$ que es justo la base de inducción.

Hipótesis de Inducción: Supongamos que para alguna $n\in \mathbb{N}$, tenemos que $(a\cdot b)\cdot n=a\cdot(b\cdot n)$

Paso Inductivo: Demostremos que $(a\cdot b)\cdot\sigma(n)=a\cdot(b\cdot \sigma(n))$. Como

\begin{align*}
(a\cdot b)\cdot\sigma(n)&\overset{*}{=}(a\cdot b)+(a\cdot b)\cdot n\\
&\overset{\text{H.I.}}{=}(a\cdot{b})+a\cdot(b\cdot n)\\
&=a\cdot (b+b\cdot n)\\
&\overset{*}{=}a\cdot(b\cdot \sigma (n))
\end{align*}

la igualdad que no está justificada es la aplicación de la propiedad distributiva.

$\square$

Ley de la cancelación

Para concluir con las propiedades del producto, enunciamos la propiedad de la cancelación del producto, recordemos que esta propiedad también es válida para la suma. Para hacer esta prueba necesitamos trabajar un poco.

Recordemos el ejercicio 2 de la Tarea moral de la entrada Principio de inducción y teoremas de recursión, el cual ya hemos ocupado anteriormente:

Si $n\neq0$, entonces existe $a\in \mathbb{N}$ tal que $n=\sigma(a)$

De la misma forma, el ejercicio 1 de la Tarea moral de la entrada pasada dice que:

Si $a,b\in\mathbb{N}$ son tales que $a+b=0$, entonces $a=b=0$

Con estos resultados en mente probamos el siguiente lema.

Lema. Si $n\neq 0$ y $m\in \mathbb{N}$ es tal que $m\cdot n=0$, entonces $m=0$.

Demostración. Como $n\neq0$, entonces existe $a\in \mathbb{N}$, tal que $n=\sigma(a)$, entonces tenemos que

\begin{align*}
0&=m\cdot n\\
&=m\cdot\sigma(a)\\
\overset{*}{=}m+(m\cdot a).
\end{align*}

Entonces tenemos que $m\cdot a=0$ y que $m=0$ que es lo que debíamos probar.

$\square$

Es común usar una equivalencia lógica del enunciado anterior, la cual dice:

Si $n,m\in \mathbb{N}\setminus\{0\}$, entonces $n\cdot m\in \mathbb{N}\setminus\{0\}$

Proposición (ley de cancelación). Si $m,n$ son números naturales y $a\neq0$ y cumplen que $a\cdot n=a\cdot m$, entonces, $n=m$

Demostración. De nuevo, procedamos por inducción sobre $n$

Base inductiva: Supongamos que $n=0$ y $a\neq0$, entonces $a\cdot m=a\cdot n=a\cdot0 =0,$ por el Lema tenemos que $m=0=n$.

Hipótesis de inducción: Supongamos que para algún $n$, tenemos que si $a\neq0$ y $a\cdot n=a\cdot m$, entonces $n=m$.

Paso inductivo: Probemos para $\sigma(n)$, sea $a\neq 0$ y supongamos que $a\cdot\sigma(n)=a\cdot m$.

Como $\sigma(n)\neq 0$, y por hipótesis, $a\neq0$, entonces por la equivalencia del lema, concluimos que $a\cdot\sigma(n)\neq 0$, de donde $a\cdot m\neq 0$, esto implica que $m\neq 0$, por lo que existe $b$ tal que $m=\sigma(b)$, entonces podemos escribir

\begin{align*}
a+a\cdot n& \overset{*}{=}a\cdot\sigma(n)\\
&=a\cdot m\\
&=a\cdot\sigma(b)\\
&\overset{*}{=}a+a\cdot b
\end{align*}

Ocupando la ley de cancelación de la suma, tenemos que $a\cdot n=a\cdot b$.

Pero por hipótesis de inducción debemos de tener que $n=b$, esto quiere decir que $\sigma(n)=\sigma(b)=m$, justo como debíamos probar.

$\square$

Con esta prueba concluimos las propiedades más fundamentales del producto.

Resumen de las propiedades del producto

Para finalizar con la entrada, haremos un compendio de las propiedades que demostramos

  • Para todo $n$ natural, se tiene que $1\cdot n=n=n \cdot 1$
  • Para todo $n$ natural, se tiene que $0\cdot n=0=n \cdot 0$
  • Para $l,m,n$ naturales cualesquiera se tiene que $(l+m)\cdot n=(l\cdot n)+(m\cdot n)$
  • Para $m,n$ naturales se tiene que $m\cdot n=n\cdot m$
  • Para $l,m,n$ naturales cualesquiera se tiene que $l\cdot(m+n)=(l\cdot m)+(l\cdot n)$
  • Para $l,m,n$ naturales cualesquiera se tiene que $(l\cdot m)\cdot n=l\cdot(m\cdot n)$
  • Para $m,n$ naturales con $m\neq 0$, si $m\cdot n=0$, entonces $n=0$
  • Para $l,m,n$ naturales con $l\neq 0$, si $l\cdot n=l\cdot m$, entonces $n=m$

Más adelante…

Con las propiedades de la suma y del producto en nuestra bolsa de herramientas, tenemos ya una rica teoría que desarrollar; nos falta aún definir una relación muy familiar en el conjunto $\mathbb{N}$, el orden, al cual ya hemos apelado en la demostración del teorema de la Recursión Débil.

Por el momento estudiaremos con mayor detalle los conjuntos infinitos, donde veremos la importancia de los naturales dentro de esta clase de conjuntos.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Prueba la Propiedad distributiva derecha.
  2. Usando únicamente la ley de cancelación el producto, demuestra el Lema previo a la demostración de la ley de cancelación.
  3. ¿Qué pasa si en el enunciado de la ley de la cancelación, no asumimos que $a\neq 0$?
  4. Demuestra usando el Lema previo a la demostración de la ley de cancelación que si $n,m\in \mathbb{N}\setminus\{0\}$, entonces $n\cdot m\in \mathbb{N}\setminus\{0\}$.
  5. Da una definición recursiva de las funciones $\eta_{m} (n)=m^n$ y prueba las leyes de los exponentes.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Álgebra Superior II: Principio de inducción y teoremas de recursión

Por Roberto Manríquez Castillo

Deja un comentario

Introducción

Inducción y recursión son dos conceptos similares con los que seguramente te has topado en tu formación matemática, e incluso tal vez antes. Muchas veces se llegan a confundir ambos conceptos, ya que ambos tienen una fuerte relación con el 5° axioma de Peano.

Aunque lo detallaremos a lo largo de la entrada, el principio de Inducción es una propiedad de los números naturales, que nos sirve para demostrar que todos los naturales satisfacen una propiedad. Es decir, es una estrategia de demostración. En contraste, la recursión es un resultado que justifica el hecho de poder dar una definición para todos los naturales, basándonos en la definición de su antecesor. En otras palabras, es una estrategia de definición.

Al final de la entrada demostraremos el teorema de recursión débil, en cuya prueba, podremos apreciar cómo es que depende directamente del Principio de inducción.

Pruebas por inducción

Recordemos el 5° axioma de Peano, el cual probamos en la entrada pasada que se satisface en nuestro modelo:

Si $S\subset \mathbb{N}$ satisface que

  • $0\in S$ y
  • si $n\in S$, implica que $\sigma(s)\in S$,

entonces $S=\mathbb{N}$.

Como hemos mencionado en entradas anteriores, esta proposición es muy similar al principio de Inducción que probablemente hayas ocupado desde el curso de Álgebra Superior I. Más aún, en la entrada pasada, seguimos la misma estrategia que en otros cursos, a la hora de ocupar el 5° axioma. Efectivamente, la equivalencia entre ambos resultados es casi inmediata, y como ejemplo ilustrativo, probaremos el Principio de Inducción a partir del 5° axioma de Peano.

Proposición (Principio de Inducción): Sea $P(n)$ una propiedad, es decir, una proposición matemática que depende de un entero $n$. Si se tiene que:

  1. $P(0)$ es verdadera y
  2. cada vez que $P(n)$ es cierto, también lo es $P(n+1)$,

entonces P(n) es cierta para todos los números naturales.

Demostración. Sea $P(n)$ una propiedad que satisface 1. y 2. y consideremos el conjunto $S:=\{n\in\mathbb{N}: P(n)\text{es verdadera}\}$.

Como $P(0)$ es verdadera, entonces $0\in S$.

Tomemos $n\in S$, entonces $P(n)$ es verdadera, y por 2., tenemos que $P(n+1)$ es verdadera; es decir, $n+1\in S$. Por el 5° Axioma de Peano, se tiene que $S=\mathbb{N}$, por lo que por la definición de $S$, se tiene que $P(n)$ es cierta para cada $n\in \mathbb{N}$

$\square$

Definiciones por recursión

Una de nuestras primeras ideas para poder construir a $\mathbb{N}$, fue intentar construir a mano cada elemento. Para esto, dimos una definición de lo que significaba el $0$ y el sucesor de un número. Después empezamos a iterar una y otra vez la función sucesor para obtener el sucesor del último número encontrado. Discutimos por qué es que esta idea no sería el mejor camino (sólo nos permite llegar hasta una cantidad finita de naturales), por lo tuvimos que introducir el Axioma del Infinito para resolver el problema. Veamos la analogía entre esta idea y el siguiente ejemplo intuitivo.

Ejemplo: Definamos la función factorial de un número natural, como:

  • $0!=1$
  • $(n+1)!=(n!)(n+1)$

Entonces, $3!:=(2!)(3)=(1!)(2)(3)=(0!)(1)(2)(3)=(1)(1)(2)(3)=6$.

Recordemos que al definir a los naturales, necesitábamos conocer un número para poder definir su sucesor. Aquí sucede lo mismo: en la definición de factorial necesitamos conocer quién es el factorial de un número para poder definir el factorial de su sucesor. A este tipo de definiciones se les conoce como definiciones recursivas, ya que para definir algo para un número, necesitamos tener conocimiento del valor de la función en los números anteriores.

Queda una pregunta muy importante. Si a los naturales no los pudimos definir de manera recursiva, ¿por qué podemos afirmar que la función factorial sí existe? A continuación enunciaremos algunos teoremas que nos garantizarán que sí podemos hacer este tipo de definiciones recursivas en nuestro modelo. Daremos una versión fuerte y una versión débil. Demostraremos la versión débil, pues basta para mucho de lo que queremos definir en los naturales (sumas, productos, potencias).

Las siguientes secciones son un poquito técnicas. Si las puedes seguir por completo, es fantástico. Pero incluso si no es así, basta con que en el fondo te quedes con la idea importante detrás: sí se vale definir de manera recursiva. Más adelante podrás regresar a este tema y entenderlo por completo.

Los teoremas de la recursión

Antes de la demostración principal de esta entrada, enunciaremos los teoremas que nos importan y hablaremos de manera intuitiva de lo que dicen. Hay dos versiones que veremos: una fuerte y una débil. Aunque parece que dicen cosas diferentes, en realidad son equivalentes. Será muy claro que la versión fuerte «implica» a la débil. Pero luego, en los problemas de tarea moral, se esbozará cómo ver que la versión débil se puede utilizar para demostrar la fuerte.

Teorema (Recursión Fuerte): Sea $X$ un conjunto y $x_{0}\in X$. Supongamos que tenemos varias funciones (una por cada natural $i$)

$$\{f_i:X\to X\}_{i\in\mathbb{N}\setminus \{0\}}.$$

Entonces existe una única función $g:\mathbb{N}\to X$ tal que:

  • $g(0)=x_{0}$
  • $g(\sigma(n))=f_{\sigma(n)}(g(n))$.

¿Qué es lo que quiere decir este teorema? Para responder esta pregunta veamos el siguiente diagrama:

Nuestro diagrama empieza en $0$, el cual queremos que sea mandado a algún $x_{0}\in X$, para la definición de los demás números, ocupamos la segunda característica que esperamos que $g$ satisfaga. Por ejemplo $g(1)=g(\sigma(0))=f_{1}(g(0))=f_{1}(x_{0})$. Este análisis coincide con lo que nos presenta el primer cuadro de flechas del diagrama anterior, que nos presenta los dos caminos que debe satisfacer $g$, para que sea la función que queremos. Como da lo mismo si «primero aplicamos $\sigma$ y luego $g$», a que si «primero aplicamos $g$ y luego $f_1$», decimos que el primer cuadrado del diagrama conmuta.

Análogamente, ya que conocemos la definición de $g(1)$ podemos fijarnos en el segundo cuadro, para poder definir $g(2)$ (de nuevo, conmuta) y seguir «recursivamente» para cualquier número natural.

Ejemplo: ¿Qué conjunto, y qué funciones necesitamos para definir el factorial?

Consideremos $X=\mathbb{N}$, definiremos intuitivamente (ya que aún no lo hemos definido formalmente), $f_{i}:\mathbb{N}\longrightarrow \mathbb{N}$, como $f_{i}(n)=i\cdot n$, es decir, el producto por $i$.

El teorema de Recursión Fuerte, nos dice que existe una única función $g$ tal que

  • $g(0)=1$
  • $g(\sigma(n))=f_{\sigma(n)}(g(n))=\sigma(n)\cdot g(n)$

Denotemos $n!:=g(n)$. Entonces tenemos que $\sigma(n)!=n!\cdot \sigma(n)$, justo como queremos.

$\triangle$

El teorema de Recursión Débil y su demostración

El teorema de Recursión Débil tiene un enunciado parecido al teorema de recursión fuerte y puede ser visto como una consecuencia directa del teorema anterior pues se obtiene de la versión fuerte tomando $f_{1}=f_{2}=\ldots=f_{n}=\ldots$

Teorema (Recursión Débil): Sea $X$ un conjunto y $x_{0}\in X$. Supongamos que tenemos una función $f:X\to X$. Entonces existe una única función $g:\mathbb{N}\to X$ tal que:

  • $g(0)=x_{0}$
  • $g(\sigma(n))=f(g(n))$.

Para concluir con esta entrada, probaremos el teorema de Recursión Débil. Antes de hacer esto introducimos un concepto auxiliar y una propiedad de los naturales.

Recordemos que como conjunto, $m=\{0,1,…,m-1\}$, lo que sugiere la siguiente definición.

Definición: Si $n,m\in \mathbb{N}$, decimos que $n<m$ si $n\in m$.

Puede probarse que esta relación en $\mathbb{N}$ es un orden total, y que sastisface la siguiente propiedad.

Teorema (Principio el Buen Orden): Sea $S\subset\mathbb{N}$ un conjunto no vacío, es decir $S\neq \emptyset$. Entonces $S$ tiene un elemento mínimo. Es decir, existe $n\in S$ tal que $n<m$ para todo $m\in S\setminus\{n\}$.

La prueba del Principio del Buen Orden y más propiedades de $<$ serán estudiadas con mayor detalle en entradas posteriores. Con esto en mente demostramos el teorema de Recursión Débil.

Demostración. Recordemos que por definición, toda función con dominio $A$ y codominio $B$, es un subconjunto de $A\times B$, por lo que una buena idea es analizar el conjunto $\wp(\mathbb{N}\times X)$, definamos

\[\Re:=\{R\in\wp(\mathbb{N}\times X)\mid (0,x_{0})\in R \text{ y si }(n,x)\in R\text{, entonces }(\sigma(n),f(x))\in R\}\]

Esta definición se ve terriblemente complicada. Pero la intuición es clara: $\Re$ tiene a todas las posibles colecciones de parejas de $\mathbb{N}\times X$ que cumplen lo que queremos. El problema es que muchas de ellas no son funciones y tenemos que «arreglar esto».

Probablemente, notarás alguna similitud entre el conjunto $\Re$ y el conjunto de los subconjuntos inductivos (que se menciona en La construcción de los naturales). Siguiendo esta analogía, definiremos $g:=\bigcap \Re$ (podemos hacer esta intersección ya que $\Re$ no es vacío pues $\mathbb{N}\times X$ está en $\Re$).

  • Demostremos que $g\in \Re$:

Por las propiedades de la intersección, tenemos que $g\subset\mathbb{N}\times X$, por lo que $g\in \wp(\mathbb{N}\times X)$. Veamos que $(0,x_{0})\in g$. Sea $R\in\Re$ arbitrario, entonces $(0,x_{0})\in R$, por lo que $(0,x_{0})\in\bigcap \Re=g$. Por último, si $(n,x)\in g$, demostremos que $(\sigma(n),f(x))\in g$, para esto, sea $R\in \Re$ arbitrario, como $(n,x)\in g$, entonces $(n,x)\in R$, por lo que $(\sigma(n),f(x))\in R$. Es decir, $(\sigma(n), f(x))\in\bigcap \Re=g$. Por todo lo anterior, $g\in\Re$.

  • Veamos ahora que $Dom(g)=\mathbb{N}$:

Usemos el quinto axioma de Peano, como $(0,x_{0})\in g$, entonces $0\in Dom(g)$. Supongamos ahora que $n\in Dom(g)$ y demostremos que $\sigma(n)\in Dom(g)$, por la hipótesis de inducción, existe $x\in X$ tal que $(n,x)\in g$, y como $g\in\Re$, tenemos que $(\sigma(n),f(x))\in g$, pero esto quiere decir que $\sigma(n)\in Dom(g)$. Entonces $Dom(g)$ es inductivo, entonces $Dom(g)=\mathbb{N}$.

  • Demostremos ahora que $g$ sí es función. Para esto, tenemos ver que «cada natural se va a un sólo elemento», en símbolos, si $(n,x),(n,y)\in g$ entonces $n=m$.

Aquí es donde ocuparemos el Principio del Buen Orden. Consideremos $S:=\{n\in\mathbb{N}\mid (n,x),(n,y)\in g \text{ y } x\neq y \}$. Procedamos por contradicción, supongamos que $S\neq\emptyset$, entonces, $S$ tiene un elemento mínimo, denotémoslo por $n$.

Si $n=0$, entonces existe $x\in X$ tal que $(0,x)\in X$ y $x\neq x_{0}$. Entonces consideremos $g’=g\setminus\{(0,x)\}$. Notemos que $g’\in\Re$, ya que $(0,x_{0})\in g’$, ya que $(0,x_{0})\neq (0,x)$. Además si $(k,a)\in g’$, entonces $(k,a)\in g$, por lo que $(\sigma(k),f(a))\in g$, y como $0$ nunca es el sucesor de otro número, tenemos que $(\sigma(k),f(a))\neq(0,x)$, por lo tanto $(\sigma(k),f(a))\in g’$, es decir, $g’\in \Re$, lo que implica que $g=\bigcap \Re\subset g’=g\setminus\{(0,x)\}$ lo cual es absurdo, por lo que $n\neq 0$.

Como $n\neq 0$, debemos tener que existe $m$ tal que $\sigma(m)=n$ ¿Por qué?. Y como $n$ es el mínimo en $S$, tenemos que $m\not\in S$, es decir, existe un único $x\in X$ tal que $(m,x)\in g$, esto implica que $(\sigma(m),f(x))=(n,f(x))\in g$, y como $n\in S$, debe existir $y\in X$, $y\neq f(x)$ tal que $(n,y)\in g$. Análogamente a como lo hicimos antes, consideremos $g’=g\setminus (n,y)$ y veamos que $g’\in \Re$. Como $(n,y)\neq(0,x_{0})$, tenemos que $(0,x_{0})\in g’$. Más aún, si $(k,a)\in g’$, demostremos que $(\sigma(k),f(a))\in g’$, para esto supongamos que no.

Como $(k,a)\in g’$, tenemos que $(k,a)\in g$, por lo que $(\sigma(k),f(a))\in g$, esto implica que $(\sigma(k),f(a))=(n,y)$ ya que este es el único elemento de $g$ que no está en $g’$. Como $\sigma(k)=n=\sigma(m)$, concluimos, por la inyectividad de $\sigma$, que $k=m$. Esto quiere decir que $(k,a)=(m,a)\in g$, pero recordando que $x$ es el único elemento relacionado con $m$, concluimos que $x=a$, en síntesis, $(k,a)=(m,x)$, por lo que $(\sigma(k),f(a))=(\sigma(m),f(x))=(n,f(x))\neq(n,y)$. Esto implica que $(\sigma(k), f(a))\in g’$, contradiciendo nuestra suposición de que no lo estaba.

Entonces hemos probado que $(0,x_{0})\in g’$ y que cada vez que $(k,a)\in g’$, también lo está $(\sigma(k), f(a))$. Esto quiere decir que $g’\in\Re$, y como lo hicimos anteriormente, tendremos que $g=\bigcap \Re\subset g’=g\setminus\{(n,y)\}$, lo cual es una contradicción. Esto quiere decir, que suponer que $S$ tiene un elemento mínimo, es absurdo, por lo que $S=\emptyset$. Lo que traducido quiere decir que para todo $n\in\mathbb{N}$, existe un único $x\in X$ tal que $(n,x)\in g$. Es decir, que $g$ sí es una función.

  • Demostremos que $g$ satisface las dos propiedades del Teorema.

Ya vimos que $g\in \Re$, por lo que $g(0)=x_{0}$. Sea ahora $n\in \mathbb{N}$ y $x=g(n)$, de nuevo, como $g\in\Re$, tenemos que $g(\sigma(n))=f(x)=f(g(n))$.

  • Por último, demostremos la unicidad de $g$.

Si $h:\mathbb{N}\longrightarrow X$ es otra función que satisface las características del Teorema, consideremos $A=\{n\in\mathbb{N}\mid h(n)=g(n)\}$, como $h(0)=x_{0}=g(0)$. Tenemos que $0\in A$. Supongamos que $n\in A$. Tendríamos entonces que $h(\sigma(n))=f(h(n))=f(g(n))=g(\sigma(n))$, es decir que $\sigma(n)\in A$, por lo que $A$ es inductivo, y por consiguiente, $A=\mathbb{N}$. En resumen, $h$ y $g$, coinciden en dominio, codominio y regla de correspondencia, entonces $h=g$, como debíamos probar.

$\square$

La demostración del teorema de Recursión Fuerte requiere de algunos detalles adicionales, pero puede deducirse del teorema de Recursión Débil. Dejamos esto como uno de los problemas de la tarea moral.

Más adelante…

El teorema de Recursión será la mayor herramienta que tendremos para poder darle una forma más familiar a los números naturales, ya que las operaciones de suma y multiplicación, que veremos en la siguiente entrada, tendrán una definición recursiva.

Y así como el teorema de la Recursión nos permitirá definir, usaremos continuamente el principio de Inducción para poder demostrar las numerosas propiedades que estas operaciones tienen.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Demuestra el 5° Axioma de Peano a partir del Principio de Inducción.
  2. Demuestra que si $n\neq 0$ entonces existe $m$ tal que $\sigma(m)=n$.
  3. ¿Qué función $g$, satisface que $g(0)=1$ y $g(\sigma(n))=2\cdot g(n)$? ¿Qué función $f$ estamos ocupando?
  4. ¿Qué conjunto y que función nos permitiría definir la sucesión de Fibonacci $a_{n+2}=a_{n+1}+a_{n}$ usando el Teorema de Recursión?
  5. Demuestra el Teorema de Recursión Fuerte, usando el Débil. Sugerencia: Considera, $F(n,x):\mathbb{N}\times X\longrightarrow \mathbb{N}\times X$, como $F(n,x)=(\sigma(n),f_{\sigma(n)}(x))$.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»