Introducción

Dos de las nociones básicas de la topología son la de homotopía y homología. La relación de homotopía describe las características topológicas de dos espacios topológicos en términos de familias de contornos que varían continuamente. Mientras que la homología es una propiedad topológica de un dominio $D\subset \mathbb{C}$, la cual se puede definir en términos de propiedades de contornos en $D$. Los dos conceptos están relacionados, pero son diferentes.

La versión local del teorema integral de Cauchy, dada en el Teorema 36.3, enfatiza la topología del dominio y cómo el camino se encuentra dentro de él. Para mejorar nuestra comprensión de este hecho, examinamos estas cuestiones topológicas con más detalle. En esta entrada lo haremos de dos maneras: mediante el concepto de homotopía y de homología, para ello consideramos deformaciones continuas de un contorno $\gamma$, dada por la noción topológica de homotopía.

Como veremos, tanto el concepto de homotopía como el de homología formalizan la idea de que un dominio $D\subset \mathbb{C}$ tiene «agujeros», y el hecho de que la integral a lo largo de un contorno $\gamma$ depende de cómo se recorre dicho contorno en el dominio $D$, en relación con estos agujeros. Sin embargo, ambos conceptos lo hacen de forma diferente, aunque relacionada. La homotopía es más fácil para visualizar y geométricamente bastante natural, mientras que la homología es algebraicamente más simple. En esta entrada reformularemos el teorema integral de Cauchy desde estos dos conceptos y extenderemos la versión local del teorema de Cauchy a dominios en el plano complejo $\mathbb{C}$ más generales.

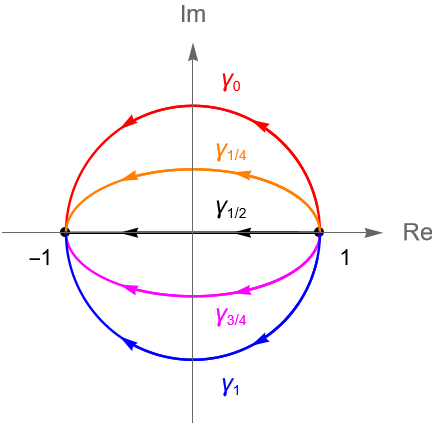
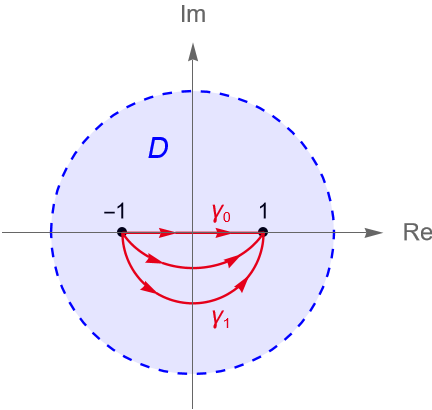
El enfoque que tomamos en esta entrada se basa en el concepto geométrico de deformación de contornos. Por ejemplo, si ${\gamma }_0$ describe a la semicircunferencia en el semiplano superior de $\mathbb{C}$ que va de $1$ a $-1$, es decir, orientada positivamente, entonces:
$${\gamma }_0(t)=e^{it},\mathrm{\forall }t\in [0,\pi ].$$

Por otra parte, si ${\gamma }_1$ describe a la semicircunferencia en el semiplano inferior de $\mathbb{C}$ que va de $1$ a $-1$, es decir, orientada negativamente, entonces:
$${\gamma }_1(t)=e^{-it},\mathrm{\forall }t\in [0,\pi ].$$

Geométricamente es fácil visualizar que podemos deformar a ${\gamma }_0$ en ${\gamma }_1$ por un desplazamiento vertical, figura 138.

Podemos formalizar lo anterior de forma analítica considerando a la función:
$${\gamma }_s(t)=(1-s)e^{it}+s{e}^{-it},$$donde $t\in [0,\pi ]$ y $s\in [0,1]$.

Entonces, ${\gamma }_0$ y ${\gamma }_1$ son dos contornos semicirculares y el contorno ${\gamma }_s$ varía continuamente conforme $s$ varía continuamente de $0$ a $1$.

Sin embargo, si los contornos no deben pasar por el origen, por ejemplo al considerar a la función $f(z)=z^{-1}$, tenemos que $f$ es continua en $D=\mathbb{C}\setminus \{0\}$, pero para ${\gamma }_{1/2}$, si $t=\pi /2$, entonces dicho contorno pasa por el origen, es decir, puede haber contornos en $D$ cuya deformación pase por el origen, como es el caso de la deformación ${\gamma }_s$. De hecho, se puede verificar que no existe ninguna deformación continua de ${\gamma }_0$ en ${\gamma }_1$ sin que algún contorno intermedio pase por el origen.

Entonces, el origen se vuelve un obstáculo para deformar el contorno, y cualquier intento de hacerlo hace que el camino ${\gamma }_s$ pase por el origen. Es decir, el origen crea un agujero y el contorno no puede cruzar el agujero.

Primeramente formalizamos lo que es una homotopía en el plano complejo $\mathbb{C}$.

Definición 38.1.(Homotopía.)
Sean $[a,b]\subset \mathbb{R}$, con $a<b$, un intervalo cerrado, $D\subset \mathbb{C}$ un dominio y ${\gamma }_0,{\gamma }_1:[a,b]\to D$ dos contornos. Una homotopía entre ${\gamma }_0$ y ${\gamma }_1$ es una función continua:
$$H:[a,b]\times [0,1]\to D,$$tal que:
$$\begin{array}{rl}H(t,0)& ={\gamma }_0(t),\mathrm{\forall }t\in [a,b],\\ H(t,1)& ={\gamma }_1(t),\mathrm{\forall }t\in [a,b].\end{array}$$

Cuando existe tal homotopía, se dice que ${\gamma }_0$ y ${\gamma }_1$ son homotópicas en $D$, lo cual se denota como ${\gamma }_0{\sim }_D{\gamma }_1$.

Observación 38.1.
Si ${\gamma }_s(t):=H(t,s)$, entonces, para cada $s\in [0,1]$ fijo, ${\gamma }_s$ es un contorno en $D$, el cual deforma continuamente a ${\gamma }_0$ en ${\gamma }_1$, conforme $s$ varía continuamente de $0$ a $1$.

Nuestro objetivo es aplicar esta definición de homotopía a la integración compleja al considerar qué sucede con ${\int }_{\gamma }f(z)dz$ cuando permitimos que el contorno $\gamma$ varíe continuamente, por lo que resulta preciso establecer condiciones bajo las cuales $\gamma$ puede deformarse continuamente sin cambiar la integral.

Una definición precisa de estas homotopías es motivado por los siguientes tres supuestos:

• Si $z_0$ y $z_1$ son puntos en un dominio $D\subset \mathbb{C}$, ${\gamma }_0$ y ${\gamma }_1$ son dos contornos en $D$ que unen a $z_0$ con $z_1$. Es, decir, ${\gamma }_0$ y ${\gamma }_1$ tienen como punto inicial a $z_0$ y como punto final a $z_1$. Entonces, es posible deformar continuamente a ${\gamma }_0$ para que coincida con ${\gamma }_1$, manteniendo los extremos fijos en $z_0$ y $z_1$, sin salir de $D$.
• Si ${\gamma }_0$ y ${\gamma }_1$ son dos contornos cerrados en un dominio $D\subset \mathbb{C}$, es posible deformar continuamente a ${\gamma }_0$ para que coincida con ${\gamma }_1$, en posición y orientación, sin salir de $D$.
• Si ${\gamma }_0$ es un contorno cerrado en un dominio $D\subset \mathbb{C}$, es posible deformar continuamente a ${\gamma }_0$ a un punto $z_0\in D$, sin salir de $D$. Esta situación es un caso particular del anterior, cuando el ${\gamma }_1(t)=z_0$ para todo $t$, es decir, se degenera en un punto.

En cualquier caso las deformaciones deben mantener al contorno dentro del dominio $D\subset \mathbb{C}$ donde la función $f$ es analítica.

Motivados en lo anterior, planteamos las siguientes definiciones.

Definición 38.2. (Homotopía con extremos fijos.)
Sean $[a,b]\subset \mathbb{R}$, con $a<b$, un intervalo cerrado, $D\subset \mathbb{C}$ un dominio, ${\gamma }_0,{\gamma }_1:[a,b]\to D$ dos contornos tales que ${\gamma }_0(0)={\gamma }_1(0)=z_0\in D$ y ${\gamma }_0(1)={\gamma }_1(1)=z_1\in D$. Se dice que ${\gamma }_0$ es {\bf homótopica con extremos fijos} a ${\gamma }_1$ si existe una función continua:
$$H:[a,b]\times [0,1]\to D,$$tal que:

1. $H(t,0)={\gamma }_0(t),\mathrm{\forall }t\in [a,b]$,
2. $H(t,1)={\gamma }_1(t),\mathrm{\forall }t\in [a,b]$,
3. $H(a,s)=z_0,\mathrm{\forall }s\in [0,1]$,
4. $H(b,s)=z_1,\mathrm{\forall }s\in [0,1]$.

La función continua $H$ se llama una homotopía con extremos fijos o una deformación continua con extremos fijos.

Observación 38.2.
Si ${\gamma }_s(t):=H(t,s)$, entonces, para cada $s\in [0,1]$ fijo, ${\gamma }_s$ es un contorno en $D$ que une a $z_0$ con $z_1$. Conforme $s$ varía continuamente de $0$ a $1$, el contorno ${\gamma }_s$ deforma continuamente a ${\gamma }_0$ en ${\gamma }_1$.

Ejemplo 38.1.
Sean $D=\{z\in \mathbb{C}:|z|<2\}=B(0,2)$, ${\gamma }_0(t)=t$ y ${\gamma }_1(t)=e^{i\pi /2(t-1)}$, ambas con $t\in [-1,1]$. Veamos que ${\gamma }_0$ es homotópica con extremos fijos a ${\gamma }_1$.

Solución. Sea $z_0=-1$ y $z_1=1$. De acuerdo con la definición 38.2 solo basta con exhibir una función continua $H:[-1,1]\times [0,1]\to D$ que satisfaga las cuatro propiedades.

Sea $H:[-1,1]\times [0,1]\to D$ dada por:
$$H(t,s)=(1-s){\gamma }_0(t)+s{\gamma }_1(t),(t,s)\in [-1,1]\times [0,1].$$

Separando a $H$ en su parte real e imaginaria, por la proposición 15.1, es claro que $H$ es continua ya que ${\gamma }_0$ y ${\gamma }_1$ son continuas. Más aún, para todo $t\in [-1,1]$ se cumple que $H(t,0)={\gamma }_0(t)$ y $H(t,1)={\gamma }_1(t)$. Mientras que para todo $s\in [0,1]$ se cumple que:
$$H(-1,s)=(1-s)(-1)+s(e^{-i\pi })=-1+s+s(-1)=-1=z_0.$$
$$H(1,s)=(1-s)(1)+s(e^0)=1-s+s(1)=1=z_1.$$

Por lo tanto ${\gamma }_0$ es homotópica con extremos fijos a ${\gamma }_1$, figura 139.

Definición 38.3. (Homotopía de contornos cerrados y homotopía a un punto.)
Sean $[a,b]\subset \mathbb{R}$, con $a<b$, un intervalo cerrado, $D\subset \mathbb{C}$ un dominio, ${\gamma }_0,{\gamma }_1:[a,b]\to D$ dos contornos cerrados en $D$. Se dice que ${\gamma }_0$ y ${\gamma }_1$ son {\bf homótopicas como contornos cerrados}, si existe una función continua:
$$H:[a,b]\times [0,1]\to D,$$tal que:

1. $H(t,0)={\gamma }_0(t),\mathrm{\forall }t\in [a,b]$,
2. $H(t,1)={\gamma }_1(t),\mathrm{\forall }t\in [a,b]$,
3. $H(a,s)=H(b,s),\mathrm{\forall }s\in [0,1]$.

La función continua $H$ se llama una homotopía de contornos cerrados o una deformación continua de contornos cerrados.

Si ${\gamma }_1$ es un contorno constante, es decir, ${\gamma }_1(t)=z_0$ para todo $t\in [a,b]$ y $z_0\in D$, entonces se dice que ${\gamma }_0$ es homotópica a un punto $z_0$ en el dominio $D$.

Observación 38.3.
Si ${\gamma }_s(t):=H(t,s)$, entonces, para cada $s\in [0,1]$ fijo, ${\gamma }_s$ es un contorno cerrado en $D$, para todo $s\in [0,1]$. Conforme $s$ varía continuamente de $0$ a $1$, el contorno ${\gamma }_s$ deforma continuamente a ${\gamma }_0$ en ${\gamma }_1$.

Más aún, si ${\gamma }_0$ es homotópica a un punto $z_0\in D$, la tercera condición de la definición 38.3 establece que el punto inicial de $H(0,s)$ y el punto final de $H(1,s)$ son el mismo.

Ejemplo 38.2.
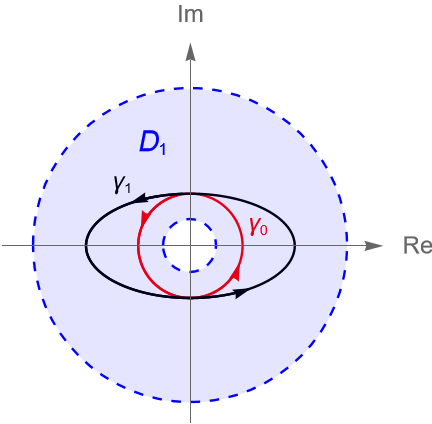
Veamos que la circunferencia unitaria y la elipse ${\displaystyle \frac{x^2}{4}}+y^2=1$, ambas orientadas positivamente, son homotópicas como curvas cerradas en la región anular:
$$D_1=\{z\in \mathbb{C}:\frac{1}{2}<|z|<3\}.$$

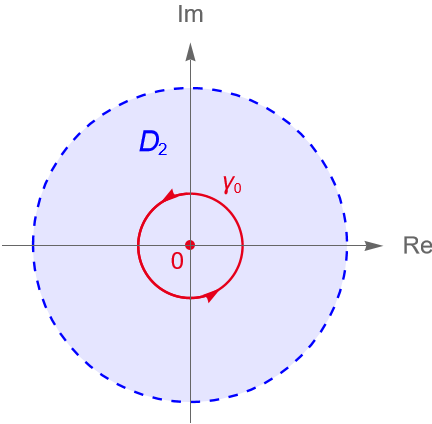
Mientras que la circunferencia unitaria es homotópica a $0$ en el dominio $D_2=B(0,3)$.

Solución. Podemos parametrizar a la circunferencia y a la elipse, respectivamente, como:
$${\gamma }_0(t)=e^{it}\text{y}{\gamma }_1(t)=2\cos (t)+i\mathrm{sen}(t),\mathrm{\forall }t\in [0,2\pi ].$$

Para la primera parte del ejercicio proponemos a la función $H_1:[0,2\pi ]\times [0,1]\to D_1$ dada por:
$$H_1(t,s)=(1+s)\cos (t)+i\mathrm{sen}(t).$$

Dado que ${\gamma }_0$ y ${\gamma }_1$ son funciones continuas, entonces $H_1$ es continua.

Por otra parte, es claro que para todo $t\in [0,2\pi ]$ se cumple que $H_1(t,0)={\gamma }_0(t)$ y $H_1(t,1)={\gamma }_1(t)$. Mientras que para todo $s\in [0,1]$ tenemos que:
$$H_1(0,s)=1+s=H_1(2\pi ,s),$$por lo que ${\gamma }_0$ y ${\gamma }_1$ son homotópicas como curvas cerradas en $D_1$, figura 140.

Para la segunda parte del ejercicio, consideramos a ${\gamma }_1(t)=0$, para todo $t\in [0,2\pi ]$. Proponemos a la función $H_2:[0,2\pi ]\times [0,1]\to D_1$ dada por:
$$H_2(t,s)=(1-s){\gamma }_0(t).$$

Claramente $H_2$ es continua. Además, para todo $t\in [0,2\pi ]$ se cumple que $H_2(t,0)={\gamma }_0(t)$ y $H_2(t,1)={\gamma }_1(t)$. Mientras que para todo $s\in [0,1]$ tenemos que:
$$H_2(0,s)=(1-s)(1)=H_2(2\pi ,s),$$por lo que ${\gamma }_0$ es homotópica a $0$ en $D_2$, figura 141.

Considerando lo anterior, ahora podemos formalizar la idea de un dominio $D\subset \mathbb{C}$ sin agujeros o sin hoyos.

Definición 38.4. (Dominio simplemente conexo y múltiplemente conexo.)
Sea $D\subset \mathbb{C}$ un dominio, es decir, un conjunto abierto y conexo. Se dice que $D$ es simplemente conexo si toda curva cerrada en $D$ es homotópica (como una curva cerrada) a un punto en $D$, es decir, a alguna curva constante en $D$.

Si $D$ no es simplemente conexo, entonces se llama múltiplemente conexo. Un dominio múltiplemente conexo con $n$ agujeros u hoyos, se llama $(n+1)$-conexo.

Ejemplo 38.3.
a) $\mathbb{C}$ es un dominio simplemente conexo.
b) Sea $r>0$ y $z_0\in \mathbb{C}$ fijo. Todo disco abierto $B(z_0,r)$ es un dominio simplemente conexo. Mientras que todo disco perforado $B^{\ast }(z_0,r)=\{z\in \mathbb{C}:0<|z-z_0|<r\}$ es un dominio doblemente conexo.
c) La región anular $\{z\in \mathbb{C}:1<|z|<2\}$ es un dominio doblemente conexo.

En este punto es importante considerar los siguientes resultados de nuestros cursos de Cálculo.

Teorema 38.1. (Igualdad de las derivadas parciales cruzadas.)
Si $U\subset {\mathbb{R}}^2$ es un conjunto abierto y $u:U\to \mathbb{R}$ es una función real de clase $C^2(U)$, entonces las derivadas parciales cruzadas son iguales, es decir:
$$\frac{{\partial }^{2}u}{\partial y\partial x}=\frac{{\partial }^{2}u}{\partial x\partial y}.$$

Teorema 38.2. (Regla de Leibniz o de diferenciación bajo el signo de integral.)
Sean $[a,b],[c,d]\subset {\mathbb{R}}^2$, con $a<b$ y $c<d$, dos intervalos cerrados y $f:[a,b]\times [c,d]\to \mathbb{R}$ una función continua en $[a,b]\times [c,d]$. Entonces la función real $g:[a,b]\to \mathbb{R}$ dada por:
$$g(x)={\int }_c^{d}f(x,y)dy,$$es continua en $[a,b]$. Más aún, si la derivada parcial ${\displaystyle \frac{\partial f}{\partial x}}$ existe y es continua en $[a,b]\times [c,d]$, entonces $g$ es diferencibale en $[a,b]$, con $g^{\prime }$ continua y dada por:
$$g^{\prime }(x)=\frac{d}{dx}{\int }_c^{d}f(x,y)dy={\int }_c^d{\displaystyle \frac{\partial f}{\partial x}}(x,y)dy.$$

• Observación 38.4.
• A lo largo de esta cuarta unidad hemos trabajado con contornos para garantizar que las curvas a lo largo de las cuales integramos sean funciones continuas de clase $C^1$ o de clase $C^1$ a trozos. Sin embargo, notemos que en las definiciones 38.1, 38.2 y 38.3 solo se pidió que la función $H$, que determina a la homotopía, sea una función continua, pero no se estableció nada sobre su diferenciabilidad, por lo que las curvas ${\gamma }_s(t)=H(t,s)$, con $s\in [0,1]$, sobre las que se integra a una función compleja, no necesariamente tienen que ser de clase $C^1$ o de clase $C^1$ a trozos, sino que simplemente son funciones continuas, por lo que es importante considerar esta pequeña sutileza, ya que la prueba que daremos del siguiente resultado considerará este supuesto adicional sobre la diferenciabilidad de las curvas ${\gamma }_s$. Una prueba completa, sin este supuesto adicional, se escapa de los objetivos de estas notas, pero puede consultarse en los siguientes textos:
• Complex Analysis de Ian Stewart, David Tall.
• Functions of One Complex Variable I de John B. Conway.
• Complex Analysis with Applications de Nakhlé H. Asmar, Loukas Grafakos.

Teorema 38.3. (Teorema integral de Cauchy, versión homotópica.)
Sean $[a,b]\subset \mathbb{R}$, con $a<b$, un intervalo cerrado, $D\subset \mathbb{C}$ un dominio, $f:D\to \mathbb{C}$ una función analítica en $D$ y ${\gamma }_0,{\gamma }_1:[a,b]\to D$ son dos contornos en $D$.

1. Si ${\gamma }_0$ y ${\gamma }_1$ son dos contornos que unen a $z_0,z_1\in D$ y son homotópicas (con extremos fijos) en $D$, entonces:
   $${\int }_{{\gamma }_0}f(z)dz={\int }_{{\gamma }_1}f(z)dz.$$
2. Si ${\gamma }_0$ y ${\gamma }_1$ son dos contornos cerrados y son homotópicas (como contornos cerrados) en $D$, entonces:
   $${\int }_{{\gamma }_0}f(z)dz={\int }_{{\gamma }_1}f(z)dz.$$

Demostración. Dadas las hipótesis, sea $H:[a,b]\times [0,1]\to D$ una homotopía entre ${\gamma }_0$ y ${\gamma }_1$. Como se mencionó en la observación 38.4, adicionalmente suponemos que $H(t,s)$ es una función de clase $C^2([a,b]\times [0,1])$.

Para cada $s\in [0,1]$ fijo, definimos al contorno ${\gamma }_s(t):=H(t,s)$, para $t\in [a,b]$. Sea $I(s)$ la integral de $f$ a lo largo del contorno ${\gamma }_s$, es decir:
$$\begin{array}{rl}I(s):& ={\int }_{{\gamma }_s}f(z)dz\\ & ={\int }_a^{b}f({\gamma }_s(t)){\gamma }_s^{\prime }(t)dt\\ & ={\int }_a^{b}f(H(t,s))\frac{\partial H(t,s)}{\partial t}dt.\end{array}$$

Veamos que $I(s)$ es una función constante, para ello determinamos su derivada. Por hipótesis sabemos que $f$ es una función analítica en $D$, en particular es continua en $D$ y como $H(t,s)$ es una función de clase $C^2$, en particular para cada $s\in [0,1]$, ${\gamma }_s(t)$ es un contorno en $D$, entonces $I(s)$ es una función bien definida y en particular continua en $[0,1]$, teorema 38.2.

Por la proposición 36.4 sabemos que $f\in C^1(D)$, ya que $f$ es analítica en $D$, por lo que $f^{\prime }$ es una función continua en $D$ y para cada $s\in [0,1]$ fijo, el contorno ${\gamma }_s$ está completamente contenido en $D$, entonces, de la regla de la cadena y la regla de Leibniz, tenemos que:
$$\begin{array}{rl}{I}^{\prime }(s)& =\frac{d}{ds}{\int }_a^{b}f(H(t,s))\frac{\partial H(t,s)}{\partial t}dt\\ & ={\int }_a^b\frac{\partial }{\partial s}[f(H(t,s))\frac{\partial H(t,s)}{\partial t}]dt\\ \text{(38.1)}& & ={\int }_a^b[f^{\prime }(H(t,s))\frac{\partial H(t,s)}{\partial s}\frac{\partial H(t,s)}{\partial t}+f(H(t,s))\frac{{\partial }^{2}H(t,s)}{\partial s\partial t}]dt.\end{array}$$

Notemos que:
$$\frac{\partial }{\partial t}[f(H(t,s))\frac{\partial H(t,s)}{\partial s}]=f^{\prime }(H(t,s))\frac{\partial H(t,s)}{\partial s}\frac{\partial H(t,s)}{\partial t}+f(H(t,s))\frac{{\partial }^{2}H(t,s)}{\partial s\partial t},$$y como $H$ es de clase $C^2$, entonces por el teorema 38.1 se cumple que:
$$\frac{{\partial }^{2}H(t,s)}{\partial t\partial s}=\frac{{\partial }^{2}H(t,s)}{\partial s\partial t},$$es decir:
$$\begin{array}{}\text{(38.2)}& \frac{\partial }{\partial t}[f(H(t,s))\frac{\partial H(t,s)}{\partial s}]=f^{\prime }(H(t,s))\frac{\partial H(t,s)}{\partial s}\frac{\partial H(t,s)}{\partial t}+f(H(t,s))\frac{{\partial }^{2}H(t,s)}{\partial t\partial s}.\end{array}$$

Entonces, de (38.1), (38.2) y la proposición 33.2, se sigue que:
$$\begin{array}{rl}{I}^{\prime }(s)& ={\int }_a^b[f^{\prime }(H(t,s))\frac{\partial H(t,s)}{\partial s}\frac{\partial H(t,s)}{\partial t}+f(H(t,s))\frac{{\partial }^{2}H(t,s)}{\partial s\partial t}]dt\\ & ={\int }_a^b\frac{\partial }{\partial t}[f(H(t,s))\frac{\partial H(t,s)}{\partial s}]dt\\ \text{(38.3)}& & =f(H(b,s))\frac{\partial H(b,s)}{\partial s}–f(H(a,s))\frac{\partial H(a,s)}{\partial s}.\end{array}$$

De acuerdo con (38.3), tenemos lo siguiente.

1. Si ${\gamma }_0$ y ${\gamma }_1$ son dos contornos que unen a $z_0,z_1\in D$ y $H$ es una homotopía (con extremos fijos) entre en ${\gamma }_0$ y ${\gamma }_1$, entonces:
   $$\begin{array}{rl}{I}^{\prime }(s)& =f(H(b,s))\frac{\partial H(b,s)}{\partial s}–f(H(a,s))\frac{\partial H(a,s)}{\partial s}\\ & =f(z_1)\frac{\partial z_1}{\partial s}–f(z_0)\frac{\partial z_0}{\partial s}\\ & =0,\end{array}$$para todo $s\in [0,1]$.
   
   Por lo que, para todo $s\in [0,1]$ tenemos que $I(s)$ es una función constante, en particular tenemos que $I(0)=I(1)$, es decir:
   $${\int }_{{\gamma }_0}f(z)dz={\int }_{{\gamma }_1}f(z)dz.$$
2. Si ${\gamma }_0$ y ${\gamma }_1$ son dos contornos cerrados y $H$ es una homotopía (como contornos cerrados) entre ${\gamma }_0$ y ${\gamma }_1$, entonces:
   $$\begin{array}{rl}{I}^{\prime }(s)& =f(H(b,s))\frac{\partial H(b,s)}{\partial s}–f(H(a,s))\frac{\partial H(a,s)}{\partial s}\\ & =f(H(b,s))\frac{\partial H(b,s)}{\partial s}–f(H(b,s))\frac{\partial H(b,s)}{\partial s}\\ & =0,\end{array}$$para todo $s\in [0,1]$.
   
   Por lo que, para todo $s\in [0,1]$ tenemos que $I(s)$ es una función constante, en particular tenemos que $I(0)=I(1)$, es decir:
   $${\int }_{{\gamma }_0}f(z)dz={\int }_{{\gamma }_1}f(z)dz.$$

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Corolario 38.1.
Sean $[a,b]\subset \mathbb{R}$, con $a<b$, un intervalo cerrado, $D\subset \mathbb{C}$ un dominio, $f:D\to \mathbb{C}$ una función analítica en $D$ y $\gamma :[a,b]\to D$ un contorno cerrado en $D$. Si $\gamma$ es homotópica a un punto en $D$, entonces:
$${\int }_{\gamma }f(z)dz=0.$$

Demostración. Dadas las hipótesis, como $\gamma$ es homotópica a un punto en $z_0\in D$, es decir, a una curva constante $\beta (t)=z_0$ para todo $t\in [a,b]$, entonces:
$${\int }_{\gamma }f(z)dz={\int }_{\beta }f(z)dz={\int }_a^{b}f(\beta (t)){\beta }^{\prime }(t)dt={\int }_a^{b}f(z_0)(0)dt=0.$$

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

El siguiente resultado generaliza el teorema integral de Cauchy para discos.

Corolario 38.2.
Sean $D\subset \mathbb{C}$ un dominio simplemente conexo y $f:D\to \mathbb{C}$ una función analítica en $D$. Entonces:
$${\int }_{\gamma }f(z)dz=0,$$ para todo contorno $\gamma$ cerrado en $D$.

Demostración. Dadas las hipótesis, consideremos al contorno cerrado $\gamma :[a,b]\subset \mathbb{R}\to D$, con $a<b$. Como el dominio $D$ es simplemente conexo, entonces al ser $\gamma$ un contorno cerrado en $D$, por definición es homotópica a un punto en $z_0\in D$, es decir, a una curva constante $\beta (t)=z_0$ para todo $t\in [a,b]$, entonces:
$${\int }_{\gamma }f(z)dz={\int }_{\beta }f(z)dz={\int }_a^{b}f(\beta (t)){\beta }^{\prime }(t)dt={\int }_a^{b}f(z_0)(0)dt=0.$$

Como $\gamma$ es arbitraria, el resultado se cumple para todo contorno cerrado en $D$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Corolario 38.3.
Sean $D\subset \mathbb{C}$ un dominio simplemente conexo y $f:D\to \mathbb{C}$ una función analítica en $D$. Las siguientes condiciones son equivalentes.

1. $f$ tiene una primitiva $F$ en $D$.
2. Si ${\gamma }_0$ y ${\gamma }_1$ son dos contornos en $D$ con los mismos puntos inicial y final, entonces:
   $${\int }_{{\gamma }_0}f(z)dz={\int }_{{\gamma }_1}f(z)dz.$$

Demostración. El resultado se sigue del corolario 38.2 y la proposición 35.2.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Observación 38.5.
Notemos que la primitiva $F$ de la función $f$, en el corolario 38.3(1) es:
$$F(z)={\int }_{{\gamma }_z}f(\zeta )d\zeta ,$$donde ${\gamma }_z$ es el contorno en $D$ que une a un punto fijo $z_0\in D$ con $z\in D$.

Ejemplo 38.4.
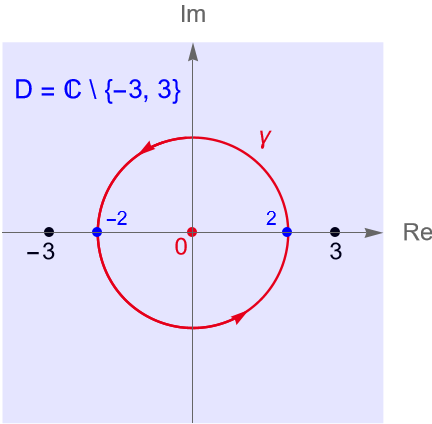
Evaluemos la integral:
$${\int }_{C(0,2)}\frac{e^z}{z^2-9}dz,$$donde la circunferencia $C(0,2)$ está orientada positivamente.

Solución. Parametrizamos a la circunferencia $C(0,2)$ como $\gamma (t)=2e^{it}$, para $t\in [0,2\pi ]$.

Sea $f(z)={\displaystyle \frac{e^z}{z^2-9}}$. Es claro que $f$ es analítica en $D=\mathbb{C}\setminus \{-3,3\}$. Dado que $C(0,2)\subset D$, entonces no pasa por los puntos donde $f$ no es analítica, por lo que, del ejemplo 38.2 concluimos que $\gamma$ es homotópica a $0\in D$, figura 142, entonces:
$${\int }_{\gamma }\frac{e^z}{z^2-9}dz=0.$$

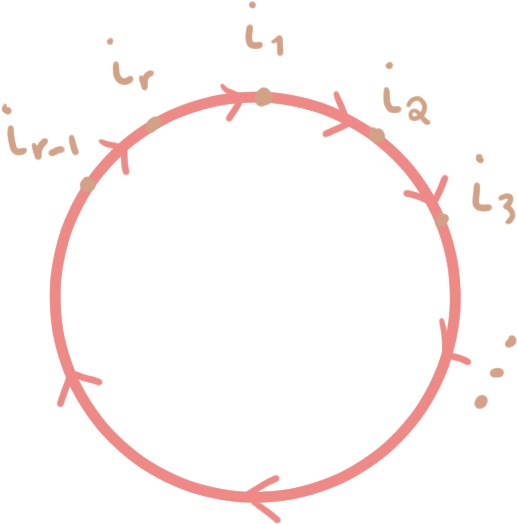
Proposición 38.1. (Extensión del teorema de Cauchy para dominios múltiplemente conexos.)
Sean $C,C_1,C_2,\dots ,C_n$ contornos cerrados simples, orientados positivamente, tales que cada contorno $C_k$ está en el interior de $C$, para $k=1,\dots ,n$ y el interior de $C_k$ no tiene puntos en común con el interior de $C_j$, si $k\ne j$, es decir, $I(C_k)\cap I(C_j)=\mathrm{\varnothing }$ para todo $k\ne j$. Sea $D\subset \mathbb{C}$ un dominio tal que $D$ contiene a todos los contornos y la región entre $C$ y $C_1+C_2+\dots +C_n$. Si $f:D\to \mathbb{C}$ es una función analítica en $D$, entonces:
$${\int }_{C}f(z)dz=\sum _{k=1}^n{\int }_{C_k}f(z)dz.$$

Demostración. Dadas las hipótesis, por simplicidad solo probaremos el caso para dos contornos cerrados simples, orientados positivamente. La prueba del caso general es completamente análoga y se deja como ejercicio al lector.

Nos apoyaremos en la figura 143 para la prueba. Debe ser claro que los contornos utilizados han sido elegidos para simplificar la gráfica, aunque el resultado sigue siendo válido para cualesquiera contornos que satisfagan las condiciones del resultado.

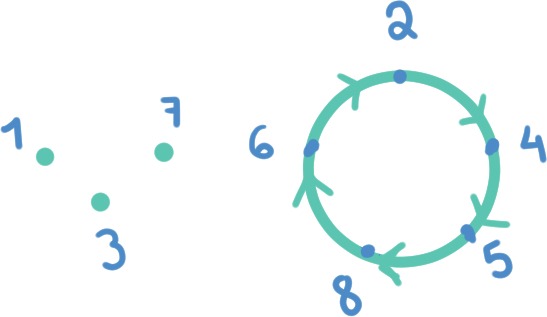
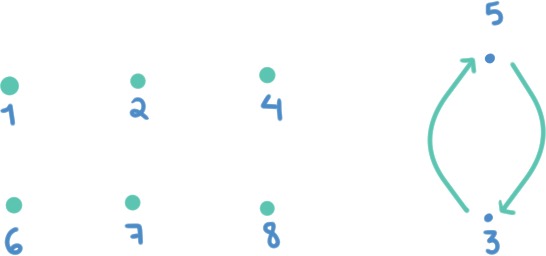
La prueba consiste en construir dos contornos disjuntos o cortes, digamos $L_1$ y $L_2$, que unen a $C_1$ con $C$. Así, el contorno $C_1$ será dividido en dos contornos $C_1^{\ast }$ y $C_1^{\ast \ast }$, mientras que el contorno $C$ será dividido en dos contornos $C^{\ast }$ y $C^{\ast \ast }$, como se muestra en la figura 144. Entonces tenemos dos nuevos contornos:
$$K_1=-C_1^{\ast }+L_1+C^{\ast }-L_2\text{y}{K}_2=-C_1^{\ast \ast }+L_2+C^{\ast \ast }-L_1.$$

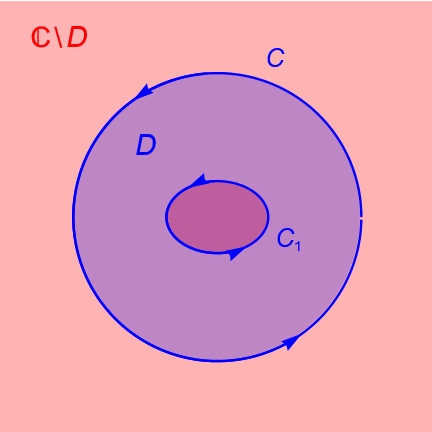
Figura 144: Los cortes $L_1$ y $L_2$ y los contornos cerrados simples $K_1$ y $K_2$.

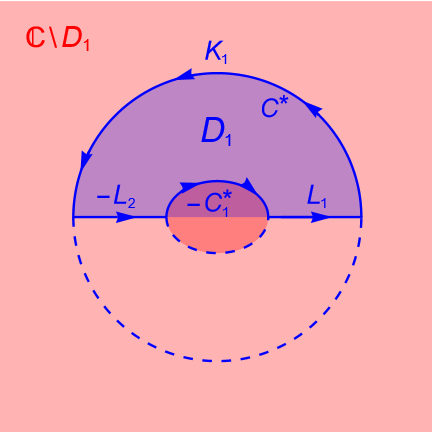
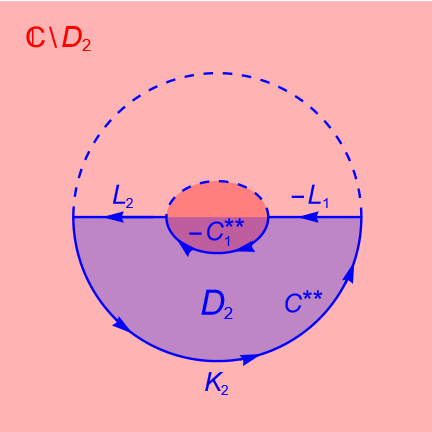
Es claro que el dominio $D$ es doblemente conexo, mientras que los nuevos dominios $D_1$ y $D_2$ son simplemente conexos y los contornos $K_1$ y $K_2$ son cerrados simples, orientados positivamente y cada uno está contenido en los dominios $D_1$ y $D_2$. respectivamente. Por hipótesis la función $f$ es analítica en el dominio $D=D_1\cup D_2$, por lo que $f{|}_{D_1}$ y $f{|}_{D_2}$ también son analíticas.

Aplicando el corolario 38.2, tenemos que:
$${\int }_{K_1}f(z)dz=0\text{y}{\int }_{K_2}f(z)dz=0.$$

Por la proposición 34.2 tenemos que:
$$\begin{array}{rl}{\int }_{K_1}f(z)dz& ={\int }_{-C_1^{\ast }+L_1+C^{\ast }-L_2}f(z)dz\\ & ={\int }_{-C_1^{\ast }}f(z)dz+{\int }_{L_1}f(z)dz+{\int }_{C^{\ast }}f(z)dz+{\int }_{-L_2}f(z)dz\\ & =-{\int }_{C_1^{\ast }}f(z)dz+{\int }_{L_1}f(z)dz+{\int }_{C^{\ast }}f(z)dz–{\int }_{L_2}f(z)dz.\end{array}$$
$$\begin{array}{rl}{\int }_{K_2}f(z)dz& ={\int }_{-C_1^{\ast \ast }+L_2+C^{\ast \ast }-L_1}f(z)dz\\ & ={\int }_{-C_1^{\ast \ast }}f(z)dz+{\int }_{L_2}f(z)dz+{\int }_{C^{\ast \ast }}f(z)dz+{\int }_{-L_1}f(z)dz\\ & =-{\int }_{C_1^{\ast \ast }}f(z)dz+{\int }_{L_2}f(z)dz+{\int }_{C^{\ast \ast }}f(z)dz–{\int }_{L_1}f(z)dz.\end{array}$$

Por lo que:
$$\begin{array}{rl}0& ={\int }_{K_1}f(z)dz+{\int }_{K_2}f(z)dz\\ & =-{\int }_{C_1^{\ast }}f(z)dz+{\int }_{C^{\ast }}f(z)dz-{\int }_{C_1^{\ast \ast }}f(z)dz+{\int }_{C^{\ast \ast }}f(z)dz\\ & ={\int }_{C^{\ast }+C^{\ast \ast }}f(z)dz-{\int }_{C_1^{\ast }+C_1^{\ast \ast }}f(z)dz\\ & ={\int }_{C}f(z)dz-{\int }_{C_1}f(z)dz.\end{array}$$

Entonces:
$${\int }_{C}f(z)dz={\int }_{C_1}f(z)dz.$$

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Proposición 38.2. (Extensión de la fórmula integral de Cauchy para dominios simplemente conexos.)
Sean $D\subset \mathbb{C}$ un dominio simplemente conexo, $f:D\to \mathbb{C}$ una función analítica en $D$ y $C$ un contorno cerrado simple, orientado positivamente, tal que está completamente contenido en $D$. Si $z_0$ es un punto en el interior de $C$, entonces:
$$f(z_0)=\frac{1}{2\pi i}{\int }_C\frac{f(z)}{z-z_0}dz.$$

Demostración. Dadas las hipótesis, como $f$ es analítica en $D$, en particular es continua en $z_0\in D$ que está en el interior de $C$, por lo que dado $\epsilon >0$ existe $\delta >0$ tal que si $|z-z_0|<\delta$, entonces $|f(z)-f(z_0)|<\epsilon$.

Notemos que la circunferencia $\gamma$ dada por $C(z_0,\delta /2)$, orientada positivamente, también está en el interior de $C$.

Dado que $f(z_0)$ es un valor fijo, entonces por el ejemplo 34.1(a) tenemos que:
$$f(z_0)=\frac{f(z_0)}{2\pi i}{\int }_{\gamma }\frac{1}{z-z_0}dz=\frac{1}{2\pi i}{\int }_{\gamma }\frac{f(z_0)}{z-z_0}dz.$$

Por el corolario 38.3(2) tenemos que:
$$\frac{1}{2\pi i}{\int }_{\gamma }\frac{f(z)}{z-z_0}dz=\frac{1}{2\pi i}{\int }_C\frac{f(z)}{z-z_0}dz.$$

Entonces, de la proposición 34.2(1) y la proposición 34.3(5), tenemos que:
$$\begin{array}{rl}|\frac{1}{2\pi i}{\int }_C\frac{f(z)}{z-z_0}dz–f(z_0)|& =\left|\frac{1}{2\pi i}{\int }_{\gamma }\frac{f(z)}{z-z_0}dz–\frac{1}{2\pi i}{\int }_{\gamma }\frac{f(z_0)}{z-z_0}dz\right|\\ & =\left|\frac{1}{2\pi i}{\int }_{\gamma }\frac{f(z)–f(z_0)}{z-z_0}dz\right|\\ & \le \frac{1}{2\pi }{\int }_{\gamma }\frac{|f(z)–f(z_0)|}{|z-z_0|}|dz|\\ & <\frac{1}{2\pi }{\displaystyle \frac{\epsilon }{\delta /2}}{\int }_{\gamma }|dz|\\ & =\frac{1}{2\pi }{\displaystyle \frac{\epsilon }{\delta /2}}\delta \pi \\ & =\epsilon .\end{array}$$

Dado que $\epsilon >0$ es arbitrario, entonces:
$$|\frac{1}{2\pi i}{\int }_C\frac{f(z)}{z-z_0}dz–f(z_0)|=0⟹f(z_0)=\frac{1}{2\pi i}{\int }_C\frac{f(z)}{z-z_0}dz.$$

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Ejemplo 38.5.
Evaluemos la integral:
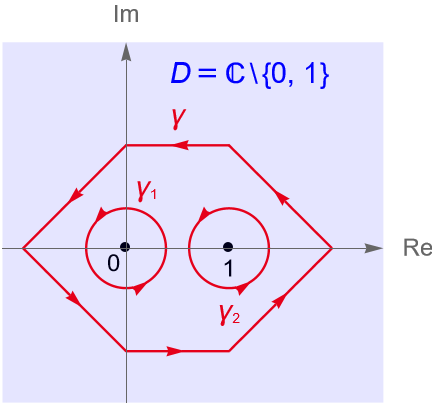
$${\int }_{\gamma }\frac{5z-2}{z^2-z}dz,$$donde $\gamma$ es el contorno cerrado dado en la figura 145.

Solución. Sea $f(z)={\displaystyle \frac{5z-2}{z^2-z}}$. Claramente $f$ es analítica en $D=\mathbb{C}\setminus \{0,1\}$, ya que en $z_1=0$ y en $z_2=-1$ el denominador de la función racional se anula. Si consideramos a dos circunferencias con centro en $z_1$ y $z_2$, de radio suficientemente pequeño para caer dentro del contorno $\gamma$ y las orientamos positivamente, entonces por la proposición 38.1 tenemos que:
$${\int }_{\gamma }f(z)dz={\int }_{{\gamma }_1}f(z)dz+{\int }_{{\gamma }_2}f(z)dz.$$

Aplicando fracciones parciales tenemos que:
$$\frac{5z-2}{z^2-z}=\frac{2}{z}+\frac{3}{z-1}.$$

Por lo que:
$$\begin{array}{rl}{\int }_{\gamma }\frac{5z-2}{z^2-z}dz& ={\int }_{{\gamma }_1}(\frac{2}{z}+\frac{3}{z-1})dz+{\int }_{{\gamma }_2}(\frac{2}{z}+\frac{3}{z-1})dz\\ & =2{\int }_{{\gamma }_1}\frac{1}{z}dz+3{\int }_{{\gamma }_1}\frac{1}{z-1}dz+2{\int }_{{\gamma }_2}\frac{1}{z}dz+3{\int }_{{\gamma }_2}\frac{1}{z-1}dz\\ & =2(2\pi i)+0+0+3(2\pi i)\\ & =10\pi i.\end{array}$$

Ejemplo 38.6.
Veamos que:
$${\int }_{\gamma }\frac{e^z}{z-1}dz=i2\pi e,$$ donde $\gamma$ es la circunferencia $C(0,2)$ orientada positivamente.

Solución. Sea $f(z)=e^z$. Claramente $f$ es una función entera, $\gamma$ está completamente contenido en $\mathbb{C}$ y $z_0=1$ es un punto en el interior de $\gamma$, entonces por la fórmula integral de Cauchy tenemos que:
$$e=f(1)=\frac{1}{2\pi i}{\int }_{\gamma }\frac{e^z}{z-1}dz,$$de donde el resultado se sigue al multiplicar por $2\pi i$ la igualdad anterior.

Cerramos esta entrada mencionando algunos resultados relacionados con la versión homológica del teorema integral de Cauchy.

Definición 38.5. (Ciclo en $\mathbb{C}$.)
A una sucesión finita de curvas cerradas suaves o suaves a trozos en $\mathbb{C}$, se le llama un ciclo y se le denota como $\sigma =({\gamma }_1,\dots ,{\gamma }_n)$. En un ciclo no importa el orden de las curvas cerradas, es decir, un ciclo es una secuencia finita, no ordenada, de contornos cerrados en $\mathbb{C}$.

Ejemplo 38.7.
Dado que $\sigma$ es una sucesión finita de contornos cerrados en $\mathbb{C}$, entonces un contorno cerrado es un ciclo.

Observación 38.6.
Denotamos a la unión de las curvas que forman a un ciclo, es decir, al conjunto compacto:
$${\gamma }_1(I_1)\cup {\gamma }_2(I_2)\cup \cdots \cup {\gamma }_n(I_n),$$como $|\sigma |$, donde $I_k$ es un intervalo real cerrado y ${\gamma }_k(I_k)$ la imagen o la curva de dicho intervalo bajo el contorno ${\gamma }_k$, para $1\le k\le n$. Entonces, diremos que un ciclo $\sigma$ está en un conjunto $S\subset \mathbb{C}$ si $|\sigma |\subset S$.

Definición 38.6.
Sean $U\subset \mathbb{C}$ un conjunto abierto, $f:U\to \mathbb{C}$ una función continua en $U$ y $\sigma$ un ciclo en $U$. Se define a la integral de $f$ a lo largo del ciclo $\sigma$ como:
$${\int }_{\sigma }f(z)dz:={\int }_{{\gamma }_1}f(z)dz+{\int }_{{\gamma }_2}f(z)dz+\cdots +{\int }_{{\gamma }_n}f(z)dz.$$

En particular, para $z\in \mathbb{C}\setminus |\sigma |$ se define el índice de $\sigma$ respecto a $z$, es decir, $n(\sigma ,z)$, como:
$$n(\sigma ,z)=\frac{1}{2\pi i}{\int }_{\sigma }\frac{d\zeta }{\zeta -z}.$$

Definición 38.7. (Ciclo homólogo a $0$.)
Sean $U\subset \mathbb{C}$ un conjunto abierto y $\sigma$ un ciclo en $U$. Se dice que $\sigma$ es como homólogo a $0$ en $U$ si $n(\sigma ,z)=0$ para todo $z\in \mathbb{C}\setminus U$.

Observación 38.7.
Dado que para $z\in \mathbb{C}\setminus |\sigma |$ se cumple que $z\in \mathbb{C}\setminus {\gamma }_k(I_k)$, para cada contorno cerrado ${\gamma }_k$ que forma a $\sigma$, entonces:
$$n(\sigma ,z)=n({\gamma }_1,z)+n({\gamma }_2,z)+\cdots +n({\gamma }_n,z).$$

Antes de continuar con el resultado esperado, podemos preguntarnos sobre ¿cuál es la relación del concepto de homología con el de homotopía? Específicamente podemos preguntarnos si ¿existe una relación entre ser un contorno homotópico a un punto y un contorno homólogo a 0? Para responder a esto tenemos la siguiente:

Proposición 38.3.
Sean $[a,b]\subset \mathbb{R}$, con $a<b$, un intervalo cerrado, $D\subset \mathbb{C}$ un dominio y $\gamma :[a,b]\to \mathbb{C}$ un contorno cerrado en $D$. Si $\gamma$ es homotópica a un punto $z_0\in D$, entonces $\gamma$ es homólogica a $0$ en $D$.

Demostración. Dadas las hipótesis, como $\gamma$ es homotópica a un punto $z_0\in D$, es decir, a una curva constante $\beta (t)=z_0$ para todo $t\in [a,b]$, entonces, del teorema 38.3 y la definición 36.1, se cumple que:
$$n(\gamma ,z)=\frac{1}{2\pi i}{\int }_{\gamma }\frac{d\zeta }{\zeta -z}=\frac{1}{2\pi i}{\int }_{\beta }\frac{d\zeta }{\zeta -z}={\int }_a^b\frac{{\beta }^{\prime }(t)}{\beta (t)-z}dt=0,$$para todo $z\in \mathbb{C}\setminus \gamma ([a,b])$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Teorema 38.4. (Teorema integral de Cauchy, versión homológica.)
Sean $U\subset \mathbb{C}$ un conjunto abierto, $f:U\to \mathbb{C}$ una función analítica en $U$ y $\sigma$ un ciclo en $U$. Entonces:
$${\int }_{\sigma }f(z)dz=0,$$si y solo si $\sigma$ es homólogo a $0$ en $U$.

Omitimos la prueba de este hecho, pero se puede consultar una prueba detallada en An Introduction to Complex Function Theory, de Bruce P. Palka, y una prueba parcial de este resultado en Notas para un curso de Variable Compleja I, de Oscar Palmas Velasco y Alberto Lazcano García.

Proposición 38.4. (Fórmula integral de Cauchy, versión homológica.)
Sean $U\subset \mathbb{C}$ un conjunto abierto, $f:U\to \mathbb{C}$ una función analítica en $U$ y $\sigma$ un ciclo en $U$. Si $\sigma$ es homólogo a $0$ en $U$, entonces:
$$n(\sigma ,z)f(z)dz=\frac{1}{2\pi i}{\int }_{\sigma }\frac{f(\zeta )}{\zeta -z}d\zeta ,$$para todo $z\in U\setminus |\sigma |$.

Demostración. Dadas las hipótesis, fijamos un punto $z\in U\setminus |\sigma |$. Definimos a la función:
$$g:U\to \mathbb{C},$$como:
$$g(\zeta )=\{\begin{array}{lcc}{\displaystyle \frac{f(\zeta )–f(z)}{\zeta –z}}& \text{si}& \zeta \ne z,\\ \\ f^{\prime }(z)& \text{si}& \zeta =z,\end{array}$$donde $\zeta$ es una variable independiente.

Es claro que $g$ es una función analítica en $U\setminus \{z\}$. Más aún, como $f$ es analítica en $U$, entonces:
$$\underset{\zeta \to z}{lim}g(\zeta )=\underset{\zeta \to z}{lim}{\displaystyle \frac{f(\zeta )–f(z)}{\zeta –z}}=f^{\prime }(z)=g(z),$$es decir, $g$ es continua en $z$, por lo que $g$ es continua en $U$, entonces, por el teorema de Morera generalizado, tenemos que $g$ es analítica en $U$.

Como $z$ no está en ninguno de los contorno cerrados ${\gamma }_k$, que conforman al ciclo $\sigma$, del teorema 38.4 y la definición 38.6, tenemos que:
$$\begin{array}{rl}0& ={\int }_{\sigma }g(\zeta )d\zeta \\ & ={\int }_{\sigma }{\displaystyle \frac{f(\zeta )–f(z)}{\zeta –z}}d\zeta \\ & ={\int }_{\sigma }{\displaystyle \frac{f(\zeta )}{\zeta –z}}d\zeta –{\int }_{\sigma }{\displaystyle \frac{f(z)}{\zeta –z}}d\zeta \\ & ={\int }_{\sigma }{\displaystyle \frac{f(\zeta )}{\zeta –z}}d\zeta –2\pi in(\sigma ,z)f(z),\end{array}$$es decir:
$$n(\sigma ,z)f(z)=\frac{1}{2\pi i}{\int }_{\sigma }{\displaystyle \frac{f(\zeta )}{\zeta –z}}d\zeta .$$

Dado que $z\in U\setminus |\sigma |$ es arbitrario, entonces se tiene el resultado.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Con los resultados previos podemos dar otra prueba del corolario 38.3.

Corolario 38.4.
Sean $D\subset \mathbb{C}$ un dominio simplemente conexo y $f:D\to \mathbb{C}$ una función analítica en $D$. Entonces existe una primitiva de $f$ en $D$.

Demostración. Dadas las hipótesis, sea $\gamma$ un contorno cerrado en $D$. Como $D$ es simplemente conexo, $\gamma$ es homotópico a un punto $z_0\in D$. Por la proposición 38.1 $\gamma$ es homólogo a $0$ en $D$ y por el teorema 38.4 se cumple que:
$$\begin{array}{}\text{(38.4)}& {\int }_{\gamma }f(z)dz=0.\end{array}$$

Dado que $\gamma$ es arbitraria, entonces (38.4) se cumple para todo contorno cerrado $\gamma$ en $D$. Por lo tanto, de la proposición 35.2 sabemos que esto es equivalente a que exista una primitiva de $f$ en $D$, es decir, una función analítica $F:D\to \mathbb{C}$ tal que $F^{\prime }(z)=f(z)$ para todo $z\in D$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Teorema 38.5.
Sean $D\subset \mathbb{C}$ un dominio. Si todo contorno cerrado en $D$ es homólogo a $0$, entonces $D$ es simplemente conexo.

Tarea moral

1. Sea $D\subset \mathbb{C}$ un dominio. Muestra que ${\sim }_D$ es una relación de equivalencia en el conjunto de contornos cerrados en $D$.
2. Sean $D=\mathbb{C}\setminus \{0\}$ y $\gamma :[-\pi /2,\pi /2]\to D$, el contorno dado por $\gamma (t)=e^{it}$. Define de manera explícita dos contornos poligonales ${\beta }_1$ y ${\beta }_2$ en $D$, que unan a $-i$ y $i$, tales que:
   $${\int }_{\beta }f(z)dz={\int }_{\gamma }f(z)dz$$se cumple para toda función analítica $f$ en $D$, si $\beta ={\beta }_1$, pero la igualdad no se cumple si $\beta ={\beta }_2$.
3. Sean $r$ y $R$ dos constantes positivas tales que $0<r<R$. Define al contorno ${\gamma }_r(t)=r{e}^{it}$, para $0\le t\le 2\pi$. Muestra que:
   $$\frac{1}{2\pi i}{\int }_{{\gamma }_r}\frac{R+z}{(R-z)z}dz=1.$$Considerando lo anterior deduce que:
   $$\frac{1}{2\pi }{\int }_0^{2\pi }\frac{R^2-r^2}{R^2+r^2-2rR\cos (t)}dt=1.$$
4. Si $\gamma$ es la circunferencia $C(i,1)$, orientada positivamente, muestra que:
   $${\int }_{\gamma }\frac{2z}{z^2+2}dz=2\pi i.$$
5. Evalúa la integral:
   $${\int }_{\gamma }\frac{1}{4z^2+4z-3}dz,$$para los siguientes contornos orientados positivamente.
   a) $\gamma$ es la circunferencia $C(0,1)$.
   b) $\gamma$ es la circunferencia $C(-3/2,1)$.
   c) $\gamma$ es la circunferencia $C(0,3)$.
6. Sea $D=\{z\in \mathbb{C}:1/2<|z|<4\}$. Determina explícitamente una homotopía $H(t,s)$ entre los contornos cerrados en $D$, orientados positivamente, dados por la elipse ${\displaystyle \frac{x^2}{4}}+{\displaystyle \frac{y^2}{9}}=1$, con punto inicial $(2,0)$ y la circunferencia unitaria $C(0,1)$, con punto inicial $(1,0)$, ambos recorridos una sola vez.
7. Sea $\gamma (t)=1+i+2e^{it}$, para $t\in [0,2\pi ]$. Evalúa las siguientes integrales.
   a) ${\displaystyle {\int }_{\gamma }\frac{1}{z-1}dz}$.
   b) ${\displaystyle {\int }_{\gamma }\frac{1}{(z-3i)(z-1)}dz}$.
   c) ${\displaystyle {\int }_{\gamma }\frac{1}{z^2+9}dz}$.
   d) ${\displaystyle {\int }_{\gamma }\frac{1}{(z-i)(z+i)}dz}$.
8. Muestra que:
   $${\int }_{\gamma }\frac{\mathrm{sen}(z)}{4z+\pi }dz=-\frac{\sqrt{2}\pi i}{4},$$donde $\gamma$ es la circunferencia unitaria $C(0,1)$, orientada positivamente.

Más adelante…

En esta entrada hemos generalizado el teorema integral de Cauchy para dominios más generales que un disco abierto, para ello recurrimos a los conceptos topológicos de homotopía y homología. Además extendimos dicho resultado para dominios múltiplemente conexos, lo cual es de mucha utilidad al evaluar integrales.

En la siguiente entrada veremos algunos resultados muy importantes que relacionan los conceptos de diferenciabilidad e integrabilidad con las sucesiones y series de funciones complejas.

Entradas relacionadas

• Ir a Variable Compleja I.
• Entrada anterior del curso: Consecuencias del teorema integral de Cauchy.
• Siguiente entrada del curso: Teoremas de Weierstrass.