(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

INTRODUCCIÓN

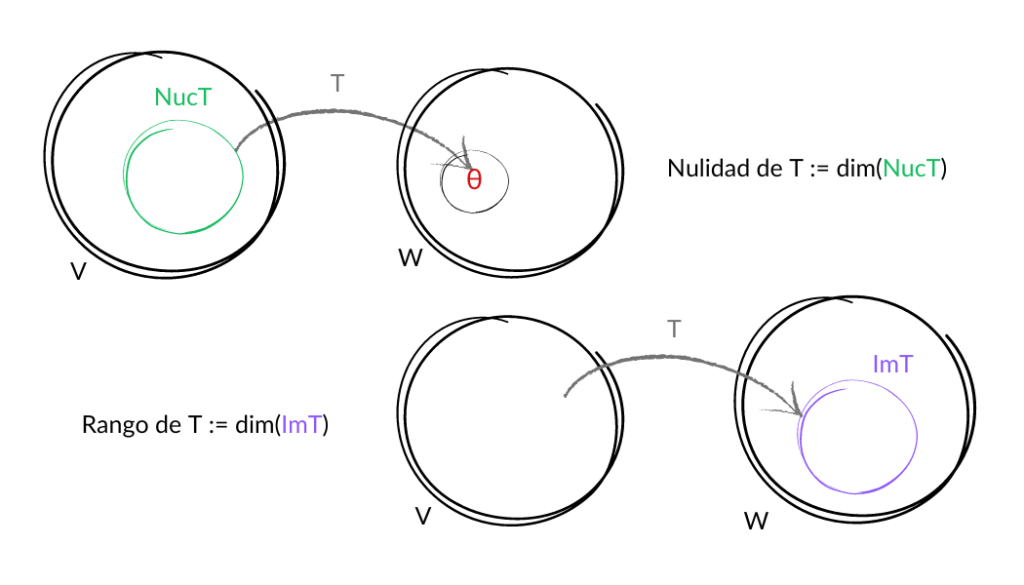
Analizaremos cuatro nuevos conceptos. Dos de ellos son conjuntos y los otros dos son las dimensiones de esos conjuntos.

Al ir avanzando en el análisis del primer concepto que estudiaremos en esta entrada, el núcleo de una transformación lineal, podrás ver que una de las aplicaciones inmediatas es pensar al núcleo como el conjunto formado por las soluciones de un sistema de ecuaciones lineales homogéneo de alguna forma a la transformación lineal. Pero todo con calma…

NÚCLEO E IMAGEN DE UNA TRANSFORMACIÓN LINEAL

Definición: Sean $V$ y $W$ $K$ – espacios vectoriales y $T\in\mathcal{L}(V,W)$.
El núcleo de $T$ es $Núc\,T=\{v\in V|T(v)=\theta_W\}$.
La imagen de $T$ es $Im\, T=\{T(v)|v\in V\}$.

Nota: El núcleo de una transformación $T$, también suele llamarse kernel y denotarse como $ker\,T$.

• Sean $K$ un campo y $T:K^\infty\longrightarrow K^\infty$ lineal donde $\forall (x_1,x_2,x_3,…)\in K^\infty (T(x_1,x_2,x_3,…)=(x_2,x_3,x_4,…))$.
  $Núc\,T=\{(x_1,0_K,0_K,…)\in K^\infty | x_1\in K\}$ ; $Im\,T=K^\infty$

Justificación. Para el núcleo de $T$:

\begin{align*} T(x_1,x_2,x_3,…)=(0_K,0_K,0_K,…) \Leftrightarrow \\ (x_2,x_3,x_4,…)=(0_K,0_K,0_K,…)\Leftrightarrow \\x_i=0_K \text{ para toda }i\in\{2,3,4,…\}. \end{align*}

Para la imagen de $T$:

Sea $(y_1,y_2,y_3,…)\in K^\infty$. Tenemos que $T(0_K,y_1,y_2,…)=(y_1,y_2,y_3,…)$, por lo cual $T$ es suprayectiva y su imagen es todo el codominio.

• Sea $T:\mathbb{R}^2\longrightarrow\mathbb{R}^2$ donde $\forall (x,y)\in\mathbb{R}^2(T(x,y)=(x,0))$
  $Núc\,T=\{(0,y)\in\mathbb{R}^2|y\in\mathbb{R}\}$ ; $Im\,T=\{(x,0)\mathbb{R}^2|x\in\mathbb{R}\}$

Justificación. Para el núcleo de $T$:

$$T(x,y)=(0,0) \Leftrightarrow (x,0)=(0,0)\Leftrightarrow x=0.$$

Para la imagen de $T$:

Sea $(a,0)\in \{ (x,0)\in\mathbb{R}^2|x\in\mathbb{R}^2\}$. Dado que $T(a,0)=(a,0)$ se tiene que $(a,0)\in Im\,T$. A la inversa, si $(a,b)\in Im\, T$ se tiene que $T(x,y)=(a,b)$ para alguna $(x,y)\in \mathbb{R}^2$, por lo que $(x,0)=(a,b)$ y así $b=0$.

• Sean $K$ un campo, $A\in\mathcal{M}_{m\times n}(K)$ y $T:K^n\longrightarrow K^m$ donde $\forall X\in K^n(T(X)=AX)$
  $Núc\,T$ es el conjunto de las soluciones del sistema homogéneo con matriz de coeficientes $A$ ; $Im\,T$ es el espacio generado por las columnas de $A$

Justificación. Para el núcleo de $T$:

$$T(X)=\theta_{m\times 1}\Leftrightarrow AX=\theta_{m\times 1} \Leftrightarrow X \text{ es solución del sistema homogéneo con matriz de coeficientes }A.$$

Para la imagen de $T$:

\begin{align*}Im\,T&=\{AX:X\in K^n\}\\&=\left\{ \begin{pmatrix} a_{11} & … & a_{1n} \\ \vdots & \ddots & \vdots \\ a_{m1} & … & a_{mn} \end{pmatrix} \begin{pmatrix} x_1\\ \vdots \\ x_n \end{pmatrix} : x_1,x_2,…,x_n\in K \right\}\\&=\left\{ \begin{pmatrix} a_{11}x_1 + … + a_{1n}x_n \\ … \\ a_{m1}x_1 + … + a_{mn}x_n \end{pmatrix} : x_1,x_2,…,x_n\in K \right\}\\&=\left\{ x_1\begin{pmatrix} a_{11}\\ \vdots \\ a_{m1} \end{pmatrix} + … + x_n\begin{pmatrix} a_{1n}\\ \vdots \\ a_{mn} \end{pmatrix} : x_1,x_2,…,x_n\in K \right\}\\&=\left\langle \begin{pmatrix} a_{11}\\ \vdots \\ a_{m1} \end{pmatrix},…,\begin{pmatrix} a_{11}\\ \vdots \\ a_{m1} \end{pmatrix} \right\rangle\end{align*}

Proposición: Sean $V,W$ $K$ – espacios vectoriales, $T\in\mathcal{L}(V,W)$. Se cumple que:

a) $Núc\,T\leqslant V$.
b) $Im\,T\leqslant W$.

Demostración: Para cada inciso es necesario demostrar dos propiedades:

a) P.D. $\theta_V\in Núc\,T$ y $\forall\lambda\in K$ $\forall u,v\in Núc\,T (\lambda u + v\in Núc\,T)$

Como $T$ es una transformación lineal tenemos que $T(\theta_V)=\theta_W$, por lo tanto, $\theta_V\in Núc\,T.$

Sean $\lambda\in K$ y $u,v\in Núc\,T$. Entonces $T(u)=\theta_W=T(v).$ Además, $T(\lambda u+v)=\lambda T(u)+T(v)$ por ser $T$ lineal. Así, $$T(\lambda u+v)=\lambda\theta_W +\theta_W=\theta_W$$
de donde $\lambda u + v\in Núc\,T.$

b) P.D. $\theta_W\in Im\,T$ y $\forall\lambda\in K$ $\forall w,z\in Im\,T (\lambda u + v\in Im\,T)$

Como $T$ es una transformación lineal tenemos que $\theta_V\in V$ cumple que $T(\theta_V)=\theta_W$, por lo tanto, $\theta_W\in Im\,T$.

Sean $\lambda\in K$ y $w,z\in Im\,T$. Entonces $\exists u,v\in V (T(u)=w\wedge T(v)=z)$. Además, $T(\lambda u+v)=\lambda T(u)+T(v)$ por ser $T$ lineal.
Así, $$T(\lambda u+v)=\lambda w+z$$
de donde $\lambda w+ z\in Im\,T.$

NULIDAD Y RANGO DE UNA TRANSFORMACIÓN LINEAL

Definición: Sea $T$ una transformación lineal con $Núc \,T$ de dimensión finita. Decimos que la dimensión de $Núc\,T$ es la nulidad de $T$.

Definición: Sea $T$ una transformación lineal con $Im \,T$ de dimensión finita. Decimos que la dimensión de $Im\,T$ es el rango de $T$.

Ejemplo

• Sea $K=\mathbb{R}$ y sean $V=\mathcal{P}_3$ y $W=\mathcal{P}_2$ $K$ – espacios vectoriales.
  Sea $T:V\longrightarrow W$ donde $\forall p(x)\in T(p(x))=p'(x)$.
  La nulidad de $T$ es $1$ y su rango es $3$

Justificación. Los polinomios con derivada cero son únicamente las constantes. Así, $Núc(T)=\{a|a\in\mathbb{R}\}$ que tiene dimensión $1$.

Por otro lado todo polinomio de grado $2$ se puede obtener derivando un polinomio de grado $3$. Basta con integrar el polinomio de grado $2$ para encontrar cómo son los polinomios de grado $3$ que cumplen lo deseado. De modo que $W\subseteq Im(T)$ y como $Im(T)\subseteq W$ por definición, entonces $Im(T)=W$ que tiene dimensión $3$.

Por lo tanto, el núcleo y la imagen son de dimensión finita y la nulidad de $T$ es $1$ y su rango es $3.$

Tarea Moral

1. Sean $K$ un campo, $V$ y $W$ $K$-espacios vectoriales y $T:V\longrightarrow W$ lineal. Sea $\{ w_1, w_2, …, w_k\}$ un subconjunto l.i. de $Im\,T$.
   Si $S=\{ v_1,v_2,…,v_k \}$ se selecciona de tal forma que $\forall i\in \{ 1,2,…,k\}(T(v_i)=w_i)$, demuestra que $S$ es l.i.
2. Para la transformación lineal $T:\mathbb{R}^3\longrightarrow \mathbb{R}^2$ con $T(a_1,a_2,a_3)=(a_1 + 2a_2, 2a_3 – a_1)$ encuentra bases para $Núc(T)$ e $Im(T)$.
3. Sean $K$ un campo y $P: \mathcal{M}_{m\times m}(K) \longrightarrow \mathcal{M}_{m\times m}(K)$ definida por $\forall A\in \mathcal{M}_{m\times m}(K) \left( P(A)=\frac{A + A^{t}}{2} \right)$. Verifica que $T$ es lineal y encuentra su núcleo e imagen.

Más adelante…

En la siguiente entrada veremos el vínculo que existe entre la dimensión del núcleo, de la imagen y del espacio vectorial que aparece como dominio de una transformación lineal. Esta relación numérica nos permite calcular cualquiera de estas dimensiones si tenemos conocimiento de las otras dos.

Entradas relacionadas

• Ir a Álgebra Lineal I
• Entrada anterior del curso: 2.1. TRANSFORMACIÓN LINEAL: definición y ejemplos
• Siguiente entrada del curso: 2.3. TEOREMA DE LA DIMENSIÓN: demostración e implicaciones