(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

INTRODUCCIÓN

Llegamos a la conclusión de que la base de un espacio vectorial (con dimensión finita) es un conjunto lo «suficientemente grande» para generar al espacio y lo «suficientemente pequeño» para ser siendo linealmente independiente.

Ahora bien, veremos que siempre será posible encontrar un base si conocemos un conjunto generador finito o un conjunto linealmente independiente.

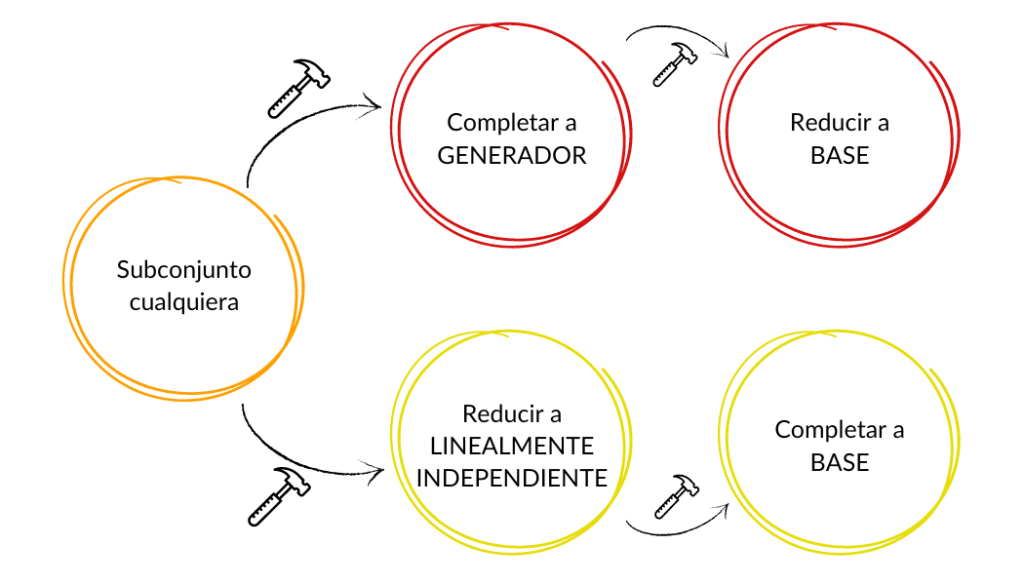
Así, con los ajustes necesarios (que ya sabremos cómo hacer), resulta que podremos construir bases en espacios de dimensión finita.

Teorema: Sea $V$ un $K$ – espacio vectorial de dimensión finita.
a) Todo conjunto generador finito o es una base o se puede reducir a una base.
b) Todo conjunto linealmente independiente o es una base o se puede completar a una base.

Demostración:

a) En la demostración de la proposición que se encuentra en la entrada anterior tomamos un conjunto generador finito $S$ de un espacio vectorial arbitrario y o bien es base o es linealmente dependiente y en ese caso recursivamente tomamos subconjuntos propios de $S$ hasta que uno de esos subconjuntos fuera base. Este método prueba que podemos reducir cualquier conjunto generador de $V$ para obtener una base.

b) Sea $S\subseteq V$ un conjunto l.i.
Ya sabemos que $S$ es finito por ser un subconjunto l.i. de un espacio $V$ de dimensión finita (ver la observación en la entrada anterior).

Caso 1. Si $\langle S \rangle = V$, entonces $S$ es base de $V$ por definición.

Caso 2. Si $\langle S \rangle \subsetneq V$, entonces existe $v_1\in V$ tal que $v_1\notin \langle S \rangle$. Por lo tanto, $ S \cup \{ v_1 \}$ es l.i.

Subaso 1. Si $\langle S \cup \{ v_1 \} \rangle = V$, entonces $S \cup \{ v_1 \}$ es base de $V$ por definición.

Subcaso 2. Si $\langle S \cup \{ v_1 \} \rangle \subsetneq V$, entonces existe $v_2\in V$ tal que $v_2\notin \langle S \cup \{ v_1 \} \rangle$ Por lo tanto, $ S \cup \{ v_1 \} \cup \{ v_2 \} $ es l.i.

Este proceso no es infinito porque los subconjuntos l.i de $V$ deben ser finitos, así que se detiene después de digamos $m$ pasos, en el momento en que obtenemos un conjunto que genera. El número $m$ es la cantidad de elementos de $V$ que tuvimos que agregar a $S$, entonces $\langle S \cup \{ v_1 \} \cup \{ v_2 \} \cup … \{ v_m \} \rangle$ es una base de $V$.

Corolario: Sea $V$ un $K$ – espacio vectorial tal que $dim_K V=n$.
a) Cualquier conjunto generador con $n$ elementos es una base de $V$.
b) Cualquier conjunto linealmente independiente con $n$ elementos es una base de $V$.

Demostración: Por definición de base tenemos que toda base $B$ de $V$ cumple que $|B|=dim_K V=n$. Es decir, toda base de $V$ tiene $n$ elementos.

a) Sea $S\subseteq V$ generador con $n$ elementos.
Por el teorema anterior $S$ es una base o se puede reducir a una base.
Pero reducir $S$ significaría quitar elementos y obtendríamos una base de $V$ con menos de $n$ elementos, lo que es una contradicción porque toda base de $V$ tiene $n$ elementos.
Por lo tanto $S$ es base.

b) Sea $S\subseteq V$ linealmente independiente.
Por el teorema anterior $S$ es una base o podemos completarlo a una base.
Pero completar $S$ significaría agregar elementos y obtendríamos una base de $V$ con más de $n$ elementos, lo que es una contradicción porque toda base de $V$ tiene $n$ elementos.
Por lo tanto $S$ es base.

Ejemplo

Sea $K=\mathbb{R}, V=\mathcal{M}_{2\times 2}(\mathbb{R})$.
Sea $W=\left\langle \begin{pmatrix} 1 & 1 \\ 0 & 0 \end{pmatrix} , \begin{pmatrix} 0 & 1 \\ 0 & 1 \end{pmatrix} , \begin{pmatrix} 0 & 0 \\ 1 & 1 \end{pmatrix} , \begin{pmatrix} 1 & 0 \\ 1 & 0 \end{pmatrix} \right\rangle$

Por construcción, $W$ es el subespacio generado por $X=\left\{\begin{pmatrix} 1 & 1 \\ 0 & 0 \end{pmatrix} , \begin{pmatrix} 0 & 1 \\ 0 & 1 \end{pmatrix} , \begin{pmatrix} 0 & 0 \\ 1 & 1 \end{pmatrix}, \begin{pmatrix} 1 & 0 \\ 1 & 0 \end{pmatrix} \right\}$
Encontremos un subconjunto de $X$ que sea base de $W$.

Observemos que $\begin{pmatrix} 1 & 1 \\ 0 & 0 \end{pmatrix}-\begin{pmatrix} 0 & 1 \\ 0 & 1 \end{pmatrix}+\begin{pmatrix} 0 & 0 \\ 1 & 1 \end{pmatrix}-\begin{pmatrix} 1 & 0 \\ 1 & 0 \end{pmatrix}=\begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix}$

Así, $X$ es l.d. y como $\begin{pmatrix} 1 & 1 \\ 0 & 0 \end{pmatrix}-\begin{pmatrix} 0 & 1 \\ 0 & 1 \end{pmatrix}+\begin{pmatrix} 0 & 0 \\ 1 & 1 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\ 1 & 0 \end{pmatrix}$, entonces $W=\langle X\rangle = \left\langle \begin{pmatrix} 1 & 1 \\ 0 & 0 \end{pmatrix}, \begin{pmatrix} 0 & 1 \\ 0 & 1 \end{pmatrix}, \begin{pmatrix} 0 & 0 \\ 1 & 1 \end{pmatrix}\right\rangle$

Veamos que $B=\left\{\begin{pmatrix} 1 & 1 \\ 0 & 0 \end{pmatrix}, \begin{pmatrix} 0 & 1 \\ 0 & 1 \end{pmatrix}, \begin{pmatrix} 0 & 0 \\ 1 & 1 \end{pmatrix}\right\}$ es l.i.

Sean $\lambda_1,\lambda_2,\lambda_3\in\mathbb{R}$ tales que $\lambda_1\begin{pmatrix} 1 & 1 \\ 0 & 0 \end{pmatrix}+\lambda_2\begin{pmatrix} 0 & 1 \\ 0 & 1 \end{pmatrix}+\lambda_3\begin{pmatrix} 0 & 0 \\ 1 & 1 \end{pmatrix}=\begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix}.$

Esto implica que $\begin{pmatrix} \lambda_1 & \lambda_1+\lambda_2 \\ \lambda_3 & \lambda_2+\lambda_3 \end{pmatrix}=\begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix}$

Así, $\lambda_1= \lambda_1+\lambda_2= \lambda_3=\lambda_2+\lambda_3=0$.
Por lo tanto, $\lambda_1=\lambda_2=\lambda_3=0$ y $B$ es l.i.

Como $\langle B\rangle=W$ y $B$ es l.i., entonces $B$ es una base y obtenemos que $dim_\mathbb{R}W=|B|=3.$

Teorema: Sean $V$ un $K$ – espacio vectorial de dimensión finita y $W$ un subespacio de $V$. Entonces se cumple lo siguiente:

a) $W$ es de dimensión finita.
b) Toda base de $W$ o es una base de $V$ o se puede completar a una base de $V$.
c) $dim_KW\leq dim_KV$.
d) Si $dim_KW=dim_KV$, entonces $W=V$.

Demostración: Analicemos cada inciso por separado:

a) Veamos que $W$ es de dimensión finita probando que tiene una base finita.

Si $W=\{\theta_V\}$ entonces $\emptyset$ es una base finita de $V$.

Supongamos que $\{\theta_V\}\subsetneq W$, consideremos $w_1\in W\setminus \{\theta_V\} $, notemos que $\{w_1\}$ es l.i. ya que $w_1\neq \theta_V$. Si $\{w_1\}$ genera a $W$, entonces es una base finita de $W$. Si por el contrario $\{w_1\}$ no genera a $W$ tendríamos que $\langle w_1\rangle\subsetneq W$ y podemos considerar $w_2\in W\setminus \langle w_1\rangle$. Debido a la elección de $w_2$ sabemos que $\{w_1, w_2\}$ es l.i. Así, si $\{w_1, w_2\}$ genera a $W$, entonces es una base finita de $W$ y si no elegimos $w_3\in W\setminus \langle w_1,w_2\rangle$.

Continuando de este modo obtenemos subconjuntos de $W$, y por lo tanto de $V$, linealmente independientes. El proceso se detiene después de un número finito de pasos ya que al ser $V$ de dimensión finita no existen conjuntos en $V$ linealmente independientes infinitos y se detiene en el momento en que el subconjunto obtenido genera a $W$. Entonces el proceso acaba después de digamos $t$ pasos obteniendo un subconjunto $\{w_1, \dots ,w_t\}$ de $W$ linealmente independiente que genera a $W$, siendo así una base finita de $W$.

b) Sea $B$ una base de $W$.
Entonces $B$ es un subconjunto l.i. en $V$ y por el teorema anterior o es una base de $V$ o se puede completar a una base de $V$.

c) Sea $B$ una base de $W$.
Por el inciso anterior tenemos $B$ es una base de $V$ o se puede completar para obtener una base de $V$, es decir, existe $A\subseteq V$ tal que $B\cup A$ es una base de $V$. Así,
$$dim_KW=|B|\leq|B\cup A|=dim_KV.$$
Por lo tanto, $dim_KW\leq\dim_KV$.

d) Supongamos que $dim_KW=\dim_KV=n$
Sea $B$ una base de $W$.
Entonces $B$ es un l.i. en $V$ con $n$ elementos. Por el corolario anterior tenemos que $B$ es una base de $V$.
Así, $W=\langle B\rangle =V$ y por lo tanto, $W=V$

Tarea Moral

1. Da tres bases diferentes para $\mathcal{M}_{2 \times 2}(\mathbb{R})$.
2. Demuestra que el conjunto $\{v_1,v_2,…\}$ (infinito) es linealmente independiente si y sólo si $\{v_1,v_2,…,v_n\}$ es linealmente independiente para toda $n\geq 1$.

Más adelante…

Veremos un nuevo concepto: Suma y suma directa de subespacios vectoriales.
¿Qué es? ¿Qué estructura tiene? ¿Dónde vive? ¿Qué relación tiene la suma de dos subespacios con sus uniones?

Entradas relacionadas

• Ir a Álgebra Lineal I
• Entrada anterior del curso: 1.9. BASE, DIMENSIÓN Y ESPACIO DE DIMENSIÓN (IN)FINITA: definiciones y ejemplos
• Siguiente entrada del curso: 1.11. SUMA Y SUMA DIRECTA DE SUBESPACIOS: definiciones y ejemplos