Archivo de la etiqueta: conjunto generador

1.10. BASE DE ESPACIOS VECTORIALES: obtención a partir de un conjunto linealmente independiente o generador

Por Jennyfer Paulina Bennetts Castillo

Deja un comentario

INTRODUCCIÓN

Llegamos a la conclusión de que la base de un espacio vectorial (con dimensión finita) es un conjunto lo «suficientemente grande» para generar al espacio y lo «suficientemente pequeño» para seguir siendo linealmente independiente.

Ahora bien, veremos que siempre será posible encontrar un base si conocemos un conjunto generador finito o un conjunto linealmente independiente.

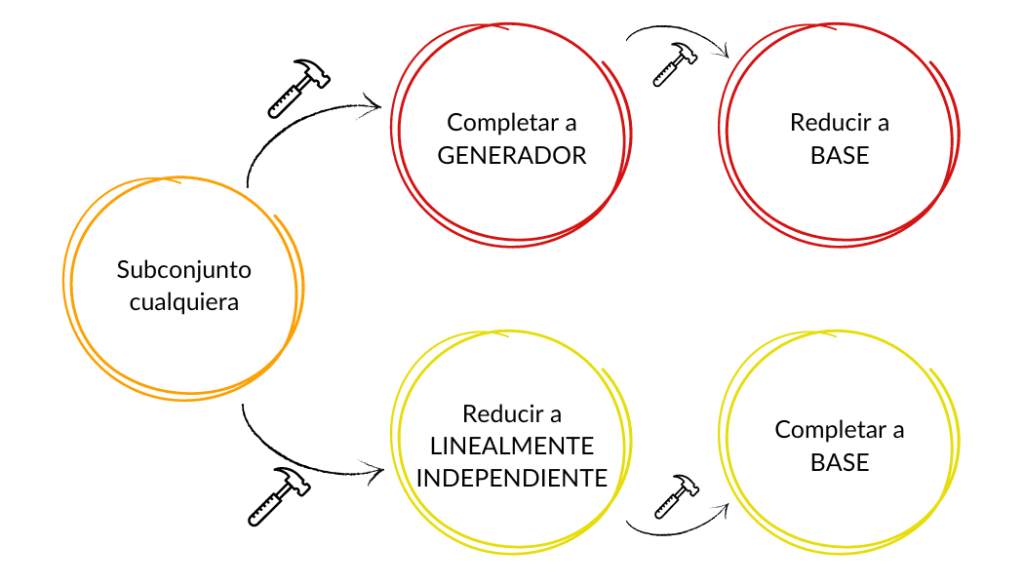
De cualquier subconjunto finito de nuestro espacio, podemos obtener un generador o un l.i. y cuando lo obtengamos, bastará con centrarnos en la cardinalidad para reducir, o bien, completar, y obtener una base.

Así, con los ajustes necesarios (que ya sabremos cómo hacer), resulta que de cualquier subconjunto en nuestro espacio podemos partir para lograr obtener una base.

Teorema: Sea $V$ un $K$ – espacio vectorial de dimensión finita.
a) Todo conjunto generador finito se puede reducir a una base.
b) Todo conjunto linealmente independiente se puede completar a una base.

Demostración:

a) En la demostración de la proposición que se encuentra en la entrada anterior tomamos un conjunto generador finito $S$ de un espacio vectorial arbitrario y recursivamente tomamos subconjuntos propios de $S$ hasta que uno de esos subconjuntos fuera base. Usando el mismo método, reducimos cualquier conjunto generador de $V$ para obtener una base.

b) Sea $S\subseteq V$ un conjunto l.i.
Ya sabemos que $S$ es finito por ser un subconjunto l.i. de $V$ de dimensión finita (observación en la entrada anterior).

Caso 1. Si $\langle S \rangle = V$, entonces $S$ es base de $V$ por definición.

Caso 2. Si $\langle S \rangle \subsetneq V$, entonces existe $v_1\in V$ tal que $v_1\notin \langle S \rangle$. Por lo tanto, $\langle S \rangle \cup \{ v_1 \}$ es l.i.

Subaso 1. Si $\langle \langle S \rangle \cup \{ v_1 \} \rangle = V$, entonces $S$ es base de $V$ por deifinición.

Subcaso 2. Si $\langle \langle S \rangle \cup \{ v_1 \} \rangle \subseteq V$, entonces existe $v_2\in V$ tal que $v_2\notin \langle \langle S \rangle \cup \{ v_1 \} \rangle$ Por lo tanto, $\langle \langle S \rangle \cup \{ v_1 \} \cup \{ v_2 \} \rangle$ es l.i.

Este proceso no es infinito porque los suconjuntos l.i de $V$ deben ser finitos.

Sea $m$ el número de elementos de $V$ que tuvimos que «aumentar» a $\langle S \rangle$ en los subcasos del caso 2, entonces $\langle \langle S \rangle \cup \{ v_1 \} \cup \{ v_2 \} \cup … \{ v_m \} \rangle$ es base de $V$.

Corolario: Sea $V$ un $K$ – espacio vectorial tal que $dim_K(V)=n$.
a) Cualquier conjunto generador con $n$ elementos es una base de $V$.
b) Cualquier conjunto linealmente independiente con $n$ elementos es una base de $V$.

Demostración: Por definición de base tenemos que toda base $B$ de $V$ cumple que $|B|=dim_K(V)=n$. Es decir, toda base de $V$ tiene $n$ elementos.

a) Sea $S\subseteq V$ generador con $n$ elementos.
Por el teorema anterior podemos reducir $S$ a una base.
Pero reducir $S$ a un conjunto de $n$ elementos implica que se conserva íntegro.
Por lo tanto $S$ es base.

b) Sea $S\subseteq V$ linealmente independiente.
Por el teorema anterior podemos completarlo a una base.
Pero completar $S$ a un conjunto de $n$ elementos implica que se conserva íntegro.
Por lo tanto $S$ es base.

Ejemplo

Sea $K=\mathbb{R}, V=\mathcal{M}_{2\times 2}(\mathbb{R})$.
Sea $W=\left\langle \begin{pmatrix} 1 & 1 \\ 0 & 0 \end{pmatrix} , \begin{pmatrix} 0 & 1 \\ 0 & 1 \end{pmatrix} , \begin{pmatrix} 0 & 0 \\ 1 & 1 \end{pmatrix} , \begin{pmatrix} 1 & 0 \\ 1 & 0 \end{pmatrix} \right\rangle$

Por construcción, $W$ es el subespacio generado por $X=\left\{\begin{pmatrix} 1 & 1 \\ 0 & 0 \end{pmatrix} , \begin{pmatrix} 0 & 1 \\ 0 & 1 \end{pmatrix} , \begin{pmatrix} 0 & 0 \\ 1 & 1 \end{pmatrix}\right\}$
Encontremos un subconjunto de $X$ que sea base de $W$.

Observemos que $\begin{pmatrix} 1 & 1 \\ 0 & 0 \end{pmatrix}-\begin{pmatrix} 0 & 1 \\ 0 & 1 \end{pmatrix}+\begin{pmatrix} 0 & 0 \\ 1 & 1 \end{pmatrix}-\begin{pmatrix} 1 & 0 \\ 1 & 0 \end{pmatrix}=\begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix}$

Así, $X$ es l.d. y como $\begin{pmatrix} 1 & 1 \\ 0 & 0 \end{pmatrix}-\begin{pmatrix} 0 & 1 \\ 0 & 1 \end{pmatrix}+\begin{pmatrix} 0 & 0 \\ 1 & 1 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\ 1 & 0 \end{pmatrix}$, entonces $W=\langle X\rangle = \left\langle \begin{pmatrix} 1 & 1 \\ 0 & 0 \end{pmatrix}-\begin{pmatrix} 0 & 1 \\ 0 & 1 \end{pmatrix}+\begin{pmatrix} 0 & 0 \\ 1 & 1 \end{pmatrix}\right\rangle$

Veamos que $B=\left\{\begin{pmatrix} 1 & 1 \\ 0 & 0 \end{pmatrix}-\begin{pmatrix} 0 & 1 \\ 0 & 1 \end{pmatrix}+\begin{pmatrix} 0 & 0 \\ 1 & 1 \end{pmatrix}\right\}$ es l.i.

Sean $\lambda_1,\lambda_2,\lambda_3\in\mathbb{R}$ tales que $\lambda_1\begin{pmatrix} 1 & 1 \\ 0 & 0 \end{pmatrix}+\lambda_2\begin{pmatrix} 0 & 1 \\ 0 & 1 \end{pmatrix}+\lambda_3\begin{pmatrix} 0 & 0 \\ 1 & 1 \end{pmatrix}=\begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix}$

De donde $\begin{pmatrix} \lambda_1 & \lambda_1+\lambda_2 \\ \lambda_3 & \lambda_2+\lambda_3 \end{pmatrix}=\begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix}$

Así, $\lambda_1, \lambda_1+\lambda_2, \lambda_3, \lambda_2+\lambda_3=0$.
Por lo tanto, $\lambda_1=\lambda_2=\lambda_3=0$.

Como $\langle B\rangle=W$ y $B$ es l.i., entonces $B$ es base y obtenemos que $dim_\mathbb{R}W=|B|=3$

Teorema: Sean $V$ un $K$ – espacio vectorial de dimensión finita y $W$ un subespacio de $V$. Entonces se cumple lo siguiente:

a) $W$ es de dimensión finita
b) Toda base de $W$ se puede completar a una base de $V$
c) $dim_KW\leq dim_KV$
d) Si $dim_KW=dim_KV$, entonces $W=V$

Demostración: Analicemos cada inciso por separado:

a) Sup. por reducción al absurdo que $W$ no es de dimensión finita.
Entonces existe $B$ base de $W$ de cardinalidad infinita.
Así, $B$ es un subconjunto de $V$ que es l.i.
Por el teorema anterior tenemos que podemos completar a $B$ para obtener una base de $V$, lo cual es una contradicción, pues existiría un abse de $V$ de cardinalidad infinita (pero por hipótesis, $V$ es de cardinalidad finita).
Por lo tanto, $W$ es de dimensión finita.

b) Sea $B$ una base de $W$.
Entonces $B$ es un subconjunto l.i. en $V$ y por el teorema anterior podemos completar $B$ a una base de $V$.

c) Sea $B$ una base de $W$.
Por el inciso anterior tenemos que podemos completar $B$ para obtener una base de $V$, es decir, $B\cup A$ es base de $V$ con $A\subseteq V$
Si $B\cup A=B$, entonces $dim_KW=|B|=dim_KV$.
Si $B\cup A\not= B$, $dim_KW=|B|\lneq|B\cup A|=dim_KV$
Por lo tanto, $dim_KW\leq\dim_KV$

d) Sup. $dim_KW=\dim_KV=n$
Sea $B$ una base de $W$.
Entonces $B$ es un l.i. en $V$ con $n$ elementos.
Por el corolario anterior tenemos que $B$ es base de $V$.
De donde $B$ es base de $V$.
Y así, $W=\langle B\rangle =V$.
Por lo tanto, $W=V$

Tarea Moral

  1. Da tres bases diferentes para $\mathcal{M}_{2 \times 2}(\mathbb{R})$.
  2. Demuestra que el conjunto $\{v_1,v_2,…\}$ (infinito) es linealmente independiente si y sólo si $\{v_1,v_2,…,v_n\}$ es linealmente independiente para toda $n\geq 1$.

Más adelante…

Veremos un nuevo concepto: Suma y suma directa de subespacios vectoriales.
¿Qué es? ¿Qué estructura tiene? ¿Dónde vive? ¿Qué relación tiene la suma de dos subespacios con sus uniones?

Entradas relacionadas

1.8. CONJUNTOS LINEALMENTE (IN)DEPENDIENTES Y CONJUNTOS GENERADORES: relación entre sí

Por Jennyfer Paulina Bennetts Castillo

Deja un comentario

Lema (Dependencia lineal): Sean $V$ un $K$ – espacio vectorial y $v_1,v_2,…,v_m$ una lista de vectores en $V$. Si $v_1,v_2,…,v_m$ es una lista l.d. y $v_1\not=\theta_V$, entonces existe $j\in\{2,3,…,m\}$ tal que
a) $v_j\in\langle\{v_1,v_2,…,v_{j-1}\}\rangle$ y
b) $\langle\{v_1,v_2,…,\widehat{v_j},…,v_m\}\rangle =\langle\{v_1,v_2,…,v_m\}\rangle$

Nota: $\langle\{v_1,v_2,…,v_{j-1},v_{j+1},…,v_m\}\rangle$ lo denotamos por $\langle v_1,v_2,…,\widehat{v_j},…,v_m\rangle$

Demostración: Sean $V$ un $K$ – espacio vectorial y $v_1,v_2,…,v_m$ una lista l.d. con $v_1\not=\theta_V$.

(*) Como la lista es l.d., entonces existen $\lambda_1,\lambda_2,…,\lambda_m\in K$ no todos nulos tales que $\lambda_1v_1+\lambda_2v_2+…+\lambda_mv_m=\theta_V$.

a) De (*) observemos que por no ser todos nulos, tenemos dos casos:

Caso 1. Únicamente $\lambda_1\not=0_K$.
Así, $\theta_V=\lambda_1v_1+\lambda_2v_2+…+\lambda_mv_m$$=\lambda_1v_1+0_Kv_2+…+0_Kv_m$$=\lambda_1v_1+\theta_V+…+\theta_V=\lambda_1v_1$.
De donde, $\lambda_1v_1=\theta_V$ con $\lambda_1\not=0_K$ y $v_1\not=\theta_V$.
Por lo tanto, este caso no es posible.

Caso 2. Existe al menos un $\lambda_j\not=0_K$ con $j\in\{2,3,…,m\}$.
Consideremos $j=m\acute{a}x\{i\in\{2,3,…,m\}|\lambda_i\not=0_K\}$
Entonces $\lambda_{j+1}v_{j+1}+…+\lambda_mv_m=0_Kv_{j+1}+…+0_Kv_m$$=\theta_V+…+\theta_V=\theta_V$ y además, existe el inverso multiplicativo de $\lambda_j.$
De lo anterior tenemos que $\theta_V=\lambda_1v_1+\lambda_2v_2+…+\lambda_mv_m$$=\lambda_1v_1+\lambda_2v_2+…+\lambda_jv_j+\theta_V$$=\lambda_1v_1\lambda_2v_2+…+\lambda_jv_j.$
Así, $\lambda_1v_1+…+\lambda_jv_j=\theta_V$, por lo cual $\lambda_jv_j=-\lambda_1v_1-\lambda_2v_2…-\lambda_{j-1}v_{j-1},$
entonces

$\begin{array}{ll}v_j&=\lambda_j^{-1}(-\lambda_1v_1-\lambda_2v_2…-\lambda_{j-1}v_{j-1})\\&=(-\lambda_j^{-1}\lambda_1)v_1+(-\lambda_j^{-1}\lambda_2)v_2+…+(-\lambda_j^{-1}\lambda_{j-1})v_{j-1}\in\langle v_1,v_2,…,v_{j-1}\rangle\end{array}$

$\therefore v_j\in\langle v_1,v_2,…,v_{j-1}\rangle$

b) Veamos que se cumplen las dos contenciones entre los subconjuntos deseados, contemplando que la $j$ para este inciso debe ser la misma que en el inciso anterior.

En primer lugar:
Tenemos que $\{v_1,v_2,…,\widehat{v_j},…,v_m\}\subseteq \{v_1,v_2,…,v_j,…,v_m\}\subseteq\langle v_1,v_2,…,v_j,…,v_m\rangle$ y este último subconjunto es un subespacio de $V$.
Además, sabemos que si $S\subseteq W\subseteq V$ con $W$ un subespacio vectorial, entonces $\langle S\rangle\subseteq W$.
$\therefore\langle v_1,v_2,…,\widehat{v_j},…,v_m\rangle\subseteq\langle v_1,v_2,…,v_j,…,v_m\rangle$.

En segundo lugar:
Si $w\in\langle v_1,v_2,…v_j,…,v_m\rangle$, entonces existen $\mu_1,\mu_2,…,\mu_j,…,\mu_m\in K$ tales que $w=\mu_1v_1+\mu_2v_2+…+\mu_jv_j+…+\mu_mv_m$.
Sabemos que $v_j=(-\lambda_j^{-1}\lambda_1)v_1+(-\lambda_j^{-1}\lambda_2)v_2+…+(-\lambda_j^{-1}\lambda_{j-1})v_{j-1}$.
De donde,

\begin{array}{ll}w&=\mu_1v_1+\mu_2v_2+…+\mu_{j-1}v_{j-1}+\\ &\mu_j[(-\lambda_j^{-1}\lambda_1)v_1+(-\lambda_j^{-1}\lambda_2)v_2+…+(-\lambda_j^{-1}\lambda_{j-1})v_{j-1}]+\\ &\mu_{j+1}v_{j+1}…+\mu_mv_m\\ &=(\mu_1-\mu_j\lambda_j^{-1}\lambda_1)v_1+(\mu_2-\mu_j\lambda_j^{-1}\lambda_2)v_2+\\ &…+(\mu_{j-1}-\mu_j\lambda_j^{-1}\lambda_{j-1})v_{j-1}+\mu_{j+1}v_{j+1}+…+\mu_mv_m\\ &\in\langle v_1,v_2,…,\widehat{v_j},…,v_m\rangle\end{array}
Así, $w\in\langle v_1,v_2,…,\widehat{v_j},…,v_m\rangle$.
$\therefore \langle v_1,v_2,…,v_j,…,v_m\rangle\subseteq\langle v_1,v_2,…,\widehat{v_j},…,v_m\rangle .$

Teorema: Sea $V$ un $K$ – espacio vectorial. Si $v_1,v_2,…,v_m$ es una lista l.i. de vectores en $V$ con $m\in\mathbb{N}$, entonces todo conjunto generador de $V$ tiene al menos $m$ elementos.

Demostración: Sea $V$ un $K$ – espacio vectorial.
Sea $v_1,v_2,…,v_m$ es una lista l.i. de vectores en $V$, llamémosle $L$ a esta lista.
Sea $S$ tal que $\langle S\rangle = V$.

Caso 1. $S$ es infinito.
Entonces $S$ tiene más de $m$ elementos.

Caso 2. $S$ es finito.
Digamos que $S=\{w_1,w_2,…,w_k\}$ y probemos que $m\leq k$.

Observemos que como $L$ es una lista l.i. de vectores en $V$, entonces para cada $i\in\{1,2,…,m\}$ tenemos que $v_i\not=\theta_V$.

(1) Como $ v_1\in V=\langle S\rangle$, entonces $v_1,w_1,w_2,…,w_k$ es una lista l.d.
Dado que $v_1\not= \theta_V$, por el lema podemos concluir que existe $j_1\in\{1,2,…,k\}$ tal que $\langle \{v_1,w_1,w_2,…,w_k\}\setminus\{w_{j_1}\}\rangle =\langle v_1,w_1,w_2,…,w_k\rangle =V.$

(2) Como $ v_2\in V=\langle \{v_1,w_1,w_2,…,w_k\}\setminus\{w_{j_1}\}\rangle$, entonces $v_2,v_1,w_1,w_2,…,\widehat{w_{j_1}},…,w_k$ es una lista l.d.
Dado que con $v_2\not= \theta_V$, por el lema podemos concluir que algún vector $v_1,w_1,w_2,…,\widehat{w_{j_1}},…,w_k$ es combinación lineal de los vectores que le anteceden en la lista $v_2,v_1,w_1,w_2,…,\widehat{w_{j_1}},…,w_k$, pero sabemos que $L$ es l.i., por lo que $v_2$ no puede ser combinación lineal de $v_1$. Así, existe algún vector $w_1,w_2,…,\widehat{w_{j_1}},…,w_k$, digamos $w_{j_2}$ con $j_2\in\{1,2,…,k\}\setminus\{j_1\}$, que es combinación lineal de los vectores que le anteceden en la lista $v_2,v_1,w_1,w_2,…,\widehat{w_{j_1}},…,w_{j_k}$, y tal que $\langle \{v_2,v_1,w_1,w_2,…,w_k\}\setminus\{w_{j_1},w_{j_2}\}\rangle$$=\langle \{v_2,v_1,w_1,w_2,…,w_k\}\setminus\{w_{j_1}\}\rangle =V.$

Continuando de este modo, en cada paso quitamos un vector $w_{j_t}$ del conjunto generador, y lo sustituimos por $v_t$, obteniendo de esta manera un nuevo conjunto generador. Observemos entonces que después de $t$ pasos hemos quitado $t$ vectores de $S$, y los hemos sustituido por $v_t,\dots ,v_2,v_1$.

Veamos que $k\geq m$. Supongamos por reducción al absurdo que $k< m$.

Continuando con el proceso anterior, después de $k$ pasos hemos quitado $k$ vectores de $S$, $w_{j_1},w_{j_2},…,w_{j_k}$ que de hecho son precisamente $w_1,w_2,…,w_k$ sólo que quizás en otro orden, y los hemos sustituido por $v_k,\dots ,v_2,v_1$. Tenemos además que:
$V=\langle \{v_{k-1},v_{k-2},…,v_2,v_1,w_1,w_2,…,w_k\}-\{w_{j_1},w_{j_2},…,w_{j_k}\}\rangle$$=\langle \{v_{k-1},v_{k-2},…,v_2,v_1\}\rangle$
Pero si $V=\langle \{v_{k-1},…,v_2,v_1\}\rangle$, entonces $v_k\in \langle \{v_{k-1},…,v_2,v_1\}\rangle$ y por lo tanto, $v_1,v_2,…,v_k$ es l.d.
Entonces $v_1,v_2,…,v_m$ es l.d., lo cual contradice nuestra hipótesis.

Por lo tanto, $m\leq k$.

Corolario: Sea $V$ un $K$-espacio vectorial. Si existe $S$ un subconjunto finito de $V$ generador con $k$ elementos, entonces todo conjunto linealmente independiente es finito y tiene a lo más $k$ elementos.
En consecuencia, no existen conjuntos infinitos l.i. en $V$.

Demostración: Sea $V$ un $K$ – espacio vectorial.
Sea $S\subseteq V$ finito con $k$ elementos tal que $\langle S\rangle =V$.
Sea $T\subseteq V$ un subconjunto l.i. Supongamos por reducción al absurdo que $T$ es infinito, consideremos entonces $\hat{T}$ un subconjunto de $T$ con $k+1$ elementos. Tenemos que $\hat{T}$ es un conjunto l.i. con $k+1$ elementos, y $S$ es un conjunto generador con $k$ elementos, lo que contradice el teorema anterior. Concluimos entonces que $T$ debe ser finito.
Nuevamente por el teorema anterior se cumple que $|T|\leq |S|$, y como $|S|=k$ entonces $|T|\leq k$.

Tarea Moral

  1. Demuestra que, dado $V$ un $K$ – espacio vectorial con $K$ un campo, sólo existe un subconjunto $S$ unitario linealmente dependiente y exhíbelo.
  2. Sea $S=\{v_1,v_2,…,v_m\}\subseteq V.$
    Demuestra que son equivalentes:
    • $S$ es l.d.
    • Existe $v_j\in S$ tal que $v_j\in \langle S-{v_j}\rangle$
  3. Recordando que $\{e_1,e_2,e_3\}$ genera a $\mathbb{R}^3$ y el Teorema de esta entrada sabemos que cualquier conjunto de solo $1$ o $2$ elementos, no podrá generar a $\mathbb{R}^3$.
    • Describe qué subespacio(s) de $\mathbb{R}^3$ se puede(n) generar con un $S\subseteq\mathbb{R}^3$ arbitrario si $|S|=1$.
    • Describe qué subespacio(s) de $\mathbb{R}^3$ se puede(n) generar con un $S\subseteq\mathbb{R}^3$ arbitrario si $|S|=2$.

Más adelante…

Ahora que sabemos la relación de cardinalidad que existe entre los conjuntos linealmente independientes y los conjuntos generadores, nos damos cuenta de que, dicho muy informalmente, los conjuntos generadores de un espacio vectorial $V$ tienen una cardinalidad mayor o igual a los l.i. en $V$.
Nos enfocaremos en aquellos conjuntos que son generadores del espacio vectorial $V$ al que pertenecen y linealmente independientes. Veremos algunas propiedades de sus cardinalidades.

Entradas relacionadas