Ecuaciones Diferenciales I: Soluciones a las ecuaciones diferenciales

Por Omar González Franco

Deja un comentario

Las matemáticas son la puerta y la llave a la ciencia.
– Roger Bacon

Introducción

En la entrada anterior vimos lo que son las ecuaciones diferenciales (ED), en particular las ecuaciones diferenciales ordinarias (EDO) con las que trabajaremos a lo largo del curso. Vimos también como clasificarlas por tipo, orden y linealidad.

Mencionábamos que lo que nos interesa al tener una ecuación diferencial es hallar la función involucrada que depende de la variable independiente, hallar dicha función significa que hemos resuelto la ecuación diferencial y a la función encontrada la llamaremos función solución, o simplemente solución. Antes de aprender a resolver ecuaciones diferenciales, en esta entrada estudiaremos las propiedades mismas de una solución.

Soluciones de ecuaciones diferenciales

Una función $f$ es solución si para una ecuación diferencial ordinaria de $n$-ésimo orden cumple lo siguiente.

$$F(x, f(x), f^{\prime}(x), \cdots, f^{(n)}(x)) = 0 \tag{1} \label{1}$$

para toda $x \in \delta$. En este curso supondremos que una solución $f$ es una función con valores reales, es decir, $\delta \in \mathbb{R}$.

El intervalo de solución $\delta$ también es conocido como intervalo de definición, intervalo de existencia, intervalo de validez o dominio de la solución y puede ser un intervalo abierto $(a, b)$, un intervalo cerrado $[a, b]$, un intervalo infinito $(a, \infty)$, etcétera.

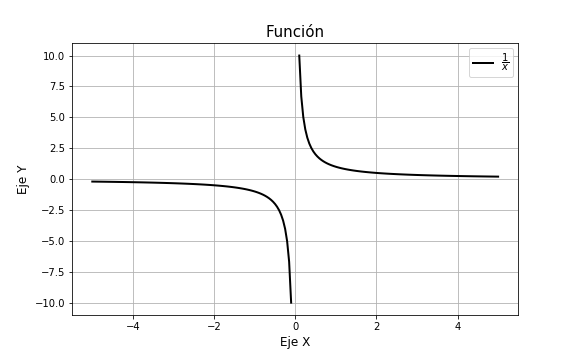
Ejemplo: Verificar que la función

$$f(x) = y = \dfrac{1}{x}$$

es solución de la ecuación diferencial

$$x \dfrac{dy}{dx} + y = 0$$

Solución: Consideremos la función $y = \dfrac{1}{x}$ para toda $x \neq 0$. La derivada de esta función es

$$\dfrac{dy}{dx} = -\dfrac{1}{x^{2}}$$

para toda $x \neq 0$. Sustituyamos estas funciones en la ecuación diferencial y verifiquemos que se satisface la igualdad.

\begin{align*}
x \dfrac{dy}{dx} + y &= x \left( -\dfrac{1}{x^{2}} \right) + \dfrac{1}{x} \\
&= -\dfrac{1}{x} + \dfrac{1}{x} \\
&= 0
\end{align*}

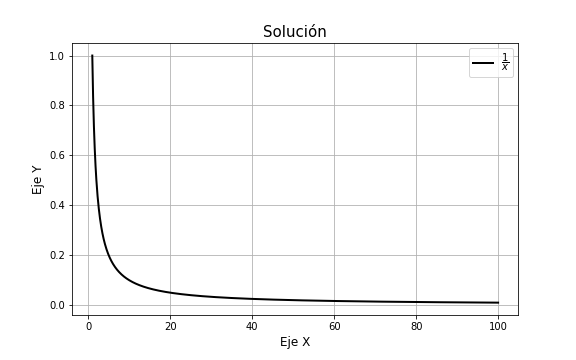
Como hemos recuperado la ecuación diferencial decimos que en efecto $y = \dfrac{1}{x}$ es solución. Observemos que la solución no está definida para $x = 0$, sin embargo, al ser solución significa que es una función definida en un intervalo $\delta$ en el que es derivable y satisface la ecuación, esto indica que $y$ es solución en cualquier intervalo que no contenga al $0$.

Como observación notemos que la función $f(x) = y = 0$ y la derivada correspondiente $\dfrac{dy}{dx} = 0$, también satisfacen la misma ecuación diferencial, entonces decimos que dicha ecuación diferencial tiene solución trivial.

Como podemos notar, tanto la función $y = \dfrac{1}{x}$, como la función constante $y = 0$, son solución de la misma ecuación diferencial, ¡esto significa que una ecuación diferencial puede tener más de una solución!.

$\square$

Curva solución de una ecuación diferencial

Las soluciones de las ecuaciones diferenciales ordinarias de una variable dependiente son funciones de una variable independiente, por lo tanto se pueden graficar en el plano $XY$. De acuerdo a la definición de solución, y al ejemplo anterior, es importante hacer una distinción entre el dominio de una función (los valores para los cuales la función está definida) y un intervalo de solución.

Si $f(x)$ es solución de una ecuación diferencial, entonces $f(x)$ es derivable, lo que también significa que es continua en su intervalo de definición $\delta$, esto es necesario para ser solución y no siempre va a ocurrir para todo el dominio de la función $f$. Puede haber diferencia entre la gráfica de la función $f(x)$ y la gráfica de la solución $f(x)$. En el ejemplo anterior el dominio de la función $y = \dfrac{1}{x}$ es $D = \mathbb{R} -\{0\}$, mientras que el intervalo de solución es cualquier intervalo que no contenga al $0$, por ejemplo $\delta = (-\infty, -1)$, $\delta = (5, 100)$ o $\delta = (1, \infty)$, etcétera. El intervalo de solución no necesita ser igual al dominio de la función $f(x)$.

Gráfica de la función $y = \dfrac{1}{x}$.
Curva solución definida por $y = \dfrac{1}{x}$ en el intervalo $\delta = (1, 100)$.

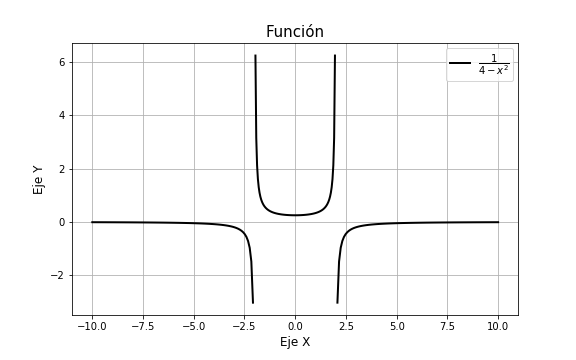
Ejemplo: Comprobar que la función

$$f(x) = y = \dfrac{1}{4 -x^{2}}$$

es solución de la ecuación diferencial

$$\dfrac{dy}{dx} = 2xy^{2}$$

y determinar al menos un intervalo de solución.

Solución: La función dada es

$$y = \dfrac{1}{4 -x^{2}}$$

La derivada de esta función es

$$\dfrac{dy}{dx} = \dfrac{2x}{(4 -x^{2})^{2}}$$

Esta ecuación se puede reescribir de la siguiente manera:

$$\dfrac{dy}{dx} = \dfrac{2x}{(4 -x^{2})^{2}} = 2x \dfrac{1}{(4 -x^{2})^{2}} = 2x \left(\dfrac{1}{4 -x^{2}}\right) ^{2} = 2xy^{2}$$

Esto es,

$$\dfrac{dy}{dx} = 2xy^{2}$$

Efectivamente, la función dada es solución de la ecuación diferencial.

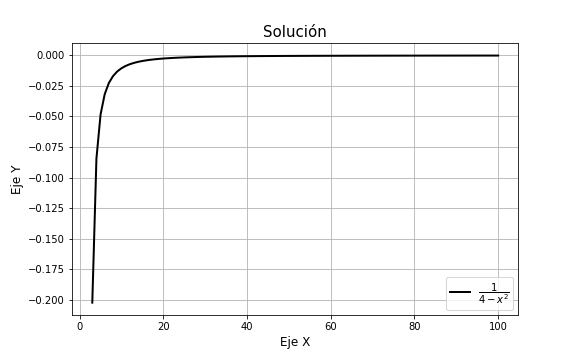
Ahora debemos determinar un intervalo de solución, para hacerlo podemos comenzar por determinar el dominio de la función. La función $y = \dfrac{1}{4 -x^{2}}$ no está definida cuando $4 = x^{2}$, es decir, cuando $x = 2$ o $x = -2$, por lo tanto el dominio de la función es

$$D = (-\infty, -2) \cup (-2, 2) \cup (2, \infty)$$

Gráfica de la función $\dfrac{1}{4 -x^{2}}$.

El intervalo de solución es cualquiera que no contenga al $-2$ ni al $2$, el ejercicio nos pide determinar al menos un intervalo de solución, podemos entonces considerar el intervalo abierto$\delta = (2, \infty)$ como el intervalo de solución.

Curva solución en el intervalo $ \delta = (2, \infty)$.

$\square$

Soluciones explícitas y soluciones implícitas

Recordemos que una función es explícita si se puede escribir como $y = f(x)$, es decir, si la variable dependiente se puede escribir en términos de la variable independiente, mientras que una función implícita esta dada por la forma $f(x, y) = 0$. Ya sabemos que las soluciones de las ecuaciones diferenciales son funciones por lo que estos conceptos se pueden extender a estas soluciones.

Una solución explicita $y = f(x)$ la podemos manejar, evaluar y derivar usando las reglas usuales. Más adelante nos encontraremos con soluciones en las que no es factible obtener la forma explicita y tendremos que hallar al menos una forma implícita de la solución.

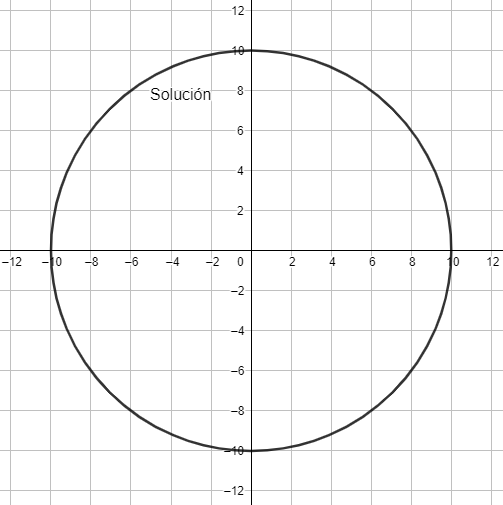
Ejemplo: Verificar que la relación

$$x^{2} + y^{2} = 100$$

es una solución implícita de la ecuación diferencial

$$\dfrac{dy}{dx} = -\dfrac{x}{y}$$

y determinar las soluciones explícitas.

Solución: Primero notemos que, de acuerdo a la definición de solución implícita, la relación dada se puede escribir como

$$G(x, y) = x^{2} + y^{2} -100 = 0$$

Derivemos esta ecuación implícitamente.

\begin{align*}
\dfrac{d}{dx} \left( x^{2} + y^{2} -100 \right) &= \dfrac{d}{dx} (0) \\
\dfrac{d}{dx} (x^{2}) + \dfrac{d}{dx} (y^{2}) -\dfrac{d}{dx} (100) &= \dfrac{d}{dx} (0) \\
2x + \dfrac{d}{dy}y^{2}\dfrac{dy}{dx} -0 &= 0 \\
2x + 2y \dfrac{dy}{dx} &= 0
\end{align*}

De la última relación despejamos $\dfrac{dy}{dx}$ obteniendo así la ecuación diferencial $\dfrac{dy}{dx} = -\dfrac{x}{y}$. Por lo tanto $x^{2} + y^{2} = 100$ es una solución implícita. El intervalo de solución es $\delta = (-10, 10)$.

Gráfica de la solución implícita $x^{2} + y^{2} = 100$

La relación $x^{2} + y^{2} = 100$ es una solución implícita ya que no es de la forma $y = f(x)$, sin embargo se puede obtener la solución explícita con sólo despejar a $y$.

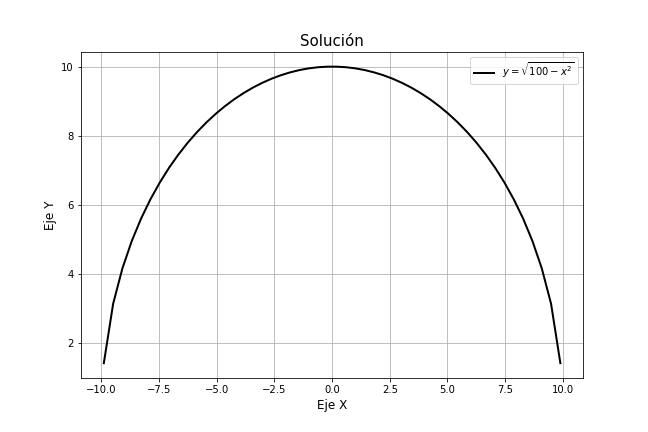
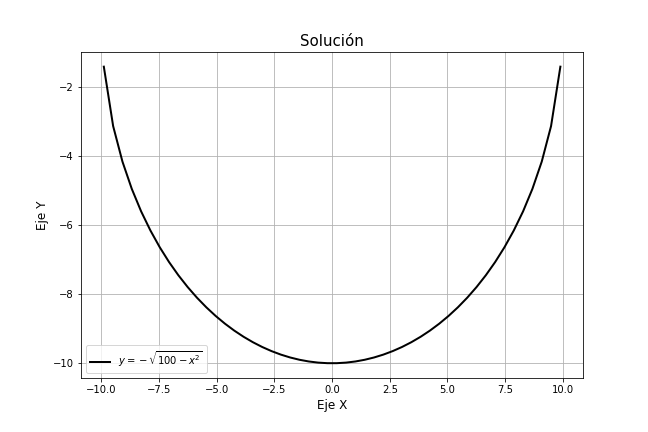
$$y = \pm \sqrt{100 -x^{2}}$$

Pero notemos que ahora tenemos dos soluciones.

$$y_{1} = \sqrt{100 -x^{2}} \hspace{1cm} y \hspace{1cm} y_{2} = -\sqrt{100 -x^{2}}$$

Estas funciones satisfacen respectivamente $x^{2} + y_{1}^{2} = 100$ y $x^{2} + y_{2}^{2} = 100$, además de la ecuación diferencial. Por lo tanto, ambas son soluciones explícitas en el mismo intervalo $\delta = (-10, 10)$ .

En las siguientes gráficas se muestran las curvas solución de cada solución explícita.

Curva solución $y_{1} = \sqrt{100 -x^{2}}$.
Curva solución $y_{2} = -\sqrt{100 -x^{2}}$.

Observamos que cada solución explícita corresponde a un tramo de la solución implícita y ambas forman dicha solución.

$\square$

Con este ejemplo vemos que es importante entender las circunstancias del problema para poder determinar la solución adecuada de la ecuación diferencial. En este caso la solución implícita involucra a las dos soluciones explícitas y nos permite conocer más acerca del problema. Cabe mencionar que no siempre será necesario o posible obtener la solución explícita, en el ejemplo fue sencillo obtener la función $y$ en términos de $x$, pero no siempre será el caso y obtener la solución implícita $G(x, y) = 0$ será suficiente.

Otro punto importante a observar es que al derivar la constante $100$ se obtiene un cero, eso significa que, independientemente del valor de la constante, al derivar siempre vamos a obtener un cero, considerando esto, la forma más general de expresar la solución anterior es

$$x^{2} + y^{2} = c$$

donde $c$ es una constante arbitraria. Si derivamos obtendremos nuevamente la ecuación diferencial

$$\dfrac{dy}{dx} = -\dfrac{x}{y}$$

Debido a que hay una infinidad de valores que puede tomar $c$ (en el campo de los reales), entonces significa que la ecuación diferencial ¡tiene infinitas soluciones!.

En efecto, una ecuación diferencial puede tener una infinidad de soluciones, así que dependerá del problema o de las condiciones, la solución que debamos considerar. A pesar de que una ecuación diferencial puede tener infinitas soluciones es posible encontrar un solución general que considere todas las posibilidades.

Familias de soluciones

Al resolver una ecuación diferencial de primer orden

$$F(x, y , y^{\prime}) = 0 \label{2} \tag{2}$$

normalmente se obtiene una solución que contiene una sola constante arbitraria $c$.

Este concepto se puede extender a una ecuación diferencial de orden $n$

$$F(x, y, y^{\prime}, \cdots, y^{(n)}) = 0 \label{4} \tag{4}$$

en este caso la solución

$$G(x, y, c_{1}, c_{2}, \cdots, c_{n}) = 0 \label{5} \tag{5}$$

corresponde a una familia de soluciones $n$-paramétrica.

En el ejemplo que vimos, la relación

$$x^{2} + y^{2} = c$$

corresponde a la solución general de la ecuación diferencial

$$\dfrac{dy}{dx} = – \dfrac{x}{y}$$

mientras que la relación

$$x^{2} + y^{2} = 100$$

corresponde a una posible solución, en este caso decimos que es una solución particular.

Concluyamos esta entrada con un último ejemplo.

Ejemplo: Mostrar que la función

$$y(x) = 3x^{2} + c_{1}x + c_{2}$$

con $c_{1}$ y $c_{2}$ constantes arbitrarias, es solución general de la ecuación diferencial

$$\dfrac{d^{2}y}{dx^{2}} = 6$$

Solución: Derivemos dos veces la función dada y veamos si obtenemos la ecuación diferencial. Derivando una vez obtenemos lo siguiente.

\begin{align*}
\dfrac{dy}{dx} &= \dfrac{d}{dx}(3x^{2}) + \dfrac{d}{dx}(c_{1}x) + \dfrac{d}{dx}(c_{2}) \\
&= 2(3x) + c_{1} + 0 \\
&= 6x + c_{1}
\end{align*}

La primer derivada es

$$ \dfrac{dy}{dx} = 6x + c_{1}$$

Derivemos nuevamente esta función.

\begin{align*}
\dfrac{d^{2}y}{dx^{2}} &= \dfrac{d}{dx}(6x) + \dfrac{d}{dx}(c_{1}) \\
&= 6 + 0 \\
&= 6
\end{align*}

Efectivamente

$$\dfrac{d^{2}y}{dx^{2}} = 6$$

Por lo tanto, la función

$$y(x) = 3x^{2} + c_{1}x + c_{2}$$

es solución de la ecuación diferencial. Sabemos que es la solución general porque satisface a la ecuación diferencial de segundo orden y contiene dos constantes arbitrarias. Una posible solución particular sería la función

$$y(x) = 3x^{2} + 10x -5$$

o

$$y(x) = 3x^{2} -0.2x + 155$$

etcétera. En este caso no hay restricción de valores para $x$ por lo que el intervalo de solución puede ser cualquiera en $\mathbb{R}$ o bien $\delta = \mathbb{R}$

$\square$

Hemos concluido la entrada.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

  1. Comprobar que las siguientes funciones $y = f(x)$ son solución de la correspondiente ecuación diferencial y establecer un adecuado intervalo de solución $\delta$.
  • $2 \dfrac{dy}{dx} + y = 0$; $\hspace{1cm}$ $y = e^{-x/2}$
  • $\dfrac{d^{2}y}{dx^{2}} -6\dfrac{dy}{dx} + 13y = 0$; $\hspace{1cm}$ $y = e^{3x} \cos{(2x)}$
  • $(y -x) \dfrac{dy}{dx} = y -x + 8$; $\hspace{1cm}$ $y = x + 4\sqrt{x + 2}$
  1. Comprobar que las siguientes familias de soluciones son solución de la correspondiente ecuación diferencial y establecer un adecuado intervalo de solución $\delta$.
  • $\dfrac{dy}{dx} = y(1 -y)$; $\hspace{1cm}$ $y = \dfrac{c_{1}e^{x}}{1 + c_{1}e^{x}}$
  • $\dfrac{d^{2}y}{dx^{2}} -4\dfrac{dy}{dx} + 4y = 0$; $\hspace{1cm}$ $y = c_{1}e^{2x} + c_{2}xe^{2x}$

Más adelante…

Ahora ya conocemos algunas características de las funciones solución de las ecuaciones diferenciales ordinarias. Sabemos que existen soluciones generales, o familias de soluciones, de una ecuación diferencial, sin embargo en algunas situaciones nos veremos en la necesidad de conocer una solución particular debido a condiciones prescritas según el problema que estemos estudiando, a estas condiciones prescritas las llamamos condiciones iniciales (o valores iniciales) y serán las que establezcan una solución particular que nos sirva para modelar nuestro problema.

En la siguiente entrada estudiaremos soluciones con condiciones iniciales y revisaremos algunos problemas del mundo real que involucran ecuaciones diferenciales ordinarias.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Álgebra Superior I: Problemas de condicionales y cuantificadores

Por Guillermo Oswaldo Cota Martínez

Deja un comentario

Introducción

En esta entrada resolveremos problemas de temas vistos en entradas anteriores. Haremos algunos ejemplos relacionados con los conectores condicionales que vimos en una entrada anterior: la implicación y la doble implicación. También veremos algunos de cuantificadores lógicos.

Problemas resueltos

Problema. Si $P$ y $R$ son verdaderas y $Q$ es falsa, di si la siguiente proposición es verdadera o falsa: $$(P \lor R) \Rightarrow \neg(Q \land R).$$

Solución. Haremos una tabla de verdad pero únicamente con los valores que nos dan, es decir, no vamos a hacer la tabla para todos los casos, sino únicamente los que nos interesan en este momento:

$P$$Q$$R$$P \lor R$ $Q \land R$$\neg (Q \land R)$$(P \lor R) \Rightarrow \neg(Q \land R)$
$1$$0$$1$  $1$ $0$  $1$   $1$

Por lo tanto la proposición es verdadera para los valores de verdad dados.

$\square$

Problema. Di si las siguientes proposiciones sobre los números enteros son verdaderas o no:

  1. $(3+1=4) \Rightarrow (0<10)$
  2. $(4=5) \Leftrightarrow (9+1=10)$
  3. $((6<7) \lor (3^2=10)) \Rightarrow (12<12^2)$
  4. $((-1<1) \land (1<-1)) \Leftrightarrow ((13-1=12-1+1)\Rightarrow (1+1<2))$

Solución.

Vamos a hacer algunas verificaciones sobre cada una de las proposiciones para encontrar su valor de verdad:

  • $(3+1=4) \Rightarrow (0<10)$

Como $3+1=4$ es verdadera y $0<10$ es verdadera también, entonces la proposición es verdadera.

  • $(4=5) \Leftrightarrow (9+1=10)$

Recordemos que la doble condicional es verdadera si ambas proposiciones tienen el mismo valor de verdad. Por un lado no es cierto que $4=5$ mientras que sí es verdad que $9+1=10$. Por lo tanto la proposición es falsa.

  • $((6<7) \lor (3^2=10)) \Rightarrow (12<12^2)$

Vamos a ver la proposición por partes. Primero veamos que $((6<7) \lor (3^2=10))$ es una disyunción verdadera pues una de las proposiciones que la componen, $6<7$, lo es. Como $12<12^2$ es verdad, entonces la implicación tiene antecedente y subsecuente verdaderos y por lo tanto es verdadera.

  • $((-1<1) \land (1<-1)) \Leftrightarrow ((13-1=12-1+1)\Rightarrow (1+1<2))$

De nuevo vamos a dividir la proposición en sus partes, $(-1<1) \land (1<-1)$ y $(13-1=12-1+1)\Rightarrow (1+1<2)$. Primero notemos que $(-1<1) \land (1<-1)$ es falsa, pues no es cierto que $1<-1$.

Ahora, veamos cómo es $(13-1=12-1+1)\Rightarrow (1+1<2)$. Nota que $12=13-1$ y $12=12-1+1$, entonces $13-1=12-1+1$. Entonces esta primera parte es verdad, mientras que $1+1=2$ pero no es cierto que $2<2$. Así que es falso que $1+1<2$. Entonces $(13-1=12-1+1)\Rightarrow (1+1<2)$ es falso.

Como $(-1<1) \land (1<-1)$, $(13-1=12-1+1)\Rightarrow (1+1<2)$ son ambas falsas, entonces $((-1<1) \land (1<-1)) \Leftrightarrow ((13-1=12-1+1)\Rightarrow (1+1<2))$ es verdadero.

Nota: En este tipo de ejercicios, ¿viste cómo se dieron las argumentaciones de las proposiciones en cada caso? El secreto aquí fue «desarmar» las proposiciones en partes más pequeñas. Esto lo hacemos pues recuerda que los conectores son binarios, esto significa que su valor de verdad depende del valor de verdad de las dos proposiciones que conectan.

Así, para ver cuál es el valor de verdad de $((6<7) \lor (3^2=10)) \Rightarrow (12<12^2)$, lo que hicimos fue deshacerlo en sus partes. Una parte $A$ fue $(6<7) \lor (3^2=10)$ y la otra parte $B$ fue $12<12^2$. Entonces bastaba con verificar cuáles eran los valores de verdad de $A$ y $B$. Para ello, volvimos a «desarmar» a $A$ en sus partes «atómicas». Es decir, desarmamos $(6<7) \lor (3^2=10)$ en $6<7$ y $3^2=10$ y estudiamos el valor de verdad de cada uno de ellos. Usualmente este tipo de pensamiento de «desarmar un problema en sus partes» te ayudará a verificar o demostrar cosas más adelante.

Problema. Sean $P(x)$, $Q(x)$ y $R(x)$ los siguientes predicados:

  • $P(x): x \leq 4$
  • $Q(x): x +1$ es par.
  • $R(x): x> 0$

Si nuestro universo de discurso son los números enteros, ¿cuáles son los valores de verdad de las siguientes proposiciones?

  1. $P(1)$
  2. $P(1) \Rightarrow Q(1)$
  3. $P(0) \Rightarrow (R(5) \Rightarrow Q(0))$
  4. $R(-1) \lor P(2)$
  5. $\neg R(-2) \lor P(-2)$

Solución.

1.$P(1)$

Es verdadera, pues $1 \leq 4$.

2. $P(1) \Rightarrow Q(1)$

Como $P(1)$ es verdadera y además $1+1=2$ es par, entonces la proposición es verdadera.

3. $P(0) \Rightarrow (R(5) \Rightarrow Q(0))$

Vamos a dividir la proposición en partes. Primero notemos que $P(0)$ es verdad. Mientras que $R(5) \Rightarrow Q(0)$ es falsa, ya que es cierto que $5>0$ pero es falso que $0+1$ sea par. Entonces la proposición es falsa.

4. $R(-1) \lor P(2)$

Como $R(-1)$ es falsa pero $P(2)$ es verdad, entonces la proposición es verdadera.

5. $\neg R(-2) \lor P(-2)$

Como $-2<0$ es verdad, entonces $\neg R(-2)$ es falso, mientras que $-2<4$ es verdad. De esta manera la proposición es verdadera.

Problema. Considera los siguientes predicados:

  • $P(x): 2x>0$
  • $Q(x):x>0$
  • $R(x): x=20$
  • $T(x):x<0$

Determina la verdad o falsedad de las siguientes proposiciones, considerando que nuestro universo de discurso son los números enteros. Si la proposición no es verdadera, da un contraejemplo o explicación de ello.

  1. $\forall x(P(x) \Rightarrow Q(x))$
  2. $\exists x (Q(x) \land T(x))$
  3. $\forall x(R(x) \Rightarrow(Q(x))$
  4. $\exists ! x(R(x))$
  5. $ \nexists x (Q(x) \land P(x))$

Solución.

  • $\forall x(P(x) \Rightarrow Q(x))$

Nota que siempre que se cumple $2x>0$ entonces $x>0$ (más adelante demostrarás esto con toda formalidad, pero de momento lo daremos por cierto). Por lo tanto la proposición es verdadera.

  • $\exists x (Q(x) \land T(x))$

Para que esto sucediera, necesitaríamos la existencia de al menos un elemento $x$ que cumpla $0<x$ y $x>0$, es decir necesitaríamos un elemento que sea positivo y negativo a la vez, pero esto no es posible. Por lo tanto la proposición es falsa.

  • $\forall x(R(x) \Rightarrow(Q(x))$

Lo que nos dice esta proposición es «Para todo número entero $x$ que cumpla $x=20$ entonces $x>0$» o dicho de otra manera: «Si un número entero es igual a 20, entonces será positivo.» Lo cuál es correcto, pues si el número es distinto a 20, la implicación será correcta (recuerda la tabla de verdad de la implicación), mientras que el único caso en donde la hipótesis se cumple es cuando $x=20$ y claramente es un número que cumple $x>0$. Entonces la proposición es verdadera.

  • $\exists ! x(R(x))$

Esto nos quiere decir que existe un único número entero que sea igual a 20, e inmediatamente podemos saber que es verdadera, pero ¿A qué nos referiremos que un número sea igual a 20? Primero tendríamos que ponernos de acuerdo de qué significa la igualdad. Aunque ahora no lo haremos, piensa el cómo nos aseguraríamos de que es el único número entero que cumple esa propiedad ¿Qué pasaría si no fuera cierto?

  • $ \nexists x (Q(x) \land P(x))$

Lo que dice la proposición es que ningún número $x$ va a cumplir a la vez $x>0$ y $2x>0$, pero esto no es cierto, pues pensemos en $x=1$. Cumple $Q(x)$ ya que $1>0$ y cumple $P(x)$ porque $2*1=2>0$. Entonces podemos decir que es falso pues dimos un contraejemplo que contradijo la proposición.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Ecuaciones Diferenciales I – Videos: Campo de pendientes asociado a una ecuación diferencial, curvas integrales y método de las isoclinas

Por Eduardo Vera Rosales

Deja un comentario

Introducción

Hola, bienvenidos a una nueva entrada del curso de Ecuaciones Diferenciales I. En la entrada anterior definimos a las soluciones de una ecuación diferencial ordinaria. Así que ahora veremos un poco de la geometría de soluciones a ecuaciones diferenciales de primer orden, en particular de la forma \begin{align*}\frac{dy}{dt}=f(t,y(t)).\end{align*}

Comenzaremos asociando un campo de pendientes a una ecuación diferencial, definiremos posteriormente el concepto de curvas integrales, y estudiaremos la relación que existe con las soluciones a la ecuación asociada.

Posteriormente revisaremos el método de las isoclinas el cual sirve para encontrar y dibujar las soluciones a una ecuación diferencial usando las curvas de nivel de $\frac{dy}{dt}=f(t,y(t))$, vista como una función $f:\mathbb{R}^{2} \rightarrow \mathbb{R}$.

Manos a la obra!

Campo de pendientes asociado a una ecuación diferencial y relación con sus soluciones

En el primer video, vemos cómo asociar un campo de pendientes a una ecuación de la forma $\frac{dy}{dt}=f(t,y(t))$ y revisamos un par de ejemplos.

Una vez que asociamos un campo de pendientes, en los siguientes dos videos definimos a las curvas integrales y estudiamos la relación que guardan con las soluciones a la ecuación diferencial.

Método de las isoclinas

Estudiamos un método bastante sencillo, llamado de las isoclinas, para conocer el comportamiento de las soluciones a una ecuación diferencial, mediante las curvas de nivel de la función $f:\mathbb{R}^{2} \rightarrow \mathbb{R}$ que define a la ecuación y el campo de pendientes asociado que definimos en los videos de la sección anterior.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero te servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

  • Esboza el campo de pendientes asociado a la ecuación $\frac{dy}{dt}=y$.
  • Dibuja las curvas integrales del campo de pendientes asociado a la ecuación $\frac{dy}{dt}=y$.
  • Prueba que si $\phi: (a,b) \rightarrow \mathbb{R}$ es una curva integral del campo de pendientes asociado a la ecuación $\frac{dy}{dt}=f(t,y(t))$ entonces $\phi(t)$ es solución a la ecuación diferencial.
  • Esboza las soluciones de la ecuación $\frac{dy}{dt}=-\frac{t}{y}$, con base en la información obtenida en el segundo ejemplo del último video. Analiza qué sucede con los puntos sobre el eje $t$, ¿forman parte de alguna solución a la ecuación?
  • En el último video hablamos acerca de las ventajas del método de las isoclinas. ¿Cuáles son las desventajas de usar este método para encontrar las soluciones a una ecuación?
  • Utiliza el método de las isoclinas para encontrar las soluciones a la ecuación $\frac{dy}{dt}=\frac{y}{t}$.

Más adelante

En la próxima entrada continuaremos analizando soluciones de una ecuación diferencial de primer orden desde un punto de vista geométrico. En esta ocasión nos enfocaremos en el caso particular de las ecuaciones del tipo $\frac{dy}{dt}=f(y)$.

Para esto analizaremos los puntos de equilibrio de la función $f(y)$ y haremos un diagrama bastante sencillo de dibujar que nos servirá para hacer un esbozo de las soluciones a la ecuación.

Nos vemos en la próxima ocasión.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Cálculo Diferencial e Integral I: Idea intuitiva de límite de una función

Por Juan Manuel Naranjo Jurado

2 respuestas

Introducción

La definición de límite de una función suele ser uno de los conceptos más retadores dentro del cálculo y es por ello que, antes de entrar a su análisis formal, queremos dar una introducción con la finalidad de desarrollar la intuición necesaria para lograr el entendimiento de esta definición.

Idea intuitiva de límite de una función

Consideremos la función $f: \mathbb{R} \to \mathbb{R}$ tal que $f(x) = 10x$.

En la gráfica de la función $f(x) = 10x$, podemos observar que si $x$ toma valores cercanos a $2$, entonces $f(x)$ se aproxima a $20$. ¿Pero qué tanto es posible aproximar los valores de la función $f(x)$ a $20$?

Por ejemplo, ¿podemos encontrar un valor de $x$ distinto de $2$ tal que $f(x)$ esté a una distancia de $20$ menor que $12$ , es decir, $|f(x) – 20| < 12$?

Consideremos $x = 1$. De esta forma, $f(1) = 10$ y $|f(1) – 20| = |10 – 20| = 10 < 12$.

¿Podemos encontrar un valor de $x$ distinto de $2$ tal que $f(x)$ esté a una distancia de $20$ menor que $1$, es decir, $|f(x) – 20| < 1$?

Si tomamos $x=1.99$, se tiene que $|f(1.99) – 20| = |19.9 – 20| = 0.1 < 1$.

Hasta este momento, se han encontrado valores puntuales de $x$ que permiten que $f(x)$ se aproxime a $20$. Sin embargo, existen más valores de $x$ que lo pueden cumplir. Retomando la última aproximación deseada, podemos ver que $x=2.02$ también cumple el propósito, pues $|f(2.02) – 20| = |20.2- 20| = 0.2 < 1$. En realidad, es posible hallar todo un intervalo que lo cumpla.

Para poder obtener dicho intervalo, procedemos estableciendo la desigualdad deseada

\begin{gather*}
& |f(x) – 20| < 1. \\ \\
\Leftrightarrow & |10x – 20|< 1. \\ \\
\Leftrightarrow & \frac{|10x – 20|}{10}< \frac{1}{10}. \\ \\
\Leftrightarrow & |x – 2| < \frac{1}{10}.
\end{gather*}

Lo anterior indica que para que $f(x)$ esté a una distancia de $20$ menor que $1$, entonces $x$ debe estar a una distancia de $2$ menor que $\frac{1}{10}$.

¿Podemos encontrar un valor de $x$ distinto de $2$ tal que $f(x)$ esté a una distancia de $20$ menor que $\varepsilon > 0$, es decir, $|f(x) – 20| < \varepsilon$?

Análogamente, se obtiene que para que $|f(x)-20| < \varepsilon$, entonces $|x-2| < \frac{\varepsilon}{10}$. Generalizando más, podemos notar que para cualquier $x_0 \in \mathbb{R}$ se tiene que $|f(x)-10x_0| < \varepsilon$ con $x \neq x_0$, siempre que $|x-x_0| < \frac{\varepsilon}{10}.$

En la siguiente entrada se proporcionará la definición formal del límite. Sin embargo, de forma provisional para esta entrada, diremos que $L \in \mathbb{R}$ es el límite de la función $f$ en $x_0$ si la distancia entre $f(x)$ y $L$ es menor que un número $\varepsilon > 0$ elegido de antemano cuando $x$ se aproxima a $x_0$, pero es distinto de $x_0$.

Considerando lo anterior para nuestro ejemplo, se tiene que el límite de $f$ en $x_0 = 2$ es $L = 20$.

Usemos como segundo ejemplo la función $f: \mathbb{R} \to \mathbb{R}$ tal que $f(x) = x^2$.

Veremos que el límite de $f$ en $x_0 = 4$ es $L=16$. Para ello, notemos que

\begin{gather*}
& |f(x) – 16| < \varepsilon. \\
\Leftrightarrow & |x^2 – 16| < \varepsilon. \\
\Leftrightarrow & |(x-4)(x+4)| < \varepsilon. \\
\Leftrightarrow &|x-4||x+4| < \varepsilon.
\end{gather*}

A diferencia del caso anterior, parece que no es tan directo llegar a nuestro objetivo, pero notemos que particularmente podemos pedir que $|x-4| < 1$, entonces

\begin{gather*}
& -1< x-4 < 1. \\
\Leftrightarrow & 3 < x < 5. \\
\Leftrightarrow & 7 < x+4<9.
\end{gather*}

En resumen, si $|x-4|<1$, entonces $|x+4| < 9$. Lo cual implica que
$$|x^2 – 16| = |x-4||x+4| < 9|x-4|.$$
Si además restringimos la distancia de $x$ respecto a $4$ de tal manera que $|x-4| < \frac{\varepsilon}{9}$ y retomando la expresión anterior llegamos a lo siguiente:

\begin{gather*}
|x^2 – 16| = |x-4||x+4| < 9|x-4| < 9 \cdot \frac{\varepsilon}{9} = \varepsilon. \\
\therefore |x^2 – 16| < \varepsilon.
\end{gather*}

Esto siempre que $|x-4|$ sea menor que $1$ y $\frac{\varepsilon}{9}$, es decir, siempre que $|x-4| < min\{1, \frac{\varepsilon}{9} \}$.


De los dos ejemplos revisados en esta entrada, podemos notar que logramos que $f(x)$ se aproxime a $L$ con una distancia menor de épsilon cuando $x$ está lo suficientemente cerca de $x_0$. Para lograr esto último, acotamos $x-x_0$ en términos de un valor positivo que depende de $\varepsilon$ (para el primer ejemplo fue $\frac{\varepsilon}{5}$ y para el segundo $min\{1, \frac{\varepsilon}{9} \}$). Vale la pena entonces darle un nombre a este valor positivo: $\delta$.

Parafraseando: Logramos que $f$ se aproxime arbitrariamente, dado $\varepsilon > 0$, a $L$ cuando $x$ está lo suficientemente cerca, $\delta > 0$, de $x_0$.

Obtenemos así un indicio muy importante, para probar que $L$ es el límite de $f$ en $x_0$, habrá que dar un valor arbitrario fijo y positivo $\varepsilon > 0$ para el cual necesitaremos encontrar otro valor positivo, $\delta > 0$, tal que si $|x-x_0|<\delta$, entonces se cumpla que $|f(x)-L| < \varepsilon$. Adicionalmente, se pide que $x \neq x_0$, tal condición puede ser compactada de la siguiente forma $0 < |x-x_0| < \delta$, pues que la distancia entre $x$ y $x_0$ sea mayor que cero implica directamente que son distintos.

Antes de finalizar con esta entrada, es conveniente aclarar que no siempre tendremos funciones tan amigables en las cuales podamos evaluar directamente el valor de $x_0$ en $f$ para encontrar $L$. Incluso habrá ocasiones en las cuales no nos podamos aproximar de la manera en la que lo hicimos en estos ejemplos, pero por ahora no daremos muchos detalles extra al respecto, será tema para entradas posteriores.

Más adelante…

En la siguiente entrada daremos la definición formal de límite de una función y veremos varios ejemplos de funciones cuyo límite existe. Una vez dominemos la definición podremos incursionar en varias de sus propiedades y podremos tomar ventaja de estos conocimientos para tener una mayor comprensión sobre el comportamiento de diversas funciones de interés.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Para corroborar que la idea intuitiva de límite de una función se ha comprendido, se queda como ejercicio realizar un análisis similar al expuesto en esta entrada. Consideremos la función $f(x) = 4x^2$ definida para todo $x \in \mathbb{R}$. En este caso, tomaremos $x_0=3$ y $f(x_0) = 4(3)^2 =36.$

  • Grafica $f(x)$.
  • Encuentra un valor de $x$ tal que $|f(x)-36| < 30$.
  • Encuentra un valor de $x$ tal que $|f(x)-36| < 1$.
  • Encuentra un intervalo de $x$ alrededor de $x_0 = 3$ tal que $|f(x)-36| < \frac{1}{100}$.
  • Encuentra un intervalo de $x$ alrededor de $x_0 = 3$ tal que $|f(x)-36| < \varepsilon$, con $\varepsilon > 0$.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Cálculo Diferencial e Integral I: Sucesiones divergentes y sus propiedades

Por Juan Manuel Naranjo Jurado

Deja un comentario

Introducción

Anteriormente estuvimos revisando el concepto de sucesiones convergentes, así como varios ejemplos y sus propiedades. Hasta este punto, deberíamos sentirnos bastante cómodos con las sucesiones convergentes puesto que en esta entrada revisaremos con mayor detalle las sucesiones divergentes.

Sucesiones divergentes a infinito

Antes de iniciar a ver las propiedades de este tipo de sucesiones, vale la pena recordar la definición que se dio previamente.

Definición. Sea $\{a_n\}$ una sucesión en $\mathbb{R}$. Decimos que $\{a_n\}$ diverge a infinito si para todo $M \in \mathbb{R}$, existe $n_0 \in \mathbb{N}$ tal que si $n \geq n_0$, entonces $M < a_n$.

La definición nos indica que una sucesión diverge a infinito si para cualquier número real $M$, existe un punto $n_0$, en el que todos los valores subsecuentes en la sucesión son mayores que $M$. Cuando una sucesión $\{a_n\}$ diverge a infinito lo denotaremos como $$\lim_{n \to \infty} a_n = \infty.$$

Propiedades de las sucesiones divergentes a infinito

Ahora sí, estamos listos para indagar las propiedades de las sucesiones que divergen a infinito. La primera propiedad que probaremos será el hecho de que si multiplicamos una sucesión divergente a infinito por una constante positiva, la sucesión resultante también diverge a infinito.

Proposición. Sea $\{a_n\}$ en $\mathbb{R}$ tal que $$\lim_{n \to \infty} a_n = \infty,$$ y sea $c > 0$ fijo, entonces $$\lim_{n \to \infty} c \cdot a_n = \infty.$$

Demostración.
Sea $M \in \mathbb{R}$. Consideremos $\frac{M}{c} \in \mathbb{R}$.
Como $\{a_n\}$ diverge a infinito, entonces existe $n_0$ tal que para todo $n \geq n_0$ se tiene

\begin{gather*}
& \frac{M}{c} < a_n. \\
\Leftrightarrow & M < c \cdot a_n.
\end{gather*}

$$\therefore \lim_{n \to \infty} c \cdot a_n = \infty.$$

$\square$

En la demostración anterior, se da un valor arbitrario de $M$ y se debe mostrar que existe un número natural $n_0 \text{,}$ tal que para todos los valores subsecuentes de la sucesión $\{c \cdot a_n\}$, son mayores que $M$. Para ello, se usa el hecho de que $\{a_n\}$ es divergente y, particularmente, para el número real $\frac{M}{c}$ existe tal número natural.

La siguiente proposición nos indica cómo se comportan la suma y la multiplicación de sucesiones divergentes que, como es de esperarse, el resultado de tales operaciones es una sucesión divergente.

Proposición. Sean $\{ a_n \}$ y $\{ b_n \}$ dos sucesiones en $\mathbb{R}$ tales que $$\lim_{n \to \infty} a_n = \infty \quad \text{ y } \quad \lim_{n \to \infty} b_n = \infty.$$

Entonces

$i)$ $$\lim_{n \to \infty} (a_n + b_n) = \infty.$$
$ii)$ $$\lim_{n \to \infty} (a_n b_n) = \infty.$$

Demostración.

$i)$ Sea $M \in \mathbb{R}$. Como $\{a_n\}$ diverge a infinito, se tiene que
$$\exists n_1 \in \mathbb{N} \text{ tal que si } n \geq n_1 \Rightarrow \frac{M}{2} < a_n.$$

Y como $\{b_n\}$ también diverge a infinito, se tiene que
$$\exists n_2 \in \mathbb{N} \text{ tal que si } n \geq n_2 \Rightarrow \frac{M}{2} < b_n.$$

Consideremos $n_0 = max\{n_1, n_2 \}$. Si $n \geq n_0$, entonces se cumplen las dos expresiones de arriba y al sumarlas obtenemos que $M < a_n+b_n.$
$$\therefore \lim_{n \to \infty} (a_n + b_n) = \infty.$$

$ii)$ Sea $M \in \mathbb{R}$.
Para $\{a_n\}$ consideremos el número real $\hat{M} = max\{M, 0\}$. Debido a que $\{a_n\}$ diverge, existe $n_1 \in \mathbb{N}$ tal que si $n \geq n_1$, entonces $\hat{M} < a_n$, lo que implica que $M < a_n$ y $0 < a_n.$

Para $\{b_n\}$ consideremos el número real $1$. Debido a que $\{b_n\}$ diverge, existe $n_2 \in \mathbb{N}$ tal que si $n \geq n_2$, entonces $1 < b_n.$

Sea $n_0 = max\{n_1, n_2 \}$. Si $n \geq n_0$, entonces se cumplen las condiciones anteriores. Como $a_n$ es positivo para todo $n \geq n_0$, podemos multiplicar la expresión $1 < b_n$ por $a_n$ y la desigualdad se preservará, es decir, $a_n < a_n b_n$ y además $M < a_n$, por transitividad concluimos que $M < a_n b_n.$

$\square$

Después de haber revisado las propiedades anteriores y sabiendo que la sucesión $\{n\}$ generada por los números naturales diverge, es posible ampliar nuestro repertorio de sucesiones divergentes. Las siguientes sucesiones divergen por implicación directa de las proposiciones vistas: $\{5n\}$, $\{n+n^2+n^3\}$, $\{7n^2+4n\}$, etc.

La siguiente propiedad hace referencia a que si tenemos una sucesión $\{a_n\}$ divergente a infinito y otra sucesión $\{b_n\}$ para la cual existe un punto a partir del cual siempre es mayor que $\{a_n\}$, entonces $\{b_n\}$ también diverge a infinito.

Proposición. Sean $\{a_n\}$ y $\{b_n\}$ sucesiones en $\mathbb{R}$ tales que
$i$) Existe $n_1 \in \mathbb{N}$ tal que para todo $n \geq n_1$ se cumple $b_n \geq a_n.$
$ii$) $\lim\limits_{n\to \infty} a_n = \infty.$
Entonces $$\lim_{n\to \infty} b_n = \infty.$$

Demostración.

Sea $M \in \mathbb{R}$. Por hipótesis, existe $n_1 \in \mathbb{N}$ tal que si $n \geq n_1$, entonces $b_n \geq a_n$. Y como $\{a_n\}$ diverge a infinito, existe $n_2 \in \mathbb{N}$ tal que para todo $n \geq n_2$, se tiene que $a_n > M$. Consideremos $n_0 = max\{n_1,n_2 \}$, entonces si $n \geq n_0$, se cumple $b_n \geq a_n$ y $a_n > M$. Se concluye que $b_n > M$ para todo $n \geq n_0.$

$$\therefore \lim_{n\to \infty} b_n = \infty.$$

$\square$

Proposición. Sea $c > 1$, entonces $$\lim_{n \to \infty} c^n = \infty.$$

Demostración.

Para realizar esta demostración haremos uso de la proposición anterior. Sea $n \in \mathbb{N}$. Como $c > 1$, entonces $c-1>0$ y por la desigualdad de Bernoulli, tenemos

\begin{gather*}
c^n = (1+c-1)^n \geq 1+n(c-1) > n(c-1). \\
\therefore c^n > n(c-1).
\end{gather*}

Además, sabemos que la sucesión $\{n\}$ diverge a infinito y si multiplicamos esta sucesión por una constante positiva, en este caso $c-1$, la sucesión $\{(c-1)n\}$ también diverge a infinito. Utilizando la proposición anterior, se concluye que $$\lim_{n \to \infty} c^n = \infty.$$

$\square$

Como última propiedad, revisaremos que una sucesión monótona no acotada es divergente. Probaremos que las sucesiones crecientes no acotadas divergen a infinito. Se dejará como tarea moral probar que las sucesiones decrecientes no acotadas divergen a $-\infty.$

Proposición. Si $\{ a_n \}$ es una sucesión creciente y no acotada, entonces $$\lim_{n \to \infty} a_n = \infty.$$

Demostración.
Sea $\{a_n \}$ una sucesión creciente y no acotada y sea $M \in \mathbb{R}$. Como la sucesión no está acotada, existe $n_0 \in \mathbb{N}$ tal que $M < a_{n_0}$ y como la sucesión es creciente $a_n \geq a_{n_0}$ para todo $n \geq n_0.$

\begin{gather*}
\therefore M < a_n \text{, para todo } n \geq n_0. \\ \\
\therefore \lim_{n \to \infty} a_n = \infty.
\end{gather*}

$\square$

En la demostración anterior hay una sutileza que vale la pena enfatizar: usamos el hecho de que la sucesión no está acotada para probar que existe al menos un elemento específico, $a_{n_0}$, que es mayor que un real arbitrario $M$, pero para probar que diverge a infinito, hay que probar que también todos los elementos subsecuentes, $a_n$ con $ n \geq n_0$, son mayores a $M$ y, en ese momento, es cuando se usa la hipótesis de monotonía.

Más adelante…

En las entradas subsecuentes revisaremos conceptos derivados de las sucesiones: el concepto de subsucesión, las sucesiones de Cauchy y culminaremos con el estudio de una de las constantes más famosas dentro de matemáticas, el número de Euler.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  • Si $\{ a_n \}$ es una sucesión decreciente y no acotada, entonces $$\lim_{n \to \infty} a_n = – \infty.$$
  • Sea $\{ a_n \}$ una sucesión divergente a infinito tal que para todo $n\in \mathbb{N}$ se cumple que $a_n \neq 0$. Entonces $$\lim_{n \to \infty} \frac{1}{a_n} = 0.$$
  • Prueba lo siguiente:
    $i)$ $\lim\limits_{n \to \infty} \frac{n^2+1}{n+1} = \infty.$
    $ii)$ $\lim\limits_{n \to \infty} (n – \sqrt{n} )= \infty.$
  • Demuestra que si $$\lim_{n \to \infty} \frac{a_n}{n} = L,$$ donde $L > 0,$ entonces $$\lim_{n\to \infty} a_n = \infty.$$

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»