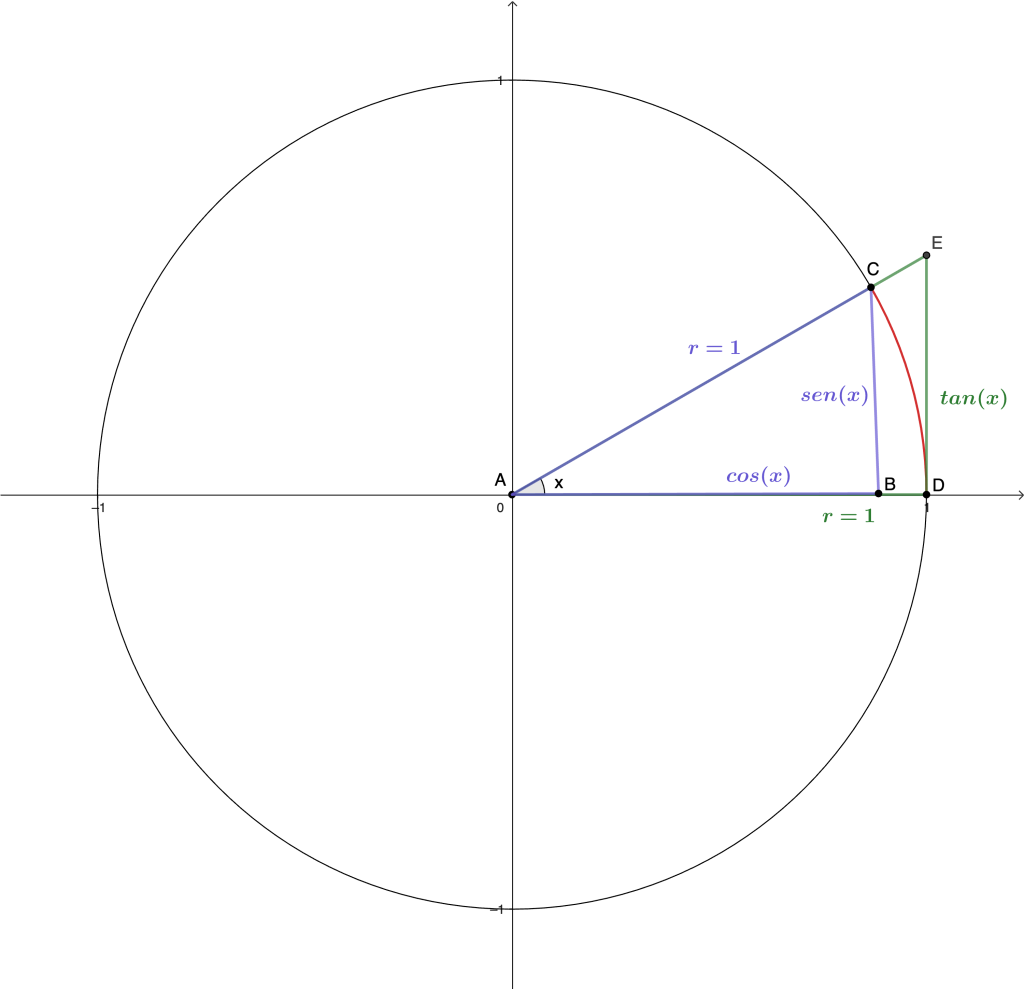
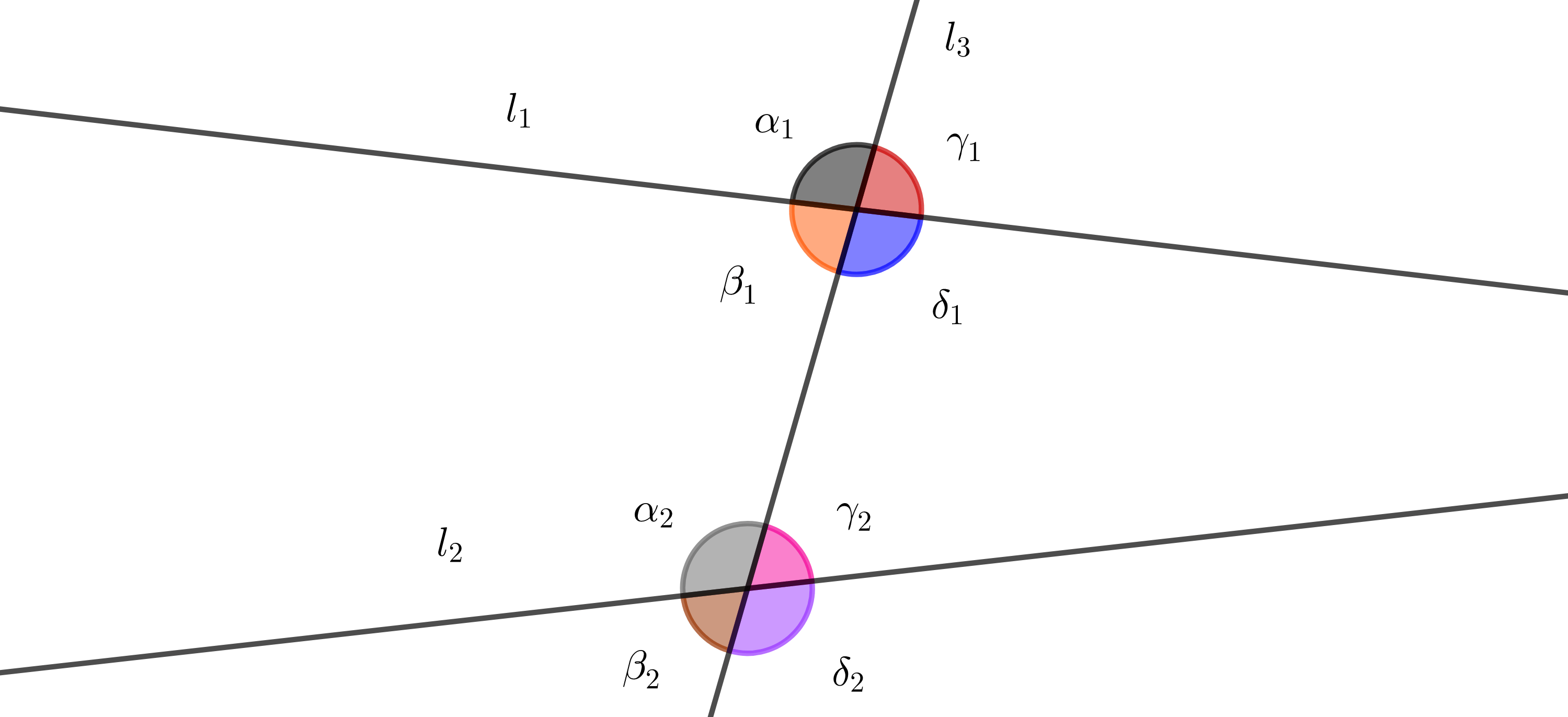Introducción
Continuando la conexión con la geometría Euclidiana con la que empezamos, hay un concepto en la geometría analítica que se conecta con la noción de ángulo, la de distancia y la de norma en la primera geometría mencionada, el producto interior. Dentro del contenido de esta entrada esta su definición en una dimensión de $2$ o mayor, ejemplos y sus propiedades. También, se discute el concepto del vector ortogonal canónico, que en conjunción con el producto interior, sirve como herramienta para detectar ciertas características de rectas y vectores.
Producto interior
Abramos esta entrada con la definición de este nuevo concepto.
Definición. Si tenemos dos vectores $u=(u_1,u_2)$ y $v=(v_1,v_2)$ en $\mathbb{R}^2$, el producto interior (o producto punto) en $\mathbb{R}^2$ de $u$ con $v$, está dado por
$u\cdot v := (u_1,u_2) \cdot (v_1,v_2) = u_1v_1 +u_2 v_2$
Esta definición se puede expresar en dimensiones mayores.
Definición. Si tenemos dos vectores $u=(u_1,u_2, \dots, u_n)$ y $v=(v_1,v_2, \dots, v_n)$ en $\mathbb{R}^n$, el producto interior (o producto punto) en $\mathbb{R}^n$ de $u_1$ con $u_2$, está definido como
\begin{align*}
u\cdot v : &= (u_1,u_2, \dots, u_n) \cdot (v_1,v_2, \dots, v_n) \\
&= u_1v_1 +u_2 v_2+u_3 v_3 + \dots + u_n v_n \\
&= \sum _{j=1} ^{n} u_j v_j
\end{align*}
Es importante notar que el resultado del producto interior (que es una operación vectorial), es un escalar.
Ejemplos:
1. Sean los vectores $(5,3)$ y $(2,-4)$ en $\mathbb{R}^2$, el producto interior de estos es
\begin{align*}
(5,3) \cdot (2,-4)&=5(2)+3(-4)\\
&=10-12\\
&=-2
\end{align*}
2. Sean los vectores $(-3,1,-1)$ y $(-6,2,-3)$ en $\mathbb{R}^3$, el producto interior de estos es
\begin{align*}
(-3,1,-1) \cdot (-6,2,-3)&=-3(-6)+1(2)+(-1)(-3)\\
&=18+2+3\\
&=23
\end{align*}
3. Sean los vectores $(1,0,-5,2,0,1)$ y $(0,-6,0,0,2,0)$ en $\mathbb{R}^6$, el resultado de su producto interior es cero, verifica.
Ahora que hemos definido una nueva operación, nos gustaría demostrar algunas propiedades asociadas a esta.
Teorema. Para todos los vectores $u,v,w \in \mathbb{R}^n$ y para todo número $t \in \mathbb{R}$ se cumple que
- $u \cdot v = v \cdot u$
- $u \cdot (tv)=t(u\cdot v)$
- $u \cdot (v + w)= u \cdot v + u \cdot w$
- $u \cdot u \geq 0$
- $u \cdot u =0 \Leftrightarrow u=(0,0)$
La primera propiedad nos dice que el producto interior es conmutativo; la siguiente que la operación saca escalares; la tercera expresa que esta abre sumas; la cuarta que al hacer el producto interior de un vector consigo mismo, el resultado es siempre mayor o igual a cero la última que la igualdad a cero sólo sucede cuando el vector $u$ es el vector cero.
Demostración
Haremos la demostración para vectores en $\mathbb{R}^2$, (el caso para dimensión $n$ es análogo) y usaremos los axiomas de los números reales.
Para empezar definamos los vectores $u=(u_1,u_2)$, $v=(v_1,v_2)$ y $w=(w_1,w_2)$ en $\mathbb{R}^2$
1. P. D. $u \cdot v = v \cdot u$. Comencemos con la definición y desarrollemos a partir de ella
\begin{align*}
u \cdot v &=(u_1,u_2) \cdot (v_1,v_2)\\
&=u_1v_1+u_2v_2 \\
&=v_1u_1+v_2u_2 \\
&=(v_1,v_2) \cdot (u_1,u_2)\\
&=v \cdot u
\end{align*}
$\therefore$ $u\cdot v= v \cdot u$
2. P.D. $u \cdot (tv)=t(u\cdot v)$
\begin{align*}
u \cdot (tv)&=(u_1,u_2) \cdot t(v_1,v_2) \\
&= (u_1,u_2) \cdot (tv_1,tv_2) \\
&= u_1(tv_1)+u_2(tv_2)\\
&= t(u_1v_1+u_2v_2) \\
&=t(u_1,u_2) \cdot (v_1,v_2)\\
&= t (u \cdot v)
\end{align*}
$\therefore u \cdot (tv)=t(u\cdot v)$
3. P.D. $u \cdot (v + w)= u \cdot v + u \cdot w$
\begin{align*}
u \cdot (v + w)&=(u_1,u_2) \cdot ((v_1,v_2) + (w_1,w_2)) \\
&= (u_1,u_2) \cdot (v_1+w_1,v_2+w_2) \\
&=u_1(v_1+w_1)+u_2(v_2+w_2) \\
&=u_1v_1+u_1w_1+u_2v_2+u_2w_2 \\
&=u_1v_1+u_2v_2+u_1w_1+u_2w_2 \\
&=(u_1v_1+u_2v_2)+(u_1w_1+u_2w_2) \\
&=((u_1,u_2)\cdot(v_1,v_2)) + ((u_1,u_2) \cdot (w_1,w_2)) \\
&= u \cdot v + u \cdot w
\end{align*}
$\therefore$ $u \cdot (v + w)= u \cdot v + u \cdot w$
4 y 5. P.D. $u \cdot u \geq 0$ y $u \cdot u =0 \Leftrightarrow u=(0,0)$
\begin{align*}
u \cdot u&=(u_1,u_2) \cdot (u_1,u_2) \\
&= u_1u_1+u_2u_2\\
&= u_1^2 + u_2^2 \geq 0
\end{align*}
La última relación se da ya que es una suma de números al cuadrado y cada término por sí sólo es mayor o igual a cero.
Resulta que si $u_1 \neq 0$ ó $u_2 \neq 0$, entonces $u_1^2 + u_2^2 > 0$, por lo que el único caso en el que se da la igualdad a cero es cuando $u=(0,0)$.
$\therefore$ $u \cdot u \geq 0$ y $u \cdot u =0 \Leftrightarrow u=(0,0)$
$\square$
Lo usado en esta demostración se restringe a los axiomas de los reales y la definición del producto interior, por lo que aunque no haya mucha descripción, espero que te sea clara.
El ortogonal canónico
Definición. Sea $v=(x,y)$ un vector en $\mathbb{R}^2$, el vector ortogonal canónico a v es el vector
$v^{\perp}=(-y,x)$
Si te das cuenta, esta definición hace referencia a lo que sucede al aplicar el ortogonal a un vector. Además, esta definición define al ortogonal canónico, pero no significa que sea el único vector perpendicular (ortogonal) a $v$.
Antes de definir o probar más cosas relacionadas al ortogonal, hagamos algunas observaciones.
Observación: Si aplicamos 4 veces el ortogonal a un vector $v$, regresamos al mismo vector:
$v^{\perp}=(x,y)^{\perp}=(-y,x)$
$(-y,x)^{\perp}=(-x,-y)$
$(-x,-y)^{\perp}=(y,-x)$
$(y,-x)^{\perp}=(x,y)$
Observación: Para cualquier $v=(x,y) \in \mathbb{R}^2$, tenemos que
$v \cdot v^{\perp} =(a,b) \cdot (-b,a)=a(-b)+b(a)=-ab+ab=0$
Para continuar, usemos el producto interior para definir y probar ciertas cosas con relación al compadre ortogonal.
Definición. Diremos que dos vectores $u,v \in \mathbb{R}^2$ son perpendiculares (ortogonales) si $u \cdot v=0$.
Proposición. Sea $u \in \mathbb{R}^2$ \ ${ 0\}$. Entonces
$\{x \in \mathbb{R}^2 : x \cdot u =0\}=L_{u_{\perp}}:=\{ru^{\perp}: r \in \mathbb{R}\}$
Demostración
Como queremos comprobar una igualdad de conjuntos, hay que probar la doble contención. Comencemos con la contención $\supseteq$.
$\supseteq$ En esta contención, queremos demostrar que cualquier vector de la forma $ru^{\perp}$ es tal que
$(ru^{\perp}) \cdot u=0$
Tomemos un vector de la forma $ru^{\perp}$ con $r \in \mathbb{R}$ y notemos que gracias a la segunda propiedad del producto interior se cumple que
$(ru^{\perp}) \cdot u = r(u^{\perp} \cdot u)= r(0)=0 $
Esto es suficiente para la demostración de la primera contención, pues hemos probado que el producto interior de cualquier vector de la forma $ru^{\perp}$ con $u$ es cero.
$\subseteq$ Para esta contención, queremos demostrar que los vectores $x$ que cumplen $x \cdot u =0$, son de la forma $x=r u^{\perp}$. Para esto, tomemos un vector $x=(r,s)$ que cumpla la primera condición y expresemos al vector $u$ con sus coordenadas $u=(u_1,u_2)$. Al realizar el producto interior obtenemos
$x \cdot u=(r,s) \cdot (u_1,u_2)=ru_1+su_2=0 $
$\Rightarrow ru_1= -su_2 \cdots (a) $
Dado que $u \neq (0,0)$, al menos una de sus entradas es distinta de cero. Supongamos que $u_1 \neq 0$, entonces podemos despejar $r$
$r=\frac{-su_2}{u_1}$
Podemos sustituir este valor en $x$ y desarrollar para obtener
\begin{align*}
x=(r,s)&=\left( \frac{-su_2}{u_1},s \right)=s\left( \frac{-u_2}{u_1}, 1 \right) \\
&=s \left( \frac{-u_2}{u_1}, \frac{u_1}{u_1} \right) \\
&=\frac{s}{u_1} \left( -u_2, u_1 \right)
\end{align*}
Y ya está el primer caso, pues sabemos que $u^{\perp}=( -u_2, u_1)$.
Así, $x \in \mathbb{R}^2$ tal que $x \cdot u=0$, es de la forma $ru^{\perp}$, con r un escalar.
En el caso en el que $u_2 \neq 0$, tenemos algo análogo. A partir de $(a)$ podemos despejar $s$
$ ru_1= -su_2$
$s=\frac{-ru_1}{u_2}$
Al sustituir en $x$ y desarrollar obtendremos que
$x=\frac{r}{-u_2}(-u_2,u_1)$
$\square$
Aplicaciones del producto punto
Para cerrar esta entrada, usemos el producto interior para describir algunas características de las rectas y vectores.
Definición. Diremos que dos líneas $l_1$ y $l_2$ son perpendiculares si al escribirlas en forma paramétrica
$l_1=\{ p_1+rq_1 : r \in \mathbb{R} \}$
$l_2=\{ p_2+rq_2 : r \in \mathbb{R} \}$
se tiene que $q_1 \cdot q_2 =0$, esto es si sus vectores dirección son ortogonales.
Proposición. Dos vectores $u$ y $v$ son paralelos si y sólo si $u$ y $v^{\perp}$ son ortogonales, es decir si $u \cdot v^{\perp}=0$.
Demostración
Ida ($\Rightarrow$). Si $u$ y $v$ son paralelos, por definición $u=cv$ con $c \in \mathbb{R}$. Como queremos que $u$ y $v^{\perp}$ sean ortogonales, realicemos su producto interior y utilicemos las propiedades de este para desarrollar
\begin{align*}
u \cdot v^{\perp}&=(cv) \cdot v^{\perp} \\
&=c(v \cdot v^{\perp}) \\
&=c(0)=0
\end{align*}
Por lo que $u$ y $v^{\perp}$ son ortogonales.
Regreso ($\Leftarrow$). Si ahora suponemos que $u$ y $v^{\perp}$ son ortogonales, pasa que
$u \cdot v^{\perp}=0$
Pero por lo visto en la proposición de la sección anterior, esto sólo pasa cuando $u=c(v^{\perp})^{\perp}$ para algún $c \in \mathbb{R}$. Si $v=(v_1,v_2)$ esto se desarrolla como
\begin{align*}
u&=c(v^{\perp})^{\perp}=c(-v_2,v_1)^{\perp}\\
&=c(-v_1,-v_2)\\
&= -cv
\end{align*}
$\therefore$ por definición de paralelismo, $u$ y $v$ son paralelos.
$\square$
Otra cosa útil del producto punto, es que cualquier recta se puede escribir en términos de este. Precisemos esto en la siguiente proposición.
Proposición. Sea la recta $l$ en su forma paramétrica
$l=\{p+rq : r \in \mathbb{R}\}$
La recta $l$ se puede escribir usando el producto punto de la siguiente manera
$l=\{x \in \mathbb{R} ^2 : q^{\perp} \cdot x=q^{\perp} \cdot p \}$
Antes de adentrarnos en la demostración, hablemos un poco de qué significa esta proposición con ayuda del siguiente interactivo aclarando que $qT$ es el vector $q{^\perp}$.
Al definir $qT$ como el vector perpendicular a la recta, tenemos que $q$ es el vector director de esta; $p$ es el punto por el que pasa la recta y $x$ representa a los puntos en ella. Como $p$ y $qt$ son fijos, entonces $qT \cdot p$ es un número constante. Si tú mueves $x$ a lo largo de la recta, veras que el producto punto $qT \cdot x$ al cual denominamos como $a$ en GeoGebra, no varia.
Es así como expresamos la recta por medio del producto punto; el conjunto de todas los $x \in \mathbb{R}^2$ tal que el producto punto con $q^{\perp}$ ($qT$ en el interactivo) es igual a $q^{\perp} \cdot p$.
Con esto claro, procedamos a la demostración.
Demostración
Como queremos demostrar que $l$ en su forma paramétrica es el mismo conjunto que el descrito por el producto punto, tenemos que explorar las dos contenciones de los conjuntos.
$\supseteq$ Tomemos $x \in \mathbb{R}^2$ tal que $q^{\perp}\cdot x =q^{\perp}\cdot p$. De esta igualdad se tiene que
\begin{align*}
0 &= q^{\perp}\cdot x – q^{\perp}\cdot p\\
&=q^{\perp}\cdot (x-p)\\
& \Rightarrow q^{\perp}\cdot (x-p) =0
\end{align*}
Dada la última igualdad, sabemos (por la primera proposición de esta entrada) que $x-p$ debe ser un múltiplo de $(q^{\perp})^{\perp}=-q$ y por lo tanto un múltiplo de $q$; por lo que para algún $s \in \mathbb{R}$ se tiene que
\begin{align*}
x-p&=sq\\
\Rightarrow x&=p+sq
\end{align*}
$\subseteq$ Ahora partamos de un punto $x=p+rq \in$ $l$ y desarrollemos su producto punto con $q^{\perp}$ para finalizar esta demostración
\begin{align*}
q^{\perp} \cdot x &= q^{\perp} \cdot (p+rq)\\
&=(q^{\perp} \cdot p) + (q^{\perp} \cdot (rq)) \\
&= q^{\perp} \cdot p
\end{align*}
Donde la última igualdad se da gracias a que $q^{\perp} \cdot (rq)=r(q^{\perp} \cdot q)=0$.
$\therefore$ Partiendo la expresión paramétrica de la recta está contenida en la expresión con producto punto y viceversa y por lo tanto son el mismo conjunto (la misma recta).
$\square$
Más adelante…
El producto interior fungirá como herramienta para establecer las nociones de distancia y ángulo en las siguientes entradas y particularmente para definir la forma normal de la recta en la siguiente entrada.
Tarea moral
- Completa los pocos pasos que omitimos en cada demostración o ejemplo.
- Demuestra el teorema de las propiedades del producto interior para $n=3$.
- Calcula el producto interior de los siguientes vectores:
- $(4,-1)$ y $(7,2)$
- $(-2,3,0)$ y $(4,-6,0)$
- $(-2,3,0)$ y $(-2)(-2,3,0)$
- $(5,0,-3,0,0)$ y $(0,4,0,-2,1)$
- Usando la definición del producto interior, demuestra que dado $ u \in \mathbb{R}^2$ se tiene que
$u \cdot x =0$, $\forall x\in \mathbb{R}^2$
si y sólo si $u=(0,0)$.
- Demuestra que para todos los vectores $ u \text{, }v \in \mathbb{R}^2$ y $\forall t \in \mathbb{R}$, se cumple que
- $(u+v)^{\perp}=u^{\perp}+v^{\perp}$
- $(tu^{\perp})=t(u^{\perp})$
- $u^{\perp} \cdot v^{\perp}=u \cdot v$
- $u^{\perp} \cdot v = -(u \cdot v^{\perp})$