Introducción
En la primera entrada del curso definimos algunos objetos importantes que nos permitirán desarrollar la teoría. Es importante mencionar que para poder empezar a construir una teoría, se tienen que suponer algunas propiedades como ciertas. A este tipo de propiedades que se aceptan a priori les llamamos axiomas.
En Lógica Matemática se requiere que los axiomas de una teoría tengan las siguientes tres características:
$i)$ ser completos, esto quiere decir que a partir de ellos todas las proposiciones referentes a objetos de la teoría puedan ser demostradas,
$ii)$ que sean independientes, es decir, que ninguno de ellos pueda ser demostrado a partir de los demás,
$iii)$ que sean consistentes, es decir, que no se contradigan.
Postulados de Euclides
Euclides fue un matemático griego que vivió alrededor del año 300 AC. En su obra reunió los conocimientos fundamentales que los matemáticos griegos habían desarrollado hasta ese momento y los expuso de manera ordenada. Sus demostraciones geométricas se basaban en el método deductivo, lo que garantizaba la validez de sus afirmaciones.
Euclides comenzó su obra definiendo los objetos con los que iba a trabajar, después estableció las reglas generales con que esos objetos se relacionaban es decir los postulados y a continuación enuncio propiedades generales sobre la igualdad de magnitudes llamadas nociones comunes. Cabe destacar que los axiomas de Euclides no cumplen con la condición de ser completos, sin embargo, a partir de ellos se puede construir gran parte de la teoría geométrica que hoy se estudia.
Para hablar del quinto postulado necesitamos presentar un concepto nuevo.
Definición. Consideremos $l_{1}$, $l_{2}$ y $l_{3}$ tres rectas distintas y tal que $l_{3}$ interseca a las primeras dos, entonces decimos que $l_{3}$ es transversal a $l_{1}$ y a $l_{2}$.
En estas condiciones se forman 8 ángulos (figura 1), decimos que $\alpha_{2}$, $\beta_{1}$, $\delta_{1}$ y $\gamma_{2}$ son ángulos internos.
Las parejas de ángulos ($\alpha_{1}$, $\alpha_{2}$), ($\beta_{1}$, $\beta_{2}$), ($\delta_{1}$, $\delta_{2}$) y ($\gamma_{1}$, $\gamma_{2}$) se llaman ángulos correspondientes, y las parejas de ángulos ($\beta_{1}$, $\gamma_{2}$) y ($\delta_{1}$, $\alpha_{2}$) son ángulos alternos internos.
A continuación enunciamos los cinco postulados de Euclides.
$i)$ Por dos puntos siempre es posible trazar una recta.
$ii)$ Es posible prolongar una recta tanto como se quiera en cualquiera de sus dos direcciones.
$iii)$ Cualquier punto del plano y segmento pueden ser usados como centro y radio, respectivamente de un círculo.
$iv)$ Todos los ángulos rectos son iguales.
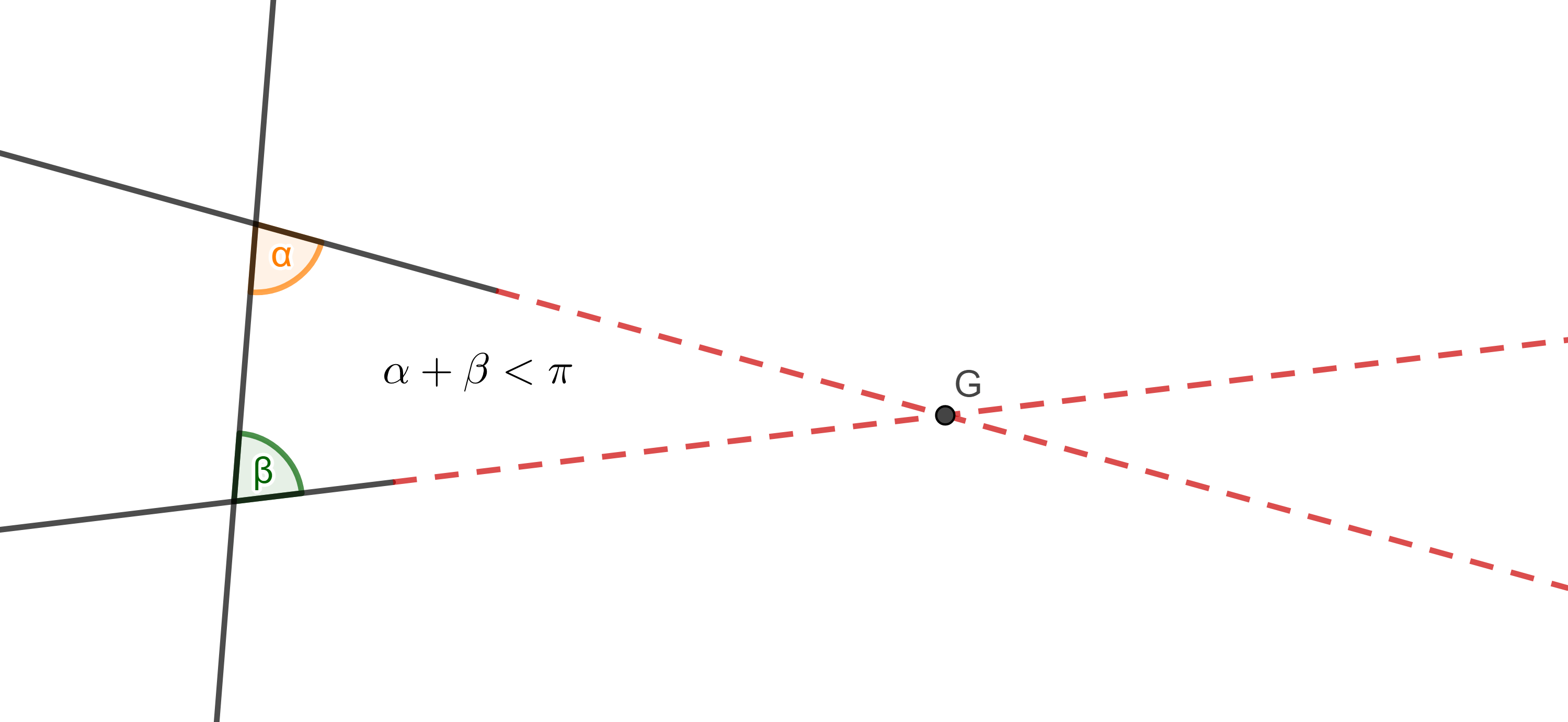
$v)$ Si por dos rectas pasa una transversal tal que, de alguno de los lados de la transversal, la suma de los ángulos interiores es menor a dos ángulos rectos, entonces si las dos rectas se prolongan lo suficientemente del lado en que dicha suma es menor a 2 ángulos rectos, las rectas se intersecan.
Nociones comunes
Las nociones comunes que enunció Euclides también son axiomas que se refieren al manejo de magnitudes del mismo tipo.
$i)$ Cosas que sean iguales a una tercera son iguales entre sí.
Si $a = c$ y $c = b$ entonces $a = b$.
$ii)$ Si a cosas iguales se añaden cosas iguales las resultantes son iguales.
Si $a = b$ entonces $a + c = b + c$.
$iii)$ Si de cosas iguales se substraen cosas iguales las resultantes son iguales.
Si $a = b$ entonces $a – c = b – c$.
$iv)$ Cosas que coinciden una con otra son iguales entre sí.
Esto se refiere, por ejemplo, a la superposición de objetos, es decir, si al superponer dos objetos estos coinciden, entonces tendrán las mismas magnitudes.
$v)$ El todo es mayor que cualquiera de sus partes.
Si $a$ y $b$ son positivos y $c = a + b$ entonces $c > a$ y $c > b$.
Hay otras nociones que también usamos frecuentemente, por ejemplo, las primeras tres nociones se preservan si usamos desigualdades.
$vi)$ Si $a > c$ y $c > b$ entonces $a > b$.
$vii)$ Si $a > b$ entonces $a + c > b + c$.
$viii)$ Si $a > b$ entonces $a – c > b – c$.
En las últimas tres nociones, podemos cambiar el mayor que ($>$) por menor que ($<$), mayor igual que ($\geq$) o menor igual que ($\leq$).
$ix)$ Tricotomía. Para $a$ y $b$ magnitudes del mismo tipo ocurre uno y solo uno de los siguientes casos:
$a = b$,
$a < b$,
$b < a$.
El quinto postulado y sus consecuencias
Como podemos apreciar, los primeros cuatro postulados son aseveraciones intuitivas mientras que el quinto está enunciado de una forma que parece establecer condiciones a partir de las cuales ocurre algo, esto causo mucha controversia por más de dos mil años, pues aparenta ser una proposición que debe ser demostrada.
Hubo numerosos intentos por demostrar el quinto postulado conocido como axioma de las paralelas. Como resultado se encontraron varias equivalencias, se llegó a la conclusión de que no era posible demostrar el quinto postulado a partir de los cuatro primeros y que además era posible aceptar otros axiomas como ciertos en lugar del quinto, lo que dio origen a las geometrías no euclidianas.
Proposición. El quinto postulado de Euclides es equivalente a la afirmación los ángulos alternos internos entre paralelas son iguales.
Demostración: Seguiremos el método de reducción al absurdo. La idea es suponer que dada una hipótesis no se cumple la tesis de la proposición y a partir de ahí tenemos que encontrar algún tipo de contradicción a algo que sabemos que si es cierto.
Primero asumimos como cierto el quinto postulado y debemos mostrar que dadas dos rectas paralelas y una transversal a ella los ángulos alternos internos son iguales.
Sean $l_{1}$ y $l_{2}$ las rectas paralelas y $l_{3}$ la transversal a ellas y supongamos que los ángulos alternos internos $\alpha$ y $\beta$ no son iguales, entonces por tricotomía uno es mayor que el otro.
Sin pérdida de generalidad supongamos que $\beta > \alpha$, podemos sumar a ambos lados de la desigualdad $\gamma$, el ángulo suplementario de $\beta$, entonces
$\pi = \beta + \gamma > \alpha + \gamma$ $\Rightarrow$ $\pi > \alpha + \gamma$.
Entonces por el quinto axioma de Euclides las rectas se cortan, lo cual es una contradicción al hecho de que las rectas son paralelas. Así, nuestra suposición de que los ángulos alternos internos eran diferentes es errónea, y por lo tanto, los ángulos alternos internos son iguales $\alpha = \beta$.
$\blacksquare$
Ahora tomemos por cierto que los ángulos alternos internos entre paralelas son iguales y mostremos que si de un lado de una transversal que corta a dos rectas la suma de los ángulos internos es menor que dos ángulos rectos entonces dichas rectas se cortan en algún punto.
Demostración. Sea $l_{3}$, transversal a $l_{1}$ y $l_{2}$ y tal que la suma de los ángulos $\alpha + \beta < \pi$, supongamos que las rectas $l_{1}$ y $l_{2}$ son paralelas, por hipótesis sabemos que los ángulos alternos internos son iguales, $\beta = \gamma$.
Pero $\gamma$ y $\alpha$ son suplementarios , entonces $\pi = \alpha + \gamma = \alpha + \beta$.
Lo que es una contradicción pues nuestra hipótesis era que la suma de los ángulos era menor que dos ángulos rectos. Por lo tanto, las rectas se cortarán en algún punto.
$\blacksquare$
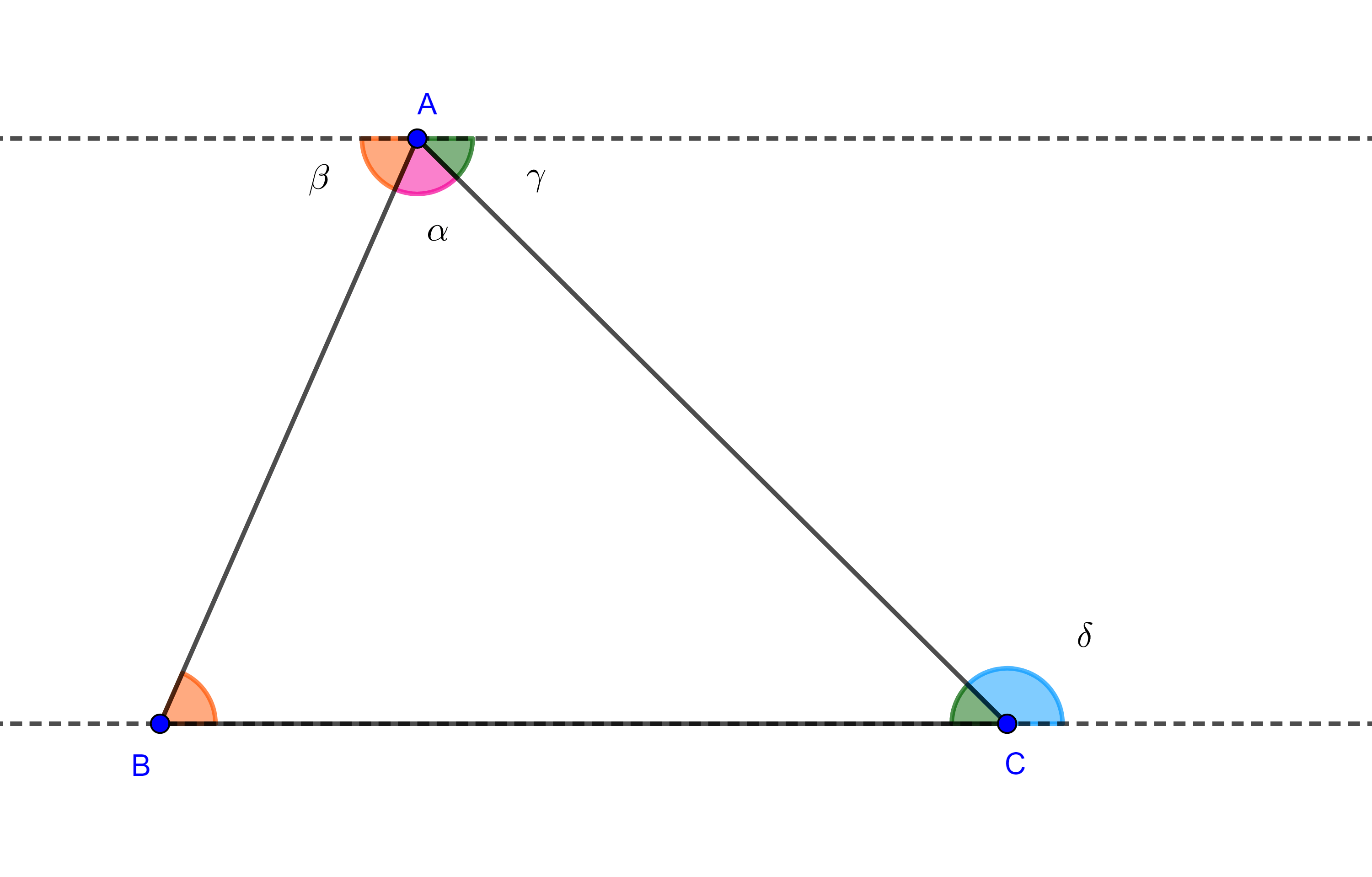
Teorema. La suma de los ángulos internos de todo triángulo es igual a dos ángulos rectos, además un ángulo exterior de un triángulo es igual a la suma de los ángulos internos no adyacentes a el.
Demostración. Sea $\triangle ABC$ un triángulo, y sea $\angle BAC = \alpha$. Consideremos la recta paralela a $BC$ que pasa por $A$.
Entonces por la proposición anterior, $\angle CBA = \beta$ y $\angle ACB = \gamma$ (figura 5), pues son ángulos alternos internos entre paralelas.
Por lo tanto, $\angle BAC + \angle CBA + \angle ACB = \alpha + \beta + \gamma = \pi$.
Por otra parte, sea $\delta$ el ángulo exterior en $C$, entonces $\gamma$ y $\delta$ son ángulos suplementarios, así que
$\gamma + \delta = \pi = \alpha + \beta + \gamma$
$\Leftrightarrow \delta = \alpha + \beta = \angle BAC + \angle CBA$.
$\blacksquare$
Más adelante…
En la siguiente entrada hablaremos de las transformaciones rígidas y estudiaremos los criterios de congruencia una herramienta muy útil en geometría.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Prueba que los ángulos correspondientes entre paralelas son iguales entre sí.
- Dados una recta y un punto fuera de ella muestra que la paralela a la recta dada por el punto dado es única.
- Sea $l_{3}$ transversal a $l_{1}$ y $l_{2}$ muestra que si los ángulos alternos internos son iguales entonces $l_{1}$ y $l_{2}$ son paralelas.
- $i)$ Muestra que dos rectas que son paralelas a una tercera son paralelas entre si.
$ii)$ Muestra que dos rectas que son perpendiculares a una tercera son paralelas entre si. - $i)$ Dados una recta y un punto fuera de ella muestra que la perpendicular a la recta dada por el punto dado es única.
$ii)$ Dados una recta y un punto en ella muestra que la perpendicular a la recta dada por el punto dado es única.
Entradas relacionadas
- Ir a Geometría Moderna I
- Entrada anterior del curso: Definiciones.
- Siguiente entrada del curso: Congruencia de triángulos.
- Otros cursos.
Fuentes
- Cárdenas, S., Notas de Geometría. México: Ed. Prensas de Ciencias, 2013, pp 5-10.
- Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 4, 8-9.
- Clark University
- Geometría interactiva
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

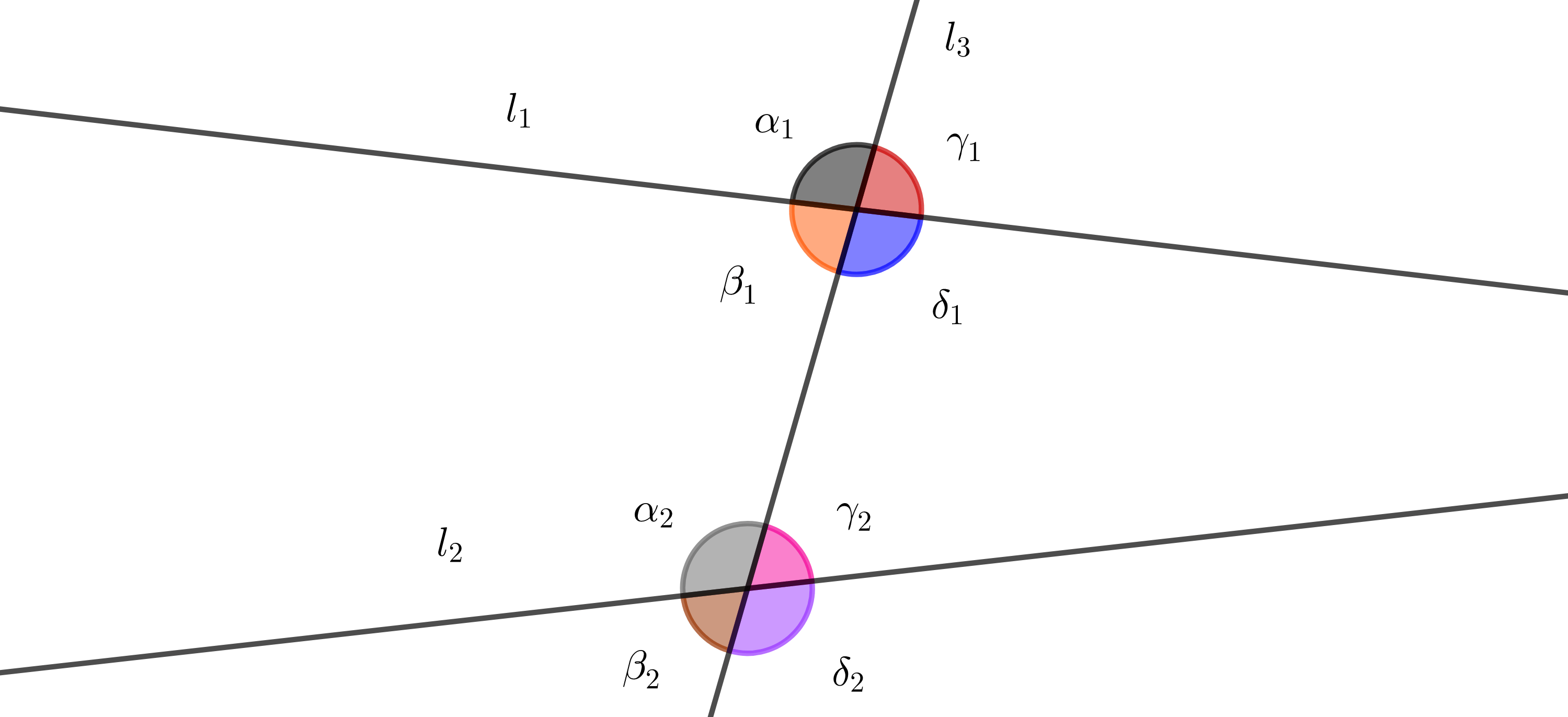

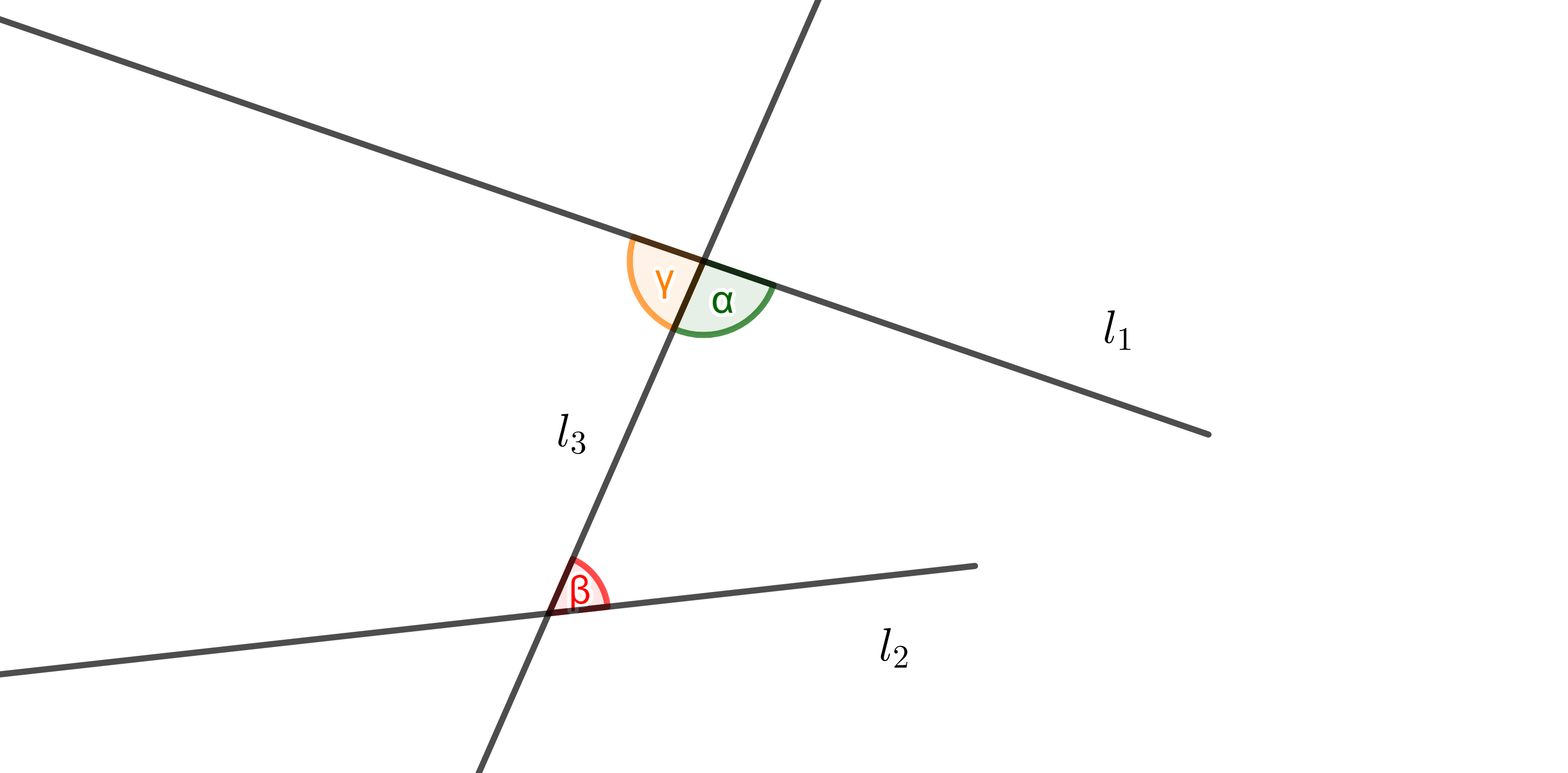
Excelente explicación , temas accesibles .
Muchas gracias por el comentario Omar.