Archivo de la etiqueta: triángulos

Seminario de Resolución de Problemas: Introducción a problemas de geometría y geometría euclideana

Por Leonardo Ignacio Martínez Sandoval

Deja un comentario

Introducción

En esta semana veremos algunas herramientas para resolver problemas de geometría. Como con otros temas que hemos visto, sería imposible tratar a profundidad el área. En vez de eso, lo que haremos es ver un poco de varias de las herramientas que se pueden usar en la solución de problemas geométricos, comenzando con geometría euclideana. Veremos ideas de lo siguiente:

  • Geometría triángulos y circunferencias
  • Geometría analítica
  • Vectores en geometría
  • Números complejos en geometría
  • Geometría discreta

En esta entrada comenzaremos con la parte de geometría euclideana. Más adelante hablaremos de las demás ideas.

Geometría euclideana

Cuando en geometría nos referimos a una solución por geometría euclideana o geometría sintética nos referimos a un argumento que no use parametrizaciones de los objetos del plano en términos de coordenadas, vectores o complejos. Simplemente usamos conceptos geométricos como ángulos, distancias, semejanza, congruencia, etc. Todas estas se pueden pensar como propiedades que se mantienen invariantes bajo movimientos rígidos del plano. Dentro de los resultados más versátiles del área tenemos los siguientes.

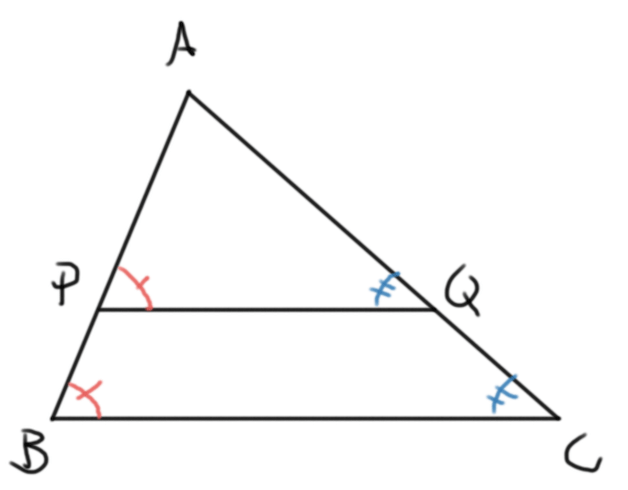
Teorema (de Tales). Tomemos puntos $P$ y $Q$ sobre los lados $AB$ y $AC$ de $\triangle ABC$. Se tiene que $AP/AQ = AB/AC$ si y sólo si la recta $PQ$ es paralela a la recta $BC$.

El teorema de Tales
Teorema de Tales

Teorema (criterios de congruencia). Sean $\triangle ABC$ y $\triangle DEF$ triángulos. Cualquiera de las siguientes condiciones (o sus simétricos) implican que $\triangle ABC$ y $\triangle DEF$ son congruentes:

  • (LLL) $AB=DE$, $BC=EF$ y $CA=FD$
  • (LAL) $AB=DE$, $\angle BAC = \angle EDF$ y $CA=FD$
  • (ALA) $\angle BAC = \angle EDF$, $CA=FD$ y $\angle BCA – \angle EFD$.

Teorema (criterios de semejanza). Sean $\triangle ABC$ y $\triangle DEF$ triángulos. Cualquiera de las siguientes condiciones (o sus simétricos) implican que $\triangle ABC$ y $\triangle DEF$ son semejantes.

  • (LLL) $\frac{AB}{DE}=\frac{BC}{EF}=\frac{CA}{FD}$.
  • (LAL) $\frac{AB}{DE}=\frac{CA}{FD}$ y $\angle BAC = \angle EDF$.
  • (AA) $\angle BAC = \angle EDF$ y $\angle BCA – \angle EFD$.

Veamos un ejemplo en el que se usan estos hechos básicos.

Problema. Sobre los lados $AB$ y $AC$ de un triángulo $ABC$ se construyen cuadrados $ABPQ$ y $ACRS$ como en la figura. Muestra que $CQ=BS$.

Sugerencia pre-solución. En geometría es típico modificar un problema. En vez de intentar medir los segmentos requeridos, es útil preguntarse si forman parte de triángulos que sean congruentes, o que sea pueda ver que son congruentes por algún criterio. Por supuesto, en todo problema de geometría es útil hacer muchas figuras.

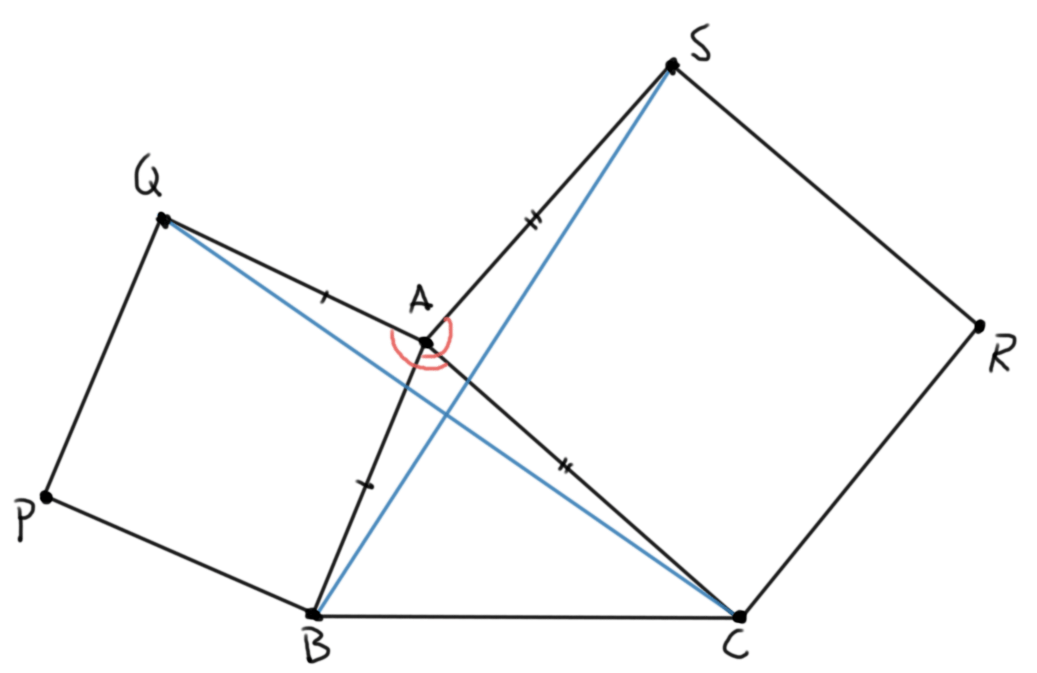
Problema de geometría euclidiana con cuadrados
Figura auxiliar para problema de cuadrados en un triángulo.

Solución. Consideremos los triángulos $ABS$ y $AQC$. Tenemos que $AB=AQ$ pues ambos son lados del cuadrado $ABPQ$. De manera similar, $AC=AS$. Finalmente, tenemos que $\angle BAS = \angle QAC$, pues ambos ángulos son iguales a $$90^\circ + \angle BAC.$$

Por esta razón, podemos usar el criterio de congruencia $LAL$ en estos triángulos para concluir que son congruentes. De aquí se concluye que $CQ=BS$, como queríamos.

$\square$

Recordatorio de puntos notables en triángulos

Otro tema relevante para la geometría euclideana es la geometría de triángulos. Tomemos un triángulo $\triangle ABC$. Hay algunos puntos y rectas notables en el triángulo, que se usan en varios problemas. A continuación enunciamos las más importantes.

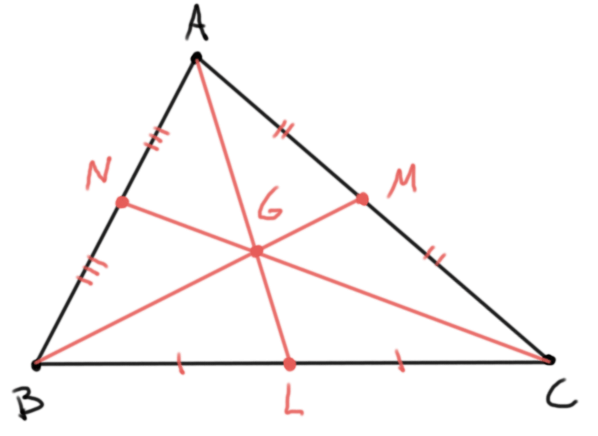
  • Si $L$, $M$ y $N$ son los puntos medios de $BC$, $CA$ y $AB$, respectivamente, entonces a cada una de las rectas $AL$, $BM$ y $CN$ se le conoce como una mediana. Las medianas de un triángulo concurren en un punto llamado el gravicentro o baricentro, que usualmente se denota por $G$.
Medianas de un triángulo y su gravicentro
Medianas de un triángulo y su gravicentro
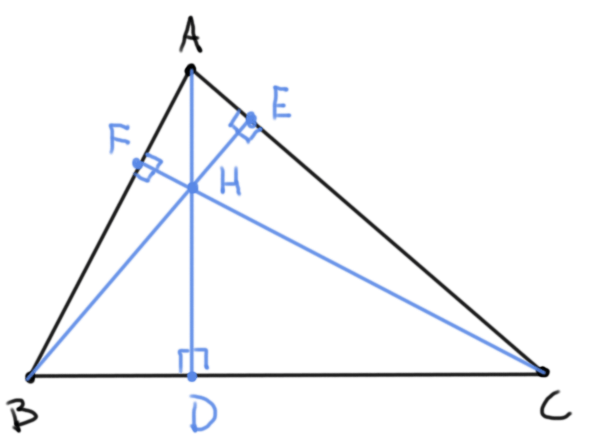
  • Si $D$, $E$ y $F$ son las proyecciones desde $A$, $B$, $C$ a los lados $BC$, $CA$ y $AB$ respectivamente, entonces a cada una de las rectas $AD$, $BE$ y $CF$ se le conoce como una altura. Las alturas de un triángulo concurren en un punto llamado el ortocentro, que usualmente se denota por $H$.
Alturas de un triángulo y su ortocentro
Alturas de un triángulo y su ortocentro
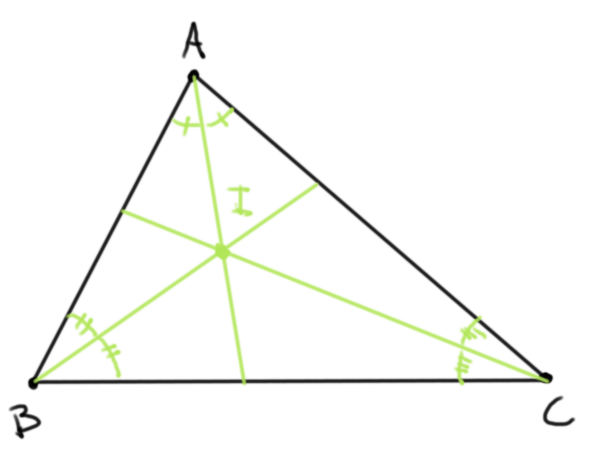
  • Las rectas que cortan a la mitad a cada uno de los ángulos internos de $\triangle ABC$ se les conoce como las bisectrices internas del triángulo. Concurren en un punto llamado el incentro, usualmente denotado por $I$. El incentro sirve como centro para la única circunferencia que es tangente a los segmentos $AB$, $BC$ y $CA$.
Bisectrices de un triángulo y su incentro
Bisectrices de un triángulo y su incentro
  • Las rectas perpendiculares a los lados del triángulo y que pasan por sus puntos medios se les llama mediatrices y concurren en un punto llamado el circuncentro, que se suele denotar $O$. Este punto sirve como centro de la única circunferencia que pasa por los tres vértices $A$, $B$ y $C$.
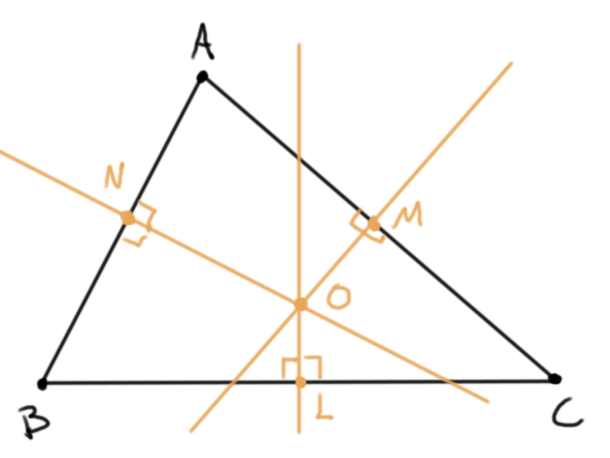
Mediatrices de un triángulo y su circuncentro
Mediatrices de un triángulo y su circuncentro

Veamos las demostraciones de algunas de estas afirmaciones, para repasar algunos argumentos geométricos.

Una idea útil es caracterizar a una recta como el conjunto de puntos que satisfacen cierta propiedad. Por ejemplo, probemos primero la siguiente caracterización de las mediatrices.

Proposición. La recta perpendicular $\ell$ a un segmento $BC$ que pasa por su punto medio $L$ consiste exactamente de los puntos $P$ tales que $PB=PC$.

Demostración. Para ver que cualquier punto en $\ell$ satisface esto, se puede usar el criterio LAL de congruencia en los triángulos $PBL$ y $PCL$, usando el ángulo recto que comparten. Para ver que cualquier punto tal que $PB=PC$ está en $\ell$, se usa que $\angle PBC = \angle PCB$ (por el triángulo isósceles $PBC$), y entonces al bajar la perpendicular desde $P$ a $BC$ a un punto $L’$, los triángulos $PBL’$ y $PCL’$ comparten dos ángulos (y por lo tanto los tres), de donde se puede usar de nuevo el criterio LAL para concluir que $L=L’$.

$\square$

Demostrar que las mediatrices concurren es entonces muy sencillo. Si $P$ es la intersección de la mediatriz en $BC$ y en $CA$, entonces por el resultado anterior tenemos $PB=PC=PA$, y entonces también por el resultado anterior se tiene que $P$ está en la mediatriz de $AB$. De manera análoga se puede mostrar que una bisectriz consiste de los puntos que equidistan de los lados que la definen, y con ello mostrar que las bisectrices internas de un triángulo concurren.

Veamos ahora un problema de geometría euclideana que involucra a las alturas y a las medianas. Es el Problema 1 del Concurso Nacional de la Olimpiada Mexicana de Matemáticas de 2009.

Problema. Sea $ABC$ un triángulo y $D$ el pie de la altura desde $A$. Con centro en $D$ se traza una circunferencia de radio $DA$. Esta circunferencia corta a los lados $AB$ y $AC$ del triángulo en puntos $P$ y $Q$ respectivamente. Muestra que los triángulos $AQP$ y $ABC$ son semejantes.

Sugerencia pre-solución. Para mostrar que estos triángulos son semejantes, basta con mostrar que tienen ángulos iguales.

Solución. Tracemos además los pies de altura $E$ y $F$ desde $B$ y $C$ respectivamente.

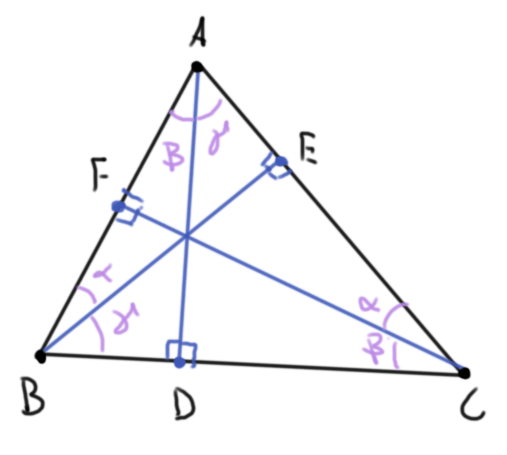
Ángulos creados por alturas de un triángulo.
Ángulos creados por alturas de un triángulo.

Observemos que $\triangle ABD$ y $\triangle CBF$ comparten los ángulos rectos y el ángulo en $B$, de modo que son semejantes y por lo tanto su tercer ángulo es igual. Este y argumentos análogos muestran que
\begin{align*}
\alpha&:=\angle ABE = \angle ACF\\
\beta&:=\angle BAD = \angle BCF\\
\gamma&:= \angle CBE = \angle CAD.
\end{align*}

De esta forma, los ángulos internos de $\triangle ABC$ miden $\angle A= \beta+\gamma$, $\angle B = \gamma+\alpha$ y $\angle C = \alpha+\beta$. Ya que la suma interna de los ángulos de un triángulo es $180^\circ$, concluimos que $\alpha+\beta+\gamma = 90^\circ$.

Ahora, usando los triángulos isósceles $\triangle ADP$ y $\triangle ADQ$ del problema, tenemos que
\begin{align*}
\angle DPA &= \angle DAP = \beta\\
\angle DQA &= \angle DAQ = \gamma.
\end{align*}

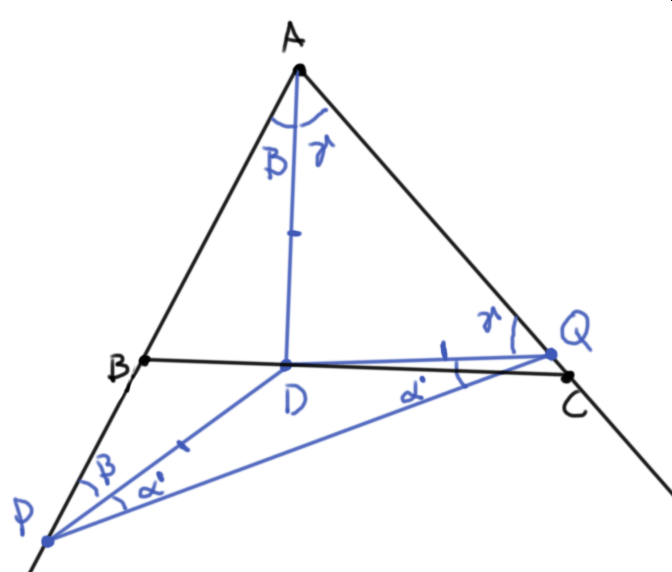
Figura auxiliar para el problema
Figura auxiliar para el problema

Como $\triangle PDQ$ también es isósceles con $PD=DQ$, tenemos que $$\alpha’=:\angle DPQ = \angle DQP.$$ Por la suma de ángulos en el triángulo $APQ$, tenemos que $\alpha’+\beta + \gamma = 90^\circ$. Así, $\alpha = \alpha’$. Concluimos entonces que en el $\triangle PAQ$ los ángulos internos son $\angle A = \beta+ \gamma$, $\angle P = \alpha+\beta$ y $\angle Q = \gamma + \alpha$.

De esta forma, los triángulos $ABC$ y $AQP$ son semejantes por el criterio AA.

$\square$

Otra técnica útil para resolver problemas de geometría consiste en mostrar que un punto está en dos rectas notables (por ejemplo, en las medianas $AL$ y $BM$), deducir que entonces es el punto notable correspondiente (en este caso el gravicentro $G$), y usar la información de que entonces la recta por el tercer vértice y el punto es la tercer recta notable (que en el ejemplo diría que $CG$ es la mediana).

Recordatorio de geometría del círculo

Un tercer ingrediente básico para la geometría euclideana es entender qué pasa con las circunferencias. Tomemos una circunferencia $\Gamma$ y dos puntos fijos $A$ y $B$ sobre ella. Tomemos $C$ y $D$ otros dos puntos sobre $\Gamma$ distintos de $A$ y $B$ sobre el mismo arco definido por $A$ y $B$ y sea $E$ otro punto sobre $\Gamma$, en el arco opuesto. Entonces

  • Los ángulos $\angle ACB$ y $\angle ADB$ son iguales.
  • Los ángulos $\angle ACB$ y $\angle AEB$ son suplementarios, es decir, suman $180^\circ$.
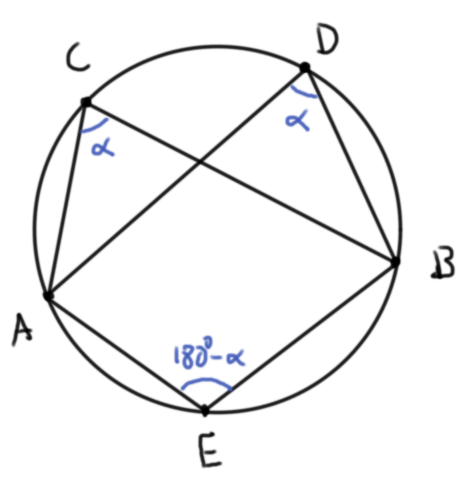
Ángulos en cuadriláteros cíclicos
Ángulos en cuadriláteros cíclicos

De hecho, este resultado es un si y sólo si. Para $A$, $B$, $C$, $D$ puntos distintos en el plano:

  • Si $\angle ACB$ y $\angle ADB$ son iguales, entonces $A$, $B$, $C$, $D$ son puntos sobre una circunferencia y $C$ y $D$ están en el mismo arco definido por $A$ y $B$ y
  • Si los ángulos $\angle ACB$ y $\angle ADB$ son suplementarios, entonces $A$, $B$, $C$, $D$ son puntos sobre una circunferencia y $C$ y $D$ están en arcos opuestos definidos por $A$ y $B$.

Cuando $A$, $B$, $C$ y $D$ son puntos distintos que yacen sobre una misma circunferencia, en ese orden, decimos que $ABCD$ es un cuadrilátero cíclico.

Teorema (potencia de un punto). Sea $P$ un punto y $\Gamma$ una circunferencia. Tomemos dos rectas por $P$ que corten a la circunferencia en puntos $A$, $B$, $C$ y $D$ como en alguna de las figuras. Entonces $PA\cdot PB = PC \cdot PD$.

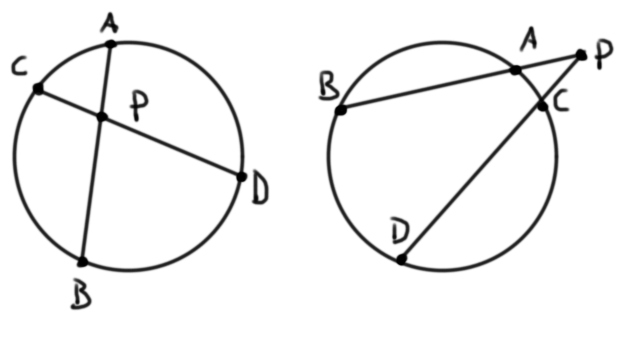
Diagrama para teorema de potencia de un punto
Diagrama para teorema de potencia de un punto

Veamos un problema de la Olimpiada Matemática de la Cuenca del Pacífico en donde confluyen algunas de estas ideas. Es el problema 1 de la edición de 2016.

Problema. Un triángulo $ABC$ es grandioso si para cualquier punto $D$ en el lado $BC$, cuando se toman los pies de las perpendiculares $P$ y $Q$ de $D$ a las rectas $AB$ y $AC$, respectivamente, sucede que la reflexión de $D$ en la recta $PQ$ cae sobre el circuncírculo del triángulo $ABC$.

Muestra que un triángulo $ABC$ es grandioso si y sólo si $\angle A = 90^\circ$ y $AB=AC$.

Sugerencia pre-solución. El problema dice que cierta condición se debe cumplir para todo punto $D$ en el lado $BC$. Considera algunos casos extremos de lo que puede ser $D$, de los que puedas obtener información de cómo debe ser el triángulo.

Solución. Para cualquier punto $D$ en el lado $BC$, vamos a llamar $D’$ a la reflexión de $D$ en la recta $PQ$. Primero veremos que si $ABC$ es grandioso, entonces es isósceles y con ángulo recto en $A$.

Como la hipótesis se cumple para cualquier punto $D$, en particular se cumple para cuando elegimos $D$ como el punto donde la bisectriz desde $A$ intersecta a $BC$. Nota que $P$ y $Q$ están en los rayos $AB$ y $AC$. Además, $P$ y $Q$ son reflexiones entre sí con respecto a la recta $AD$, de modo que $PQ$ es perpendicular a $AD$. Por esto, se tiene que $D’$ está en la recta $AD$, así que o es $A$, o es el segundo punto de intersección de la bisectriz en $A$ con el circuncírculo del triángulo. Como además $APDQ$ es un cuadrilátero cíclico, se tiene que $AD$ intersecta a $PQ$ y por lo tanto $D’=A$.

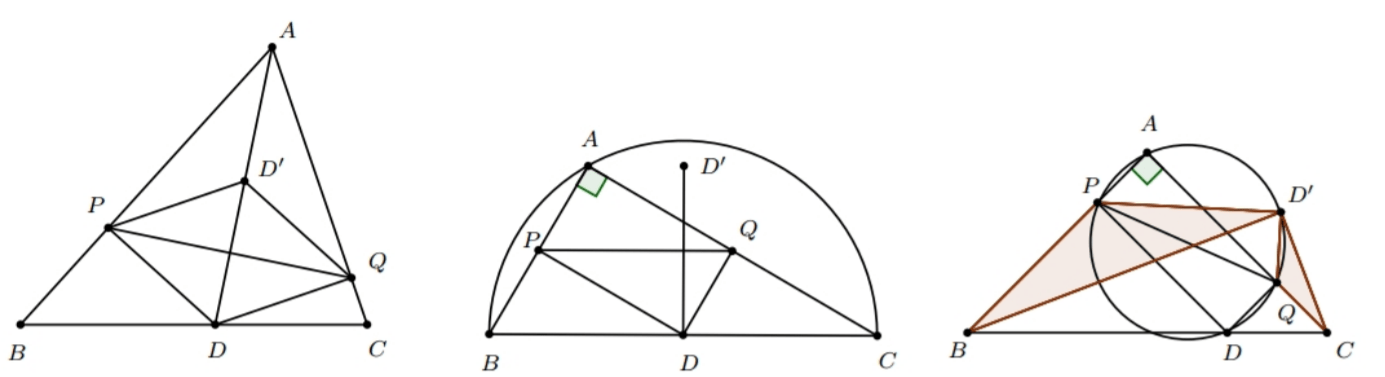
Imagen auxiliar para problema APMO
Imagen auxiliar para problema APMO

Tenemos entonces las igualdades de ángulos
\begin{align*}
\angle BAC &= \angle PD’Q \\
&= \angle PDQ \\
&= 180^\circ – \angle BAC.
\end{align*}

Concluimos entonces que $\angle BAC = 90^\circ$, que muestra que el triángulo es rectángulo en $A$.

Ahora tomamos a $D$ como el punto medio de $BC$, lo cual hace que $P$ y $Q$ sean los puntos medios de $AB$ y $AC$ respectivamente. Pero entonces $PQ$ es paralelo a $BC$ y por lo tanto $DD’$ es perpendicular a $BC$. La distancia de $D’$ a $BC$ es igual al circunradio del triángulo (pues $D’$ debe caer en el circuncírculo), y es igual a la distancia de $A$ a $BC$. Esto sólo puede suceder cuando $ABC$ es isósceles y con ángulo recto en $A$, como queríamos.

Veamos ahora que si $ABC$ es isósceles y de ángulo recto en $A$, entonces se cumple la propiedad para todo punto $D$ en $BC$. Como $D$ es la reflexión en $PQ$, tendríamos $D’P=DP=BP$. De manera similar, $D’Q=DQ=CQ$.

El cuadrilátero $APDQD’$ es cíclico de diámetro $PQ$, pues todos los ángulos $\angle PAQ$, $\angle PD’Q$ y $\angle PDQ$ son de $90^\circ$. De aquí, $\angle APD’= \angle AQD’$, de donde obtenemos que $\angle BPD’= \angle CQD’$. Con esto concluimos que $\triangle D’PB$ y $\triangle D’QC$ son semejantes. De aquí se sigue que

\begin{align*}
\angle PD’Q &= \angle PD’C+ \angle CD’Q\\
&=\angle PD’C + \angle BD’P\\
&= \angle BD’C.
\end{align*}

Como además tenemos $\frac{D’P}{D’Q}= \frac{D’B}{D’C}$, concluimos que también $\triangle D’PQ$ y $\triangle D’BC$ son semejantes. Pero como $\triangle DPQ$ y $\triangle D’PQ$ son congruentes, se obtiene que $$\angle BD’C=\angle PD’Q = \angle PDQ = 90^\circ.$$ Con esto concluimos que $D’$ yace en la circunferencia de diámetro $BC$, que es precisamente el circuncírculo de $\triangle ABC$.

$\square$

Más problemas

Puedes encontrar más problemas de geometría euclideana en la sección 8.1 del libro Problem Solving through Problems de Loren Larson. Para tener buenos fundamentos en geometría euclideana, se pueden revisar algunos textos en el área, como los cuadernos de la Olimpiada Mexicana de Matemáticas de Geometría y de Geometría: Ejercicios y problemas.

Seminario de Resolución de Problemas: Desigualdades básicas

Por Leonardo Ignacio Martínez Sandoval

2 respuestas

Introducción

En las entradas correspondientes a esta parte del curso aprenderemos varias técnicas que nos permitirán resolver problemas que involucren desigualdades. El área es enorme y hay libros enteros dedicados a ello. Nosotros sólo veremos algunas técnicas. Comenzaremos con desigualdades básicas y nos enfocaremos en los siguientes temas:

  • Desigualdad $x^2\geq 0$ y desigualdad del triángulo
  • Desigualdades de medias
  • La desigualdad de Cauchy-Schwarz
  • Técnicas de cálculo en desigualdades

En esta entrada veremos el primer inciso, que consiste de dos ideas muy sencillas:

Desigualdad $x^2\geq 0$. El cuadrado de cualquier número real es mayor o igual a cero. Es cero si y sólo si el número es cero.

Desigualdad del triángulo. Si $V$ es un espacio vectorial con norma $\norm{\cdot}$, entonces para cualesquiera vectores $u$ y $v$ se tiene que $$\norm{u}+\norm{v}\geq \norm{u+v}.$$

La desigualdad $x^2\geq 0$ parece muy inocente. Sin embargo, es una herramienta muy versátil cuando se combina con manipulaciones algebraicas creativas. La desigualdad del triángulo la estamos enunciando para espacios vectoriales con norma en general. Dos casos particulares que a lo mejor te son más familiares son los siguientes:

Desigualdad del triángulo para $\mathbb{R}$. Si $a$ y $b$ son números reales, entonces $|a|+|b| \geq |a+b|$.

Desigualdad del triángulo en $\mathbb{R}^n$. Si $ABC$ es un triángulo en el plano (o dimensiones más altas) , de lados de longitudes $\overline{AB}=c$, $\overline{BC}=a$ y $\overline{CA}=b$, entonces
\begin{align*}
a+b&\geq c\\
b+c &\geq a\\
c+a &\geq b.
\end{align*}

Si una de las igualdades se da, $ABC$ es un triángulo degenerado, es decir, con sus tres vértices alineados. En otro caso, todas las desigualdades son estrictas.

Veamos aplicaciones de estas desigualdades básicas.

La desigualdad $\frac{a^2+b^2}{2}\geq \sqrt{ab}$

Comenzaremos probando de dos formas distintas una desigualdad que también resulta útil en otras ocasiones.

Problema. Sean $a$ y $b$ números reales mayores o iguales a cero. Muestra que $$\frac{a+b}{2}\geq \sqrt{ab},$$ y que la igualdad se da si y sólo si $a$ y $b$ son iguales.

A esta desigualdad se le conoce como la desigualdad MA-MG para dos números reales. También forma parte de las desigualdades básicas que te ayudará conocer. Se llama así pues en el lado izquierdo tenemos a la media aritmética de los números $a$ y $b$, y al lado derecho tenemos la media geométrica de los números $a$ y $b$. En realidad la desigualdad se vale para más reales no negativos, pero esto lo veremos en otra entrada.

Sugerencia pre-solución. El problema se puede resolver tanto de manera algebraica, (usando $x^2\geq 0$) como de manera geométrica (usando la desigualdad del triángulo).

Para resolverlo de la primera forma, trabaja hacia atrás. Haz manipulaciones algebraicas para formular problemas equivalentes hasta que llegues a una desigualdad obvia.

Para resolverlo de la segunda forma, haz una figura en la que puedas representar tanto a la media geométrica como a la aritmética. Una forma de hacerlo es comenzar con una semicircunferencia de diámetro $a+b$.

Para identificar el caso de igualdad, haz un análisis de casos.

Solución algebraica. Queremos mostrar que $$\frac{a+b}{2}\geq \sqrt{ab}.$$ Pasando el dos multiplicando, y luego $2\sqrt{ab}$ restando al lado izquierdo, esta desigualdad igualdad ocurre si y sólo si $$a+b-2\sqrt{ab}\geq 0.$$ En el lado izquierdo identificamos un binomio al cuadrado, que se puede factorizar para dar la desigualdad equivalente $$\left(\sqrt{a}-\sqrt{b}\right)^2\geq 0.$$

Esta desigualdad es de la forma $x^2\geq 0$, así que es claramente cierta. La igualdad ocurre si y sólo si $\sqrt{a}-\sqrt{b}=0$, lo cual sucede si y sólo si $a=b$. Todos los pasos que hicimos son reversibles. Esto termina la solución.

$\square$

Solución geométrica. Consideremos la siguiente figura, en donde tenemos una semicircunferencia de diámetro $\overline{AB}=a+b$ y centro $O$. Aquí $C$ es un punto en $AB$ tal que $\overline{AC}=a$ y entonces $\overline{CB}=b$. Además, $D$ es un punto sobre la circunferencia tal que $DC$ es perpendicular a $AB$. Llamemos $d=\overline{CD}$.

Prueba visual de la desigualdad entre la media aritmética y media geométrica usando desigualdades básicas
Prueba visual de MA-MG

Como $\triangle AOD$ y $\triangle BOD$ son isósceles por tener dos lados iguales al radio de la circunferencia, tenemos que $\angle ADO = \angle DAO$ y $\angle BDO = \angle DBO$. Usando estas igualdades y que la suma de los ángulos internos de $\triangle ABD$ es $180^\circ$, se puede mostrar que el ángulo $ADB$ es de $90^\circ$.

De este modo, $\triangle ACD$ y $\triangle DCB$ son semejantes (por ser ambos semejantes a $\triangle ABD$ por criterio AA). Por la semejanza, tenemos que $$\frac{a}{d}=\frac{d}{b},$$ de donde $d=\sqrt{ab}$.

Para terminar la demostración, tomamos un punto $E$ sobre $DO$ tal que $\angle EOC = \angle ECO$. Por la desigualdad del triángulo en $\triangle DEC$, tenemos que

\begin{align*}
\sqrt{ab}&=\overline{DC}\\
&\leq \overline{DE} + \overline{EC}\\
&= \overline{DE} + \overline {EO}\\
&= \overline{DO}\\
&=\frac{a+b}{2}.
\end{align*}

Con esto demostramos la desigualdad. Para terminar el problema, necesitamos ver cuándo se dan los casos de igualdad. Se tiene la igualdad si y sólo si $\triangle DEC$ es un triángulo degenerado, lo cual sucede si y sólo si $E$ está en el segmento $DC$. Esto sólo es posible cuando $DO$ es perpendicular a $AB$, lo cual sucede si y sólo si $C=O$, si y sólo si $AC=CB$, si y sólo si $a=b$.

$\square$

Desigualdades básicas aplicadas a un problema de la Olimpiada Mexicana de Matemáticas

El siguiente problema apareció como parte de los exámenes selectivos que el Comité Nacional de la Olimpiada Mexicana de Matemáticas envía a los estados para seleccionar a sus estudiantes en distintas etapas. Tiene muchas formas de resolverse, pero veamos cómo se puede resolver con desigualdades básicas.

Problema. Sean $a,b,c,d$ reales positivos con $a^2+b^2+c^2+d^2=4$. Muestra que $$a^5+b^5+c^5+d^5 \geq a+b+c+d$$

Sugerencia pre-solución. Modifica el problema a mostrar como desigualdad auxiliar que para un real no negativo $x$ se tiene que $$x^5-2x^2-x+2\geq 0.$$ Esta desigualdad se puede demostrar usando que los cuadrados son no negativos.

Solución. Vamos a probar primero la desigualdad $$x^5-2x^2-x+2\geq 0.$$ Para que sea un poco más fácil, factorizaremos la expresión del lado izquierdo.

Notemos que $1$ es una raíz de $x^5-2x^2-x+2$, de modo que por el teorema del factor podemos factorizar $x-1$ del polinomio. Obtenemos que $$x^5-2x^2-x+2=(x-1)(x^4+x^3+x^2-x-2).$$

Notemos que, nuevamente, $1$ es una raíz de $(x^4+x^3+x^2-x-2)$. Al factorizar $x-1$ de nuevo, obtenemos que $$x^5-2x^2-x+2=(x-1)^2(x^3+2x^2+3x+2).$$

Ya estamos listos para probar la desigualdad que queremos. Notemos que $(x-1)^2\geq 0$ y que $x^3+2x^2+3x+2$ es mayor o igual que cero para $x\geq 0$ pues es un polinomio con puros coeficientes positivos. Esto prueba la desigualdad auxiliar. Reescribiéndola, tenemos que $$x^5\geq 2x^2+x-2.$$ Aplicándola en esta forma a los cuatro reales positivos $a,b,c,d$ del problema, y usando que la suma de cuadardos es $4$, obtenemos que
\begin{align*}
a^5 & + b^5+c^5+d^5\\
&\geq 2(a^2+b^2+c^2+d^2)+a+b+c+d-8\\
&=2\cdot 4 + a+b+c+d-8\\
&=a+b+c+d.
\end{align*}

Esto termina el problema.

$\square$

El primer paso parece un poco artificial. ¿Por qué queremos probar esa desigualdad auxiliar? En otra entrada de blog escribí cómo se puede llegar a las ideas de esta solución.

Desigualdad del triángulo aplicada a la construcción de tetraedros

Si pegamos cuatro triángulos equiláteros en el espacio se hace un tetraedro regular. De manera similar, si pegamos cuatro triángulos como el siguiente, también se hace un tetraedro en el espacio:

Pegar cuatro triángulos congruentes para hacer un tetraedro

La intuición nos dice que debería poderse con cualquier triángulo. Pero esta intuición está mal.

Problema. Sea $ABC$ un triángulo con un ángulo mayor a $90^\circ$. Muestra que no existe ningún tetraedro en el espacio tal que sus cuatro caras sean congruentes a $ABC$.

Sugerencia pre-solución. Procede por contradicción. Por simetría, puedes asumir que el ángulo mayor a $90^\circ$ es el ángulo en $A$. Usa como punto auxiliar al punto medio de $BC$ y usa desigualdades.

Solución. Una observación inicial es que si $ABC$ es un triángulo, $M$ es el punto medio de $BC$ y su ángulo interno en $A$ es mayor a $90^\circ$, entonces $2\overline{AM}<\overline{BC}$. Esto se muestra trazando una circunferencia de diámetro $BC$.

Desigualdad para la mediana en términos del ángulo que hace.

De hecho,

  • Un punto $X$ está sobre la circunfencia si y sólo si $\angle BXC = 90 ^\circ$, si y sólo si $\overline{OX}=\overline{OA}$.
  • $X$ está dentro de la circunferencia si y sólo si $\angle BXC > 90^\circ$, si y sólo si $\overline{OX}<\overline{OA}$ y
  • $X$ está fuera de la circunferencia si y sólo si $\angle BXC < 90^\circ$, si y sólo si $\overline{OX}>\overline{OA}$.

Resolvamos el problema. Sin pérdida de generalidad, el ángulo en $A$ es mayor a $90^\circ$. Entonces $\overline{AM}<\frac{\overline{BC}}{2}$, de donde $2\overline{AM}<\overline{BC}$.

Supongamos que se pudiera hacer en el espacio un tetraedro $WXYZ$ tal que cada una de las caras es congruente al triángulo $ABC$. Sin pérdida de generalidad, tenemos que
\begin{align*}
\overline{WX}&=\overline{YZ}=\overline{AB}\\
\overline{XY}&=\overline{ZW}=\overline{BC}\\
\overline{WY}&=\overline{XZ}=\overline{CA}.
\end{align*}

Tomemos el punto medio $M$ de $XY$. En $\triangle ZMW$, tenemos que
\begin{align*}
\overline{ZM}&=\overline{AM}\\
\overline{WM}&=\overline{AM}.
\end{align*}

Así, usando la desigualdad del triángulo en $\triangle ZMW$ tenemos que \begin{align*}
2\overline{AM}&=\overline{ZM}+\overline{WM}\\
&\geq \overline{ZW}\\
&=\overline{BC}.
\end{align*}

Esto es una contradicción con la desigualdad $2\overline{AM}<\overline{BC}$ que ya habíamos mostrado.

$\square$

Más problemas

Puedes encontrar más problemas de desigualdades básicas en la sección 7.1 del libro Problem Solving through Problems de Loren Larson. También puedes consultar más técnicas y problemas en el libro Desigualdades de la Olimpiada Mexicana de Matemáticas.

Hacer una figura

Por Leonardo Ignacio Martínez Sandoval

Deja un comentario

HeuristicasOtra herramienta muy importante para resolver problemas es poder plantear el problema de forma visual. Los seres humanos llevamos muchísimas generaciones viendo, mucho más de lo que llevamos platicando y por tanto hay algunos conocimientos que se facilitan utilizando la vista.

Veremos algunos ejemplos de problemas en los cuales hacer una figura es útil y en algunos casos necesario.

Ir a los videos…