Archivo de la etiqueta: Puntos críticos

Cálculo Diferencial e Integral III: Puntos críticos de campos escalares

Por Alejandro Antonio Estrada Franco

Deja un comentario

Introducción

En las unidades anteriores hemos desarrollado varias herramientas de la teoría de diferenciabilidad que nos permiten estudiar tanto a los campos escalares, como a los campos vectoriales. Hemos platicado un poco de las aplicaciones que esta teoría puede tener. En esta última unidad, profundizamos un poco más en cómo dichas herramientas nos permitirán hacer un análisis geométrico y cuantitativo de las funciones. Es decir, a partir de ciertas propiedades analíticas, hallaremos algunas cualidades de su comportamiento geométrico. En esta entrada estudiaremos una pregunta muy natural: ¿cuándo una función diferenciable alcanza su máximo o su mínimo? Para ello, necesitaremos definir qué quiere decir que algo sea un punto crítico de una función. Esto incluirá a los puntos más altos, los más bajos, local y globalmente y ciertos «puntos de quiebre» que llamamos puntos silla.

Introducción al estudio de los puntos críticos

Si tenemos un campo escalar $f:\mathbb{R}^n\to \mathbb{R}$, en muchas aplicaciones nos interesa poder decir cuándo alcanza sus valores máximos o mínimos. Y a veces eso sólo nos importa en una vecindad pequeña. La siguiente definición hace ciertas precisiones.

Definición. Sea $f:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}$ un campo escalar, y $\bar{a}\in S$.

  • Decimos que $f$ tiene un máximo absoluto (o máximo global) en $\bar{a}$ si $f(\bar{x})\leq f(\bar{a})$ para todo $\bar{x}\in S$. A $f(\bar{a})$ le llamamos el máximo absoluto (o máximo global) de $f$ en $S$.
  • Decimos que $f$ tiene un máximo relativo (o máximo local) en $\bar{a}$ si existe una bola abierta $B_{r}(\bar{a})$ tal que para todo $\bar{x}\in B_{r}(\bar{a})$ $f(\bar{x})\leq f(\bar{a})$.
  • Decimos que $f$ tiene un mínimo absoluto (o mínimo global) en $\bar{a}$ si $f(\bar{x})\geq f(\bar{a})$ para todo $\bar{x}\in S$. A $f(\bar{a})$ le llamamos el mínimo absoluto (o mínimo global) de $f$ en $S$.
  • Decimos que $f$ tiene un mínimo relativo (o mínimo local) en $\bar{a}$ si existe una bola abierta $B_{r}(\bar{a})$ tal que para todo $\bar{x}\in B_{r}(\bar{a})$ $f(\bar{x})\geq f(\bar{a})$.

En cualquiera de las situaciones anteriores, decimos que $f$ tiene un valor extremo (ya sea relativo o absoluto) en $\bar{a}$. Notemos que todo extremo absoluto en $S$ será extremo relativo al tomar una bola $B_{r}(\bar{a})$ que se quede contenida en $S$. Y de manera similar, todo extremo relativo se vuelve un extremo absoluto para la función restringida a la bola $B_{r}(\bar{a})$ que da la definición.

Usualmente, cuando no sabemos nada de una función $f$, puede ser muy difícil, si no imposible estudiar sus valores extremos. Sin embargo, la intuición que tenemos a partir de las funciones de una variable real es que deberíamos poder decir algo cuando la función que tenemos tiene cierta regularidad, por ejemplo, cuando es diferenciable. Por ejemplo, para funciones diferenciables $f:S\subseteq \mathbb{R}\to\mathbb{R}$ quizás recuerdes que si $f$ tiene un valor extremo en $\bar{a}\in S$, entonces $f'(\bar{a})=0$.

El siguiente teorema es el análogo en altas dimensiones de este resultado.

Teorema. Sea $f:S\subseteq \mathbb{R}^n\to \mathbb{R}$ un campo escalar. Supongamos que $f$ tiene un valor extremo en un punto interior $\bar{a}$ de $S$, y que $f$ es diferenciable en $\bar{a}$. Entonces el gradiente de $f$ se anula en $\bar{a}$, es decir, $$\triangledown f(\bar{a})=0.$$

Demostración. Demostraremos el resultado para cuando hay un máximo relativo en $\bar{a}$. El resto de los casos quedan como tarea moral. De la suposición, obtenemos que existe un $r>0$ tal que $f(\bar{x})\leq f(\bar{a})$ para todo $\bar{x}\in B_r(\bar{a})$. Escribamos $\bar{a}=(a_{1},\dots ,a_{n})$.

Para cada $i=1,\dots ,n$ tenemos:

\[ \frac{\partial f}{\partial x_{i}}(\bar{a})=\lim\limits_{\xi \to a_{i}}\frac{f(\xi \hat{e}_{i})-f(\bar{a})}{\xi -a_{i}}. \]

Además, ya que $f$ es diferenciable en $\bar{a}$ también se cumple

\[\lim\limits_{\xi \to a_{i}-}\frac{f(\xi e_{i})-f(a)}{\xi -a_{i}}=\lim\limits_{\xi \to a_{i}+}\frac{f(\xi e_i)-f(a)}{\xi -a_{i}}. \]

Dado que $f$ alcanza máximo en $\bar{a}$ tenemos que $f(\xi \hat{e}_{i})-f(\bar{a})\leq 0$. Para el límite por la izquierda tenemos $\xi-a_{i}\leq 0$, por lo tanto, en este caso

\[ \lim\limits_{\xi \to a_{i}-}\frac{f(\xi e_{i})-f(\bar{a})}{\xi -a_{i}}\geq 0.\]

Para el límite por la derecha tenemos $\xi-a_{i}\geq 0$, por lo cual

\[ \lim\limits_{\xi \to a_{i}+}\frac{f(\xi \hat{e}_{i})-f(\bar{a})}{\xi -a_{i}}\leq 0.\]

Pero la igualdad entre ambos límites dos dice entonces que

\[\frac{\partial f}{\partial x_{i}}(\bar{a}) =\lim\limits_{\xi \to a_{i}-}\frac{f(\xi \hat{e}_{i})-f(\bar{a})}{\xi -a_{i}}=0. \]

Por lo cual cada derivada parcial del campo vectorial es cero, y así el gradiente también lo es.

$\square$

Parece ser que es muy importante saber si para un campo vectorial su gradiente se anula, o no, en un punto. Por ello, introducimos dos nuevas definiciones.

Definición. Sea $f:S\subseteq \mathbb{R}^n \to \mathbb{R}$ un campo escalar diferenciable en un punto $\bar{a}$ en $S$. Diremos que $f$ tiene un punto estacionario en $\bar{a}$ si $\triangledown f(\bar{a})=0$.

Definición. Sea $f:S\subseteq \mathbb{R}^n \to \mathbb{R}$ un campo escalar y tomemos $\bar{a}$ en $S$. Diremos que $f$ tiene un punto crítico en $\bar{a}$ si o bien $f$ no es diferenciable en $\bar{a}$, o bien $f$ tiene un punto estacionario en $\bar{a}$.

Si $f$ tiene un valor extremo en $\bar{a}$ y no es diferenciable en $\bar{a}$, entonces tiene un punto crítico en $\bar{a}$. Si sí es diferenciable en $\bar{a}$ y $\bar{a}$ es un punto interior del dominio, por el teorema de arriba su gradiente se anula, así que tiene un punto estacionario y por lo tanto también un punto crítico en $\bar{a}$. La otra opción es que sea diferenciable en $\bar{a}$, pero que $\bar{a}$ no sea un punto interior del dominio.

Observación. Los valores extremos de $f$ se dan en los puntos críticos de $f$, o en puntos del dominio que no sean puntos interiores.

Esto nos da una receta para buscar valores extremos para un campo escalar. Los puntos candidatos a dar valores extremos son:

  1. Todos los puntos del dominio que no sean interiores.
  2. Aquellos puntos donde la función no sea diferenciable.
  3. Los puntos la función es diferenciable y el gradiente se anule.

Ya teniendo a estos candidatos, hay que tener cuidado, pues desafortunadamente no todos ellos serán puntos extremos. En la teoría que desarrollaremos a continuación, profundizaremos en el entendimiento de los puntos estacionarios y de los distintos comportamientos que las funciones de varias variables pueden tener.

Intuición geométrica

Para entender mejor qué quiere decir que el gradiente de un campo escalar se anuele, pensemos qué pasa en términos geomértricos en un caso particular, que podamos dibujar. Tomemos un campo escalar $f:\mathbb{R}^2\to \mathbb{R}$. La gráfica de la función $f$ es la superficie en $\mathbb{R}^{3}$ que se obtiene al variar los valores de $x,y$ en la expresión $(x,y,f(x,y))$.

Otra manera de pensar a esta gráfica es como un conjunto de nivel. Si definimos $F(x,y,z)=z-f(x,y)$, entonces la gráfica es precisamente el conjunto de nivel para $F$ en el valor $0$, pues precisamente $F(x,y,z)=0$ si y sólo si $z=f(x,y)$.

Si $f$ alcanza un extremo en $(a,b)$, entonces $\triangledown f(a,b)=0$ por lo cual $\triangledown F (a,b,f(a,b))=(0,0,1)$. Así, el gradiente es paralelo al eje $z$ y por lo tanto es un vector normal a la superficie $F(x,y,z)=0$. Esto lo podemos reinterpretar como que el plano tangente a la superficie citada en el punto $(a,b,f(a,b))$ es horizontal.

Puntos silla

Cuando la función es diferenciable y el gradiente se anula, en realida tenemos pocas situaciones que pueden ocurrir. Sin embargo, falta hablar de una de ellas. Vamos a introducirla mediante un ejemplo.

Ejemplo. Consideremos $f(x,y)=xy$. En este caso

$$\frac{\partial f}{\partial x}=y\hspace{0.5cm}\textup{y}\hspace{0.5cm}\frac{\partial f}{\partial y}=x.$$

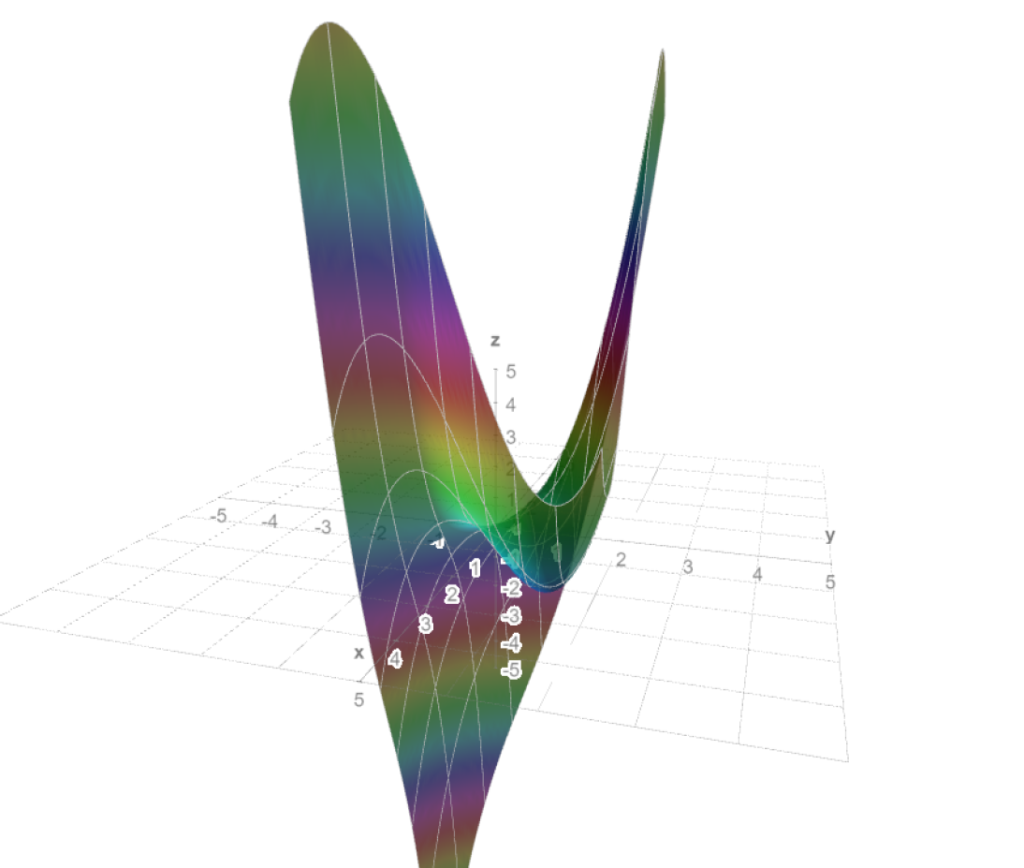
Si $(x,y)=(0,0)$, entonces las parciales se anulan, así que el gradiente también. Por ello, $(0,0)$ es un punto estacionario (y por lo tanto también crítico). Pero veremos a continuación que $f(0,0)=0$ no es máximo relativo ni mínimo relativo.

Tomemos $r>0$ abitrario y $\varepsilon= r/\sqrt{8}$. El punto $(\varepsilon ,\varepsilon)\in B_{r}(0)$ pues $\sqrt{\varepsilon ^{2}+\varepsilon ^{2}}$ es igual a $\sqrt{r^{2}/8\hspace{0.1cm}+\hspace{0.1cm}r^{2}/8}=r/2<r$. Análogamente, tenemos que el punto $(\varepsilon,-\varepsilon)\in B_{r}(0)$. Sin embargo $f(\varepsilon,-\varepsilon)=-r^{2}/8<0$, por lo que $0$ no es un mínimo local, también $f(\varepsilon,\varepsilon)=r^{2}/8>0$, por lo que $0$ tampoco es máximo local. En la Figura 1 tenemos un bosquejo de esta gráfica.

Figura 1

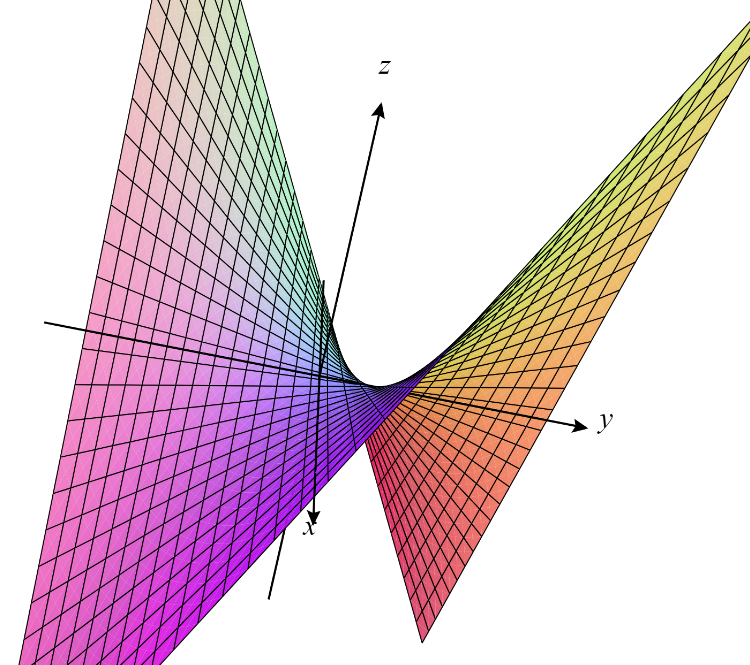
$\triangle$

Los puntos como los de este ejemplo tienen un nombre especial que definimos a continuación.

Definición. Sea $f:S\subseteq \mathbb{R}^n\to\mathbb{R}$ un campo escalar y $\bar{a}$ un punto estacionario de $f$. Diremos que $\bar{a}$ es un punto silla si para todo $r>0$ existen $\bar{u},\bar{v}\in B_{r}(\bar{a})$ tales que $f(\bar{u})<f(\bar{a})$ y $f(\bar{v})>f(\bar{a})$.

Determinar la naturaleza de un punto estacionario

Cuando tenemos un punto estacionario $\bar{a}$ de una función $f:\mathbb{R}^n\to \mathbb{R}$, tenemos diferenciabilidad de $f$ en $\bar{a}$. Si tenemos que la función es de clase $C^2$ en ese punto, entonces tenemos todavía más. La intuición nos dice que probablemente podamos decir mucho mejor cómo se comporta $f$ cerca de $\bar{a}$ y con un poco de suerte entender si tiene algún valor extremo o punto silla ahí, y bajo qué circunstancias.

En efecto, podemos enunciar resultados de este estilo. Por la fórmula de Taylor tenemos que

$$f(\bar{a}+\bar{y})=f(\bar{a})+\triangledown f (\bar{a}) \cdot y + \frac{1}{2}[\bar{y}]^tH(\bar{a})[\bar{y}]+||\bar{y}||^{2}E_{2}(\bar{a},\bar{y}),$$

en donde el error $||\bar{y}||^{2}E_{2}(\bar{a},\bar{y})$ se va a cero conforme $||\bar{y}||\to 0$. Recuerda que aquí $H(\bar{a})$ es la matriz hessiana de $f$ en $\bar{a}$. Como $f:\mathbb{R}^n\to \mathbb{R}$, se tiene que $H(\bar{a})\in M_n(\mathbb{R})$.

Para un punto estacionario $\bar{a}$ se cumple que $\triangledown f(\bar{a})=0$, así que de lo anterior tenemos

\[ f(\bar{a}+\bar{y})-f(\bar{a})=\frac{1}{2}[\bar{y}]^tH(\bar{a})[\bar{y}]+||\bar{y}||^{2}E_{2}(\bar{a},\bar{y}).\]

De manera heurística, dado que $\lim\limits_{||\bar{y}||\to 0}||\bar{y}||^{2}E_{2}(\bar{a},\bar{y})=0$, estamos invitados a pensar que el signo de $f(\bar{a}+\bar{y})-f(\bar{a})$ es el mismo que el la expresión $[\bar{y}]^tH(\bar{a})[\bar{y}]$. Pero como hemos platicado anteriormente, esto es una forma cuadrática en la variable $\bar{y}$, y podemos saber si es siempre positiva, siempre negativa o una mezcla de ambas, estudiando a la matriz hessiana $H(\bar{a})$.

Esta matriz es simétrica y de entradas reales, así que por el teorema espectral es diagonalizable mediante una matriz ortogonal $P$. Tenemos entonces que $P^tAP$ es una matriz diagonal $D$. Sabemos también que las entradas de la diagonal de $D$ son los eigenvalores $\lambda_1,\ldots,\lambda_n$ de $A$ contados con la multiplicidad que aparecen en el polinomio característico.

Teorema. Sea $X$ una matriz simétrica en $M_n(\mathbb{R})$. Consideremos la forma bilineal $\mathfrak{B}(\bar{v})=[\bar{v}]^tX[\bar{v}]$. Se cumple:

  1. $\mathfrak{B}(\bar{v})>0$ para todo $\bar{v}\neq \bar{0}$ si y sólo si todos los eigenvalores de $X$ son positivos.
  2. $\mathfrak{B}(\bar{v})<0$ para todo $\bar{v}\neq \bar{0}$ si y sólo si todos los eigenvalores de $X$ son negativos.

Demostración. Veamos la demostración del inciso 1.

$\Rightarrow )$ Por la discusión anterior, existe una matriz ortogonal $P$ tal que $P^tXP$ es diagonal, con entradas $\lambda_1,\ldots,\lambda_n$ que son los eigenvalores de $X$. Así, en alguna base ortonormal $\beta$ tenemos $$\mathfrak{B}(\bar{v})=\sum_{i=1}^{n}\lambda _{i}a_{i}^{2}$$ donde $\bar{a}=(a_{1},\dots ,a_{n})$ es el vector $\bar{v}$ en la base $\beta$. Si todos los eigenvalores son positivos, claramente $\mathfrak{B}(\bar{v})>0$, para todo $\bar{v}\neq \bar{0}$.

$\Leftarrow )$ Si $\mathfrak{B}(\bar{v})>0$ para todo $\bar{v}\neq \bar{0}$ podemos elegir $\bar{v}$ como el vector $e_k$ de la base $\beta$. Para esta elección de $\bar{v}$ tenemos $\mathfrak{B}(\hat{e_{k}})=\lambda _{k}$, de modo que para toda $k$, $\lambda _{k}>0$.

El inciso $2$ es análogo y deja como tarea moral su demostración.

$\square$

A las formas cuadráticas que cumplen el primer inciso ya las habíamos llamado positivas definidas. A las que cumplen el segundo inciso las llamaremos negativas definidas.

Combinando las ideas anteriores, podemos formalmente enunciar el teorema que nos habla de cómo son los puntos estacionarios en términos de los eigenvalores de la matriz hessiana.

Teorema. Consideremos un campo escalar $f:S\subseteq \mathbb{R}^n\to \mathbb{R}$ de clase $C^2$ en un cierto punto interior $\bar{a}\in S$. Supongamos que $\bar{a}$ es un punto estacionario.

  1. Si todos los eigenvalores de $H(\bar{a})$ son positivos, $f$ tiene un mínimo relativo en $\bar{a}$.
  2. Si todos los eigenvalores de $H(\bar{a})$ son negativos, $f$ tiene un máximo relativo en $\bar{a}$.
  3. Si $H(\bar{a})$ tiene por lo menos un eigenvalor positivo, y por lo menos un eigenvalor negativo, $f$ tiene punto silla en $\bar{a}$.

Antes de continuar, verifica que los tres puntos anteriores no cubren todos los casos posibles para los eigenvalores. ¿Qué casos nos faltan?

Demostración: Definamos la forma bilineal $\mathfrak{B}(\bar{v})=[\bar{v}]^tH(\bar{a})[\bar{v}]$ y usemos el teorema de Taylor para escribir

\[ \begin{equation}\label{eq:taylor}f(\bar{a}+\bar{v})-f(\bar{a})=\frac{1}{2}\mathfrak{B}(\bar{v})+||\bar{v}||^{2}E(\bar{a},\bar{v}) \end{equation} \]

con

\[ \begin{equation}\label{eq:error}\lim\limits_{\bar{v}\to \bar{0}}E(\bar{a},\bar{v})=0. \end{equation} \]

En primer lugar haremos el caso para los eigenvalores positivos. Sean $\lambda _{1},\dots ,\lambda_{n}$ los eigenvalores de $H(\bar{a})$. Sea $\lambda _{*}=\min\{ \lambda _{1},\dots ,\lambda _{n}\}$. Si $\varepsilon <\lambda_{*}$, para cada $i=1,\dots , n$ tenemos $\lambda _{i}-\varepsilon>0$. Además, los números $\lambda _{i}-\varepsilon$ son los eigenvalores de la matriz $H(\bar{a})-\varepsilon I$, la cual es simétrica porque $H(\bar{a})$ lo es. De acuerdo con nuestro teorema anterior la forma cuadrática $[\bar{v}]^t(H(\bar{a})-\varepsilon I)[\bar{v}]$ es definida positiva, y por lo tanto

$$[\bar{v}]^tH(\bar{a})[\bar{v}]>[\bar{v}]^t\varepsilon I [\bar{v}] = \varepsilon ||\bar{v}||^2.$$

Esto funciona para todo $\varepsilon <\lambda _{*}$. Tomando $\varepsilon =\frac{1}{2}\lambda _{*}$ obtenemos $\mathfrak{B}(\bar{v})>\frac{1}{2}||\bar{v}||^2$ para todo $\bar{v}\neq \bar{0}$. Por el límite de \eqref{eq:error} tenemos que existe $r>0$ tal que $|E(\bar{a},\bar{v})|<\frac{1}{4}\lambda _{*}$ para $0<||\bar{v}||<r$. En este caso se cumple

\begin{align*}0&\leq ||\bar{v}||^{2}|E(\bar{a},\bar{v})|\\ &<\frac{1}{4}\lambda _{*}||\bar{v}||^{2}\\ &<\frac{1}{2}\mathfrak{B}(\bar{v}),\end{align*}

Luego por la ecuación \eqref{eq:taylor} tenemos
\begin{align*}
f(\bar{a}+\bar{v})-f(\bar{a})&=\frac{1}{2}\mathfrak{B}(\bar{v})+||\bar{v}||^{2}E(\bar{a},\bar{v})\\
&\geq \frac{1}{2}\mathfrak{B}(\bar{v})-||\bar{v}||^{2}|E(\bar{a},\bar{v})|\\
&>0.
\end{align*}

Esto muestra que $f$ tiene un mínimo relativo en $\bar{a}$ para la vecindad $B_{r}(\bar{a})$.

Para probar la parte $2$ se usa exactamente el mismo proceder sólo que hay que considerar la función $-f$, lo cual quedará hacer como tarea moral.

Revisemos pues la parte del punto silla, la parte $3$. Consideremos $\lambda _{1}$ y $\lambda _{2}$ dos eigenvalores de $H(\bar{a})$ tales que $\lambda _1 <0$ y $\lambda _2 >0$. Pongamos $\lambda _{*}=\min\{ |\lambda _{1}|,|\lambda _{2}|\}$. Notemos que para todo $\varepsilon \in (-\lambda _{*},\lambda _{*})$ se tiene que $\lambda _{1}-\varepsilon$ y $\lambda _{2}-\varepsilon$ son números de signos opuestos y además eigenvalores de la matriz $H(\bar{a})-\varepsilon I$. Tomando vectores en dirección de los eigenvectores $\bar{v}_1$ y $\bar{v}_2$ correspondientes a $\lambda_1$ y $\lambda_2$ notamos que $[\bar{v}](H(\bar{a})-\varepsilon I)[\bar{v}]^{t}$ toma valores positivos y negativos en toda vecindad de $\bar{0}$. Finalmente escojamos $r>0$ de tal manera que $|E(\bar{a},\bar{v})|<\frac{1}{4}\varepsilon$ cuando $0<||\bar{v}||<r$. Usando las mismas desigualdades del la parte $1$, vemos que para $\bar{v}$ en la dirección de $\bar{v}_1$ la diferencia $f(\bar{a}+\bar{v})-f(\bar{a})$ es negativa y para $\bar{v}$ en la dirección de $\bar{v}_2$ es positiva. Así, $f$ tiene un punto silla en $\bar{a}$.

$\square$

Hay algunas situaciones en las que el teorema anterior no puede ser usado. Por ejemplo, cuando los eigenvalores de $H(\bar{a})$ son todos iguales a cero. En dicho caso, el teorema no funciona y no nos dice nada de si tenemos máximo, mínimo o punto silla, y de hecho cualquiera de esas cosas puede pasar.

Ejemplos de análisis de puntos críticos

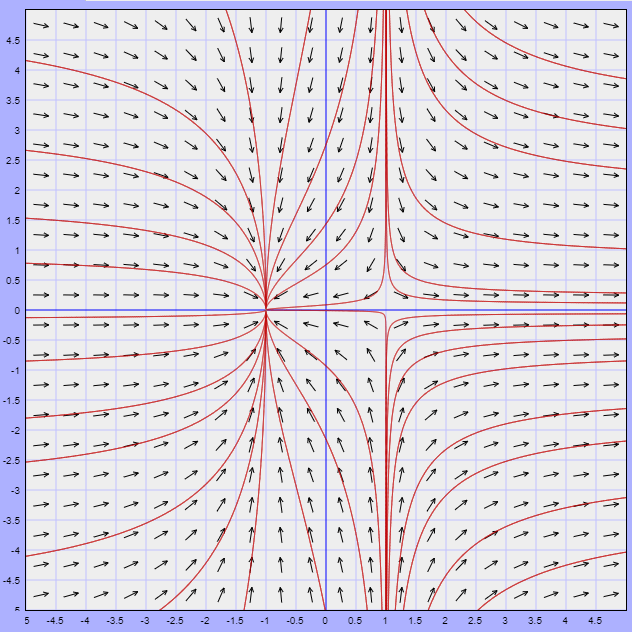
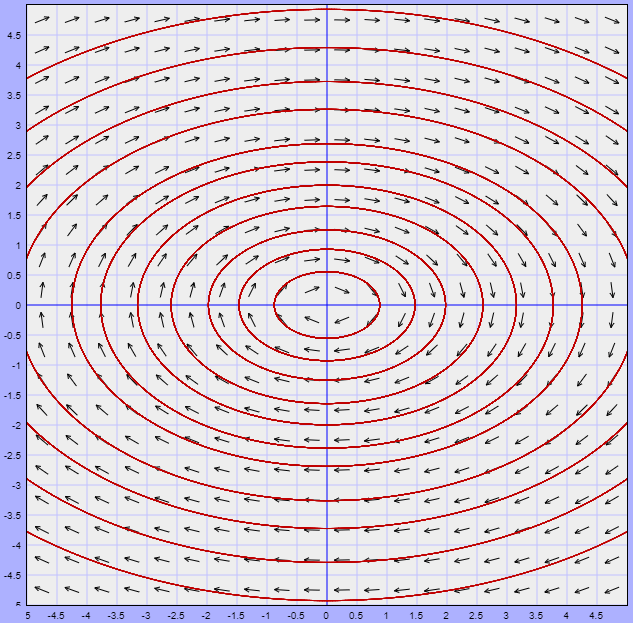
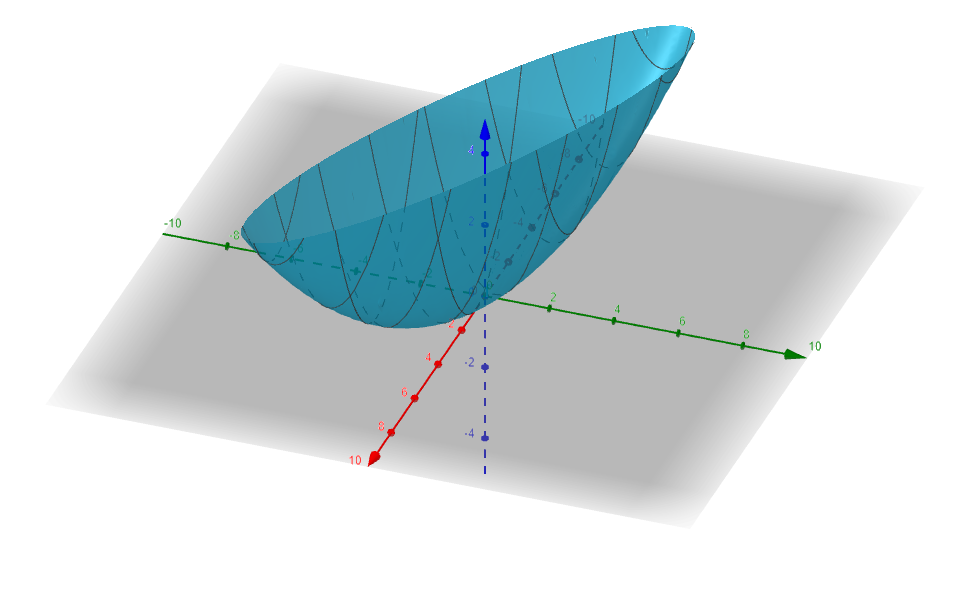
Ejemplo. Tomemos el campo escalar $f(x,y)=x^{2}+(y-1)^{2}$ y veamos cómo identificar y clasificar sus puntos estacionarios. Lo primero por hacer es encontrar el gradiente, que está dado por $$\triangledown f(x,y)=(2x,2(y-1)).$$ El gradiente se anula cuando $2x=0$ y $2(y-1)=0$, lo cual pasa si y sólo si $x=0$ y $y=1$. Esto dice que sólo hay un punto estacionario. Para determinar su naturaleza, encontraremos la matriz hessiana en este punto, así como los eigenvalores que tiene. La matriz hessiana es

\[ H(\bar{v})=\begin{pmatrix} \frac{\partial ^{2}f}{\partial x^{2}}(\bar{v}) & \frac{\partial ^{2}f}{\partial y \partial x}(\bar{v}) \\ \frac{\partial ^{2}f}{\partial x \partial y}(\bar{v}) & \frac{\partial ^{2}f}{\partial y^{2}}(\bar{v}) \end{pmatrix}=\begin{pmatrix} 2 & 0 \\ 0 & 2 \end{pmatrix}.\]

Notemos que la matriz hessiana ya está diagonalizada y es la misma para todo $\bar{v}$. En particular, en $(0,1)$ sus valores propios son $2$ y $2$, que son positivos. Así, la matriz hessiana es positiva definida y por lo tanto tenemos un mínimo local en el punto $(0,1)$. Esto lo confirma visualmente la gráfica de la Figura 2.

$\triangle$

Figura 2

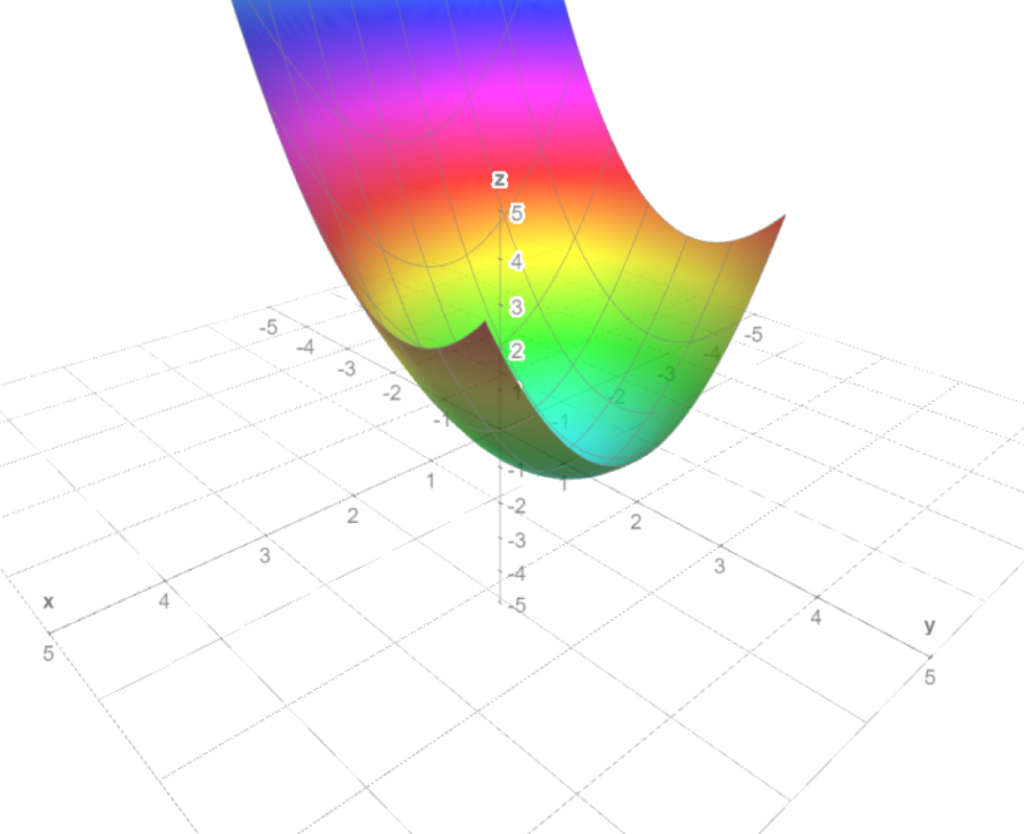
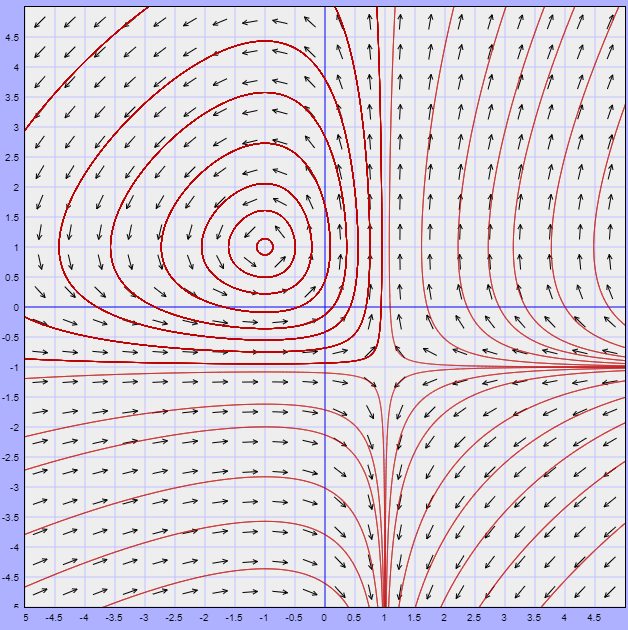
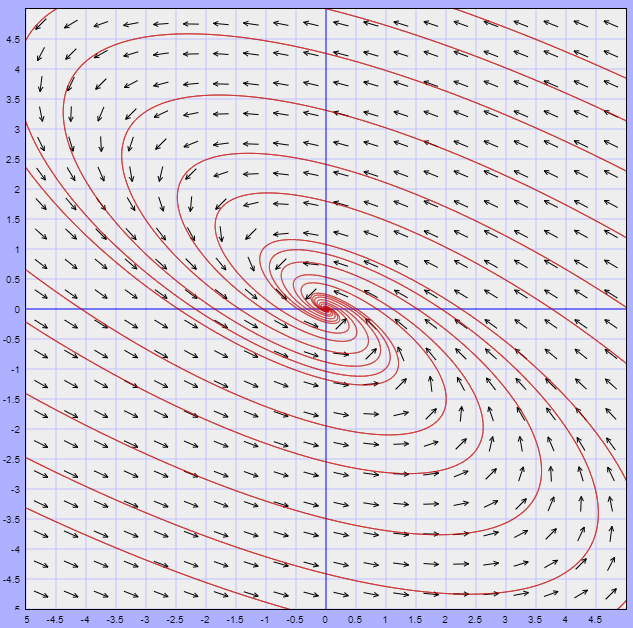
Ejemplo. Veamos cómo identificar y clasificar los puntos estacionarios del campo escalar $f(x,y)=x^{3}+y^{3}-3xy.$ Localicemos primero los puntos estacionarios. Para ello calculemos el gradiente $\triangledown f(x,y)=(3x^{2}-3y,3y^{2}-3x)$. Esto nos dice que los puntos estacionarios cumplen el sistema de ecuaciones

\[\left\{ \begin{matrix} 3x^2-3y=0\\ 3y^2-3x=0.\end{matrix} \right.\]

Puedes verificar que las únicas soluciones están dadas son los puntos $(0,0)$ y $(1,1)$ (Sugerencia. Multiplica la segunda ecuación por $x$ y suma ambas). La matriz hessiana es la siguiente:

\[ H(x,y)=\begin{pmatrix} 6x & -3 \\ -3 & 6y \end{pmatrix}.\]

En $(x,y)=(0,0)$ la matriz hessiana es $\begin{pmatrix} 0 & -3 \\ -3 & 0 \end{pmatrix}$. Para encontar sus eigenvalores calculamos el polinomio característico

\begin{align*} \det(H(0,0)-\lambda I)&=\begin{vmatrix} -\lambda & -3 \\ -3 & -\lambda \end{vmatrix} \\ &= \lambda ^{2}-9.\end{align*}

Las raíces del polinomio característico (y por lo tanto los eigenvalores) son $\lambda _{1}=3$ y $\lambda _{2}=-3$. Ya que tenemos valores propios de signos distintos tenemos un punto silla en $(0,0)$.

Para $(x,y)=(1,1)$ la cuenta correspondiente de polinomio característico es

\begin{align*} \det(H(1,1)-\lambda I)&=\begin{vmatrix} 6-\lambda & -3 \\ -3 & 6-\lambda\end{vmatrix}\\ &=(6-\lambda )^{2}-9.\end{align*}

Tras manipulaciones algebraicas, las raíces son $\lambda _{1}=9$, $\lambda _{2}=3$. Como ambas son positivas, en $(1,1)$ tenemos un mínimo.

Puedes confirmar visualmente todo lo que encontramos en la gráfica de esta función, la cual está en la Figura 3.

$\triangle$

Figura 3

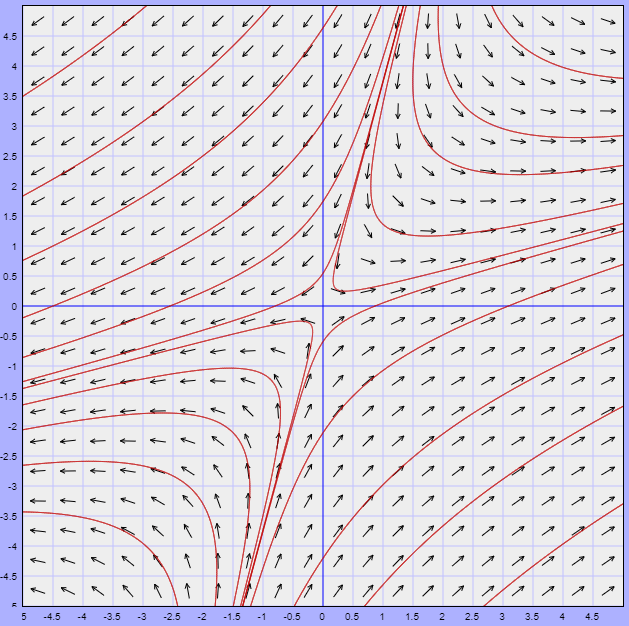
A continuación se muestra otro problema que se puede resolver con lo que hemos platicado. Imaginemos que queremos aproximar a la función $x^2$ mediante una función lineal $ax+b$. ¿Cuál es la mejor forma de elegir $a,b$ para que las funciones queden «cerquita» en el intervalo $[0,1]$? Esa cercanía se puede medir de muchas formas, pero una es pidiendo que una integral se haga chiquita.

Ejemplo. Determinemos qué valores de las constantes $a,b\in \mathbb{R}$ minimizan la siguiente integral

\[ \int_{0}^{1}[ax+b-x^2]^2 dx.\]

Trabajemos sobre la integral.

\begin{align*} \int_{0}^{1}[ax+b-x^{2}]^{2}dx&=\int_{0}^{1}(2abx+(a^{2}-2b)x^{2}-2ax^{3}+x^{4}+b^{2})dx\\ &=\int_{0}^{1}2abx\hspace{0.1cm}dx+\int_{0}^{1}(a^{2}-2b)x^{2}dx-\int_{0}^{1}2ax^{3}dx+\int_{0}^{1}x^{4}dx+\int_{0}^{1}b^{2}dx\\ &=b^{2}+\frac{1}{3}a^{2}+ab-\frac{2}{3}b-\frac{1}{2}a+\frac{1}{5}. \end{align*}

Es decir, tenemos

\[ \int_{0}^{1}[ax+b-x^{2}]^{2}dx=b^{2}+\frac{1}{3}a^{2}+ab-\frac{2}{3}b-\frac{1}{2}a+\frac{1}{5}.\]

Ahora definamos $f(a,b)=b^{2}+\frac{1}{3}a^{2}+ab-\frac{2}{3}b-\frac{1}{2}a+\frac{1}{5}$; basándonos en la forma general de la ecuación cuadrática de dos variables podemos comprobar rápidamente que $f$ nos dibuja una elipse en cada una de sus curvas de nivel. Continuando con nuestra misión, tenemos que $\triangledown f(a,b)=(\frac{2}{3}a+b-\frac{1}{2},2b+a-\frac{2}{3})$. Al resolver el sistema
\[\left\{\begin{matrix}\frac{2}{3}a+b-\frac{1}{2}=0\\2b+a-\frac{2}{3}=0,\end{matrix}\right.\]

hay una única solución $a=1$ y $b=-\frac{1}{6}$. Puedes verificar que la matriz hessiana es la siguiente en todo punto.

\[ H(\bar{v})=\begin{pmatrix} \frac{2}{3} & 1 \\ 1 & 2 \end{pmatrix}.\]

Para determinar si tenemos un mínimo, calculamos el polinomio característico como sigue

\begin{align*} \det(H(\bar{v})-\lambda I)&=\begin{vmatrix} \frac{2}{3}-\lambda & 1 \\ 1 & 2-\lambda \end{vmatrix}\\ &=\left( \frac{2}{3}-\lambda \right)\left( 2-\lambda\right)-1\\ &=\lambda ^{2}-\frac{8}{3}\lambda + \frac{1}{3}.\end{align*}

Esta expresión se anula para $\lambda _{1}=\frac{4+\sqrt{13}}{3}$ y $\lambda_{2}=\frac{4-\sqrt{13}}{3}$. Ambos son números positivos, por lo que en el único punto estacionario de $f$ tenemos un mínimo. Así el punto en el cual la integral se minimiza es $(a,b)=(1,-\frac{1}{6})$. Concluimos que la mejor función lineal $ax+b$ que aproxima a la función $x^2$ en el intervalo $[0,1]$ con la distancia inducida por la integral dada es la función $x-\frac{1}{6}$.

En la Figura 3 puedes ver un fragmento de la gráfica de la función $f(a,b)$ que nos interesa.

Figura 3. Gráfica de la función $f(a,b)$.

$\triangle$

Mas adelante…

La siguiente será nuestra última entrada del curso y nos permitirá resolver problemas de optimización en los que las variables que nos dan tengan ciertas restricciones. Esto debe recordarnos al teorema de la función implícita. En efecto, para demostrar los resultados de la siguiente entrada se necesitará este importante teorema, así que es recomendable que lo repases y recuerdes cómo se usa.

Tarea moral

  1. Identifica y clasifica los puntos estacionarios de los siguientes campos escalares:
    • $f(x,y)=(x-y+1)^{2}$
    • $f(x,y)=(x^{2}+y^{2})e^{-(x^{2}+y^{2})}$
    • $f(x,y)=\sin(x)\cos(x)$.
  2. Determina si hay constantes $a,b\in \mathbb{R}$ tales que el valor de la integral \[\int_{0}^{1}[ax+b-f(x)]^{2}dx \] sea mínima para $f(x)=(x^{2}+1)^{-1}$. Esto en cierto sentido nos dice «cuál es la mejor aproximación lineal para $\frac{1}{x^2+1}$».
  3. Este problema habla de lo que se conoce como el método de los mínimos cuadrados. Consideremos $n$ puntos $(x_{i},y_{i})$ en $\mathbb{R}^2$, todos distintos. En general es imposible hallar una recta que pase por todos y cada uno de estos puntos; es decir, hallar una función $f(x)=ax+b$ tal que $f(x_{i})=y_{i}$ para cada $i$. Sin embargo, sí es posible encontrar una función lineal $f(x)=ax+b$ que minimice el error cuadrático total que está dado por \[ E(a,b)=\sum_{i=1}^{n}[f(x_{i})-y_{i}]^{2}.\] Determina los valores de $a$ y $b$ para que esto ocurra. Sugerencia. Trabaja con el campo escalar $E(a,b)$ recuerda que los puntos $(x_{i},y_{i})$ son constantes.
  4. Completa la demostración de que si una matriz $X$ tiene puros eigenvalores negativos, entonces es negativa definida.
  5. En el teorema de clasificación de puntos estacionarios, muestra que en efecto si la matriz hessiana es negativa definida, entonces el punto estacionario es un punto en donde la función tiene máximo local.

Entradas relacionadas

Ecuaciones Diferenciales I: Sistemas autónomos, puntos de equilibrio y su estabilidad

Por Omar González Franco

2 respuestas

Si hay un Dios, es un gran matemático.
– Paul Dirac

Introducción

En la entrada anterior realizamos un desarrollo geométrico y un tanto cualitativo de un sistema de dos ecuaciones diferenciales lineales de primer orden homogéneas con coeficientes constantes con el fin de introducirnos a la teoría cualitativa de las ecuaciones diferenciales. En dicha entrada justificamos la razón por la que estudiaremos principalmente los sistemas compuestos por dos ecuaciones de primer orden.

En esta entrada presentaremos formalmente la teoría cualitativa y geométrica de los sistemas tanto lineales como no lineales compuestos por dos ecuaciones diferenciales de primer orden.

Teoría cualitativa

A lo largo del curso nos hemos centrado en el problema de obtener soluciones, hemos desarrollado una serie de métodos de resolución de ciertos tipos de ecuaciones diferenciales y sistemas lineales. Lo que haremos ahora es dar otro enfoque al estudio de las ecuaciones diferenciales planteándonos obtener información cualitativa sobre el comportamiento de las soluciones.

Hemos visto que, a medida que aumenta la complejidad de las ecuaciones diferenciales, o los sistemas lineales, mayor es la dificultad que tenemos para obtener soluciones. Existen incluso ecuaciones que no se sabe cómo se resuelven o ecuaciones en las que obtener su solución es bastante costoso, por lo que una alternativa será hacer un análisis cualitativo, pues muchas veces bastará conocer el comportamiento de las soluciones.

Recordemos que, además de hacer un análisis cualitativo, estamos interesados en hacer un análisis geométrico, así que centraremos nuestra atención en los sistemas de dos ecuaciones diferenciales ya que, como vimos en la entrada anterior, tenemos la oportunidad de hacer gráficas en dos dimensiones, es decir, podremos visualizar sin ningún problema el plano fase.

Sistemas autónomos

En la entrada anterior vimos la importancia de que el sistema no dependa explícitamente de la variable independiente $t$ para poder hacer nuestro desarrollo geométrico. Este tipo de sistemas tienen un nombre particular.

El sistema se denomina autónomo debido a que la variable independiente $t$ no aparece explícitamente en las ecuaciones del sistema. Las condiciones de $F_{1}$ y $F_{2}$ garantizan la existencia y unicidad de la solución definida $\forall$ $t \in \mathbb{R}$ del problema de valores iniciales

\begin{align*}
x^{\prime} &= F_{1}(x, y) \hspace{1.2cm} x(t_{0}) = x_{0} \\
y^{\prime} &= F_{2}(x, y), \hspace{1cm} y(t_{0}) = y_{0} \label{2} \tag{2}
\end{align*}

para cualquier $t_{0} \in \mathbb{R}$ y $(x_{0},y_{0}) \in \mathbb{R}^{2}$.

En el caso en el que tenemos una ecuación de segundo orden autónoma

$$\dfrac{d^{2}x}{dt^{2}} = f \left( x, \dfrac{dx}{dt} \right) \label{3} \tag{3}$$

Se puede convertir en un sistema autónomo introduciendo una nueva variable $y = \dfrac{dx}{dt}$, obteniendo el sistema

\begin{align*}
x^{\prime} &= y \\
y^{\prime} &= f(x, y) \label{4} \tag{4}
\end{align*}

Sistemas autónomos lineales

En el caso en el que el sistema autónomo es lineal y con coeficientes constantes, entonces lo podemos escribir como

\begin{align*}
x^{\prime} &= ax + by \\
y^{\prime} &= cx + dy \label{5} \tag{5}
\end{align*}

En donde $a, b, c$ y $d$ son constantes, $x = x(t): \mathbb{R} \rightarrow \mathbb{R}$ y $y = y(t): \mathbb{R} \rightarrow \mathbb{R}$.

Definimos las funciones $F_{1}: \mathbb{R}^{2} \rightarrow \mathbb{R}$ y $F_{2}: \mathbb{R}^{2} \rightarrow \mathbb{R}$ como

$$F_{1}(x, y) = ax + by \hspace{1cm} y \hspace{1cm} F_{2}(x, y) = cx + dy \label{6} \tag{6}$$

Podemos definir la función vectorial $F: \mathbb{R}^{2} \rightarrow \mathbb{R}^{2}$ como

$$F(x, y) = (F_{1}(x, y), F_{2}(x, y)) = (ax +by, cx +dy) \label{7} \tag{7}$$

Entonces el sistema autónomo (\ref{5}) se puede escribir como

$$Y^{\prime} = F(x, y) \label{8} \tag{8}$$

Por su puesto, si se define la matriz de coeficientes

$$\mathbf{A} = \begin{pmatrix}
a & b \\ c & d
\end{pmatrix} \label{9} \tag{9}$$

entonces el sistema lineal (\ref{5}) se puede escribir como

$$\begin{pmatrix}
x^{\prime} \\ y^{\prime}
\end{pmatrix} = \begin{pmatrix}
a & b \\ c & d
\end{pmatrix} \begin{pmatrix}
x \\ y
\end{pmatrix} \label{10} \tag{10}$$

o bien,

$$\mathbf{Y}^{\prime} = \mathbf{AY} \label{11} \tag{11}$$

como es costumbre.

Notación: Hemos visto que no necesariamente haremos uso de la notación vectorial como en la unidad anterior, así que con fines de notación usaremos letras en negrita cuando trabajemos con vectores (o matrices) y letras sin negrita cuando no usemos la notación vectorial a pesar de indicar lo mismo. Por ejemplo, la solución de un sistema en notación vectorial la escribiremos como

$$\mathbf{Y}(t) = \begin{pmatrix}
x(t) \\ y(t)
\end{pmatrix}$$

mientras que la misma solución sin notación vectorial como

$$Y(t) = (x(t), y(t))$$

Está última notación nos será de utilidad para representar coordenadas en el plano $\mathbb{R}^{2}$.

Algunas definiciones

Las siguientes definiciones son generales, para cualquier sistema autónomo de dos ecuaciones diferenciales de primer orden.

Las soluciones de un sistema autónomo reciben un nombre especial.

En la entrada anterior ya trabajamos con el plano fase, definámoslo formalmente.

Cada punto de la curva $C$ determina el estado del sistema en un instante $t$ correspondiente a una condición inicial determinada.

En la entrada anterior vimos que en cada punto $(x, y)$ de una curva solución, el vector

$$F(x, y) = (F_{1}(x, y), F_{2}(x, y))$$

es un vector tangente a dicha curva en cada punto $(x, y)$. El conjunto de vectores tangentes recibe un nombre.

Con estas definiciones podemos decir que el plano fase es una representación geométrica de todas las trayectorias de un sistema dinámico en el plano, donde cada curva representa una condición inicial diferente. Entendemos por sistema dinámico al sistema cuyo estado evoluciona con el tiempo.

Como ejemplo visualicemos el campo vectorial de dos sistemas de ecuaciones diferenciales sencillos usando la herramienta que ya conocemos.

Ejemplo: Visualizar el campo vectorial del sistema lineal

\begin{align*}
x^{\prime} &= x \\
y^{\prime} &= y
\end{align*}

Solución: La función vectorial es

$$F(x, y) = (x, y)$$

El campo vectorial en el plano fase se ilustra a continuación.

Campo vectorial $F(x, y) = (x, y)$.

Los vectores del campo vectorial siempre señalan directamente alejándose del origen.

$\square$

Ejemplo: Visualizar el campo vectorial del sistema lineal

\begin{align*}
x^{\prime} &= -x \\
y^{\prime} &= -y
\end{align*}

Solución: La función vectorial es

$$F(x, y)= (-x, -y)$$

El campo vectorial se ilustra a continuación.

Campo vectorial $F(x, y)= (-x, -y)$.

En este caso los vectores del campo vectorial apuntan directamente hacia el origen.

$\square$

Como el campo vectorial es tangente a las soluciones del sistema, entonces en los dos ejemplos anteriores deducimos que las soluciones son rectas con distintas pendientes para cada solución particular.

En la herramienta que utilizamos se puede dar clic sobre el campo vectorial para trazar distintas soluciones. Inténtalo con los ejemplos anteriores.

Puntos de equilibrio

Por sí solo el campo vectorial de un sistema ya nos da información sobre el comportamiento que presentan las trayectorias sin siquiera conocer explícitamente las soluciones del sistema, sin embargo en cada plano fase existe al menos un punto particular sobre el cual dependerá casi por completo el comportamiento de las soluciones, dichos puntos se conocen como puntos de equilibrio.

Una solución constante

$$Y(t) = (x(t), y(t)) = (x_{0}, y_{0}) \label{13} \tag{13}$$

para todo $t \in \mathbb{R}$ define únicamente un punto $(x_{0}, y_{0})$ en el plano fase y verifica que

$$F_{1}(x_{0}, y_{0}) = F_{2}(x_{0}, y_{0}) = 0 \label{14} \tag{14}$$

es decir,

$$F(x_{0}, y_{0}) = (0, 0) \label{15} \tag{15}$$

Como ejemplo determinemos los puntos de equilibrio de dos sistemas de ecuaciones diferenciales.

Ejemplo: Hallar los puntos de equilibrio del siguiente sistema de ecuaciones diferenciales y visualizar que ocurre alrededor de ellos.

\begin{align*}
x^{\prime} &= (x -1)(y -1) \\
y^{\prime} &= (x + 1)(y + 1)
\end{align*}

Solución: La función vectorial es

$$F(x, y) = ((x -1)(y -1), (x + 1)(y + 1))$$

Los puntos de equilibrio $(x_{0}, y_{0})$ son tales que

$$F(x_{0},y_{0}) = (0, 0)$$

es decir, tales que

$$((x_{0} -1)(y_{0} -1), (x_{0} + 1)(y_{0} + 1)) = (0, 0)$$

El sistema de ecuaciones que se forma es

\begin{align*}
(x_{0} -1) (y_{0} -1) &= 0 \\
(x_{0} + 1) (y_{0} + 1) &= 0
\end{align*}

Los puntos que verifican el sistema son

$$(x_{0}, y_{0}) = (1, -1) \hspace{1cm} y \hspace{1cm} (x_{0}, y_{0}) = (-1, 1)$$

Hemos encontrado dos puntos de equilibrio. Veamos cómo se ve el campo vectorial del sistema y que forma tienen las soluciones alrededor de estos puntos.

Plano fase: Campo vectorial, puntos de equilibrio y trayectorias del sistema.

Recordemos que la dirección de las trayectorias está definida por la dirección del campo vectorial. En el plano fase observamos que alrededor del punto de equilibrio $(-1, 1)$ las soluciones son trayectorias cerradas que giran en torno a dicho punto, mientras que alrededor del punto de equilibrio $(1, -1)$ las trayectorias tienden a acercarse a dicho punto, pero cuando se aproximan a él inmediatamente se alejan.

$\square$

Más adelante caracterizaremos a los puntos de equilibrio de acuerdo al tipo de comportamiento que tienen las trayectorias alrededor de él. Por ahora notemos estas características. Veamos un ejemplo más.

Ejemplo: Hallar los puntos de equilibrio del siguiente sistema de ecuaciones diferenciales y visualizar que ocurre alrededor de ellos.

\begin{align*}
x^{\prime} &= x^{2} -1 \\
y^{\prime} &= -y
\end{align*}

Solución: La función vectorial es

$$F(x, y) = (x^{2} -1, -y)$$

Si

$$F(x_{0}, y_{0}) = (0,0)$$

entonces,

$$(x^{2}_{0} -1, -y_{0}) = (0, 0)$$

El sistema de ecuaciones que se obtiene es

\begin{align*}
x^{2}_{0} -1 &= 0 \\
-y_{0} &= 0
\end{align*}

De la segunda ecuación obtenemos inmediatamente que $y_{0} = 0$ y de la primer ecuación obtenemos que $x^{2}_{0}= 1$. Por lo tanto, los puntos de equilibrio son

$$(x_{0}, y_{0}) = (-1, 0) \hspace{1cm} y \hspace{1cm} (x_{0}, y_{0}) = (1, 0)$$

Veamos cómo se ve el plano fase.

Plano fase: Campo vectorial, puntos de equilibrio y trayectorias del sistema.

En esta ocasión observamos que las trayectorias tienden hacía el punto de equilibrio $(-1, 0)$, mientras que alrededor del punto de equilibrio $(1, 0)$ las trayectorias tienden a alejarse de él.

$\square$

Con estos dos ejemplos observamos tres cualidades de las trayectorias alrededor de los puntos de equilibrio. El primero de ellos es que hay trayectorias cerradas que permanecen cerca de un punto de equilibrio, pero que nunca llegan a él, por otro lado, hay trayectorias que tienden directamente hacía a un punto de equilibrio y finalmente hay puntos de equilibrio en los que las trayectorias tienden a alejarse de él. A esto se le conoce como estabilidad de los puntos de equilibrio y lo estudiaremos más adelante en esta entrada.

Un hecho importante es que los sistemas de los dos ejemplos anteriores son sistemas no lineales y ya comenzamos a caracterizar y visualizar el comportamiento de las soluciones a pesar de no conocer ningún método para obtener las soluciones explícitamente, de ahí la importancia de este análisis cualitativo.

Cabe mencionar que resolver sistemas no lineales puede ser muy complejo, al menos para un primer curso de ecuaciones diferenciales, es por ello que dedicamos la unidad anterior al caso exclusivamente lineal.

Por otro lado, es claro que cada punto del plano fase, o bien es un punto de equilibrio, o bien pasa por él una única trayectoria. Existe un resultado importante que nos permite saber cuando el único punto de equilibrio de un sistema lineal es el origen.

Demostración: Consideremos el sistema lineal ${\mathbf{Y}}’ = \mathbf{AY}$ cuya matriz de coeficientes es (\ref{9}), entonces podemos escribir al sistema lineal como

$$\begin{pmatrix}
x^{\prime} \\ y^{\prime}
\end{pmatrix} = \begin{pmatrix}
a & b \\ c & d
\end{pmatrix} \begin{pmatrix}
x \\ y
\end{pmatrix}$$

Sabemos que un punto $Y_{0} = (x_{0}, y_{0})$ es un punto de equilibrio del sistema si el campo vectorial en $Y_{0}$ es cero, es decir, si

$$F(x_{0}, y_{0}) = (0, 0)$$

Sabemos, por otro lado, que el sistema lineal también se puede escribir en términos de la función vectorial $F$ como

$$F(x, y) = (F_{1}(x, y), F_{2}(x, y)) = (ax + by, cx + dy)$$

Entonces $Y_{0} = (x_{0}, y_{0})$ es un punto de equilibrio si ocurre que

$$F(x_{0}, y_{0}) = (ax_{0} + by_{0}, cx_{0} + dy_{0}) = (0, 0) \label{16} \tag{16}$$

es decir, debe ocurrir que

$$\begin{pmatrix}
a & b \\ c & d
\end{pmatrix} \begin{pmatrix}
x_{0} \\ y_{0}
\end{pmatrix} = \begin{pmatrix}
ax_{0} + by_{0} \\ cx_{0} + dy_{0}
\end{pmatrix} = \begin{pmatrix}
0 \\ 0
\end{pmatrix} \label{17} \tag{17}$$

El par de ecuaciones que se tiene es

\begin{align*}
ax_{0} + by_{0} &= 0 \\
cx_{0} + dy_{0} &= 0 \label{18} \tag{18}
\end{align*}

Es claro que $(x_{0}, y_{0}) = (0, 0)$ es una solución de las ecuaciones (\ref{18}). Por tanto, $Y_{0} = (0, 0)$ es un punto de equilibrio y la función constante

$$Y(t) = (0, 0) \label{19} \tag{19}$$

para toda $t \in \mathbb{R}$ es una solución del sistema lineal. Ahora veamos si existe otra solución que no sea la trivial.

Cualesquiera puntos de equilibrio $(x_{0}, y_{0}) \neq (0, 0)$ deben también satisfacer el sistema (\ref{18}). Para encontrarlos supongamos por ahora que $a\neq 0$, de la primer ecuación se obtiene que

$$x_{0} = -\dfrac{b}{a}y_{0} \label{20} \tag{20}$$

Sustituyendo en la segunda ecuación, se tiene

$$c \left( -\dfrac{b}{a} \right) y_{0} + dy_{0} = 0$$

que puede escribirse como

$$(ad -bc)y_{0} = 0 \label{21} \tag{21}$$

Entonces,

$$y_{0} = 0 \hspace{1cm} o \hspace{1cm} ad -bc =0$$

Si $y_{0} = 0$, entonces $x_{0} = 0$ y de nuevo obtenemos la solución trivial. Por tanto, un sistema lineal tiene puntos de equilibrio no triviales sólo si

$$ad -bc = 0$$

es decir si el determinante de $\mathbf{A}$ es igual a cero. Esto significa que si $|\mathbf{A}| \neq 0$, entonces el único punto de equilibrio del sistema lineal es el origen.

$\square$

Una observación importante en la demostración es que el cálculo que hicimos no depende de los valores de los coeficientes $a, b, c$ y $d$, sólo de la condición $a \neq 0$, por tanto ¡todo sistema lineal tiene un punto de equilibrio en el origen!.

Estabilidad de puntos de equilibrio

Veíamos que hay tres cualidades de las trayectorias alrededor de puntos de equilibrio. De acuerdo al comportamiento que tengan las trayectorias alrededor de los puntos de equilibrio éstos recibirán un nombre.

Lo que esta definición nos dice es que si una trayectoria está cerca del punto de equilibrio $(x_{0}, y_{0})$, entonces se mantendrá cerca de él para $t_{0} \leq t \rightarrow \infty$.

Es este caso las trayectorias cercanas al punto de equilibrio $(x_{0}, y_{0})$ no sólo se mantendrán cerca de dicho punto, sino que tenderán a él para $t_{0} \leq t \rightarrow \infty$.

Contrario a un punto de equilibrio estable, si las trayectorias están cerca del punto de equilibrio $(x_{0}, y_{0})$, entonces se alejarán de él para $t_{0} \leq t \rightarrow \infty$.

Las definiciones anteriores son aplicables a cualquier punto de equilibrio $(x_{0}, y_{0})$, sin embargo las definiciones se vuelven más intuitivas si el punto de equilibrio sobre el que se trabaja es el origen $(x_{0}, y_{0}) = (0, 0)$ del plano $XY$ o plano fase.

Supongamos que el punto de equilibrio del sistema (\ref{1}) es el origen y que está aislado, esto es que existe un entorno donde no hay otro punto de equilibrio. Notemos que el hecho de que el punto de equilibrio sea el origen no supone ningún tipo de restricción ya que se puede hacer el cambio de variable

\begin{align*}
\hat{x} &= x -x_{0} \\
\hat{y} &= y -y_{0} \label{24} \tag{24}
\end{align*}

y transformar al sistema (\ref{1}) en

\begin{align*}
\hat{x}^{\prime} &= F(\hat{x} + x_{0}, \hat{y} + y_{0}) \\
\hat{y}^{\prime} &= G(\hat{x} + x_{0}, \hat{y} + y_{0}) \label{25} \tag{25}
\end{align*}

cuyo punto de equilibrio es el punto $(0, 0)$. En estas condiciones definimos de manera más intuitiva la estabilidad de un punto de equilibrio.

Realicemos algunos ejemplos de manera gráfica.

Ejemplo: Definir el tipo de punto de equilibrio del siguiente sistema visualizando el comportamiento de las trayectorias alrededor de dicho punto.

\begin{align*}
x^{\prime} &= 5y \\
y^{\prime} &= -2x
\end{align*}

Solución: Es claro que el punto de equilibrio es el origen ya que si $x = 0$ y $y = 0$, entonces

$$F(0, 0) = (0, 0)$$

El campo vectorial y algunas trayectorias del sistema se muestran a continuación.

Plano fase del sistema.

Observamos que las trayectorias son cerradas, lo que significa que todas las que están cerca del punto de equilibrio permanecerán cerca de él, pero nunca llegarán a él conforme $t \rightarrow \infty$. De acuerdo a las definiciones anteriores, el punto de equilibrio corresponde a un punto estable. Veremos más adelante que este tipo de trayectorias corresponden a soluciones periódicas.

$\square$

Ejemplo: Definir el tipo de punto de equilibrio del siguiente sistema visualizando el comportamiento de las trayectorias alrededor de dicho punto.

\begin{align*}
x^{\prime} &= -3x -4y \\
y^{\prime} &= 2x + y
\end{align*}

Solución: Como el sistema es lineal podemos aplicar el teorema visto para verificar que el único punto de equilibrio del sistemas es el origen. La matriz de coeficientes es

$$\mathbf{A} = \begin{pmatrix}
-3 & -4 \\ 2 & 1
\end{pmatrix} $$

Calculemos el determinante.

$$\begin{vmatrix}
-3 & -4 \\ 2 & 1
\end{vmatrix} = -3 + 8 = 5 \neq 0$$

Como $|A| \neq 0$, entonces el único punto de equilibrio es el origen.

El plano fase del sistema se ilustra a continuación.

Plano fase del sistema.

Es este caso se logra observar que las trayectorias cerca del punto de equilibrio tienden a él conforme $t \rightarrow \infty$, lo que lo define como un punto de equilibrio asintóticamente estable.

$\square$

Veamos un último ejemplo.

Ejemplo: Definir el tipo de punto de equilibrio del siguiente sistema visualizando el comportamiento de las trayectorias alrededor de dicho punto.

\begin{align*}
x^{\prime} &= 5x -2y \\
y^{\prime} &= 2x -3y
\end{align*}

Solución: Nuevamente se puede verificar que el único punto de equilibrio del sistema es el origen. Observemos el plano fase.

Plano fase del sistema.

En este caso se observa que cerca del punto de equilibrio las trayectorias se alejan de él, por lo que dicho punto es un punto inestable.

$\square$

Al menos geométricamente ya somos capaces de identificar el tipo de comportamiento que tienen las trayectorias alrededor de los puntos de equilibrio según su clasificación.

Más adelante resolveremos algunos sistemas lineales y haremos este mismo análisis desde una perspectiva analítica analizando las soluciones que obtengamos. Más aún, veremos que de acuerdo al valor de los eigenvalores del sistema será el tipo de punto de equilibrio que tendrá dicho sistema. Pero antes de ello, en la siguiente entrada estudiemos algunas propiedades cualitativas de las trayectorias.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

  1. Visualizar el campo vectorial y algunas trayectorias de los siguientes sistemas. ¿Tienen puntos de equilibrio?.
  • $x^{\prime} = (y -x)(y -1)$
    $y^{\prime} = (x- y)(x -1)$
  • $x^{\prime} = -y(y -2)$
    $y^{\prime} = (x -2)(y -2)$
  1. Determinar los puntos de equilibrio de los siguientes sistemas y clasificarlos como estables, asintóticamente estables o inestables. Visualizar el campo vectorial y algunas trayectorias.
  • $x^{\prime} = 2y$
    $y^{\prime} = 2x$
  • $x^{\prime} = -8y$
    $y^{\prime} = 18x$
  • $x^{\prime} = 2x + y + 3$
    $y^{\prime} = -3x -2y -4$
  • $x^{\prime} =-5x + 2y$
    $y^{\prime} = x -4y$
  • $x^{\prime} = 2x + 13y$
    $y^{\prime} = -x -2y$
  • $x^{\prime} = x(7 -x -2y)$
    $y^{\prime} = y(5 -x -y)$
  1. Analizar el comportamiento de las curvas solución del siguiente sistema.
  • $x^{\prime} = 3/y$
    $y^{\prime} = 2/x$

    ¿Qué se puede observar?. ¿Hay puntos de equilibrio?.

Más adelante…

Conforme avanzamos nos damos cuenta que es posible describir cualitativamente las soluciones de un sistema tanto lineal como no lineal compuesto por dos ecuaciones diferenciales de primer orden homogéneas con coeficientes contantes, esto tiene la enorme ventaja de que ya no es necesario conocer explícitamente las soluciones del sistema para poder trabajar.

Continuando con nuestro desarrollo cualitativo, en la siguiente entrada estudiaremos algunas propiedades de las trayectorias en el plano fase.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Ecuaciones Diferenciales I: Ecuaciones diferenciales autónomas

Por Omar González Franco

2 respuestas

¿Cómo es posible un error en las matemáticas?.
– Henri Poincare

Introducción

Continuando con la descripción cualitativa de las ecuaciones diferenciales, en esta entrada estudiaremos las ecuaciones diferenciales en las que la función razón no depende explícitamente de la variable independiente $x$.

En la entrada anterior vimos una propiedad geométrica interesante de las ecuaciones diferenciales de la forma

$$\dfrac{dy}{dx} = f(y) \label{1} \tag{1}$$

dicha propiedad es que los elementos lineales en dos puntos distintos del plano $XY$, pero con la misma coordenada $y$, tienen la misma pendiente, esta propiedad tiene interesantes consecuencias y las estudiaremos en esta entrada.

Ecuaciones de primer orden autónomas

Una ecuación autónoma en su forma normal se ve como (\ref{1}).

La ecuación diferencial

$$\dfrac{dy}{dx} = 1 + 2y$$

es una ecuación diferencial autónoma, mientras que la ecuación

$$\dfrac{dy}{dx} = 2xy$$

es una ecuación no autónoma ya que la función razón

$$f(x, y) = 2xy$$

sí depende de la variable independiente $x$.

Hay muchos procesos físicos que son modelados con ecuaciones diferenciales autónomas donde la variable independiente puede ser por ejemplo el tiempo $t$, en estos casos dichos procesos no cambiarían en el tiempo.

Puntos críticos

En la ecuación diferencial autónoma (\ref{1}) las raíces de la función razón son de especial importancia.

Un punto crítico también es llamado punto de equilibrio o punto estacionario.

Con estas dos definiciones podemos observar que si $k$ es un punto crítico de la ecuación (\ref{1}), entonces $y(x) = k$ es una solución constante de la ecuación diferencial autónoma.

Esquema de fases

En la entrada anterior vimos que una propiedad geométrica de las ecuaciones autónomas es que los elementos lineales son paralelos a lo largo de líneas horizontales en el plano $XY$, esto quiere decir que si conocemos el campo de pendientes a lo largo de una sola línea vertical $x = x_{0}$, entonces lo conocemos para todo el plano $XY$. Esta propiedad nos permite, en lugar de dibujar todo el plano, dibujar una sola línea que contiene la misma información. Esta línea se llama línea fase para la ecuación autónoma.

Para ver cómo obtener los puntos críticos, soluciones de equilibrio y líneas fase realicemos el siguiente ejemplo con una ecuación logística.

Ejemplo: Obtener los puntos críticos, soluciones de equilibrio y línea fase de la siguiente ecuación diferencial autónoma.

$$\dfrac{dy}{dx} = y(\alpha -\beta y) \label{3} \tag{3}$$

con $\alpha$ y $\beta$ constantes positivas.

Solución: Para obtener las soluciones de equilibrio y los puntos críticos igualamos la función razón a cero.

$$f(y) = y(\alpha -\beta y) = 0$$

La ecuación se satisface si $y = 0$ o $\alpha -\beta y = 0$, es decir, si

$$y(x) = 0 \hspace{1cm} o \hspace{1cm} y(x) = \dfrac{\alpha}{\beta}$$

Estas funciones corresponden a las soluciones de equilibrio de la ecuación diferencial y los puntos críticos no son más que las constantes $k_{1} = 0$ y $k_{2} = \dfrac{\alpha}{\beta} > 0$.

Para esbozar la línea fase comencemos por colocar dos puntos sobre una línea vertical, dichos puntos corresponden a los puntos críticos obtenidos.

Puntos críticos en la línea fase.

La línea fase es paralela al eje $Y$, o bien puede ser el mismo eje $Y$.

En este caso los puntos críticos dividen a la línea fase en tres intervalos:

$$(-\infty, 0), \hspace{1cm} \left( 0, \dfrac{\alpha}{\beta} \right) \hspace{1cm} y \hspace{1cm} \left(\dfrac{\alpha}{\beta}, \infty\right)$$

Por definición los puntos críticos son los valores en los que

$$\dfrac{dy}{dx} = f(k) = 0$$

esto significa que la pendiente de los elementos lineales en los puntos críticos debe ser cero, mientras que por encima y por debajo de los puntos críticos la pendiente tiene que ser distinta de cero, así que puede haber elementos lineales con pendiente negativa o pendiente positiva.

Veamos en cada uno de los intervalos de nuestro ejemplo que signo tiene la pendiente de los elementos lineales, como se trata de un diagrama unidimensional dicho valor lo representaremos con flechas sobre la línea fase, si la pendiente es positiva colocaremos una flecha apuntando hacia arriba y si es una pendiente negativa colocaremos una flecha apuntando hacia abajo.

Para ver si la pendiente es positiva o negativa estudiemos el signo de la función razón (que es equivalente al signo de la derivada $\dfrac{dy}{dx}$) en cada uno de los intervalos. Comencemos con el intervalo $(-\infty, 0)$, en este caso $-\infty < y < 0$.

\begin{align*}
y &< 0 \\
\beta y &< 0 \\
-\beta y &> 0 \\
-\beta y + \alpha > \alpha &> 0 \\
f(y) = y(\alpha -\beta y) &< 0 \\
\dfrac{dy}{dx} &< 0
\end{align*}

Este análisis nos indica que la pendiente de los elementos lineales en el intervalo $(-\infty, 0)$ es negativa.

Haciendo un análisis similar en los intervalos $\left( 0, \dfrac{\alpha}{\beta} \right)$ y $\left(\dfrac{\alpha}{\beta}, \infty \right)$ obtenemos los siguientes resultados:

  • En $(-\infty, 0)$ $\hspace{0.2cm}$ $\Rightarrow$ $f(y) = y(\alpha -\beta y) < 0$ $\Rightarrow$ La pendiente es negativa
  • En $\left( 0, \dfrac{\alpha}{\beta} \right)$ $\hspace{0.2cm}$ $\Rightarrow$ $f(y) = y(\alpha -\beta y) > 0$ $\Rightarrow$ La pendiente es positiva.
  • En $\left( \dfrac{\alpha}{\beta}, \infty \right)$ $\hspace{0.05cm}$ $\Rightarrow$ $f(y) = y(\alpha -\beta y) < 0$ $\Rightarrow$ La pendiente es negativa.

Como mencionamos antes, en el intervalo $(-\infty, 0)$ de la línea fase colocaremos una flecha apuntando hacia abajo debido a que la pendiente es negativa. En el intervalo $\left( 0, \dfrac{\alpha}{\beta} \right)$ colocaremos una flecha apuntando hacia arriba ya que la pendiente es positiva y finalmente en el intervalo $\left(\dfrac{\alpha}{\beta}, \infty \right)$ colocaremos nuevamente una flecha hacia abajo debido a que la pendiente vuelve a ser negativa. La línea fase de la ecuación diferencial dada se muestra en la siguiente figura.

Línea fase de la ecuación $\dfrac{dy}{dx} = y(\alpha-\beta y)$.

Como caso particular consideremos la ecuación diferencial autónoma

$$\dfrac{dy}{dx} = y(6 -3y)$$

Las soluciones de equilibrio son $y(x) = 0$ y $y(x) = \dfrac{\alpha}{\beta} = \dfrac{6}{3} = 2$. A continuación se muestra el campo de pendientes de esta ecuación.

Campo de pendientes de la ecuación diferencial $\dfrac{dy}{dx} = y(6 -3y)$.

Notamos que, en efecto, el valor de la pendiente de los elementos lineales en las soluciones de equilibrio es cero, por encima de $y(x) = 2$ y por debajo de $y(x) = 0$ la pendiente es negativa y entre las soluciones de equilibrio la pendiente de los elementos lineales es positiva, tal como lo mostramos en la línea fase del caso general.

$\square$

Como podemos ver, la línea fase es una gran herramienta que nos permite analizar el comportamiento de las soluciones de una ecuación diferencial autónoma gracias a que las pendientes de los elementos lineales en líneas horizontales del plano $XY$ son siempre iguales.

Con el ejemplo en mente ahora podemos establecer los pasos necesarios para dibujar una línea fase de una ecuación diferencial autónoma.

  • Comenzamos por dibujar una línea vertical paralela al eje $Y$ para cualquier valor de $x$.
  • Determinamos las soluciones de equilibrio y los puntos críticos, marcamos los puntos críticos sobre la línea vertical.
  • Determinamos los intervalos de $y$ en los que $f(y) > 0$ y dibujamos flechas apuntando hacia arriba en esos intervalos.
  • Determinamos los intervalos de $y$ en los que $f(y) < 0$ y dibujamos flechas apuntando hacia abajo en esos intervalos.

Las líneas fase nos permiten obtener una aproximación cualitativa de las curvas solución de una ecuación diferencial autónoma.

Nota: En ocasiones se usan de forma indistinta los términos puntos críticos y soluciones de equilibrio, sin embargo podemos pensar a un punto crítico como el punto $c = k$ que se coloca en la línea fase, mientras que una solución de equilibrio $y(x) = k$ como la gráfica en el plano $XY$ de una función constante para toda $x$. Cuando estamos analizando líneas fase puede ser que al punto crítico también se le llame solución de equilibrio y es correcto debido a que la línea fase representa al eje de la variable dependiente $y$ para cualquier valor de la variable independiente $x$. Lo importante es que tengamos presente las definiciones de punto crítico y de solución de equilibrio que establecimos al inicio para evitar confusiones.

Ahora veamos que nos dice esta descripción cualitativa acerca de la forma de una curva solución de una ecuación diferencial autónoma.

Curvas solución de una ecuación diferencial autónoma

En la ecuación diferencial autónoma (\ref{1}) la función $f$ es independiente de la variable $x$, esto nos permite suponer que $f$ está definida en $x \in (-\infty, \infty)$, o en $x \in [0, \infty)$. Consideremos una región $U$ en el plano $XY$ en el que se cumple el teorema de existencia y unicidad de una solución, por este teorema sabemos que existe una solución que pasa por el punto $(x_{0}, y_{0})$. En la región $U$ supongamos que una ecuación diferencial autónoma tiene dos puntos críticos $c_{1}$ y $c_{2}$ tales que $c_{1} < c_{2}$. Las gráficas de las soluciones

$$y(x) = c_{1} \hspace{1cm } y \hspace{1cm} y(x) = c_{2}$$

son rectas horizontales que dividen a la región $U$ en tres regiones: $U_{1}, U_{2}$ y $U_{3}$, esto se puede visualizar en la siguiente figura.

Subregiones $U_{1}, U_{2}$ y $U_{3}$ de $U$.

Con estas condiciones podemos establecer las siguientes propiedades.

  • Si el punto $(x_{0}, y_{0})$ está en alguna subregión $U_{i}$, $i = 1, 2, 3$ y $y(x)$ es una solución cuya curva solución pasa por $(x_{0}, y_{0})$, entonces $y(x)$ debe permanecer en esa subregión $U_{i}$ para toda $x$.

Esto indica que una solución $y(x)$ no puede cruzar la grafica de una solución de equilibrio $y(x) = c$. Para argumentar este hecho consideremos a $k$ como un punto crítico de una ecuación diferencial autónoma tal que $f(k) = 0$, considerando que $f(y)$ es continua, si las soluciones $y(x)$ son cercanas a $k$, entonces el valor de $f$ debe ser pequeño, esto nos indica que las soluciones se están desplazando lentamente cuando están próximas a los puntos críticos, dicho de otra manera, una solución que se acerca a un punto crítico cuando $x$ crece (o decrece) se mueve cada vez más lento al acercarse a éste. Por el teorema de existencia y unicidad, una solución que se acerca a un punto crítico nunca llega realmente a él, es decir, la solución de equilibrio se vuelve una asíntota para todas las soluciones $y(x)$ que se aproximan al punto crítico.

En la figura anterior, por ejemplo, la curva $y(x)$ que pasa por el punto $(x_{0}, y_{0})$ debe mantenerse dentro de $U_{2}$ para toda $x$, $y(x)$ está acotada por arriba con $c_{2}$ y por abajo con $c_{1}$, esto es, $c_{1} < y(x) < c_{2}$.

Otra propiedad es la siguiente.

  • Por continuidad de la función $f$, debe ser $f(y) > 0$ o $f(y) < 0$ para toda $x$ en una subregión $U_{i}$, $i = 1, 2, 3$.

Vimos anteriormente que el signo de la pendiente se mantiene igual dentro de toda la región limitada por los puntos críticos, esto nos permite deducir que una curva solución $y(x)$ no puede oscilar o tener extremos relativos (máximos o mínimos) dentro de una misma región. Esto lo podemos describir con la siguiente propiedad.

  • Debido a que $\dfrac{dy}{dx} = f(y(x))$ es positiva o negativa en una subregión $U_{i}$, $i = 1, 2, 3$, una solución $y(x)$ es estrictamente monótona, por lo tanto no puede oscilar ni tener extremos relativos.

Ahora que conocemos estas propiedades podemos establecer una más que se puede deducir de las anteriores. Basándonos en el caso general de la imagen anterior podemos decir lo siguiente.

  • Si $y(x)$ es una solución dentro de la región $U_{1}$, entonces está acotada por arriba con el punto crítico $c_{1}$, esto es, $\forall$ $x$ en el intervalo $$y(x) < c_{1}$$ Esto indica que la curva solución $y(x)$ debe tender a la gráfica de la solución de equilibrio $y(x) = c_{1}$ a medida que $x \rightarrow \infty$ o $x \rightarrow -\infty$. Por otro lado, una solución $y(x)$ que este en la región $U_{2}$ está acotada por abajo con $c_{1}$ y arriba con $c_{2}$, esto es, $\forall$ $x$ en el intervalo $$c_{1} < y(x) < c_{2}$$ Entonces la curva solución $y(x)$ debe tender a las gráficas de las soluciones de equilibrio $y(x) = c_{1}$ y $y(x) = c_{2}$ conforme $x \rightarrow \infty$ en una y $x \rightarrow -\infty$ en la otra. Finalmente, si la solución está en la region $U_{3}$ entonces está acotada por abajo con $c_{2}$, es decir, $\forall$ $x$ $$y(x) > c_{2}$$ En este caso la grafica $y(x)$ debe tender a la gráfica de la solución de equilibrio $y(x) = c_{2}$ conforme $x \rightarrow \infty$ o $x \rightarrow -\infty$.

Veamos la importancia de estas propiedades en un ejemplo.

Modelo logístico de la población

En esta entrada ya estudiamos como ejemplo la ecuación logística (\ref{3}), usemos los resultados obtenidos para resolver de manera cualitativa el problema del modelo logístico de la población visto en la entrada anterior. El modelo que establecimos fue

$$\dfrac{dP}{dt} = k \left(1 -\dfrac{P}{N}\right) P \label{4} \tag{4}$$

Este modelo corresponde a una ecuación diferencial autónoma.

$$\dfrac{dP}{dt} = f(P) \label{5} \tag{5}$$

así que las curvas solución las podemos describir con la teoría que hemos construido en esta entrada.

El problema que analizábamos era el crecimiento de la población en función de su entorno y los recursos limitados a los que están sujetos. Resolvamos la ecuación diferencial de manera cualitativa aplicando lo que hemos aprendido hasta ahora e interpretemos los resultados.

Comencemos por determinar las soluciones de equilibrio y los puntos críticos, para ello igualemos la ecuación a cero.

$$\dfrac{dP}{dt} = k \left(1 -\dfrac{P}{N}\right) P = 0$$

Esta relación se satisface si

$$kP = 0 \hspace{1cm} o \hspace{1cm} 1 -\dfrac{P}{N} = 0$$

Es decir, si $P = 0$ o $P = N$. Por lo tanto, los puntos críticos son $c_{1} = 0$ y $c_{2} = N$, mientras que las soluciones de equilibrio son $P(t) = 0$ y $P(t) = N$.

Coloquemos los puntos críticos sobre la línea fase.

Puntos críticos en la línea fase.

Los puntos críticos definen tres intervalos para $P$, estos son

$$(-\infty, 0), \hspace{1cm} (0, N) \hspace{1cm} y \hspace{1cm} (N, \infty)$$

Sin embargo, como se trata de un problema real es claro que no tiene sentido que la variable población $P(t)$ sea negativa (no hay individuos negativos), así mismo no hay tiempos negativos por lo que $t > 0$, por lo tanto en este problema sólo consideraremos los intervalos $(0, N)$ y $(N, \infty)$ para $P$, así como $0 < t < \infty$.

Del caso general (\ref{3}) deducimos que en el intervalo $(0, N)$ las pendientes son positivas, así que la función $P(t)$ será creciente en dicho intervalo y en $(N, \infty)$ las pendientes son negativas, por tanto la función $P(t)$ será decreciente. La línea fase final queda de la siguiente manera.

Línea fase del modelo logístico.

Un ejemplo de como se ve el campo de pendientes, las soluciones de equilibrio y algunas curvas solución de la ecuación logística (\ref{4}) se muestra en la siguiente figura.

Campo de pendientes de la ecuación logística (4) para valores particulares de $k$ y $N$.

De este gráfico notamos que las curvas solución cumplen con las hipótesis que establecimos al plantear el modelo, dichas hipótesis eran

  • Si la población es pequeña $(P(t) < N)$, la tasa de crecimiento de la población es proporcional a su tamaño.
  • Si la población es demasiado grande para ser soportada por su entorno y recursos $(P(t) > N)$, la población disminuirá, en este caso la tasa de crecimiento será negativa.

Las soluciones de equilibrio $P(t) = 0$ y $P(t) = N$ tienen sentido, pues si la población es cero permanecerá en cero indefinidamente y si la población es exactamente la asociada con la capacidad de soporte, entonces no crecerá ni disminuirá.

Es así que a partir de la línea fase y el campo de pendientes de una ecuación diferencial autónoma podemos esbozar varias curvas solución con distintas condiciones iniciales. En este ejemplo la única información que necesitamos es el hecho de que $P = 0$ y $P = N$ son soluciones de equilibrio, $P(t)$ crece si $0 < P < N$ y disminuye si $P > N$ o $P < 0$. Los valores exactos de $P(t)$ en cualquier tiempo dado $t$ dependerán de los valores $P(0)$, $k$ y $N$.

$\square$

Clasificación de puntos de equilibrio

Como vimos, alrededor de un punto crítico las soluciones pueden tener distintos comportamientos. Básicamente hay tres tipos de comportamiento que $y(x)$ puede tener alrededor de un punto crítico y en base a estos comportamientos podemos clasificarlos.

Supongamos que $y(x) = y_{0}$ es una solución de equilibrio de la ecuación diferencial autónoma (\ref{1}), los tres tipos de comportamiento que $y(x)$ puede tener alrededor del punto crítico $y_{0}$ son:

  • Caso 1: Por arriba de $y_{0}$ la función $y(x)$ es decreciente y por debajo de $y_{0}$ la función $y(x)$ es creciente, en este caso decimos que el punto crítico es un atractor.
$y_{0}$ es un atractor.
  • Caso 2: Por arriba de $y_{0}$ la función $y(x)$ es creciente y por debajo de $y_{0}$ la función $y(x)$ es decreciente, en este caso decimos que el punto crítico es un repulsor.
$y_{0}$ es un repulsor.
  • Caso 3: Tanto por arriba y por abajo de $y_{0}$ la función $y(x)$ es creciente o decreciente, en este caso decimos que el punto crítico es un nodo o punto semiestable.
$y_{0}$ es un nodo o punto semiestable.

En resumen, sea $y(x)$ solución de una ecuación diferencial autónoma (\ref{1}).

  • Si $f(y_{0}) = 0$, entonces $y_{0}$ es un punto crítico y $y(x) = y_{0}$ es la solución de equilibrio para toda $x$.
  • Si $f(y_{0}) > 0$, entonces $y(x)$ es creciente para toda $x$ y $y(x) \rightarrow \infty$, cuando $x$ incrementa, o bien $y(x)$ tiende al primer punto de equilibrio mayor que $y_{0}$.
  • Si $f(y_{0}) < 0$, entonces $y(x)$ es decreciente para toda $x$ y $y(x) \rightarrow -\infty$, cuando $x$ incrementa, o bien $y(x)$ tiende al primer punto de equilibrio menor que $y_{0}$.

Importante mencionar que esto también es valido para $x$ negativas. Cuando $x$ decrece podemos encontrar resultados similares.

  • Si $f(y_{0}) > 0$, entonces $y(x) \rightarrow -\infty$ o al siguiente punto de equilibrio menor conforme $x$ aumenta en valores negativos.
  • Si $f(y_{0}) < 0$, entonces $y(x) \rightarrow \infty$ o al siguiente punto de equilibrio mayor conforme $x$ aumenta en valores negativos.

Un caso especial

Consideremos la ecuación diferencial autónoma

$$\dfrac{dy}{dx} = \dfrac{1}{1 -y}$$

Intentemos esbozar la línea fase. Por definición, los puntos críticos son los valores para los que $f(y) = 0$, sin embargo en este caso $f(y)$ no puede ser cero.

Notemos que si $y > 1$, entonces $f(y) < 0$ y si $y < 1$, entonces $f(y) > 0$, pero si $y = 1$, $f(y)$ no esta definida. En este caso decimos que la línea fase tiene un agujero en $y =1$ y lo denotamos como un circulo vacío.

Agujero en la línea fase.

Las soluciones $y(x)$ de la ecuación tienden hacia $y = 1$ cuando $x$ aumenta.

Concluyamos esta entrada con el enunciado de un teorema importante.

Teorema de linearización

Existe un teorema conocido como teorema de linearización que nos ayuda a determinar el tipo de puntos críticos de una ecuación diferencial autónoma (\ref{1}), de acuerdo al comportamiento que tiene la función $f(y)$. El enunciado de este teorema es el siguiente.

La demostración a este teorema la podemos encontrar en la sección de videos.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

  1. Para las siguientes ecuaciones diferenciales, esbozar las líneas fase y clasificar a los puntos críticos como atractores, repulsores o nodos según sea el caso.
  • $\dfrac{dy}{dx} = 3y(1 -y)$
  • $\dfrac{dv}{du} = \dfrac{1}{v -2}$
  • $\dfrac{dy}{dt} = \cos(y)$
  • $\dfrac{dw}{dt} = w^{2} -6w -16$
  1. Para cada condición inicial dada, describir cualitativamente el comportamiento a largo plazo de las soluciones de la ecuación diferencial

    $\dfrac{dy}{dx} = y^{2} -4y + 2$

    con condición inicial
  • $y(0) = 0$
  • $y(0) = 10$
  • $y(3) = 1$

Más adelante…

En estas dos últimas entradas hemos estudiado a las ecuaciones diferenciales ordinarias de primer orden desde una perspectiva cualitativa, esto nos ha permitido esbozar las curvas solución y encontrar propiedades interesantes sin siquiera conocer la forma explicita de la solución. En particular, las ecuaciones diferenciales autónomas presentan propiedades interesantes que son útiles para analizar modelos que describen algún fenómeno real.

Ha llegado el momento de estudiar los distintos métodos de resolución de las ecuaciones diferenciales ordinarias de primer orden. Comenzaremos con un método sencillo que funciona sólo para ecuaciones diferenciales lineales.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»