Introducción
En las unidades anteriores hemos desarrollado varias herramientas de la teoría de diferenciabilidad que nos permiten estudiar tanto a los campos escalares, como a los campos vectoriales. Hemos platicado un poco de las aplicaciones que esta teoría puede tener. En esta última unidad, profundizamos un poco más en cómo dichas herramientas nos permitirán hacer un análisis geométrico y cuantitativo de las funciones. Es decir, a partir de ciertas propiedades analíticas, hallaremos algunas cualidades de su comportamiento geométrico. En esta entrada estudiaremos una pregunta muy natural: ¿cuándo una función diferenciable alcanza su máximo o su mínimo? Para ello, necesitaremos definir qué quiere decir que algo sea un punto crítico de una función. Esto incluirá a los puntos más altos, los más bajos, local y globalmente y ciertos «puntos de quiebre» que llamamos puntos silla.
Introducción al estudio de los puntos críticos
Si tenemos un campo escalar $f:\mathbb{R}^n\to \mathbb{R}$, en muchas aplicaciones nos interesa poder decir cuándo alcanza sus valores máximos o mínimos. Y a veces eso sólo nos importa en una vecindad pequeña. La siguiente definición hace ciertas precisiones.
Definición. Sea $f:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}$ un campo escalar, y $\bar{a}\in S$.
- Decimos que $f$ tiene un máximo absoluto (o máximo global) en $\bar{a}$ si $f(\bar{x})\leq f(\bar{a})$ para todo $\bar{x}\in S$. A $f(\bar{a})$ le llamamos el máximo absoluto (o máximo global) de $f$ en $S$.
- Decimos que $f$ tiene un máximo relativo (o máximo local) en $\bar{a}$ si existe una bola abierta $B_{r}(\bar{a})$ tal que para todo $\bar{x}\in B_{r}(\bar{a})$ $f(\bar{x})\leq f(\bar{a})$.
- Decimos que $f$ tiene un mínimo absoluto (o mínimo global) en $\bar{a}$ si $f(\bar{x})\geq f(\bar{a})$ para todo $\bar{x}\in S$. A $f(\bar{a})$ le llamamos el mínimo absoluto (o mínimo global) de $f$ en $S$.
- Decimos que $f$ tiene un mínimo relativo (o mínimo local) en $\bar{a}$ si existe una bola abierta $B_{r}(\bar{a})$ tal que para todo $\bar{x}\in B_{r}(\bar{a})$ $f(\bar{x})\geq f(\bar{a})$.
En cualquiera de las situaciones anteriores, decimos que $f$ tiene un valor extremo (ya sea relativo o absoluto) en $\bar{a}$. Notemos que todo extremo absoluto en $S$ será extremo relativo al tomar una bola $B_{r}(\bar{a})$ que se quede contenida en $S$. Y de manera similar, todo extremo relativo se vuelve un extremo absoluto para la función restringida a la bola $B_{r}(\bar{a})$ que da la definición.
Usualmente, cuando no sabemos nada de una función $f$, puede ser muy difícil, si no imposible estudiar sus valores extremos. Sin embargo, la intuición que tenemos a partir de las funciones de una variable real es que deberíamos poder decir algo cuando la función que tenemos tiene cierta regularidad, por ejemplo, cuando es diferenciable. Por ejemplo, para funciones diferenciables $f:S\subseteq \mathbb{R}\to\mathbb{R}$ quizás recuerdes que si $f$ tiene un valor extremo en $\bar{a}\in S$, entonces $f'(\bar{a})=0$.
El siguiente teorema es el análogo en altas dimensiones de este resultado.
Teorema. Sea $f:S\subseteq \mathbb{R}^n\to \mathbb{R}$ un campo escalar. Supongamos que $f$ tiene un valor extremo en un punto interior $\bar{a}$ de $S$, y que $f$ es diferenciable en $\bar{a}$. Entonces el gradiente de $f$ se anula en $\bar{a}$, es decir, $$\triangledown f(\bar{a})=0.$$
Demostración. Demostraremos el resultado para cuando hay un máximo relativo en $\bar{a}$. El resto de los casos quedan como tarea moral. De la suposición, obtenemos que existe un $r>0$ tal que $f(\bar{x})\leq f(\bar{a})$ para todo $\bar{x}\in B_r(\bar{a})$. Escribamos $\bar{a}=(a_{1},\dots ,a_{n})$.
Para cada $i=1,\dots ,n$ tenemos:
\[ \frac{\partial f}{\partial x_{i}}(\bar{a})=\lim\limits_{\xi \to a_{i}}\frac{f(\xi \hat{e}_{i})-f(\bar{a})}{\xi -a_{i}}. \]
Además, ya que $f$ es diferenciable en $\bar{a}$ también se cumple
\[\lim\limits_{\xi \to a_{i}-}\frac{f(\xi e_{i})-f(a)}{\xi -a_{i}}=\lim\limits_{\xi \to a_{i}+}\frac{f(\xi e_i)-f(a)}{\xi -a_{i}}. \]
Dado que $f$ alcanza máximo en $\bar{a}$ tenemos que $f(\xi \hat{e}_{i})-f(\bar{a})\leq 0$. Para el límite por la izquierda tenemos $\xi-a_{i}\leq 0$, por lo tanto, en este caso
\[ \lim\limits_{\xi \to a_{i}-}\frac{f(\xi e_{i})-f(\bar{a})}{\xi -a_{i}}\geq 0.\]
Para el límite por la derecha tenemos $\xi-a_{i}\geq 0$, por lo cual
\[ \lim\limits_{\xi \to a_{i}+}\frac{f(\xi \hat{e}_{i})-f(\bar{a})}{\xi -a_{i}}\leq 0.\]
Pero la igualdad entre ambos límites dos dice entonces que
\[\frac{\partial f}{\partial x_{i}}(\bar{a}) =\lim\limits_{\xi \to a_{i}-}\frac{f(\xi \hat{e}_{i})-f(\bar{a})}{\xi -a_{i}}=0. \]
Por lo cual cada derivada parcial del campo vectorial es cero, y así el gradiente también lo es.
$\square$
Parece ser que es muy importante saber si para un campo vectorial su gradiente se anula, o no, en un punto. Por ello, introducimos dos nuevas definiciones.
Definición. Sea $f:S\subseteq \mathbb{R}^n \to \mathbb{R}$ un campo escalar diferenciable en un punto $\bar{a}$ en $S$. Diremos que $f$ tiene un punto estacionario en $\bar{a}$ si $\triangledown f(\bar{a})=0$.
Definición. Sea $f:S\subseteq \mathbb{R}^n \to \mathbb{R}$ un campo escalar y tomemos $\bar{a}$ en $S$. Diremos que $f$ tiene un punto crítico en $\bar{a}$ si o bien $f$ no es diferenciable en $\bar{a}$, o bien $f$ tiene un punto estacionario en $\bar{a}$.
Si $f$ tiene un valor extremo en $\bar{a}$ y no es diferenciable en $\bar{a}$, entonces tiene un punto crítico en $\bar{a}$. Si sí es diferenciable en $\bar{a}$ y $\bar{a}$ es un punto interior del dominio, por el teorema de arriba su gradiente se anula, así que tiene un punto estacionario y por lo tanto también un punto crítico en $\bar{a}$. La otra opción es que sea diferenciable en $\bar{a}$, pero que $\bar{a}$ no sea un punto interior del dominio.
Observación. Los valores extremos de $f$ se dan en los puntos críticos de $f$, o en puntos del dominio que no sean puntos interiores.
Esto nos da una receta para buscar valores extremos para un campo escalar. Los puntos candidatos a dar valores extremos son:
- Todos los puntos del dominio que no sean interiores.
- Aquellos puntos donde la función no sea diferenciable.
- Los puntos la función es diferenciable y el gradiente se anule.
Ya teniendo a estos candidatos, hay que tener cuidado, pues desafortunadamente no todos ellos serán puntos extremos. En la teoría que desarrollaremos a continuación, profundizaremos en el entendimiento de los puntos estacionarios y de los distintos comportamientos que las funciones de varias variables pueden tener.
Intuición geométrica
Para entender mejor qué quiere decir que el gradiente de un campo escalar se anuele, pensemos qué pasa en términos geomértricos en un caso particular, que podamos dibujar. Tomemos un campo escalar $f:\mathbb{R}^2\to \mathbb{R}$. La gráfica de la función $f$ es la superficie en $\mathbb{R}^{3}$ que se obtiene al variar los valores de $x,y$ en la expresión $(x,y,f(x,y))$.
Otra manera de pensar a esta gráfica es como un conjunto de nivel. Si definimos $F(x,y,z)=z-f(x,y)$, entonces la gráfica es precisamente el conjunto de nivel para $F$ en el valor $0$, pues precisamente $F(x,y,z)=0$ si y sólo si $z=f(x,y)$.
Si $f$ alcanza un extremo en $(a,b)$, entonces $\triangledown f(a,b)=0$ por lo cual $\triangledown F (a,b,f(a,b))=(0,0,1)$. Así, el gradiente es paralelo al eje $z$ y por lo tanto es un vector normal a la superficie $F(x,y,z)=0$. Esto lo podemos reinterpretar como que el plano tangente a la superficie citada en el punto $(a,b,f(a,b))$ es horizontal.
Puntos silla
Cuando la función es diferenciable y el gradiente se anula, en realida tenemos pocas situaciones que pueden ocurrir. Sin embargo, falta hablar de una de ellas. Vamos a introducirla mediante un ejemplo.
Ejemplo. Consideremos $f(x,y)=xy$. En este caso
$$\frac{\partial f}{\partial x}=y\hspace{0.5cm}\textup{y}\hspace{0.5cm}\frac{\partial f}{\partial y}=x.$$
Si $(x,y)=(0,0)$, entonces las parciales se anulan, así que el gradiente también. Por ello, $(0,0)$ es un punto estacionario (y por lo tanto también crítico). Pero veremos a continuación que $f(0,0)=0$ no es máximo relativo ni mínimo relativo.
Tomemos $r>0$ abitrario y $\varepsilon= r/\sqrt{8}$. El punto $(\varepsilon ,\varepsilon)\in B_{r}(0)$ pues $\sqrt{\varepsilon ^{2}+\varepsilon ^{2}}$ es igual a $\sqrt{r^{2}/8\hspace{0.1cm}+\hspace{0.1cm}r^{2}/8}=r/2<r$. Análogamente, tenemos que el punto $(\varepsilon,-\varepsilon)\in B_{r}(0)$. Sin embargo $f(\varepsilon,-\varepsilon)=-r^{2}/8<0$, por lo que $0$ no es un mínimo local, también $f(\varepsilon,\varepsilon)=r^{2}/8>0$, por lo que $0$ tampoco es máximo local. En la Figura 1 tenemos un bosquejo de esta gráfica.
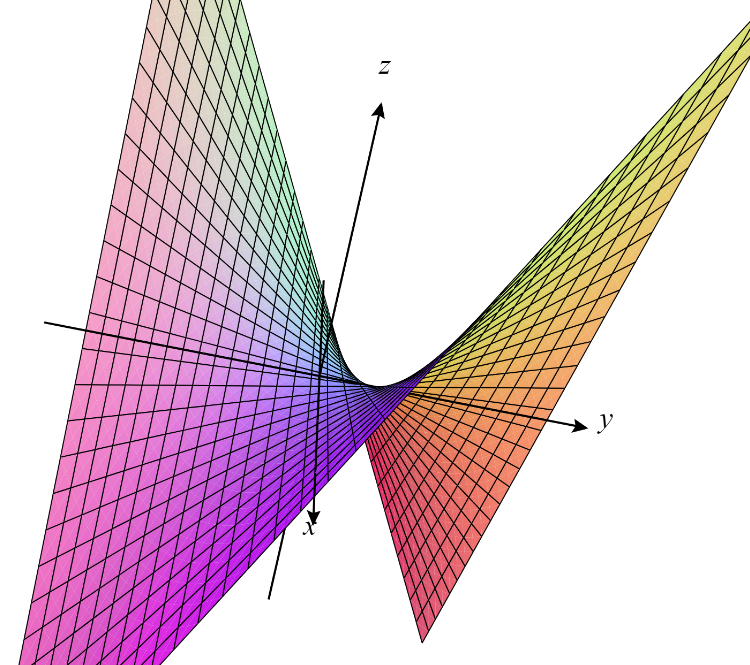
$\triangle$
Los puntos como los de este ejemplo tienen un nombre especial que definimos a continuación.
Definición. Sea $f:S\subseteq \mathbb{R}^n\to\mathbb{R}$ un campo escalar y $\bar{a}$ un punto estacionario de $f$. Diremos que $\bar{a}$ es un punto silla si para todo $r>0$ existen $\bar{u},\bar{v}\in B_{r}(\bar{a})$ tales que $f(\bar{u})<f(\bar{a})$ y $f(\bar{v})>f(\bar{a})$.
Determinar la naturaleza de un punto estacionario
Cuando tenemos un punto estacionario $\bar{a}$ de una función $f:\mathbb{R}^n\to \mathbb{R}$, tenemos diferenciabilidad de $f$ en $\bar{a}$. Si tenemos que la función es de clase $C^2$ en ese punto, entonces tenemos todavía más. La intuición nos dice que probablemente podamos decir mucho mejor cómo se comporta $f$ cerca de $\bar{a}$ y con un poco de suerte entender si tiene algún valor extremo o punto silla ahí, y bajo qué circunstancias.
En efecto, podemos enunciar resultados de este estilo. Por la fórmula de Taylor tenemos que
$$f(\bar{a}+\bar{y})=f(\bar{a})+\triangledown f (\bar{a}) \cdot y + \frac{1}{2}[\bar{y}]^tH(\bar{a})[\bar{y}]+||\bar{y}||^{2}E_{2}(\bar{a},\bar{y}),$$
en donde el error $||\bar{y}||^{2}E_{2}(\bar{a},\bar{y})$ se va a cero conforme $||\bar{y}||\to 0$. Recuerda que aquí $H(\bar{a})$ es la matriz hessiana de $f$ en $\bar{a}$. Como $f:\mathbb{R}^n\to \mathbb{R}$, se tiene que $H(\bar{a})\in M_n(\mathbb{R})$.
Para un punto estacionario $\bar{a}$ se cumple que $\triangledown f(\bar{a})=0$, así que de lo anterior tenemos
\[ f(\bar{a}+\bar{y})-f(\bar{a})=\frac{1}{2}[\bar{y}]^tH(\bar{a})[\bar{y}]+||\bar{y}||^{2}E_{2}(\bar{a},\bar{y}).\]
De manera heurística, dado que $\lim\limits_{||\bar{y}||\to 0}||\bar{y}||^{2}E_{2}(\bar{a},\bar{y})=0$, estamos invitados a pensar que el signo de $f(\bar{a}+\bar{y})-f(\bar{a})$ es el mismo que el la expresión $[\bar{y}]^tH(\bar{a})[\bar{y}]$. Pero como hemos platicado anteriormente, esto es una forma cuadrática en la variable $\bar{y}$, y podemos saber si es siempre positiva, siempre negativa o una mezcla de ambas, estudiando a la matriz hessiana $H(\bar{a})$.
Esta matriz es simétrica y de entradas reales, así que por el teorema espectral es diagonalizable mediante una matriz ortogonal $P$. Tenemos entonces que $P^tAP$ es una matriz diagonal $D$. Sabemos también que las entradas de la diagonal de $D$ son los eigenvalores $\lambda_1,\ldots,\lambda_n$ de $A$ contados con la multiplicidad que aparecen en el polinomio característico.
Teorema. Sea $X$ una matriz simétrica en $M_n(\mathbb{R})$. Consideremos la forma bilineal $\mathfrak{B}(\bar{v})=[\bar{v}]^tX[\bar{v}]$. Se cumple:
- $\mathfrak{B}(\bar{v})>0$ para todo $\bar{v}\neq \bar{0}$ si y sólo si todos los eigenvalores de $X$ son positivos.
- $\mathfrak{B}(\bar{v})<0$ para todo $\bar{v}\neq \bar{0}$ si y sólo si todos los eigenvalores de $X$ son negativos.
Demostración. Veamos la demostración del inciso 1.
$\Rightarrow )$ Por la discusión anterior, existe una matriz ortogonal $P$ tal que $P^tXP$ es diagonal, con entradas $\lambda_1,\ldots,\lambda_n$ que son los eigenvalores de $X$. Así, en alguna base ortonormal $\beta$ tenemos $$\mathfrak{B}(\bar{v})=\sum_{i=1}^{n}\lambda _{i}a_{i}^{2}$$ donde $\bar{a}=(a_{1},\dots ,a_{n})$ es el vector $\bar{v}$ en la base $\beta$. Si todos los eigenvalores son positivos, claramente $\mathfrak{B}(\bar{v})>0$, para todo $\bar{v}\neq \bar{0}$.
$\Leftarrow )$ Si $\mathfrak{B}(\bar{v})>0$ para todo $\bar{v}\neq \bar{0}$ podemos elegir $\bar{v}$ como el vector $e_k$ de la base $\beta$. Para esta elección de $\bar{v}$ tenemos $\mathfrak{B}(\hat{e_{k}})=\lambda _{k}$, de modo que para toda $k$, $\lambda _{k}>0$.
El inciso $2$ es análogo y deja como tarea moral su demostración.
$\square$
A las formas cuadráticas que cumplen el primer inciso ya las habíamos llamado positivas definidas. A las que cumplen el segundo inciso las llamaremos negativas definidas.
Combinando las ideas anteriores, podemos formalmente enunciar el teorema que nos habla de cómo son los puntos estacionarios en términos de los eigenvalores de la matriz hessiana.
Teorema. Consideremos un campo escalar $f:S\subseteq \mathbb{R}^n\to \mathbb{R}$ de clase $C^2$ en un cierto punto interior $\bar{a}\in S$. Supongamos que $\bar{a}$ es un punto estacionario.
- Si todos los eigenvalores de $H(\bar{a})$ son positivos, $f$ tiene un mínimo relativo en $\bar{a}$.
- Si todos los eigenvalores de $H(\bar{a})$ son negativos, $f$ tiene un máximo relativo en $\bar{a}$.
- Si $H(\bar{a})$ tiene por lo menos un eigenvalor positivo, y por lo menos un eigenvalor negativo, $f$ tiene punto silla en $\bar{a}$.
Antes de continuar, verifica que los tres puntos anteriores no cubren todos los casos posibles para los eigenvalores. ¿Qué casos nos faltan?
Demostración: Definamos la forma bilineal $\mathfrak{B}(\bar{v})=[\bar{v}]^tH(\bar{a})[\bar{v}]$ y usemos el teorema de Taylor para escribir
\[ \begin{equation}\label{eq:taylor}f(\bar{a}+\bar{v})-f(\bar{a})=\frac{1}{2}\mathfrak{B}(\bar{v})+||\bar{v}||^{2}E(\bar{a},\bar{v}) \end{equation} \]
con
\[ \begin{equation}\label{eq:error}\lim\limits_{\bar{v}\to \bar{0}}E(\bar{a},\bar{v})=0. \end{equation} \]
En primer lugar haremos el caso para los eigenvalores positivos. Sean $\lambda _{1},\dots ,\lambda_{n}$ los eigenvalores de $H(\bar{a})$. Sea $\lambda _{*}=\min\{ \lambda _{1},\dots ,\lambda _{n}\}$. Si $\varepsilon <\lambda_{*}$, para cada $i=1,\dots , n$ tenemos $\lambda _{i}-\varepsilon>0$. Además, los números $\lambda _{i}-\varepsilon$ son los eigenvalores de la matriz $H(\bar{a})-\varepsilon I$, la cual es simétrica porque $H(\bar{a})$ lo es. De acuerdo con nuestro teorema anterior la forma cuadrática $[\bar{v}]^t(H(\bar{a})-\varepsilon I)[\bar{v}]$ es definida positiva, y por lo tanto
$$[\bar{v}]^tH(\bar{a})[\bar{v}]>[\bar{v}]^t\varepsilon I [\bar{v}] = \varepsilon ||\bar{v}||^2.$$
Esto funciona para todo $\varepsilon <\lambda _{*}$. Tomando $\varepsilon =\frac{1}{2}\lambda _{*}$ obtenemos $\mathfrak{B}(\bar{v})>\frac{1}{2}||\bar{v}||^2$ para todo $\bar{v}\neq \bar{0}$. Por el límite de \eqref{eq:error} tenemos que existe $r>0$ tal que $|E(\bar{a},\bar{v})|<\frac{1}{4}\lambda _{*}$ para $0<||\bar{v}||<r$. En este caso se cumple
\begin{align*}0&\leq ||\bar{v}||^{2}|E(\bar{a},\bar{v})|\\ &<\frac{1}{4}\lambda _{*}||\bar{v}||^{2}\\ &<\frac{1}{2}\mathfrak{B}(\bar{v}),\end{align*}
Luego por la ecuación \eqref{eq:taylor} tenemos
\begin{align*}
f(\bar{a}+\bar{v})-f(\bar{a})&=\frac{1}{2}\mathfrak{B}(\bar{v})+||\bar{v}||^{2}E(\bar{a},\bar{v})\\
&\geq \frac{1}{2}\mathfrak{B}(\bar{v})-||\bar{v}||^{2}|E(\bar{a},\bar{v})|\\
&>0.
\end{align*}
Esto muestra que $f$ tiene un mínimo relativo en $\bar{a}$ para la vecindad $B_{r}(\bar{a})$.
Para probar la parte $2$ se usa exactamente el mismo proceder sólo que hay que considerar la función $-f$, lo cual quedará hacer como tarea moral.
Revisemos pues la parte del punto silla, la parte $3$. Consideremos $\lambda _{1}$ y $\lambda _{2}$ dos eigenvalores de $H(\bar{a})$ tales que $\lambda _1 <0$ y $\lambda _2 >0$. Pongamos $\lambda _{*}=\min\{ |\lambda _{1}|,|\lambda _{2}|\}$. Notemos que para todo $\varepsilon \in (-\lambda _{*},\lambda _{*})$ se tiene que $\lambda _{1}-\varepsilon$ y $\lambda _{2}-\varepsilon$ son números de signos opuestos y además eigenvalores de la matriz $H(\bar{a})-\varepsilon I$. Tomando vectores en dirección de los eigenvectores $\bar{v}_1$ y $\bar{v}_2$ correspondientes a $\lambda_1$ y $\lambda_2$ notamos que $[\bar{v}](H(\bar{a})-\varepsilon I)[\bar{v}]^{t}$ toma valores positivos y negativos en toda vecindad de $\bar{0}$. Finalmente escojamos $r>0$ de tal manera que $|E(\bar{a},\bar{v})|<\frac{1}{4}\varepsilon$ cuando $0<||\bar{v}||<r$. Usando las mismas desigualdades del la parte $1$, vemos que para $\bar{v}$ en la dirección de $\bar{v}_1$ la diferencia $f(\bar{a}+\bar{v})-f(\bar{a})$ es negativa y para $\bar{v}$ en la dirección de $\bar{v}_2$ es positiva. Así, $f$ tiene un punto silla en $\bar{a}$.
$\square$
Hay algunas situaciones en las que el teorema anterior no puede ser usado. Por ejemplo, cuando los eigenvalores de $H(\bar{a})$ son todos iguales a cero. En dicho caso, el teorema no funciona y no nos dice nada de si tenemos máximo, mínimo o punto silla, y de hecho cualquiera de esas cosas puede pasar.
Ejemplos de análisis de puntos críticos
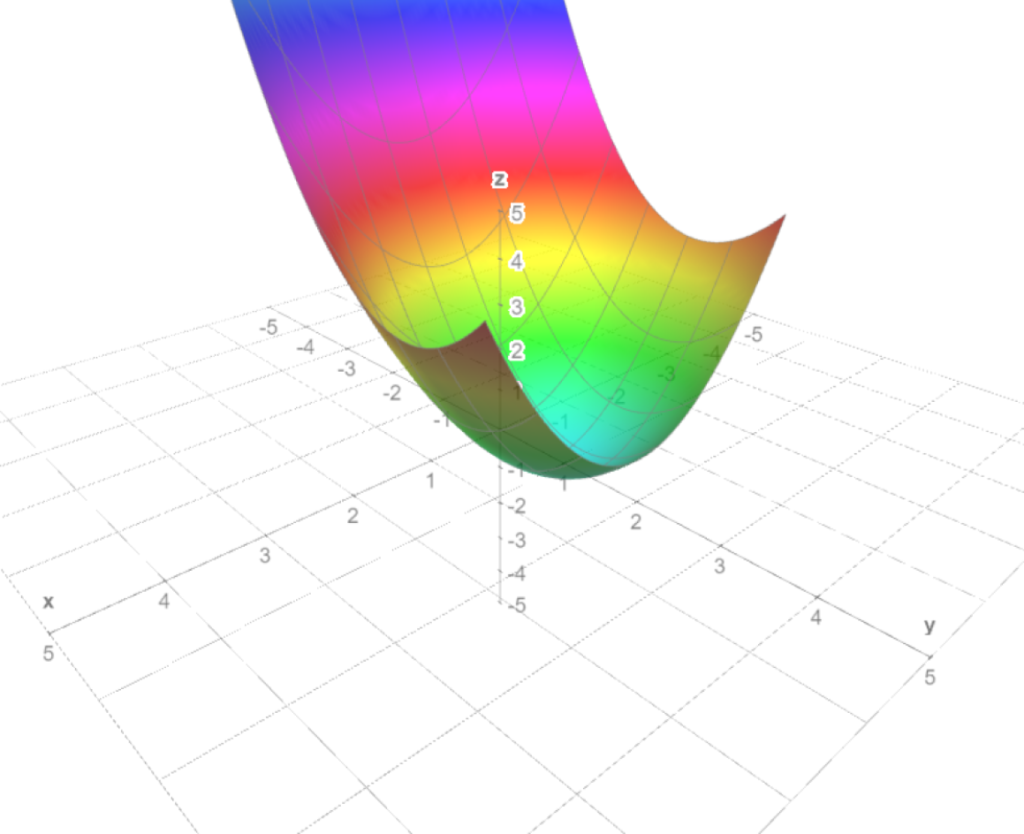
Ejemplo. Tomemos el campo escalar $f(x,y)=x^{2}+(y-1)^{2}$ y veamos cómo identificar y clasificar sus puntos estacionarios. Lo primero por hacer es encontrar el gradiente, que está dado por $$\triangledown f(x,y)=(2x,2(y-1)).$$ El gradiente se anula cuando $2x=0$ y $2(y-1)=0$, lo cual pasa si y sólo si $x=0$ y $y=1$. Esto dice que sólo hay un punto estacionario. Para determinar su naturaleza, encontraremos la matriz hessiana en este punto, así como los eigenvalores que tiene. La matriz hessiana es
\[ H(\bar{v})=\begin{pmatrix} \frac{\partial ^{2}f}{\partial x^{2}}(\bar{v}) & \frac{\partial ^{2}f}{\partial y \partial x}(\bar{v}) \\ \frac{\partial ^{2}f}{\partial x \partial y}(\bar{v}) & \frac{\partial ^{2}f}{\partial y^{2}}(\bar{v}) \end{pmatrix}=\begin{pmatrix} 2 & 0 \\ 0 & 2 \end{pmatrix}.\]
Notemos que la matriz hessiana ya está diagonalizada y es la misma para todo $\bar{v}$. En particular, en $(0,1)$ sus valores propios son $2$ y $2$, que son positivos. Así, la matriz hessiana es positiva definida y por lo tanto tenemos un mínimo local en el punto $(0,1)$. Esto lo confirma visualmente la gráfica de la Figura 2.
$\triangle$
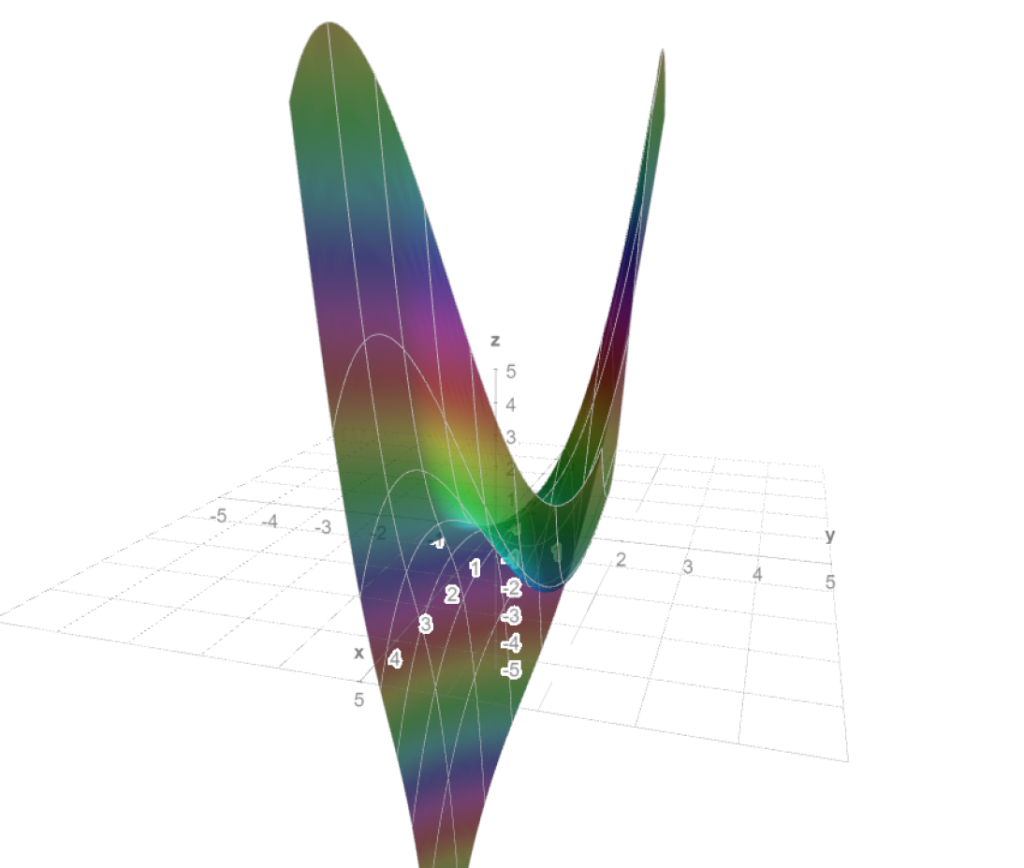
Ejemplo. Veamos cómo identificar y clasificar los puntos estacionarios del campo escalar $f(x,y)=x^{3}+y^{3}-3xy.$ Localicemos primero los puntos estacionarios. Para ello calculemos el gradiente $\triangledown f(x,y)=(3x^{2}-3y,3y^{2}-3x)$. Esto nos dice que los puntos estacionarios cumplen el sistema de ecuaciones
\[\left\{ \begin{matrix} 3x^2-3y=0\\ 3y^2-3x=0.\end{matrix} \right.\]
Puedes verificar que las únicas soluciones están dadas son los puntos $(0,0)$ y $(1,1)$ (Sugerencia. Multiplica la segunda ecuación por $x$ y suma ambas). La matriz hessiana es la siguiente:
\[ H(x,y)=\begin{pmatrix} 6x & -3 \\ -3 & 6y \end{pmatrix}.\]
En $(x,y)=(0,0)$ la matriz hessiana es $\begin{pmatrix} 0 & -3 \\ -3 & 0 \end{pmatrix}$. Para encontar sus eigenvalores calculamos el polinomio característico
\begin{align*} \det(H(0,0)-\lambda I)&=\begin{vmatrix} -\lambda & -3 \\ -3 & -\lambda \end{vmatrix} \\ &= \lambda ^{2}-9.\end{align*}
Las raíces del polinomio característico (y por lo tanto los eigenvalores) son $\lambda _{1}=3$ y $\lambda _{2}=-3$. Ya que tenemos valores propios de signos distintos tenemos un punto silla en $(0,0)$.
Para $(x,y)=(1,1)$ la cuenta correspondiente de polinomio característico es
\begin{align*} \det(H(1,1)-\lambda I)&=\begin{vmatrix} 6-\lambda & -3 \\ -3 & 6-\lambda\end{vmatrix}\\ &=(6-\lambda )^{2}-9.\end{align*}
Tras manipulaciones algebraicas, las raíces son $\lambda _{1}=9$, $\lambda _{2}=3$. Como ambas son positivas, en $(1,1)$ tenemos un mínimo.
Puedes confirmar visualmente todo lo que encontramos en la gráfica de esta función, la cual está en la Figura 3.
$\triangle$
A continuación se muestra otro problema que se puede resolver con lo que hemos platicado. Imaginemos que queremos aproximar a la función $x^2$ mediante una función lineal $ax+b$. ¿Cuál es la mejor forma de elegir $a,b$ para que las funciones queden «cerquita» en el intervalo $[0,1]$? Esa cercanía se puede medir de muchas formas, pero una es pidiendo que una integral se haga chiquita.
Ejemplo. Determinemos qué valores de las constantes $a,b\in \mathbb{R}$ minimizan la siguiente integral
\[ \int_{0}^{1}[ax+b-x^2]^2 dx.\]
Trabajemos sobre la integral.
\begin{align*} \int_{0}^{1}[ax+b-x^{2}]^{2}dx&=\int_{0}^{1}(2abx+(a^{2}-2b)x^{2}-2ax^{3}+x^{4}+b^{2})dx\\ &=\int_{0}^{1}2abx\hspace{0.1cm}dx+\int_{0}^{1}(a^{2}-2b)x^{2}dx-\int_{0}^{1}2ax^{3}dx+\int_{0}^{1}x^{4}dx+\int_{0}^{1}b^{2}dx\\ &=b^{2}+\frac{1}{3}a^{2}+ab-\frac{2}{3}b-\frac{1}{2}a+\frac{1}{5}. \end{align*}
Es decir, tenemos
\[ \int_{0}^{1}[ax+b-x^{2}]^{2}dx=b^{2}+\frac{1}{3}a^{2}+ab-\frac{2}{3}b-\frac{1}{2}a+\frac{1}{5}.\]
Ahora definamos $f(a,b)=b^{2}+\frac{1}{3}a^{2}+ab-\frac{2}{3}b-\frac{1}{2}a+\frac{1}{5}$; basándonos en la forma general de la ecuación cuadrática de dos variables podemos comprobar rápidamente que $f$ nos dibuja una elipse en cada una de sus curvas de nivel. Continuando con nuestra misión, tenemos que $\triangledown f(a,b)=(\frac{2}{3}a+b-\frac{1}{2},2b+a-\frac{2}{3})$. Al resolver el sistema
\[\left\{\begin{matrix}\frac{2}{3}a+b-\frac{1}{2}=0\\2b+a-\frac{2}{3}=0,\end{matrix}\right.\]
hay una única solución $a=1$ y $b=-\frac{1}{6}$. Puedes verificar que la matriz hessiana es la siguiente en todo punto.
\[ H(\bar{v})=\begin{pmatrix} \frac{2}{3} & 1 \\ 1 & 2 \end{pmatrix}.\]
Para determinar si tenemos un mínimo, calculamos el polinomio característico como sigue
\begin{align*} \det(H(\bar{v})-\lambda I)&=\begin{vmatrix} \frac{2}{3}-\lambda & 1 \\ 1 & 2-\lambda \end{vmatrix}\\ &=\left( \frac{2}{3}-\lambda \right)\left( 2-\lambda\right)-1\\ &=\lambda ^{2}-\frac{8}{3}\lambda + \frac{1}{3}.\end{align*}
Esta expresión se anula para $\lambda _{1}=\frac{4+\sqrt{13}}{3}$ y $\lambda_{2}=\frac{4-\sqrt{13}}{3}$. Ambos son números positivos, por lo que en el único punto estacionario de $f$ tenemos un mínimo. Así el punto en el cual la integral se minimiza es $(a,b)=(1,-\frac{1}{6})$. Concluimos que la mejor función lineal $ax+b$ que aproxima a la función $x^2$ en el intervalo $[0,1]$ con la distancia inducida por la integral dada es la función $x-\frac{1}{6}$.
En la Figura 3 puedes ver un fragmento de la gráfica de la función $f(a,b)$ que nos interesa.
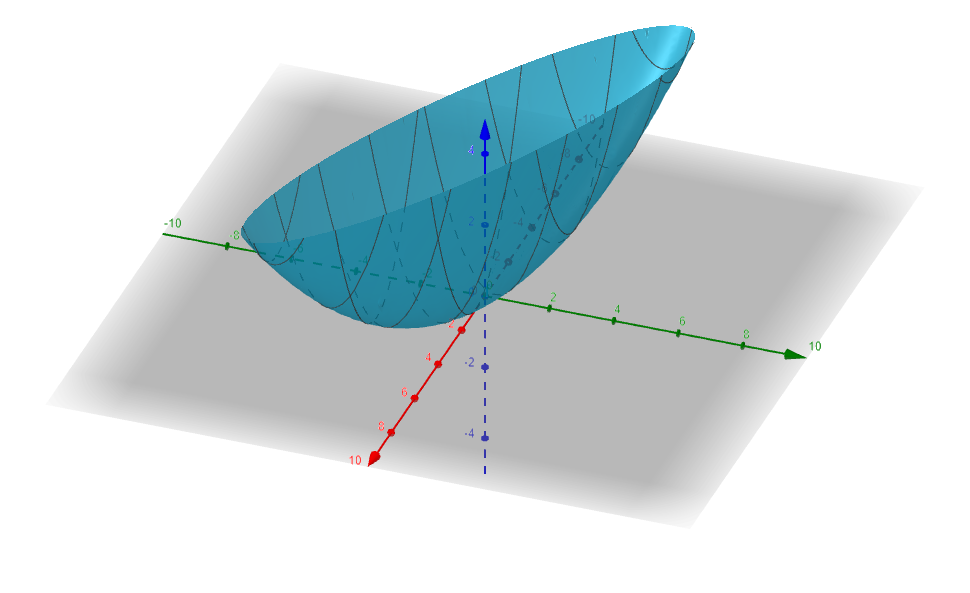
$\triangle$
Mas adelante…
La siguiente será nuestra última entrada del curso y nos permitirá resolver problemas de optimización en los que las variables que nos dan tengan ciertas restricciones. Esto debe recordarnos al teorema de la función implícita. En efecto, para demostrar los resultados de la siguiente entrada se necesitará este importante teorema, así que es recomendable que lo repases y recuerdes cómo se usa.
Tarea moral
- Identifica y clasifica los puntos estacionarios de los siguientes campos escalares:
- $f(x,y)=(x-y+1)^{2}$
- $f(x,y)=(x^{2}+y^{2})e^{-(x^{2}+y^{2})}$
- $f(x,y)=\sin(x)\cos(x)$.
- Determina si hay constantes $a,b\in \mathbb{R}$ tales que el valor de la integral \[\int_{0}^{1}[ax+b-f(x)]^{2}dx \] sea mínima para $f(x)=(x^{2}+1)^{-1}$. Esto en cierto sentido nos dice «cuál es la mejor aproximación lineal para $\frac{1}{x^2+1}$».
- Este problema habla de lo que se conoce como el método de los mínimos cuadrados. Consideremos $n$ puntos $(x_{i},y_{i})$ en $\mathbb{R}^2$, todos distintos. En general es imposible hallar una recta que pase por todos y cada uno de estos puntos; es decir, hallar una función $f(x)=ax+b$ tal que $f(x_{i})=y_{i}$ para cada $i$. Sin embargo, sí es posible encontrar una función lineal $f(x)=ax+b$ que minimice el error cuadrático total que está dado por \[ E(a,b)=\sum_{i=1}^{n}[f(x_{i})-y_{i}]^{2}.\] Determina los valores de $a$ y $b$ para que esto ocurra. Sugerencia. Trabaja con el campo escalar $E(a,b)$ recuerda que los puntos $(x_{i},y_{i})$ son constantes.
- Completa la demostración de que si una matriz $X$ tiene puros eigenvalores negativos, entonces es negativa definida.
- En el teorema de clasificación de puntos estacionarios, muestra que en efecto si la matriz hessiana es negativa definida, entonces el punto estacionario es un punto en donde la función tiene máximo local.
Entradas relacionadas
- Ir a Cálculo Diferencial e Integral III
- Entrada anterior del curso: Divergencia, laplaciano y rotacional
- Entrada siguiente del curso: Multiplicadores de Lagrange
