Introducción

En la entrada anterior comenzamos el estudio a la teoría cualitativa de sistemas de dos ecuaciones de primer orden, definiendo el plano fase del sistema que es el plano $x(t)-y(t)$ junto con todas las curvas que representan a las soluciones al sistema de ecuaciones, vistas como funciones de $\mathbb{R}$ a $\mathbb{R}^{2}$. Una vez que escribimos al sistema de ecuaciones en la forma $$\dot{\textbf{X}}=\textbf{F}(x,y)$$ notamos que la función $\textbf{F}(x,y)$ puede ser vista como una función de $\mathbb{R}^{2}$ a $\mathbb{R}^{2}$. Más aún, podemos ver que a cada punto $(x,y)$ podemos anclar el vector $\textbf{F}(x,y)$ en el plano $x(t)-y(t)$. Este es el campo vectorial asociado al sistema, el cual nos da la información de cómo se ven las curvas solución y su comportamiento.

Para poder dibujar el plano fase de la forma más fiel posible aún debemos estudiar los puntos donde el campo $\textbf{F}$ se anula. A estos puntos los llamaremos puntos de equilibrio. De ellos dependerá casi por completo el comportamiento de las soluciones en el plano fase, por lo que estudiaremos su estabilidad. Es decir, veremos el comportamiento de las soluciones cercanas a los puntos de equilibrio conforme cambia la variable independiente $t$. Finalizaremos estudiando el plano fase de diversos sistemas e interpretando la estabilidad de los puntos de equilibrio según se recorren las curvas solución.

Puntos de equilibrio de sistemas de ecuaciones de primer orden

Definimos los puntos de equilibrio de un sistema de ecuaciones de primer orden y analizamos varios ejemplos. Además, probamos que $$\textbf{X}(t)=\begin{pmatrix} x_{0} \\ y_{0} \end{pmatrix}$$ es solución al sistema de ecuaciones lineal homogéneo con coeficientes constantes $$\dot{\textbf{X}}=\textbf{A}\textbf{X}$$ si $(x_{0},y_{0})$ es punto de equilibrio del sistema.

Estabilidad de puntos de equilibrio

Definimos los conceptos de puntos de equilibrio estables, asintóticamente estables e inestables. Mediante el plano fase estudiamos la estabilidad de puntos de equilibrio de diversos sistemas de ecuaciones.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero te servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

Los campos vectoriales de las imágenes fueron realizados en el siguiente enlace.

• Considera el sistema lineal homogéneo con coeficientes constantes $\dot{\textbf{X}}=\textbf{A}\textbf{X}$. Muestra que si $\det{A} \neq 0$, entonces el único punto de equilibrio del sistema es $(0,0)$.

• Considera nuevamente el sistema del ejercicio anterior $\dot{\textbf{X}}=\textbf{A}\textbf{X}$. Supongamos que $$\textbf{A}=\begin{pmatrix} a & b \\ c &d \end{pmatrix}$$ con $a\neq 0$ y $\det{A}=0$. ¿Qué puedes decir acerca de los puntos de equilibrio del sistema?

• Encuentra un sistema de ecuaciones no lineales de primer orden sin puntos de equilibrio.

• Calcula los puntos de equilibrio de los siguientes sistemas: $$\dot{\textbf{X}}=\begin{pmatrix} 1 & 4 \\ -2 & 7 \end{pmatrix}+\begin{pmatrix} 2 \\ 2 \end{pmatrix}.$$ $$\dot{\textbf{X}}=\begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}+\begin{pmatrix} 0 \\ -\cos{x} \end{pmatrix}.$$ $$\dot{\textbf{X}}=\begin{pmatrix} 0 & 1 \\ 0 & -1 \end{pmatrix}+\begin{pmatrix} 0 \\ -\cos{x} \end{pmatrix}.$$

• Determina la estabilidad de los puntos de equilibrio, según los campos vectoriales que aparecen a continuación:

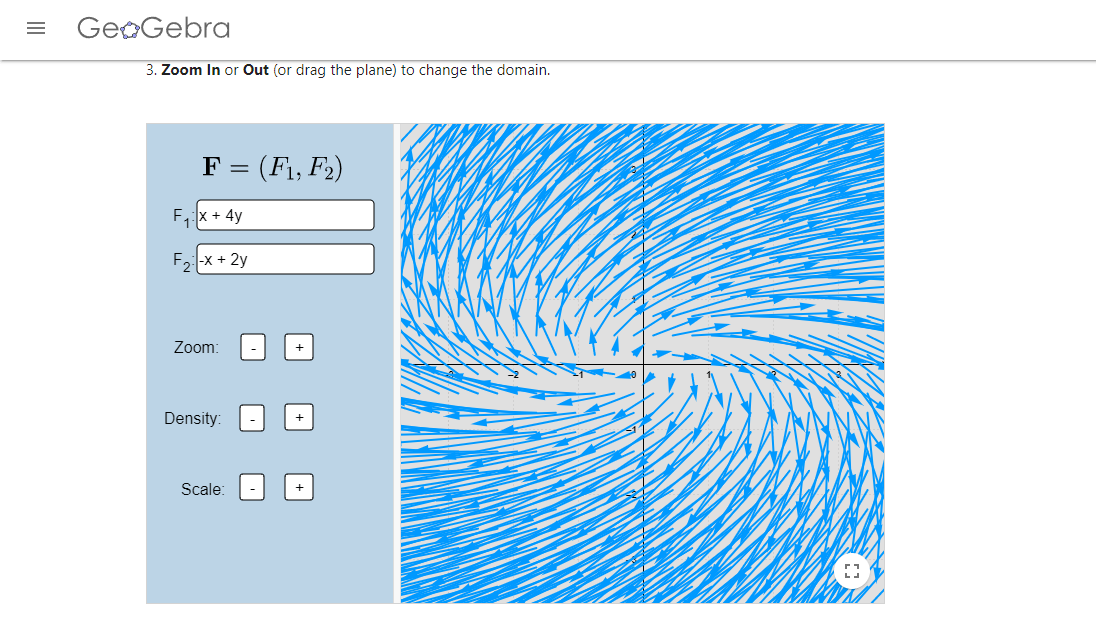
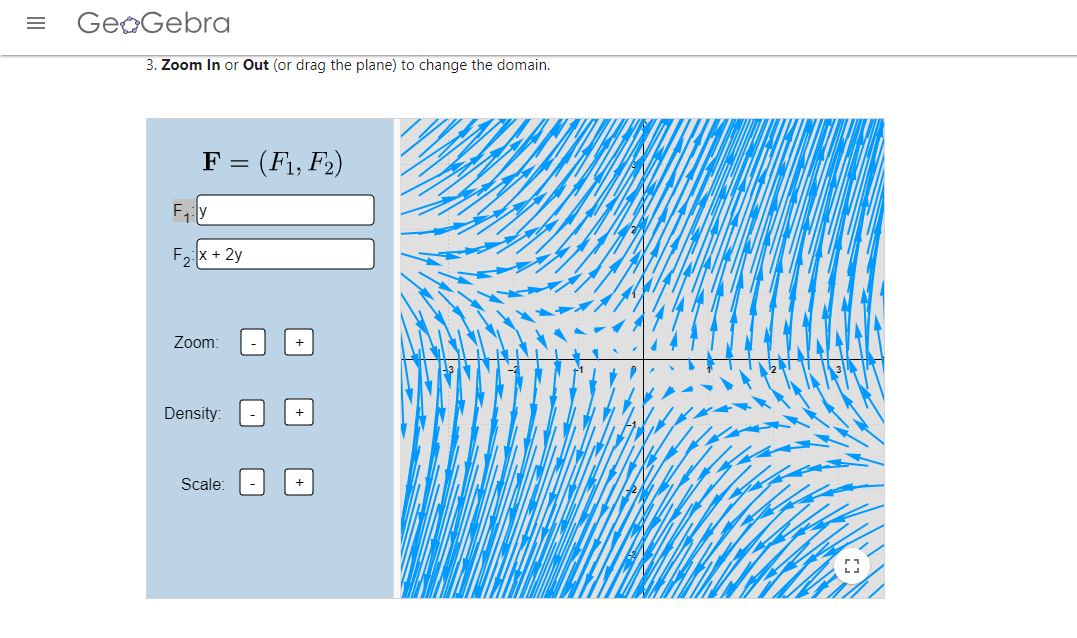
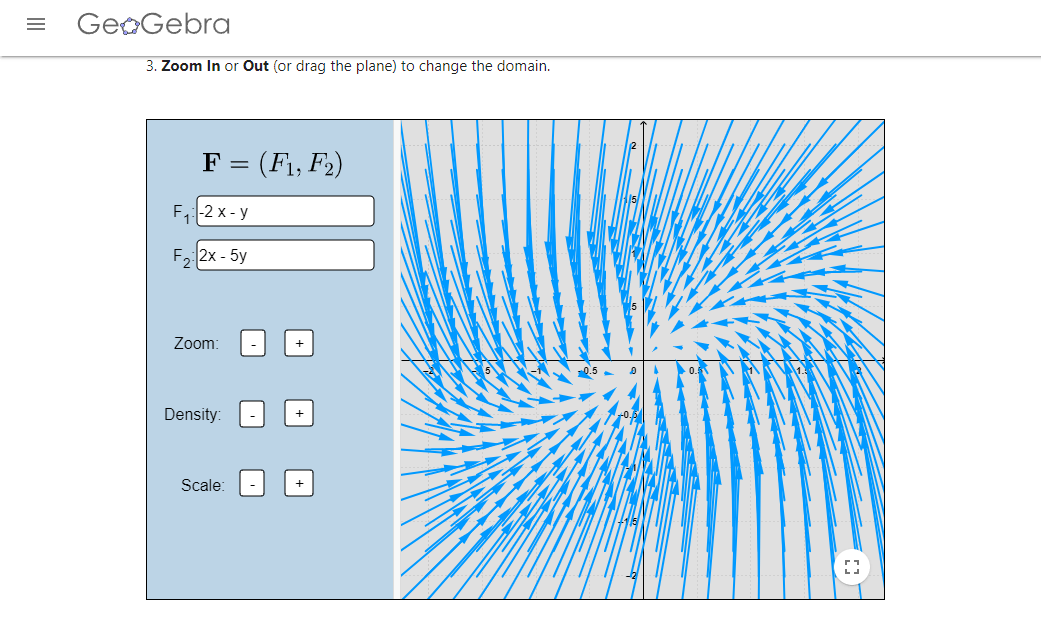
Más adelante

Una vez que conocemos los puntos de equilibrio de un sistema de ecuaciones de primer orden y definimos la estabilidad de estos, es momento para analizar el plano fase de los sistemas de dos ecuaciones con coeficientes constantes. Afortunadamente el plano fase y la estabilidad del (único) punto de equilibrio quedará determinado por la forma de los valores propios del sistema.

Comenzaremos en la siguiente entrada con el caso cuando el sistema tiene dos valores propios reales distintos y no nulos.

Entradas relacionadas

• Ir a Ecuaciones Diferenciales I
• Entrada anterior del curso: Geometría de soluciones a sistemas de dos ecuaciones de primer orden. Plano fase y campo vectorial asociado
• Siguiente entrada del curso: Plano fase para sistemas lineales con valores propios reales distintos no nulos

• Notas escritas relacionadas con el tema: Sistemas autónomos, puntos de equilibrio y su estabilidad

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»