Archivo de la etiqueta: lógica

Álgebra Superior I: Demostraciones por contradicción

Por Guillermo Oswaldo Cota Martínez

2 respuestas

Introducción

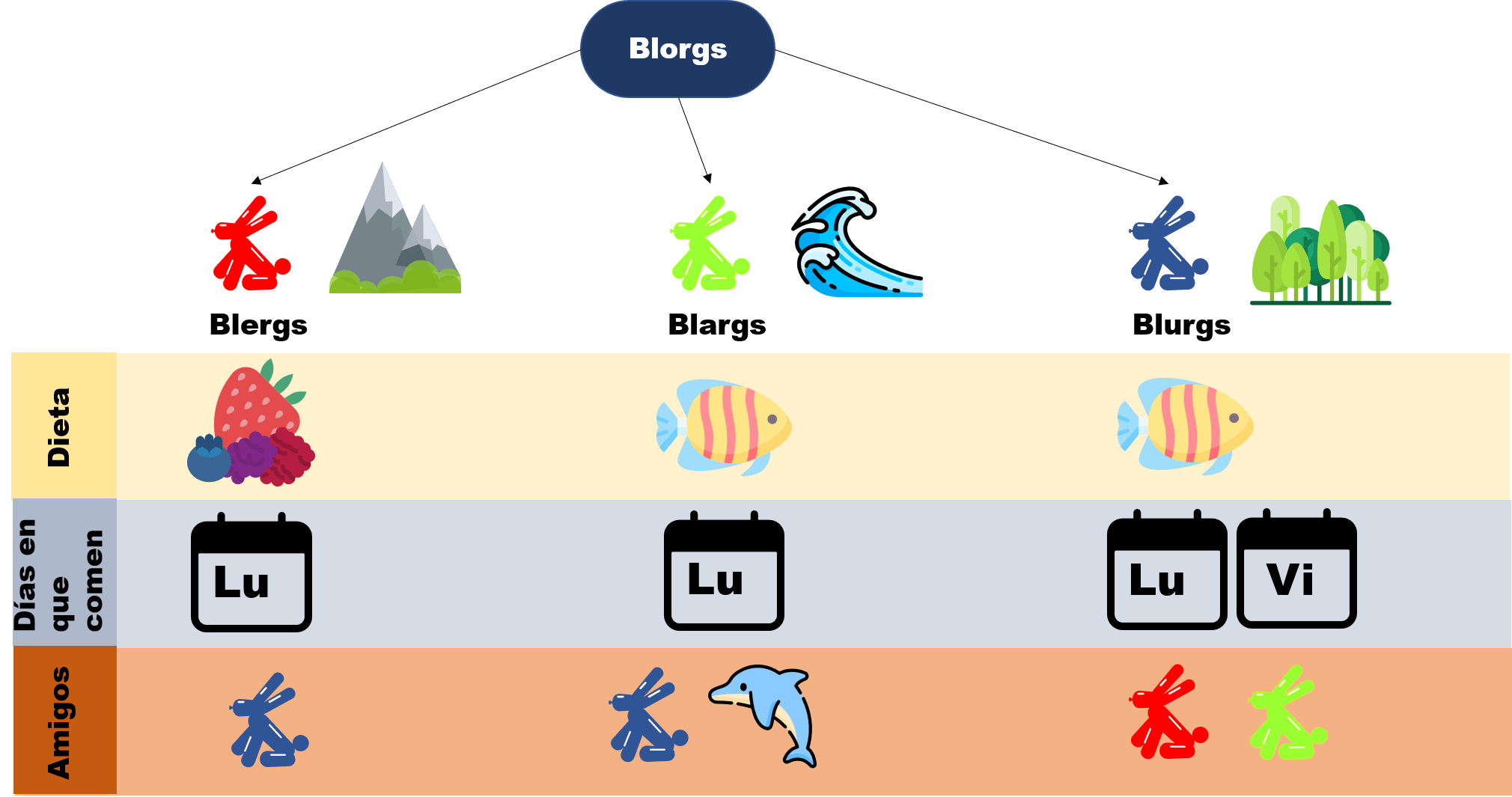
Esta entrada es parte de una serie de notas introductorias sobre técnicas de demostración. En esta entrada se habla sobre demostraciones por contradicción. Cada entrada está ligeramente relacionada con las otras. Para entenderlas bien, usamos el siguiente diagrama que recopila cómo se comporta un mundo fantástico llamado Axios, en donde habitan creaturas llamadas Blorgs. Para leer más sobre ello, haz click aquí.

Ya hemos empezado a ver algunas estrategias para empezar a demostrar cosas. Ahora veremos una siguiente que es muy común de encontrar: las demostraciones por contradicción. Comenzando con una proposición que queremos demostrar, supondremos que no es cierta. Puede sonarte que es un poco extraño, pero en esta entrada revisaremos de qué forma esta suposición nos ayudará.

La contradicción

Puede que en tu vida hayas escuchado la palabra contradicción usada en alguno u otro contexto. Podemos decir por ejemplo que una persona se contradice a sí misma cuando dice que es alérgica al camarón después de haberse comido un coctél de camarón. Esto suena poco convincente, ¿no? Pues al decir que alguien es alérgico al camarón sabemos que no puede comer camarón, al mismo tiempo que vemos a la persona haciéndolo. Esta idea va a ser similar en las matemáticas. Pero recuerda que aquí estamos en el lenguaje de las proposiciones.

Definición. Una contradicción es una fórmula proposicional en la cual sin importar la asignación de verdad de las variables proposicionales, siempre se obtiene algo falso.

Un ejemplo muy sencillo es la fórmula proposicional $(P \land \neg P)$. Si $P$ es falso, entonces la conjunción es falsa. Y si $P$ es verdadero, entonces $\neg P$ es falso y entonces también la conjunción es falsa.

Ahora observa la siguiente regla de inferencia:

\begin{array}{rl}
P \\
\neg P \\
\hline
\therefore Q.
\end{array}

Se puede probar que esta es una inferencia válida (es uno de los ejercicios al final de la entrada). Analiza un poco la regla y piensa: ¿esto qué significa? Observa que en ningún momento aparece el término $Q$ en las premisas y sin embargo es una conclusión. La parte de las premisas de la regla de inferencia sería $P\land \neg P$. En pocas palabras, esto nos quiere decir que «de una contradicción se puede deducir lo que sea». Es decir, si en algún momento llegamos a una contradicción, ya nada tiene sentido, pues cualquier cosa sería cierta. Si cambiamos $Q$ por «La luna es de queso», podemos concluirlo de una contradicción, y esto no tiene sentido. Es por eso que si en algún momento en las matemáticas llegamos a una contradicción, es que algo está raro. Bajo esta idea funcionarán las demostraciones por contradicción.

Demostraciones por contradicción

Hablemos ahora sí de la estrategia de hacer demostraciones por contradicción. Como platicamos en la sección anterior, de una contradicción podemos concluir cualquier cosa. En particular, podemos concluir lo que queremos demostrar. Esto, ¿cómo se ve en pasos específicos que tenemos que hacer? La estrategia general es la siguiente.

  1. Pensemos que de ciertas premisas $Q_1, Q_2, \ldots, Q_n$ queremos llegar a la conclusión $P$.
  2. Supongamos que además de dichas premisas, también tenemos a $\neg P$ como premisa.
  3. A partir de $Q_1,\ldots,Q_n,\neg P$, obtengamos todas las cosas ciertas que podamos, con el objetivo de simultáneamente probar que tanto cierta proposición $R$ como cierta proposición $\neg R$ son ciertas.
  4. Como ya tendremos $R$ y $\neg R$ en nuestras premisas, podremos concluir lo que sea, en particular, $P$.
  5. Otra manera de pensarlo es que en el momento en que hemos encontrado tanto $R$ como $\neg R$. En matemáticas las contradicciones nos dicen que hay algo raro, pues sabemos que una proposición no puede ser verdadera y falsa a la vez (recuerda que esto es una contradicción). Así, habremos encontrado un problema lógico. Entonces nuestra suposición de que $\neg P$ es verdadera es imposible. Por lo tanto, $P$ es verdadera.

Otra manera en la que en que te puedas imaginar la reducción al absurdo es mediante la validez de la siguiente regla de inferencia (también tendrás que justificarla como uno de los ejercicios):

$$ \begin{array}{rl} & \neg P \Rightarrow (R \land \neg R) \\ \hline \therefore & P \end{array}.$$

Esto nos dice que si $P$ es falso (es decir, que $\neg P$ es verdad) implica tanto cierta proposición $Q$, como su negación $\neg Q$, entonces en realidad $P$ no puede ser falso, y por lo tanto es verdadero. Piénsalo como mejor te acomodes.

Ejemplo de demostración por contradicción

Hagamos una prueba en el mundo Axios.

Proposición. Para todo Blurg $x$, si $x$ come un cierto día, entonces pasan como mínimo tres días antes de que $x$ vuelva a comer.

Demostración. Vamos a hacer esta prueba por contradicción. Como dijimos antes, las pruebas por contradicción se basan en que para demostrar una proposición $P$, se empieza suponiendo $\neg P$, y a partir de ahí se ven las consecuencias y se intenta llegar a una contradicción. Ahora veamos la traducción de esto a nuestra proposición.

$P$ = Para todo Blurg $x$, si $x$ come un cierto día, entonces pasan como mínimo tres días antes de que $x$ vuelva a comer.

La negación es (recuerda que la negación de $\forall x: A(x)\Rightarrow B(x)$ es $\exists x: A\land \neg B$):

$\neg P$ = Existe un Blurg $x$ que comió cierto día, y no pasaron como mínimo tres días antes que de $x$ volviera a comer.

Otra manera de escribir esto es

$\neg P$ = Existe un Blurg $x$ que comió cierto día, y pasaron máximo dos días antes que de $x$ volviera a comer.

Entonces empecemos con $ \neg P$ y veamos qué obtenemos. Tomemos dicho Blurg $x$ que existe. Uno de nuestros axiomas dice que $Q =\text {Para todo Blurg $x$, se tiene que $x$ come exactamente los lunes y los viernes}$. Así, la primera vez que $x$ comió fue o lunes, o viernes.

  • Si comió el lunes, entonces como estamos suponiendo $\neg P$, tenemos que $x$ comió máximo el martes o el jueves. Pero esto es $\neg Q$, pues existió un Blurg que no comió exactamente los lunes o viernes. Así, tendríamos $Q$ y $\neg Q$, una contradicción.
  • Si comió el viernes, entonces como estamos suponiendo $\neg P$, tenemos que $x$ comió máximo el sábado, o el domingo. Pero esto es $\neg Q$ también, pues existió un Blurg que no comió exactamente los lunes o viernes. Una vez más tenemos $Q$ y $\neg Q$, una contradicción.

En cualquiera de los casos, llegamos a una contradicción. Nuestro error fue suponer que $P$ no era cierta, por lo tanto tiene que ser cierta $P$.

$\square$

Algunos ejemplos famosos de demostraciones por contradicción.

Ahorita estamos en Axios y seguiremos en él. Pero para acercárte un poco más a cómo se usa esta estrategia en matemáticas, aquí te compartimos unos ejemplos de demostraciones por contradicción. Para fines de este curso no necesitas saber demostrar estas proposiciones, únicamente son ejemplos que podrías checar para entender mejor cómo se utiliza esta estrategia.

  • La demostración de que el $0$ es el único neutro aditivo en los números reales (es el único número que al sumarlo a otro número resulta el mismo otro número) utiliza esta estrategia, pues al suponer que no es único, se llega a una contradicción. Puedes checar la demostración aquí.
  • En geometría euclideana, existen criterios para decir si dos triángulos son congruentes (son el «mismo» triángulo salvo quizá la reflexión y rotación, es decir hay una forma de rotarlo o reflejarlo para notar que se trata del «mismo» triángulo). Uno de estos se llama el criterio LAL que nos dice que si dos triángulos tienen dos lados que miden lo mismo y comparten el ángulo entre esos lados, entonces son congruentes. Una técnica para demostrar esto es con reducción a lo absurdo y supone que dos lados y el ángulo entre ellos son iguales, pero que el lado restante es distinto. De ahí se puede llegar a una contradicción. Puedes checar la demostración aquí.
  • En el estudio de los tipos de números, se usa una prueba por contradicción para mostrar que el número $\sqrt{2}$ es irracional. Si fuera racional, se podría escribir como $\sqrt{2}=\frac{a}{b}$ con $a$ y $b$ enteros positivos que no comparten factores en común. Pero de esa igualdad se llega a $2b^2=a^2$, de donde se puede justificar con algunos pasos que tanto $a$ como $b$ son pares. Así, ¡simultáneamente $a$ y $b$ deberían y no deberían tener factores en común! Esa contradicción muestra la irracionalidad de $\sqrt{2}$.
  • También puedes ver una colección de videos con pruebas por contradicción en el siguiente enlace: Busca una contradicción.

Más adelante…

En las siguientes entradas seguiremos hablando de cómo hacer demostraciones. Más que estrategias generales, serán una guía sobre cómo demostrar proposiciones que involucran conectores lógicos o cuantificadores. Ya hemos visto algunos de estos ejemplos y ahora profundizaremos un poco más en su estructura.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Usa tablas de verdad para ver que $(P\Rightarrow Q) \land (Q\Rightarrow P) \land P \land \neg Q$ es una contradicción.
  2. Prueba que $$ \begin{array}{rl} & P \Rightarrow (R \land \neg R) \\ \hline \therefore & \neg P \end{array}$$ es una regla de inferencia válida.
  3. Prueba que
    \begin{array}{rl}
    P \\
    \neg P \\
    \hline
    \therefore R
    \end{array}
    es una regla de inferencia válida.
  4. Prueba por contradicción que «Para todo Blorg $x$, si $x$ no come fresas, ni come los viernes, entonces $x$ es un Blarg». Como ayuda, la negación es «Existe un Blorg $x$ tal que ni come fresas, ni come los viernes, ni es Blarg». Si no es Blarg, ¿qué casos hay y cómo llegas a una contradicción en cada uno de ellos?
  5. El viernes pasado iba caminando y encontré un Blorg $A$ que estaba platicando con un amigo suyo, un Blorg $B$ el cual estaba comiendo. Luego, el Blorg $B$ se encontró a un amigo suyo que estaba comiendo lo mismo. ¿Tiene sentido mi historia? ¿Qué sucedería si toda mi historia es verdadera?

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Álgebra Superior I: Problemas de condicionales y cuantificadores

Por Guillermo Oswaldo Cota Martínez

Deja un comentario

Introducción

En esta entrada resolveremos problemas de temas vistos en entradas anteriores. Haremos algunos ejemplos relacionados con los conectores condicionales que vimos en una entrada anterior: la implicación y la doble implicación. También veremos algunos de cuantificadores lógicos.

Problemas resueltos

Problema. Si $P$ y $R$ son verdaderas y $Q$ es falsa, di si la siguiente proposición es verdadera o falsa: $$(P \lor R) \Rightarrow \neg(Q \land R).$$

Solución. Haremos una tabla de verdad pero únicamente con los valores que nos dan, es decir, no vamos a hacer la tabla para todos los casos, sino únicamente los que nos interesan en este momento:

$P$$Q$$R$$P \lor R$ $Q \land R$$\neg (Q \land R)$$(P \lor R) \Rightarrow \neg(Q \land R)$
$1$$0$$1$  $1$ $0$  $1$   $1$

Por lo tanto la proposición es verdadera para los valores de verdad dados.

$\square$

Problema. Di si las siguientes proposiciones sobre los números enteros son verdaderas o no:

  1. $(3+1=4) \Rightarrow (0<10)$
  2. $(4=5) \Leftrightarrow (9+1=10)$
  3. $((6<7) \lor (3^2=10)) \Rightarrow (12<12^2)$
  4. $((-1<1) \land (1<-1)) \Leftrightarrow ((13-1=12-1+1)\Rightarrow (1+1<2))$

Solución.

Vamos a hacer algunas verificaciones sobre cada una de las proposiciones para encontrar su valor de verdad:

  • $(3+1=4) \Rightarrow (0<10)$

Como $3+1=4$ es verdadera y $0<10$ es verdadera también, entonces la proposición es verdadera.

  • $(4=5) \Leftrightarrow (9+1=10)$

Recordemos que la doble condicional es verdadera si ambas proposiciones tienen el mismo valor de verdad. Por un lado no es cierto que $4=5$ mientras que sí es verdad que $9+1=10$. Por lo tanto la proposición es falsa.

  • $((6<7) \lor (3^2=10)) \Rightarrow (12<12^2)$

Vamos a ver la proposición por partes. Primero veamos que $((6<7) \lor (3^2=10))$ es una disyunción verdadera pues una de las proposiciones que la componen, $6<7$, lo es. Como $12<12^2$ es verdad, entonces la implicación tiene antecedente y subsecuente verdaderos y por lo tanto es verdadera.

  • $((-1<1) \land (1<-1)) \Leftrightarrow ((13-1=12-1+1)\Rightarrow (1+1<2))$

De nuevo vamos a dividir la proposición en sus partes, $(-1<1) \land (1<-1)$ y $(13-1=12-1+1)\Rightarrow (1+1<2)$. Primero notemos que $(-1<1) \land (1<-1)$ es falsa, pues no es cierto que $1<-1$.

Ahora, veamos cómo es $(13-1=12-1+1)\Rightarrow (1+1<2)$. Nota que $12=13-1$ y $12=12-1+1$, entonces $13-1=12-1+1$. Entonces esta primera parte es verdad, mientras que $1+1=2$ pero no es cierto que $2<2$. Así que es falso que $1+1<2$. Entonces $(13-1=12-1+1)\Rightarrow (1+1<2)$ es falso.

Como $(-1<1) \land (1<-1)$, $(13-1=12-1+1)\Rightarrow (1+1<2)$ son ambas falsas, entonces $((-1<1) \land (1<-1)) \Leftrightarrow ((13-1=12-1+1)\Rightarrow (1+1<2))$ es verdadero.

$\square$

Nota: En este tipo de ejercicios, ¿viste cómo se dieron las argumentaciones de las proposiciones en cada caso? El secreto aquí fue «desarmar» las proposiciones en partes más pequeñas. Esto lo hacemos pues recuerda que los conectores son binarios, esto significa que su valor de verdad depende del valor de verdad de las dos proposiciones que conectan.

Así, para ver cuál es el valor de verdad de $((6<7) \lor (3^2=10)) \Rightarrow (12<12^2)$, lo que hicimos fue deshacerlo en sus partes. Una parte $A$ fue $(6<7) \lor (3^2=10)$ y la otra parte $B$ fue $12<12^2$. Entonces bastaba con verificar cuáles eran los valores de verdad de $A$ y $B$. Para ello, volvimos a «desarmar» a $A$ en sus partes «atómicas». Es decir, desarmamos $(6<7) \lor (3^2=10)$ en $6<7$ y $3^2=10$ y estudiamos el valor de verdad de cada uno de ellos. Usualmente este tipo de pensamiento de «desarmar un problema en sus partes» te ayudará a verificar o demostrar cosas más adelante.

Problema. Sean $P(x)$, $Q(x)$ y $R(x)$ los siguientes predicados:

  • $P(x): x \leq 4$
  • $Q(x): x +1$ es par.
  • $R(x): x> 0$

Si nuestro universo de discurso son los números enteros, ¿cuáles son los valores de verdad de las siguientes proposiciones?

  1. $P(1)$
  2. $P(1) \Rightarrow Q(1)$
  3. $P(0) \Rightarrow (R(5) \Rightarrow Q(0))$
  4. $R(-1) \lor P(2)$
  5. $\neg R(-2) \land P(-2)$

Solución.

1.$P(1)$

Es verdadera, pues $1 \leq 4$.

2. $P(1) \Rightarrow Q(1)$

Como $P(1)$ es verdadera y además $1+1=2$ es par, entonces la proposición es verdadera.

3. $P(0) \Rightarrow (R(5) \Rightarrow Q(0))$

Vamos a dividir la proposición en partes. Primero notemos que $P(0)$ es verdad. Mientras que $R(5) \Rightarrow Q(0)$ es falsa, ya que es cierto que $5>0$ pero es falso que $0+1$ sea par. Entonces la proposición es falsa.

4. $R(-1) \lor P(2)$

Como $R(-1)$ es falsa pero $P(2)$ es verdad, entonces la proposición es verdadera.

5. $\neg R(-2) \land P(-2)$

Como $-2>0$ es falsa, entonces $\neg R(-2)$ es verdad. Además, $-2<4$ es verdad. De esta manera la proposición es verdadera.

$\square$

Problema. Considera los siguientes predicados:

  • $P(x): 2x>0$
  • $Q(x):x>0$
  • $R(x): x=20$
  • $T(x):x<0$

Determina la verdad o falsedad de las siguientes proposiciones, considerando que nuestro universo de discurso son los números enteros. Si la proposición no es verdadera, da un contraejemplo o explicación de ello.

  1. $\forall x: (P(x) \Rightarrow Q(x))$
  2. $\exists x: (Q(x) \land T(x))$
  3. $\forall x: (R(x) \Rightarrow Q(x))$
  4. $\exists ! x:(R(x))$
  5. $ \nexists x :(Q(x) \land P(x))$

Solución.

  • $\forall x:(P(x) \Rightarrow Q(x))$

Nota que siempre que se cumple $2x>0$ entonces $x>0$ (más adelante demostrarás esto con toda formalidad, pero de momento lo daremos por cierto). Por lo tanto la proposición es verdadera.

  • $\exists x: (Q(x) \land T(x))$

Para que esto sucediera, necesitaríamos la existencia de al menos un elemento $x$ que cumpla $0<x$ y $x>0$, es decir necesitaríamos un elemento que sea positivo y negativo a la vez, pero esto no es posible. Por lo tanto la proposición es falsa.

  • $\forall x:(R(x) \Rightarrow Q(x))$

Lo que nos dice esta proposición es «Para todo número entero $x$ que cumpla $x=20$ entonces $x>0$» o dicho de otra manera: «Si un número entero es igual a 20, entonces será positivo.» Lo cuál es correcto, pues si el número es distinto a 20, la implicación será correcta (recuerda la tabla de verdad de la implicación), mientras que el único caso en donde la hipótesis se cumple es cuando $x=20$ y claramente es un número que cumple $x>0$. Entonces la proposición es verdadera.

  • $\exists ! x:(R(x))$

Esto nos quiere decir que existe un único número entero que sea igual a 20, e inmediatamente podemos saber que es verdadera, pero ¿A qué nos referiremos que un número sea igual a 20? Primero tendríamos que ponernos de acuerdo de qué significa la igualdad. Aunque ahora no lo haremos, piensa el cómo nos aseguraríamos de que es el único número entero que cumple esa propiedad. ¿Qué pasaría si no fuera cierto?

  • $ \nexists x: (Q(x) \land P(x))$

Lo que dice la proposición es que ningún número $x$ va a cumplir a la vez $x>0$ y $2x>0$, pero esto no es cierto, pues pensemos en $x=1$. Cumple $Q(x)$ ya que $1>0$ y cumple $P(x)$ porque $2\cdot 1=2>0$. Entonces podemos decir que es falso pues dimos un contraejemplo que contradijo la proposición.

$\square$

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Álgebra Superior I: Cuantificadores existenciales y universales

Por Guillermo Oswaldo Cota Martínez

4 respuestas

Introducción

Hasta ahora hemos visto proposiciones, variables proposicionales, conectores y fórmulas lógicas. Por ello, ya podemos decir cómo se manejan las proposiciones al combinarlas o qué significa que dos proposiciones sean equivalentes.

Sin embargo, hasta ahora no hemos trabajado con tanto rigor los objetos a los que nos referimos dentro de una proposición. Por ejemplo cuando decimos la proposición «Este número es impar» puede que sea o no verdadera, pero esto depende de una cosa: el contexto. ¿A qué número nos estamos refiriendo? Podríamos estar en la siguiente conversación: «Hay números distintos a los múltiplos de 2, por ejemplo el 3. Este número es impar.» A esto último, estando en contexto, ya le podríamos asociar un valor de verdad.

En general esto no es así. Podemos ir variando a qué número nos referimos. En ocasiones las proposiciones tienen una variable y, dependiendo el valor de esa variable, cambian su significado o su valor de verdad. En esta entrada formalizamos estas ideas y hablamos de cuantificadores, que nos permitirán «recorrer» todos los valores posibles de una variable.

Términos variables y predicados

Volvamos a nuestro ejemplo. Al tomar la proposición $P$ «el número es impar», podríamos referirnos al $1$, $2$, $3$, $80$ o $20,000$. Así, es más conveniente pensar en que la proposición depende de una variable como sigue:

$P(\text{el número})$ = «$\text{el número}$ es impar».

Visto de esta manera, $P(2)$ es la proposición «$2$ es impar». En general $P(x)$ es la proposición «$x$ es impar» y esta hace referencia a que el número es una variable que puede tomar distintos valores «permitidos». Observa que en este caso no tendría sentido decir si $P(\text{azul})$ es verdadero o falso. A este tipo de proposiciones que tienen una variable (o más), se les llama predicados.

¿Notas que tenemos que ponernos de acuerdo sobre cuál es el contexto sobre el que estamos hablando al momento de asignarle un valor a nuestra variable? Esto debido a que no podríamos decir que «azul es impar» o «la luna es impar». A este «conjunto» dentro del cual pueden tomar valores nuestras variables le llamamos universo de discurso. Aunque suena algo sofisticado, puedes pensarlo como el contexto al que nos estamos acoplando.

Es muy importante siempre tener claro el universo de discurso cuando usamos predicados. No será lo mismo estar hablando de número pares, que de números enteros. Sabemos que todos los números pares no son impares. Mientras que algunos números enteros son impares. Estas palabras enfatizadas son las que nos van a permitir hablar más sobre cómo es nuestro universo de discurso. No es lo mismo que solo un objeto del universo cumpla un predicado (tenga valor de verdad verdadero) a que todos los objetos de nuestro universo las cumplan.

Cuantificador universal

Cuando tenemos un predicado $P(x)$, no podemos decir si es verdadero o falso hasta que no hayamos decidido quién es exactamente el objeto $x$ dentro de nuestro universo de discurso del que estamos hablando. Pero lo que sí podemos hacer es pensar en si ninguno, alguno o todos los elementos de dicho universo de discurso hacen que $P(x)$ sea verdadero, o no. A esto se le llama cuantificar un predicado.

El primer cuantificador que nos interesa es el cuantificador universal que transforma un predicado en una afirmación de que todo objeto de nuestro universo de discurso hace que la proposición $P(x)$ sea verdadera. Dicho cuantificador universal puede pensarse como agregar un «Para todo $x$ en el universo de discurso,» antes del predicado $P(x)$ que nos interesa. Lo que esto hace es que transforma el predicado $P(x)$ en la proposición $\forall x: P(x)$, la cual acordamos que es cierta siempre y cuando cualquier objeto $x$ de nuestro universo de discurso hace que $P(x)$ sea cierta. Entonces la veracidad de $\forall x: P(x)$ depende fuertemente tanto de:

  • La proposición $P(x)$
  • El universo de discurso en el que estemos.

Cotidianamente también decimos simpemente «Para todo $x$, $P(x)$», pero es muy importante que el universo de discurso sea claro.

Veamos un ejemplo poco a poco. Consideremos el siguiente predicado:

$$P(x)= \text{$x$ es múltiplo de $2$.}$$

Este predicado no tiene ningún valor de verdad. Lo podemos pensar como que es una proposición cuyo contenido depende de una variable $x$ que no hemos decidido. Ahora acordemos como universo a los números múltiplos de $4$. A partir de ello, podemos crear la siguiente proposición con el cuantificador universal $\forall$:

$$\forall x \text{ múltiplo de $4$}: P(x).$$

En palabras «todo múltiplo de $4$ es múltiplo de $2$». Al cuantificar el predicado, ya se convierte en una proposición. ¿Es verdadera? Sí, en efecto, sin importar cuál $x$ tomemos que sea múltiplo de $4$, cumplirá que es múltiplo de $2$.

Pero, ¡cuidado! Podríamos estar trabajando en otro universo de discurso, donde los objetos que nos interesan son todos los enteros. Si ese fuera el caso, al cuantificar universalmente tendríamos lo siguiente:

$$\forall x \text{ entero}: P(x).$$

Esta es una proposición, pero es falsa, pues podemos encontrar un entero, digamos $5$, para el cual $P(5)=\text{$5$ es múltiplo de $2$.}$ es falso. Por ello, la proposición con el cuantificador es falsa.

Algunos otros ejemplos de cómo podemos usar este cuantificador son los siguientes. Observa cómo se deja claro el universo de discurso.

  • $\forall x$ número par, $x$ es múltiplo de 2.
  • $\forall x$ grupo cíclico, $x$ es generado por un único elemento.
  • $\forall x$ año bisiesto, $x$ tiene 366 días.
  • $\forall (x,y)$ vector en $\mathbb{R}^2$, $\norm{x+y}\leq\norm{x}+\norm{y}.$ *

Recuerda que ahora no es necesario que conozcamos a la perfección el universo de discurso del que estamos hablando en estos ejemplos. En estas entradas no nos interesa estudiar a los pares, a los grupos cíclicos, o a los años bisiestos. Los ponemos como ejemplos únicamente para ver que las ideas de lógica aplican a todos ellos. Por ejemplo para el segundo ejemplo el objetivo es que entiendas que siempre que consideremos un grupo cíclico (sea lo que signifique un grupo o un grupo cíclico), ese grupo es generado por un único elemento (sea lo que signifique que un grupo se genere por un único elemento). En este caso nuestro universo de discurso serán los grupos cíclicos, mientras que $P(x)$ es el predicado «$x$ es generado por un único elemento». En estos renglones sólo nos interesa entender cuándo estamos hablando de un universo de discurso, un cuantificador y un predicado.

Cuantificador existencial

El cuantificador «para todo» establece que una proposición es verdadera para todos los objetos de un universo de discurso. Pero esto no siempre pasa. Por ejemplo, pensemos en que nuestro universo de discurso es $$A=\{\text{pescados, reptiles, aves, piedras, felinos}\}$$ y nuestro predicado $P(x)$ es «Los gatos son $x$». En este caso no todas las formas de asignar un objeto del universo a la variable $x$ darán proposiciones verdaderas. Los gatos no son pescados, reptiles ni mucho menos piedras o aves. Pero los gatos sí son felinos. En este caso la asignación $x=\text{felinos}$ será la única en la que se cumpla el esquema proposicional.

El cuantificador existencial permite enunciar una proposición que acordamos que se vuelve verdadera cuando uno (o más) de los objetos del universo de discurso hacen que obtengamos una proposición verdadera. Así, una vez acordado un universo de discurso y un predicado $P(x)$, diremos que la proposición $\exists x:P(x)$ es verdadera cuando logremos encontrar algún $x$ para el cual $P(x)$ sea verdadera.

En palabras, esto se dice a veces como «existe $x$ en el universo de discurso que cumple $P(x)$», o simplemente como «existe $x$, $P(x)$», cuando el universo de discurso se sobreentiende.

Algunos ejemplos del uso de este cuantificador son los siguientes:

  • $\exists n$ número entero que es solución a $n^2=4$.
  • $\exists n$ número entero que cumple $e^{i\pi}+n=0.$ **

Nuevamente, es muy importante que se acuerde el universo de discurso para poder concluir la veracidad de una proposición que involucra un cuantificador existencial. Por ejemplo, la proposición

$$\exists x \text{ número real}: x^2=-1$$

es falsa, pues no existe tal real (al elevar un real al cuadrado siempre queda mayor o igual a cero), mientras que la proposición

$$\exists x \text{ número complejo}: x^2=-1$$

es verdadera, pues el número complejo $x=i$ cumple que $x^2=-1$ es verdadero.

Cuantificador «existe un único»

El cuantificador «existe» tiene una variante más restrictiva. Cuando decimos que existe al menos un elemento en nuestro universo de discurso que cumple una propiedad, también tenemos que puede haber $2$, $3$ o $20$ elementos que lo cumplen. Por ejemplo: «$\exists n$ número entero que es solución a $n^2=4$» tiene dos posibilidades, pues al tomar $n=-2$ o $n=2$ el predicado se transforma en una proposición verdadera.

Pero es muy frecuente en matemáticas que se busque que uno y sólo un elemento que haga verdadero a a un predicado. Para referirnos a estas ocasiones, usamos el cuantificador «$\exists!$», que se lee como «existe un único«. Por ejemplo, sabemos que el único número primo par es 2. Así que podríamos decir: «$\exists! x$ número entero que es primo y par».

La regla de asignación de verdad es que $\exists! x: P(x)$ será verdadera si hay un único $x$ del universo de discurso que haga que $P(x)$ sea verdadera. Si no hay, o hay más de uno, entonces $\exists! x:P(x)$ será falsa.

Otros ejemplos (algunos informales) de su uso son:

  • $\exists!x$ día de la semana tal que $x$ empieza con la letra L
  • $\exists!x$ número real tal que $x$ es neutro aditivo. ***
  • $\exists!n$ número entero que cumple $e^{i\pi}+n=0.$

¿Observas que la última oración se parece mucho al último ejemplo del cuantificador anterior? Y con esto no estamos contradiciendo nada, en el ejemplo anterior solo estamos diciendo «Existe un número entero $n$ que es solución a $e^{i\pi}+n=0$» con lo que queremos decir que existe al menos uno, mientras que en el último ejemplo, decimos «Existe un único número entero $n$ que es solución a $e^{i\pi}+n=0$». Aquí, el objetivo solo es ser más específicos, lo que quiere decir que sólo estamos dando información extra acerca de la proposición.

Tabla resumen de conjunciones y cuantificadores

A continuación resumimos en una tabla varios símbolos lógicos que hemos discutido.

Negaciones$\neg$
Conjunciones$\land$
Disyunciones$\lor$
Implicaciones$\Rightarrow$
Dobles implicaciones$\Leftrightarrow$
Para todos los casos$\forall$
Para al menos un caso$\exists$
Para un único caso$\exists!$

Combinando conectores y cuantificadores

Habiendo conocido los distintos cuantificadores, podríamos hacer afirmaciones un poco más extensas usando otros conectores lógicos en los predicados que usamos. Por ejemplo, pensemos en que nuestro universo de discurso son los números enteros. Consideremos los predicados $P(x)=x<0$ y $Q(x)=x<1$. Entonces podríamos decir

$$\forall \text{$x$ número entero: } (P(x) \Rightarrow Q(x))$$

En palabras: «Para todo número entero $x$, si $x$ es menor a 0, entonces $x$ es menor a 1». Esto es una afirmación verdadera.

También podríamos poner algo del estilo

$$\exists \text{$x$ número entero: } (x+3=8) \land (x^2-2=23).$$

Esta también es una afirmación verdadera pues $x=5$ es un número entero que cumple la proposición $x+3=8$ y la proposición $x^2-2=23$.

También podemos tener predicados con más de una variable e irlos cuantificando poco a poco. Por ejemplo, pensemos nuevamente a los números enteros como nuestro universo de discurso y $P(x,y)$ como la afirmación $x+y=0$. Tenemos que $P(2,-2)$ es verdadero, mientras que $P(2,2)$ es falso, pues es falso que $2+2=0$. Podemos cuantificar a $y$ con un existencial de unicidad para obtener lo siguiente: $$\exists ! y: P(x,y).$$ Esto todavía no es una proposición de la que podamos saber si es cierta o verdadera. Aunque $y$ ya está cuantificado, $x$ sigue siendo variable. Lo que sí es que entonces es un predicado que de la variable $x$ y ahora podemos cuantificarlo con respecto a $x$ para obtener, por ejemplo,

$$\forall x: (\exists! y: P(x,y)).$$

Aquí estaríamos diciendo «para cada número entero $x$, existe un único número entero $y$ tal que $x+y=0$». Dicho de otra forma, cada vez que consideramos un número entero $x$, digamos $3$, existirá un único número entero $y$ que cumplirá la ecuación $x+y=0$. En este caso ese número $y$ es $-3$, pues dijimos que $x=3$ y sólo hay un número que al sumarlo a $3$ nos da $0$.

Entender estas dobles cuantificaciones será crucial para entender, por ejemplo, la definición de límite en Cálculo Diferencial e Integral I.

Notas

Estas son algunas anotaciones del artículo y no es necesario que las sepas, únicamente son curiosidades o temas por aparte que forman parte de la cultura matemática.

* Esta se conoce como la desigualdad del triángulo y nos dice básicamente que la suma de la longitud de dos lados de un triángulo siempre será mayor a la longitud del tercer lado.

** Esta afirmación está relacionada con la llamada identidad de Euler y algunos piensan que es una de las ecuaciones más hermosas de las matemáticas. En otros cursos como Álgebra Superior 2 o Variable Compleja 1 puede que vuelvas a ver esta identidad con su demostración.

*** El único neutro aditivo es el $0$, y esto quiere decir que al sumarle este a cualquier otro número, dará el mismo número.

Más adelante…

Cuando estamos hablando de cuantificadores, también nos van a interesar sus negaciones. Por ejemplo, ¿a qué nos referiremos cuando digamos $\neg (\forall x P(x))$? ¿o cuando digamos $\neg (\exists x (P(x) \Rightarrow Q(x)))$? Lo primero que tenemos que entender es qué quiere decir negar un cuantificador universal y uno existencial. Eso es justo lo que estudiaremos en la siguiente entrada.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Imagina que definitivamente quieres comprar un helado. Cuando vas a la heladería, sólo venden un sabor. Esto tiene desventajas, por supuesto. Pero, ¿qué ventajas tiene que sólo haya un sabor de helado? Enlista todas las que puedas.
  2. En los ejemplos siguientes encuentra el universo de discurso y su predicado.
    1. $\forall x$ número par,$x$ es múltiplo de 2.
    2. $\forall x$ año bisiesto, $x$ tiene 366 días.
    3. $\forall (x,y)$ vector en $\mathbb{R}^2$, $\norm{x+y}\leq\norm{x}+\norm{y}$.
  3. Considera el predicado $P(x)=«x$ es múltiplo de 11». Da cuatro universos de discurso tales que los siguientes enunciados sean ciertos:
    • $\forall x P(x)$
    • $\exists x P(x)$
    • $\exists! x P(x)$
    • $\nexists x P(x)$
  4. Considera la proposición: $P(x,y,z)$ = «$x^3+y^3=z^3$». ¿Cuál de los siguientes enunciados representa la oración «No existen números enteros $x,y,z$ que cumplen $P(x,y,z)$»?:
    • $\forall x (\exists y (\exists z P(x,y,z)))$
    • $\nexists (x,y,z)P(x,y,z)$
    • $\forall x (\nexists(y,z)P(x,y,z))$
    • $\nexists x (\forall (x,y) P(x,y,z))$
  5. ¿El ejercicio anterior sólo tiene una solución? Si hay más de una opción correcta, ¿cómo argumentarías que dos enunciados representan el mismo enunciado?

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Álgebra Superior I: Condicionales y dobles condicionales

Por Guillermo Oswaldo Cota Martínez

Deja un comentario

Introducción

Hemos hablado en las últimas entradas de tres conectores muy importantes: la negación, la conjunción y la disyunción. Sin embargo, como recordarás en la introducción al tema, mencionamos más de tres conectores. Ha llegado el momento en que veamos a los conectores condicionales: la implicación y la doble implicación.

Pensar en consecuencias

Para introducir mejor la implicación, pensemos en qué significa la palabra sin algún contexto matemático. ¿Qué se te viene a la mente cuando oyes la palabra «implicación»? Quizá se te venga a la mente «consecuencia», que a su vez significa cosas o acciones que derivan otras más.

Un ejemplo es el siguiente: ¿qué implicación tiene que se acabe la pila de un celular? Pues en principio se apaga el teléfono. Entonces podríamos decir «Si se acaba la pila del celular, entonces se apagará». Otro ejemplo: ¿qué consecuencias tiene llegar tarde a una cita médica? Pues muy probablemente se cancelará. Esto mismo lo podemos decir así: «Si llego tarde a una cita médica, entonces la cancelarán». Un último ejemplo sería el siguiente: «Si sube el nivel de dióxido de carbono en la atmósfera, entonces los polos se derretirán».

Todas estas oraciones son ejemplos de condicionales, y para entender su estructura, volvamos al primer ejemplo. Pensemos en las proposiciones
\begin{align*}
P &= \text{El celular se queda sin pila.}\\
Q &= \text{El celular se apaga.}
\end{align*}

Podemos reescribir la oración «Si se acaba la pila del celular entonces se apagará» como «Si pasa $P$, entonces pasa $Q$». Observa que siempre que pase $P$, entonces pasará $Q$. Esto lo escribiremos como $P \Rightarrow Q$ y se lee «$P$ implica $Q$». Lo que estamos diciendo con esta oración es que si el valor de verdad de $P$ es verdadero entonces el valor de verdad de $Q$ es verdadero.

Observa que si al celular no se le acaba la pila, entonces no tendría porqué apagarse, entonces si $P$ es falso, $Q$ puede ser falso y no hay problema. También puede pasar que apagues el celular, pero no necesariamente sea porque se le acabó la pila, entonces si $P$ es falso, $Q$ también puede ser verdadero y no hay algún problema con ello. El único problema sería decir que se le acabó la pila al celular y sigue prendido, eso sería algo que no puede suceder, porque sabemos que «Si se acaba la pila del celular, entonces se apagará».

Todo esto lo resumimos en la tabla de verdad de la siguiente sección.

Tabla de verdad de la implicación

Dadas proposiciones $P$ y $Q$, pensamos en la implicación $P\Rightarrow Q$ como la proposición que tiene la siguiente tabla de verdad.

$P$$Q$$P \Rightarrow Q$
$0$$0$$1$ 
$0$$1$$1$ 
$1$$0$ $0$
$1$$1$ $1$

Quizá sigas teniendo dificultades para entender porqué si $P$ es falso, $Q$ puede tener cualquier valor y seguir haciendo la expresión verdadera. Para ello, piensa en lo siguiente: lo que dice la implicación es que siempre que pase la primera condición $P$, también llamada hipótesis, ocurrirá $Q$, también conocida como tesis. Puede ser que se cumpla $Q$ y no se cumpla $P$, pero eso no contradice lo que dice la implicación, o puede que igual no se cumpla ni $Q$ ni $P$. Lo único que nos dice la implicación es que siempre que se cumpla $P$ va a tener como consecuencia que se cumpla $Q$. Entonces el único caso en donde desobedecemos a la implicación (donde es falsa), es cuando pasa $P$ y no pasa $Q$, que corresponde al penúltimo renglón de la tabla de verdad.

Condiciones suficientes y necesarias

El siguiente y último conector que vamos a ver es la doble implicación. A diferencia de la implicación, asumimos que para que una proposición sea verdadera, es necesaria que la otra también y viceversa. Para esto, refiramos a la doble implicación como una equivalencia lógica $P \Leftrightarrow Q :\equiv (P \Rightarrow Q) \land (Q \Rightarrow P)$. En otras palabras decimos que hay una doble implicación entre $P$ y $Q$ si $P$ implica $Q$ y además $Q$ implica $P$.

Además de este nombre, algunas formas de referirse a la doble implicación que encontrarás serán:

  • «$P$ es equivalente a $Q$»
  • «Una condición necesaria y suficiente para $Q$ es $P$»
  • «$P$ si y sólo si $Q$»

Esta última se utiliza mucho en enunciados matemáticos como proposiciones y teoremas.

Tabla de verdad de la doble implicación

$P$$Q$$P \Rightarrow Q$$Q \Rightarrow P$$(P \Rightarrow Q) \land (Q \Rightarrow P)$$P\Leftrightarrow Q$
$0$$0$ $1$$1$$1$  $1$ 
$0$$1$$1$ $0$ $0$ $0$ 
$1$$0$  $0$$1$ $0$ $0$
$1$$1$  $1$$1$ $1$   $1$

Nota que la doble implicación es verdad cuando los valores de $P$ y $Q$ son ambos verdaderos o ambos falsos. Esto quiere decir que en este caso si alguno es verdadero, entonces los dos son verdaderos, mientras que si uno es falso, los dos lo serán.

La implicación en términos de otros conectores

El hecho de que hayamos aprendido los primeros tres conectores (negación, conjunción y disyunción) antes que estos no es coincidencia. Resulta que la implicación y la doble implicación se «pueden construir» a partir de los primeros tres. Con esto nos referimos a que la implicación es equivalente a una expresión hecha únicamente por los anteriores.

Para ello, primero recuerda cómo construimos la implicación. La única forma en que la implicación $P \Rightarrow Q$ sea falsa es que $P$ sea verdadero y $Q$ falso. Entonces si $P$ es falso, no importa qué valor tome $Q$. De esta forma, cada vez que $\neg P$ sea verdad, la implicación también será verdadera. Pero si $P$ es verdadero, entonces $Q$ debe serlo también. Eso lo podemos expresar como $\neg P \lor Q$ que quiere decir «$P$ no pasa o $Q$ es verdadero» y coincide con lo que acabamos de decir. Para convencerte de eso, revisa con cuidado la siguiente tabla.

$P$$Q$$\neg P$ $\neg P \lor Q$$P \Rightarrow Q$
$0$$0$ $1$$1$  $1$ 
$0$$1$$1$  $1$ $1$ 
$1$$0$  $0$ $0$ $0$
$1$$1$  $0$ $1$   $1$

Entonces $\neg P \lor Q \equiv P \Rightarrow Q$. Entonces cada vez que digamos que «Una cosa implica la otra», podemos pensarlo como «La negación de la primera cosa o la otra». Siempre es útil regresar a ejemplos concretos. Piensa cuidadosamente por qué es lo mismo decir «si llueve el piso se moja» y decir «no llueve o el piso está seco».

La contrapositiva de una implicación

Una propiedad que más adelante nos servirá sobre la implicación es el hecho de que en ocasiones es más sencillo trabajar con las negaciones de las proposiciones que con las proposiciones normales. No te preocupes si no entiendes a qué nos referimos con esto, más adelante lo veremos con más calma.

Un ejemplo de esto es verificar la siguiente proposición: «Si un número al cuadrado es par, entonces el número es par». A primera vista no es tan fácil verificar directamente esta proposición que es de la forma $P \Rightarrow Q$. Resulta que la forma en que se comprueba esto es con una equivalencia de la implicación. Para llegar a esta equivalencia, como primer paso, notaremos que podemos poner a la implicación en términos de la negación. Para esto, vamos a usar el resultado anterior para encontrar lo que buscamos.

Recordemos que $\neg P \lor Q \equiv P \Rightarrow Q$, y la conjunción es conmutativa, es decir $\neg P \lor Q \equiv Q \lor \neg P$.

¿Podemos ver esto de otra forma?

Pues resulta que sí. Veamos a $Q$ como la negación de la negación de $Q$, dicho de otra forma, $Q \equiv \neg \neg Q$. Esto último nos ayuda a ver la equivalencia de otra forma: $Q \lor \neg P \equiv\neg \neg Q \lor \neg P$. El siguiente paso es pensar a $\neg Q$ como un término por sí mismo y a $\neg P$ como otro término. Dicho de otra forma agrupemos términos para ver la equivalencia de manera distinta: $$Q \lor \neg P \equiv\neg (\neg Q) \lor (\neg P).$$ Ahora, pensemos a $\neg Q$ como una proposición y a $\neg P$ como otra. La expresión está diciendo «La negación de $\neg Q$ una cosa o $\neg P$» ¿Suena familiar? Esto justamente es la equivalencia de la implicación. Dicho de otra manera, fíjate que tenemos una equivalencia:

$$Q \lor \neg P \equiv\neg (\neg Q) \lor (\neg P) \equiv \neg Q \Rightarrow \neg P.$$

Es decir,

$$P \Rightarrow Q \equiv \neg Q \Rightarrow \neg P.$$

Cuando tenemos una implicación de la forma $P\Rightarrow Q$, a la fórmula proposicional $\neg Q \Rightarrow \neq P$ le llamamos la contrapositiva.

Regresando al ejemplo inicial de esta sección, la proposición «Si un número al cuadrado es par, entonces el número es par» podemos pensarla como «Si un número es impar entonces su cuadrado es impar», lo cual es mucho más fácil de verificar. En entradas posteriores retomaremos esta forma de pensar. Por lo mientras es suficiente que entiendas que la implicación es equivalente a su contrapositiva.

El caso en donde todo es verdadero

Antes de terminar esta entrada, introduciremos un concepto que resultará útil cuando llegue el momento de estudiar inferencias. Para ello, observa la tabla de verdad de la fórmula proposicional $((Q \Rightarrow P) \land Q) \Rightarrow P$:

$P$$Q$$Q \Rightarrow P$$Q \Rightarrow P \land Q$$(Q \Rightarrow P \land Q) \Rightarrow P$
$0$$0$ 1 01 
$0$$1$ 0 0 1
$1$$0$ 1 0 1
$1$$1$ 11  1

¿Notas algo peculiar? Toda la columna final es verdadera. Esto quiere decir que no importa qué valores tomen las variables proposicionales, siempre es verdadera la expresión. A una fórmula matemática que cumpla esto le llamamos una tautología.

Sucede algo que une aún más los conceptos de tautología y doble condicional. ¿Recuerdas que las fórmulas proposicionales $\neg(P \land Q)$ y $\neg P \lor \neg Q$ son equivalentes? Pues veamos ahora sus tablas de verdad:

$P$$Q$$P \land Q$$\neg (P \land Q)$$\neg P$$\neg Q$$\neg P \lor \neg Q$$\neg (P \land Q)\Leftrightarrow (\neg P \lor \neg Q)$
$0$$0$ 01 1111 
$0$$1$ 01 101 1
$1$$0$ 01 011 1
$1$$1$ 10000 1

Hemos agregado una última columna, la correspondiente a $\neg (P \land Q))\Leftrightarrow (\neg P \lor \neg Q)$. ¡Es una tautología! Esto sucede siempre: dos fórmulas proposicionales $F_1$ y $F_2$ son equivalentes siempre que $F_1 \Leftrightarrow F_2$ sea una tautología.

Más adelante…

Recuerda el ejemplo que mencionamos anteriormente «Un número al cuadrado es par si el número es par», no especificamos de qué número se trataba, sin embargo hay una infinidad de números los cuales podemos tomar como ejemplo para verificar la propiedad. Entonces podemos decir «$1^2$ es par si $1$ es par» o «$38^2$ es par si $38$ es par», o en general podemos decir «$x^2$ es par si $x$ es par». ¿Pero quién es $x$? ¿Qué valores puede tomar? En la siguiente entrada veremos algo conocido como predicados y cuantificadores. Estos ampliarán el poder de las proposiciones introduciendo variables dentro de las proposiciones. Con ello, se puede cambiar el objeto al que se refiere una proposición y, dependiendo de esto, su valor de verdad.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Escribe las siguientes frases en lógica proposicional:
    • Si hoy es lunes, entonces mañana será viernes.
    • El caos implica el orden.
    • Para que crezcan las plantas, tienes que regarlas.
    • Hoy es lunes si mañana es martes y mañana es martes si hoy es lunes.
    • Hoy es lunes si y sólo si mañana es martes.
  2. Verifica que siempre «Una cosa siempre se implica a sí misma», es decir, verifica que si $P$ es una proposición, entonces $P \Rightarrow P$ siempre es verdadera.
  3. Haz la tabla de verdad de la implicación $P\Rightarrow Q$ y de su contrapositiva $\neg Q \Rightarrow \neg P$ para convencerte de que en verdad son equivalentes.
  4. ¿Cómo verificarías que  $P \Leftrightarrow Q \equiv (\neg Q \lor P)\land(\neg P \lor Q)$? Recuerda que la doble implicación $P \Leftrightarrow Q$ es equivalente a $(P \Rightarrow Q) \land (Q \Rightarrow P)$.
  5. Verifica que la doble condicional es conmutativa, es decir $P \Leftrightarrow Q \equiv Q \Leftrightarrow P $. ¿La condicional es conmutativa?

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Álgebra Superior I: Propiedades de la negación, conjunción y disyunción

Por Guillermo Oswaldo Cota Martínez

Deja un comentario

Introducción

En la entrada pasada vimos que con conectores podemos construir nuevas proposiciones a partir de otras. Y nombramos a tres de ellas: la negación, la conjunción y la disyunción.

Ahora, discutiremos sobre algunas consecuencias que tiene juntar unas con otras y diremos en términos formales qué significa que una fórmula lógica sea «igual» a otra.

Recordatorio de proposiciones vs. variables proposicionales vs. fórmulas lógicas

Como breve recordatorio, tenemos las siguientes distinciones conceptuales importantes.

  • «Proposición» es una afirmación que puede ser verdadera o falsa, y lo estamos usando para una proposición específica. Como ejemplo, tenemos «El cielo es azul» o «El número $5$ es primo».
  • «Variable proposicional» es una letra que usamos para representar una proposición arbitraria, aún no definida. Por ejemplo, $P,Q,R$. Sin saber qué proposición representa, no podemos determinar su valor de verdad.
  • «Fórmula proposicional» es una expresión que armamos a través de variables proposicionales y conectores lógicos. Por ejemplo, $(P\land Q) \lor (R \land \neg P)$. Sin saber quiénes son exactamente $P,Q,R$, no podemos determinar el valor de verdad. Pero sí podemos considerar todas las posibilidades mediante una tabla de verdad.

Equivalencia de fórmulas proposicionales

Volvamos a retomar un ejemplo que ya habíamos revisado anteriormente.

$P$$\neg P$$\neg(\neg P)$
$0$$1$ $0$
$1$$0$$1$ 

Habíamos dicho que al coincidir las columnas de $\neg ( \neg P)$ con $P$ entonces $\neg(\neg P) \equiv P$. Esto leeremos como «$\neg(\neg P)$ es equivalente a $P$». La equivalencia de fórmulas proposicionales nos dice que sus valores de verdad siempre coinciden, sin importar el valor de verdad de las variables proposicionales que las conforman. En este ejemplo, en cualquier caso en que $\neg(\neg P)$ sea verdad, sucede que $P$ es verdad. De igual forma, cada vez que suceda que $\neg(\neg P)$ sea falso, $P$ también lo será.

Podemos dar un ejemplo más concreto. Pensemos en que nuestra proposición $P$ es: «El 2 es un número impar». En este caso $\neg(\neg P)$ corresponde a: «No es cierto que 2 no es un número impar». Observa que la proposición $P$ es falsa, y que también la proposición $\neg(\neg P)$ es falsa.

Ahora, nota que acabamos de hacer una definición, pues nombramos a dos fórmulas proposicionales que tienen la misma tabla de verdad como equivalentes. Como lo mencionamos en la entrada de los tipos de enunciados, les estamos poniendo un nombre a un objeto matemático que cumple ciertas propiedades.

Definición. Dos fórmulas proposicionales son equivalentes si sus tablas de verdad coinciden.

Esta «igualdad» en las fórmulas proposicionales nos será muy útil, pues en la matemática nos ayudará a ver algunos resultados de otra manera. Por ejemplo, retomemos $\neg(\neg P) = P$. Como sabemos que es falso que 2 es impar, en consecuencia también sabemos que es falso que «No sea cierto que 2 no es impar» y esto lo sabemos sin tener que verificar algo más, pues el hecho de que tengamos la equivalencia a nivel de fórmulas proposicionales, en particular la tenemos para cualquier proposición específica que reemplaze las variables proposicionales. Esta equivalencia también nos ayudará a demostrar otros resultados en el futuro.

Nota además lo siguiente. Piensa que $F_1$, $F_2$ y $F_3$ son fórmulas proposicionales (cada una conformada por varias variables proposicionales y conectivos). Si $F_1$ y $F_2$ son equivalentes, y $F_2$ y $F_3$ son equivalentes (es decir $F_1\equiv F_2$ y $F_2\equiv F_3$) entonces $F_1$ y $F_3$ también son equivalentes. Puedes convencerte de esto como sigue. Del hecho de que $F_1$ y $F_2$ lo sean, sale que $F_1$ y $F_2$ tienen la misma tabla de verdad. Del hecho de que $F_2$ y $F_3$ lo sean, sale que $F_2$ y $F_3$ tienen la misma tabla de verdad. Pero entonces $F_1$ y $F_3$ tienen la misma tabla de verdad (la de $F_2$). A esto se le conoce como la propiedad transitiva. No es importante que recuerdes este nombre, sin embargo después volveremos a estudiar esta propiedad con más calma. Y para recordar mejor esto, piensa en que funciona similar a la igualdad entre números, por ejemplo $2+2=4$ y $4=2^2$, entonces $2+2=2^2$.

Algunas propiedades de la conjunción y la disyunción

Hemos hablado un poco sobre la negación, pero ahora cambiemos el foco a la conjunción y la disyunción. Para empezar, recordemos que la conjunción $P\land Q$ sólo es verdadera cuando tanto $P$ como $Q$ son verdaderas, y en la entrada anterior verificamos que $Q \land P$ es equivalente a $P \land Q$.

También nos va a interesar el caso en donde combinamos más de dos proposiciones. Sin embargo, hay que tener cuidado. Por definición, la conjunción es un conector que combina únicamente dos proposiciones. Así, para unir a más de dos proposiciones mediante la conjunción, tendremos que agruparlas.

Piensa el agrupamiento como piensas la suma: si quieres sumar $2+3+4$, lo más habitual es sumar primero $2+3$ que resulta en cinco, y después sumárselo a $4$, de manera que podemos escribir la suma como $2+3+4=(2+3)+4$. Algo similar va a pasar con las proposiciones, pues podemos pensar a $P \land Q \land R$ como $(P \land Q) \land R$. Ahora piensa de nuevo en la suma $2+3+4$. El resultado de esta suma es $9$ y nosotros decidimos agrupar $2+3$ y después sumar el resultado con $4$. Pero esto es lo mismo que haber agrupado primero $3+4$ y después sumarlo a $2$. Esto no es coincidencia, pues la suma tiene una propiedad que se llama asociatividad que nos dice que $(2+3)+4=2+(3+4)$. ¿Pasará lo mismo con la conjunción? Veamos que sí.

Lo que queremos ver es si $P \land (Q \land R)\equiv (P \land Q) \land R$ es decir, queremos ver si $P \land (Q \land R)$ es equivalente a $(P \land Q) \land R$. La equivalencia está dada en términos de tablas de verdad, así que tenemos que hacer la tablas para ambas fórmulas lógicas. La presentamos a continuación.

$P$$Q$$R$$Q \land R$$P \land ( Q\land R)$$P \land Q$$(P \land Q) \land R$
$0$$0$$0$$0$$0$$0$$0$
$0$$0$$1$$0$$0$$0$$0$
$0$$1$$0$$0$$0$$0$$0$
$0$$1$$1$$1$$0$$0$$0$
$1$$0$$0$$0$$0$$0$$0$
$1$$0$$1$$0$$0$$0$$0$
$1$$1$$0$$0$$0$$1$$0$
$1$$1$$1$$1$$1$$1$$1$

Como puedes notar, las columnas $P \land (Q \land R)$ y $(P \land Q) \land R$ coinciden, es decir, coinciden en sus tablas de verdad, por lo tanto son equivalentes.

Con este ejemplo, vimos cómo la conjunción tiene la propiedad asociativa, es decir, cuando combinamos tres o más proposiciones mediante la conjunción, no importa «dónde pongamos los paréntesis». Lo mismo pasará con la disyunción que de igual manera es asociativa.

Combinando la conjunción con la disyunción

También podemos juntar los conectores de conjunción y disyunción. Por ejemplo, piensa que tenemos tres proposiciones $P, Q, R$ donde,

$P = \text{Toda persona es mortal}$

$Q = \text{2 es un número impar}$

$R = \text{2 es un número par}$

¿Qué significaría la proposición $P \lor (Q \land R)$? Si lo escribieramos en palabras, sería «Toda persona es mortal o (2 es un número impar y 2 es un número par)». Sabemos que toda persona es mortal, y también sabemos que 2 no puede ser impar y par a la vez (por ahora parece que sabemos que 2 es un número par, en otros cursos profundizarás más en lo que significa ser par). Entonces nuestra proposición está formada por dos componentes, la proposición $P$ y la proposición $Q \land R$. Como un número no puede ser par e impar a la vez, entonces la segunda proposición es falsa. Pero la primera proposición $P$ es verdadera, entonces la proposición $P \lor (Q \land R)$ es verdadera, porque para la disyunción basta que alguna de las dos sea verdadera.

Vayamos un poco más lejos. ¿Será que esta es la única forma de escribir la proposición? Resulta que no. Resulta que la disyunción y la conjunción cumplen una propiedad que se llama la propiedad distributiva. Para no quedarnos sólo con el ejemplo específico del párrafo anterior, la describimos en términos de fórmulas proposicionales: $$P \lor (Q \land R) \equiv (P \lor Q) \land (P \lor R).$$

Si te resulta un poco confuso esto, puedes pensarlo por ahora como la distribución de una multiplicación con la suma, es decir la operación $2 \times (1+3) = (2 \times 1) + (2 \times 3)$, en donde nuestra disyunción $\lor$ queda distribuida a causa de la conjunción $\land$ los distribuye.

Para convencernos de que se satisface la propiedad distributiva, veamos las tablas de verdad de cada una de las expresiones que están involucradas.

$P$$Q$$R$$Q \land R$$P \lor ( Q\land R)$$P \lor Q$$P \lor R$$(P \lor Q) \land (P \lor R)$
$0$$0$$0$$0$$0$$0$$0$$0$
$0$$0$$1$$0$$0$$0$$1$$0$
$0$$1$$0$$0$$0$$1$$0$$0$
$0$$1$$1$$1$$1$$1$$1$$1$
$1$$0$$0$$0$$1$$1$$1$$1$
$1$$0$$1$$0$$1$$1$$1$$1$
$1$$1$$0$$0$$1$$1$$1$$1$
$1$$1$$1$$1$$1$$1$$1$$1$

Nota que las columnas coloreadas corresponden a las fórmulas lógicas que nos interesan y son iguales, entonces $P \lor (Q \land R) \equiv (P \lor Q) \land (P \lor R)$. Lo mismo sucede si cambiamos el orden de los conectores, es decir $P \land (Q \lor R) \equiv (P \land Q) \lor (P \land R)$, así podemos distribuir los conectores conjuntivos y disyuntivos como más nos convenga.

Agregando la negación a la mezcla

Por último, vamos a incluir a la negación en nuestra mezcla de conjunciones y disyunciones. ¿Qué pasará cuando tenemos proposiciones del estilo $\neg (P \land Q)$ y $\neg (P \lor Q)$? Sería lógico pensar en un inicio que igual la negación se va a distribuir, pero eso no es cierto. Para esto, piensa en el siguiente ejemplo:

$$P = \text{32 es un número perfecto} $$

$$ Q = 2^7-1 \text{ es un número primo} $$

Aquí hablamos de dos cosas que quizá aún no sepas: números perfectos y números primos, no te preocupes por lo que signifiquen, en otros cursos los verás con más detalle, aunque te puedo decir que sólo una de estas dos afirmaciones es correcta (¿Puedes adivinar cuál es?), entonces la conjunción es falsa, por lo que la negación de la conjunción es verdadera.

Lo que acabamos de decir es que $P \land Q$ es falsa y por consecuente $\neg (P \land Q)$ es verdadera. Si sucediera que la negación se distribuyera sobre la conjunción, entonces $\neg (P \land Q)$ sería equivalente a $\neg P \land \neg Q$. Pero esto no es cierto, porque $\neg P$ es verdadero, y $\neg Q$ es falso, y entonces $\neg P \land \neg Q$ es falso. Acabamos de llegar a una contradicción en nuestro pensar matemático es decir, primero dijimos que $\neg (P \land Q)$ es verdadera y después observamos que si la negación se distribuyera sobre la conjunción, sería falso, pero recuerda que una proposición es verdadera o falsa, no puede ser verdadera y falsa al mismo tiempo, entonces alguna de las dos suposiciones que hicimos es incorrecta. Si quieres pensarlo de otra forma, $\neg P \land \neg Q$ y $\neg (P \land Q)$ no son equivalentes pues sus tablas de verdad difieren en el renglón en el que $P$ es verdadero y $Q$ es falso.

Nuestro error fue haber distribuido la negación sin cuidado. Resulta que la negación no cumple esa propiedad, pero «casi» es distributiva. Veamos sus reglas.

$$ \neg (P \land Q) \equiv \neg P \lor \neg Q $$

$$ \neg (P \lor Q) \equiv \neg P \land \neg Q $$

En el ejemplo concreto de arriba, esto quiere decir que es lo mismo decir «No es cierto que (32 sea un número perfecto y $2^7-1$ sea un número primo)» a decir «No es cierto que 32 es un número perfecto, o no es cierto que $2^7-1$ es un número primo». Para que lo entiendas más claro, revisa la tabla de verdad:

$P$$Q$$P \land Q$$\neg (P \land Q)$$\neg P$$\neg Q$$\neg P \lor \neg Q$
$0$$0$$0$$1$$1$$1$$1$
$0$$1$$0$$1$$1$$0$$1$
$1$$0$$0$$1$$0$$1$$1$
$1$$1$$1$$0$$0$$0$$0$

Observa que las columnas correspondientes a las fórmulas proposicionales que queremos coinciden, lo que quiere decir que son equivalentes. Lo mismo puedes verificar para comprobar que $ \neg (P \lor Q) \equiv \neg P \land \neg Q $. A estas propiedades se les conoce como las leyes de De Morgan (más adelante volverás a oír ese nombre).

Más adelante…

Recapitulando, en esta entrada hablamos sobre las propiedades que tienen tres conectores. Vimos lo siguiente:

  • Hablamos de la equivalencia de fórmulas proposicionales que ocurre cuando dichas fórmulas coinciden en todos los renglones de sus tablas de verdad, sin importar la asignación de veracidad de las variables proposicionales que las conforman.
  • Observamos tres propiedades de los conectores: la asociatividad, la distributividad y las leyes de DeMorgan.

Todo esto nos da herramientas suficientes para ya empezar a hablar de lógica proposicional, pero esto apenas empieza. Recuerda que tenemos más conectores. Aún nos faltan revisar dos muy importantes: la implicación y la doble implicación. Estos dos las vamos a ver con más calma en la siguiente entrada.

Tarea Moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Demuestra que $\neg ( \neg (\neg P))$ es equivalente a $\neg P$.
  2. En la entrada vimos que podemos asociar la conjunción como queramos. Ahora verifica que lo mismo pasa con la disyunción, es decir $P \lor (Q \lor R) \equiv (P \lor Q) \lor R$.
  3. Verifica con la tabla de verdad que $P \land (Q \lor R) \equiv(P \land Q) \lor (P \land R)$.
  4. Verifica con la tabla de verdad que $ \neg (P \lor Q) \equiv\neg P \land \neg Q $.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»