Introducción

En las entradas anteriores hemos abordado de manera formal el concepto de función en el sentido complejo así como algunas de sus propiedades más importantes como la continuidad y la diferenciablidad.

Para esta entrada, así como para las últimas dos entradas de esta unidad, nuestro objetivo será darle una interpretación geométrica a las funciones complejas de variable compleja. Para ello recurriremos al concepto de transformación, desde una perspectiva Geométrica, es decir, como una transformación del plano en sí mismo y desde la perspectiva del Álgebra Lineal considerando lo que sabemos de $\mathbb{R}^2$ como un $\mathbb{R}$-espacio vectorial.

Observación 24.1.
Recordemos que una transformación del plano $\mathbb{R}^2$ es una función $T:\mathbb{R}^2 \to \mathbb{R}^2$, es decir, una función del plano en sí mismo. En algunos textos suele pedirse que $T$ sea una función biyectiva, sin embargo, como veremos en esta entrada, la mayoría de las transformaciones con las que trabajaremos cumplirán esta propiedad.

Definición 24.1. (Transformación compleja.)
Una transformación compleja o simplemente una transformación del plano complejo es una función $T: \mathbb{C} \to \mathbb{C}$, es decir, una función del plano complejo $\mathbb{C}$ en sí mismo.

Considerando que hemos construido a $\mathbb{C}$ mediante $\mathbb{R}^2$ y el hecho de que $\mathbb{R}^2$ es un $\mathbb{R}$-espacio vectorial, podemos definir el concepto de linealidad para transformaciones complejas.

Definición 24.2. (Transformación compleja $\mathbb{R}$-lineal.)
Sea $T : \mathbb{C} \to \mathbb{C}$ una transformación. Entonces, $T$ es $\mathbb{R}$-lineal si:

1. $T(z_1 + z_2) = T(z_1) + T(z_2)$, para todo $z_1,z_2\in\mathbb{C}$,
2. $T(\lambda z) = \lambda T(z)$, para todo $\lambda\in\mathbb{R}$ y para todo $z\in\mathbb{C}$.

Definición 24.3. (Transformación compleja $\mathbb{C}$-lineal.)
Sea $T : \mathbb{C} \to \mathbb{C}$ una transformación. Entonces, $T$ es $\mathbb{C}$-lineal si:

1. $T(z_1 + z_2) = T(z_1) + T(z_2)$, para todo $z_1,z_2\in\mathbb{C}$,
2. $T(\lambda z) = \lambda T(z)$, para todo $\lambda\in\mathbb{C}$ y para todo $z\in\mathbb{C}$.

Proposición 24.1.
Toda transformación $T : \mathbb{C} \to \mathbb{C}$ que es $\mathbb{R}$-lineal es de la forma:
\begin{equation*}
T(z) = \lambda z + \mu \overline{z},
\end{equation*}
donde $\lambda = \dfrac{a – ib}{2}$, $\mu = \dfrac{a + ib}{2}$, con $a = T(1)$ y $b=T(i)$.

Demostración. Dadas las hipótesis, sea $z=x+iy\in\mathbb{C}$. Como $T$ es $\mathbb{R}$-lineal, entonces:
\begin{equation*}
T(z) = T(x+iy) = x T(1) + y T(i).
\end{equation*}

Definimos $a := T(1)$ y $b := T(i)$, dado que:
\begin{equation*}
x = \frac{z + \overline{z}}{2} \quad \text{y} \quad y = -i\left(\frac{z – \overline{z}}{2}\right),
\end{equation*}

entonces:
\begin{equation*}
T(z) = a\left(\frac{z + \overline{z}}{2}\right) -ib\left(\frac{z – \overline{z}}{2}\right) = \lambda z + \mu \overline{z},
\end{equation*} donde $\lambda = \dfrac{a – ib}{2}$ y $\mu = \dfrac{a + ib}{2}$.

$\blacksquare$

Proposición 24.2.
Toda transformación $T:\mathbb{C}\to\mathbb{C}$ que es $\mathbb{C}$-lineal es de la forma:
\begin{equation*}
T(z) = \lambda z,
\end{equation*} donde $\lambda = T(1) \in\mathbb{C}$ es una constante.

Demostración. Se deja como ejercicio al lector.

$\blacksquare$

Proposición 24.3.
Sea $T$ una transformación $\mathbb{R}$-lineal, cuya matriz asociada es $A\in M_{2\times 2}(R)$ (considerando la base estándar de $\mathbb{R}^2$). Entonces las siguientes condiciones son equivalentes:

1. $T$ es $\mathbb{C}$-lineal, definición 24.3.
2. $T(iz) = i\,T(z)$ para todo $z\in\mathbb{C}$.
3. $A = \begin{pmatrix} a & -b\\ b & a \end{pmatrix}$ para algunos $a, b\in\mathbb{R}$.
4. $T$ es una multiplicación compleja, es decir, existe algún $\lambda \in\mathbb{C}$ tal que $T(z) = \lambda z$ para todo $z\in\mathbb{C}$.

Demostración.

1. $\Rightarrow )$ 2.

Es inmediata de la definición.

2. $\Rightarrow )$ 3.

Sea $A = \begin{pmatrix}
a & c\\
b & d
\end{pmatrix}$, con $a,b,c,d\in\mathbb{R}$ la matriz asociada a $T$. Entonces tenemos:
\begin{align*}
T(i) & = \begin{pmatrix}
a & c\\
b & d
\end{pmatrix} \begin{pmatrix}
0\\
1
\end{pmatrix}\\
& = \begin{pmatrix}
c\\
d
\end{pmatrix}\\
&= c + id.
\end{align*}

Por otra parte:
\begin{align*}
i\,T(1) & = i \begin{pmatrix}
a & c\\
b & d
\end{pmatrix} \begin{pmatrix}
1\\
0
\end{pmatrix}\\
& = i\begin{pmatrix}
a\\
b
\end{pmatrix}\\
&= i(a + ib)\\
& = -b + ia.
\end{align*}

Por hipótesis tenemos que $T(i) = i \, T(1)$, por lo que $c = -b$ y $d = a$, de donde se sigue el resultado.

3. $\Rightarrow )$ 4.

Sea $z = x+iy\in\mathbb{C}$, entonces:
\begin{align*}
T(z) & = A\,z\\
& = \begin{pmatrix}
a & -b\\
b & a
\end{pmatrix} \begin{pmatrix}
x\\
y
\end{pmatrix}\\
&= (ax – by) + i(bx + ay)\\
& = (a+ib)(x+iy),
\end{align*}

por lo que tomando $\lambda = a + ib\in\mathbb{C}$ se tiene que $T(z) = \lambda z$, para toda $z\in\mathbb{C}$.

4. $\Rightarrow )$ 1.

Se deja como ejercicio al lector.

$\blacksquare$

Observación 24.2.
El resultado anterior nos dice cuáles transformaciones $\mathbb{R}$-lineales, pueden ser vistas también como transformaciones $\mathbb{C}$-lineales.

Más aún, dado que $\mathbb{R}\subset\mathbb{C}$, debe ser claro que una transformación que es $\mathbb{C}$-lineal en particular es $\mathbb{R}$-lineal, sin embargo el recíproco no se cumple.

Ejemplo 24.1.
a) Sea $T:\mathbb{C} \to \mathbb{C}$ dada por $T(z) = \overline{z}$. Es fácil verificar que $T$ es una transformación $\mathbb{R}$-lineal, por lo que se deja como ejercicio al lector. Por otra parte, notemos que para todo $z=x+iy\in\mathbb{C}$:
\begin{equation*}
T(z) = \overline{z} = x – iy,
\end{equation*} por lo que:
\begin{equation*}
T(i) = \overline{i} = -i,
\end{equation*} mientras que:
\begin{equation*}
i\,T(1) = i\,\overline{1} = i(1) = i,
\end{equation*} entonces considerando la proposición 16.2 es claro que $T$ no es $\mathbb{C}$-lineal.

b) Sea $T:\mathbb{C}\setminus\{0\} \to \mathbb{C}\setminus\{0\}$ dada por $T(z) = \dfrac{1}{z}$. Es fácil verificar que $T$ no es una transformación $\mathbb{R}$-lineal ni tampoco $\mathbb{C}$-lineal, por lo que se deja como ejercicio al lector. A esta transformación se le llama inversión.

De acuerdo con los resultados de la entrada 18 y considerando la proposición 24.3, debe ser claro que existe una estrecha relación entre a diferenciabilidad en el sentido complejo y las transformaciones $\mathbb{C}$-lineales, pues como sabemos, la diferenciabilidad en el sentido real de una función $f:\mathbb{R}^2\to\mathbb{R}^2$ no basta para garantizar la diferenciabilidad compleja.

Proposición 24.4.
Sean $U\subset\mathbb{C}$ un conjunto abierto y $f:U\to\mathbb{C}$ una función. Se dice que $f$ es complejo diferenciable en $z\in U$ si existe:
\begin{equation*}
\lim_{h\to 0} \frac{f(z+h) – f(z)}{h}. \tag{24.1}
\end{equation*}

Mientras que, se dice que $f$ es real diferenciable en $z\in U$ si existe una transformación $\varphi : \mathbb{C} \to \mathbb{C}$, la cual es $\mathbb{R}$-lineal, tal que:
\begin{equation*}
\lim_{h\to 0} \frac{f(z+h) – f(z) – \varphi(h)}{h} = 0. \tag{24.2}
\end{equation*}

Entonces se cumple que:

1. si $f$ es complejo diferenciable en $z\in U$, entonces $f$ es real diferenciable en $z\in U$;
2. si $f$ es real diferenciable en $z\in U$ y la transformación $\mathbb{R}$-lineal $\varphi : \mathbb{C} \to \mathbb{C}$ también es $\mathbb{C}$-lineal, entonces $f$ es complejo diferenciable en $z\in U$;
3. si $f$ es real diferenciable en $z\in U$ y existe el límite:
   \begin{equation*}
   \lim_{h\to 0} \left|\frac{f(z+h) – f(z)}{h}\right|, \tag{24.3}
   \end{equation*} entonces $f$ ó $\overline{f}$ es complejo diferenciable en $z\in U$.

Demostración. Dadas las hipótesis.

1. Se deja como ejercicio al lector.
2. Se deja como ejercicio al lector.
3. Como $f$ es real diferenciable en $z\in U$, entonces existe una transformación $R$-lineal $\varphi:\mathbb{C} \to \mathbb{C}$ tal que (24.2) se cumple. De acuerdo con la desiguladad del triángulo, proposición 3.3, tenemos que:
   \begin{equation*} 0 \leq \left| \left|\frac{f(z+h) – f(z)}{h} \right| – \left| \frac{\varphi(h)}{h}\right| \right| \leq \left|\frac{f(z+h) – f(z) – \varphi(h)}{h}\right|. \end{equation*} Por hipótesis el límite (24.2) existe, entonces al tomar limites en las desigualdades anteriores se sigue que:
   \begin{equation*} \lim_{h\to 0}\left| \left|\frac{f(z+h) – f(z)}{h} \right| – \left| \frac{\varphi(h)}{h}\right| \right| = 0, \end{equation*} de donde:
   \begin{equation*} \lim_{h\to 0} \left|\frac{f(z+h) – f(z)}{h} \right| = \lim_{h\to 0} \left| \frac{\varphi(h)}{h}\right|, \end{equation*} dado que (24.3) existe, entonces el límite del lado derecho de la igualdad existe.
   
   Como $\varphi$ es $R$-lineal, entonces, proposición 24.1, es de la forma $\varphi(h) = \lambda h + \mu \overline{h}$ donde: \begin{equation*} \lambda = \dfrac{\varphi(1) – i\varphi(i)}{2} \quad \text{y} \quad \mu = \dfrac{\varphi(1) + i\varphi(i)}{2}. \tag{24.4} \end{equation*} Notemos que: \begin{equation*} \left| \frac{\varphi(h)}{h}\right|^2 = \left| \frac{\lambda h + \mu \overline{h}}{h}\right|^2 = |\lambda|^2 + |\mu|^2 + 2 \operatorname{Re}\left(\lambda \overline{\mu} \frac{h}{\overline{h}}\right), \end{equation*} por lo que, al tomar límites en ambos lados de la igualdad, al existir el límite del lado izquierdo, también debe existir el límite: \begin{equation*} \lim_{h\to 0} \operatorname{Re}\left(\lambda \overline{\mu} \, \frac{h}{\overline{h}}\right). \end{equation*} Sea $h = a+ib$. Procedemos a calcular el límite cuando $h\to 0$ a lo largo de las rectas $a = 0$ y $b=0$, respectivamente. Por la unicidad del límite tenemos que: \begin{equation*} \lim_{b\to 0} \operatorname{Re}\left(\lambda \overline{\mu} \left[\frac{ib}{-ib}\right]\right) = \lim_{a\to 0} \operatorname{Re}\left(\lambda \overline{\mu} \left[\frac{a}{a}\right]\right), \end{equation*} es decir: \begin{equation*} -\operatorname{Re}\left(\lambda \overline{\mu}\right) = \operatorname{Re}\left(-\lambda \overline{\mu}\right) = \operatorname{Re}\left(\lambda \overline{\mu}\right), \end{equation*} de donde: \begin{equation*} \operatorname{Re}\left(\lambda \overline{\mu}\right) = 0. \end{equation*} Procediendo de manera análoga, si ahora consideramos el límite cuando $h\to 0$ a lo largo de las rectas $a=b$ y $a=-b$, respectivamente, por la unicidad del límite tenemos que: \begin{equation*} \operatorname{Re}\left(i\lambda \overline{\mu}\right) = – \operatorname{Re}\left(i\lambda \overline{\mu}\right) \quad \Longleftrightarrow \quad -\operatorname{Im}\left(\lambda \overline{\mu}\right) = \operatorname{Im}\left(\lambda \overline{\mu}\right), \end{equation*} de donde: \begin{equation*} \operatorname{Im}\left(\lambda \overline{\mu}\right) = 0. \end{equation*} Por lo tanto $\lambda \overline{\mu} = 0$, es decir, $\lambda = 0$ ó $\overline{\mu} = 0$.
   
   De $(24.4)$ se sigue que: \begin{equation*} \varphi(1) = i \varphi(i) \quad \text{ó} \quad \overline{\varphi}(1) = i \overline{\varphi}(i). \end{equation*} Del primer caso se sigue de la proposición 24.3 que $\varphi$ es $\mathbb{C}$-lineal y por el inciso anterior de esta proposición, tenemos que $f$ es complejo diferenciable en $z\in U$.
   
   Por último, notemos que si $f$ es real diferenciable con respecto a $\varphi$, entonces $\overline{f}$ es real diferenciable con respecto a $\overline{\varphi}$ desde que: \begin{align*} \lim_{h\to 0} \frac{f(z+h) – f(z) – \varphi(h)}{h} &= 0\\ \Longleftrightarrow \quad \lim_{h\to 0} \left| \frac{f(z+h) – f(z) – \varphi(h)}{h} \right| &= 0\\ \Longleftrightarrow \quad \lim_{h\to 0} \frac{\left| \overline{f(z+h) – f(z) – \varphi(h)}\right|}{\left|h\right|} &= 0\\ \Longleftrightarrow \quad \lim_{h\to 0} \frac{\overline{f}(z+h) – \overline{f}(z) – \overline{\varphi}(h)}{h} &= 0. \end{align*} Por lo que, para el segundo caso se sigue de la proposición 24.3, que $\overline{\varphi}$ es $\mathbb{C}$-lineal y por tanto $\overline{f}$ es complejo diferenciable en $z\in U$.
   
   Entonces $f$ ó $\overline{f}$ es complejo diferenciable en $z\in U$.

$\blacksquare$

Procedemos ahora a definir algunas de las transformaciones del plano complejo más importantes, con las que ya estamos familiarizados por nuestros cursos de Geometría.

Definición 24.4. (Transformación identidad en $\mathbb{C}$.)
La transformación $\mathbb{I}_\mathbb{C} : \mathbb{C} \to \mathbb{C}$ dada por $\mathbb{I}_\mathbb{C}(z)=z$, es llamada la transformación identidad del plano complejo $\mathbb{C}$.

Definición 24.5. (Homotecia.)
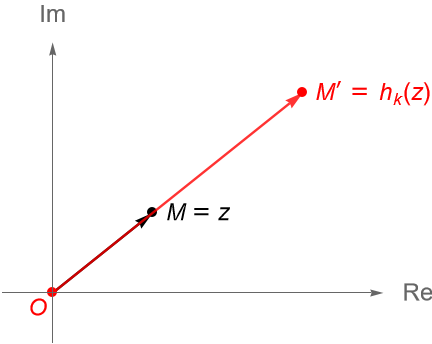
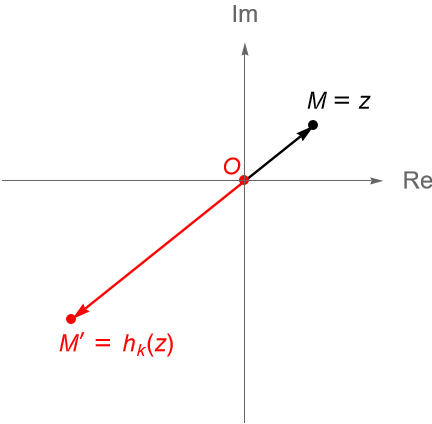
Sea $k\in\mathbb{R}\setminus\{0\}$. Se define a una homotecia del plano complejo $\mathbb{C}$, con centro en el origen y razón (o factor) $k$ como la transformación $h_k:\mathbb{C} \to \mathbb{C}$ dada por $h_k(z) = kz$.

Si el punto $O$ es el origen, $M$ es un punto cualquiera en el plano complejo, dado por $z\in\mathbb{C}$, entonces la posición del punto $M’=h_k(z) \in \mathbb{C}$ depende del signo de $k$, es decir, si $k>0$ figura 83, ó $k<0$ figura 84. Al punto $M’$ se le llama el punto homotético de $M$ con centro en $O$ y razón $k$.

En cualquiera de ambos caso se cumple que:
\begin{equation*}
|\overline{OM’}| = |k| \, |\overline{OM}|,
\end{equation*} es decir, el módulo del punto homotético $M’$ es igual al valor absoluto de $k$ por el módulo del punto $M$.

No es difícil verificar que la composición de dos homotecias también es una homotecia.

Definición 24.6. (Traslación.)
Sea $z_0 \in \mathbb{C}$ fijo y sea $t_{z_0}:\mathbb{C} \to \mathbb{C}$ la transformación dada por:
\begin{equation*}
t_{z_0}(z) = z + z_0.
\end{equation*}

La transformación $t_{z_0}$ es llamada la traslación del plano complejo $\mathbb{C}$ por un número $z_0$.

Teniendo en cuenta la interpretación geométrica de la suma de dos números complejos, entrada 3, podemos dar fácilmente una interpretación geométrica de la traslación analizando la imagen de cualquier $z\in\mathbb{C}$, bajo $t_{z_0}$, figura 85.

En la figura 85, $O M_0 M’ M$ es un paralelogramo y el segmento $\overline{OM’}$ es una de sus diagonales. Por lo que, la transfromación $t_{z_0}$ corresponde en el plano complejo $\mathbb{C}$ con la traslación $t_{\overrightarrow{OM_0}}$ dada por el vector $\overrightarrow{OM_0}$ en el caso del plano Euclidiano.

Debe ser claro que la composición de dos traslaciones $t_{z_1}$ y $t_{z_2}$ cumple que:
\begin{equation*}
t_{z_1} \circ t_{z_2} = t_{z_1 + z_2}.
\end{equation*}

Observación 24.3.
Notemos que el conjunto $\tau$ de todas las traslaciones del plano complejo forma un grupo con respecto de la composición de funciones. El grupo $\left(\tau,\circ\right)$ es abeliano y su unidad es la transformación identidad $\mathbb{I}_{\mathbb{C}} = t_0$, es decir, la traslación por el número complejo $0$.

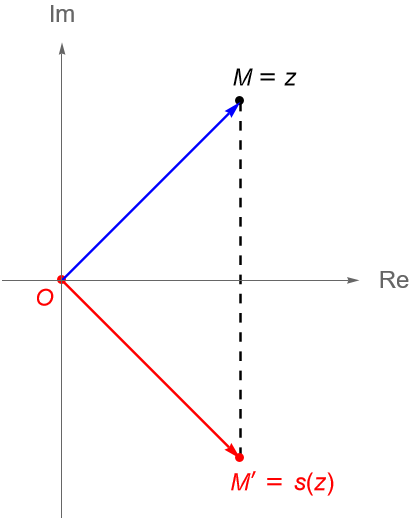
Definición 24.7. (Reflexión respecto al eje real y respecto a un punto.)
Sea $s:\mathbb{C} \to \mathbb{C}$ dada por $s(z) = \overline{z}$. A la transformación $s$ se le llama la reflexión con respecto al eje real.

Si $M$ es un punto en el plano dado por el número complejo $z\in\mathbb{C}$, entonces el punto $M’=s(z) \in\mathbb{C}$ es obtenido al reflejar a $M$ respecto al eje real, figura 86. Además, es claro que:
\begin{equation*}
s \circ s = \mathbb{I}_{\mathbb{C}}.
\end{equation*}

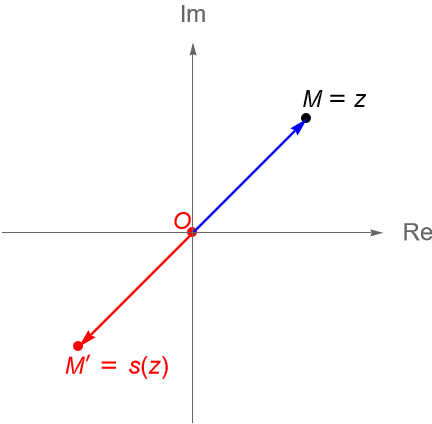
Por otra parte, a la transformación $s_0 : \mathbb{C} \to \mathbb{C}$ dada por $s_0(z) = -z$, se le llama la reflexión con respecto al origen, desde que $s_0(z) + z = 0$, entonces para un punto $M = z\in\mathbb{C}$, el origen $O$ es el punto medio del segmento $\overline{MM’}$, con $M’=s_0(z)$, es decir, el punto $M’$ es la reflexión del punto $M$ en el origen, figura 87.

Debe ser claro que:
\begin{equation*}
s_{0} \circ s_{0} = \mathbb{I}_{\mathbb{C}}.
\end{equation*}

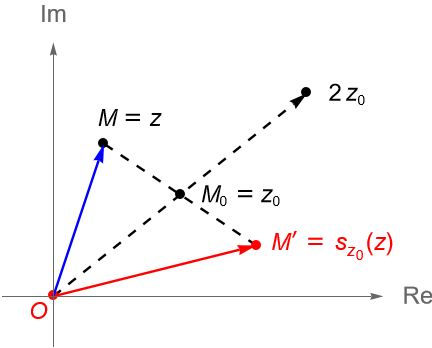
Por último, para $z_0\in\mathbb{C}$ fijo, se define a la reflexión con respecto a $\pmb{z_0}$ como la transformación $s_{z_0} : \mathbb{C} \to \mathbb{C}$ dada por $s_{z_0}(z) = 2z_0-z$.

Si $M, M_0$ y $M’$ son los puntos en el plano dados por $z,z_0,s_{z_0}(z) \in \mathbb{C}$, respectivamente, entonces $M_0$ es el punto medio del segmento $\overline{MM’}$ y así $M’$ es la reflexión de $M$ en $M_0$, figura 88.

Es sencillo verificar que:
\begin{equation*}
s_{z_0} \circ s_{z_0} = \mathbb{I}_{\mathbb{C}}.
\end{equation*}

Observación 24.4.
A pesar de que la transformación $T(z) = \overline{z}$ no es $\mathbb{C}$-lineal, es importante recordar su interpretación geométrica, ya que dicha transformación nos representa una reflexión en el plano complejo a través del eje real.

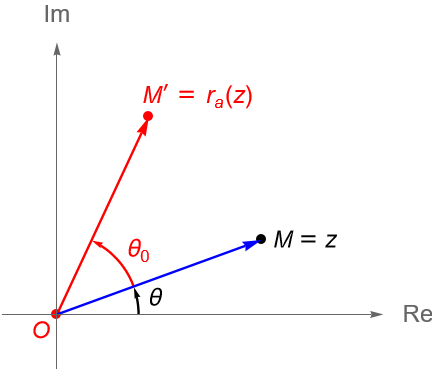
Definición 24.8. (Rotación.)
Sea $a = \in \mathbb{C}$ tal que $|a|=1$, es decir, $a=e^{i\theta_0}$. Se define a la rotación de $z=\rho e^{i\theta}\in\mathbb{C}$ alrededor del origen, en un ángulo $\theta_0\in\mathbb{R}$, como la transformación $r_a:\mathbb{C} \to \mathbb{C}$ dada por:
\begin{equation*}
r_a(z) = az = \rho e^{i(\theta+\theta_0)}.
\end{equation*}

Así, si $M$ es un punto en el plano complejo dado por $z=\rho e^{i\theta}\in\mathbb{C}$, entonces $M’ = r_a(z)$ se obtiene al rotar $M$ alrededor del origen un ángulo $\theta_0$, figura 89.

Observación 24.5.
De manera general es posible definir una reflexión en el plano complejo respecto a una recta $\mathcal{L}$ arbitraria, la cual está dada por la composición de una rotación y/o una traslación del eje real, una reflexión respecto al eje real y las inversas de la rotación y la traslación, por lo que será de la forma:
\begin{equation*}
s_\mathcal{L}(z) = e^{i\theta} \overline{z} + b,
\end{equation*} para algún ángulo $\theta\in\mathbb{R}$ y una constante $b\in\mathbb{C}$.

Analicemos lo anterior mediante el siguiente:

Ejemplo 24.2.
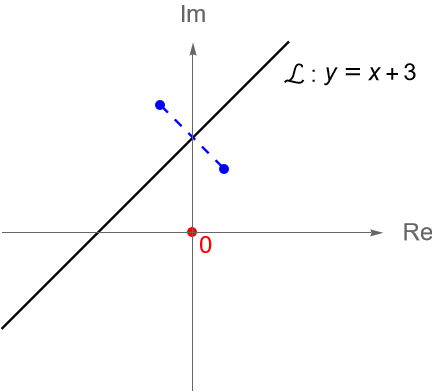
Determinemos la reflexión en el plano complejo dada sobre la recta $\mathcal{L} : y=x+3$.

Solución. Primeramente, notemos que la recta dada se obtiene al rotar el eje real alrededor del origen un ángulo de $\pi/4$ y luego trasladarlo verticalmente por $3i$.

Así, para reflejar a $z\in\mathbb{C}$ respecto a $\mathcal{L}$, primero trasladamos verticalmente dicho punto por $-3i$, luego lo rotamos alrededor del origen un ángulo de $-\pi/4$, después lo reflejamos respecto al eje real y por último, lo rotamos alrededor del origen un ángulo de $\pi/4$ y lo trasladamos por $3i$.

Es decir, sean:
\begin{align*}
t_{-3i}(z) &= z-3i,\\
r_{e^{-i\frac{\pi}{4}}}(z) &= e^{-i\frac{\pi}{4}} z,\\
s(z) &= \overline{z},\\
t_{3i}(z) & = z+3i,\\
r_{e^{i\frac{\pi}{4}}}(z) &= e^{i\frac{\pi}{4}} z,
\end{align*}

por lo que:
\begin{align*}
\left(s\circ r_{e^{-i\frac{\pi}{4}}} \circ t_{-3i}\right)(z) & = s\left(r_{e^{-i\frac{\pi}{4}}}(t_{-3i}(z))\right)\\
& = s\left(r_{e^{-i\frac{\pi}{4}}}(z-3i)\right)\\
& = s\left(e^{-i\frac{\pi}{4}}(z-3i)\right)\\
& = \overline{e^{-i\frac{\pi}{4}}(z-3i)}\\
& = e^{i\frac{\pi}{4}}(\overline{z}+3i).
\end{align*}

Luego, como $e^{i\frac{\pi}{2}} = i$, tenemos que:
\begin{align*}
\left(t_{3i} \circ r_{e^{i\frac{\pi}{4}}}\right)(e^{i\frac{\pi}{4}}(\overline{z}+3i)) & = t_{3i} \left(r_{e^{i\frac{\pi}{4}}}(e^{i\frac{\pi}{4}}(\overline{z}+3i))\right)\\
& = t_{3i} \left(e^{i\frac{\pi}{4}} e^{i\frac{\pi}{4}}(\overline{z}+3i)\right)\\
& = e^{i\frac{\pi}{2}}(\overline{z}+3i) + 3i\\
& = i (\overline{z}+3i) + 3i\\
& = i\overline{z} – 3(1-i).
\end{align*}

Entonces, la reflexión sobre la recta $\mathcal{L} : y=x+3$, figura 90, está dada por:
\begin{equation*}
s_{\mathcal{L}}(z) = i\overline{z} – 3(1-i).
\end{equation*}

Por ejemplo, si consideramos al punto $z=-1+4i$, entonces:
\begin{align*}
s_{\mathcal{L}}(z) & = i(\overline{-1+4i}) – 3(1-i)\\
& = i(-1-4i)-3+3i\\
& = -i+4-3+3i\\
& = 1+2i.
\end{align*}

Observación 24.6.
Como se verá en el ejercicio 7 de esta entrada, las reflexiones son transformaciones más sencillas que las rotaciones y las traslaciones, desde que estas últimas transformaciones son simplemente composiciones dos reflexiones particulares.

Recordemos ahora otro concepto importante visto en nuestros cursos de Geometría.

Definición 24.9. (Isometría.)
Sea $S\subset \mathbb{C}$. Una transformación $T:\mathbb{C} \to \mathbb{C}$ se llama una isometría si no modifica las distancias, es decir, si:
\begin{equation*}
|\,T(z_1) – T(z_2)\,| = |\,z_1 – z_2\,|, \quad \forall z_1, z_2 \in\mathbb{C}.
\end{equation*}

Mientras que una función $f:S \to \mathbb{C}$ se llama una isometría si:
\begin{equation*}
|\,f(z_1) – f(z_2)\,| = |\,z_1 – z_2\,|,
\end{equation*} para todo par de números complejos $z_1$ y $z_2$ en el dominio $S$ de $f$.

Observación 24.7.
No es difícil verificar que la composición de dos isometrías es también una isometría. Más aún, el conjunto de todas las isometrías del plano complejo, denotado como $\text{Iso}(\mathbb{C})$ es un grupo con respecto a la composición de funciones y el grupo de las traslaciones, $(\tau, \circ)$, es un subgrupo de dicho grupo.

Proposición 24.5.
Las traslaciones, reflexiones y las rotaciones alrededor de un punto $z_0$ son isometrías del plano.

Demostración. Se deja como ejercicio al lector.

$\blacksquare$

De acuerdo con el ejercicio 9 de esta entrada tenemos el siguiente:

Ejemplo 24.3.
a) Las transformaciones $s_{\mathcal{L}_1}(z) = \overline{z}+3i$, $s_{\mathcal{L}_2}(z) = \overline{z}+5i$ y $s_{\mathcal{L}_3}(z) = -\overline{z}+1$ corresponden con tres reflexiones, las primeras dos respecto a las rectas horizontales $\mathcal{L}_1 : -iz+i\overline{z}-3=0$ y $\mathcal{L}_2 : -iz+i\overline{z}-5=0$, respectivamente, y la última respecto a la recta vertical $\mathcal{L}_3 : z+\overline{z}-1=0$.

La composición:
\begin{align*}
\left(s_{\mathcal{L}_1} \circ s_{\mathcal{L}_2}\right)(z) & = s_{\mathcal{L}_1}\left( s_{\mathcal{L}_2}(z)\right)\\
& = s_{\mathcal{L}_1}\left( \overline{z}+5i\right)\\
& = \overline{\overline{z}+5i}+3i\\
& = z – 2i,
\end{align*} corresponde con la traslación $t_{-2i}(z)$ en el plano complejo.

Por otra parte, la composición:
\begin{align*}
\left(s_{\mathcal{L}_1} \circ s_{\mathcal{L}_3}\right)(z) & = s_{\mathcal{L}_1}\left( s_{\mathcal{L}_3}(z)\right)\\
& = s_{\mathcal{L}_1}\left(- \overline{z}+1\right)\\
& = \overline{- \overline{z}+1}+3i\\
& = -z + \left(1 + 3i\right),
\end{align*} corresponde con la rotación $r_{a}(z)$ alrededor del punto $z_0 = \dfrac{1}{2} + i \dfrac{1}{2}$ y un ángulo $\pi$, es decir, $a = e^{i\pi}$, en el plano complejo.

b) La transformación $h(z)=\overline{z}+1$ está dada por la composición de la reflexión respecto al eje real $s(z) = \overline{z}$ y la traslación $t_{1}(z)=z+1$.

c) La transformación $h(z)=\overline{z}+2i = (\overline{z}+i)+i$ está dada por la composición de la reflexión $s_{\mathcal{L}}(z) = \overline{z} + i$, respecto a la recta horizontal $\mathcal{L} : -iz+i\overline{z}-1=0$, y la traslación $t_{i}(z)=z+i$.

Definición 24.10.(Punto fijo.)
Sea $T: \mathbb{C} \to \mathbb{C}$ una transformación. Diremos que un punto $z_0 \in \mathbb{C}$ es un punto fijo de $T$ si y solo si $T(z_0) = z_0$.

Ejemplo 24.4.
a) La transformación identidad fija a todos los puntos de $\mathbb{C}$.

b) Si $z_0\in\mathbb{C}$ es tal que $z_0 \neq 0$, entonces la transformación $t_{z_0}(z)=z+z_0$ no tiene puntos fijos.

c) Si $a\in\mathbb{C}$ es tal que $|a|=1$ y $a\neq 1$, entonces la rotación $r_a(z) = az$ alrededor del origen solo fija al origen.

Lema 24.1.
Una isometría del plano que fija a los puntos $0, 1$ e $i$ debe ser la identidad.

Demostración. Dadas las hipótesis, sea $h:\mathbb{C}\to\mathbb{C}$ una isometría tal que: \begin{equation*}
h(0)=0, \quad h(1) = 1 \quad \text{y} \quad h(i)=i.
\end{equation*}

Dado que $h$ es una isometría, entonces para cualesquiera $z,w\in\mathbb{C}$ se cumple que:
\begin{equation*}
|h(z)-h(w)| = |z-w|,
\end{equation*} en particular, para $w \in \{0,1,i\}$ tenemos que:
\begin{equation*}
|h(z)| = |z|, \quad |h(z)-1| = |z-1| \quad \text{y} \quad |h(z)-i| = |z-i|.
\end{equation*}

Elevando al cuadrado las tres igualdades anteriores tenemos que:
\begin{align*}
h(z) \overline{h(z)} & = z \overline{z}, \tag{24.4}\\
(h(z)-1)\overline{(h(z)-1)} &= (z-1)\overline{(z-1)}, \tag{24.5}\\
(h(z)-i)\overline{(h(z)-i)} &= (z-i)\overline{(z-i)}.\tag{24.6}
\end{align*}

Desarrollando (24.5) tenemos:
\begin{equation*}
h(z) \overline{h(z)} – h(z) – \overline{h(z)} + 1 = z \overline{z} – z \overline{z} + 1.
\end{equation*}

Considerando (24.4) se tiene que:
\begin{equation*}
h(z) + \overline{h(z)} = z + \overline{z}, \tag{24.7}
\end{equation*}

Análogamente, de (24.6) obtenemos que:
\begin{equation*}
h(z) – \overline{h(z)} = z – \overline{z}, \tag{24.8}
\end{equation*}

Entonces, de (24.7) y (24.8) se sigue que:
\begin{equation*}
h(z) = z.
\end{equation*}

$\blacksquare$

Proposición 24.6.
Toda isometría del plano complejo es de la forma:
\begin{equation*}
h_1(z) = \alpha z + \beta \quad \text{ó} \quad h_2(z) = \alpha \overline{z} + \beta,
\end{equation*} con $\alpha, \beta\in\mathbb{C}$, únicos y $|\,\alpha\,|=1$.

La primera función es una isometría que preserva la orientación y la segunda una isometría que la invierte.

Demostración. Sea $h:\mathbb{C} \to \mathbb{C}$ una isometría arbitraria. Primeramente notemos que una función de la forma:
\begin{equation*}
h_1(z) = \alpha z + \beta \quad \text{ó} \quad h_2(z) = \alpha \overline{z} + \beta,
\end{equation*} con $\alpha, \beta\in\mathbb{C}$, constantes y $|\,\alpha\,|=1$ es una isometría desde que:
\begin{align*}
|h_1(z) – h_1(w)| = |\alpha(z-w)| = |z-w|,\\
|h_2(z) – h_2(w)| = |\alpha\overline{(z-w)}| = |z-w|,
\end{align*} para cualesquiera $z, w\in\mathbb{C}$.

Definimos:
\begin{equation*}
\beta : = h(0) \quad \text{y} \quad \alpha:= h(1) – h(0),
\end{equation*} de donde se sigue la unicidad de dichas constantes. Además:
\begin{equation*}
|\alpha|= |h(1) – h(0)| = |1 – 0| = 1.
\end{equation*}

Consideremos a la función:
\begin{equation*}
H(z) : = \frac{h(z) – \beta}{\alpha} = \frac{h(z) – h(0)}{h(1) – h(0)},
\end{equation*} la cual está bien definida desde que $\alpha\neq 0$, pues cualquier isometría del plano en particular es una función inyectiva.

Veamos que $H$ también es una isometría, en particular que dicha función es igual a $z$ ó $\overline{z}$.

Sean $z, w\in\mathbb{C}$, entonces:
\begin{align*}
|H(z) – H(w)| & = \left|\frac{h(z) – \beta}{\alpha} – \frac{h(z) – \beta}{\alpha} \right|\\
& = \frac{|h(z) – h(w)|}{|\alpha|}\\
& = |z-w|.
\end{align*}

Por otra parte, tenemos que:
\begin{align*}
H(0) = \frac{h(0) – h(0)}{h(1) – h(0)} = 0,\\
H(1) = \frac{h(1) – h(0)}{h(1) – h(0)} = 1.
\end{align*}

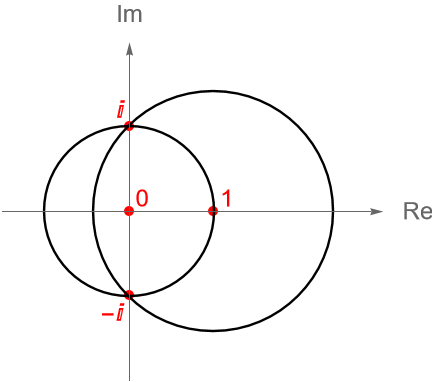
Dado que $H$ es una isometría que fija a $0$ y a $1$, se sigue que:
\begin{align*}
|H(i)| = |H(i) – H(0)| = |i-0| = 1, \tag{24.9}\\
|H(i)-1| = |H(i) – H(1)| = |i-1| = \sqrt{2}. \tag{24.10}
\end{align*}

Geométricamente, lo anterior nos dice que $H(i)$ está en la intersección de la circunferencia unitaria y la circunferencia de radio $\sqrt{2}$ y centro en $1$, pero en tal intersección únicamente están los puntos $i$ y $-i$, figura 91.

Es fácil verificar este hecho de manera algebraica elevando al cuadrado las ecuaciones (24.9) y (24.10) y resolviendo el sistema de ecuaciones como en la prueba del lema 24.1, por lo que esta verificación se deja como ejercicio al lector.

Si $H(i)=i$, entonces por el lema 24.1 tenemos que:
\begin{equation*}
H(z) = z \quad \Longrightarrow \quad h(z) = \alpha z + \beta, \quad \forall z\in\mathbb{C}.
\end{equation*}

Si $H(i)=-i$, entonces $\overline{H(z)}$ es una isometría del plano que fija a $0, 1$ e $i$, por lo que, lema 24.1, debe ser la identidad:
\begin{equation*}
\overline{H(z)} = z \quad \Longrightarrow \quad H(z) = \overline{z}, \quad \forall z\in\mathbb{C},
\end{equation*}

de donde:
\begin{equation*}
h(z) = \alpha \overline{z} + \beta.
\end{equation*}

$\blacksquare$

Corolario 24.1.
Toda isometría del plano complejo es una función biyectiva y su inversa es también una isometría.

Demostración. Se deja como ejercicio al lector.

$\blacksquare$

Corolario 24.2.
Una isometría del plano está determinada por sus imágenes en tres puntos no colineales, es decir, si $z_1, z_2, z_3\in\mathbb{C}$ son tres puntos no colineales y $h_1$ y $h_2$ son dos isometrías tales que $h_1(z_i) = h_2(z_i)$, para $i=1,2,3$, entonces $h_1 = h_2$.

Demostración. Se sigue de la observación 24.5 y del corolario 24.1, por lo que los detalles se deja como ejercicio al lector.

$\blacksquare$

Cerraremos esta entrada con la siguiente caracterización de las transformaciones $\mathbb{C}$-lineales.

Observación 24.8.
Sean $\lambda=a_1 + i a_2$, $\mu=b_1 + i b_2$, $z=x + i y$ y $w = u+iv$ números complejos y sea $T:\mathbb{C} \to \mathbb{C}$ una transformación $\mathbb{R}$-lineal. Por la proposición 24.1 sabemos que $T$ es de la forma:
\begin{align*}
w = T(z) & = \lambda z + \mu \overline{z}\\
& = (a_1+b_1) x – (a_2 – b_2) y + i \left[(a_2 + b_2) x + (a_1-b_1)y\right].
\end{align*}

De lo anterior se sigue que podemos representar a dicha transformación mediante las ecuaciones reales:
\begin{align*}
u = (a_1+b_1) x – (a_2 – b_2) y,\\
v = (a_2 + b_2) x + (a_1-b_1)y.
\end{align*}

Por lo que, geométricamente una transformación $\mathbb{R}$-lineal del plano complejo, es una transformación afín de un plano $\overline{y} = A \overline{x}$ con:
\begin{equation*}
A = \begin{pmatrix}
a_1+b_1 & -(a_2-b_2)\\
a_2+b_2& a_1 – b_1
\end{pmatrix}.
\end{equation*}

El Jacobiano de dicha transformación es:
\begin{equation*}
J = a_1^2 – b_1^2 + a_2^2 -b_2^2 = |\lambda|^2 – |\mu|^2,
\end{equation*} es decir, la transformación es invertible si $|\lambda| \neq |\mu|$. Dicha transformación envía rectas en rectas, rectas paralelas en rectas paralelas y cuadrados en paralelogramos. Además, preserva la orientación cuando $|\lambda|>|\mu|$ y la invierte cuando $|\lambda| < |\mu|$.

Sin embargo, una transformación $\mathbb{C}$-lineal, digamos $T(z) = \lambda z$, puede no invertir la orientación desde que su Jacobiano es:
\begin{equation*}
J = |\lambda|^2 \geq 0.
\end{equation*}

En tal caso, dicha transformación no es invertible si $\lambda=0$. Considerando la interpretación geométrica de la multiplicación de dos números complejos, para $\lambda= |\lambda| e^{i\theta_0}$, tenemos que $T(z) = |\lambda| e^{i\theta_0} z$ es la composición de una homotecia de razón $|\lambda|$ y una rotación alrededor del origen de un ángulo $\theta_0$. Tal transformación preserva ángulos y envía cuadrados en cuadrados.

Considerando lo anterior tenemos la siguiente caracterización de las transformaciones $\mathbb{C}$-lineales.

Proposición 24.7.
Si una transformación $\mathbb{R}$-lineal, digamos $T(z) = \lambda z +\mu \overline{z}$, preserva la orientación y los ángulos entre tres vectores no paralelos $e^{i\theta_1}, e^{i\theta_2}, e^{i\theta_3}\in\mathbb{C}$, con $\theta_k \in\mathbb{R}$ para $k=1,2,3$, entonces $T$ es $\mathbb{C}$-lineal.

La prueba de este resultado, así como de algunos otros resultados de ésta entrada se pueden consultar en el texto Introduction to Complex Analysis – excerpts de B.V.Shabat.

Tarea moral

1. Realiza la demostración de las proposiciones 24.2 y 24.5.
2. Completa la demostración de la proposiciones 24.3 y 24.4.
3. Prueba las observaciones 24.3 y 24.7.
4. Demuestra los corolarios 24.1 y 24.2.
5. Sean $z_1, z_2 \in\mathbb{C}$. Supón que una isometría del plano complejo tiene como puntos fijos a $z_1$ y a $z_2$. Demuestra que todo punto $z$ del segmento $[z_1, z_2]$ es un punto fijo de dicha transformación.
6. Prueba que las siguientes transformaciones son una isometría. En cada caso muestra que cada función se puede ver como la composición de una rotación con una traslación y posiblemente con una reflexión sobre el eje real.
   a) $f:\mathbb{C} \to \mathbb{C}$ dada por $f(z) = i \overline{z} + 4 – i$.
   b) $g:\mathbb{C} \to \mathbb{C}$ dada por $g(z) = -iz+ 1 + 2i$.
   c) $h:\mathbb{C} \to \mathbb{C}$ dada por $h(z) = -\overline{z} + i$.
7. Muestra que una traslación del plano complejo es la composición de dos reflexiones respecto dos rectas paralelas, mientras que una rotación en $\mathbb{C}$, alrededor de un punto fijo $z_0 \in\mathbb{C}$, es la composición de dos reflexiones respecto dos rectas que se cortan en $z_0$.
8. En cada inciso determina una expresión que describa a una reflexión en el plano complejo respecto a la recta dada.
   a) $y=k$ con $k\in\mathbb{R}$ constante.
   b) $x=k$ con $k\in\mathbb{R}$ constante.
   c) $y=mx+b$, con $m, b\in\mathbb{R}$ y $m\neq 0$.
9. Muestra que las siguientes transformaciones corresponden con una reflexión respecto a la recta dada.
   a) $s_{\mathcal{L}}(z) = \overline{z}+3i$ con $\mathcal{L}: -iz+i\overline{z}-3=0$.
   b) $s_{\mathcal{L}}(z) = \overline{z}+5i$ con $\mathcal{L} : -iz+i\overline{z}-5=0$.
   c) $s_{\mathcal{L}}(z) = -\overline{z}+1$ con $\mathcal{L} : z+\overline{z}-1=0$.
   d) $s_{\mathcal{L}}(z) = \overline{z}+i$ con $\mathcal{L} : -iz+i\overline{z}-1=0$.

Más adelante…

En esta entrada hemos recordado algunos conceptos de Geometría Analítica y Álgebra Lineal relacionados con las transformaciones del plano Euclidiano. Como es de esperarse, las definiciones de estos conceptos para el caso complejo coinciden con las que se dan para $\mathbb{R}^2$. Sin embargo, debe ser claro que a través de las propiedades de los números complejos resulta más sencilla la prueba de los resultados dados en esta entrada.

La siguiente entrada estudiaremos algunas transformaciones del plano complejo muy particulares, llamadas transformaciones de Möbius, mediante las cuales podremos caracterizar la geometría de las funciones complejas.

Entradas relacionadas

• Ir a Variable Compleja I.
• Entrada anterior del curso: Funciones inversas de las funciones trigonométricas e hiperbólicas complejas.
• Siguiente entrada del curso: Transformaciones lineales y transformaciones de Möbius.