Archivo de la etiqueta: hiperplanos

Seminario de Resolución de Problemas: Geometría discreta

Por Leonardo Ignacio Martínez Sandoval

Deja un comentario

Introducción

Como última entradaen esta parte de geometría, hablaremos de algunos temas de geometría discreta. Esta área de las matemáticas se dedica a estudiar propiedades combinatorias de familias de objetos geométricos. Estos objetos pueden ser puntos, rectas, rectángulos, convexos, politopos, etc. Las relaciones que nos interesan son que formen un tipo de acomodo especial, que se intersecten, que podamos contar ciertas configuraciones, etc.

Sólo hablaremos superficialmente de un área que es profunda y bastante interesante. Un libro genial que cubre varios temas de geometría discreta de manera sistemática es Lectures on Discrete Geometry de Jiří Matoušek.

Convexos y el teorema de Helly

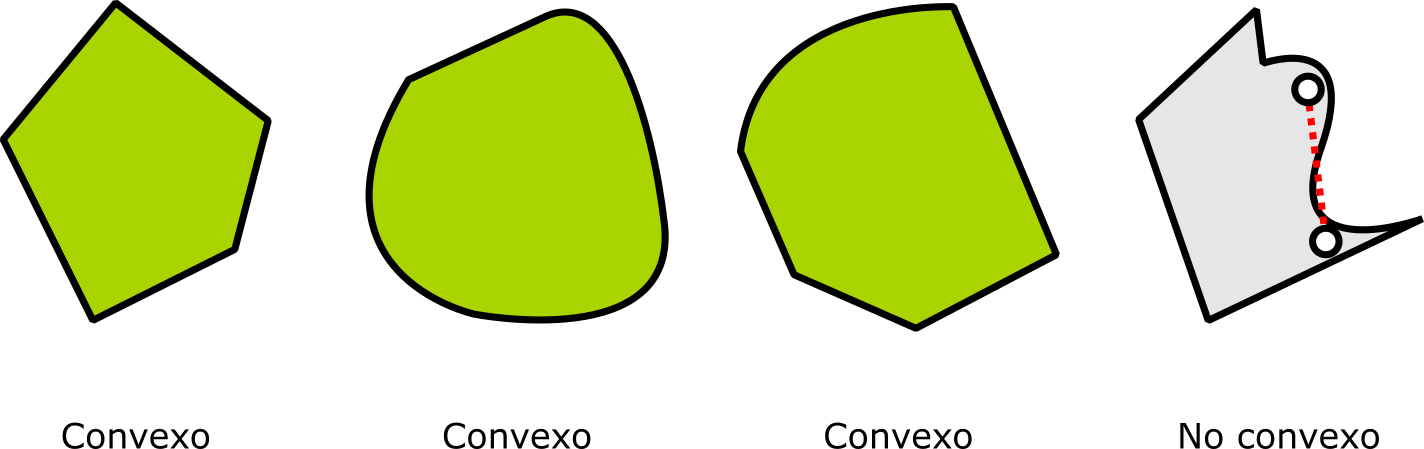
Un convexo de $\mathbb{R}^d$ es un conjunto tal que cualquier segmento recto definido por dos de sus puntos queda totalmente contenido en el conjunto. Por ejemplo, los convexos de $\mathbb{R}$ son los intervalos, mientras que en el plano hay muchos más ejemplos, como lo muestra la figura.

Ejemplos de conjuntos convexos y no convexos
Ejemplos de conjuntos convexos y no convexos

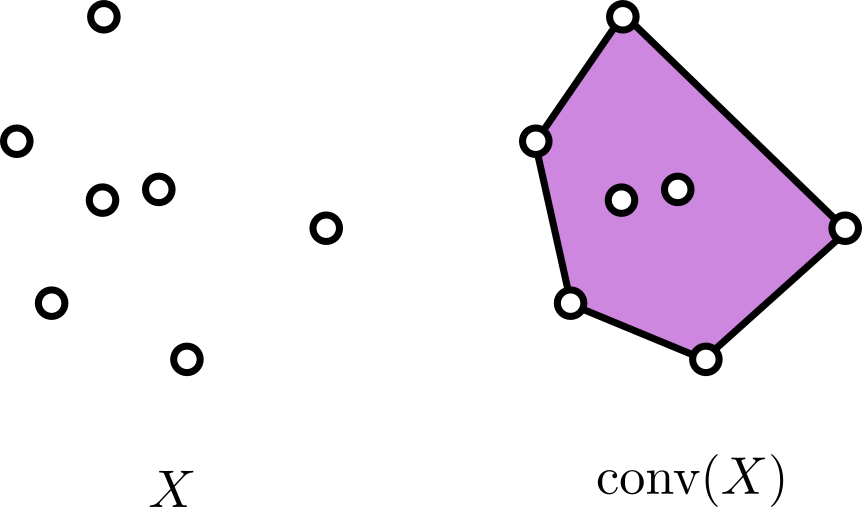
Si tenemos un conjunto $X$ de $\mathbb{R}^d$, su envolvente convexa es el conjunto convexo más pequeño (por contención), que contiene a $X$. Cuando $X$ es un conjunto de puntos, tenemos algo como lo de la figura. Si todos los puntos de $X$ están sobre la frontera de su envolvente convexa, y no hay tres alineados, decimos que $X$ son puntos en posición convexa.

Envolvente convexa de un conjunto de puntos
Envolvente convexa de un conjunto de puntos. El conjunto $X$ no está en posición convexa.

Los conjuntos convexos son especiales en muchos sentidos. Uno de ellos es que la intersección de una familia de convexos se puede detectar «localmente».

Problema. A una plática de matemáticas de una hora asistieron una cantidad finita de matemáticos. La plática estaba tan aburrida, que cada matemático se durmió en cierto intervalo de tiempo de esa hora, pero sólo una vez. A la hora del café, los matemáticos platicaron entre sí, y si se dieron cuenta de que para cualesquiera dos de ellos, $I$ y $J$, hubo un momento en el que $I$ y $J$ estuvieron dormidos simultáneamente. Muestra que hubo un momento de la plática en la que todos los matemáticos estuvieron dormidos.

Sugerencia pre-solución. Hay muchas soluciones. Una es mediante un argumento de maximalidad.

Solución. En términos matemáticos, queremos ver que si tenemos una cantidad finita de intervalos acotados y cerrados en la recta real que se intersectan de dos en dos, entonces todos ellos se intersectan.

Tomemos el intervalo $I$ cuyo extremo derecho sea mínimo. Llamemos $x$ a este extremo derecho. Afirmamos que cualquier otro intervalo tiene a $x$. Sea $J$ cualquiera de estos intervalos, con extremo izquierdo $y$ y extremo derecho $z$.

Imagen auxiliar para intersección de intervalos
Imaten auxiliar para intersección de intervalos

Por la minimalidad de $x$, tenemos que $x\leq z$. Si $y>x$, entonces $J$ no intersecta a $I$ y se contradice la hipótesis. Entonces, para que $J$ pueda intersectar a $I$, necesitamos que $y \leq x$. Pero entonces $x$ queda entre los extremos del intervalo $J$ y por lo tanto $x$ está en $J$. Esto termina la prueba.

$\square$

En dimensiones más altas, tenemos el siguiente resultado.

Teorema (Helly). Sea $\mathcal{F}$ una familia finita de al menos $d+1$ conjuntos convexos compactos en $\mathbb{R}^d$. Si cada subfamilia de $\mathcal{F}$ de $d+1$ convexos tiene intersección no vacía, entonces $\mathcal{F}$ tiene intersección no vacía.

El teorema de Helly es una de las piedras angulares de la geometría discreta. Una cantidad de enorme de investigación ha resultado de considerar variantes del teorema con hipótesis más débiles o más fuertes.

Politopos y la fórmula de Euler

Otra área muy rica de la geometría discreta es la teoría de politopos. Un politopo es la generalización a altas dimensiones de un polígono, o de un poliedro. Hay dos formas de definir politopos. Una es tomar puntos en $\mathbb{R}^d$ y considerar su envolvente convexa. Esto es un $V$-politopo. Para la otra necesitamos algunas definiciones adicionales.

Un subespacio afín de $\mathbb{R}^d$ es la traslación de un subespacio lineal, y su dimensión es la dimensión del subespacio lineal trasladado. Por ejemplo, cualquier punto de $\mathbb{R}^d$ es un subespacio afín de dimensión $0$ pues es la traslación del subespacio trivial $\{0\}$. Las rectas en $\mathbb{R}^d$, incluso aquellas que no pasan por el $0$, son subespacios afines de dimensión $0$. A los subespacios afines de dimensión $n-1$ les llamamos hiperplanos. Así, las líneas son los hiperplanos de $\mathbb{R}^2$, los planos los hiperplanos de $\mathbb{R}^3$, etc.

Si $P$ es un hiperplano de $\mathbb{R}^d$, un semiespacio definido por $P$ es todo lo que queda en uno de los lados de $P$. Si es abierto, no incluye a $P$, y si es cerrado, sí incluye a $P$. Un hiperplano siempre define dos semiespacios abiertos, y dos cerrados.

Hay otra forma de pensar a los politopos: tomamos una cantidad finita de semiespacios cerrados y los intersectamos. Si esa intersección está acotada, entonces a lo que obtenemos le llamamos un $H$-politopo. Piensa, por ejemplo, en los hiperplanos que determinan las caras de un cubo, y en los semiespacios «hacia adentro».

Un resultado clásico es que todo $H$-politopo es un $V$-politopo, así que podemos usar la descripción que nos convenga de acuerdo al problema que estemos resolviendo.

Un hiperplano $H$ es hiperplano soporte de un politopo $P$ si el politopo se queda totalmente contenido en alguno de los semiespacios definidos por $H$. Una cara de $P$ es la intersección de $P$ con alguno de sus hiperplanos soporte. Resulta que las caras de politopos son politopos. Para que todo funcione bien, debemos considerar al vacío como un politopo.

La dimensión de un politopo es la menor dimensión de un subespacio afín que lo contiene. Por definición, la dimensión del vacío es $-1$. Si una cara de un politopo es $k$, entonces la llamamos una $k$-cara. Los valores de $k$ sólo pueden ir de $0$ a $d$. A las $0$-caras les llamamos los vértices de $P$. A las $1$-caras les llamamos las aristas.

Para cada $k$ de $0$ a $n$, usamos $f_k$ para denotar la cantidad de $k$ caras del politopo, y a $$(f_0,f_1,f_2,\ldots,f_d)$$ le llamamos el $f$-vector del politopo. Estamos listos para enunciar un resultado crucial en la teoría de politopos.

Teorema (fórmula de Euler). Sea $P$ un politopo de dimensión $d$ en $\mathbb{R}^d$. Entonces

$$f_0-f_1+f_2-\ldots + (-1)^d f_d = 1.$$

Observa que $f_d$ siempre es $1$ pues la única $d$ cara de un politopo $P$ de dimensión $d$ es $P$ mismo.

En $\mathbb{R}^2$ esta fórmula no es tan útil, pues simplemente nos dice que si un polígono tiene $V$ vértices y $A$ aristas, entonces $V-A=0$, es decir, que tiene la misma cantidad de vértices y aristas, lo cual es inmediato.

En $\mathbb{R}^3$ la fórmula nos dice que si un poliedros tiene $V$ vértices, $A$ aristas y $F$ caras, entonces $$V-A+F=2.$$ Este fórmula se puede usar en varios problemas matemáticos de poliedros.

Problema. Muestra que el tetraedro, el cubo, el octaedro, el dodecaedro y el icosaedro son los únicos poliedros en $\mathbb{R}^3$ tales que a cada vértice una misma cantidad $a$ de caras, y cada cara consiste de la misma cantidad $b$ de vértices.

Sugerencia pre-solución. Usa notación adecuada, poniendo la cantidad de vértices, aristas y caras en términos de $a$ y $b$. Usa la fórmula de Euler. Luego, da un argumento de desigualdades.

Solución. A cada vértice llegan por lo menos $3$ caras, y cada cara tiene por lo menos $3$ vértices. Así, $a\geq 3$ y $b\geq 3$.

Si hay $A$ aristas, entonces tanto $2A$ como $bF$ cuentan la cantidad de parejas $(e,c)$ donde $e$ es una arista y $c$ una cara que lo tiene. Esto se debe a que cada arista está exactamente en dos caras, y a que como cada cara tiene $b$ vértices, entonces tiene $b$ aristas. Por lo tanto, $2A=bF$, de donde $$A=\frac{bF}{2}.$$

De manera similar, si hay $V$ vértices y $F$ caras, entonces tanto $aV$ como $bF$ cuentan la cantidad de parejas $(v,c)$, donde $v$ es un vértice y $c$ es una cara que lo tiene. De esta forma, $aV=bF$, de lo cual $$V=\frac{bF}{a}.$$

Por la fórmula de Euler, tenemos entonces que $$\frac{bF}{a}-\frac{bF}{2}+F = 2.$$ Esta igualdad implica, en particular, que al determinar los valores de $a$ y $b$, se determinan $F$ y entonces $V$ y $A$.

Si multiplicamos por $\frac{2}{bF}$ de ambos lados, y sumamos $1$ de ambos lados, tenemos que \begin{equation}
\frac{2}{a}+\frac{2}{b}= \frac{4}{bF}+1 > 1.
\end{equation}

Como $a\geq 3$, entonces $\frac{2}{a}\leq \frac{2}{3}$. De este modo,
\begin{align*}
\frac{2}{b}&> 1 – \frac{2}{a}\\
&\geq 1-\frac{2}{3} \\
&= \frac{1}{3}.
\end{align*}

Esto muestra que $b<6$, de modo que $b\leq 5$. Por simetría, $a\leq 5$. Podemos entonces simplemente estudiar los casos $a=2,3,4$ y $b=2,3,4$.

Si $a=5$, entonces la desigualdad (1) se cumple sólo si $b=3$. Si $a=4$, la desigualdad (1) se cumple sólo si $b=3$. Finalmente, si $a=3$, la desigualdad se cumple para $b=3,4,5$. De este modo, las únicas parejas de $(a,b)$ que sirven son:

  • $(3,3)$, que nos da el tetraedro.
  • $(3,4)$, que nos da el cubo.
  • $(4,3)$, que nos da el octaedro.
  • $(3,5)$, que nos da el dodecaedro.
  • $(5,3)$, que nos da el icosaedro.

$\square$

La fórmula de Euler es sólo una de las relaciones lineales que satisfacen las entradas del $f$-vector de un politopo. Otros dos resultados interesantes del área son:

  • Las relaciones de Dehn-Sommerville, que dan otras relaciones lineales que satisfacen las entradas del $f$-vector.
  • El teorema de la cota superior que para $d$, $n$ y $k$ fijas acota el número de $k$-caras que puede tener un politopo de dimensión $d$ con $n$-vértices.

Un libro canónico para aprender de politopos de manera sistemática es el Lectures on Polytopes de Günter M. Ziegler.

Conjuntos de puntos y teoremas extremales

La última área de la que hablaremos serán los problemas extremales en geometría discreta. Nos enfocaremos únicamente en problemas sobre conjuntos de puntos, pero se podrían hacer preguntas análogas para otras familias de objetos geométricos. De manera informal, pero intuitiva, un problema extremal de geometría consiste en mostrar que si un número es suficientemente grande, entonces empiezan a pasar cosas interesantes con ciertos objetos geométricos.

Uno de los resultados clásicos es el teorema de Erdős-Szekeres. A grandes rasgos, lo que dice es que si tenemos muchos puntos en posición general en el plano (no hay tres colineales), entonces siempre es posible encontrar un subconjunto grande de ellos que está en posición convexa.

Teorema (Erdős-Szekeres). Sea $n$ un entero positivo. Entonces, existe un entero $f(n)$ tal que si se tiene un conjunto $S$ con $f(n)$ o más puntos en el plano en posición general, entonces hay un subconjunto de tamaño $n$ de $S$ que consiste de puntos en posición convexa.

Típicamente, es bastante difícil encontrar los valores exactos de las funciones involucradas en problemas extremales de geometría discreta. El tipo de resultados de interés para la investigación matemática es encontrar las mejores «cotas asintóticas», que digan, más o menos, cómo se comporta la función que se está estudiando. En el caso del teorema de Erdős-Szekeres, las mejores cotas se enuncian así:

$$1+2^{n-2}\leq f(n) \leq 2^{n+o(n)}.$$

La notación $h(n)=o(g(n))$ quiere decir que $\frac{h(n)}{g(n)}\to 0$ cuando $n\to \infty$.

Aunque sea difícil determinar los valores exactos de $f(n)$ para toda $n$, hay algunos valores pequeños que sí se pueden determinar.

Problema. Demuestra que $f(4)=5$, es decir:

  • Que hay conjuntos de $4$ puntos en posición general en el plano que no tienen subconjuntos de tamaño $4$ en posición convexa.
  • Que cualquier subconjunto de $5$ puntos en posición general en el plano tiene un subconjunto de $4$ puntos en posición convexa.

Sugerencia pre-solución. Encontrar el ejemplo para el primer punto es fácil, simplemente explora el problema haciendo varias figuras. Divide el problema en casos de acuerdo a la cantidad de puntos que forman la envolvente convexa. Para uno de los casos, usa el principio de las casillas.

Solución. El siguiente ejemplo son $4$ puntos que no están en posición convexa, y que por lo tanto no tienen subconjuntos de tamaño $4$ en posición convexa.

Cuatro puntos que no están en posición convexa
Cuatro puntos que no están en posición convexa

Mostraremos ahora que $5$ puntos en posición general en el plano siempre tienen un subconjunto de tamaño $4$ en posición convexa. Procedemos por casos de acuerdo a la cantidad de puntos que están en la frontera de la envolvente convexa. Si son $4$ ó $5$, entonces inmediatamente entre ellos hay $4$ en posición convexa.

Si son $3$, entonces llamemos $A$, $B$, $C$ a esos puntos y $D$ y $E$ a los otros dos, que quedan dentro de $\triangle ABC$. La recta $DE$ divide al plano en dos semiplanos. Por principio de las casillas, hay dos puntos de entre $A$, $B$ y $C$ que yacen en el mismo semiplano, digamos $A$ y $B$.

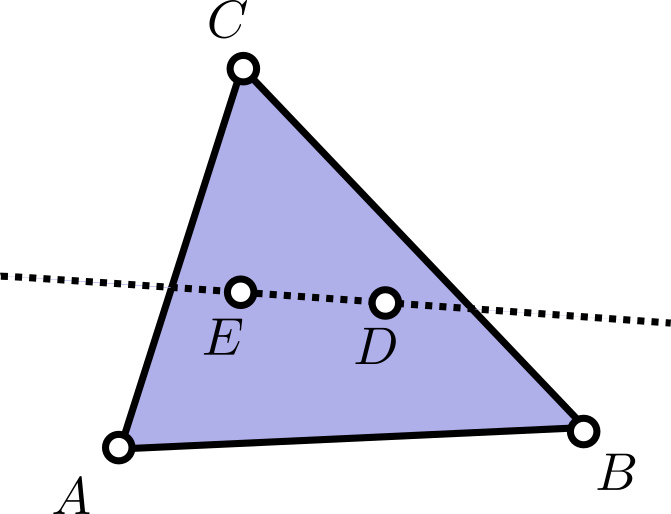
Caso con tres puntos en la envolvente convexa
Caso con tres puntos en la envolvente convexa

Como la recta $DE$ no corta al segmento $AB$ (por estar $D$ y $E$ en el mismo semiplano), y la recta $AB$ no corta al segmento $DE$ (por ser $AB$ un lado de la envolvente convexa), entonces los puntos $A$, $B$, $D$, $E$ están en posición convexa.

$\square$

Finalmente, presentamos un par de resultados más. También son problemas extremales, pero en vez de hablar de envolventes convexas, hablan acerca de distancias.

Si lo piensas un poco, es imposible colocar $4$ puntos distintos en el plano de modo que todas las parejas estén a distancia uno. Si tienes $n$ puntos en el plano, entonces ellos definen $\binom{n}{2}=\frac{n(n-1)}{2}\approx \frac{n^2}{2}$ parejas de puntos. ¿Cuántos de ellos pueden estar a distancia $1$? Estudiar esta cantidad es un problema que fue propuesto por Paul Erdős. Si $u(n)$ denota este máximo, las mejores cotas que hay para el problema son $$n^{1+d/\log \log n} \leq f(n) \leq O(n^{4/3}).$$

Aquí $d$ es una constante que sirve para toda $n$. La notación $h(n)\leq O(g(n))$ se refiere a que existe una constante $c$ tal que $h(n)\leq cg(n)$ para $n$ suficientemente grande.

Por supuesto, la distancia $1$ no tiene nada de especial. En realidad, ninguna distancia puede repetirse demasiado. Ya que ninguna distancia aparece muchas veces, la intuición (por principio de las casillas), nos debe decir que entonces para un conjunto de puntos, sus parejas deben definir muchas distancias diferentes. Llamemos $d(n)$ a la cantidad de distancias diferentes que define un conjunto de $n$ puntos en el plano. Erdős también preguntó, ¿cómo se comporta este número?. Las mejores cotas son $$\Omega\left(\frac{n}{\log }\right)\leq d(n) \leq O\left(\frac{n}{\sqrt{\log n}}\right).$$

La notación $h(n)\geq\Omega(g(n))$ se refiere a que existe una constante $c$ tal que $h(n)\geq cg(n)$ para $n$ suficientemente grande.

El problema de las distancias unitarias y el problema de las distancias diferentes han estimulado mucha de la investigación en geometría discreta. Las demostraciones de sus cotas, han introducido al área varias técnicas de teoría de números, del método probabilista y de geometría algebraica.

Un libro con mucho material de problemas extremales y otros temas es Combinatorial Geometry and its Algorithmic Applications de Janos Pach y Micha Sharir.

Más problemas

En resumen, en los siguientes libros hay bastante material para aprender los temas de esta entrada:

Álgebra Lineal I: Problemas de ortogonalidad, ecuaciones e hiperplanos

Por Ayax Calderón

11 respuestas

Introducción

En esta entrada ejercitaremos los conceptos introducidos recientemente. Abordamos los temas de espacio ortogonal e hiperplanos. Para ello, resolveremos problemas de ortogonalidad relacionados con encontrar una base para el espacio ortogonal y de escribir subespacios en términos de ecuaciones e intersecciones de hiperplanos.

Problemas resueltos de espacio ortogonal

Problema 1. Sea $S=\{x^3+x, x^2+x ,-x^3+x^2+1\} \subseteq \mathbb{R}_3[x]$.
Describe $S^{\bot}$ dando una base de este espacio.

Solución. Una forma lineal $l$ sobre $\mathbb{R}_3[x]$ es de la forma

$l(a_0 + a_1x+a_2x^2+a_3x^3)=aa_0+ba_1+ca_2+da_3$

para algunos $a, b,c,d\in \mathbb{R}$, pues basta decidir quiénes son $a=l(1)$, $b=l(x)$, $c=l(x^2)$ y $d=l(x^3)$.

La condición $l\in S^{\bot}$ es equivalente a

$l(x^3+x)=l(x^2+x)=l(-x^3+x^2+1)=0.$

Esto es
\begin{align*}
l(x^3+x)&=b+d=0\\
l(x^2+x)&=b+c=0\\
l(-x^3+x^2+1)&=a+c-d=0.
\end{align*}

La matriz asociada al sistema es

$A=\begin{pmatrix}
0 & 1 & 0 & 1\\
0 & 1 & 1 & 0\\
1 & 0 & 1 & -1\end{pmatrix}$

y su forma escalonada reducida es

$A_{red}=\begin{pmatrix}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 1\\
0 & 0 & 1 & -1\end{pmatrix}.$

Así, $d$ es variable libre y \begin{align*} a&=0\\ b&=-d\\ c&=d.\end{align*}

De aquí, el conjunto de soluciones del sistema es
$$\{(0,-u,u,u) : u\in \mathbb{R}\}.$$

Las correspondientes formas lineales son $$l_u(a_0+a_1x+a_2x^2+a_3x^3)=u(-a_1+a_2+a_3).$$

Este es un subespacio de dimensión $1$, así que para determinar una base para $S^{\bot}$, basta con elegir una de estas formas lineales con $u\neq 0$, por ejemplo, para $u=1$ tenemos
$$l_1(a_o+a_1x+a_2x^2+a_3x^3)=-a_1+a_2+a_3.$$

$\triangle$

Problema 2. Sea $V$ un espacio vectorial sobre un campo $F$, sea $V^\ast$ su espacio dual y tomemos subconjuntos $S, S_1, S_2\subseteq V^\ast$ tales que $S_1\subseteq S_2$. Prueba lo siguiente.

  1. $S_2^{\bot}\subseteq S_1^{\bot}$.
  2. $S\subseteq (S^{\bot})^{\bot}$.

Solución.

  1. Sea $l\in S_2^{\bot}$. Por definición $l(s)=0$ para toda $s\in S_2$.
    Luego, si $s\in S_1$, entonces $s\in S_2$ y así $l(s)=0$. Por consiguiente $l\in S_1^{\bot}$. Concluimos $S_2^{\bot}\subseteq S_1^{\bot}$.
  2. Sea $s\in S$. Para cualquier $l\in S^{\bot}$ se cumple que $l(s)=0$ y así $s\in (S^{\bot})^{\bot}$

$\square$

Observación. El problema anterior también es cierto si suponemos que $S, S_1, S_2\subseteq V$ tales que $S_1\subseteq S_2$ y la prueba es idéntica a la anterior.

Observación. Por muy tentador que sea pensar que la igualdad se da en el inciso 2 del problema anterior, esto es totalmente falso: $(S^{\bot})^{\bot}$ es un subespacio de $V$ (o de $V^\ast$), mientras que no hay razón para que $S$ lo sea, pues este es solamente un subconjunto arbitrario de $V$ (o $V^\ast$). Como vimos en una entrada anterior, la igualdad se da si $S$ es un subespacio de $V$ (o de $V^\ast$) cuando $V$ es un subespacio de dimensión finita.

Problemas resueltos de ecuaciones lineales y de hiperplanos

Veamos ahora problemas de ortogonalidad relacionados con encontrar expresiones para un subespacio en términos de ecuaciones lineales y de hiperplanos.

Problema 1. Sea $W$ el subespacio de $\mathbb{R}^4$ generado por los vectores

$v_1=(1,1,0,1)$
$v_2=(1,2,2,1).$

Encuentra ecuaciones lineales en $\mathbb{R}^4$ cuyo conjunto solución sea $W$.

Solución. Necesitamos encontrar una base para $W^{\bot}$.
Recordemos que $W^{\bot}$ consiste de todas las formas lineales

$l(x,y,z,t)=ax+by+cz+dt$

tales que $l(v_1)=l(v_2)=0$, es decir
\begin{align*}
a+b+d&=0\\
a+2b+2c+d&=0.
\end{align*}

La matriz asociada al sistema anterior es

$A=\begin{pmatrix}
1 & 1 & 0 & 1\\
1 & 2 & 2 & 1\end{pmatrix}$

y por medio de reducción gaussiana llegamos a que su forma reducida escalonada es

$A_{red}=\begin{pmatrix}
1 & 0 & -2 & 1\\
0 & 1 & 2 & 0\end{pmatrix}.$

De aquí, $c$ y $d$ son variables libres y $a$ y $b$ son variables pivote determinadas por
\begin{align*}a&=2c-d\\b&=-2c.\end{align*}

Por lo tanto,
\begin{align*}
l(x,y,z,t)&=(2c-d)x-2cy+cz+dt\\
&=c(2x-2y+z)+d(-x+t).
\end{align*}

Así, deducimos que una base para $W^{\bot}$ está dada por

$l_1(x,y,z,t)=2x-2y+z$ y $l_2(x,y,z,t)=-x+t$

y por consiguiente $W=\{v\in \mathbb{R}^4 : l_1(v)=l_2(v)=0\}$, de donde $$l_1(v)=0, l_2(v)=0$$ son ecuaciones cuyo conjunto solución es $W$.

$\triangle$

Problema 2. Considera el espacio vectorial $V=\mathbb{R}_3[x]$. Escribe el subespacio vectorial generado por $p(x)=1-2x^2$ y $q(x)=x+x^2-x^3$ como la intersección de dos hiperplanos linealmente independientes en $V$.

Solución. Sea $\mathcal{B}=\{1,x,x^2,x^3\}=\{e_1,e_2,e_3,e_4\}$ la base canónica de $V$.

Entonces

\begin{align*}
p(x)&=e_1-2e_3\\
q(x)&=e_2+e_3-e_4.
\end{align*}

Escribir $W=\text{span}(p(x),q(x))$ como intersección de dos hiperplanos es equivalente a encontrar dos ecuaciones que definan a $W$, digamos $l_1(v)=l_2(v)=0$ pues entonces $$W=H_1 \cap H_2,$$ donde $H_1=\ker(l_1)$ y $H_2=\ker(l_2)$.

Así que sólo necesitamos encontrar una base $l_1,l_2$ de $W^{\bot}$.

Recordemos que una forma lineal en $\mathbb{R}_3[x]$ es de la forma $$l_1(x_1e_1+x_2e_2+x_3e_3+x_4e_4)=ax_1+bx_2+cx_3+dx_4$$

para algunos $a,b,c,d \in \mathbb{R}$.

Esta forma lineal $l$ pertenece a $W^{\bot}$ si y sólo si $$l(p(x))=l(q(x))=0,$$ o bien

\begin{align*}
a-2c&=0\\
b+c-d&=0.
\end{align*}

Podemos fijar $c$ y $d$ libremente y despejar $a$ y $b$ como sigue:

\begin{align*}a&=2c\\b&=-c+d.\end{align*}

Por consiguiente

\begin{align*}
l(x_1e_1&+x_2e_2+x_3e_3+x_4e_4)\\
&=2cx_1+(-c+d)x_2+cx_3+dx_4\\
&=c2x_1-x_2+x_3)+d(x_2+x_4).
\end{align*}

Así deducimos que una base $l_1,l_2$ de $W^{\bot}$ está dada por

\begin{align*}
l_1(x_1e_1+x_2e_2+x_3e_3+x_4e_4)&=2x_1-x_2+x_3\\
l_2(x_1e_1+x_2e_2+x_3e_3+x_4e_4)&=x_2+x_4.
\end{align*}

y así $W=H_1\cap H_2$, donde

\begin{align*}
H_1&=\ker(l_1)=\{a+bx+cx^2+dx^3\in V : 2a-b+c=0\}\\
H_2&=\ker(l_2)=\{a+bx+cx^2+dx^3\in V : b+d=0\}.
\end{align*}


$\triangle$

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104721 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM»

Álgebra Lineal I: Ortogonalidad, hiperplanos y ecuaciones lineales

Por Leonardo Ignacio Martínez Sandoval

Deja un comentario

Introducción

En entradas anteriores hablamos de formas lineales, del espacio dual y de ortogonalidad. Con la teoría que hemos desarrollado en esas entradas, podemos cosechar uno de los hechos más importantes para espacios vectoriales de dimensión finita $n$: todos los subespacios se pueden obtener a partir de intersectar hiperplanos, es decir, subespacios de dimensión $n-1$. El objetivo de esta entrada es dar las definiciones necesarias para enunciar y demostrar este resultado formalmente.

Hiperplanos

Antes de demostrar el resultado mencionado en la introducción, tomaremos un poco de intuición geométrica de $\mathbb{R}^3$.

En $\mathbb{R}^3$ tenemos sólo un subespacio de dimensión $0$, que es $\{(0,0,0)\}$, un punto. Para obtener un subespacio de dimensión $1$, tenemos que tomar un vector $v\neq 0$ y considerar todos los vectores $rv$ con $r$ en $\mathbb{R}$. Esto corresponde geométricamente a una línea por el origen, con la misma dirección que $v$. En otras palabras, los subespacios de dimensión $1$ son líneas por el origen.

¿Quiénes son los subespacios de dimensión $2$? Debemos tomar dos vectores linealmente independientes $u$ y $v$ y considerar todas las combinaciones lineales $au+bv$ de ellos. Es más o menos fácil convencerse de que obtendremos al plano que pasa por $u$, $v$ y el $(0,0,0)$. Es decir, los subespacios de dimensión $2$ de $\mathbb{R}^3$ son planos por el origen.

Esto motiva la siguiente definición.

Definición 1. Sea $V$ un espacio vectorial de dimensión finita $n$. Un hiperplano de $V$ es un subespacio de dimensión $n-1$.

Ejemplo. El subespacio $U=\mathbb{R}_5[x]$ de $V=\mathbb{R}_6[x]$ es un hiperplano. Esto es ya que $U$ es de dimesión $6$ y $V$ es de dimensión $7$. Sin embargo, aunque $U$ también es un subespacio de $W=\mathbb{R}_7[x]$, no se cumple que $U$ sea hiperplano de $W$ pues $W$ es de dimensión $8$ y $6\neq 8-1$.

Las matrices simétricas de $M_2(\mathbb{R})$ forman un subespacio $S$ de dimensión $3$ de $M_2(\mathbb{R})$, pues son de la forma $\begin{pmatrix} a & b \\ b & c \end{pmatrix}$. De esta forma, $S$ es un hiperplano de $M_2(\mathbb{R})$. Sin embargo, el conjunto de matrices simétricas de $M_n(\mathbb{R})$ no es un hiperplano ni para $n=1$, ni para $n\geq 3$.

$\triangle$

Los hiperplanos nos pueden ayudar a obtener subespacios. De hecho, veremos que en el caso de dimensión finita nos ayudan a obtener a todos los subespacios. Para continuar construyendo la intuición, notemos que en $\mathbb{R}^3$ los hiperplanos son simplemente los planos por el origen y que:

  • Podemos obtener a cualquier plano por el origen como intersección de planos por el origen: simplemente lo tomamos a él mismo.
  • Podemos obtener a cualquier línea por el origen como la intersección de dos planos distintos por el origen que la contengan. Por ejemplo, el eje $z$ es la intersección de los planos $xz$ y $yz$. En otras palabras: todo subespacio de dimensión $1$ de $\mathbb{R}^3$ se puede obtener como la intersección de dos hiperplanos de $\mathbb{R}^3$.
  • A $\{0\}$ lo podemos expresar como la intersección de los planos $xy$, $yz$ y $xz$, osea, al único espacio de dimensión cero lo podemos expresar como intersección de $3$ hiperplanos.

Ya obtenida la intuición, lo que veremos a continuación es que el resultado anterior en realidad es un fenómeno que sucede en cualquier espacio vectorial de dimensión finita. Así, nos enfocaremos en entender las definiciones del siguiente teorema, y demostrarlo.

Teorema. Sea $V$ un espacio vectorial de dimensión finita $n$.

  • Todo subespacio $W$ de $V$ de dimensión $m$ es la intersección de $n-m$ hiperplanos de $V$ linealmente independientes.
  • Toda intersección de $n-m$ hiperplanos de $V$ linealmente independientes es un subespacio vectorial de dimensión $m$.

Los hiperplanos son subespacio y la definición de independencia lineal que tenemos es para vectores. Pero el teorema anterior habla de «hiperplanos linealmente independientes». ¿A qué se refiere esto? Como veremos más adelante, a cada hiperplano se le puede asignar de manera natural un elemento del espacio dual de $V$.

Recordatorio de espacio ortogonal

En la entrada anterior mostramos el siguiente resultado:

Teorema (teorema de dualidad). Sea $V$ un espacio vectorial de dimensión finita sobre $F$ y $W$ un subespacio de $V$ (o de $V^\ast)$. Entonces $$\dim W + \dim W^\bot = \dim V.$$

Además, obtuvimos como corolario lo siguiente:

Corolario. Si $V$ es un espacio vectorial de dimensión finita sobre un campo $F$ y $W$ un subespacio de $V$ (o de $V^\ast$), entonces $(W^\bot)^\bot=W$.

Usaremos estos resultados para dar una definición alternativa de hiperplanos, para entender a los subespacios de dimensión $n-1$ y para mostrar el teorema principal de esta entrada.

Subespacios de dimensión $n-1$ y definición alternativa de hiperplanos

Tomemos un espacio vectorial $V$ de dimensión finita $n$. Un caso especial, pero muy importante, del teorema de dualidad es cuando $W$ es un subespacio de $V^\ast$ de dimensión $1$, es decir, cuando $W$ está generado por una forma lineal $l\neq 0$. En este caso, $W^\bot$ es un subespacio de $V$ y por el teorema de dualidad, es de dimensión $n-1$.

De manera inversa, si $W$ es un subespacio de $V$ de dimensión $n-1$, por el teorema de dualidad tenemos que $W^\bot$ es de dimensión $1$, así que hay una forma lineal $l\neq 0$ que lo genera. Por el corolario, $W=(W^\bot)^\bot$, que en otras palabras quiere decir que $W=\{v\in V: l(v)=0\}.$ En resumen:

Proposición. Un subespacio $W$ de un espacio de dimensión finita $d$ tiene dimensión $d-1$ si y sólo si es el kernel de una forma lineal $l\neq 0$ de $V$.

Ejemplo 1. Considera la forma lineal $\text{ev}_0$ en el espacio vectorial $V=\mathbb{C}_n[x]$ de polinomios con coeficientes complejos y grado a lo más $n$. Los polinomios $p$ tales que $\text{ev}_0(p)=0$ son exactamente aquellos cuyo término libre es $0$. Este es un subespacio vectorial de $V$ de dimensión $n=\dim V – 1$, pues una base para él son los polinomios $x, x^2, \ldots, x^n$.

$\triangle$

Problema. Considera el espacio vectorial $V=M_{2,3}(\mathbb{R})$. Considera $W$ el subconjunto de matrices cuya suma de entradas en la primer columna es igual a la suma de entradas de la segunda columna. Muestra que $W$ es un subespacio de dimensión $5$ y escríbelo como el kernel de una forma lineal.

Solución. Mostrar que $W$ es un subespacio de $V$ es sencillo y se queda como tarea moral. Se tiene que $W$ no puede ser igual a todo $V$ pues, por ejemplo, la matriz $\begin{pmatrix} 1 & 0 & 0\\ 0 & 0 & 0 \end{pmatrix}$ no está en $W$, así que $\dim W\leq 5$.

Las matrices $\begin{pmatrix} 1 & 1 & 0\\ 0 & 0 & 0 \end{pmatrix}$, $\begin{pmatrix} 1 & 1 & 1\\ 0 & 0 & 0 \end{pmatrix}$, $\begin{pmatrix} 1 & 1 & 0\\ 0 & 0 & 1 \end{pmatrix}$, $\begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 0 \end{pmatrix}$, $\begin{pmatrix} 0 & 1 & 0\\ 1 & 0 & 0 \end{pmatrix}$ son linealmente independientes y están en $W$, así que $\dim W\geq 5$, y junto con el párrafo anterior concluimos que $\dim W = 5$.

Finalmente, tomemos la forma lineal $$l\begin{pmatrix} a & b & c\\ d& e& f\end{pmatrix}=a+d-b-e.$$ Tenemos que una matriz está en el kernel de $l$ si y sólo si $a+d-b-e=0$, si y sólo si $a+d=b+e$, es decir, si y sólo si las entradas de la primer columna tienen la misma suma que las de la segunda. Así, $W=\ker l$.

$\square$

La proposición anterior nos permite dar una definición alternativa de hiperplano y hablar de hiperplanos linealmente independientes.

Definición 2. Sea $V$ un espacio vectorial. Un hiperplano es el kernel de una forma lineal $l\neq 0$ en $V^\ast$. Una familia de hiperplanos es linealmente independiente si sus formas lineales correspondientes son linealmente independientes en $V^\ast$.

Observa además que la definición anterior también sirve para espacios vectoriales de dimensión infinita, pues nunca hace referencia a la dimensión que debe tener un hiperplano.

Ejemplo 2. El conjunto de funciones continuas $f$ en el intervalo $[0,1]$ tales que $$\int_0^1 f(x) \, dx = 0$$ son un subespacio $W$ de $\mathcal{C}[0,1]$. Este subespacio es un hiperplano pues es el kernel de la forma lineal $I$ tal que $$I(f)=\int_0^1 f(x)\, dx.$$

$\square$

No mencionaremos más de espacios de dimensión infinita en esta entrada.

Escribiendo subespacios como intersección de hiperplanos

Ya podemos entender el teorema principal de esta entrada y demostrarlo. Lo enunciamos nuevamente por conveniencia.

Teorema 2. Sea $V$ un espacio vectorial de dimensión finita $n$.

  • Todo subespacio $W$ de $V$ de dimensión $m$ es la intersección de $n-m$ hiperplanos de $V$ linealmente independientes.
  • Toda intersección de $n-m$ hiperplanos de $V$ linealmente independientes es un subespacio vectorial de dimensión $m$.

Demostración. Tomemos un espacio vectorial $V$ de dimensión finita $n$ y un subespacio $W$ de dimensión $m$. Por el teorema de dualidad, la dimensión de $\dim W^\bot$ es $n-m$. Tomemos una base $B=\{l_1,l_2,\ldots,l_{n-m}\}$ de $W^\bot$. Por el corolario al teorema de dualidad, podemos expresar a $W$ como $$W=(W^\bot)^\bot=\{v\in V: l_1(v)=\ldots=l_{n-m}(v)=0\}.$$

Si definimos $L_i=\{v\in V: l_i(v)=0\}$, por la proposición de la sección anterior tenemos que cada $L_i$ es un hiperplano de $V$. Además, $$W=L_1\cap \ldots\cap L_{n-m}.$$ Como los $l_i$ son linealmente independientes, con esto logramos expresar a $W$ como intersección de $n-m$ hiperplanos linealmente independientes.

Probemos ahora la segunda parte de la proposición. Tomemos el conjunto $S=\{l_1,\ldots,l_{n-m}\}$ de formas linealmente independientes que definen a los hiperplanos. Un vector $v$ está en la intersección de todos estos hiperplanos si y sólo si $l_1(v)=\ldots=l_{n-m}(v)=0$, si y sólo si está en $S^\bot=\text{span}(S)^\bot$. Es decir, la intersección de los hiperplanos es precisamente el subespacio $\text{span}(S)^\bot$. Como $S$ es linealmente independiente, tenemos que $ \text{span}(S)$ es de dimensión $n-m$, de modo que por el teorema de dualidad, $\dim \text{span}(S)^\bot = n-(n-m)=m$. Esto muestra lo que queremos.

$\square$

Algunos problemas prácticos

Si tenemos un espacio $V$ de dimensión finita $n$, un subespacio $W$ de dimensión finita $m$ y queremos encontrar de manera práctica la expresión de $W$ como intersección de hiperplanos de $V$, podemos hacer el siguiente procedimiento:

  • Determinamos una base $l_1,\ldots,l_{n-m}$ para $W^\bot$ (la cual consiste de formas lineales de $V^\ast$). Esto lo podemos hacer con los pasos que mencionamos en la entrada anterior.
  • Definimos $L_i=\{v\in V: l_i(v)=0\}$.
  • Tendremos que $W$ es la intersección de los $L_i$.

Una última observación es que cada $L_i$ está definido por una ecuación lineal. Esto nos permite poner a cualquier subespacio como el conjunto solución a un sistema lineal. Esto lo cual podemos ver de forma práctica de la siguiente manera:

  • Tomamos una base $e_1,\ldots,e_n$ de $V$.
  • Tomemos un vector $v=a_1e_1+\ldots+a_ne_n$ que queremos determinar si está en $W$. Para ello, debe estar en cada $L_i$.
  • Cada $L_i$ está definido mediante la ecuación $l_i(v)=0$ de modo que si $v$ está en $L_i$ sus coordenadas $a_1,\ldots,a_n$ en la base $e_1,\ldots,e_n$ deben satisfacer la ecuación lineal $$l_i(e_1)a_1+\ldots+l_i(e_n)a_n=0.$$
  • De esta forma, los vectores $v$ en $W$ son aquellos cuyas coordenadas en la base $e_1,\ldots, e_n$ satisfacen el sistema de ecuaciones obtenido de las ecuaciones lineales para cada $i$ del punto anterior.

Veremos algunos ejemplos de estos procedimientos en la siguiente entrada.

La receta anterior nos permite concluir la siguiente variante del teorema de esta entrada, escrito en términos de ecuaciones lineales.

Teorema. Sea $V$ un espacio vectorial de dimensión finita $n$ y $B$ una base de $V$.

  • Un subespacio $W$ de dimensión $m$ se puede definir mediante un sistema de ecuaciones lineales independientes que deben satisfacer las coordenadas de los vectores de $W$ escritos en la base $B$.
  • Aquellos vectores cuyas coordenadas en la base $B$ satisfacen un sistema de ecuaciones lineales independientes homogéneo, forman un subespacio de $V$ de dimensión $n-m$.

La moraleja de esta entrada es que podemos pensar que los sistemas de ecuaciones, las intersecciones de hiperplanos y los subespacios de un espacio vectorial de dimensión finita son «prácticamente lo mismo».

Más adelante…

A lo largo de esta entrada enunciamos las definiciones necesarias para llegar al teorema que mencionamos al inicio: para un espacio vectorial de dimension finita $n$, todos los subespacios se pueden obtener a partir de intersectar hiperplanos, es decir, subespacios de dimensión $n-1$.

En la siguiente entrada utilizaremos este resultado para resolver algunos ejercicios y veremos en acción este importante teorema.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  • Considera el plano $P$ en $\mathbb{R}^3$ que pasa por el origen y por los vectores $(1,1,1)$, $(0,2,0)$. Encuentra reales $a,b,c$ tales que $$P=\{(x,y,z): ax+by+cz = 0 \}.$$
  • En todos los ejemplos en los que se menciona que algo es subespacio, verifica que en efecto lo sea. En los que se menciona que un conjunto es base, también verifica esto.
  • Encuentra una base para el espacio de polinomios $p$ en $M_n(\mathbb{C})$ tales que $\text{ev}(1)(p)=0$.
  • Sea $W$ el subconjunto de matrices de $V:=M_n(\mathbb{R})$ tal que la sumas de las entradas de todas las filas son iguales. Muestra que $W$ es un subespacio de $V$. Determina la dimensión de $W$ y exprésalo como intersección de hiperplanos linealmente independientes.
  • ¿Qué sucede cuando intersectas hiperplanos que no corresponden a formas linealmente independientes? Más concretamente, supongamos que tienes formas lineales $l_1,\ldots,l_m$ de $F^n$. Toma $B=\{e_1,\ldots,e_n\}$ la base canónica de $F^n$. Considera la matriz $A=[l_i(e_j)]$. ¿Qué puedes decir de la dimensión de la intersección de los hiperplanos correspondientes a los $l_i$ en términos del rango de la matriz $A$?

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104721 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM»