Introducción

Como última entradaen esta parte de geometría, hablaremos de algunos temas de geometría discreta. Esta área de las matemáticas se dedica a estudiar propiedades combinatorias de familias de objetos geométricos. Estos objetos pueden ser puntos, rectas, rectángulos, convexos, politopos, etc. Las relaciones que nos interesan son que formen un tipo de acomodo especial, que se intersecten, que podamos contar ciertas configuraciones, etc.

Sólo hablaremos superficialmente de un área que es profunda y bastante interesante. Un libro genial que cubre varios temas de geometría discreta de manera sistemática es Lectures on Discrete Geometry de Jiří Matoušek.

Convexos y el teorema de Helly

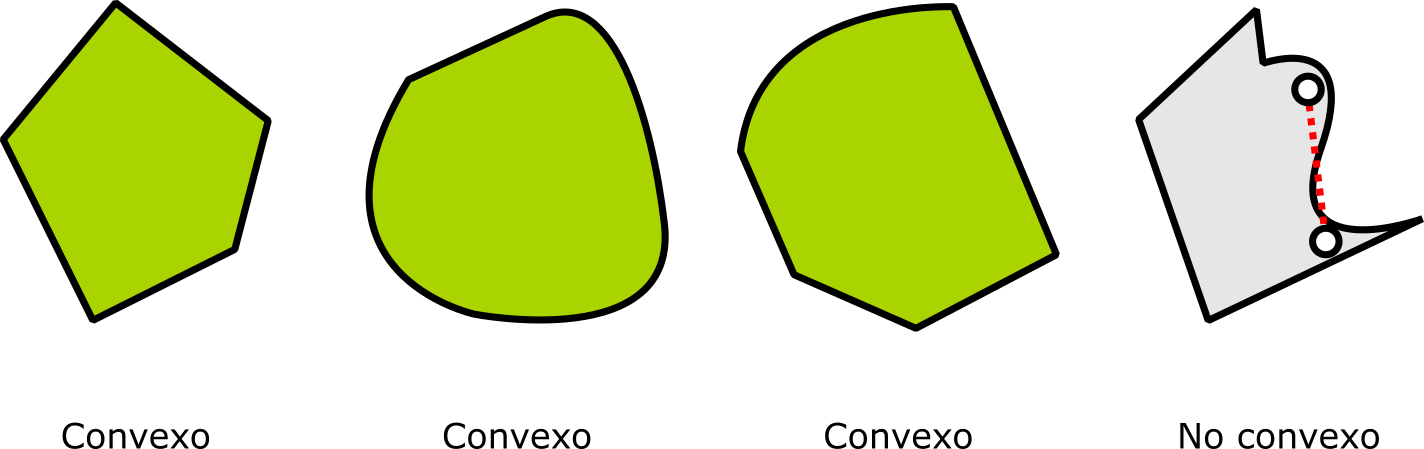
Un convexo de $\mathbb{R}^d$ es un conjunto tal que cualquier segmento recto definido por dos de sus puntos queda totalmente contenido en el conjunto. Por ejemplo, los convexos de $\mathbb{R}$ son los intervalos, mientras que en el plano hay muchos más ejemplos, como lo muestra la figura.

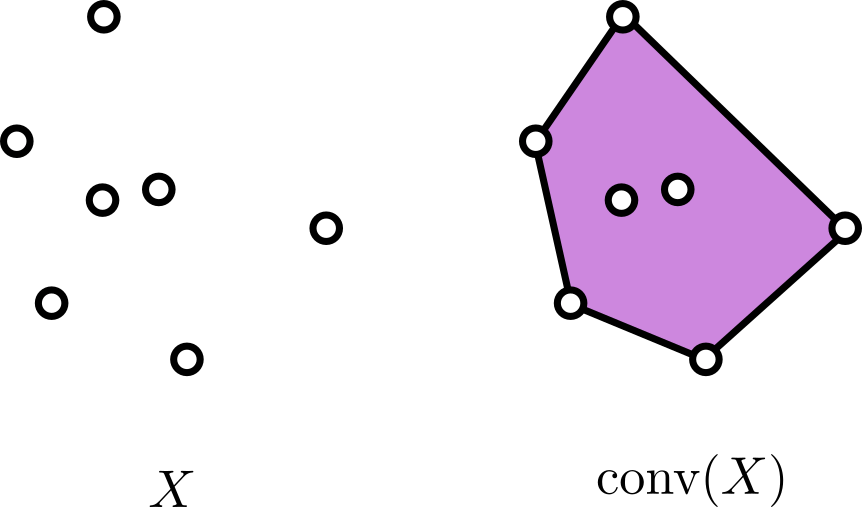
Si tenemos un conjunto $X$ de $\mathbb{R}^d$, su envolvente convexa es el conjunto convexo más pequeño (por contención), que contiene a $X$. Cuando $X$ es un conjunto de puntos, tenemos algo como lo de la figura. Si todos los puntos de $X$ están sobre la frontera de su envolvente convexa, y no hay tres alineados, decimos que $X$ son puntos en posición convexa.

Los conjuntos convexos son especiales en muchos sentidos. Uno de ellos es que la intersección de una familia de convexos se puede detectar “localmente”.

Problema. A una plática de matemáticas de una hora asistieron una cantidad finita de matemáticos. La plática estaba tan aburrida, que cada matemático se durmió en cierto intervalo de tiempo de esa hora, pero sólo una vez. A la hora del café, los matemáticos platicaron entre sí, y si se dieron cuenta de que para cualesquiera dos de ellos, $I$ y $J$, hubo un momento en el que $I$ y $J$ estuvieron dormidos simultáneamente. Muestra que hubo un momento de la plática en la que todos los matemáticos estuvieron dormidos.

Sugerencia pre-solución. Hay muchas soluciones. Una es mediante un argumento de maximalidad.

Solución. En términos matemáticos, queremos ver que si tenemos una cantidad finita de intervalos acotados y cerrados en la recta real que se intersectan de dos en dos, entonces todos ellos se intersectan.

Tomemos el intervalo $I$ cuyo extremo derecho sea mínimo. Llamemos $x$ a este extremo derecho. Afirmamos que cualquier otro intervalo tiene a $x$. Sea $J$ cualquiera de estos intervalos, con extremo izquierdo $y$ y extremo derecho $z$.

Por la minimalidad de $x$, tenemos que $x\leq z$. Si $y>x$, entonces $J$ no intersecta a $I$ y se contradice la hipótesis. Entonces, para que $J$ pueda intersectar a $I$, necesitamos que $y \leq x$. Pero entonces $x$ queda entre los extremos del intervalo $J$ y por lo tanto $x$ está en $J$. Esto termina la prueba.

$\square$

En dimensiones más altas, tenemos el siguiente resultado.

Teorema (Helly). Sea $\mathcal{F}$ una familia finita de al menos $d+1$ conjuntos convexos compactos en $\mathbb{R}^d$. Si cada subfamilia de $\mathcal{F}$ de $d+1$ convexos tiene intersección no vacía, entonces $\mathcal{F}$ tiene intersección no vacía.

El teorema de Helly es una de las piedras angulares de la geometría discreta. Una cantidad de enorme de investigación ha resultado de considerar variantes del teorema con hipótesis más débiles o más fuertes.

Politopos y la fórmula de Euler

Otra área muy rica de la geometría discreta es la teoría de politopos. Un politopo es la generalización a altas dimensiones de un polígono, o de un poliedro. Hay dos formas de definir politopos. Una es tomar puntos en $\mathbb{R}^d$ y considerar su envolvente convexa. Esto es un $V$-politopo. Para la otra necesitamos algunas definiciones adicionales.

Un subespacio afín de $\mathbb{R}^d$ es la traslación de un subespacio lineal, y su dimensión es la dimensión del subespacio lineal trasladado. Por ejemplo, cualquier punto de $\mathbb{R}^d$ es un subespacio afín de dimensión $0$ pues es la traslación del subespacio trivial $\{0\}$. Las rectas en $\mathbb{R}^d$, incluso aquellas que no pasan por el $0$, son subespacios afines de dimensión $0$. A los subespacios afines de dimensión $n-1$ les llamamos hiperplanos. Así, las líneas son los hiperplanos de $\mathbb{R}^2$, los planos los hiperplanos de $\mathbb{R}^3$, etc.

Si $P$ es un hiperplano de $\mathbb{R}^d$, un semiespacio definido por $P$ es todo lo que queda en uno de los lados de $P$. Si es abierto, no incluye a $P$, y si es cerrado, sí incluye a $P$. Un hiperplano siempre define dos semiespacios abiertos, y dos cerrados.

Hay otra forma de pensar a los politopos: tomamos una cantidad finita de semiespacios cerrados y los intersectamos. Si esa intersección está acotada, entonces a lo que obtenemos le llamamos un $H$-politopo. Piensa, por ejemplo, en los hiperplanos que determinan las caras de un cubo, y en los semiespacios “hacia adentro”.

Un resultado clásico es que todo $H$-politopo es un $V$-politopo, así que podemos usar la descripción que nos convenga de acuerdo al problema que estemos resolviendo.

Un hiperplano $H$ es hiperplano soporte de un politopo $P$ si el politopo se queda totalmente contenido en alguno de los semiespacios definidos por $H$. Una cara de $P$ es la intersección de $P$ con alguno de sus hiperplanos soporte. Resulta que las caras de politopos son politopos. Para que todo funcione bien, debemos considerar al vacío como un politopo.

La dimensión de un politopo es la menor dimensión de un subespacio afín que lo contiene. Por definición, la dimensión del vacío es $-1$. Si una cara de un politopo es $k$, entonces la llamamos una $k$-cara. Los valores de $k$ sólo pueden ir de $0$ a $d$. A las $0$-caras les llamamos los vértices de $P$. A las $1$-caras les llamamos las aristas.

Para cada $k$ de $0$ a $n$, usamos $f_k$ para denotar la cantidad de $k$ caras del politopo, y a $$(f_0,f_1,f_2,\ldots,f_d)$$ le llamamos el $f$-vector del politopo. Estamos listos para enunciar un resultado crucial en la teoría de politopos.

Teorema (fórmula de Euler). Sea $P$ un politopo de dimensión $d$ en $\mathbb{R}^d$. Entonces

$$f_0-f_1+f_2-\ldots + (-1)^d f_d = 1.$$

Observa que $f_d$ siempre es $1$ pues la única $d$ cara de un politopo $P$ de dimensión $d$ es $P$ mismo.

En $\mathbb{R}^2$ esta fórmula no es tan útil, pues simplemente nos dice que si un polígono tiene $V$ vértices y $A$ aristas, entonces $V-A=0$, es decir, que tiene la misma cantidad de vértices y aristas, lo cual es inmediato.

En $\mathbb{R}^3$ la fórmula nos dice que si un poliedros tiene $V$ vértices, $A$ aristas y $F$ caras, entonces $$V-A+F=2.$$ Este fórmula se puede usar en varios problemas matemáticos de poliedros.

Problema. Muestra que el tetraedro, el cubo, el octaedro, el dodecaedro y el icosaedro son los únicos poliedros en $\mathbb{R}^3$ tales que a cada vértice una misma cantidad $a$ de caras, y cada cara consiste de la misma cantidad $b$ de vértices.

Sugerencia pre-solución. Usa notación adecuada, poniendo la cantidad de vértices, aristas y caras en términos de $a$ y $b$. Usa la fórmula de Euler. Luego, da un argumento de desigualdades.

Solución. A cada vértice llegan por lo menos $3$ caras, y cada cara tiene por lo menos $3$ vértices. Así, $a\geq 3$ y $b\geq 3$.

Si hay $A$ aristas, entonces tanto $2A$ como $bF$ cuentan la cantidad de parejas $(e,c)$ donde $e$ es una arista y $c$ una cara que lo tiene. Esto se debe a que cada arista está exactamente en dos caras, y a que como cada cara tiene $b$ vértices, entonces tiene $b$ aristas. Por lo tanto, $2A=bF$, de donde $$A=\frac{bF}{2}.$$

De manera similar, si hay $V$ vértices y $F$ caras, entonces tanto $aV$ como $bF$ cuentan la cantidad de parejas $(v,c)$, donde $v$ es un vértice y $c$ es una cara que lo tiene. De esta forma, $aV=bF$, de lo cual $$V=\frac{bF}{a}.$$

Por la fórmula de Euler, tenemos entonces que $$\frac{bF}{a}-\frac{bF}{2}+F = 2.$$ Esta igualdad implica, en particular, que al determinar los valores de $a$ y $b$, se determinan $F$ y entonces $V$ y $A$.

Si multiplicamos por $\frac{2}{bF}$ de ambos lados, y sumamos $1$ de ambos lados, tenemos que \begin{equation}
\frac{2}{a}+\frac{2}{b}= \frac{4}{bF}+1 > 1.
\end{equation}

Como $a\geq 3$, entonces $\frac{2}{a}\leq \frac{2}{3}$. De este modo,
\begin{align*}
\frac{2}{b}&> 1 – \frac{2}{a}\\
&\geq 1-\frac{2}{3} \\
&= \frac{1}{3}.
\end{align*}

Esto muestra que $b<6$, de modo que $b\leq 5$. Por simetría, $a\leq 5$. Podemos entonces simplemente estudiar los casos $a=2,3,4$ y $b=2,3,4$.

Si $a=5$, entonces la desigualdad (1) se cumple sólo si $b=3$. Si $a=4$, la desigualdad (1) se cumple sólo si $b=3$. Finalmente, si $a=3$, la desigualdad se cumple para $b=3,4,5$. De este modo, las únicas parejas de $(a,b)$ que sirven son:

• $(3,3)$, que nos da el tetraedro.
• $(3,4)$, que nos da el cubo.
• $(4,3)$, que nos da el octaedro.
• $(3,5)$, que nos da el dodecaedro.
• $(5,3)$, que nos da el icosaedro.

$\square$

La fórmula de Euler es sólo una de las relaciones lineales que satisfacen las entradas del $f$-vector de un politopo. Otros dos resultados interesantes del área son:

• Las relaciones de Dehn-Sommerville, que dan otras relaciones lineales que satisfacen las entradas del $f$-vector.
• El teorema de la cota superior que para $d$, $n$ y $k$ fijas acota el número de $k$-caras que puede tener un politopo de dimensión $d$ con $n$-vértices.

Un libro canónico para aprender de politopos de manera sistemática es el Lectures on Polytopes de Günter M. Ziegler.

Conjuntos de puntos y teoremas extremales

La última área de la que hablaremos serán los problemas extremales en geometría discreta. Nos enfocaremos únicamente en problemas sobre conjuntos de puntos, pero se podrían hacer preguntas análogas para otras familias de objetos geométricos. De manera informal, pero intuitiva, un problema extremal de geometría consiste en mostrar que si un número es suficientemente grande, entonces empiezan a pasar cosas interesantes con ciertos objetos geométricos.

Uno de los resultados clásicos es el teorema de Erdős-Szekeres. A grandes rasgos, lo que dice es que si tenemos muchos puntos en posición general en el plano (no hay tres colineales), entonces siempre es posible encontrar un subconjunto grande de ellos que está en posición convexa.

Teorema (Erdős-Szekeres). Sea $n$ un entero positivo. Entonces, existe un entero $f(n)$ tal que si se tiene un conjunto $S$ con $f(n)$ o más puntos en el plano en posición general, entonces hay un subconjunto de tamaño $n$ de $S$ que consiste de puntos en posición convexa.

Típicamente, es bastante difícil encontrar los valores exactos de las funciones involucradas en problemas extremales de geometría discreta. El tipo de resultados de interés para la investigación matemática es encontrar las mejores “cotas asintóticas”, que digan, más o menos, cómo se comporta la función que se está estudiando. En el caso del teorema de Erdős-Szekeres, las mejores cotas se enuncian así:

$$1+2^{n-2}\leq f(n) \leq 2^{n+o(n)}.$$

La notación $h(n)=o(g(n))$ quiere decir que $\frac{h(n)}{g(n)}\to 0$ cuando $n\to \infty$.

Aunque sea difícil determinar los valores exactos de $f(n)$ para toda $n$, hay algunos valores pequeños que sí se pueden determinar.

Problema. Demuestra que $f(4)=5$, es decir:

• Que hay conjuntos de $4$ puntos en posición general en el plano que no tienen subconjuntos de tamaño $4$ en posición convexa.
• Que cualquier subconjunto de $5$ puntos en posición general en el plano tiene un subconjunto de $4$ puntos en posición convexa.

Sugerencia pre-solución. Encontrar el ejemplo para el primer punto es fácil, simplemente explora el problema haciendo varias figuras. Divide el problema en casos de acuerdo a la cantidad de puntos que forman la envolvente convexa. Para uno de los casos, usa el principio de las casillas.

Solución. El siguiente ejemplo son $4$ puntos que no están en posición convexa, y que por lo tanto no tienen subconjuntos de tamaño $4$ en posición convexa.

Mostraremos ahora que $5$ puntos en posición general en el plano siempre tienen un subconjunto de tamaño $4$ en posición convexa. Procedemos por casos de acuerdo a la cantidad de puntos que están en la frontera de la envolvente convexa. Si son $4$ ó $5$, entonces inmediatamente entre ellos hay $4$ en posición convexa.

Si son $3$, entonces llamemos $A$, $B$, $C$ a esos puntos y $D$ y $E$ a los otros dos, que quedan dentro de $\triangle ABC$. La recta $DE$ divide al plano en dos semiplanos. Por principio de las casillas, hay dos puntos de entre $A$, $B$ y $C$ que yacen en el mismo semiplano, digamos $A$ y $B$.

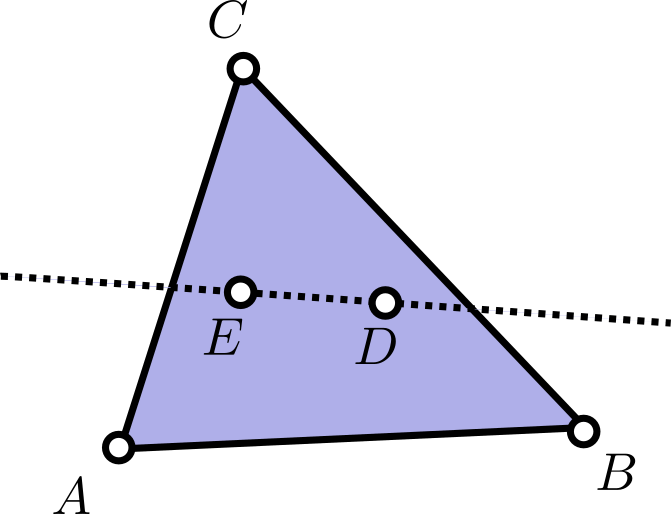
Como la recta $DE$ no corta al segmento $AB$ (por estar $D$ y $E$ en el mismo semiplano), y la recta $AB$ no corta al segmento $DE$ (por ser $AB$ un lado de la envolvente convexa), entonces los puntos $A$, $B$, $D$, $E$ están en posición convexa.

$\square$

Finalmente, presentamos un par de resultados más. También son problemas extremales, pero en vez de hablar de envolventes convexas, hablan acerca de distancias.

Si lo piensas un poco, es imposible colocar $4$ puntos distintos en el plano de modo que todas las parejas estén a distancia uno. Si tienes $n$ puntos en el plano, entonces ellos definen $\binom{n}{2}=\frac{n(n-1)}{2}\approx \frac{n^2}{2}$ parejas de puntos. ¿Cuántos de ellos pueden estar a distancia $1$? Estudiar esta cantidad es un problema que fue propuesto por Paul Erdős. Si $u(n)$ denota este máximo, las mejores cotas que hay para el problema son $$n^{1+d/\log \log n} \leq f(n) \leq O(n^{4/3}).$$

Aquí $d$ es una constante que sirve para toda $n$. La notación $h(n)\leq O(g(n))$ se refiere a que existe una constante $c$ tal que $h(n)\leq cg(n)$ para $n$ suficientemente grande.

Por supuesto, la distancia $1$ no tiene nada de especial. En realidad, ninguna distancia puede repetirse demasiado. Ya que ninguna distancia aparece muchas veces, la intuición (por principio de las casillas), nos debe decir que entonces para un conjunto de puntos, sus parejas deben definir muchas distancias diferentes. Llamemos $d(n)$ a la cantidad de distancias diferentes que define un conjunto de $n$ puntos en el plano. Erdős también preguntó, ¿cómo se comporta este número?. Las mejores cotas son $$\Omega\left(\frac{n}{\log }\right)\leq d(n) \leq O\left(\frac{n}{\sqrt{\log n}}\right).$$

La notación $h(n)\geq\Omega(g(n))$ se refiere a que existe una constante $c$ tal que $h(n)\geq cg(n)$ para $n$ suficientemente grande.

El problema de las distancias unitarias y el problema de las distancias diferentes han estimulado mucha de la investigación en geometría discreta. Las demostraciones de sus cotas, han introducido al área varias técnicas de teoría de números, del método probabilista y de geometría algebraica.

Un libro con mucho material de problemas extremales y otros temas es Combinatorial Geometry and its Algorithmic Applications de Janos Pach y Micha Sharir.

Más problemas

En resumen, en los siguientes libros hay bastante material para aprender los temas de esta entrada:

• Lectures on Discrete Geometry de Jiří Matoušek
• Lectures on Polytopes de Günter M. Ziegler
• Combinatorial Geometry and its Algorithmic Applications de Janos Pach y Micha Sharir