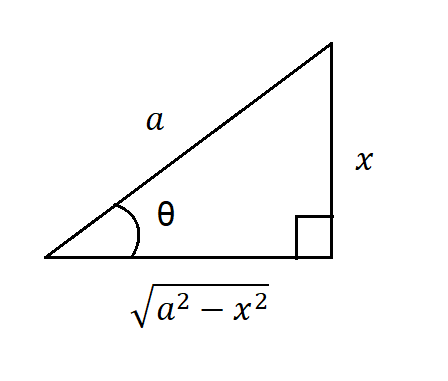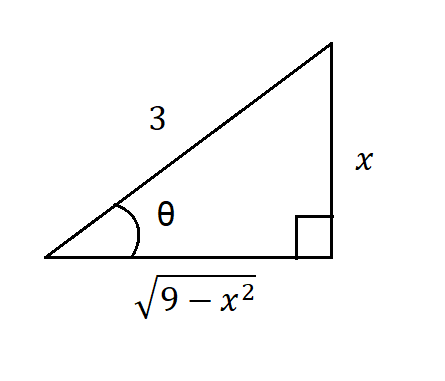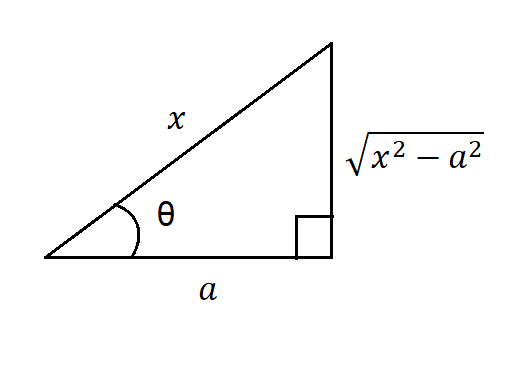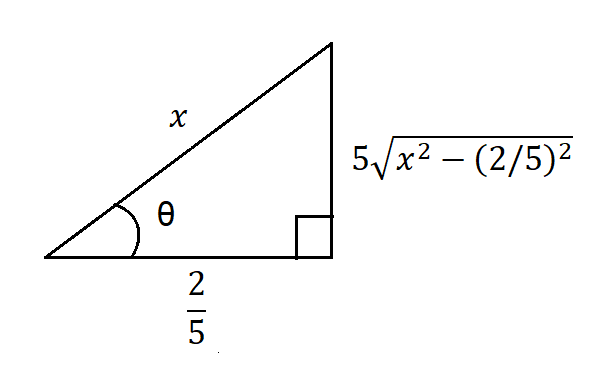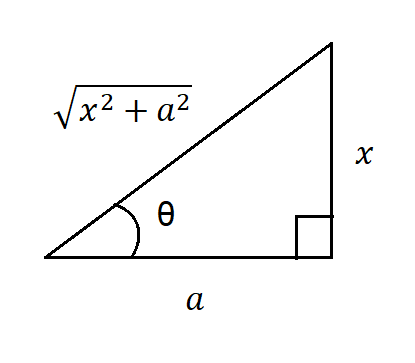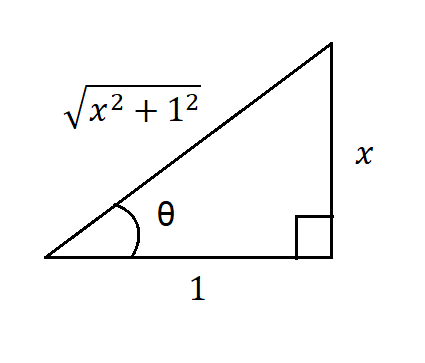Introducción
En las últimas dos secciones anteriores vimos integrales trigonométricas que contiene producto de potencias de las funciones trigonométricas básicas, en esta sección veremos integrales que se resuelven con sustituciones utilizando las funciones trigonométricas, veamos como.
Método de sustitución trigonométrica
El método de sustitución trigonométrica consiste en resolver integrales que contienen términos de la forma:
- $$\sqrt{a^{2}-x^{2}}$$
- $$\sqrt{x^{2}-a^{2}}$$
- $$\sqrt{x^{2}+a^{2}}$$
Para hacer estas sustituciones con las funciones trigonométricas básicas se debe ver cada caso según corresponda.
Caso 1: Integrales de la forma: $\sqrt{a^{2}-x^{2}}$
Podemos auxiliarnos con un triángulo rectángulo como vemos en la figura $(1)$, y recordar un poco de trigonometría básica, recordemos que en un triángulo rectángulo:
$$\sin(\theta)=\frac{Cateto \space opuesto}{Hipotenusa}=\frac{x}{a}\Rightarrow a \cdot \sin\theta=x $$
Podemos hacer la sustitución:
$$x=a \cdot \sin(\theta) \tag{1}$$
Por otro lado:
$$\cos(\theta)=\frac{Cateto \space adyacente}{Hipotenusa}=\frac{\sqrt{a^{2}-x^{2}}}{a} \Rightarrow \sqrt{a^{2}-x^{2}}=a \cdot \cos(\theta) \tag{2}$$
Estas son las sustituciones que debemos de hacer para integrales del tipo $\sqrt{a^{2}-x^{2}}$, en este punto talvez pueda ser un poco confuso de utilizarlas, así que veamos el ejemplo siguiente.
- $\int \frac{dx}{x^{2}\sqrt{9-x^{2}}}$
Vemos que lo que está adentro de la raíz es similar al del caso $(1)$, por lo que podemos hacer la siguiente figura:
De la figura $(2)$ y de la relación $(1)$, podemos escribir:
$$\frac{x}{3}=\sin(\theta) \Rightarrow x=3\sin(\theta) \Rightarrow dx=3\cos(\theta)d\theta$$
Elevamos al cuadrado la variable $x$ como:
$$x^{2}=9\sin^{2}(\theta)$$
Por otro lado, utilizando la relación $(2)$ tenemos que:
$$\frac{\sqrt{9-x^{2}}}{3}=\cos(\theta) \Rightarrow \sqrt{9-x^{2}}=3\cos(\theta)$$
Así sustituimos estas variables en la integral obteniendo lo siguiente:
$$\int \frac{dx}{x^{2}\sqrt{9-x^{2}}}=\int \frac{3\cos(\theta)d\theta}{9\sin^{2}(\theta)3\cos(\theta)}=\frac{1}{9}\int \frac{1}{\sin^{2}(\theta)}d\theta=\frac{1}{9}\int csc^{2}(\theta)d\theta$$
La resolución de esta integral se utiliza los métodos de integrales trigonométricas vistos en esta entrada, por lo que:
$$\frac{1}{9}\int \csc^{2}(\theta)d\theta=\frac{1}{9}(-\cot(\theta))+C$$
Volvemos a la variable original $x$, reescribimos a la función cotangente como: $$\cot(\theta)=\frac{\cos(\theta)}{\sin(\theta)}$$
Con los cambios de variable que hicimos, tenemos que:
$$\cot(\theta)=\frac{\cos(\theta)}{\sin(\theta)}=\frac{\frac{\sqrt{9-x^{2}}}{3}}{\frac{x}{3}}=\frac{{\sqrt{9-x^{2}}}}{{x}}$$
Así la resolución de la integral es:
$$\int \frac{dx}{x^{2}\sqrt{9-x^{2}}}= -\frac{1}{9}\frac{{\sqrt{9-x^{2}}}}{{x}}+C$$
Caso 2: Integrales de la forma $\sqrt{x^{2}-a^{2}}$
Análogamente, nos auxiliamos de un triángulo rectángulo como vemos en la figura $(3)$, recordamos que:
$$\sec(\theta)=\frac{1}{\cos(\theta)}=\frac{Hipotenusa}{Cateto \space adyacente}=\frac{x}{a} $$
Podemos hacer la sustitución:
$$x=a \cdot \sec(\theta) \tag{3}$$
Por otro lado:
$$\tan(\theta)=\frac{Cateto \space opuesto}{Cateto \space adyacente}=\frac{\sqrt{x^{2}-a^{2}}}{a} \Rightarrow \sqrt{x^{2}-a^{2}}=a \cdot \tan(\theta) \tag{4}$$
Por lo que estas son las sustituciones que debemos hacer en este caso, veamos un ejemplo.
- $\int \frac{dx}{\sqrt{25x^{2}-4}}$
Nos fijamos en el radicando y notamos que es similar al caso $(2)$, pero vemos que tenemos un problema con el número que va multiplicando $x^{2}$, ya que se quiere que sea de la forma: $\sqrt{x^{2}-a^{2}}$, por lo que podemos rescribir el radical como sigue: $$\sqrt{25x^{2}-4}=\sqrt{25(x^{2}-\frac{4}{25}})=5\sqrt{x^{2}-\left (\frac{2}{5} \right )^{2}} \tag{5}$$.
Así podemos hacer la siguiente figura:
De la figura $(4)$ y de la relación $(3)$, hacemos la sustitución:
$$x=\frac{2}{5}\sec(\theta) \Rightarrow dx=\frac{2}{5}\sec(\theta)\tan(\theta)d\theta$$
Por otro lado, utilizando la relación $(4)$, tenemos que:
$$\frac{\sqrt{x^{2}-(\frac{2}{5})^{2}}}{\frac{2}{5}}=\tan(\theta) \Rightarrow \sqrt{x^{2}-\left ( \frac{2}{5} \right )^{2}}=\frac{2}{5}\tan(\theta)$$
Sustituyendo en la integral tenemos que:
$$\int \frac{dx}{\sqrt{25x^{2}-4}}=\int \frac{\frac{2}{5}\sec(\theta)\tan(\theta)}{5(\frac{2}{5}\tan(\theta))}d\theta=\frac{1}{5}\int \sec(\theta )d\theta$$
Recordemos que el 5 que está multiplicando en el divisor viene de la relación $(5)$.
Sabemos que la solución de esta integral está dada como:
$$\int \sec(\theta )d\theta = ln|\sec(\theta)+\tan(\theta )|+C$$
Por lo que:
$$\frac{1}{5}\int \sec(\theta )d\theta=\frac{1}{5}ln|\sec(\theta)+\tan(\theta )|+C$$
Volviendo a la variable original $x$, el resultado de la integral es:
$$\int \frac{dx}{\sqrt{25x^{2}-4}}=\frac{1}{5}ln\bigg|\frac{5x}{2}+\frac{5\sqrt{x^{2}-\left (\frac{2}{5} \right )^{2}}}{2}\bigg|+C$$
Caso 3: Integrales de la forma $\sqrt{x^{2}+a^{2}}$
Análogamente, nos auxiliamos de un triángulo rectángulo, como se muestra en la figura $(5)$, sabemos que: $$\tan(\theta)=\frac{Cateto \space opuesto}{Cateto \space adyacente}=\frac{x}{a}$$
Podemos hacer la sustitución:
$$x=a \cdot \tan(\theta) \tag{6}$$
Por otro lado:
$$\sec(\theta)=\frac{1}{\cos(\theta)}=\frac{Hipotenusa}{Cateto \space adyacente}=\frac{\sqrt{x^{2}+a^{2}}}{a} \Rightarrow \sqrt{x^{2}+a^{2}}=a \cdot \sec(\theta) \tag{7}$$
Veamos el siguiente ejemplo para ejemplar este caso.
- $\int \frac{dx}{(x^{2}+1)^{\frac{3}{2}}}$
Podemos expresar el integrando de la siguiente forma:
$$\int \frac{dx}{(x^{2}+1)^{\frac{3}{2}}}=\int \frac{dx}{(\sqrt{x^{2}+1})^{3}}$$
Vemos que es igual al caso $(3)$, por lo que nos ayudamos de la figura $(6)$ y utilizando la relación $(6)$, tenemos que:
$$\frac{x}{1}=\tan(\theta) \Rightarrow dx=\sec^{2}(\theta)d\theta$$
Por otro lado, utilizando la relación $(7)$, se tiene que:
$$\frac{\sqrt{x^{2}+1}}{1}=\sec(\theta) \Rightarrow (\sqrt{x^{2}+1})^{3} =\sqrt[3]{x^{2}+1}=\sec^{3}(\theta)$$
Sustituyendo en la integral tenemos que:
$$\int \frac{dx}{(x^{2}+1)^{\frac{3}{2}}}=\int \frac{\sec^{2}(\theta )d\theta}{\sec^{3}(\theta )}=\int \frac{1}{\sec(\theta )}d\theta=\int \cos(\theta)d\theta=\sin\theta+C$$
Para regresar a la variable $x$ volvemos a auxiliarnos de la figura $(6)$, recordemos que:
$$\sin(\theta)=\frac{Cateto \space opuesto}{Hipotenusa}=\frac{x}{\sqrt{x^{2}+1}}$$
Así:
$$\int \frac{dx}{(x^{2}+1)^{\frac{3}{2}}}=\frac{x}{\sqrt{x^{2}+1}}+C$$
Tarea moral
Los siguientes ejercicios no son para evaluación, pero son ejercicios para que practiques lo aprendido que te ayudaran en el desarrollo del entendimiento del tema, por lo que te invitamos a resolver los siguientes ejercicios propuestos relacionados con el tema visto.
Resolver las siguientes integrales:
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- $$\int \frac{\sqrt{9-x^{2}}}{x^{2}}dx$$
- $$\int \frac{dx}{\sqrt{4x^{2}+1}}dx$$
- $$\int \frac{\sqrt{x^{2}-1}}{x}dx$$
- $$\int \sqrt{x^{2}+x}dx$$
- $$\int_{0}^{2\sqrt{3}} \frac{x^{3}}{\sqrt{16-x^{2}}}dx$$
- $$\int_{\sqrt{3}}^{2} \frac{\sqrt{x^{2}-3}}{x}dx$$
Más adelante…
En esta sección vimos el método de sustitución trigonométrica viendo las condiciones para poder aplicar este método auxiliándonos con triángulos rectángulos en el cual nos ayuda a resolver integrales fácilmente, por lo que en esta entrada vimos que se pueden resolver integrales utilizando las funciones trigonométricas. En la siguiente sección veremos el método de fracciones parciales para poder integrar polinomios que tengan el grado del numerador menor que el del denominador.
Entradas relacionadas
- Ir a Cálculo Diferencial e Integral II.
- Entrada anterior del curso: Cálculo Diferencial e Integral II: Integrales trigonométricas – Productos de potencias de tan(x) y sec(x) – El blog de Leo (nekomath.com)
- Siguiente entrada del curso: Cálculo Diferencial e Integral II: Integración de funciones racionales por fracciones parciales – El blog de Leo (nekomath.com)