Introducción
Durante las últimas clases hemos visto problemas y teoremas que nos demuestran que las bases ortogonales son extremadamente útiles en la práctica, ya que podemos calcular fácilmente varias propiedades una vez que tengamos a nuestra disposición una base ortogonal del espacio que nos interesa. Veamos más problemas de bases ortogonales y otros resultados que nos permitirán reforzar estas ideas.
Problemas resueltos de bases ortogonales y proyecciones
Para continuar con este tema, veremos que las bases ortogonales nos permiten encontrar de manera sencilla la proyección de un vector sobre un subespacio. Primero, recordemos que si $V=W\oplus W_2$, para todo $v\in V$ podemos definir su proyección en $W$, que denotamos $\pi_W(v)$, como el único elemento en $W$ tal que $v-\pi_W(v) \in W_2$.
Debido a las discusiones sobre bases ortogonales, no es difícil ver que si $\langle w,u \rangle =0$ para todo $w\in W$, entonces $u\in W_2$. Como consecuencia de esto, tenemos el siguiente resultado:
Teorema. Sea $V$ un espacio vectorial sobre $\mathbb{R}$ con producto interior $\langle \cdot , \cdot \rangle$, y sea $W$ un subespacio de $V$ de dimensión finita. Sea $v_1,\cdots,v_n$ una base ortogonal de $W$. Entonces para todo $v\in V$ tenemos que
$\pi_W(v)=\sum_{i=1}^n \frac{\langle v,v_i \rangle}{\norm{v_i}^2} v_i .$
Demostración. Escribimos $v$ como $v=\pi_W(v)+u$ con $u\in W_2$. Por la observación previa al teorema, $\langle u,v_i \rangle =0$ para todo $i$. Además existen $a_1,\cdots,a_n$ tales que $\pi_W(v)=a_1 v_1+\cdots+a_n v_n$. Entonces
\begin{align*}
0 &= \langle u,v_i \rangle =\langle v,v_i \rangle – \langle \pi_W(v),v_i \rangle \\
&= \langle v,v_i \rangle – \sum_{j=1}^n a_j \langle v_j,v_i \rangle \\
&= \langle v,v_i \rangle – a_i \langle v_i,v_i \rangle,
\end{align*}
porque $v_1,\cdots,v_n$ es una base ortogonal. Por lo tanto, para todo $i$, obtenemos
$a_i=\frac{\langle v,v_i \rangle}{\norm{v_i}^2}.$
$\square$
Distancia de un vector a un subespacio y desigualdad de Bessel
En la clase de ayer, vimos la definición de distancia entre dos vectores. También se puede definir la distancia entre un vector y un subconjunto como la distancia entre el vector y el vector «más cercano» del subconjunto, en símbolos:
$d(v,W)=\min_{x\in W} \norm{x-v}.$
Dado que $x\in W$, $x-\pi_W(v) \in W$, y por definición de proyección $v-\pi_W(v) \in W_2$, entonces
\begin{align*}
\norm{x-v}^2 &=\norm{(x-\pi_W(v))+(\pi_W(v)-v)}^2 \\
&= \norm{x-\pi_W(v)}^2+2\langle x-\pi_W(v),\pi_W(v)-v \rangle+\norm{\pi_W(v)-v}^2 \\
&= \norm{x-\pi_W(v)}^2+\norm{\pi_W(v)-v}^2\\
&\geq \norm{\pi_W(v)-v}^2.
\end{align*}
Y dado que la proyección pertenece a $W$, la desigualdad anterior muestra que la proyección es precisamente el vector en $W$ con el que $v$ alcanza la distancia a $W$. En conclusión, $$d(v,W)=\norm{\pi_W(v)-v}.$$
Teorema. Sea $V$ un espacio vectorial sobre $\mathbb{R}$ con producto interior $\langle \cdot , \cdot \rangle$, y sea $W$ un subespacio de $V$ de dimensión finita. Sea $v_1,\ldots,v_n$ una base ortonormal de $W$. Entonces para todo $v\in V$ tenemos que
$\pi_W(v)=\sum_{i=1}^n \langle v,v_i \rangle v_i,$
y
\begin{align*}
d(v,W)^2&=\norm{v-\sum_{i=1}^n \langle v,v_i \rangle v_i }^2\\
&=\norm{v}^2-\sum_{i=1}^n \langle v,v_i \rangle^2.
\end{align*}
En particular
$\sum_{i=1}^n \langle v,v_i \rangle^2\leq \norm{v}^2.$
A esta última desigualdad se le conoce como desigualdad de Bessel.
Demostración. Por el teorema anterior y dado que $v_1,\cdots,v_n$ es una base ortonormal, obtenemos la primera ecuación. Ahora, por Pitágoras,
$d(v,W)^2=\norm{v-\pi_W(v)}^2=\norm{v}^2-\norm{\pi_W(v)}^2.$
Por otro lado, tenemos que
\begin{align*}
\norm{\pi_W(v)}^2 &=\norm{\sum_{i=1}^n \langle v,v_i \rangle v_i}^2 \\
&= \sum_{i,j=1}^n \langle \langle v,v_i \rangle v_i, \langle v,v_j \rangle v_j \rangle \\
&= \sum_{i,j=1}^n \langle v,v_i \rangle \langle v,v_j \rangle \langle v_i,v_j \rangle \\
&=\sum_{i=1}^n \langle v,v_i \rangle^2.
\end{align*}
Por lo tanto, se cumple la igualdad de la distancia. Finalmente como $d(v,W)^2 \geq 0$, inmediatamente tenemos la desigualdad de Bessel.
$\square$
Veamos ahora dos problemas más en los que usamos la teoría de bases ortonormales.
Aplicación del proceso de Gram-Schmidt
Primero, veremos un ejemplo más del uso del proceso de Gram-Schmidt.
Problema. Consideremos $V$ como el espacio vectorial de polinomios en $[0,1]$ de grado a lo más $2$, con producto interior definido por $$\langle p,q \rangle =\int_0^1 xp(x)q(x) dx.$$
Aplica el algoritmo de Gram-Schmidt a los vectores $1,x,x^2$.
Solución. Es fácil ver que ese sí es un producto interior en $V$ (tarea moral). Nombremos $v_1=1, v_2=x, v_3=x^2$. Entonces
$$e_1=\frac{v_1}{\norm{v_1}}=\sqrt{2}v_1=\sqrt{2},$$
ya que $$\norm{v_1}^2=\int_0^1 x \, dx=\frac{1}{2}.$$
Sea $z_2=v_2-\langle v_2,e_1 \rangle e_1$. Calculando, $$\langle v_2,e_1 \rangle=\int_0^1 \sqrt{2}x^2 dx=\frac{\sqrt{2}}{3}.$$ Entonces $z_2=x-\frac{\sqrt{2}}{3}\sqrt{2}=x-\frac{2}{3}.$ Esto implica que
$e_2=\frac{z_2}{\norm{z_2}}=6\left(x-\frac{2}{3}\right)=6x-4.$
Finalmente, sea $z_3=v_3-\langle v_3,e_1\rangle e_1 -\langle v_3,e_2 \rangle e_2$. Haciendo los cálculos obtenemos que
$z_3=x^2-\left(\frac{\sqrt{2}}{4}\right)\sqrt{2}-\left(\frac{1}{5}\right)(6x-4)$
$z_3=x^2-\frac{6}{5}x+\frac{3}{10}.$
Por lo tanto
$e_3=\frac{z_3}{\norm{z_3}}=10\sqrt{6}(x^2-\frac{6}{5}x+\frac{3}{10}).$
$\triangle$
El teorema de Plancherel y una fórmula con $\pi$
Finalmente, en este ejemplo, usaremos técnicas de la descomposición de Fourier para solucionar un problema bonito de series.
Problema. Consideremos la función $2\pi-$periódica $f:\mathbb{R}\rightarrow \mathbb{R}$ definida como $f(0)=f(\pi)=0,$ $f(x)=-1-\frac{x}{\pi}$ en el intervalo $(-\pi,0)$, y $f(x)=1-\frac{x}{\pi}$ en el intervalo $(0,\pi)$.
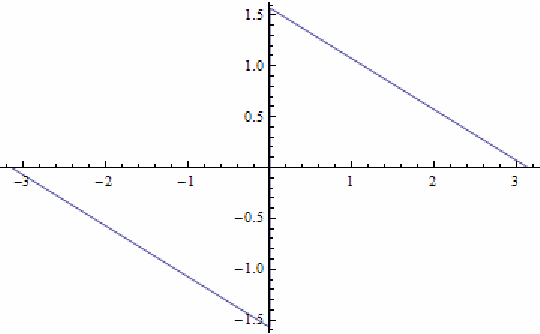
Usa el teorema de Plancherel para deducir las identidades de Euler
\begin{align*}
\sum_{n=1}^\infty \frac{1}{n^2} &= \frac{\pi^2}{6},\\
\sum_{n=0}^\infty \frac{1}{(2n+1)^2} & = \frac{\pi^2}{8}.
\end{align*}
Solución. Notemos que no sólo es $2\pi-$periódica, también es una función impar, es decir, $f(-x)=-f(x)$. Por lo visto en la clase del miércoles pasado tenemos que calcular
$a_0(f)=\frac{1}{\pi} \int_{-\pi}^{\pi} f(x) dx,$
$a_k(f)=\frac{1}{\pi} \int_{-\pi}^{\pi} f(x) cos(kx) dx,$
$b_k(f)=\frac{1}{\pi} \int_{-\pi}^{\pi} f(x)sen(kx) dx.$
Para no hacer más larga esta entrada, la obtención de los coeficientes de Fourier se los dejaremos como un buen ejercicio de cálculo. Para hacer las integrales hay que separar la integral en cada uno de los intervalos $[-\pi,0]$ y $[0,\pi]$ y en cada uno de ellos usar integración por partes.
El resultado es que para todo $k\geq 1$, $$a_0=0, a_k=0, b_k=\frac{2}{k\pi}.$$
Entonces por el teorema de Plancherel,
\begin{align*}
\sum_{k=1}^\infty \frac{4}{k^2\pi^2} &=\frac{1}{\pi} \int_{-\pi}^{\pi} f^2(x) dx \\
&= \frac{1}{\pi} \left( \int_{-\pi}^0 \left(1+\frac{x}{\pi}\right)^2 dx + \int_0^\pi \left(1-\frac{x}{\pi}\right)^2 dx \right) \\
&= \frac{2}{3},
\end{align*}
teniendo que $$\sum_{k=1}^\infty \frac{1}{k^2} =\frac{2}{3}\frac{\pi^2}{4}=\frac{\pi^2}{6}.$$
Ahora para obtener la otra identidad de Euler, notemos que
\begin{align*}
\sum_{n=0}^\infty \frac{1}{(2n+1)^2} &= \sum_{n=1}^\infty \frac{1}{n^2} – \sum_{n=1}^\infty \frac{1}{(2n)^2} \\
&= \frac{\pi^2}{6}-\frac{\pi^2}{4\cdot6}= \frac{\pi^2}{8}.
\end{align*}
$\triangle$
Entradas relacionadas
- Ir a Álgebra Lineal I
- Entrada anterior del curso: Proceso de Gram-Schmidt
- Siguiente entrada del curso: Transformaciones multilineales
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104721 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM»
