Archivo de la etiqueta: Conjuntos

Geometría Analítica I: Introducción a resultados de clasificación

Por Leonardo Ignacio Martínez Sandoval

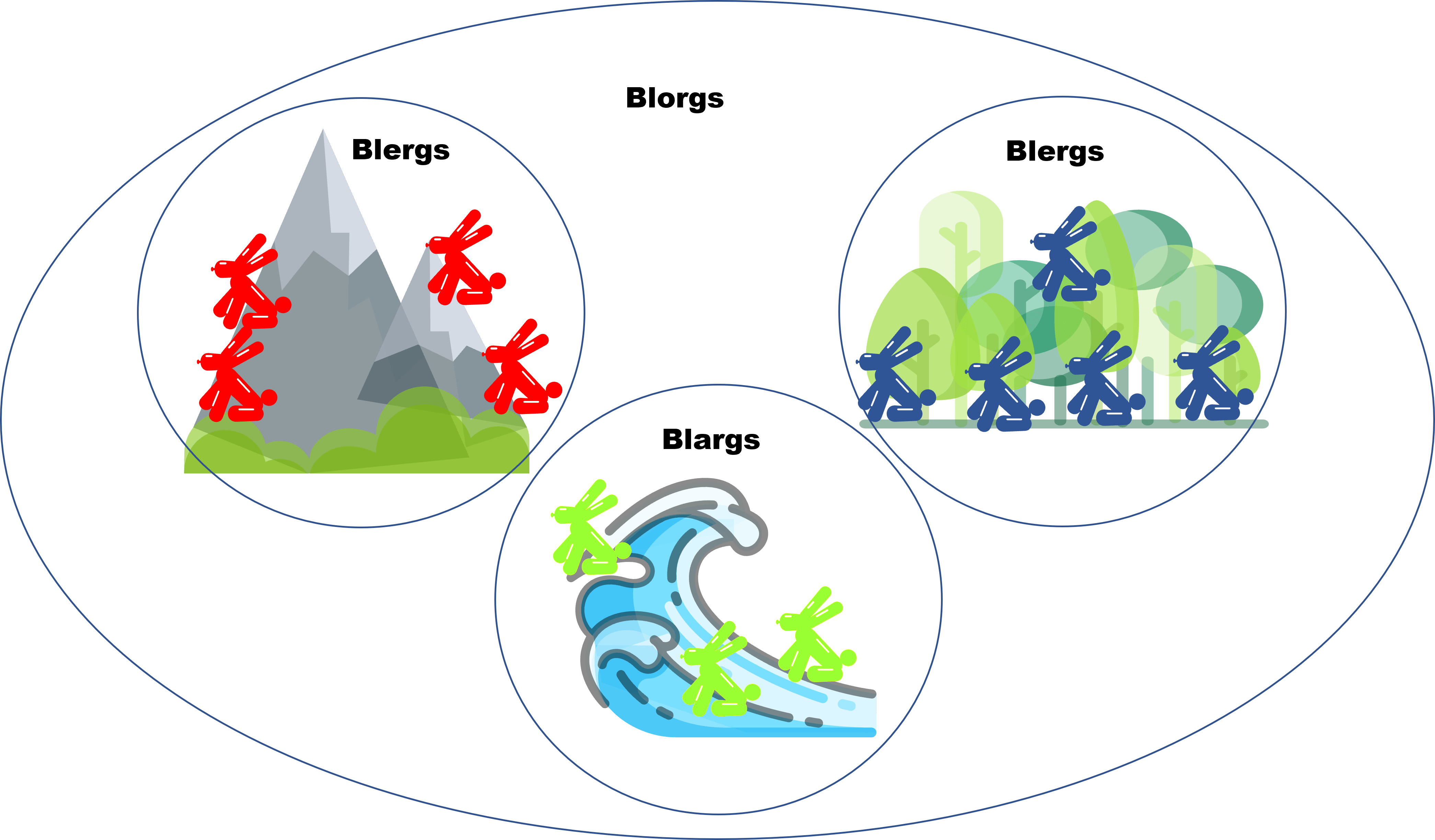
Introducción

En tu formación matemática muchas veces te encontrarás con resultados de clasificación. Pero, ¿qué es clasificar en este contexto? A grandes rasgos, consiste en poder decir de manera sencilla cómo son todos los objetos matemáticos que se estén estudiando en un contexto dado.

En esta entrada hablaremos un poco más del problema de clasificar ciertos objetos matemáticos. Iniciaremos con un ejemplo «de juguete» muy básico. Luego, hablaremos de cómo en las clasificaciones geométricas podemos usar transformaciones. Finalmente, daremos un ejemplo sencillo de cómo usar estas ideas en la clasificación de los segmentos del plano.

Ejemplo básico de clasificación

Cuando queremos hacer una clasificación, en el sentido matemático, lo que queremos hacer es tomar algunos objetos matemáticos y decir, bajo algún criterio cómo son todos los «tipos posibles» que existen para esos objetos. Esto puede ser respondido de muchas formas, así que es fundamental acordar dos cosas con precisión:

¿Cuáles son los objetos que queremos clasificar?
¿Bajo qué criterio diremos que dos de esos objetos son «del mismo tipo»?

Al final del proceso, nos gustaría tener una lista relativamente fácil de escribir de todas las posibilidades. Esto puede ayudar posteriormente a resolver otros problemas matemáticos o bien a desarrollar más teoría.

Comencemos con un ejemplo «de juguete». Será muy sencillo, pero nos permitirá hablar de algunas de las sutilezas que nos encontraremos en contextos más abstractos. Considera la siguiente figura en la que hay varias figuras geométricas.

Imagina que nos piden «clasificar todas las figuras que están aquí». Lo que nos gustaría obtener al final es una lista con la clasificación, es decir con «todas las posibilidades» de figuras que hay. Si sólo nos dan esta instrucción, entonces estaríamos en problemas: hay muchas formas de clasificar estos objetos.

Una posible clasificación es por forma. Si consideramos equivalentes a dos de estas figuras cuando tienen la misma forma, entonces nuestra lista de posibilidades se reduce a tres: triángulos, cuadrados y círculos. Nuestro teorema de clasificación se vería así:

Teorema. Cualquier figura de la imagen tiene alguna de las siguientes formas:

Triángulo
Cuadrado
Círculo

Este teorema de clasificación está padre. Pero puede ser inútil en algunos contextos. Por ejemplo, imagina que las figuras son muestras que está regalando una tienda de pinturas para que puedas llevarlas a tu casa y usarlas para ver si te gustaría pintar una pared con el color dado. Para estos fines es (prácticamente) lo mismo que te den un cuadrado azul o un triángulo azul. Lo único que importa es el color.

Pensar de esta manera nos da otra manera de clasificar a las figuras: por color. Si usamos esta noción de equivalencia, entonces nuestro resultado de clasificación sería muy distinto.

Teorema. Cualquier figura de la imagen es de alguno de los siguientes colores:

Rojo
Naranja
Amarillo
Verde
Azul

Pero podríamos querer ser mucho más estrictos y querer clasificar considerando ambos criterios: tanto la forma como el color. Quizás uno podría pensar que como hay tres figuras y cinco colores, entonces hay $3\cdot 5=15$ posibilidades en esta clasificación. Obtendríamos el siguiente resultado.

Teorema. Cualquier figura de la imagen es de alguno de los siguientes 15 tipos: triángulo rojo, triángulo naranja, triángulo amarillo, triángulo verde, triángulo azul, cuadrado rojo, cuadrado naranja, cuadrado amarillo, cuadrado verde, cuadrado azul, círculo rojo, círculo naranja, círculo amarillo, círculo verde, círculo azul.

Estrictamente hablando, este resultado es correcto: cualquier figura es de alguno de esos tipos. Pero el teorema tiene algo incómodo: nos está dando posibilidades que no suceden. Por ejemplo, no hay cuadrados amarillos, ni círculos azules.

Una clasificación con forma y color que nos dejaría más satisfecho sería la siguiente:

Teorema. Cualquier figura de la imagen es de alguno de los siguientes 11 tipos:

Triángulo rojo
Triángulo naranja
Triángulo amarillo
Triángulo azul
Cuadrado rojo
Cuadrado naranja
Cuadrado azul
Círculo rojo
Círculo naranja
Círculo amarillo
Círculo verde

Más aún, cualquiera de estas posibilidades sucede.

Este resultado se siente mucho más satisfactorio. Por un lado, no está agregando a la lista «opciones de más». Por otro lado, a partir de él podemos demostrar proposiciones sin tener que volver a ver la figura. Algunos ejemplos son los siguientes:

Ningún círculo de nuestra figuras es azul.
Todas las figuras verdes son círculos.
Ninguna figura amarilla es un cuadrado.

Para mostrar cualquiera de estas, basta ver nuestra clasificación.

¿Podemos dar una clasificación mucho más estricta? Sí, por supuesto. Por ejemplo, podemos considerar dos figuras iguales sólo cuando tienen exactamente la misma figura, color y posición. En este caso nuestro teorema de clasificación tendría un tipo por cada una de las 19 figuras. Esta clasificación también se siente un poco insatisfactoria pues en realidad no estamos «agrupando» figuras, sino simplemente «poniendo a cada una en su propio grupo». Pero bueno, es una clasificación válida también.

Uso de relaciones de equivalencia y particiones

Una manera de formalizar una clasificación es a partir de relaciones de equivalencia y particiones. Recordemos las siguientes dos definiciones:

Definición. Una relación de equivalencia en un conjunto $X$ es una colección de parejas $(x,y)$ en $X\times X$ tales que:

(Reflexividad) Para cualquier $x$ en $X$ la pareja $(x,x)$ está en la colección.
(Simetría) Si para algunos $x,y$ en $X$ se cumple que la pareja $(x,y)$ está en la colección, entonces la pareja $(y,x)$ también está en la colección.
(Transitividad) Si para algunos $x,y,z$ en $X$ se cumple que tanto las parejas $(x,y)$ como $(y,z)$ están en la colección, entonces la pareja $(x,z)$ también está.

Las relaciones de equivalencia nos ayudan a decir cuándo dos objetos de $X$ «son iguales» o «son el mismo» bajo algún criterio usualmente más relajado que la igualdad.

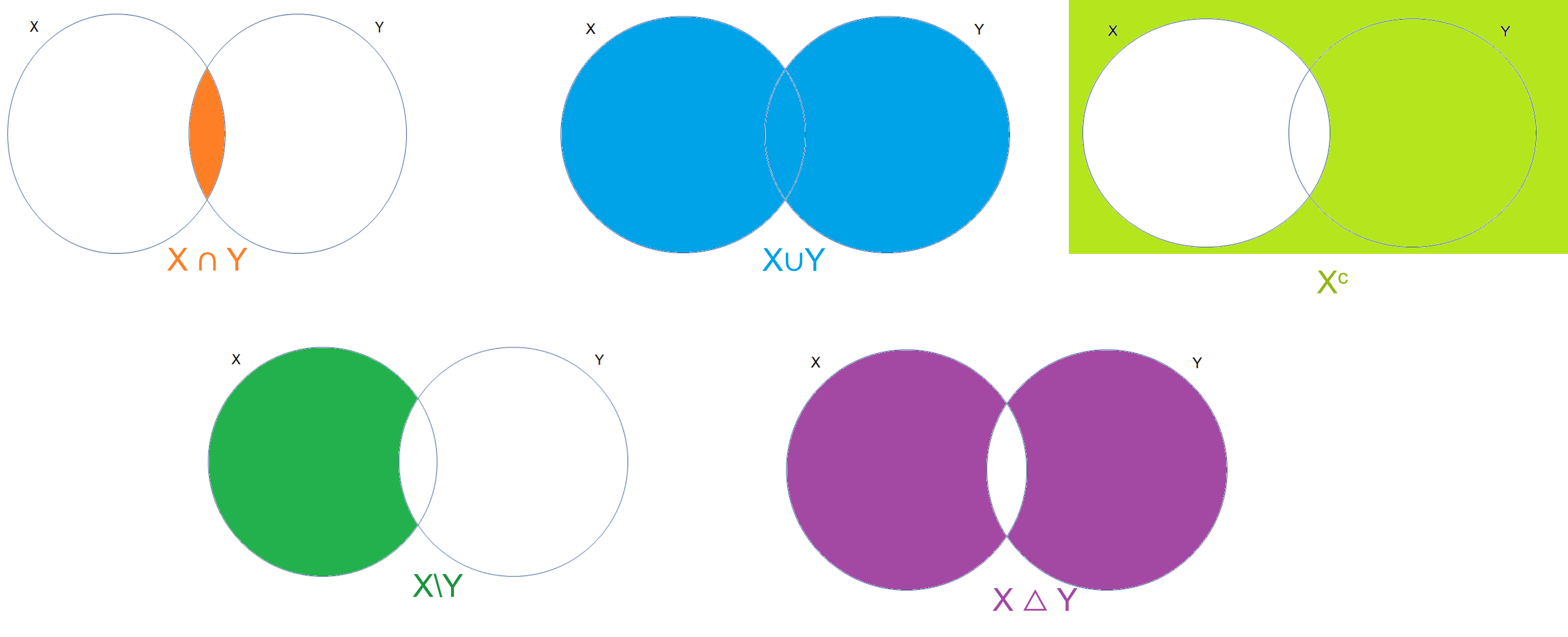
Definición. Una partición de un conjunto $X$ es una colección de conjuntos $(A_i)_{i \in I}$ para algún conjunto de índices $I$ tal que ninguno de los $A_i$ es vacío, cualesquiera dos de ellos tienen intersección vacía y $X=\cup_{i\in I}A_i$.

Un resultado clásico de teoría de conjuntos dice que «una relación de equivalencia da una partición, y viceversa». Formalmente, dada una relación de equivalencia $R$ en un conjunto $X$, podemos crear la clase de equivalencia de un elemento $x$ en $X$ como sigue: $$\overline(x):=\{y \in X: (x,y)\in R\}.$$ El conjunto $\{\overline{x}:x\in X\}$ da una colección de conjuntos que es una partición de $X$. Y viceversa, si tenemos una partición $(A_i)_{i \in I}$, entonces podemos considerar las parejas $(x,y)$ de elementos tales que $x$ y $y$ están en un mismo $A_i$, de donde obtenemos una relación de equivalencia.

Regresando a la idea de clasificar, podemos realizar una clasificación a través de una relación de equivalencia o de una partición. Las clases de equivalencia son los «tipos» de objetos que tenemos. Podemos dar un representante «sencillo» dentro de cada clase de equivalencia para hacer nuestra lista de los posibles «tipos» que existen.

Ejemplo. En los números enteros podemos decir que dos enteros $x$ y $y$ están relacionados cuando $x-y$ es un número par. Es fácil mostrar que esto da una relación de equivalencia y que las clases de equivalencia en este caso son los conjuntos:

\begin{align*}
P&=\{\ldots,-4,-2,0,2,4,\ldots\},
Q&=\{\ldots,-3,-1,1,3,\ldots\}.
\end{align*}

Tenemos que $P$ y $Q$ forman una partición del conjunto $\mathbb{Z}$ de números enteros. Así, esta relación clasifica a los enteros en dos tipos: los pares y los impares. Otra forma de dar esta clasificación es diciendo que «Cualquier entero es equivalente al $0$ o al $1$», o más explícitamente, «Para cualquier entero $z$ se tiene que o bien $z$ es par, o bien $z-1$ es par».

$\triangle$

Clasificación de segmentos del plano con transformaciones

Hacia donde queremos ir es hacia una clasificación relacionada con la geometría. Por esta razón, las relaciones de equivalencia, particiones o «tipos» de objetos que obtendremos estarán relacionados con nociones geométricas. Una manera de hacer esto es mediante las transformaciones que estuvimos estudiando en la unidad anterior: transformaciones afines, traslaciones, isometrías, transformaciones ortogonales, etc.

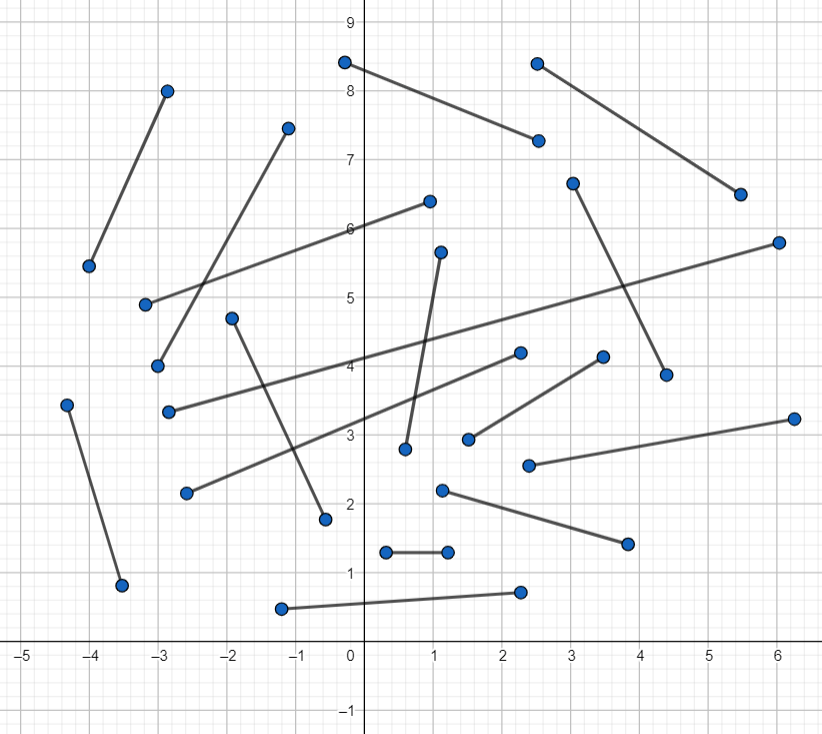
Por ejemplo, pensemos en que estamos hablando de los segmentos cerrados y acotados en el plano cartesiano. Es decir, de acuerdo a lo que estudiamos en la primera unidad, para cualesquiera dos puntos distintos $P$ y $Q$ en el plano estamos considerando el conjunto $$\overline{PQ}=\{pP+qQ:0\leq p \leq 1, 0 \leq q \leq 1, p+q=1\}.$$ En la siguiente figura puedes ver algunos de los (muchos) segmentos que hay en el plano:

¿Cómo podemos clasificar a todos los segmentos que hay en el plano? Antes de cualquier cosa, tenemos que ponernos de acuerdo en la clasificación. Una manera de hacer esto es mediante transformaciones del plano. Veamos un par de ejemplos.

Ejemplo. Una primer opción es que digamos que dos segmentos son del mismo tipo cuando podamos trasladar uno de ellos al otro. Si hacemos esto, casi todos los segmentos de la siguiente figura serían del mismo tipo.

El único que no es del mismo tipo que los demás sería el segmento punteado que, aunque lo dibujamos intencionalmente de la misma longitud que los demás, no resulta ser equivalente pues es imposible trasladarlo a alguno de los otros segmentos. Con esta noción de segmentos equivalentes, ¿qué posibilidades tendríamos? Es más o menos fácil convencerse de que para que dos segmentos sean del mismo tipo con esta clasificación necesitamos que a) sean paralelos y b) tengan la misma longitud. Por ello mismo, no es tampoco difícil convencerse del siguiente teorema de clasificación.

Teorema. Cualquier segmento del plano es equivalente bajo traslaciones a un segmento tal que uno de sus extremos es el origen.

$\square$

Veamos otra manera de clasificar los segmentos del plano.

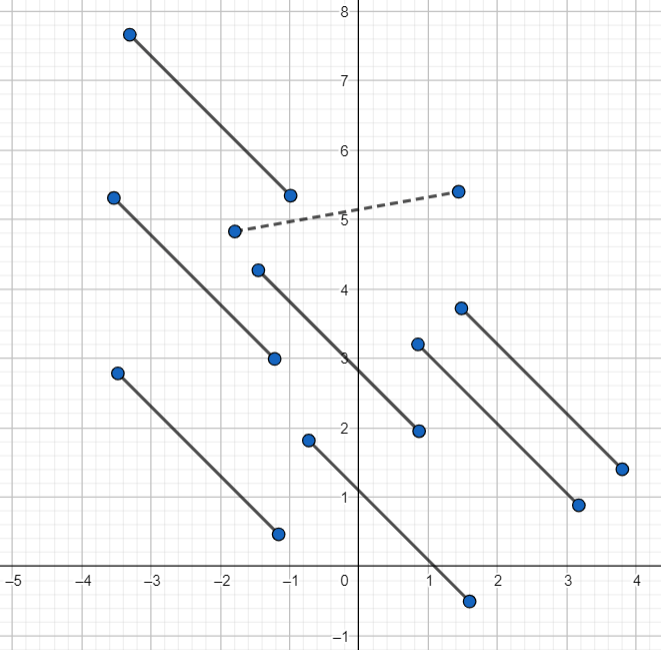
Ejemplo. Diremos que dos segmentos son del mismo tipo si podemos llevar uno al otro a través de una isometría. Si hacemos esto entonces ahora sí todos los segmentos de la siguiente figura son equivalentes (pensando en que el segmento punteado tiene la misma longitud que los otros).

De hecho, por lo que sabemos de las isometrías podemos afirmar que bajo este criterio dos segmentos son del mismo tipo si y sólo si tienen la misma longitud. Esto nos llevaría a un teorema de clasificación un poco distinto.

Teorema. Cualquier segmento se puede mediante isometrías a un segmento que sale del origen y termina en un punto del la forma $(x,0)$ con $x>0$. Más aún, todos estos segmentos son de distinto tipo.

$\square$

En los dos ejemplos anteriores hemos sido un poco informales, pues dejamos varias cosas sin demostrar. Seguramente podrás detectarlas e intentar completar los argumentos que faltan. Algunas de estas cosas faltantes están en los ejercicios.

Más adelante…

En esta entrada hablamos de la noción de «clasificar» de manera muy general, con el fin de entenderla y ver algunas de las sutilezas que nos encontraremos más adelante. A partir de ahora nos enfocaremos en probar resultados de clasificación muy específicos, relacionados con las cónicas.

Sin embargo, queremos ser muy precisos con respecto a la clasificación que daremos. Por esta razón, en las siguientes dos entradas hablaremos de los objetos específicos que queremos clasificar y de las nociones de equivalencia que permitiremos.

Tarea moral

Verifica que en nuestro ejemplo de juguete la relación «tener el mismo color» es una relación de equivalencia.
Para cada una de las clasificaciones que dimos en nuestro ejemplo de juguete encuentra cuántas de las figuras originales hay en cada una de las clases.
Demuestra que la relación en $\mathbb{Z}$ en la cual tenemos a $(x,y)$ si y sólo si $x-y$ es un número par es una relación de equivalencia. Muestra que en este caso la partición consiste en el conjunto de los números pares, y el conjunto de los números impares.
Sea $S$ el conjunto de segmentos en el plano. Diremos un elemento $s_1$ de $S$ es traslacionalmente equivalente a otro elemento $s_2$ de $S$ si existe una traslación $T$ de $\mathbb{R}^2$ tal que $T(s_1)=s_2$. Demuestra que «ser traslacionalmente equivalente a» es una relación de equivalencia en $S$.
Da teoremas de clasificación de las rectas en $\mathbb{R}$ usando transformaciones para cada una de las siguientes posibilidades:
1. Dos rectas son del mismo tipo si se puede llevar una a otra mediante una traslación.
2. Dos rectas son del mismo tipo si se puede llevar una a la otra mediante una rotación.
3. Dos rectas son del mismo tipo si se puede llevar una a la otra mediante una isometría.

Entradas relacionadas

Ir a Geometría Analítica I
Entrada anterior del curso: Homotecias y semejanzas
Siguiente entrada del curso: Polinomios cuadráticos y curvas cuadráticas

Álgebra Superior I: Parejas ordenadas y producto cartesiano de conjuntos

Por Guillermo Oswaldo Cota Martínez

Deja un comentario

Introducción

En la primera unidad revisamos los conceptos básicos de la teoría de conjuntos. Estos nos permitirán a partir de ahora manejar conjuntos con los operadores que vimos y nos permitirán armar nueva teoría a partir de ellos. En esta unidad nos enfocaremos en las relaciones y funciones. Estas son maneras de «agrupar» unos conjuntos con otros y serán útiles no solo en este curso, sino que en muchos otros que se basan en la idea de las funciones entre conjuntos.

Agrupando zapatos

Empecemos considerando una tienda de zapatos muy disfuncional, pues no se preocupa por hacer coincidir sus zapatos derechos con los izquierdos. Describimos al conjunto $D = \{d_1,d_2, \dots, d_n\}$ como los $n$ zapatos derechos que tiene la tienda, y por $I = \{ i_1, i_2, \dots i_m\}$ como los $m$ zapatos izquierdos. Nota que al ser una tienda poco organizada, puede ser que haya distinto número de zapatos derechos que de izquierdos (puede pasar que $m \neq n$). Cuando un cliente llega a la tienda, el mismo cliente tiene la posibilidad de elegir su par de zapatos. El primer cliente llega y elige el zapato derecho $d_3$ con el zapato izquierdo $i_2$, y eso está permitido, pues la tienda deja que los clientes eligan sus pares como quieran. Llamemos a este par de zapatos, el par $(d_3,i_2)$. Esto es lo que nos va a dar una idea intuitiva de lo que llamaremos parejas ordenadas, que en términos simples es considerar elementos de dos conjuntos y agruparlos en una misma expresión. A continuación damos su definición conjuntista.

Definición. Sean $X$ y $Y$ dos conjuntos. Una pareja ordenada de $X$ y $Y$ es una pareja de dos términos $x \in X$ y $y \in Y$ escrita mediante la expresión $(x,y)$. En términos de conjuntos se define como: $$(x,y) = \{ \{ x\}, \{x,y \} \} $$

El nombre de pareja ordenada viene del hecho de que los dos elementos a considerar respetan un orden de conjuntos, esto quiere decir a que si nos referimos a la pareja ordenada $(x,y)$ de $X$ con $Y$, eso significa que $x \in X \land y \in Y$. Por lo que la pareja $(y,x)$ no es la misma, puesto que esta es una pareja de $Y$ con $X$. Además nota que hay un «orden», pues en su expresión conjuntista, el término $x$ aparece en los dos conjuntos que conforman $(x,y)$, mientras que $y$ solo aparece una vez.

Digamos ahora que $n=4$ y $m=2$, de manera que los zapatos derechos son $D = \{ d_1,d_2,d_3,d_4 \}$ y los izquierdos son $I = \{ i_1,i_2 \}$. Entonces los zapatos que se pueden formar de estos conjuntos son:

$$\{ (d_1,i_1), (d_1,i_2), (d_2,i_1), (d_2,i_2), (d_3,i_1), (d_3,i_2), (d_4,i_1), (d_4,i_2) \} $$

Y como posiblemente te habrás imaginado, los distintos zapatos que se pueden formar con esos conjuntos, corresponden a las distintas parejas ordenadas entre $X$ y $Y$.

Igualdad entre parejas ordenadas

Ahora vamos a definir cuándo diremos que dos pares de parejas ordenadas (zapatos) son el mismo. Para esto observa que en la vida cotidiana, diríamos que dos pares son iguales si el zapato derecho de un par es exactamente el mismo que el zapato derecho del otro par, de la misma manera que el izquierdo de uno será el mismo izquierdo del otro. Anotemos eso como una proposición que habrá que demostrar.

Proposición. Sean $X$ y $Y$ dos conjuntos y $(x,y),(x’, y’)$ dos parejas ordenadas de $X$ con $Y$. Entonces las parejas son la misma ($(x,y)=(x’,y’)$) si y solo si $(x=x’) \land (y=y’)$.

Demostración. $\Rightarrow)$ Para demostrar la primera implicación, notemos que por hipótesis $(x,y)=(x’,y’)$. Esto quiere decir que $$\{\{ x\} ,\{x,y \} \} = \{\{ x’\} ,\{x’,y’ \} \} $$. Para $x$ tenemos dos casos:

Caso 1. $x =y$

En este caso, notemos que $\{\{ x\} ,\{x,y \} \} = \{\{x\}\}$. Al tener este conjunto un único elemento, entonces $\{\{ x’\} ,\{x’,y’ \} \}$ también tiene un único elemento, ya que de otra manera no serían el mismo conjunto. Enseguida, se sigue que $\{\{x\}\} = \{\{x’\}\}$. Donde se tiene que $x=x’$. Ahora notemos que al ser $x=y$, entonces $x’=y’$ y puesto que $\{\{x’\}\} = \{\{ x’\} ,\{x’,y’ \} \}$ entonces $x’=y’$.

Caso 2. $x \neq y$

Ahora, si son distintos, tenemos que $$(x,y) = \{ \{x\}, \{ x,y\} \}$$. Notemos ahora que $\{ \{x\}, \{ x,y\} \} = \{ \{x’\}, \{ x’,y’\} \}$ son conjuntos con ambos dos elementos. Al ser estos conjuntos iguales, entonces cada elemento de un conjunto está en el otro, es decir $\{x\} \in \{ \{x’\}, \{ x’,y’\} \}$ y $\{x,y\} \in \{ \{x’\}, \{ x’,y’\} \}$. Ahora, como $\{x\} \in \{ \{x’\}, \{ x’,y’\} \}$ entonces $(\{x\} = \{x’\} ) \lor (\{x\} = \{x’,y’\})$, al ser $\{x’\}$ el único elemento con un elemento, entonces deducimos que $\{x\} = \{x’\}$. De manera análoga $\{x,y\} = \{x’,y’\}$.

Ahora, como $\{x\} = \{x’\}$ entonces $x=x’$. Y después como $\{x,y\} = \{x’,y’\}$, podemos sustituir $x$ por $x’$, pues son el mismo elemento. Así, $\{x’,y\} = \{x’,y’\}$. Y nota que esto significa que $y=y’$, pues tenemos la igualdad de conjuntos. De esta manera $x=x’$ y $y=y’$ como se quería demostrar.

$\Leftarrow)$. Ahora supongamos que $x=x’$ y $y=y’$. Al tener esta igualdad, entonces $\{x\}=\{x’\}$ y además $\{x,y\} = \{ x’,y’\}$ pues tienen los mismos elementos. De esta forma, los siguientes conjuntos son iguales:$$ \{\{ x\} ,\{x,y \} \} = \{\{ x’\} ,\{x’,y’ \} \}.$$ Por lo tanto $(x,y)=(x’,y’)$

$\square$

Algunos ejemplos de parejas ordenadas que sí son la misma:

$(1,4) = (1,4) $
$(\frac{1}{2}, 0) = (1- \frac{1}{2}, 9 -9) $
$(\{x:P(x)\}, \{x: R(x) \land \neg R(x) \}) = (\{x: P(x) \land P(x) \}, \emptyset) $

Algunos ejemplos de parejas ordenadas que no son la misma:

$(1,4) \neq (4,1)$
$(1,0) \neq (1, \{0\})$
$(\{x: P(x)\}, \{x: P(x) \}) \neq (\{x: P(x) \land R(x)\}, \{x: \neg P(x) \})$

Producto Cartesiano

Hemos hablado ya de las parejas ordenadas particulares entre dos conjuntos. Sin embargo, al estar hablando de parejas ordenadas entre dos conjuntos, realmente el término que usaremos de ahora en adelante será el de producto cartesiano.

Definición. Sean $X$ y $Y$ dos conjuntos. El producto cartesiano $X \times Y$ entre $X$ y $Y$ es el conjunto: $$X \times Y = \{(x,y): (x \in X) \land (y \in Y) \}. $$

De esta manera, volviendo al ejemplo de los zapatos, en párrafos anteriores mencionamos un caso particular en donde $D = \{ d_1,d_2,d_3,d_4 \}$ y $I = \{ i_1,i_2 \}$, entonces:

$$D \times I = \{ (d_1,i_1), (d_1,i_2), (d_2,i_1), (d_2,i_2), (d_3,i_1), (d_3,i_2), (d_4,i_1), (d_4,i_2) \}. $$

Otro ejemplo, podríamos considerarlo tomando $X = \{1, \{1,2\} \}, Y = \{\emptyset, \text{perro}, 1\}$. Entonces:

\begin{align*}
&X \times Y = \{ (1,\emptyset), (1,\text{perro}),(1,1),(\{1,2\},\emptyset),(\{1,2\},\text{perro}), (\{1,2\},1)\} \\
&Y \times X = \{ (\emptyset,1), (\text{perro},1),(1,1),(\emptyset,\{1,2\}),(\text{perro},\{1,2\}), (1,\{1,2\}) \} \\
\end{align*}

Como puedes observar, aquí vemos que no es lo mismo $X \times Y$ que $Y \times X$, de hecho no coinciden en casi ningún elemento, salvo uno:

$(X \times Y) \cap (Y \times X) = \{ (1,1)\}.$

Así que hay que tener cuidado en el orden del producto cartesiano, pues como pudiste ver, no conmutan.

Otra cosa que podemos observar es que tampoco es asociativo el producto cartesiano. Esto quiere decir que no es lo mismo por ejemplo $\mathbb{Z} \times (\mathbb{Z} \times \mathbb{Z})$ que $(\mathbb{Z} \times \mathbb{Z}) \times \mathbb{Z}$. Para convencerte de esto, observa cómo son los elementos del primer conjunto y del segundo conjunto. Para empezar, un elemento de $\mathbb{Z} \times (\mathbb{Z} \times \mathbb{Z})$ es $(1,(1,1))$ mientras que un elemento del segundo es $((1,1),1)$, que no son el mismo elemento. Y de manera general, no es lo mismo para $a,b,c \in \mathbb{Z}$ la pareja $(a,(b,c))$ que la pareja $((a,b),c)$ pues siempre la primera componente de la primera pareja es un número, mientras que de la segunda, es una pareja ordenada.

Más adelante…

En la siguiente entrada, vamos a ver algunas propiedades del producto cartesiano. Algunas de las cuales ya hemos revisado en esta entrada, añadiendo otras sobre cómo se comportan con los conectores entre conjuntos.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

¿Cuántas parejas ordenadas hay en el producto cartesiano de $X \times Y$ si $X$ y $Y$ tienen un número finito de elementos?
Demuestra que si $X,Y$ son dos conjuntos no vacíos, entonces $X \times Y = Y \times X$ si y solo si $X=Y$
¿Cómo es $ \emptyset \times Y$? ¿Cuántos elementos tiene?
Encuentra el producto cartesiano $X \times X$ donde $X = \{x \in \mathbb{Z} : (x \leq 20)\land (x \ \text{es un número primo)} \}$
Encuentra el producto cartesiano de $X \times Y$ donde $X= \{1, 5, 10 \}$ y $Y = X \times X$

Entradas relacionadas

Ir a Álgebra Superior I
Entrada anterior del curso: Problemas de intersecciones, complementos, uniones y diferencia simétrica
Siguiente entrada del curso: Propiedades del producto cartesiano

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Álgebra Superior I: Leyes de De Morgan y diferencia simétrica de conjuntos

Por Guillermo Oswaldo Cota Martínez

2 respuestas

Introducción

Hasta ahora ya hemos visto cómo juntar dos conjuntos (unión), cómo encontrar elementos en común entre dos conjuntos (intersección), y hemos considerado cualquier elemento excepto los que están dentro de un conjunto (complemento). Ahora vamos a hablar de otros dos conectores: La diferencia y la diferencia simétrica. Estos dos nos permitirán a hablar de los elementos de un conjunto $A$ sin considerar los elementos de otro conjunto $B$, así como de la unión de ambos conjuntos a excepción de su intersección. Después hablaremos de algunas propiedades conocidas como las leyes de De Morgan.

La Diferencia

Habrá ocasiones en que nos interesará diferencias algunos conjuntos de otros. Por ejemplo, imagina que quieres comprar una chamarra, visitando un sitio web te das cuenta de que hay una promoción en algunas prendas, incluidas las chamarras, entonces decides que compraras una chamarra solo si tiene descuento. Considera los conjuntos que describen artículos de la página web:

$$A = \{x : x \text{ es chamarra} \} $$

$$B = \{x : x \text{ no tiene descuento} \} $$

Si solo pudiéramos distinguir entre esos dos conjuntos, a nosotros nos gustaría encontrar una chamarra $x$ del conjunto $A$ que no esté en el conjunto $B$. Esto puede describirse como:

$$\{ x: x \in A \land x \not \in B \} = \{x: x \in A \land x \in B^c \} $$

Nota ahora que esto se puede escribir como:

$$ A \cap B^c =\{x: x \in A \land x \in B^c \} $$

Esto es justamente a lo que nosotros llamamos diferencia entre conjuntos, que representa la idea de «restar conjuntos», es decir, considerar los elementos de un conjunto exceptuando los elementos que también están en otro conjunto específico.

Definición. Sean $X$ y $Y$ dos conjuntos. Definimos la diferencia de conjuntos $X/Y$ como:

$$X \setminus Y = X \cap Y^c .$$

Y gráficamente se ve de la siguiente manera:

Diferencia simétrica

Ahora imagina que en una universidad se ofrece el curso de Lógica y el curso de Teoría de Conjuntos. La universidad quiere ver cuántos alumnos se interesan únicamente por la materia de Lógica sin la Teoría de Conjuntos y viceversa para ver cuántos grupos abrir.

Puesto que la universidad piensa abrir un curso que abarca Conjuntos y Lógica para los alumnos que quieren tomar los dos cursos a la vez, por ahora no nos interesan los alumnos que estén en la intersección del conjunto de alumnos que quieren tomar el curso de Lógica con el conjunto de alumnos que quieren tomar el curso de Teoría de Conjuntos. Dicho de otra manera, si el conjunto de los alumnos interesados en un curso de Lógica lo representamos por $L$ y al conjunto de los alumnos interesados en un curso de Teoría de Conjuntos lo representamos por $C$, entonces los alumnos que están interesados en un curso de Lógica y no de Conjuntos es $L \setminus C$ y el conjunto de alumnos que están interesados en un curso de Conjuntos y no de Lógica es $C \setminus L$.

Nota ahora que entre los dos conjuntos, hay $(L \setminus C) \cup (C \setminus L)$ alumnos que no tomarán el curso de Conjuntos y Lógica pero si una materia en alguna de esas dos disciplinas. A este conjunto lo llamamos la diferencia simétrica o unión disyuntiva entre conjuntos.

Definición . Sean $X$ y $Y$ dos conjuntos. La diferencia simétrica o unión disyuntiva de los conjuntos $X$ y $Y$ se define como:

$$X \vartriangle Y = (X \setminus Y) \cup (Y \setminus X) $$

Y gráficamente se ve como:

Leyes de De Morgan

Una vez que ya definimos los operadores que vamos a usar en la teoría de conjuntos, vamos a anotar una propiedad importante de los conjuntos que tiene su contraparte en la lógica proposicional. Y nos habla de cómo encontrar el complemento de la unión y la intersección.

Teorema (Leyes de De Morgan). Sean $X$ y $Y$ dos conjuntos dentro del conjunto universal $U$. Entonces:

$(X \cap Y)^c = X^c \cup Y^c$
$(X \cup Y)^c = X^c \cap Y^c$

Demostración. En esta entrada, solo demostraremos la primera parte, la segunda parte tendrá un argumento muy similar a la demostración que presentaremos a continuación.

Para demostrar que $(X \cup Y)^c = X^c \cap Y^c$, necesitaremos considerar un elemento $x$ y probar que $x \in (X \cup Y)^c$ si y solo si $ x\in X^c \cap Y^c$. Para ello, nota lo siguiente:

\begin{align*}
x \in (X \cap Y)^c &\Leftrightarrow x \in \{x \in U : \neg(x \in X \cap Y) \} \\
&\Leftrightarrow x \in \{x \in U: \neg (x \in X \land x \in Y) \} \\
&\Leftrightarrow x \in \{x \in U: \neg( x \in X ) \lor \neg (x \in Y) \} \ \ \ \ \text{ ( Por las leyes de De Morgan de la lógica)} \\
&\Leftrightarrow x \in \{x \in U: x \in X^c \lor x \in Y^c \}\\
&\Leftrightarrow x \in X^c \cup Y^c
\end{align*}

De esta manera, $(X \cap Y)^c = X^c \cup Y^c$. De manera análoga se cumple la otra proposición.

$\square$

Este teorema lo que nos quiere decir es que la forma de encontrar el complemento de la unión es intersectando el complemento de los conjuntos, y el complemento de la intersección es la unión de los complementos.

Corolario. Las siguientes proposiciones se cumplen con $X,Y,Z$ tres conjuntos:

$(X \cup Y \cup Z)^c = X^c \cap Y^c \cap Z^c $
$(X \cap Y \cap Z)^c = X^c \cup Y^c \cup Z^c$

Demostración. De manera similar al teorema anterior, solo demostraremos el primer inciso.

Para esto, notemos que:

\begin{align*}
(X \cup Y \cup Z)^c &= (X \cup Y)^c \cap Z^c \\
&= X^c \cap Y^c \cap Z^c
\end{align*}

De manera análoga se cumple la segunda proposición.

$\square$

Más adelante, tendremos herramienta matemática para demostrar que las leyes no solo se cumplen para la dos o tres variables, sino que para una cantidad arbitraria de términos. En otras palabras, podremos demostrar que:

Proposición. Sea $X = \{X_1,X_2,\dots,X_n\}$ una colección finita de conjuntos. Entonces:

$(X_1 \cup X_2 \cup \dots \cup X_n)^c = X_1^c \cap X_2^c \cap \dots \cap X_n^c $
$(X_1 \cap X_2 \cap \dots \cap X_n)^c = X_1^c \cup X_2^c \cup \dots \cup X_n^c$

Por ahora, nos quedaremos únicamente en el caso de tres variables. A este punto, conviene también decir que a veces encontrarás en la literatura la el término $X_1 \cup X_2 \cup \dots \cup X_n$ escrito como $\bigcup_{i=1}^nX_i$ y esta es únicamente una forma de notación que representa la unión de una colección de conjuntos. De manera similar, $X_1 \cap X_2 \cap \dots \cap X_n = \bigcap_{i=1}^nX_i $. De esta manera, la proposición anterior se resume en:

$\big( \bigcup_{i=1}^n X_i \big)^c = \bigcap_{i=1}^n X_i^c$
$\big( \bigcap_{i=1}^n X_i \big)^c = \bigcup_{i=1}^n X_i^c$

Otras propiedades de los conjuntos

A continuación anotamos otras propiedades que tienen los conjuntos, algunas de las cuales ya hemos revisado. Sean $X,Y$ y $Z$ tres conjuntos en el conjunto universal $U$, la siguiente tabla resume algunas propiedades que se cumplen.

Propiedad
Asociatividad de los conjuntos	\begin{align} X \cup (Y \cup Z) &= (X \cup Y) \cup Z \\ X \cap (Y \cap Z) &= (X \cap Y) \cap Z \end{align}
Distributividad de la unión y la intersección	\begin{align} X \cap (Y \cup Z) &= (X \cap Y) \cup (X \cap Z) \\ X \cup (Y \cap Z) &= (X \cup Y) \cap (X \cup Z) \end{align}
Idempotencia de la unión e intersección	\begin{align} X \cup X = X = X \cap X \end{align}
Conmutatividad de unión e intersección	\begin{align} X \cup Y = Y \cup X \\ X \cap Y = Y \cap X \end{align}
Leyes de identidad de unión	\begin{align} X \cup \emptyset &= X \\ X \cup U &= U \end{align}
Leyes de identidad de intersección	\begin{align} X \cap \emptyset &= \emptyset \\ X \cap U &= X \end{align}
Unión de complementos	\begin{align} X \cup X^c = U \end{align}
Intersección de complementos	\begin{align} X \cap X^c = \emptyset \end{align}
	\begin{align} (X^c)^c = X \end{align}
Leyes de De Morgan	\begin{align} (X \cap Y)^c &= X^c \cup Y^c\\ (X \cup Y)^c &= X^c \cap Y^c \end{align}

Y para resumir los operadores entre conjuntos, se encuentra la siguiente imagen:

Notas

*: En la literatura, también puedes encontrar la diferencia entre dos conjuntos $X$ y $Y$ escrita como $X – Y$ en lugar de $X \setminus Y$.

Más adelante…

Con esta entrada acabamos la primer unidad. Hasta ahora hemos sentado las bases matemáticas de la teoría de conjuntos, en la siguiente unidad vamos a seguir hablando de conjuntos, pero introduciremos un nuevo concepto: las relaciones entre conjuntos. Estas nos permitirán empezar a hablar de funciones, un recurso muy utilizado en todas las áreas de las matemáticas.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Sean $P, Q, R, S$ cuatro proposiciones y $A = \{x: (P(x) \land Q(x)) \lor R(x) \}$, $B = \{x: (R(x) \land \neg P(x)) \lor S(x) \}$, $C = \{ x: S(x)\}$. Encuentra:
- $A \cup B$
- $B^c$
- $A \setminus B$
- $A \cap (B \cap C)$
- $A \vartriangle C$
Demuestra que $(X \cup Y)^c = X^c \cap Y^c$
Demuestra que $(X^c)^c = X$
Describe al conjunto $(X \vartriangle Y)^c \setminus (X \setminus Y)^c$ en términos de complementos, la unión y la intersección.

Entradas relacionadas

Ir a Álgebra Superior I
Entrada anterior del curso: Intersecciones, uniones y complementos de conjuntos
Siguiente entrada del curso: Problemas de intersecciones, complementos, uniones y diferencia simétrica

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Álgebra Superior I: Intersecciones, uniones y complementos de conjuntos

Por Guillermo Oswaldo Cota Martínez

2 respuestas

Introducción

Habiendo establecido los axiomas de la teoría de conjuntos, ahora vamos a empezar a trabajar con ellos. En particular en esta entrada nos intereseran tres operaciones: La intersección, la unión y el complemento de conjuntos.

Pensando en conjuntos

Para empezar a hablar de las operaciones que usaremos, pues primero debemos de ponernos de acuerdo a qué nos referiremos y qué queremos construir cuando hablamos de operaciones. Para estos fines, nos interesa qué podemos hacer con los conjuntos y cómo se relacionan los unos a los otros. Por ejemplo: ¿Habrá algunos elementos que pertenezcan a dos conjuntos a la vez? o ¿Qué pasa con el con elementos que sí están en unos conjuntos y en otros no? Pues veremos algunas operaciones, sin embargo hay que ver la idea intuitiva detrás de algunos de ellos.

Será bueno que de igual manera tengas los axiomas a la mano, pues serán útiles para la definición de algunas de estas operaciones:

Axioma 1	Existe un conjunto.
Axioma 2	Podemos hacer conjuntos a partir de proposiciones que cumplen o no cumplen elementos de algún conjunto.
Axioma 3	Si $X$ y $Y$ son conjuntos, entonces $\{X,Y\}$ es un conjunto.
Axioma 4	Dos conjuntos son iguales si todos sus elementos son iguales.
Axioma 5	Existe un conjunto que tiene como elementos a todos los elementos que pertenecen a algún elemento de $X$.
Axioma 6	Para cada conjunto $X$, existe su conjunto potencia $\mathcal P (X)$ cuyos elementos son los subconjuntos de $X$.

Intersección

Supongamos que tenemos dos conjuntos $X,Y$ de números enteros positivos del 1 al 20. $X$ es el conjunto de los números pares y $Y$ es el conjunto de los números primos. Entonces $X$ lo podemos ver como:

Mientras que $Y$ se podría ver como:

Nota que hay un elemento en común con ambos conjuntos, pues $2$ es el único par primo, es decir hay un punto de intersección que es el $2$:

En este caso diremos que $2$ se encuentra en la intersección de $X$ con $Y$, pues está en ambos conjuntos. Con esto en mente definiremos la intersección:

Definición. Sean $X$ y $Y$ dos conjuntos, entonces el conjunto intersección de $X$ y $Y$, $X \cap Y$ es: $$X\cap Y = \{x \in X : x \in Y\} $$

En nuestro ejemplo anterior, $X=\{2,4,6,8,10,12,14,16,18,20\}, Y=\{2,3,5,7,11,13,17,19\}$, y $X \cap Y = \{2\}$ pues es el único par primo.

Como puedes ver, gráficamente el área que representa la intersección entre dos conjuntos es:

Ahora vamos a ver algunas propiedades como: la conmutatividad y la asociatividad .

Proposición. La intersección es conmutativa, es decir: $$X \cap Y = Y \cap X .$$

Demostración. Recuerda que por el axioma 4, tenemos que demostrar dos cosas: primero que $X \cap Y \subset Y \cap X$ y después que $Y \cap X \subset X \cap Y$. Vas a ver una similitud en demostrar este tipo de proposiciones de igualdad de conjuntos a las demostraciones que usan el «si y solo si», pues primero tendremos que demostrar la contención de «ida» y después la del «regreso». Y esto tiene sentido, pues demostrar la igualdad entre conjuntos es demostrar la doble implicación de que un elemento pertenezca a alguno de los dos conjuntos, pues habría que demostrar:

$$\forall x \big( x \in X \cap Y \Leftrightarrow x \in Y \cap X) .$$

Así que empezamos nuestra demostración probando una contención.

$\subset)$ Consideremos $x \in X\cap Y$. Para demostrar que $X \cap Y \subset Y \cap X$, habría que demostrar que cada elemento del primer conjunto se encuentra en el segundo, así que hay que demostrar que $ x \in Y \cap X$. Para ello, nota que $$X \cap Y = \{x \in X: x \in Y\} = \{x \in X: P(x)\}$$ son los elementos de $X$ que cumplen la proposición $P(x):x \in Y$. Entonces sabemos que $x \in Y$. Por otro lado, sabemos que la proposición $Q(x): x \in X$ se cumple, entonces $x$ pertenece al conjunto

$$x \in \{y \in Y: Q(y)\} = \{y \in Y: y \in X\} = Y \cap X$$

puesto que $x$ pertenece a $Y$ y cumple $Q(x)$. De esta forma $X \cap Y \subset Y \cap X$.

$\supset )$ Nota que para demostrar la otra contención, únicamente deberíamos copiar la demostración anterior cambiando de lugar $X$ con $Y$, es decir que nuestra demostración sería muy parecida a la primera contención que hicimos. Lo podríamos poner tal cual haciendo los cambios mencionados, sin embargo puede ser redundante. En este caso diremos que «La demostración de este caso es análoga a la anterior», que significa: para hacer esta demostración tendríamos un razonamiento muy parecido a la anterior sin ningún modificación interesante, pues seguiríamos los mismos pasos. Muchas veces verás este tipo de oraciones en demostraciones, siendo una herramienta para ahorrar palabras y no ser redundante, pues el razonamiento para hacer alguna demostración (en este caso la segunda contención), sigue un razonamiento casi idéntico a algo ya hecho (en este caso la primera contención).

De esta manera, al ser esta contención análoga a la anterior, $Y \cap X \subset X \cap Y$

$\square$

Proposición. La intersección es asociativa, es decir $$X \cap (Y \cap Z) = (X \cap Y) \cap Z$$.

Demostración. Podríamos hacer esta demostración como la anterior donde hicimos la conmutatividad, sin embargo emplearemos otro razonamiento en donde cada uno de los pasos es válido. Para ello nota que queremos demostrar que $$X \cap (Y \cap Z) = (X \cap Y) \cap Z$$ y que $$(X \cap Y) \cap Z = X \cap (Y \cap Z)$$. Y para esto debemos de demostrar que $$\big( x \in X \cap (Y \cap Z) \big) \Leftrightarrow \big(x \in (X \cap Y) \cap Z\big).$$

Ahora nota que

\begin{align*}
x \in X \cap (Y \cap Z)& \Leftrightarrow (x \in X) \land \big((x \in Y)\land(x \in Z) \big)\\
& \Leftrightarrow \big((x \in X) \land (x \in Y)\big) \land (x \in Z) \ \ \ (\text{Por la asociatividad de la disyunción}) \\
& \Leftrightarrow x \in (X \cap Y) \cap Z \\
\end{align*}

De esta manera hicimos una cadena de equivalencias lógicas válidas, empezamos con un elemento en el conjunto $X \cap (Y \cap Z)$ y demostramos que ese elemento estaba en $(X \cap Y) \cap Z$ y viceversa. Esto lo hicimos con el conocimiento que ya sabíamos, y como antes ya habíamos demostrado que la disyunción es asociativa, entonces cada paso lógico es válido y con esto demostramos la igualdad entre conjuntos.

$\square$

Unión

Ahora en vez de fijarnos en donde dos conjuntos se intersectan, pensemos en cuando dos conjuntos se unen. Para esto, considera el siguiente ejemplo. Digamos que $X = \{ 1,2,3,4,5\}$ y $Y = \{4, 5,6,7 \}$ son conjuntos de números enteros.

Los conjuntos $X,Y$ son los siguientes:

El siguiente paso es construir el conjunto que tiene como elementos a los elementos de ambos conjuntos ¿Recuerdas el axioma 4? Este nos hablaba de un conjunto que contiene a todos los elementos que son elementos del mismo conjunto. Suena confuso pero este axioma junto al axioma 3 justifican la existencia de este conjunto. Veamos como lo podemos construir:

Por el axioma 3, existe el conjunto $\{X,Y\}$, es decir que existe el conjunto $A = \{\{1,2,3,4,5\}\{4,5,6,7\}\}$.

Después, como existe este conjunto $A$, por el axioma 4, existe un conjunto cuyos elementos son elementos que pertenecen a elementos de $\{X,Y\}$, entonces para dicho conjunto que llamaremos $X \cup Y$, sus elementos son $$X \cup Y = \{x: x \in X \lor x \in Y\}$$.

Entonces el conjunto unión de $X$ y $Y$ $X \cup Y = \{1,2,3,4,5,6,7\}$, pues es el conjunto que contiene a todos los elementos de ambos conjuntos.

Definición. El conjunto unión de dos conjuntos $X,Y$ es el conjunto: $$X \cup Y = \{x: x \in X \lor x \in Y\} $$

De manera gráfica, podemos ver la unión como:

Ahora enunciaremos las proposiciones que demostramos para la intersección, pero ahora usando la unión:

Proposición. La unión es conmutativa.

Demostración. Considera a $X$ y $Y$ dos conjuntos, entonces

\begin{align*}
x \in X \cup Y & \Leftrightarrow (x \in X) \lor (x \in Y)\\
& \Leftrightarrow (x \in Y) \lor (x \in X) \ \ \ (\text{Por la conmutatividad de la conjunción}) \\
& \Leftrightarrow x \in Y \cup X
\end{align*}

$\square$

Proposición. La unión es asociativa.

Para esta última no daremos demostración, sin embargo es una demotración parecida a su contraparte de la intersección.

Una vez que hemos establecido estas dos operaciones, solo falta una más por revisar ahora. Si la intersección es la disyunción y la unión es la conjunción, la siguiente que definiremos es la negación.

Complemento de conjuntos

Cuando estemos hablando de conjuntos, muchas veces estaremos dentro de un contexto de conjuntos, o un Conjunto universal, dentro del cual siempre estaremos trabajando. Por ejemplo, si estamos en cálculo de una variable, todos los conjuntos o casi todos sobre los que estemos trabajando serán conjuntos de números reales. Nota ahora que cuando estuvimos dando los ejemplos de conjuntos paraexplicar la unión y la intersección, decíamos que $X,Y$ eran conjuntos de números enteros. Es decir, estábamos acordando que nuestro conjunto universal eran los números enteros $\mathbb{Z}$.

Muchas veces el contexto sobre el conjunto universal sobre el que estamos trabajando no será especificado y se puede inferir, pues si estamos trabajando por ejemplo con números reales, no es posible que un conjunto tenga números complejos, por ejemplo.

Ahora con esto acordado, vamos a ver que cualquier conjunto $X$ en un conjunto universal $U$ se puede escribir de la siguiente manera: $$ X = \{x \in U: x \in X\}.$$

Es decir, podemos escribir al conjunto $X$ como los elementos del conjunto universal que están en $X$. Así, definiremos el complemento de $X$ o $X^c$ como: $$X^c = \{x \in U:x \not \in X\}. $$

Definición. Sea $X$ un conjunto sobre el conjunto universal $U$, entonces definimos el complemento de $X$ como $$X^c = \{x \in U: x\not \in X\}^* $$

Por ejemplo, considera $X = \{2,4,6,8,10\}$ al conjunto de los números pares dentro del conjunto de los números enteros del 1 al 10. Entonces en este caso $U = \{1,2,3,4,5,6,7,8,9,10\}$ y su complemento es $X^c = \{1,3,5,7,9\}$.

Gráficamente, podemos ver al complemento como:

Algunas de las cosas que podemos decir del complemento son:

Proposición. Sea $X$ un conjuntos dentro del conjunto universal $U$. Entonces:

$X \cup X^c = U$
$U^c = \emptyset$

Demostración.

Esta proposición nos quiere decir que un conjunto junto al complemento «llenan» todo el espacio. Para esto, nota que
\begin{align*}
x \in X^c \cup X & \Leftrightarrow x \in X^c \lor x \in X \\
& \Leftrightarrow x \in \{x \in U : x \in X \lor x \not \in X\}
\end{align*}
Ahora nota que $P(x): x \in X \lor x \not \in X$ es una tautología, es decir, cualquier elemento de $U$ cumple dicha definición, así,
\begin{align*}
x \in X^c \cup X & \Leftrightarrow x \in X^c \lor x \in X \\
& \Leftrightarrow x \in \{x \in U : x \in X \lor x \not \in X\}\\
& \Leftrightarrow x \in U
\end{align*}
Nota primero que ya hemos dicho que $\emptyset$ es subconjunto de cualquier conjunto, así se tiene la contención $\emptyset \subset U$. Para la otra contención, supón que no sucede que $U \subset \emptyset$. Entonces se tiene que existe un elemento $x\in U$ que cumple:$$ x\in \{x \in U: x \not \in U\}. $$ Donde se tendría que $x \in U \land x \not \in U$, lo cual es imposible. Entonces $U \subset \emptyset$. De esta manera se tiene la igualdad entre conjuntos.

$\square$

Nota

*: En la literatura, también puedes encontrar escrito el complemento de un conjunto $A$ escrito como $\bar A$ en lugar de $A^c$

Más adelante…

Ahora ya hemos visto tres operaciones básicas en la teoría de conjuntos, junto a la definición del conjunto universal, que recuerda: no siempre verás implícitamente y puede ser un conjunto que dependa del contexto. En la siguiente entrada veremos dos operaciones más que se pueden definir en términos de las que vimos ahora, así como otras propiedades de las operaciones.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Sea $N = \{1,2,3,4,6,9,10,15,20,30\}$ y $X = \{x \in \mathbb{Z}: x= 2n, n \in N \}$, encuentra:
- $X \cap N$
- $X \cup N$
Demuestra que la unión es asociativa.
Demuestra que la unión de subconjuntos de un conjunto $X$ siempre está contenida en $X$.
Demuestra que si $Y \subset X $ y $Z \subset X$ entonces $Y \cup Z \subset X$
Demuestra que si $X \subset Y$ son dos conjuntos, entonces:
- $X \cap Y = X$
- $X \cup Y = Y$
Demuestra que:
- $X^c \cap X^c = \emptyset$
- $\emptyset^c = U$

Entradas relacionadas

Ir a Álgebra Superior I
Entrada anterior del curso: Problemas de conjuntos y subconjuntos
Siguiente entrada del curso: Leyes de De Morgan y diferencia simétrica de conjuntos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Álgebra Superior I: Axiomas de los conjuntos.

Por Guillermo Oswaldo Cota Martínez

Deja un comentario

Introducción

Hasta ahora, hemos introducido intuitivamente la idea de qué es un conjunto, cómo describirlos y qué representan. En esta entrada vamos a hablar de tres temas importantes para trabajar con más ideas de los conjuntos: contención, subconjuntos y conjunto potencia.

Las primeras dos van de la mano, y serán una forma de definir subcolecciones dentro de una colección (a la que ahora llamamos conjunto) y nos permitirán manejar con mayor facilidad conceptos que veremos más adelante sobre las operaciones entre conjuntos.

Mientras tanto, el conjunto potencia nos hablará de la forma de combinar elementos dentro de un mismo conjunto, que es un concepto que tiene propiedades muy interesantes.

Estos tres conceptos serán fundamentales para axiomatizar la teoría de los conjuntos.

Axiomatizando los conjuntos

En la entrada pasada, dimos una peequeña introducción a la teoría de conjuntos. Hablamos de su idea intuitiva y algunos ejemplos de su uso en otras materias. Ahora nos toca entrar un poco más en fondo a sus reglas, esto es, sus axiomas.

Para poder hablar de los conjuntos, su idea y la forma en que se manejan, vamos a establecer algunos axiomas que describirán la teoría de conjuntos. Todo objeto matemático que sigan el sistema axiomático, serán conjuntos. Para ello, primero es fundamental declarar que existen los conjuntos, de otra forma no estaríamos trabajando con nada:

Axioma 1. Existe al menos un conjunto.

Este axioma nos permitirá trabajar con conjuntos, pues nos asegurará que al menos existe un conjunto $V$ con el que podremos trabajar los siguientes axiomas. Sin este axioma, no podríamos seguir trabajando la teoría, pues no tendríamos con qué trabajar.

Los siguientes axiomas serán los que nos darán la intuición de qué se puede y no puede hacer con un conjunto.

Axioma 2. Si X es un conjunto y $P(x)$ es una proposición que depende de elementos $x \in X$, entonces:

$$\{x \in X : P(x) \text{ se cumple}\} $$

también es un conjunto.

En la entrada pasada, dimos una idea intuitiva de este axioma, que nos dice que si tenemos un conjunto $X$ y cualquier proposición $P(x)$ de elementos de $X$ entonces podemos construir nuevos conjuntos a partir de los elementos de $X$ que cumplen cierta propiedad. Por ejemplo, piensa que $X$ es el conjunto de todos los zapatos, entonces un conjunto nuevo puede formarse a partir de la proposición $P(x): $»$x$ es amarillo», entonces el nuevo conjunto $\{ x \in X : P(x) $ se cumple $\}$ es el conjunto de los zapatos amarillos. Otro ejemplo de esto, sería el conjunto de los números pares que podemos definir a partir de los números enteros $\mathbb{Z} = \{\dots,-3,-2,-1,0,1,2,3,\dots\}$. Los número pares se pueden definir como: $2\mathbb{Z} = \{x \in \mathbb{Z} : x = 2n, n \in \mathbb{Z} \}$ es decir, es el conjunto creado por los número enteros multiplicados por dos.

Creando el conjunto vacío.

Antes de seguir con los demás axiomas, vamos a mostrar una consecuencia de los dos primeros axiomas. Observa que por el primer axioma, existe al menos un conjunto al que llamaremos $X$. Y el segundo axioma nos dice que con cualquier conjunto, se puede obtener un conjunto a partir de aquellos elementos que cumplan alguna proposición que depende de elementos de $X$, entonces consideremos la siguiente propocisión:

$$P(x) : x \neq x $$

Esta proposición nos dice que un objeto $x$ no es igual a sí mismo, lo cual es imposible, ninguna cosa u objeto matemático va a cumplir esta proposición. Es decir:

$$\forall x (\neg P(x)) $$

se cumple. ¿Entonces qué conjunto será el conjunto: $\{x \in X : P(x)\} = \{x \in X : x \neq x\} $?

Pues es un conjunto que no tiene a ningún elemento, pues ningún elemento $x$ de $X$ puede cumplir esa definición. Esto no representa ninguna contradicción a algún axioma, lo que nos dice es que existe un conjunto que no tiene a ningún elemento. A este conjunto lo conocemos como conjunto vacío y lo representamos como $\emptyset$. A veces también lo encontrarás como unas llaves sin nada adentro, es decir $\{\}$.

Una vez dicho esto, vamos construyendo poco a poco más resultados, sigamos con los siguientes axiomas:

Axioma 3. Si $X$ y $Y$ son conjuntos, entonces $\{X,Y\}$ es un conjunto.

Esto nos permite «poner» conjuntos, dentro de un conjunto. Es decir, podemos hacer dos conjuntos en los que cada elemento sea un conjunto. Por ejemplo, considera $X = $ el conjunto de zapatos amarillos y $Y = $ el conjunto de los Blergs. Entonces existe el conjunto $Z=\{X,Y\}$ un conjunto que solo tiene dos elementos: el conjunto de los zapatos amarillos y el conjunto de los Blergs. OJO: un zapato amarillo NO pertenece al conjunto $Z$, lo que sí pertenece al conjunto es el conjunto de todos los zapatos amarillos. Es decir, si $x$ es un zapato amarillo, entonces $x \in X$ pero no sucede que $x \in Z$. Lo que sí sucede es $X \in Z$.

De este axioma, podemos deducir la siguiente proposición:

Proposición: Si $X$ es un conjunto entonces $\{X\}$ tambien es un conjunto.

Demostración. Sea $X$ un conjunto. No hay nada en la definición del axioma 3 que impida que $X=Y$, entonces lo que nos dice el axioma es que si tenemos dos conjuntos $X,Y$ donde $X=Y$ entonces el conjunto $W=\{X,Y\}$ es un conjunto, y podemos reescribir este como $\{X,X\}$. Ahora, recuerda que hemos dicho con anterioridad que realmente al describir a un conjunto, solo nos interesan los elementos distintos que lo conforman, es decir, está de más repetir dos veces $X$ dentro de los corchetes que representan los elementos del conjunto $W$, entonces $W=\{X\}$ es un conjunto.

$\square$

Axioma 4. Si $X$ y $Y$ son dos conjuntos, diremos que $X=Y$ (el conjunto $X$ es igual al conjunto $Y$) si tienen exactamente los mismos elementos. Esto se puede describir usando lógica proposicional de la siguiente manera:

$$\big( X=Y\big) \Leftrightarrow \forall x\big(x \in X \Leftrightarrow x \in Y \big)$$

Axioma 5. Si $X$ es un conjunto, entonces el conjunto de los elementos que pertenecen a por lo menos un elemento de $X$ forman un conjunto (unión).

Vamos a leer con más calma el axioma. Primero tenemos un conjunto $X$, digamos el conjunto de todos los grupos dentro de una universidad. Entonces un alumno de esa universidad pertenece al menos a algún grupo. De esta manera, el conjunto de todos los alumnos de la universidad, forma un conjunto. Veamos esto con notación matemática:

Sea $U$ los grupos de la universidad: $\{G_1,G_2,G_3\}$, es decir, cada elemento cada grupo está formado de estudiantes, es decir cada alumno es elemento de un grupo, digamos

$$G_1 = \{A_1,A_2,A_3\}$$

$$G_2 = \{B_1,B_2,B_3\}$$

$$G_3 = \{C_1,C_2,C_3\}$$

Entonces el axioma nos dice que el conjunto de todos los elementos (alumnos) que pertenecen al menos a un elemento de $X$ (grupos del conjunto $U$), forma otro conjunto. En nuestro caso, sería el conjunto de todos los alumnos: $\{A_1,A_2,A_3,B_1,B_2,B_3,C_1,C_2,C_3\}$.

Quizá esta idea de «los elementos de un conjunto a su vez también tienen elementos» puede ser un poco difícil de entender y quizá hasta un poco filosófica: ¿Hasta qué punto podríamos usar el raciocinio para extraer las partes que componen a un todo? Es decir: Si consideramos el conjunto de todos los zapatos: ¿Qué significa ahora que haya un elemento que pertenezca a un zapato? las respuestas pueden ser variadas, y puede que incluso se te ocurran unas distintas a otra persona que lea esto, así que velo de la siguiente forma: si tenemos la capacidad de hacer una intuición de separar un elemento de algún conjunto en sus partes, entonces podemos hacer otro conjunto con esas partes. Conforme vayas avanzando en tu carrera matemática, vas a poder ir aclarando muchas de estas ideas, volveremos a este axioma más adelante.

Para el siguiente axioma, primero introduciremos algunos conceptos:

Contención entre conjuntos

Recuerda que los conjuntos los pensamos como «colecciones de algo», pueden ser conjuntos de zapatos, conuntos de autos o conjuntos de animales, por mencionar algunos. Para introducir el axioma que sigue, primero hablaremos de la contención y para explicarlo, veamos el conjunto de unas criaturas a las que les llamamos Blorgs y nos ayudaron en la entrada anterior. Lo que tienes que saber de ellos, es que se dividen en Blargs, Blergs y Blurgs según su color (amarillo,rojo y azul respectivamente), como lo puedes ver en la siguiente imagen:

Ahora, llamemos a los 3 Blargs: «blargmino», «blargastacia» y «blargencio», de manera que el conjunto de los Blargs es:

$$\text{Blargs} = \{ \text{ blargmino, blargastacia , blargencio }\}$$.

Ahora, nota que decimos que «blargmino pertenece al conjunto de los Blorgs», pero a su vez también pertenece al conjunto de los Blargs, entonces también podríamos decir blargmino pertenece al conjunto de los Blorgs». ¿Notas que no necesitamos rigor al decir qué es y qué no es un conjunto? Con el simple hecho de poder abstraer sus partes o elementos, es suficiente. Pero ahora surge una pregunta natural: ¿Existe alguna relación entre el conjunto de los $B_a$ Blargs y el conjunto $B_o$ de todos los Blorgs? En cuyo caso, nota que:

$$\forall x(x \in B_a \Rightarrow x \in B_o) $$

Es decir, todo blarg es un blorg. Diremos entonces que los Blargs con un subconjunto de los Blorgs. Ya que todo elemento de $B_a$ está en $B_o$.

Definición. Sean $A$ y $B$ dos conjuntos. Diremos que $A$ es un subconjunto de $B$ o que $A$ está contenido en $B$ si:

$$\forall x(x \in A \Rightarrow x \in B). $$

Y lo escribiremos como $A \subset B$*

Ahora, nota que cualquier conjunto contiene al conjunto vacío.

Proposición. Sea $X$ un conjunto, entonces $\emptyset \subset X$.

Demostración. Vamos a demostrar esto por contradicción, suponiendo que $\emptyset \not \subset X$, es decir supongamos que $\neg \big( \forall x(x \in \emptyset \Rightarrow x \in X) \big) = \exists x(x \in \emptyset \land x \not \in X) $. Entonces bajo nuestra suposición, existe un elemento $x$ en $\emptyset$ pero $x \not \in X$. ¿Puedes ver porqué esto es una contraidcción? Pues estamos suponiendo que existe un elemento en $\emptyset$, pero por la forma en que definimos al conjunto vacío, esto significaría que existe un elemento $x$ que cumple que $x \neq x$, lo cual es imposible. ¿Cuál fue nuestro error? Pues suponer que no se cumplía $\emptyset \subset X$. Por lo tanto, $\emptyset \subset X$

$\square$

Axioma 6. Si $X$ es un conjunto, entonces existe un conjunto conformado por todos los subconjuntos de $X$. Nos referiremos a este conjunto como el conjunto potencia y lo denotaremos por $\mathcal P (X)$.

Nota que nuestra definición de un subconjunto $Y$ de $X$ nos pide que todo elemento de $Y$ esté en $X$, así que el conjunto potencia será aquel conjunto en el que cada elemento será un conjunto que es subconjunto de nuestro conjunto original. Pongamos un ejemplo para que lo veas mejor:

Ejemplo. Considera al conjunto $X = \{1,2,3\}$ el conjunto con los números enteros del $1$ al $3$, entonces el conjunto potencia está dado por todos sus subconjuntos: $\emptyset, \{1\},\{2\},\{3\},\{1,2\},\{2,3\},\{1,3\},\{1,2,3\}$ es decir, el conjunto potencia de $X$ es: $$\mathcal P(X) =\{\emptyset, \{1\},\{2\},\{3\},\{1,2\},\{2,3\},\{1,3\}, X\} $$

Con estos seis axiomas serán con los que trabajaremos, en resumen, los axiomas son los siguientes:

Axioma 1	Existe un conjunto.
Axioma 2	Podemos hacer conjuntos a partir de proposiciones que cumplen o no cumplen elementos de algún conjunto.
Axioma 3	Si $X$ y $Y$ son conjuntos, entonces $\{X,Y\}$ es un conjunto.
Axioma 4	Dos conjuntos son iguales si todos sus elementos son iguales.
Axioma 5	Existe un conjunto que tiene como elementos a todos los elementos que pertenecen a algún elemento de $X$.
Axioma 6	Para cada conjunto $X$, existe su conjunto potencia $\mathcal P (X)$ cuyos elementos son los subconjuntos de $X$.

Notas

*: Algunos autores usan la notación $\subseteq$ para detonar que «el subconjunto está contenido estrictamente o es igual», por ejemplo si decimos «X \subseteq Y» diremos que cada elemento de $X$ está en $Y$ entonces puede que $X$ sea el mismo que $Y$, nosotros nos apegaremos a la notación $\subset$ para decir que un subconjunto está contenido estrictamente o es igual, y usaremos la notación $\subsetneq$ para denotar la contención estricta, es decir, $X \subsetneq Y$ si y solo si para cada $x \in X \rightarrow x \in Y$ pero existe $y \in Y \land y \not \in X$.

Más adelante…

Ahora que ya hemos establecido las reglas que seguirán los conjuntos, es hora de hablar sobre algunas operaciones dentro de esta teoría. Sobre todo hablaremos de Intersecciones, Uniones y Complementos de conjuntos.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Demuestra que las siguientes afirmaciones son equivalentes:
- $X=Y$
- $ \forall x (x \in X \Leftrightarrow x \in Y)$
- $(X \subset Y) \land (Y \subset X) $
¿Es cierto que el conjunto vacío es único?
¿Cuál es el conjunto potencia de $\{1,2,3,4\}$?
Demuestra que $X=Y$ si y solo si $\mathcal P(X) = \mathcal P(Y)$.

Entradas relacionadas

Ir a Álgebra Superior I
Entrada anterior del curso: Conjuntos y elementos
Siguiente entrada del curso: Problemas de conjuntos y subconjuntos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»