Archivo de la etiqueta: Operaciones de conjuntos

Álgebra Superior I: Leyes de De Morgan y diferencia simétrica de conjuntos

Por Guillermo Oswaldo Cota Martínez

2 respuestas

Introducción

Hasta ahora ya hemos visto cómo juntar dos conjuntos (unión), cómo encontrar elementos en común entre dos conjuntos (intersección), y hemos considerado cualquier elemento excepto los que están dentro de un conjunto (complemento). Ahora vamos a hablar de otros dos conectores: La diferencia y la diferencia simétrica. Estos dos nos permitirán a hablar de los elementos de un conjunto $A$ sin considerar los elementos de otro conjunto $B$, así como de la unión de ambos conjuntos a excepción de su intersección. Después hablaremos de algunas propiedades conocidas como las leyes de De Morgan.

La Diferencia

Habrá ocasiones en que nos interesará diferencias algunos conjuntos de otros. Por ejemplo, imagina que quieres comprar una chamarra, visitando un sitio web te das cuenta de que hay una promoción en algunas prendas, incluidas las chamarras, entonces decides que compraras una chamarra solo si tiene descuento. Considera los conjuntos que describen artículos de la página web:

$$A = \{x : x \text{ es chamarra} \} $$

$$B = \{x : x \text{ no tiene descuento} \} $$

Si solo pudiéramos distinguir entre esos dos conjuntos, a nosotros nos gustaría encontrar una chamarra $x$ del conjunto $A$ que no esté en el conjunto $B$. Esto puede describirse como:

$$\{ x: x \in A \land x \not \in B \} = \{x: x \in A \land x \in B^c \} $$

Nota ahora que esto se puede escribir como:

$$ A \cap B^c =\{x: x \in A \land x \in B^c \} $$

Esto es justamente a lo que nosotros llamamos diferencia entre conjuntos, que representa la idea de «restar conjuntos», es decir, considerar los elementos de un conjunto exceptuando los elementos que también están en otro conjunto específico.

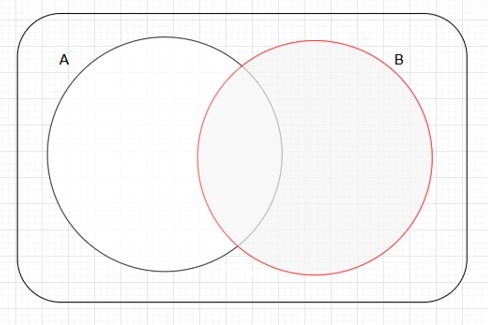
Definición. Sean $X$ y $Y$ dos conjuntos. Definimos la diferencia de conjuntos $X/Y$ como:

$$X \setminus Y = X \cap Y^c .$$

Y gráficamente se ve de la siguiente manera:

Diferencia simétrica

Ahora imagina que en una universidad se ofrece el curso de Lógica y el curso de Teoría de Conjuntos. La universidad quiere ver cuántos alumnos se interesan únicamente por la materia de Lógica sin la Teoría de Conjuntos y viceversa para ver cuántos grupos abrir.

Puesto que la universidad piensa abrir un curso que abarca Conjuntos y Lógica para los alumnos que quieren tomar los dos cursos a la vez, por ahora no nos interesan los alumnos que estén en la intersección del conjunto de alumnos que quieren tomar el curso de Lógica con el conjunto de alumnos que quieren tomar el curso de Teoría de Conjuntos. Dicho de otra manera, si el conjunto de los alumnos interesados en un curso de Lógica lo representamos por $L$ y al conjunto de los alumnos interesados en un curso de Teoría de Conjuntos lo representamos por $C$, entonces los alumnos que están interesados en un curso de Lógica y no de Conjuntos es $L \setminus C$ y el conjunto de alumnos que están interesados en un curso de Conjuntos y no de Lógica es $C \setminus L$.

Nota ahora que entre los dos conjuntos, hay $(L \setminus C) \cup (C \setminus L)$ alumnos que no tomarán el curso de Conjuntos y Lógica pero si una materia en alguna de esas dos disciplinas. A este conjunto lo llamamos la diferencia simétrica o unión disyuntiva entre conjuntos.

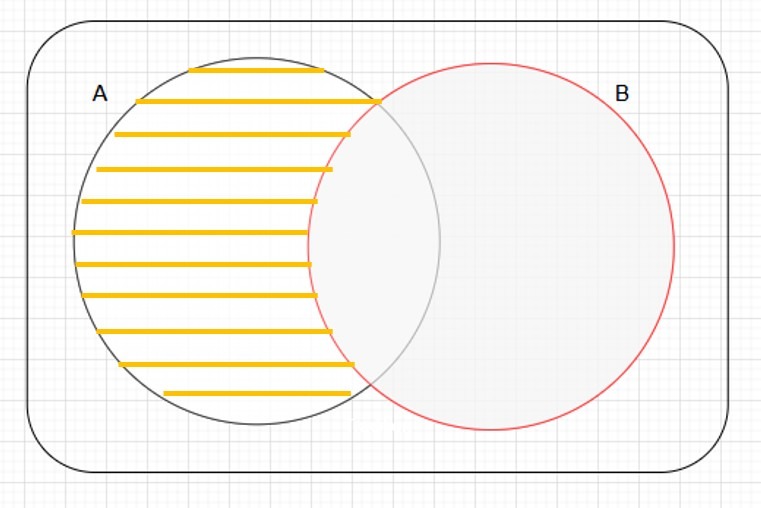
Definición . Sean $X$ y $Y$ dos conjuntos. La diferencia simétrica o unión disyuntiva de los conjuntos $X$ y $Y$ se define como:

$$X \vartriangle Y = (X \setminus Y) \cup (Y \setminus X) $$

Y gráficamente se ve como:

Leyes de De Morgan

Una vez que ya definimos los operadores que vamos a usar en la teoría de conjuntos, vamos a anotar una propiedad importante de los conjuntos que tiene su contraparte en la lógica proposicional. Y nos habla de cómo encontrar el complemento de la unión y la intersección.

Teorema (Leyes de De Morgan). Sean $X$ y $Y$ dos conjuntos dentro del conjunto universal $U$. Entonces:

  1. $(X \cap Y)^c = X^c \cup Y^c$
  2. $(X \cup Y)^c = X^c \cap Y^c$

Demostración. En esta entrada, solo demostraremos la primera parte, la segunda parte tendrá un argumento muy similar a la demostración que presentaremos a continuación.

Para demostrar que $(X \cup Y)^c = X^c \cap Y^c$, necesitaremos considerar un elemento $x$ y probar que $x \in (X \cup Y)^c$ si y solo si $ x\in X^c \cap Y^c$. Para ello, nota lo siguiente:

\begin{align*}
x \in (X \cap Y)^c &\Leftrightarrow x \in \{x \in U : \neg(x \in X \cap Y) \} \\
&\Leftrightarrow x \in \{x \in U: \neg (x \in X \land x \in Y) \} \\
&\Leftrightarrow x \in \{x \in U: \neg( x \in X ) \lor \neg (x \in Y) \} \ \ \ \ \text{ ( Por las leyes de De Morgan de la lógica)} \\
&\Leftrightarrow x \in \{x \in U: x \in X^c \lor x \in Y^c \}\\
&\Leftrightarrow x \in X^c \cup Y^c
\end{align*}

De esta manera, $(X \cap Y)^c = X^c \cup Y^c$. De manera análoga se cumple la otra proposición.

$\square$

Este teorema lo que nos quiere decir es que la forma de encontrar el complemento de la unión es intersectando el complemento de los conjuntos, y el complemento de la intersección es la unión de los complementos.

Corolario. Las siguientes proposiciones se cumplen con $X,Y,Z$ tres conjuntos:

  1. $(X \cup Y \cup Z)^c = X^c \cap Y^c \cap Z^c $
  2. $(X \cap Y \cap Z)^c = X^c \cup Y^c \cup Z^c$

Demostración. De manera similar al teorema anterior, solo demostraremos el primer inciso.

Para esto, notemos que:

\begin{align*}
(X \cup Y \cup Z)^c &= (X \cup Y)^c \cap Z^c \\
&= X^c \cap Y^c \cap Z^c
\end{align*}

De manera análoga se cumple la segunda proposición.

$\square$

Más adelante, tendremos herramienta matemática para demostrar que las leyes no solo se cumplen para la dos o tres variables, sino que para una cantidad arbitraria de términos. En otras palabras, podremos demostrar que:

Proposición. Sea $X = \{X_1,X_2,\dots,X_n\}$ una colección finita de conjuntos. Entonces:

  1. $(X_1 \cup X_2 \cup \dots \cup X_n)^c = X_1^c \cap X_2^c \cap \dots \cap X_n^c $
  2. $(X_1 \cap X_2 \cap \dots \cap X_n)^c = X_1^c \cup X_2^c \cup \dots \cup X_n^c$

Por ahora, nos quedaremos únicamente en el caso de tres variables. A este punto, conviene también decir que a veces encontrarás en la literatura la el término $X_1 \cup X_2 \cup \dots \cup X_n$ escrito como $\bigcup_{i=1}^nX_i$ y esta es únicamente una forma de notación que representa la unión de una colección de conjuntos. De manera similar, $X_1 \cap X_2 \cap \dots \cap X_n = \bigcap_{i=1}^nX_i $. De esta manera, la proposición anterior se resume en:

  1. $\big( \bigcup_{i=1}^n X_i \big)^c = \bigcap_{i=1}^n X_i^c$
  2. $\big( \bigcap_{i=1}^n X_i \big)^c = \bigcup_{i=1}^n X_i^c$

Otras propiedades de los conjuntos

A continuación anotamos otras propiedades que tienen los conjuntos, algunas de las cuales ya hemos revisado. Sean $X,Y$ y $Z$ tres conjuntos en el conjunto universal $U$, la siguiente tabla resume algunas propiedades que se cumplen.

Propiedad
Asociatividad de los conjuntos\begin{align*}
X \cup (Y \cup Z) &= (X \cup Y) \cup Z \\
X \cap (Y \cap Z) &= (X \cap Y) \cap Z
\end{align*}
Distributividad de la unión y la intersección\begin{align*}
X \cap (Y \cup Z) &= (X \cap Y) \cup (X \cap Z) \\
X \cup (Y \cap Z) &= (X \cup Y) \cap (X \cup Z)
\end{align*}
Idempotencia de la unión e intersección\begin{align*}
X \cup X = X = X \cap X
\end{align*}
Conmutatividad de unión e intersección\begin{align*}
X \cup Y = Y \cup X \\
X \cap Y = Y \cap X
\end{align*}
Leyes de identidad de unión\begin{align*}
X \cup \emptyset &= X \\
X \cup U &= U
\end{align*}
Leyes de identidad de intersección\begin{align*}
X \cap \emptyset &= \emptyset \\
X \cap U &= X
\end{align*}
Unión de complementos\begin{align*}
X \cup X^c = U
\end{align*}
Intersección de complementos\begin{align*}
X \cap X^c = \emptyset
\end{align*}
\begin{align*}
(X^c)^c = X
\end{align*}
Leyes de De Morgan\begin{align*}
(X \cap Y)^c &= X^c \cup Y^c\\
(X \cup Y)^c &= X^c \cap Y^c
\end{align*}

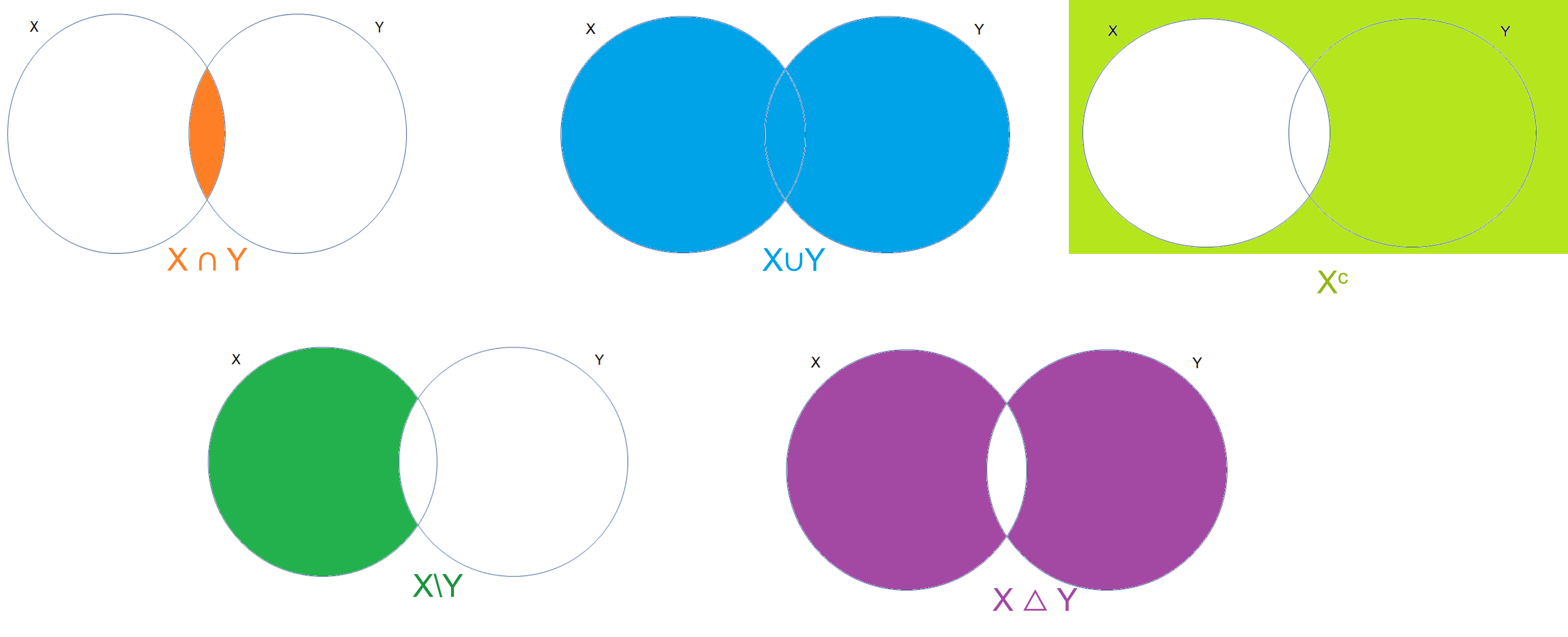
Y para resumir los operadores entre conjuntos, se encuentra la siguiente imagen:

Notas

*: En la literatura, también puedes encontrar la diferencia entre dos conjuntos $X$ y $Y$ escrita como $X – Y$ en lugar de $X \setminus Y$.

Más adelante…

Con esta entrada acabamos la primer unidad. Hasta ahora hemos sentado las bases matemáticas de la teoría de conjuntos, en la siguiente unidad vamos a seguir hablando de conjuntos, pero introduciremos un nuevo concepto: las relaciones entre conjuntos. Estas nos permitirán empezar a hablar de funciones, un recurso muy utilizado en todas las áreas de las matemáticas.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Sean $P, Q, R, S$ cuatro proposiciones y $A = \{x: (P(x) \land Q(x)) \lor R(x) \}$, $B = \{x: (R(x) \land \neg P(x)) \lor S(x) \}$, $C = \{ x: S(x)\}$. Encuentra:
    • $A \cup B$
    • $B^c$
    • $A \setminus B$
    • $A \cap (B \cap C)$
    • $A \vartriangle C$
  2. Demuestra que $(X \cup Y)^c = X^c \cap Y^c$
  3. Demuestra que $(X^c)^c = X$
  4. Describe al conjunto $(X \vartriangle Y)^c \setminus (X \setminus Y)^c$ en términos de complementos, la unión y la intersección.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Cálculo Diferencial e Integral I: Repaso. Teoría de Conjuntos. (Parte 2)

Por Karen González Cárdenas

Deja un comentario

Introducción

En la entrada anterior vimos qué significa ser un conjunto y cuál es la notación que se utiliza para denotarlos. Además de un par de conceptos: pertenencia a un conjunto y subconjunto.

Retomaremos todo lo antes mencionado para ahora presentar las llamadas Operaciones con conjuntos. Éstas estarán presentes no sólo en este curso, sino también en varios de los textos de matemáticas que consultarás a lo largo de tu vida académica.

Operaciones con conjuntos

A lo largo de esta entrada haremos uso de una representación gráfica de los conjuntos llamada Diagramas de Venn para poder visualizar cada una de las operaciones que definiremos a continuación.

Ejemplo de diagrama de Venn

Definición (Unión): Sean $A$ y $B$ dos conjuntos. Decimos que la unión de $A$ con $B$ está definida como:

\[ A \cup B:=\left\{ x\mid x\in A \vee x\in B\right\} \text{.}\]

Esto quiere decir que está conformada por los elementos que se encuentran en $A$ o los que se encuentran en $B$. En el siguiente diagrama queda representada por la zona sombreada de azul.

Notación: Utilizamos el símbolo matemático $\vee$ para sustituir a la disyunción «o».

Observación. En este caso al hacer uso de la «o» estamos considerando que esta es inclusiva, lo que quiere decir que es válido que $x$ se encuentre tanto en $A$ como en $B$.

A continuación mostraremos un ejemplo para hacer más clara la definición.

Ejemplo: Supongamos que tenemos los siguientes conjuntos:

\[ A=\left\{0,1, 2, 3, 4\right\} \text{,}\]
\[ B=\left\{0, a,b,c,d,e\right\} \text{.}\]

Si nosotros queremos obtener $A \cup B$, al aplicar la definición anterior tenemos:

\[ A \cup B=\left\{0,1, 2, 3, 4,0,a,b,c,d,e \right\} \text{.} \]

Observamos que al realizar la unión de este par de conjuntos «unimos sus elementos en un sólo conjunto llamado $A \cup B$». Veamos que el 0 es un elemento tanto de $A$ como de $B$, por lo que sólo será necesario escribirlo una vez y así nos queda:

\[ A \cup B=\left\{0,1, 2, 3, 4,a,b,c,d,e \right\} \text{.}\]

Definición (Intersección): Sean $A$ y $B$ dos conjuntos. Decimos que la intersección de $A$ con $B$ está definida como:

\[ A \cap B:=\left\{ x\mid x\in A \wedge x\in B\right\} \text{.}\]

Esto quiere decir que está conformada por los elementos que se encuentran en $A$ y los que se encuentran en $B$. En otras palabras, la intersección está conformada por los elementos en común de $A$ y $B$.

Notación: Utilizamos el símbolo matemático $\wedge$ para sustituir a la conjunción «y».

En el diagrama anterior queda representada por la zona sombreada de verde.

Ejemplo: Retomamos los siguientes conjuntos:

\[ A=\left\{0,1, 2, 3, 4\right\} \text{,}\]
\[ B=\left\{0, a,b,c,d,e\right\} \text{.}\]

Si nosotros queremos obtener $A \cap B$, al aplicar la definición anterior tenemos:

\[ A \cap B=\left\{0 \right\}\text{.} \]

Definición (Diferencia): Sean $A$ y $B$ dos conjuntos. Decimos que la diferencia de $A$ con $B$ está definida como:

\[ A \setminus B:=\left\{ x\mid x\in A \wedge x\notin B\right\}\text{.} \]

Esto quiere decir que está conformada por los elementos que se encuentran en $A$ y que no se encuentran en $B$.

Ejemplo: Retomamos los conjuntos:

\[ A=\left\{0,1, 2, 3, 4\right\} \text{,}\]
\[ B=\left\{0, a,b,c,d,e\right\} \text{.}\]

Si nosotros queremos obtener $A \setminus B$, al aplicar la definición anterior tenemos:

\[ A \setminus B=\left\{1,2,3,4 \right\} \text{.}\]

Vemos que le hemos quitado los elementos a $A$ que tenía en común con $B$. Por lo que el diagrama nos quedaría como:

Teorema: Sean $A$, $B$ y $C$ conjuntos. Tenemos que:

  1. Propiedades conmutativas:
    • \[A \cup B = B \cup A\quad \text{.}\]
    • \[A \cap B = B \cap A\quad\text{.}\]
  2. Propiedades asociativas:
    • \[A \cup (B\cup C) = (A \cup B)\cup C \quad \text{.}\]
    • \[A \cap (B\cap C) = (A \cap B)\cap C \quad\text{.}\]
  3. Propiedades distributivas:
    • \[A \cap (B\cup C) = (A \cap B)\cup (A\cap C)\quad\text{.}\]
    • \[A \cup (B\cap C) = (A \cup B)\cap (A\cup C) \quad\text{.}\]
  4. \[ A\cup A= A \quad\text{.}\] \[A\cap A= A \quad\text{.}\]
  5. \[ A\subseteq A\cup B \quad\text{.} \] \[ A\cap B \subseteq A \quad\text{.}\]
  6. \[ A\cup \emptyset = A \quad\text{.}\] \[A\cap \emptyset= \emptyset\quad\text{.}\]
    • Nota.-$\emptyset$ denota al conjunto vacío: es aquel que no posee elementos.
  7. \[A \setminus (B\cap C) = (A \setminus B)\cup (A\setminus C) \quad\text{.} \]

Demostración:

1.Probaremos la igualdad $A \cup B = B \cup A$, haciendo uso de la definición de igualdad de conjuntos, así tenemos:

$A \cup B = B \cup A$ si y sólo si $A\cup B\subseteq B \cup A$ y $B\cup A\subseteq A\cup B$

Comencemos con $A\cup B\subseteq B \cup A$. Sea $x\in A\cup B$, por la definición de subconjunto queremos probar que $x\in B\cup A$.

Por definición de unión se sigue que $x \in B$ o $x\in A$.

Caso 1: $x \in B$.

Como $x \in B$ entonces $x \in B$ o $x \in A$. Así, por la definición de unión concluimos que: $x\in B\cup A$.

Caso 2: $x \in A$.

Ahora como $x \in A$ entonces $x \in A$ o $x \in B$. Y como el conectivo «o» es conmutativo tenemos: $x \in A$ entonces $x \in B$ o $x \in A$. Así, por la definición de unión concluimos que: $x\in B\cup A$.

Del Caso 1 y Caso 2 concluimos que: $x\in B\cup A$. Por lo tanto, $A\cup B\subseteq B \cup A$.

Ahora probemos la segunda contención: $B\cup A\subseteq A\cup B$. Sea $x\in B\cup A$, así lo que queremos probar es $x\in A\cup B$.

Por definición de unión se sigue que $x \in B$ o $x\in A$.

Caso 3: $x \in B$.

Como $x \in B$ entonces $x \in B$ o $x \in A$, y como el conectivo «o» es conmutativo tenemos $x \in B$ entonces $x \in A$ o $x \in B$. Así, por la definición de unión concluimos que $x\in A\cup B$.

Caso 4: $x \in A$.

Ahora como $x \in A$ entonces $x \in A$ o $x \in B$. Así, por la definición de unión concluimos que $x\in A\cup B$.

Del Caso 3 y Caso 4 concluimos que: $x\in B\cup A$. Por lo tanto, $B\cup A\subseteq A\cup B$.

Por lo que finalmente probamos: $A\cup B = B \cup A$. La igualdad $A \cap B = B \cap A$ se dejará como ejercicio al lector.

2. Los incisos de las Propiedades asociativas quedan como ejercicio de Tarea moral.

3. Probaremos sólo la igualdad $A \cup (B\cap C) = (A \cup B)\cap (A\cup C)$.

Comenzaremos con probar la siguiente contención: $A \cup (B\cap C)\subseteq (A \cup B)\cap (A\cup C)$. Así tomemos $x\in A \cup (B\cap C)$, queremos demostrar que $x\in (A \cup B)\cap (A\cup C)$.

Caso 1: $x\in A$
Así tenemos que se cumple:
\begin{align}
x \in A\vee x\in B &\Rightarrow x\in A\cup B
\end{align}
Y también sucede que:
\begin{align}
x \in A\vee x\in C &\Rightarrow x\in A\cup C
\end{align}
En (1) y (2) aplicamos la propiedad de adición para la disyunción y la definición de la unión. Por lo que concluimos, al aplicar la definición de la intersección en (3):
\begin{align}
x\in A\cup B \wedge x\in A\cup C \Rightarrow x\in (A\cup B) \cap (A\cup C)
\end{align}

Caso 2: $x \in B\cap C$
Así por definición de intersección, tenemos que:
\begin{align}
x\in B \wedge x\in C &\Rightarrow (x\in B \wedge x\in C) \vee x\in A\\
&\Rightarrow (x\in B \vee x\in A) \wedge (x\in C \vee x \in A)\\
&\Rightarrow x\in B\cup A \wedge x\in C\cup A\\
&\Rightarrow x\in A\cup B \wedge x\in A\cup C\\
&\Rightarrow x\in (A\cup B) \cap (A\cup C)\\
\end{align}
Aplicamos en (4) la propiedad aditiva de la disyunción; para (5) usamos las Leyes distributivas de los conectivos disyunción y conjunción; para (6) y (7) aplicamos la unión y su propiedad conmutativa. Finalizamos aplicando en (8) la definición de intersección.


Por (3) y (8) de los Casos 1 y 2, podemos concluir que: $A \cup (B\cap C)\subseteq (A \cup B)\cap (A\cup C)$.

Ahora probaremos la contención: $(A \cup B)\cap (A\cup C)\subseteq A \cup (B\cap C)$.
Tomamos $ x\in (A \cup B)\cap (A\cup C)$. Así por definición de intersección, tenemos que:
\begin{align}
x\in (A \cup B) \wedge x \in (A\cup C) &\Rightarrow (x\in A \vee x\in B) \wedge (x \in A\vee x\in C)\\
&\Rightarrow x\in A \vee (x \in B \wedge x\in C)\\
&\Rightarrow x\in A \vee x \in B\cap C\\
&\Rightarrow x\in A \cup (B \cap C)
\end{align}
Vemos que (9) se sigue de la definición de unión. En (10) utilizamos las leyes distributivas de la disyunción con la conjunción; para (11) aplicamos la definición de intersección para $B$ y $C$.
Y por último en (12) aplicamos la definición de unión para $A$ y $B\cup C$.

Así concluimos que: $A \cup (B\cap C) = (A \cup B)\cap (A\cup C) \text{.}$

4. Tarea moral
5. Tarea moral
6. Tarea moral
7. Tarea moral


$\square$

Notación: El símbolo «$\Rightarrow$» se lee como «entonces».

Más adelante

Ahora que hemos terminado con el repaso de los conceptos básicos de Teoría de Conjuntos, en la siguiente entrada veremos el método de demostración llamado: Inducción matemática, el cuál será utilizado frecuentemente en los diferentes cursos a lo largo de tu preparación profesional.

Tarea moral

  • Realiza la demostración de la siguiente Ley distributiva: $A \cap (B\cup C) = (A \cap B)\cup (A\cap C)$.
  • Prueba que $A \setminus (B\cap C) = (A \setminus B)\cup (A\setminus C)$.
  • Determina si las siguientes afirmaciones son verdaderas o falsas, argumenta tu respuesta:
    • Si $x\in A$ y $A\subseteq B$, sucede que $x\in B$.
    • Si $x\in A$ y $A\in B$, sucede que $x\in B$.
    • Si tenemos $A$ y $B$ conjuntos, sucede siempre que $A\setminus B = B \setminus A$.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»