Introducción
Hasta ahora hemos hablado de una parte muy particular de la matemática, la Lógica. Esta te ayudará a entender a lo largo de los cursos de matemáticas, pues es uno de los lenguajes que muchas veces verás escrito y con la que las y los matemáticos nos comunicamos. Pero esta solo es lo que muchos considerarían, la mitad del lenguaje. Ahora introduciremos la noción de la otra mitad del lenguaje, esta es llamada la «teoría de los conjuntos».
Desarmando y armando
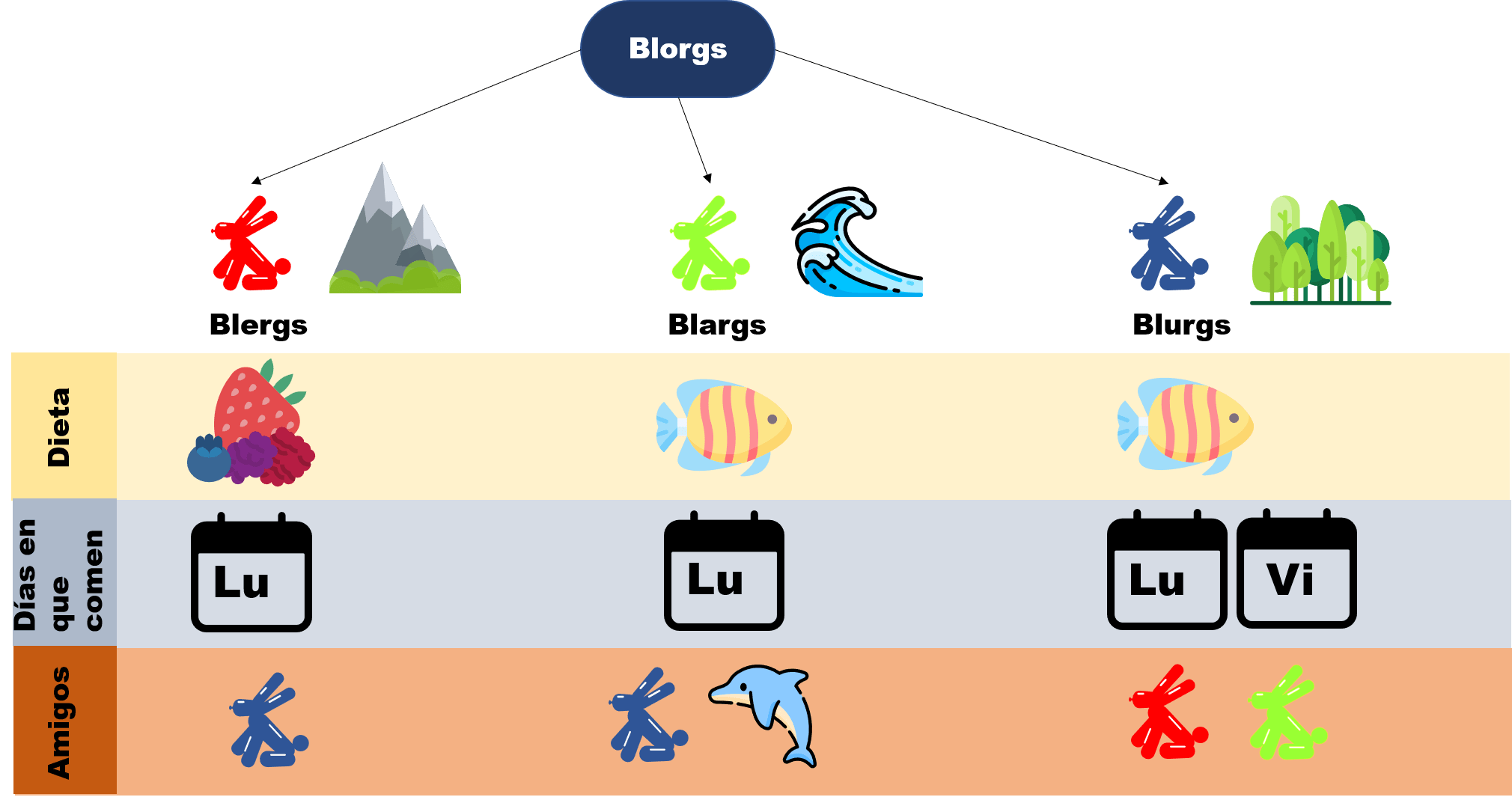
Para entender un poco más de esta otra parte del lenguaje, vamos a ayudarnos nuevamente de nuestros amigos Blorgs. Para recordar, los Blorgs son unos seres imaginarios que viven en otro planeta. Estos se dividen en tres especies: Los Blargs, Blergs y Blurgs. Cada uno vive en terrenos distintos y come cosas distintas en diferentes días. Así como tienen sus amigos de distintas especies.
Ahora, veamos un poco cómo es que se vería la isla Blorg, que estaría dividida según las regiones en donde vive cada especie:
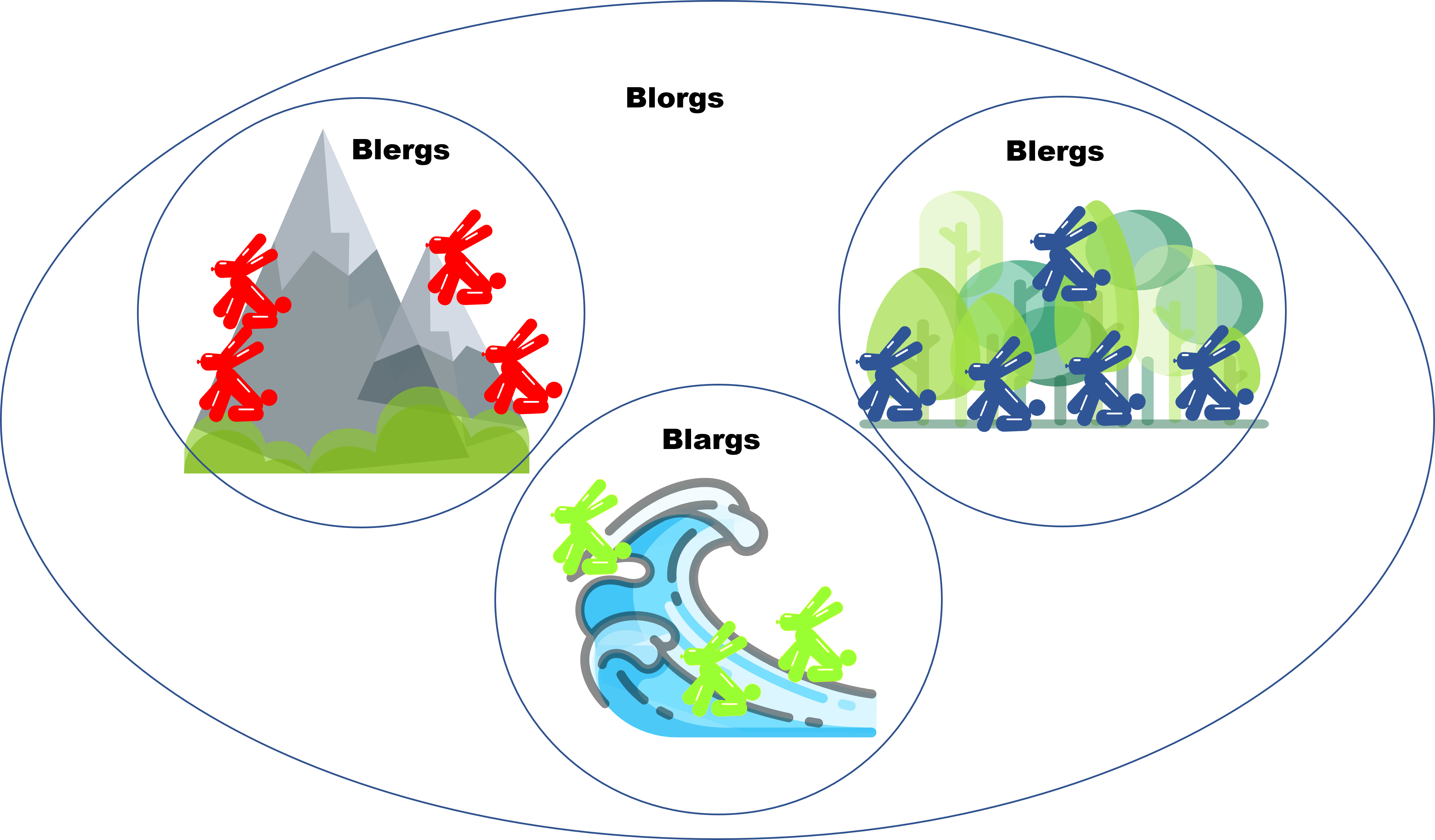
Como pudiste observar, cada uno de los Blorgs vive en regiones distintas, como los Blergs viven en las montañas y los Blurgs en bosques, nunca encontrarás un blurg viviendo donde viven los Blergs. Pero cada uno de ellos es un blorg, puesto que blorg es el «conjunto» que describe a la criatura. Es decir «todo blerg es un blorg», pero «no todo blorg es un blerg». La primera idea de la palabra conjunto que vamos a tener es: una colección de objetos. En este caso, podríamos decir que todos los Blergs, Blargs y Blurgs forman el conjunto de los Blorgs.
Por ejemplo, cuando empezamos a hablar de demostraciones, siempre usábamos la frase «Consideremos a $x$ un blorg …» o «Sea $x$ un blerg …», a lo que nos referimos es que dentro del conjunto de los Blorgs, «seleccionábamos» a algun blorg. Por ejemplo, cuando decíamos «Sea $x$ un blorg», podríamos referirnos a este:
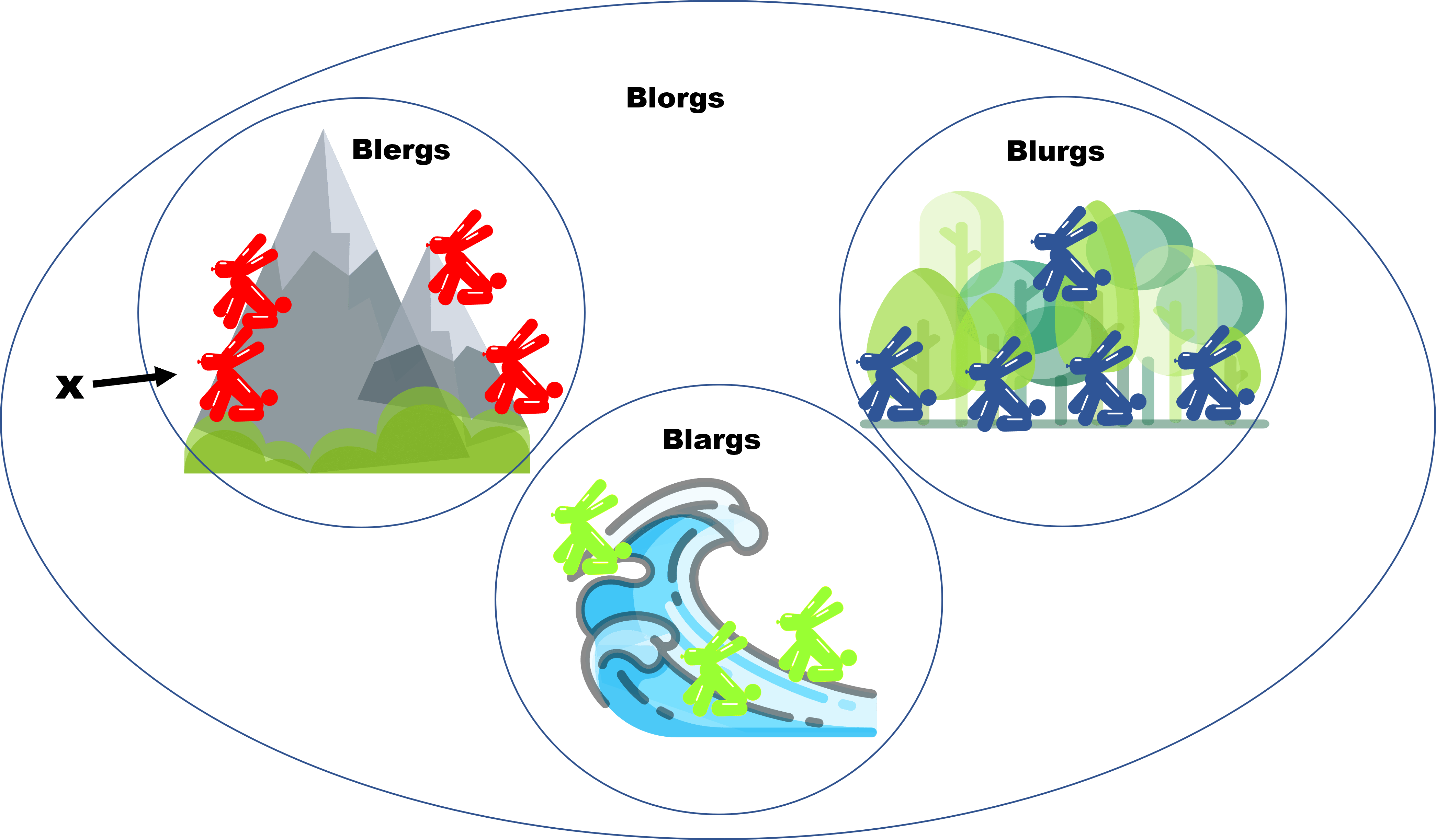

O este:
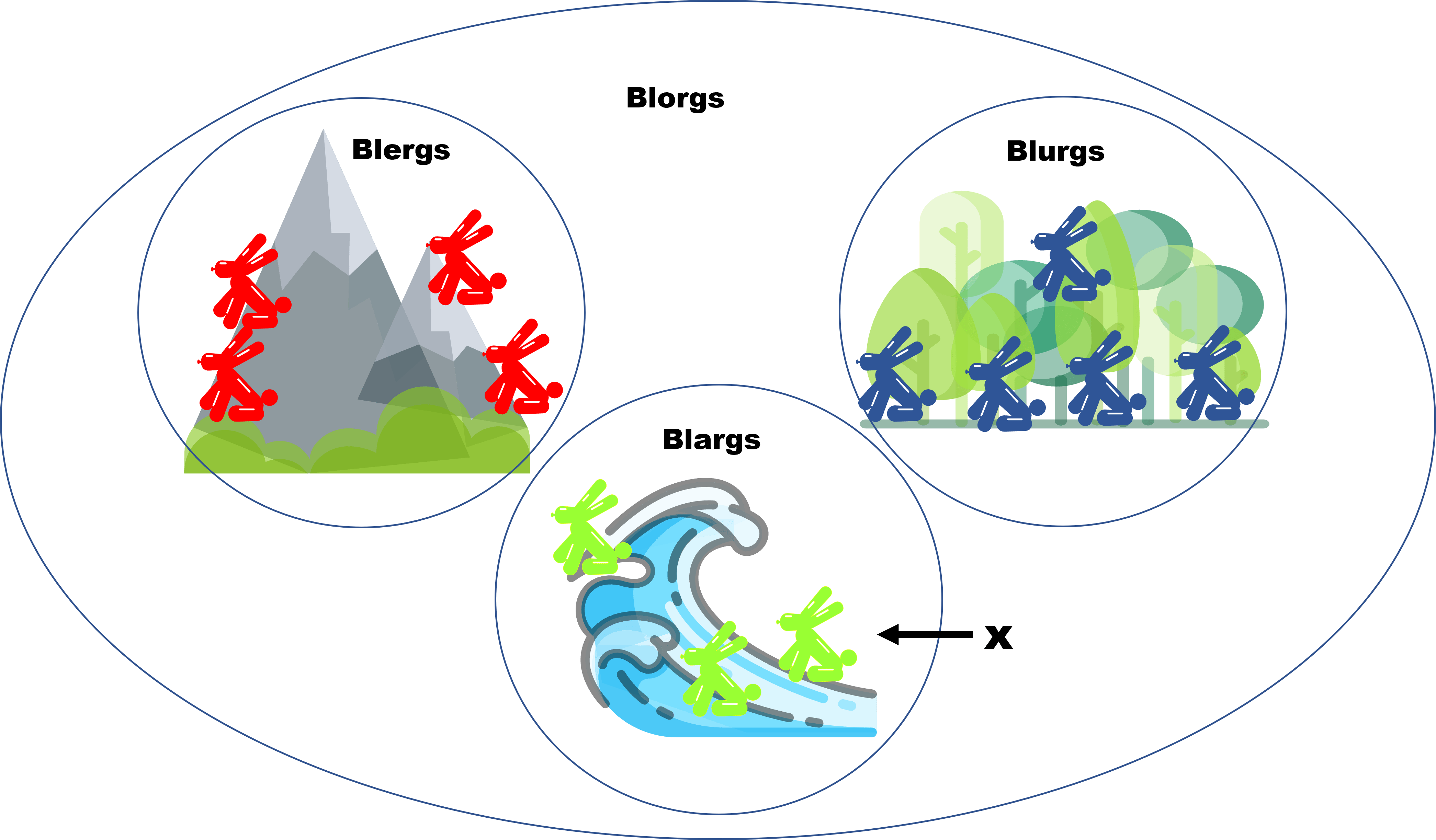

O aquel:
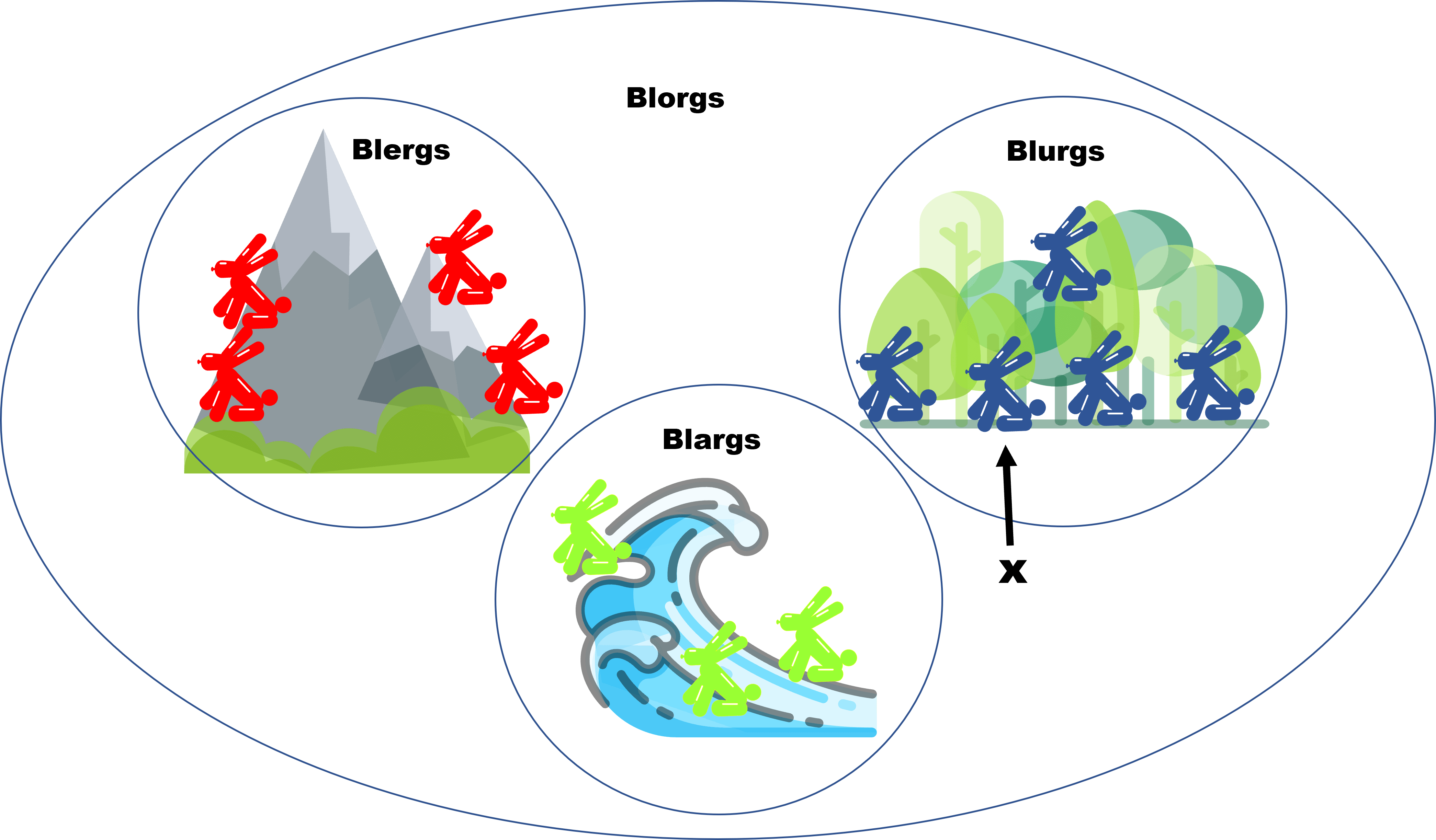

Incluso este:
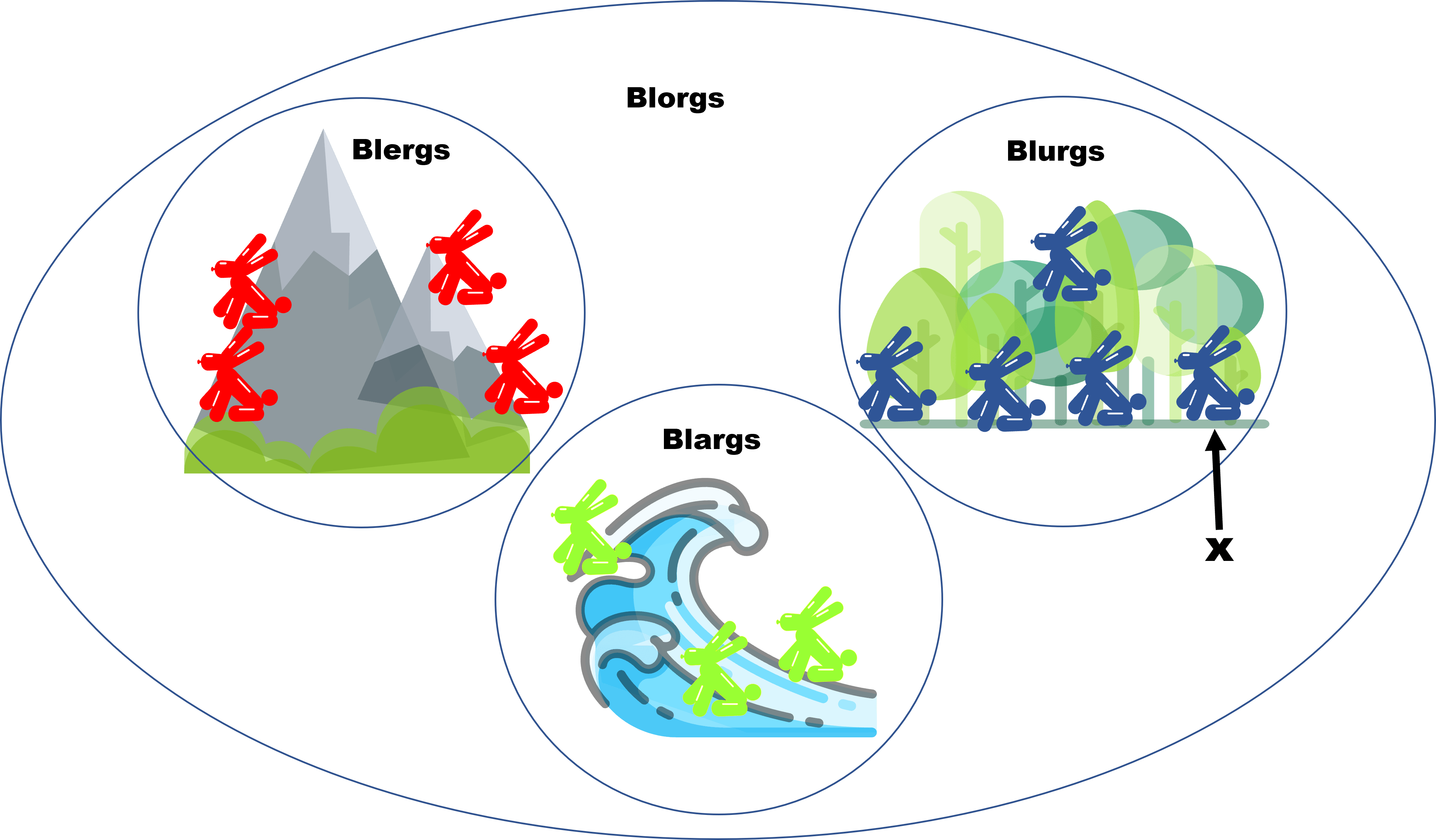

Lo que nos importaba al momento de hacer las demostraciones, era verificar que sin importar cuál blorg nos «tomaramos», la proposición se cumplía. Y quizá teníamos que verificar algunas particularidades dependiendo de su especie, pero lo importante es que cada uno de estos blorgs que considerábamos, «pertenecía» al conjunto de los Blorgs.
Hemos dicho una palabra fundamental en la teoría de conjuntos, y esta es la noción de pertenecer. Como vimos anteriormente, vamos a decir que un conjunto es una colección de objetos. En este caso el conjunto son los Blorgs y cada blorg es un objeto de dicho conjunto. Así que vamos a decir, en este caso que si $x$ es un blorg y $B$ es el conjunto de los Blorgs, entonces $$x \in B.$$ Y se lee «$x$ pertenece a $B$».
Describiendo conjuntos
Existen dos forma de describir o enunciar a los conjuntos: por extensión y por comprensión. Un conjunto descrito por extensión es aquel en donde decimos explícitamente todos sus elementos, mientras que al describirlo por comprensión, los describimos mediante alguna propiedad que tengan en común.
Por ejemplo, imagina que existen tres Blargs: blargmino, blargastacia y blargencio. Entonces podríamos describir por extensión al conjunto de los Blargs por:
$$\text{Blargs} = \{ \text{ blargmino, blargastacia , blargencio }\}$$.
Pero recordemos que todos los Blargs son Blorgs amarillos, así que igual podríamos describir al conjunto de los Blargs por comprensión:
$$ \text{Blargs} = \{ x \text{ tal que } x \text{ es un blorg amarillo} \} .$$
Este «tal que» se refiere a que $x$ cumple con ser un blorg amarillo. Sin embargo en la práctica no vas a ver escrito esto, y en su lugar se usa la siguiente notación:
$$ \text{Blargs} = \{ x \in B : x \text{ es amarillo} \} .$$
Como podrás ver, hicimos dos reemplazos, el primero de la frase «tal que», y esto nos sirve para ahorrarnos un poco la escritura. El otro simplemente es decir en un inicio a qué conjunto pertenece $x$. Recuerda que $B$ es el conjunto de los Blorgs, así que decimos que los Blargs son los objetos $x$ pertenecientes al conjunto de los Blorgs, tal que $x$ es amarillo. De esta forma simplificamos la escritura escribiendo la pertenencia de conjunto de los objetos.
Cualquiera de las dos formas de describir a un conjunto es correcta, sin embargo es más usual trabajar con la segunda, puesto que si quisiéramos describir al conjunto $X$ de todos los números enteros del 1 al 20, sería poco cómodo escribir:
$$X = \{ 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20\} $$
Y en su lugar, es más fácil escribir:
$$X = \{ x \in \mathbb{Z} : 1 \leq x \leq 20\}. $$
Donde $\mathbb{Z}$ representa a los números enteros.*
Una cosa además de notar de los conjuntos, es que solo nos importan los elementos diferentes entre sí, esto quiere decir que si queremos describir al conjunto de los números primos menores a 15: $\{2,3,5,7,13\}$, si ya lo hemos descrito una vez, no hace falta volverlo a describir, es decir es redundante decir que el conjunto se conforma por $\{2,2,3,2,5,7,2,13\}$ pues la redundancia del número $2$ ya la hemos escrito en la descripción del conjunto, esto quiere decir que $\{2,2,3,2,5,7,2,13\}$ y $ \{2,3,5,7,13\}$ describen al mismo conjunto, pues la colección que representan es la misma.
Conjuntos y lógica
Si te das cuenta, estamos diciendo cómo es un conjunto en relación a cómo cumple una propiedad. Esto lo podemos traducir a términos de lógica proposicional. Por ejemplo, consideremos $$P(x)= x \text{ es amarillo}.$$
Al escribir
$$\{x \in B: P(x) \}, $$
estaremos describiendo al conjunto de los $x \in B$ para los cuales $P(x)$ es verdadera. Observa que
$$\{x \in B: P(x) \}, $$
describe al mismo conjunto que
$$ \{ x \in B : x \text{ es amarillo} \} .$$
Entonces, es el mismo conjunto que describe a los Blargs:
$$ \text{Blargs} = \{ x \in B : P(x) \} .$$
Esto nos permitirá usar conectores, proposiciones e incluso cuantificadores para describir conjuntos. Y realmente es aquí donde reluce la lógica proposicional que hemos estudiado. Pues el poder escribir conjuntos como elementos que cumplen cierta condición, da más forma a la lógica. Hay quienes dicen que no puede existir la lógica sin los conjuntos y viceversa, pues a lo que antes llamábamos «Universo de Discurso», realmente se refiere a un conjunto.
La importancia de la teoría de conjuntos
Quizá a estas alturas te preguntarás: ¿Por qué estos dos temas grandes que hemos visto (lógica y conjuntos) son algo que se ve en un primer curso de preparación matemática? Pues bien, esto no es coincidencia. En otras materias introductorias a la carrera de matemáticas como Cálculo Diferencial e Integral I, Geometría Moderna I o Geometría Analítica I empiezan a generar resultados, demostraciones, proposiciones, teoremas y demás material basándose en estas dos. Pues al hablar por ejemplo en las primeras notas de cálculo, se ve este tipo de proposiciones:
Proposición: El neutro aditivos es único en $\mathbb{R}$.
Lo que nos traduce este enunciado y su significado es la lógica y la teoría de conjuntos (que vamos a ir desarrollando en las próximas entradas) independientemente de que tengamos claros los conceptos de neutro aditivo (en el sentido del cáclulo diferencial) o del conjunto de los números reales ($\mathbb{R}$). Aún sin saber esos conceptos, la lógica y conjuntos nos dicen lo siguiente:
La teoría de conjuntos nos dice: Estamos trabajando en el conjunto $\mathbb{R}$.
La lógica nos dice: Si $x \in \mathbb{R}$ ($x$ está en el conjunto dentro del que estamos trabajando) es un neutro aditivo, entonces es único.
De esta forma, si $P(x)= x$ es un neutro aditivo, entonces:
$$\exists ! x \in \mathbb{R} (P(x)). $$
Y con nuestro conocimiento de las demostraciones, podríamos reescribir esto como:
$$\forall x,y \in \mathbb{R} \big((P(x)\land P(y)) \Rightarrow (x=y)\big) .$$
Nota que la gran diferencia al considerar a la teoría de los conjuntos, es el ingrediente de saber sobre qué conjunto estamos hablando. Ya que no es lo mismo decir
$$\exists ! x \in \mathbb{R} (P(x)). $$
A decir:
$$\exists ! x \in \mathbb{R}^2 (P(x)). $$
Y este solo es un ejemplo de cómo afecta la teoría de conjuntos en la comprensión de proposiciones, enunciados y teoremas. Nos ayudará a poner contexto, a encontrar propiedades de elementos dentro del mismo conjunto y comprender su relación los unos con los otros.
Notas
*Comúnmente los número enteros se denotan por $\mathbb{Z}$, esta
convención viene de la notación que matemáticos alemanes en el siglo XVIII como Gauss y Euler usaban para referirse a «die Zahlen», cuya traducción del alemán es «los números».
Más adelante…
Hasta ahora hemos hablado de las primeras nociones básicas de la teoría de conjuntos. Aún faltan un par de conceptos por ver y estos son la contención y el conjunto potencia. Estos resolverán algunas dudas como ¿Qué relación tienen el conjunto de los Blargs y los Blorgs? a su vez, estos nos ayudarán a axiomatizar la teoría de los conjuntos,que como recordarás, ayudarán a ponernos de acuerdo las reglas de los conjuntos para empezar a sacar resultados de ellos.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Describe por comprensión al conjunto de los Blergs.
- Describe al conjunto de los números del 10 al 10,000.
- Considera al conjunto $$\{ x \in B : P(x) \land \neg Q(x)\}.$$ Donde $$ P(x) = x \text{ come peces}$$ y $$ Q(x) = x \text{ vive en el mar}.$$ ¿A qué especie de Blorgs pertenece este conjunto?
- ¿Qué conjunto genera la proposición $ P (x) := \exists n \in \mathbb{N}\big( x = 2n + 1 \big)$ donde $x$ es un número entero ?
Entradas relacionadas
- Ir a Álgebra Superior I
- Entrada anterior del curso: Problemas de demostraciones de condicionales y dobles condicionales.
- Siguiente entrada del curso: Axiomas de los conjuntos
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»