Introducción

Esta entrada es parte de una serie de notas sobre demostraciones matemáticas. Sin embargo, para llegar a la importancia de demostrar, hablaremos previamente de un pequeño mundo en donde habitan seres fantásticos a quienes les interesa mucho la lógica y para quienes es fundamental poder deducir únicamente verdades. Este lugar lo vistaremos a lo largo de varias entradas y lo que acordemos a partir de ahora será cierto más adelante. Así que presta atención.

El mundo de los Blorgs

Antes de que pienses que te equivocaste de entrada debido al cuento que está por comenzar, déjame decirte que todo está relacionado con la teoría que hemos estado platicando. Sin embargo, antes de comenzar a aplicarla, vamos a conocer a los Blorgs.

Imagina el mundo de los Blorgs. Es un mundo paralelo al nuestro que se puede encontrar en aquel mundo que existe más allá de lo que la esquina del espejo deja ver. Es un lugar que se parece un poco al piso sobre el que estamos, despierta con casi los mismos tonos del alba por la mañana pero con algunas cosas distintas.

Para empezar estamos hablando de un mundo en el que habitan mayoritariamente criaturas llamadas Blorgs. Aquellos que alguna vez los vieron, comentan que curiosamente son pequeñas criaturas parecidas a los conejos. Y con algunas otras descripciones en mente, podríamos empezar a clasificar los Blorgs de acuerdo a distintas características como por ejemplo su dieta, su rutina, dónde viven, etc. Pero se decidió que era mejor clasificarlos según su color, y aquí es donde las cosas se ponen interesantes.

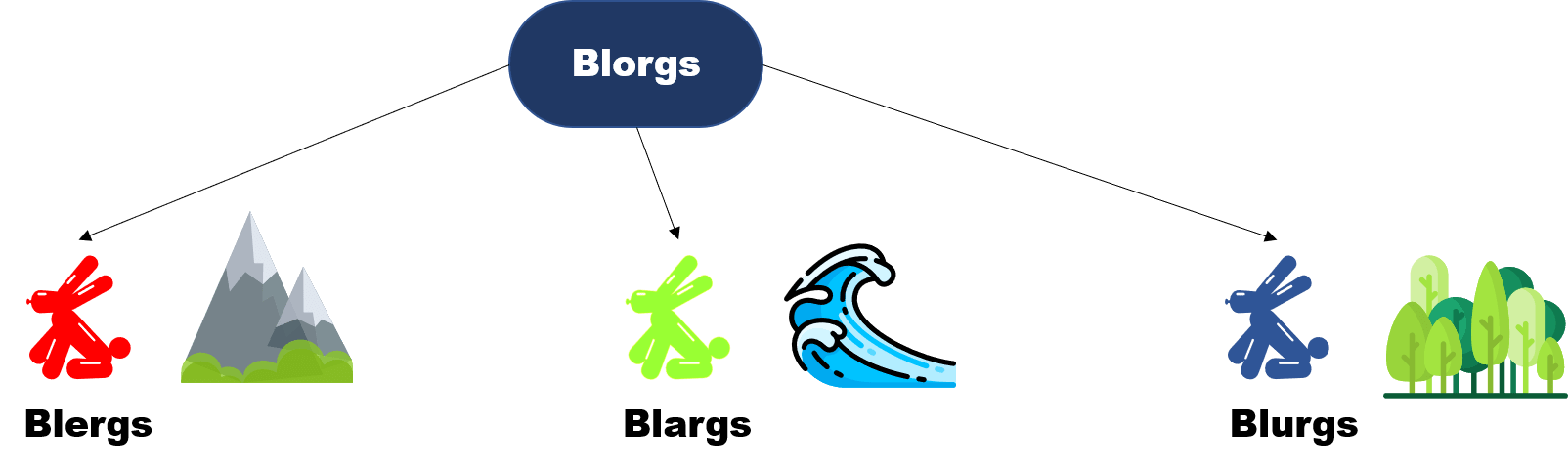
Por un lado están los Blergs, estos son las criaturas rojas que viven por las montañas. Después podemos considerar a los Blargs que son aquellos Blorgs verdes y viven debajo del mar, no son muy sociales pero es lo que hay. Finalmente están los Blurgs que son azules y prefieren vivir en el bosque. Entonces, podemos dividir a los Blorgs en sus razas: Blergs, Blargs y Blurgs. Algo importante que tenemos que decir también: ningún Blorg tiene más de un color.

Quizá sean de color distinto y vivan en lugares diferentes, pero esto no les impide tener algunas cosas en común. Por ejemplo, todos los Blurgs comen pescados, pues tienen un lago cerca de su bosque, y al ser los Blargs marinos, también comen pescados. El hecho de haber vivido tanto tiempo en terreno alto, hizo que los Blergs prefieran cultivar sus cosechas: frutos dulces y verduras siempre comen. Por alguna razón, será costumbre o creencia, todos los Blorgs comen los lunes, es decir, que cada criatura come una vez a la semana. Eso les ha ayudado a no depender tanto de la comida en el día a día. Aunque aquí es donde los Blurgs no coinciden: ellos no esperan tanto y también comen algo los viernes.

La vida siendo Blorg

Tristemente, los Blargs no pueden salir del mar, pues a pesar de ser Blorgs, el salir del agua les despinta lo verde y les quita fuerza. Es por esto que casi no hablan con sus contrapartes terrestres. Por otro lado los Blerg y los Blurg se llevan muy bien. Los Blurgs comparten la madera que tienen con los Blergs y los Blergs comparten los cultivos que hacen con los Blurgs (aunque no para comer, los Blurgs más bien usan los lindos colores de los frutos rojos para pintar).

No está de más decir que todos los Blergs son amigos de todos los Blurgs. Esto hace que los Blargs se sientan más ajenos a ellos, pues aunque sí se llevan con los Blurgs, prefieren juntarse con los delfines que viven junto a ellos. Los blurgs son amistosos con los Blargs y Blergs, y siempre están dispuestos a negociar peces a cambio de paseos a lo largo del mar. Pero nadie se queja, así es la vida siendo un Blorg.

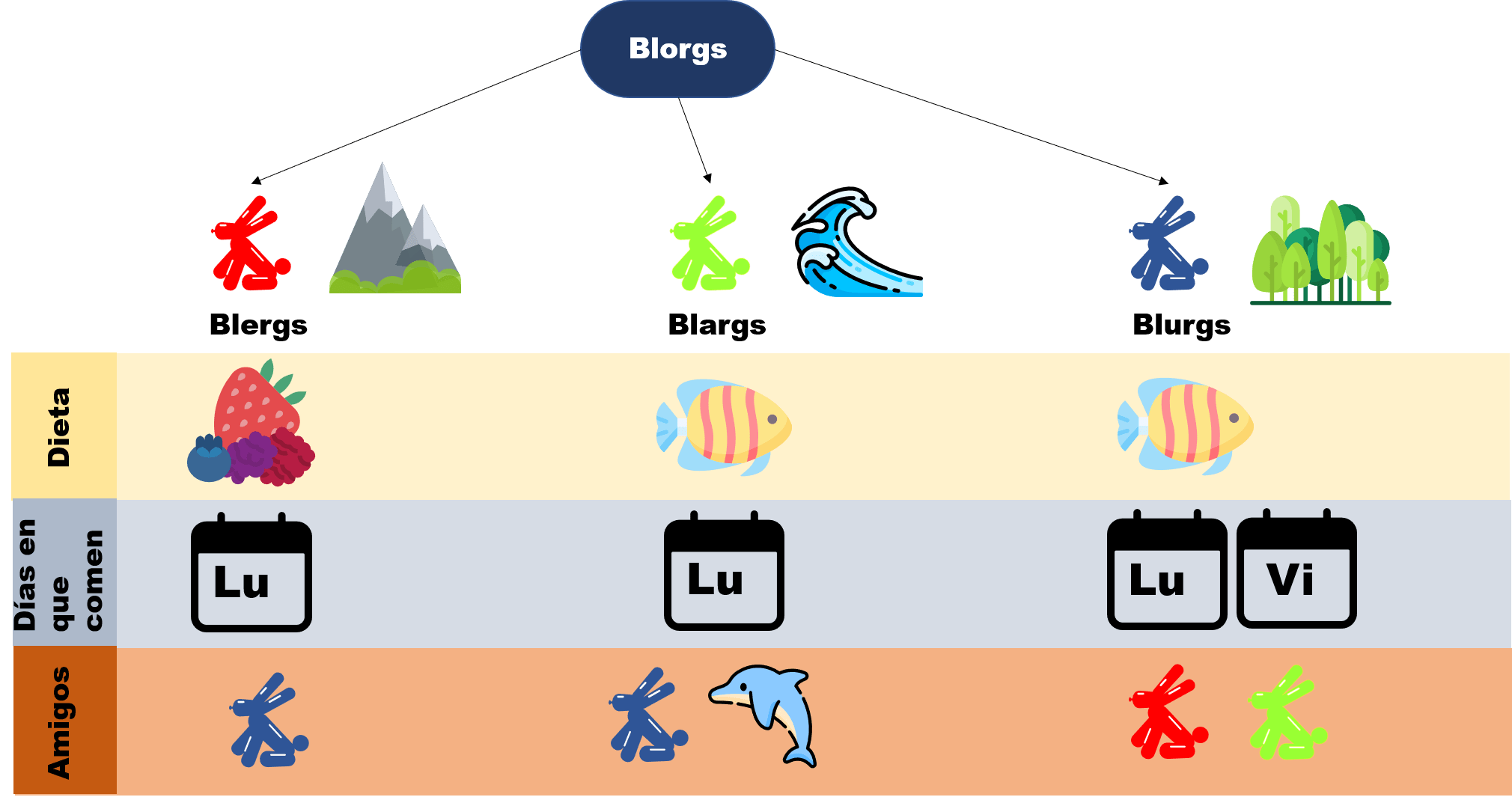
De esta manera, podemos resumir la información que sabemos de los Blorgs en el siguiente diagrama:

Sobre Axios y demostraciones matemáticas

Una cualidad que podemos saber de los Blorgs es que ellos le llaman al lugar en donde viven «Axios» y dentro de ella, no hacen diferencia entre lo que es una característica o costumbre, ellos no tienen una palabra para cada una de ellas. En su lugar usan la palabra «Axioma«* (¿recuerdas qué significa esta palabra?). Esto quiere decir que para los Blargs, ser verdes es un axioma, al igual que para ellos hablar con delfines o comer peces es un axioma.

Así que es natural poder hacer conclusiones a partir de estos Axiomas. Por ejemplo: ¿Qué opinarías si te digo que todos los Blorgs comen peces? ¿O si te digo que todos los Blorgs que viven en montañas comen los lunes? Pues quizá puedas dar respuesta a estas preguntas intuitivamente. Pero, ¿cómo es que nos aseguramos que la respuesta es correcta o no?

En Axios no basta con decir que todos los Blorgs que viven en las montañas comen los lunes. Los Blorgs no entienden la intuición, pero nosotros sí. A ellos hay que convencerlos con demostraciones, a ellos tenemos que explicarles mediante lógica el porqué una proposición sucede. Es decir que si queremos afirmar que todos los Blorgs que viven en las montañas comen los lunes, tenemos que decir paso a paso el porqué es así. Y esto lo lograremos sólo mediante reglas de inferencia válidas. Vamos a anotar esto que acabamos de decir como una definición (¿recuerdas qué era una definición?):

Definición. Una demostración matemática es el uso de pasos lógicos usando reglas de inferencia válidas para llegar de la veracidad de ciertas hipótesis a la veracidad de una conclusión.

La intuición con inferencia

Para introducir un poco más qué van a ser las demostraciones en las matemáticas, vamos a pensar en Legos, aquellos pequeños bloques que encajan unos con otros con los que se pueden armar lo que se te ocurra. Y piensa a las reglas de inferencia como las instrucciones para armar algo.

Imagina que queremos armar un cuarto con una mesa, cama y lámpara con estas piezas. Primero, tendríamos que armar una mesa, para lo cual necesitamos armar las patas y después la superfice. Las reglas de inferencia nos van a ayudar diciéndonos: las patas hay que acomodarlas de cierta manera junto a la superficie para que se haga una mesa. Y una vez construida la mesa, ahora podemos usar otras reglas de inferencia para crear la cama y otras para la lámpara, juntando las tres partes (mesa, cama y lámpara) tendríamos hecho un cuarto.

Así, si quisiéramos «demostrar» cómo se hace un cuarto con estas piezas de Lego, tendríamos que explicar cómo se hace la lámpara, cómo se hace la cama y cómo la mesa. Esto es lo que haremos en matemáticas: construir cosas dando las instrucciones adecuadas. Incluso podríamos ir más allá: Una vez que sabemos cómo construir un cuarto, podríamos también demostrar cómo se hace una cocina y un baño. Entonces si tuviéramos ese conocimiento de cómo se hacen estos tres, podríamos construir una casa. Y después sabiendo cómo se construyen casas, podríamos crear ciudades y países enteros. Pero como todo: un paso a la vez.

Armando piezas con los Blorgs

Nuestras piezas de Lego con los Blorgs van a ser los axiomas. Ahora si le dijeramos a un Blorg que los Blorgs verdes comen peces, no nos creería. Debemos darle una demostración de esto:

Proposición. Los Blorgs verdes comen peces.

Demostración. Para empezar, vamos a notar que es una proposición del tipo «Si $x$ es un Blorg verde, entonces $x$ come peces». Esto es lo que queremos demostrar. Para ello, vamos a ir armando poco a poco el argumento con las piezas que sí conocemos:

• Usaremos que todos los Blorgs verdes son Blargs. Es decir «si $x$ es un Blorg verde, entonces $x$ es un Blarg»
• Usaremos que todos los Blargs comen peces. Es decir «si $x$ es un Blarg, entonces $x$ come peces»

En las demostraciones vamos a ir usando cosas que ya conocemos (en este caso los axiomas) para poder ir aplicando pasos lógicos y reglas de inferencia para llegar a la conclusión deseada. Entonces como queremos ver que todos los Blorgs verdes comen peces, entonces resulta natural «agarrar» o «elegir» un Blorg verde y ver que ese Blorg come peces (si pasa con un Blorg verde, pasará para todos los Blorgs verdes pues todos nuestros pasos lógicos aplicarán para todos los Blorgs verdes). Así que empecemos considerando a $x$ un Blorg verde . Sabemos que «si $x$ es un Blorg verde, entonces $x$ es un Blarg» entonces como nuestro $x$ es un Blorg verde, entonces es un Blarg.

Ahora, sabemos que nuestro $x$ es un Blarg, pero además sabemos que «si $x$ es un Blarg, entonces $x$ come peces» entonces también nuestro Blarg come peces. Por lo tanto los Blorgs verdes comen peces.

$\square$

¿Viste cómo es que hicimos la demostración? Si consideramos

• $ P(x) : x$ es blorg verde,
• $ Q(x) : x$ es blarg,
• $ R(x) : x$ come peces,

entonces realmente lo que hicimos fue usar la siguiente regla de inferencia válida:

$$ \begin{array}{rl} & P \Rightarrow Q \\ & Q \Rightarrow R \\ \hline \therefore & P \Rightarrow R \end{array}.$$

La razón por la que $P\Rightarrow Q$ y $Q\Rightarrow R$ los tomamos como premisas, es porque acordamos que son axiomas. Recuerda que los axiomas los tomamos como verdaderos.

En este caso solo usamos una regla de inferencia. Más veremos cómo se pueden usar varias reglas de inferencia en una misma demostración. Apenas estamos empezando este tema, así que si aún tienes muchas dudas, no te preocupes y vuelve a leer la demostración si es necesario.

* Esta palabra viene del griego ἀξίωμα que significa «lo que se considera justo» y de hecho viene de la palabra ἄξιος (áxios) que significa «valioso» y en la antigua grecia se consideraban aquellas cosas que parecían evidentes y no hacía falta justificar.

Más adelante…

Apenas estamos empezando a explicar qué son estas «demostraciones matemáticas». En el mundo de la matemática no hay algo como el recetario de las demostraciones, pero hay ideas o formas de pensar los problemas que te servirán para tener una idea de por dónde empezar a pensar a la hora de demostrar. Así que en las siguientes entradas vamos a ver algunas de estas «formas» de pensar los problemas y lo haremos con ayuda de los Blorgs.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

1. ¿Qué color necesita tener un Blorg para ser amigo de los delfines?
2. ¿Es cierto que existe un Blorg que coma frutos rojos en viernes?
3. ¿Qué argumentos lógicos podrías usar para demostrar que todo Blorg rojo come los lunes? ¿Y qué argumentos usarías para demostrar que si un Blorg vive en el mar, entonces no come los viernes? Finalmente, ¿puedes argumentar por que si un Blorg no es Blurg, entonces sus Blorg amigos comen los viernes?
4. Verifica que

$$ \begin{array}{rl} & P \Rightarrow Q \\ & Q \Rightarrow R \\ \hline \therefore & P \Rightarrow R \end{array}$$

es una regla de inferencia válida.

Entradas relacionadas

• Ir a Álgebra Superior I
• Entrada anterior del curso: Inferencias matemáticas
• Siguiente entrada del curso: Demostraciones directas e indirectas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»