Archivo del Autor: Guillermo Oswaldo Cota Martínez

Acerca de Guillermo Oswaldo Cota Martínez

Soy Guillermo. Soy pasante de la Licenciatura en Matemáticas en la Facultad de Ciencias de la UNAM, y estudiante de la Licenciatura en Ciencia de Datos del IIMAS, UNAM. Me interesan los problemas referente al análisis de datos y a la docencia.

Álgebra Superior I: Demostraciones matemáticas (El mundo de los Blorg)

Por Guillermo Oswaldo Cota Martínez

Deja un comentario

Introducción

Esta entrada es parte de una serie de notas sobre demostraciones matemáticas. Sin embargo, para llegar a la importancia de demostrar, hablaremos previamente de un pequeño mundo en donde habitan seres fantásticos a quienes les interesa mucho la lógica y para quienes es fundamental poder deducir únicamente verdades. Este lugar lo vistaremos a lo largo de varias entradas y lo que acordemos a partir de ahora será cierto más adelante. Así que presta atención.

El mundo de los Blorgs

Antes de que pienses que te equivocaste de entrada debido al cuento que está por comenzar, déjame decirte que todo está relacionado con la teoría que hemos estado platicando. Sin embargo, antes de comenzar a aplicarla, vamos a conocer a los Blorgs.

Imagina el mundo de los Blorgs. Es un mundo paralelo al nuestro que se puede encontrar en aquel mundo que existe más allá de lo que la esquina del espejo deja ver. Es un lugar que se parece un poco al piso sobre el que estamos, despierta con casi los mismos tonos del alba por la mañana pero con algunas cosas distintas.

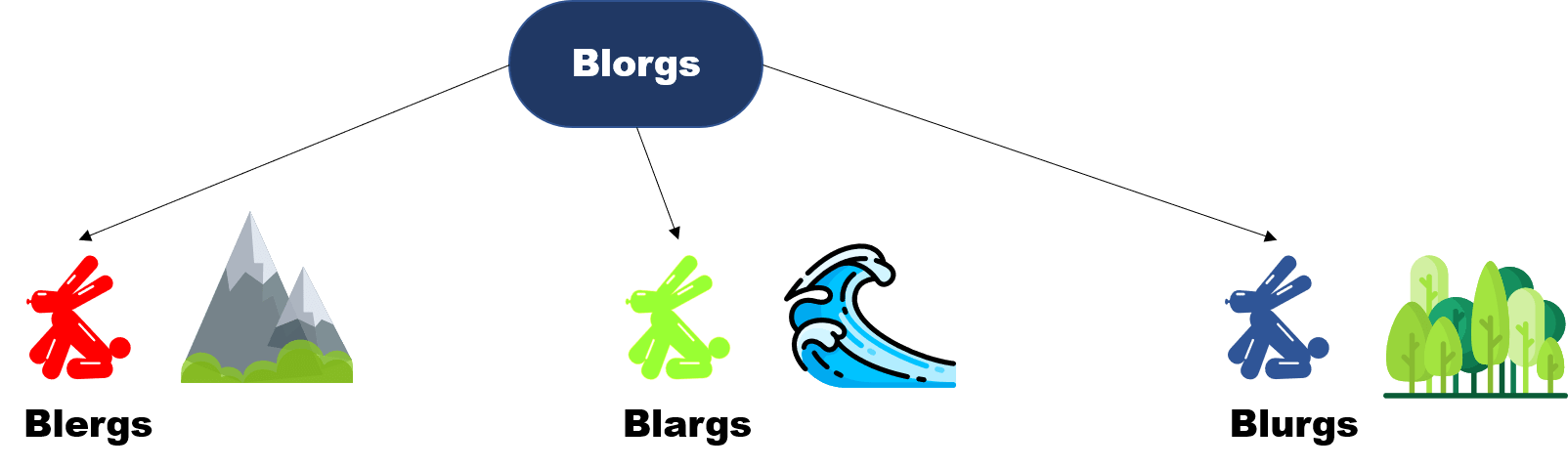
Para empezar estamos hablando de un mundo en el que habitan mayoritariamente criaturas llamadas Blorgs. Aquellos que alguna vez los vieron, comentan que curiosamente son pequeñas criaturas parecidas a los conejos. Y con algunas otras descripciones en mente, podríamos empezar a clasificar los Blorgs de acuerdo a distintas características como por ejemplo su dieta, su rutina, dónde viven, etc. Pero se decidió que era mejor clasificarlos según su color, y aquí es donde las cosas se ponen interesantes.

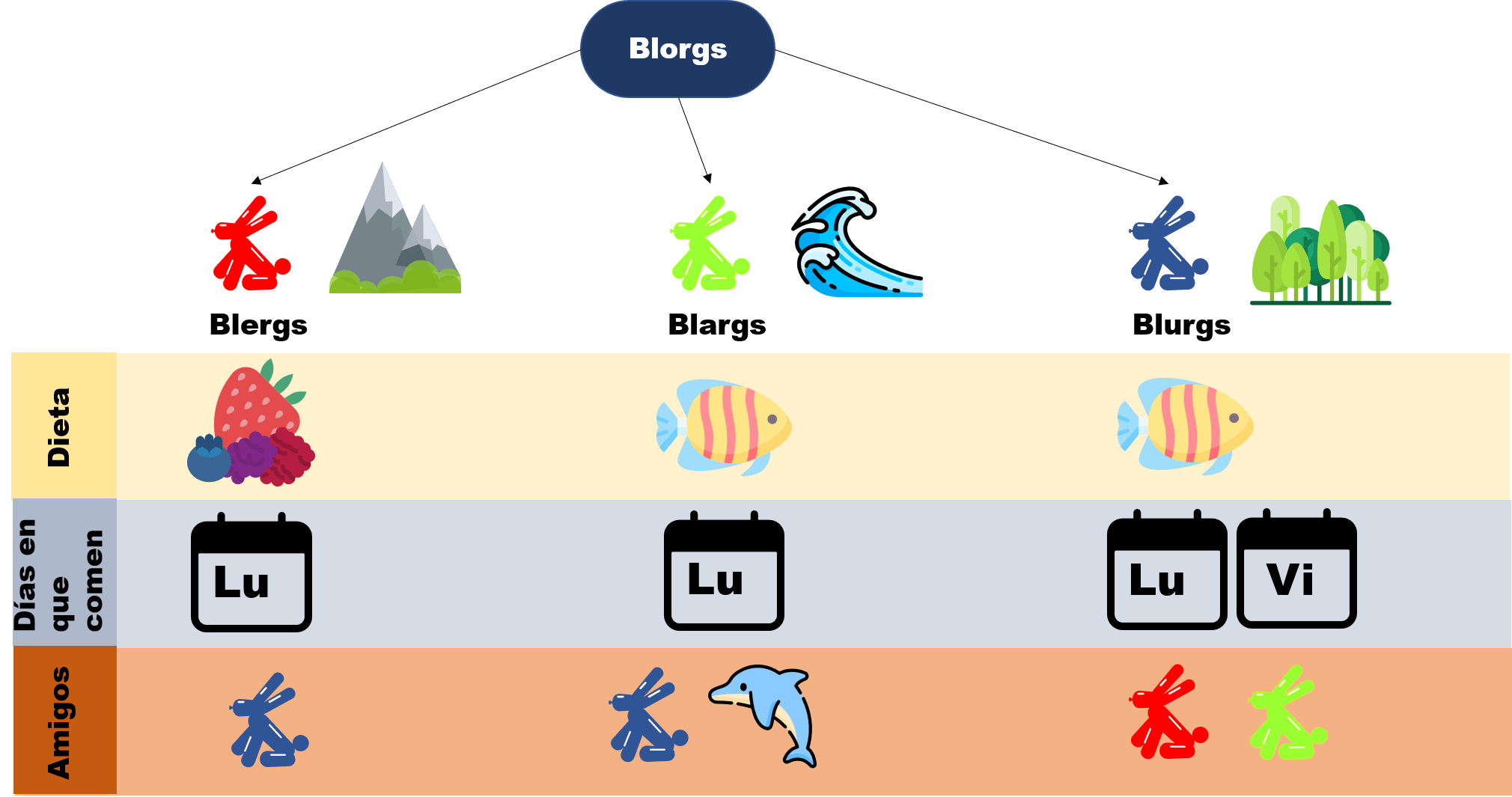
Por un lado están los Blergs, estos son las criaturas rojas que viven por las montañas. Después podemos considerar a los Blargs que son aquellos Blorgs verdes y viven debajo del mar, no son muy sociales pero es lo que hay. Finalmente están los Blurgs que son azules y prefieren vivir en el bosque. Entonces, podemos dividir a los Blorgs en sus razas: Blergs, Blargs y Blurgs. Algo importante que tenemos que decir también: ningún Blorg tiene más de un color.

Quizá sean de color distinto y vivan en lugares diferentes, pero esto no les impide tener algunas cosas en común. Por ejemplo, todos los Blurgs comen pescados, pues tienen un lago cerca de su bosque, y al ser los Blargs marinos, también comen pescados. El hecho de haber vivido tanto tiempo en terreno alto, hizo que los Blergs prefieran cultivar sus cosechas: frutos dulces y verduras siempre comen. Por alguna razón, será costumbre o creencia, todos los Blorgs comen los lunes, es decir, que cada criatura come una vez a la semana. Eso les ha ayudado a no depender tanto de la comida en el día a día. Aunque aquí es donde los Blurgs no coinciden: ellos no esperan tanto y también comen algo los viernes.

La vida siendo Blorg

Tristemente, los Blargs no pueden salir del mar, pues a pesar de ser Blorgs, el salir del agua les despinta lo verde y les quita fuerza. Es por esto que casi no hablan con sus contrapartes terrestres. Por otro lado los Blerg y los Blurg se llevan muy bien. Los Blurgs comparten la madera que tienen con los Blergs y los Blergs comparten los cultivos que hacen con los Blurgs (aunque no para comer, los Blurgs más bien usan los lindos colores de los frutos rojos para pintar).

No está de más decir que todos los Blergs son amigos de todos los Blurgs. Esto hace que los Blargs se sientan más ajenos a ellos, pues aunque sí se llevan con los Blurgs, prefieren juntarse con los delfines que viven junto a ellos. Los blurgs son amistosos con los Blargs y Blergs, y siempre están dispuestos a negociar peces a cambio de paseos a lo largo del mar. Pero nadie se queja, así es la vida siendo un Blorg.

De esta manera, podemos resumir la información que sabemos de los Blorgs en el siguiente diagrama:

Sobre Axios y demostraciones matemáticas

Una cualidad que podemos saber de los Blorgs es que ellos le llaman al lugar en donde viven «Axios» y dentro de ella, no hacen diferencia entre lo que es una característica o costumbre, ellos no tienen una palabra para cada una de ellas. En su lugar usan la palabra «Axioma«* (¿recuerdas qué significa esta palabra?). Esto quiere decir que para los Blargs, ser verdes es un axioma, al igual que para ellos hablar con delfines o comer peces es un axioma.

Así que es natural poder hacer conclusiones a partir de estos Axiomas. Por ejemplo: ¿Qué opinarías si te digo que todos los Blorgs comen peces? ¿O si te digo que todos los Blorgs que viven en montañas comen los lunes? Pues quizá puedas dar respuesta a estas preguntas intuitivamente. Pero, ¿cómo es que nos aseguramos que la respuesta es correcta o no?

En Axios no basta con decir que todos los Blorgs que viven en las montañas comen los lunes. Los Blorgs no entienden la intuición, pero nosotros sí. A ellos hay que convencerlos con demostraciones, a ellos tenemos que explicarles mediante lógica el porqué una proposición sucede. Es decir que si queremos afirmar que todos los Blorgs que viven en las montañas comen los lunes, tenemos que decir paso a paso el porqué es así. Y esto lo lograremos sólo mediante reglas de inferencia válidas. Vamos a anotar esto que acabamos de decir como una definición (¿recuerdas qué era una definición?):

Definición. Una demostración matemática es el uso de pasos lógicos usando reglas de inferencia válidas para llegar de la veracidad de ciertas hipótesis a la veracidad de una conclusión.

La intuición con inferencia

Para introducir un poco más qué van a ser las demostraciones en las matemáticas, vamos a pensar en Legos, aquellos pequeños bloques que encajan unos con otros con los que se pueden armar lo que se te ocurra. Y piensa a las reglas de inferencia como las instrucciones para armar algo.

Imagina que queremos armar un cuarto con una mesa, cama y lámpara con estas piezas. Primero, tendríamos que armar una mesa, para lo cual necesitamos armar las patas y después la superfice. Las reglas de inferencia nos van a ayudar diciéndonos: las patas hay que acomodarlas de cierta manera junto a la superficie para que se haga una mesa. Y una vez construida la mesa, ahora podemos usar otras reglas de inferencia para crear la cama y otras para la lámpara, juntando las tres partes (mesa, cama y lámpara) tendríamos hecho un cuarto.

Así, si quisiéramos «demostrar» cómo se hace un cuarto con estas piezas de Lego, tendríamos que explicar cómo se hace la lámpara, cómo se hace la cama y cómo la mesa. Esto es lo que haremos en matemáticas: construir cosas dando las instrucciones adecuadas. Incluso podríamos ir más allá: Una vez que sabemos cómo construir un cuarto, podríamos también demostrar cómo se hace una cocina y un baño. Entonces si tuviéramos ese conocimiento de cómo se hacen estos tres, podríamos construir una casa. Y después sabiendo cómo se construyen casas, podríamos crear ciudades y países enteros. Pero como todo: un paso a la vez.

Armando piezas con los Blorgs

Nuestras piezas de Lego con los Blorgs van a ser los axiomas. Ahora si le dijeramos a un Blorg que los Blorgs verdes comen peces, no nos creería. Debemos darle una demostración de esto:

Proposición. Los Blorgs verdes comen peces.

Demostración. Para empezar, vamos a notar que es una proposición del tipo «Si $x$ es un Blorg verde, entonces $x$ come peces». Esto es lo que queremos demostrar. Para ello, vamos a ir armando poco a poco el argumento con las piezas que sí conocemos:

  • Usaremos que todos los Blorgs verdes son Blargs. Es decir «si $x$ es un Blorg verde, entonces $x$ es un Blarg»
  • Usaremos que todos los Blargs comen peces. Es decir «si $x$ es un Blarg, entonces $x$ come peces»

En las demostraciones vamos a ir usando cosas que ya conocemos (en este caso los axiomas) para poder ir aplicando pasos lógicos y reglas de inferencia para llegar a la conclusión deseada. Entonces como queremos ver que todos los Blorgs verdes comen peces, entonces resulta natural «agarrar» o «elegir» un Blorg verde y ver que ese Blorg come peces (si pasa con un Blorg verde, pasará para todos los Blorgs verdes pues todos nuestros pasos lógicos aplicarán para todos los Blorgs verdes). Así que empecemos considerando a $x$ un Blorg verde . Sabemos que «si $x$ es un Blorg verde, entonces $x$ es un Blarg» entonces como nuestro $x$ es un Blorg verde, entonces es un Blarg.

Ahora, sabemos que nuestro $x$ es un Blarg, pero además sabemos que «si $x$ es un Blarg, entonces $x$ come peces» entonces también nuestro Blarg come peces. Por lo tanto los Blorgs verdes comen peces.

$\square$

¿Viste cómo es que hicimos la demostración? Si consideramos

  • $ P(x) : x$ es blorg verde,
  • $ Q(x) : x$ es blarg,
  • $ R(x) : x$ come peces,

entonces realmente lo que hicimos fue usar la siguiente regla de inferencia válida:

$$ \begin{array}{rl} & P \Rightarrow Q \\ & Q \Rightarrow R \\ \hline \therefore & P \Rightarrow R \end{array}.$$

La razón por la que $P\Rightarrow Q$ y $Q\Rightarrow R$ los tomamos como premisas, es porque acordamos que son axiomas. Recuerda que los axiomas los tomamos como verdaderos.

En este caso solo usamos una regla de inferencia. Más veremos cómo se pueden usar varias reglas de inferencia en una misma demostración. Apenas estamos empezando este tema, así que si aún tienes muchas dudas, no te preocupes y vuelve a leer la demostración si es necesario.

Notas

Estas son algunas anotaciones del artículo y no es necesario que las sepas, únicamente son curiosidades o temas por aparte que forman parte de cultura matemática

* Esta palabra viene del griego ἀξίωμα que significa «lo que se considera justo» y de hecho viene de la palabra ἄξιος (áxios) que significa «valioso» y en la antigua grecia se consideraban aquellas cosas que parecían evidentes y no hacía falta justificar.

Más adelante…

Apenas estamos empezando a explicar qué son estas «demostraciones matemáticas». En el mundo de la matemática no hay algo como el recetario de las demostraciones, pero hay ideas o formas de pensar los problemas que te servirán para tener una idea de por dónde empezar a pensar a la hora de demostrar. Así que en las siguientes entradas vamos a ver algunas de estas «formas» de pensar los problemas y lo haremos con ayuda de los Blorgs.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. ¿Qué color necesita tener un Blorg para ser amigo de los delfines?
  2. ¿Es cierto que existe un Blorg que coma frutos rojos en viernes?
  3. ¿Qué argumentos lógicos podrías usar para demostrar que todo Blorg rojo come los lunes? ¿Y qué argumentos usarías para demostrar que si un Blorg vive en el mar, entonces no come los viernes? Finalmente, ¿puedes argumentar por que si un Blorg no es Blurg, entonces sus Blorg amigos comen los viernes?
  4. Verifica que

$$ \begin{array}{rl} & P \Rightarrow Q \\ & Q \Rightarrow R \\ \hline \therefore & P \Rightarrow R \end{array}$$

es una regla de inferencia válida.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Álgebra Superior I: Inferencias matemáticas

Por Guillermo Oswaldo Cota Martínez

2 respuestas

Introducción

Antes de entrar de lleno a lo que será una parte importante en tu carrera en las matemáticas, vamos a establecer algunas definiciones que nos permiten aterrizar un poco la idea de usar una serie de proposiciones para ‘demostrar’ otras cosas. En esta entrada veremos algo llamado inferencias matemáticas.

La implicación para deducir verdades

Pensemos un momento en las siguientes dos expresiones:

$$P \qquad P\Rightarrow Q,.$$

¿Qué sucedería si acordamos o sabemos por cualquier razón, que $P$ es verdadera y que $P\Rightarrow Q$ es verdadera? Entonces, debe pasar forzosamente que $Q$ debe ser verdadera. En efecto, esto podemos verificarlo en una tabla de verdad:

$P$$Q$$P\Rightarrow Q$
$0$$0$$1$ 
$0$$1$$1$ 
$1$$0$$0$ 
$1$$1$$1$ 

El único renglón en donde $P$ es $1$ y $P\Rightarrow Q$ es $1$ es el cuarto renglón, en el cual en efecto $Q$ es $1$. De la veracidad de $P$ y $P\Rightarrow Q$ se obtiene la veracidad de $Q$. Esto es muy importante, pues nos dice que de $P$ y de $P\Rightarrow Q$ se puede deducir $Q$.

Pensemos ahora en la siguiente fórmula proposicional:

$$(P \land (P \Rightarrow Q)) \Rightarrow Q $$

Por lo que entendemos del $\Rightarrow$ de la derecha, estamos diciendo algo similar a lo que pusimos arriba: «$P$ y $P\Rightarrow Q$ implican $Q$». Abajo haremos una conexión más explícita.

Por el momento, puedes tomar el siguiente ejemplo. Imagina que sabes que las siguientes dos cosas son ciertas simultáneamente:

  • Si $n$ es un entero impar, entonces $n+1$ es un entero par.
  • $n$ es un entero impar.

¿Qué podrías concluir a partir de la veracidad de estas dos oraciones? Que $n+1$ es un entero par. Más concretamente, imagina por un momento que no sabes si 8 es impar o par, pero que sí sabemos la veracidad de la primera oración de arriba y que $7$ es impar. Esta información es suficiente para saber que 8 es par, ¿No lo crees?

Inferencias matemáticas: premisas y conclusiones

Lo que hicimos en el ejemplo de la sección anterior fue tomar dos proposiciones $P\Rightarrow Q$ y $Q$ y que acordamos/sabemos que simultánteamente eran verdaderas. A partir de las veracidades de ellas, logramos concluir la veracidad de otra proposición $P$. Nuestro argumento de que «la veracidad de las premisas hizo que la conclusión fuera verdadera» fue a través de la tabla de verdad. Decimos que usamos una inferencia matemática o una regla de inferencia.

Más formalmente, una regla de inferencia está conformada por unas premisas $P_1, P_2,\ldots, P_n$, que son usualmente fórmulas proposicionales en ciertas variables proposicionales que estamos usando; y una conclusión $Q$ que también es una fórmula proposicional. La regla de inferencia es entonces la fórmula proposicional

$$( P_1 \land P_2 \land \dots \land P_n) \Rightarrow Q.$$

La forma en que escribiremos las reglas de inferencia es la siguiente:

$$ \begin{array}{rl}& P_1\\&P_2\\ & \vdots \\ &P_n\\ \hline \therefore & Q\end{array}$$

El símbolo $\therefore$ se lee «por lo tanto».

Hasta aquí hemos definido qué es una regla de inferencia. Pero hay reglas de inferencia válidas y otras que no lo son. Es decir, hay algunas inferencias matemáticas que son válidas: a partir de la veracidad de las premisas se puede obtener la veracidad de la conclusión (como en el ejemplo que discutimos en la sección anterior). Y hay otras que no, que son inválidas. Es decir, son inferencias matemáticas en las que aunque las premisas sean verdaderas, no podemos concluir nada de la veracidad de la conclusión. ¿Cómo saber cuáles reglas de inferencia son válidas y cuáles no?

Volvamos de nuevo a nuestro ejemplo. Las premisas en este caso son $P$ y $P \Rightarrow Q$ y la conclusión es $Q$. Ahora veamos la tabla de verdad de la regla de inferencia $(P \land (P \Rightarrow Q)) \Rightarrow Q $:

$P$$Q$$P \Rightarrow Q$$P \land (P \Rightarrow Q)$$(P \land (P \Rightarrow Q)) \Rightarrow Q $
$0$$0$ 0 01 
$0$$1$ 0 0 1
$1$$0$ 1 0 1
$1$$1$ 11  1

¿Notas algo peculiar? ¡Pues resulta que la regla de inferencia que dijimos es una tatuología!

En el caso en donde una regla de inferencia sea una tautología, diremos que es una regla de inferencia válida .

Los ingredientes de la validez

Ahora que tenemos las partes de las inferencias matemáticas, veamos un poco su comportamiento para ver cuándo en efecto es verdadera. Esto a la vez nos ayudará a entender la noción de «de la veracidad de las premisas sale la veracidad de la conclusión».

Supongamos que tenemos una regla de inferencia

$$ (P_1 \land P_2 \land \dots \land P_n) \Rightarrow Q $$

y queremos ver si es válida, pero no queremos hacer todos los renglones de la tabla de verdad. Podemos ahorrarnos mucho trabajo como sigue.

En el lado izquierdo tenemos la conjunción $P_1 \land P_2 \land \dots \land P_n$. Si alguna de las premisas fuera falsa, esta conjunción sería falsa. Pero entonces la implicación $\text{Lado izquierdo}\Rightarrow Q$ sería verdadera (recuerda que en las implicaciones si el lado izquierdo es falso, la implicación es verdadera). Así, todos los renglones de la tabla de verdad donde alguna premisa sea falsa, tendremos gratuitamente que la regla de inferencia es verdadera.

Nos quedan los casos en los que todas las premisas son verdaderas. En ellos, tenemos que ver que la conclusión $Q$ también es verdadera. Así, para ver que la regla de inferencia es válida, basta ver que «en aquellos casos que las premisas son verdaderas, la conclusión también lo es».

Y al revés también se vale. Imagina que sabes que la regla de inferencia es válida y que sabes la veracidad de todas las premisas. Entonces, la conjunción $P_1 \land P_2 \land \dots \land P_n$ es verdadera y, así, forzosamente $Q$ es verdadera. En resumen:

«Si una regla de inferencia es válida (es una tautología), y sus premisas son verdaderas, entonces la conclusión es verdadera. Y viceversa, una regla de inferencia es válida cuando hemos visto que en todas las situaciones que las premisas son verdaderas, la conclusión también».

Algunos ejemplos sencillos de inferencias matemáticas válidas

A continuación vamos a ver algunos ejemplos de algunas inferencias matemáticas válidas.

La regla de inferencia válida más simple que se nos puede ocurrir es la siguiente:

$$ \begin{array}{rl}& P\\ \hline \therefore & P \end{array}$$

En donde básicamente estamos diciendo que si tenemos la premisa $P$ entonces va a pasar $P$, lo cual es muy fácil de verificar incluso platicado. Para ver que esta inferencia es válida, necesitamos que $P\Rightarrow P$ sea una tautología. Si $P$ es verdadero, la implicación es verdadera. Si $P$ es falso, la implicación (al tener su antecedente falso), es verdadera.

Veamos otro ejemplo. Considera que tenemos como premisas a $P$ y $Q$ y como conclusión a $P\land Q$. En este caso tendríamos la regla de inferencia:

$$ \begin{array}{rl} & P\\ & Q\\ \hline \therefore & P \land Q \end{array}$$

Esto claramente es válido, pues la proposición $(P \land Q) \Rightarrow (P \land Q)$ siempre es cierta.

Nota que para que una regla de inferencia no sea válida, se tenga que tener ‘un caso’ en que las premisas sean ciertas y la conclusión no. Por ejemplo, considera la siguiente regla de inferencia que nos diría algo así como que «de cualquier cosa $P$ podemos deducir cualquier cosa $Q$»:

$$ \begin{array}{rl} & P \\ \hline \therefore & Q \end{array}$$

Esta regla de inferencia no es válida (¡qué bueno!). La razón es que la implicación $P\Rightarrow Q$ no es una tautología. Para ver esto, notemos que si $P$ es verdadero y $Q$ es falso, entonces $P\Rightarrow Q$ es falso.

Un ejemplo más complicado de inferencia válida

Ahora hagamos un ejemplo más elaborado, en el que aprovecharemos lo que platicamos sobre «pensar que las premisas son verdaderas». Imaginemos que queremos pensar que la siguiente inferencia es válida:

$$ \begin{array}{rl} & P \Rightarrow Q \\ & Q \Rightarrow R \\ & Q\Rightarrow S \\ &(R\land S) \Rightarrow T \\ & P \\ \hline \therefore & T.\end{array}$$

Si alguna premisa fuera falsa, entonces el antecedente de la conjunción de las premisas es falso, y así la implicación de la inferencia sería verdadera: en los casos en los que alguna premisa es falsa, entonces no hay nada que hacer. Así, pensemos, ¿qué pasa si todas las premisas son verdaderas?

Como $P$ es verdadera y $P\Rightarrow Q$ es verdadera, entonces $Q$ es verdadera. Pero ahora, sabiendo que $Q$ es verdadera y $Q\Rightarrow R$ es verdadera, entonces $R$ es verdadera. De manera similar, $S$ es verdadera.

Como tenemos que $R$ y $S$ son verdaderas, entonces $R\land S$ es verdadera. Y como también $(R\land S) \Rightarrow T$ es verdadera, entonces $T$ es verdadera. ¡Hemos logrado el objetivo! A partir de la veracidad de las premisas llegamos a la veracidad de $T$. ¡Yay! Entonces al suponer que todas nuestras premisas fueron verdaderas, y aplicando un poco de «lógica» llegamos a que nuestra conclusión es verdadera.

Un poco de esto se va a tratar la matemática que sigue. A partir de ahora vamos a empezar a usar esta forma de pensar, estamos rascando la fibra de la matemática y con ello empieza el viaje hacia un bosque lleno de distintas áreas, desde el álgebra y el cálculo, pasando por la geometría y la probabilidad. Todas ellas llevan la capa de la matemática porque partirán de un tronco común que nosotros estamos sentando en estas entradas. Dentro de poco verás cómo todo esto se relaciona al quehacer matemático.

Más adelante…

Acabamos de establecer uno de los cimientos sobre el cuál se sustenta el pensamiento deductivo: realizar inferencias matemáticas. Es como pensaremos de ahora en adelante. No te preocupes si aún no puedes expresar bien la lógica detrás de las reglas de inferencia o sus trucos. Esto apenas comienza, pues en las siguientes entradas relacionaremos lo visto ahora con los bloques que construirán a la matemática: las demostraciones. Y por ahí conocerás un cuento que te introducirá a esta idea.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Prueba que $P \Rightarrow P$ es una regla de inferencia válida.
  2. Verifica que las siguientes reglas de inferencia son válidas con tablas de verdad:
  • $$ \begin{array}{rl} & \neg P \Rightarrow \neg Q \\ & \neg P \\ \hline \therefore & \neg Q \end{array}$$
  • $$ \begin{array}{rl} & P \lor Q \\ & \neg P \\ \hline \therefore & Q \end{array}$$

Ahora haz lo mismo pero da un razonamiento «deductivo» (supón que todas las premisas y explica por qué la conclusión es cierta) de porqué es válida la siguiente regla de inferencia:

  • $$ \begin{array}{rl} & P \Rightarrow Q \\ & Q \Rightarrow R \\ \hline \therefore & P \Rightarrow R \end{array}$$
  1. Revisa la Tabla de reglas de inferencia en la página de Wikipedia para conocer más reglas de inferencia válidas. Muestra que en efecto son reglas de inferencia válidas haciendo las tablas que verifiquen la tautología requerida.
  2. Cuando estamos viendo si una regla de inferencia es válida, podemos «ir agregando cosas verdaderas que vayamos deduciendo a las premisas» y usarlas a su vez para seguir deduciendo nuevas cosas. El objetivo de este ejercicio es que demuestres esto. Muestra que si $P_1 \land P_2 \land \ldots \land P_n \Rightarrow Q$ es una inferencia válida y $P_1 \land P_2 \land \ldots \land P_n \land Q \Rightarrow R$ es una inferencia válida, entonces $P_1 \land P_2 \land \ldots \land P_n \Rightarrow R$ es una inferencia válida. En otras palabras, ¡prueba que la siguiente inferencia es válida!
    $$ \begin{array}{rl} & P_1 \land P_2 \land \ldots \land P_n \Rightarrow Q\\ & P_1 \land P_2 \land \ldots \land P_n \land Q \Rightarrow R \\ \hline \therefore & P_1 \land P_2 \land \ldots \land P_n \Rightarrow R. \end{array}$$

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Álgebra Superior I: Negaciones de proposiciones con conectores y cuantificadores

Por Guillermo Oswaldo Cota Martínez

Deja un comentario

Introducción

Ya hemos visto cómo podemos crear proposiciones complejas a partir de proposiciones básicas usando conectores y cuantificadores. En esta entrada repasaremos cómo hacer negaciones de los distintos conectores lógicos de los que hemos platicado, y hablaremos de cómo hacer eso mismo para los cuantificadores universales y existenciales.

Recordatorio de negaciones de conectores lógicos.

Hemos hablado de cinco conectores lógicos: negación, conjunción, disyunción, implicación y doble implicación. En entradas anteriores hemos platicado de qué sucede con algunos de ellos si los negamos.

Negación, conjunción y disyunción

Negar una negación es sencillo. Ya vimos con anterioridad que $\neg(\neg P)\equiv P$. Para la conjunción y disyunción hablamos de las leyes de De Morgan en la entrada correspondiente. Nos dicen que estos conectores se niegan como sigue:

  • $\neg (P \lor Q) \equiv \neg P \land \neg Q$
  • $\neg (P \land Q) \equiv \neg P \lor \neg Q$

Siendo que trabajemos con alguna de estas, solo es necesario recordar: «la conjunción se niega con la disyunción de las negaciones y la disyunción se niega con la conjunción de las negaciones».

Implicación

Para ver cómo es que se niega este conector, recordemos su equivalencia lógica: $$P \Rightarrow Q \equiv \neg P \lor Q.$$

Lo siguiente que podemos hacer es aplicar una ley de De Morgan:

$$\neg (P \Rightarrow Q) \equiv \neg(\neg P \lor Q) \equiv P \land \neg Q.$$

Lo cuál nos quiere decir: «la negación de la implicación es que se cumpla la hipótesis y no la tesis» o «una promesa falla cuando pasa la condición requerida, pero no sucede lo requerido».

Doble implicación

Ahora, recordemos que la doble implicación $P \Leftrightarrow Q$ la definimos mediante $(P\Rightarrow Q) \land (Q \Rightarrow P)$. De esta manera, podemos usar nuevamente leyes de De Morgan para obtener:

$$ \begin{aligned} \neg(P \Leftrightarrow Q) &\equiv \neg((P\Rightarrow Q) \land (Q \Rightarrow P))\\ &\equiv \neg(P\Rightarrow Q) \lor \neg(Q \Rightarrow P) \\ &\equiv (P \land \neg Q) \lor (Q \land \neg P)\end{aligned}$$

Esto lo podemos pensar como «Las negación de un doble condicional es que las dos proposiciones tengan valores de verdad distintos». Para que la negación de la doble implicación sea verdadera necesitamos que $P$ sea verdad y $Q$ falsa o $Q$ verdad y $P$ falsa.

Para recapitular esta parte, recuerda la siguiente tabla:

ConectorNegación
$\neg P$$P$
$P \lor Q$$\neg P \land \neg Q$
$P \land Q$$\neg P \lor \neg Q$
$P \Rightarrow Q$$P \land \neg Q $
$P \Leftrightarrow Q$$(P \land \neg Q) \lor (Q \land \neg P)$

Negaciones de cuantificadores

Ahora que ya hemos visto sobre las negaciones de los conectores, es turno de que hablemos un poco de los cuantificadores. Y para esto recordemos que un cuantificador nos da información sobre los posibles valores de verdad de un predicado a través de un universo.

Negación de cuantificadores universales

Observa por un momento el siguiente predicado:

«Todos los números primos son impares»

Esta proposición la podemos ver de la forma $\forall x: P(x)$ en el universo de discurso de los números enteros. Y la proposición nos dice que cada número primo que tomemos, será impar. ¿Esto es verdad? Pues resulta que no. Y de hecho el único número primo que no es impar es el 2. En este caso no podemos decir que sea verdad la proposición cuantificada, esto pues existe al menos un número entero que no cumple la proposición. ¿Ves a dónde vamos con las palabras resaltadas?

Para negar el cuantificador $\forall$ usamos el cuantificador $\exists$ diciendo que existe un elemento que no cumple la propiedad:

$\neg(\forall x: P(x)) \equiv \exists x: \neg P(x)$

Pensemos en el significado de la expresión. Si tenemos $\neg(\forall x: P(x))$ significa que en el universo de discurso, existe una manera de elegir a $x$, digamos $x=a$ donde $P(a)$ es falsa, es decir $\neg P(a)$ es verdadera.

Negación de cuantificadores existenciales

Por otro lado, pensemos en el siguiente ejemplo:

«Existe un número entero mayor a 1 y menor a 2»

Para poder decir si es verdad o no, deberíamos ponernos de acuerdo en qué es un número entero o qué significa que sea menor o mayor que otro. Pero nuestra intuición nos dice que esto no es cierto (y estamos en lo correcto al pensar así). Ahora ¿Cómo se te ocurre que podríamos negar la expresión $\exists x: P(x)$, donde nuestro universo de discurso son los números enteros y $P(x) : 1<x \land x<2$? Pues necesitaríamos que no exista algún elemento que cumpla la condición. Entonces podemos notar que lo que nos dice esta negación es que cualquier elemento que tomemos de nuestro universo de discurso, no cumplirá con la proposición. Es decir, «Para todo $x$ en el universo de discurso, no se cumplirá el predicado». Dicho de otra forma:

$\neg (\exists x: P(x)) \equiv \forall x: \neg (P(x)).$

Vayamos un paso más allá, pues $P(x) : 1<x \land x<2$ es una conjunción. Al negarla, por leyes de De Morgan obtenemos una disyunción $\neg P(x): \neg(1<x) \lor \neg (x<2)$. Así, podríamos concluir entonces que la negación de

«Existe un número entero $x$ tal que $x>1$ y $x<2$.»

es

«Para todo número entero $x$, o bien no se cumple $x>1$ o bien no se cumple $x<2$.»

Negar hasta lo más profundo posible

Cuando hablamos de negar una proposición matemática compuesta por proposiciones específicas, o bien de negar una fórmula proposicional, nuestro objetivo es llevar las negaciones hasta las proposiciones básicas o las variables proposicionales o las variables de predicado. Por ejemplo, pensemos en simplificar la siguiente negación:

$$\neg(\exists x: (P(x)\lor Q(x)) \land (\neg R(x)\Rightarrow P(x))).$$

Aquí la primera negación está afectando al cuantificador existencial, entonces lo primero que hacemos es cambiarlo en un cuantificador universal de la negación:

$$\forall x: \neg((P(x)\lor Q(x)) \land (\neg R(x)\Rightarrow P(x))).$$

Ahora la negación está actuando en una conjunción, entonces usamos De Morgan para simplificar a

$$\forall x: \neg(P(x)\lor Q(x)) \lor \neg (\neg R(x) \Rightarrow P(x)).$$

Ahora hay una negación en una disyunción y una en una implicación. Entonces, usamos las reglas que vimos arriba para simplificar a lo siguiente

$$\forall x: (\neg P(x)\land \neg Q(x)) \lor (\neg R(x) \land \neg P(x)).$$

Esta ya es la forma final que nos interesa. Nota que las negaciones ya están sólo junto a $P(x), Q(x), R(x)$, pero ya no afectan conjunciones, disyunciones, condicionales ni cuantificadores.

Más adelante…

Llegando a este punto, ya tenemos el conocimiento necesario para hablar de una sustancia muy importante en la matemática: las demostraciones. Esto es, ¿cómo podemos estar seguros de cuándo algo se cumple y cuándo no?, ¿qué significa que un enunciado se derive de otros enunciados? Y más importante: vamos a introducir algunas técnicas de demostración que te ayudarán a entender de qué estamos hablando en matemáticas cuando haya que verificar algo. Y para esto usaremos algo conocido como reglas de inferencia.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. ¿Cuál es la negación de las siguientes proposiciones?
    • $P\lor (Q \Rightarrow S)$
    • $(P \Leftrightarrow (Q\land \neg S))$
    • $P \land (Q\lor R)$
    • $P \Rightarrow(Q \Rightarrow P)$
  2. ¿Cuál es la negación de las siguientes proposiciones que involucran cuantificadores?
    • $\forall x:(P(x)\Rightarrow Q(x))$
    • $\exists y: (\forall x: (P(x)\land Q(y)))$

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Álgebra Superior I: Problemas de condicionales y cuantificadores

Por Guillermo Oswaldo Cota Martínez

Deja un comentario

Introducción

En esta entrada resolveremos problemas de temas vistos en entradas anteriores. Haremos algunos ejemplos relacionados con los conectores condicionales que vimos en una entrada anterior: la implicación y la doble implicación. También veremos algunos de cuantificadores lógicos.

Problemas resueltos

Problema. Si $P$ y $R$ son verdaderas y $Q$ es falsa, di si la siguiente proposición es verdadera o falsa: $$(P \lor R) \Rightarrow \neg(Q \land R).$$

Solución. Haremos una tabla de verdad pero únicamente con los valores que nos dan, es decir, no vamos a hacer la tabla para todos los casos, sino únicamente los que nos interesan en este momento:

$P$$Q$$R$$P \lor R$ $Q \land R$$\neg (Q \land R)$$(P \lor R) \Rightarrow \neg(Q \land R)$
$1$$0$$1$  $1$ $0$  $1$   $1$

Por lo tanto la proposición es verdadera para los valores de verdad dados.

$\square$

Problema. Di si las siguientes proposiciones sobre los números enteros son verdaderas o no:

  1. $(3+1=4) \Rightarrow (0<10)$
  2. $(4=5) \Leftrightarrow (9+1=10)$
  3. $((6<7) \lor (3^2=10)) \Rightarrow (12<12^2)$
  4. $((-1<1) \land (1<-1)) \Leftrightarrow ((13-1=12-1+1)\Rightarrow (1+1<2))$

Solución.

Vamos a hacer algunas verificaciones sobre cada una de las proposiciones para encontrar su valor de verdad:

  • $(3+1=4) \Rightarrow (0<10)$

Como $3+1=4$ es verdadera y $0<10$ es verdadera también, entonces la proposición es verdadera.

  • $(4=5) \Leftrightarrow (9+1=10)$

Recordemos que la doble condicional es verdadera si ambas proposiciones tienen el mismo valor de verdad. Por un lado no es cierto que $4=5$ mientras que sí es verdad que $9+1=10$. Por lo tanto la proposición es falsa.

  • $((6<7) \lor (3^2=10)) \Rightarrow (12<12^2)$

Vamos a ver la proposición por partes. Primero veamos que $((6<7) \lor (3^2=10))$ es una disyunción verdadera pues una de las proposiciones que la componen, $6<7$, lo es. Como $12<12^2$ es verdad, entonces la implicación tiene antecedente y subsecuente verdaderos y por lo tanto es verdadera.

  • $((-1<1) \land (1<-1)) \Leftrightarrow ((13-1=12-1+1)\Rightarrow (1+1<2))$

De nuevo vamos a dividir la proposición en sus partes, $(-1<1) \land (1<-1)$ y $(13-1=12-1+1)\Rightarrow (1+1<2)$. Primero notemos que $(-1<1) \land (1<-1)$ es falsa, pues no es cierto que $1<-1$.

Ahora, veamos cómo es $(13-1=12-1+1)\Rightarrow (1+1<2)$. Nota que $12=13-1$ y $12=12-1+1$, entonces $13-1=12-1+1$. Entonces esta primera parte es verdad, mientras que $1+1=2$ pero no es cierto que $2<2$. Así que es falso que $1+1<2$. Entonces $(13-1=12-1+1)\Rightarrow (1+1<2)$ es falso.

Como $(-1<1) \land (1<-1)$, $(13-1=12-1+1)\Rightarrow (1+1<2)$ son ambas falsas, entonces $((-1<1) \land (1<-1)) \Leftrightarrow ((13-1=12-1+1)\Rightarrow (1+1<2))$ es verdadero.

$\square$

Nota: En este tipo de ejercicios, ¿viste cómo se dieron las argumentaciones de las proposiciones en cada caso? El secreto aquí fue «desarmar» las proposiciones en partes más pequeñas. Esto lo hacemos pues recuerda que los conectores son binarios, esto significa que su valor de verdad depende del valor de verdad de las dos proposiciones que conectan.

Así, para ver cuál es el valor de verdad de $((6<7) \lor (3^2=10)) \Rightarrow (12<12^2)$, lo que hicimos fue deshacerlo en sus partes. Una parte $A$ fue $(6<7) \lor (3^2=10)$ y la otra parte $B$ fue $12<12^2$. Entonces bastaba con verificar cuáles eran los valores de verdad de $A$ y $B$. Para ello, volvimos a «desarmar» a $A$ en sus partes «atómicas». Es decir, desarmamos $(6<7) \lor (3^2=10)$ en $6<7$ y $3^2=10$ y estudiamos el valor de verdad de cada uno de ellos. Usualmente este tipo de pensamiento de «desarmar un problema en sus partes» te ayudará a verificar o demostrar cosas más adelante.

Problema. Sean $P(x)$, $Q(x)$ y $R(x)$ los siguientes predicados:

  • $P(x): x \leq 4$
  • $Q(x): x +1$ es par.
  • $R(x): x> 0$

Si nuestro universo de discurso son los números enteros, ¿cuáles son los valores de verdad de las siguientes proposiciones?

  1. $P(1)$
  2. $P(1) \Rightarrow Q(1)$
  3. $P(0) \Rightarrow (R(5) \Rightarrow Q(0))$
  4. $R(-1) \lor P(2)$
  5. $\neg R(-2) \land P(-2)$

Solución.

1.$P(1)$

Es verdadera, pues $1 \leq 4$.

2. $P(1) \Rightarrow Q(1)$

Como $P(1)$ es verdadera y además $1+1=2$ es par, entonces la proposición es verdadera.

3. $P(0) \Rightarrow (R(5) \Rightarrow Q(0))$

Vamos a dividir la proposición en partes. Primero notemos que $P(0)$ es verdad. Mientras que $R(5) \Rightarrow Q(0)$ es falsa, ya que es cierto que $5>0$ pero es falso que $0+1$ sea par. Entonces la proposición es falsa.

4. $R(-1) \lor P(2)$

Como $R(-1)$ es falsa pero $P(2)$ es verdad, entonces la proposición es verdadera.

5. $\neg R(-2) \land P(-2)$

Como $-2>0$ es falsa, entonces $\neg R(-2)$ es verdad. Además, $-2<4$ es verdad. De esta manera la proposición es verdadera.

$\square$

Problema. Considera los siguientes predicados:

  • $P(x): 2x>0$
  • $Q(x):x>0$
  • $R(x): x=20$
  • $T(x):x<0$

Determina la verdad o falsedad de las siguientes proposiciones, considerando que nuestro universo de discurso son los números enteros. Si la proposición no es verdadera, da un contraejemplo o explicación de ello.

  1. $\forall x: (P(x) \Rightarrow Q(x))$
  2. $\exists x: (Q(x) \land T(x))$
  3. $\forall x: (R(x) \Rightarrow Q(x))$
  4. $\exists ! x:(R(x))$
  5. $ \nexists x :(Q(x) \land P(x))$

Solución.

  • $\forall x:(P(x) \Rightarrow Q(x))$

Nota que siempre que se cumple $2x>0$ entonces $x>0$ (más adelante demostrarás esto con toda formalidad, pero de momento lo daremos por cierto). Por lo tanto la proposición es verdadera.

  • $\exists x: (Q(x) \land T(x))$

Para que esto sucediera, necesitaríamos la existencia de al menos un elemento $x$ que cumpla $0<x$ y $x>0$, es decir necesitaríamos un elemento que sea positivo y negativo a la vez, pero esto no es posible. Por lo tanto la proposición es falsa.

  • $\forall x:(R(x) \Rightarrow Q(x))$

Lo que nos dice esta proposición es «Para todo número entero $x$ que cumpla $x=20$ entonces $x>0$» o dicho de otra manera: «Si un número entero es igual a 20, entonces será positivo.» Lo cuál es correcto, pues si el número es distinto a 20, la implicación será correcta (recuerda la tabla de verdad de la implicación), mientras que el único caso en donde la hipótesis se cumple es cuando $x=20$ y claramente es un número que cumple $x>0$. Entonces la proposición es verdadera.

  • $\exists ! x:(R(x))$

Esto nos quiere decir que existe un único número entero que sea igual a 20, e inmediatamente podemos saber que es verdadera, pero ¿A qué nos referiremos que un número sea igual a 20? Primero tendríamos que ponernos de acuerdo de qué significa la igualdad. Aunque ahora no lo haremos, piensa el cómo nos aseguraríamos de que es el único número entero que cumple esa propiedad. ¿Qué pasaría si no fuera cierto?

  • $ \nexists x: (Q(x) \land P(x))$

Lo que dice la proposición es que ningún número $x$ va a cumplir a la vez $x>0$ y $2x>0$, pero esto no es cierto, pues pensemos en $x=1$. Cumple $Q(x)$ ya que $1>0$ y cumple $P(x)$ porque $2\cdot 1=2>0$. Entonces podemos decir que es falso pues dimos un contraejemplo que contradijo la proposición.

$\square$

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Álgebra Superior I: Cuantificadores existenciales y universales

Por Guillermo Oswaldo Cota Martínez

4 respuestas

Introducción

Hasta ahora hemos visto proposiciones, variables proposicionales, conectores y fórmulas lógicas. Por ello, ya podemos decir cómo se manejan las proposiciones al combinarlas o qué significa que dos proposiciones sean equivalentes.

Sin embargo, hasta ahora no hemos trabajado con tanto rigor los objetos a los que nos referimos dentro de una proposición. Por ejemplo cuando decimos la proposición «Este número es impar» puede que sea o no verdadera, pero esto depende de una cosa: el contexto. ¿A qué número nos estamos refiriendo? Podríamos estar en la siguiente conversación: «Hay números distintos a los múltiplos de 2, por ejemplo el 3. Este número es impar.» A esto último, estando en contexto, ya le podríamos asociar un valor de verdad.

En general esto no es así. Podemos ir variando a qué número nos referimos. En ocasiones las proposiciones tienen una variable y, dependiendo el valor de esa variable, cambian su significado o su valor de verdad. En esta entrada formalizamos estas ideas y hablamos de cuantificadores, que nos permitirán «recorrer» todos los valores posibles de una variable.

Términos variables y predicados

Volvamos a nuestro ejemplo. Al tomar la proposición $P$ «el número es impar», podríamos referirnos al $1$, $2$, $3$, $80$ o $20,000$. Así, es más conveniente pensar en que la proposición depende de una variable como sigue:

$P(\text{el número})$ = «$\text{el número}$ es impar».

Visto de esta manera, $P(2)$ es la proposición «$2$ es impar». En general $P(x)$ es la proposición «$x$ es impar» y esta hace referencia a que el número es una variable que puede tomar distintos valores «permitidos». Observa que en este caso no tendría sentido decir si $P(\text{azul})$ es verdadero o falso. A este tipo de proposiciones que tienen una variable (o más), se les llama predicados.

¿Notas que tenemos que ponernos de acuerdo sobre cuál es el contexto sobre el que estamos hablando al momento de asignarle un valor a nuestra variable? Esto debido a que no podríamos decir que «azul es impar» o «la luna es impar». A este «conjunto» dentro del cual pueden tomar valores nuestras variables le llamamos universo de discurso. Aunque suena algo sofisticado, puedes pensarlo como el contexto al que nos estamos acoplando.

Es muy importante siempre tener claro el universo de discurso cuando usamos predicados. No será lo mismo estar hablando de número pares, que de números enteros. Sabemos que todos los números pares no son impares. Mientras que algunos números enteros son impares. Estas palabras enfatizadas son las que nos van a permitir hablar más sobre cómo es nuestro universo de discurso. No es lo mismo que solo un objeto del universo cumpla un predicado (tenga valor de verdad verdadero) a que todos los objetos de nuestro universo las cumplan.

Cuantificador universal

Cuando tenemos un predicado $P(x)$, no podemos decir si es verdadero o falso hasta que no hayamos decidido quién es exactamente el objeto $x$ dentro de nuestro universo de discurso del que estamos hablando. Pero lo que sí podemos hacer es pensar en si ninguno, alguno o todos los elementos de dicho universo de discurso hacen que $P(x)$ sea verdadero, o no. A esto se le llama cuantificar un predicado.

El primer cuantificador que nos interesa es el cuantificador universal que transforma un predicado en una afirmación de que todo objeto de nuestro universo de discurso hace que la proposición $P(x)$ sea verdadera. Dicho cuantificador universal puede pensarse como agregar un «Para todo $x$ en el universo de discurso,» antes del predicado $P(x)$ que nos interesa. Lo que esto hace es que transforma el predicado $P(x)$ en la proposición $\forall x: P(x)$, la cual acordamos que es cierta siempre y cuando cualquier objeto $x$ de nuestro universo de discurso hace que $P(x)$ sea cierta. Entonces la veracidad de $\forall x: P(x)$ depende fuertemente tanto de:

  • La proposición $P(x)$
  • El universo de discurso en el que estemos.

Cotidianamente también decimos simpemente «Para todo $x$, $P(x)$», pero es muy importante que el universo de discurso sea claro.

Veamos un ejemplo poco a poco. Consideremos el siguiente predicado:

$$P(x)= \text{$x$ es múltiplo de $2$.}$$

Este predicado no tiene ningún valor de verdad. Lo podemos pensar como que es una proposición cuyo contenido depende de una variable $x$ que no hemos decidido. Ahora acordemos como universo a los números múltiplos de $4$. A partir de ello, podemos crear la siguiente proposición con el cuantificador universal $\forall$:

$$\forall x \text{ múltiplo de $4$}: P(x).$$

En palabras «todo múltiplo de $4$ es múltiplo de $2$». Al cuantificar el predicado, ya se convierte en una proposición. ¿Es verdadera? Sí, en efecto, sin importar cuál $x$ tomemos que sea múltiplo de $4$, cumplirá que es múltiplo de $2$.

Pero, ¡cuidado! Podríamos estar trabajando en otro universo de discurso, donde los objetos que nos interesan son todos los enteros. Si ese fuera el caso, al cuantificar universalmente tendríamos lo siguiente:

$$\forall x \text{ entero}: P(x).$$

Esta es una proposición, pero es falsa, pues podemos encontrar un entero, digamos $5$, para el cual $P(5)=\text{$5$ es múltiplo de $2$.}$ es falso. Por ello, la proposición con el cuantificador es falsa.

Algunos otros ejemplos de cómo podemos usar este cuantificador son los siguientes. Observa cómo se deja claro el universo de discurso.

  • $\forall x$ número par, $x$ es múltiplo de 2.
  • $\forall x$ grupo cíclico, $x$ es generado por un único elemento.
  • $\forall x$ año bisiesto, $x$ tiene 366 días.
  • $\forall (x,y)$ vector en $\mathbb{R}^2$, $\norm{x+y}\leq\norm{x}+\norm{y}.$ *

Recuerda que ahora no es necesario que conozcamos a la perfección el universo de discurso del que estamos hablando en estos ejemplos. En estas entradas no nos interesa estudiar a los pares, a los grupos cíclicos, o a los años bisiestos. Los ponemos como ejemplos únicamente para ver que las ideas de lógica aplican a todos ellos. Por ejemplo para el segundo ejemplo el objetivo es que entiendas que siempre que consideremos un grupo cíclico (sea lo que signifique un grupo o un grupo cíclico), ese grupo es generado por un único elemento (sea lo que signifique que un grupo se genere por un único elemento). En este caso nuestro universo de discurso serán los grupos cíclicos, mientras que $P(x)$ es el predicado «$x$ es generado por un único elemento». En estos renglones sólo nos interesa entender cuándo estamos hablando de un universo de discurso, un cuantificador y un predicado.

Cuantificador existencial

El cuantificador «para todo» establece que una proposición es verdadera para todos los objetos de un universo de discurso. Pero esto no siempre pasa. Por ejemplo, pensemos en que nuestro universo de discurso es $$A=\{\text{pescados, reptiles, aves, piedras, felinos}\}$$ y nuestro predicado $P(x)$ es «Los gatos son $x$». En este caso no todas las formas de asignar un objeto del universo a la variable $x$ darán proposiciones verdaderas. Los gatos no son pescados, reptiles ni mucho menos piedras o aves. Pero los gatos sí son felinos. En este caso la asignación $x=\text{felinos}$ será la única en la que se cumpla el esquema proposicional.

El cuantificador existencial permite enunciar una proposición que acordamos que se vuelve verdadera cuando uno (o más) de los objetos del universo de discurso hacen que obtengamos una proposición verdadera. Así, una vez acordado un universo de discurso y un predicado $P(x)$, diremos que la proposición $\exists x:P(x)$ es verdadera cuando logremos encontrar algún $x$ para el cual $P(x)$ sea verdadera.

En palabras, esto se dice a veces como «existe $x$ en el universo de discurso que cumple $P(x)$», o simplemente como «existe $x$, $P(x)$», cuando el universo de discurso se sobreentiende.

Algunos ejemplos del uso de este cuantificador son los siguientes:

  • $\exists n$ número entero que es solución a $n^2=4$.
  • $\exists n$ número entero que cumple $e^{i\pi}+n=0.$ **

Nuevamente, es muy importante que se acuerde el universo de discurso para poder concluir la veracidad de una proposición que involucra un cuantificador existencial. Por ejemplo, la proposición

$$\exists x \text{ número real}: x^2=-1$$

es falsa, pues no existe tal real (al elevar un real al cuadrado siempre queda mayor o igual a cero), mientras que la proposición

$$\exists x \text{ número complejo}: x^2=-1$$

es verdadera, pues el número complejo $x=i$ cumple que $x^2=-1$ es verdadero.

Cuantificador «existe un único»

El cuantificador «existe» tiene una variante más restrictiva. Cuando decimos que existe al menos un elemento en nuestro universo de discurso que cumple una propiedad, también tenemos que puede haber $2$, $3$ o $20$ elementos que lo cumplen. Por ejemplo: «$\exists n$ número entero que es solución a $n^2=4$» tiene dos posibilidades, pues al tomar $n=-2$ o $n=2$ el predicado se transforma en una proposición verdadera.

Pero es muy frecuente en matemáticas que se busque que uno y sólo un elemento que haga verdadero a a un predicado. Para referirnos a estas ocasiones, usamos el cuantificador «$\exists!$», que se lee como «existe un único«. Por ejemplo, sabemos que el único número primo par es 2. Así que podríamos decir: «$\exists! x$ número entero que es primo y par».

La regla de asignación de verdad es que $\exists! x: P(x)$ será verdadera si hay un único $x$ del universo de discurso que haga que $P(x)$ sea verdadera. Si no hay, o hay más de uno, entonces $\exists! x:P(x)$ será falsa.

Otros ejemplos (algunos informales) de su uso son:

  • $\exists!x$ día de la semana tal que $x$ empieza con la letra L
  • $\exists!x$ número real tal que $x$ es neutro aditivo. ***
  • $\exists!n$ número entero que cumple $e^{i\pi}+n=0.$

¿Observas que la última oración se parece mucho al último ejemplo del cuantificador anterior? Y con esto no estamos contradiciendo nada, en el ejemplo anterior solo estamos diciendo «Existe un número entero $n$ que es solución a $e^{i\pi}+n=0$» con lo que queremos decir que existe al menos uno, mientras que en el último ejemplo, decimos «Existe un único número entero $n$ que es solución a $e^{i\pi}+n=0$». Aquí, el objetivo solo es ser más específicos, lo que quiere decir que sólo estamos dando información extra acerca de la proposición.

Tabla resumen de conjunciones y cuantificadores

A continuación resumimos en una tabla varios símbolos lógicos que hemos discutido.

Negaciones$\neg$
Conjunciones$\land$
Disyunciones$\lor$
Implicaciones$\Rightarrow$
Dobles implicaciones$\Leftrightarrow$
Para todos los casos$\forall$
Para al menos un caso$\exists$
Para un único caso$\exists!$

Combinando conectores y cuantificadores

Habiendo conocido los distintos cuantificadores, podríamos hacer afirmaciones un poco más extensas usando otros conectores lógicos en los predicados que usamos. Por ejemplo, pensemos en que nuestro universo de discurso son los números enteros. Consideremos los predicados $P(x)=x<0$ y $Q(x)=x<1$. Entonces podríamos decir

$$\forall \text{$x$ número entero: } (P(x) \Rightarrow Q(x))$$

En palabras: «Para todo número entero $x$, si $x$ es menor a 0, entonces $x$ es menor a 1». Esto es una afirmación verdadera.

También podríamos poner algo del estilo

$$\exists \text{$x$ número entero: } (x+3=8) \land (x^2-2=23).$$

Esta también es una afirmación verdadera pues $x=5$ es un número entero que cumple la proposición $x+3=8$ y la proposición $x^2-2=23$.

También podemos tener predicados con más de una variable e irlos cuantificando poco a poco. Por ejemplo, pensemos nuevamente a los números enteros como nuestro universo de discurso y $P(x,y)$ como la afirmación $x+y=0$. Tenemos que $P(2,-2)$ es verdadero, mientras que $P(2,2)$ es falso, pues es falso que $2+2=0$. Podemos cuantificar a $y$ con un existencial de unicidad para obtener lo siguiente: $$\exists ! y: P(x,y).$$ Esto todavía no es una proposición de la que podamos saber si es cierta o verdadera. Aunque $y$ ya está cuantificado, $x$ sigue siendo variable. Lo que sí es que entonces es un predicado que de la variable $x$ y ahora podemos cuantificarlo con respecto a $x$ para obtener, por ejemplo,

$$\forall x: (\exists! y: P(x,y)).$$

Aquí estaríamos diciendo «para cada número entero $x$, existe un único número entero $y$ tal que $x+y=0$». Dicho de otra forma, cada vez que consideramos un número entero $x$, digamos $3$, existirá un único número entero $y$ que cumplirá la ecuación $x+y=0$. En este caso ese número $y$ es $-3$, pues dijimos que $x=3$ y sólo hay un número que al sumarlo a $3$ nos da $0$.

Entender estas dobles cuantificaciones será crucial para entender, por ejemplo, la definición de límite en Cálculo Diferencial e Integral I.

Notas

Estas son algunas anotaciones del artículo y no es necesario que las sepas, únicamente son curiosidades o temas por aparte que forman parte de la cultura matemática.

* Esta se conoce como la desigualdad del triángulo y nos dice básicamente que la suma de la longitud de dos lados de un triángulo siempre será mayor a la longitud del tercer lado.

** Esta afirmación está relacionada con la llamada identidad de Euler y algunos piensan que es una de las ecuaciones más hermosas de las matemáticas. En otros cursos como Álgebra Superior 2 o Variable Compleja 1 puede que vuelvas a ver esta identidad con su demostración.

*** El único neutro aditivo es el $0$, y esto quiere decir que al sumarle este a cualquier otro número, dará el mismo número.

Más adelante…

Cuando estamos hablando de cuantificadores, también nos van a interesar sus negaciones. Por ejemplo, ¿a qué nos referiremos cuando digamos $\neg (\forall x P(x))$? ¿o cuando digamos $\neg (\exists x (P(x) \Rightarrow Q(x)))$? Lo primero que tenemos que entender es qué quiere decir negar un cuantificador universal y uno existencial. Eso es justo lo que estudiaremos en la siguiente entrada.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Imagina que definitivamente quieres comprar un helado. Cuando vas a la heladería, sólo venden un sabor. Esto tiene desventajas, por supuesto. Pero, ¿qué ventajas tiene que sólo haya un sabor de helado? Enlista todas las que puedas.
  2. En los ejemplos siguientes encuentra el universo de discurso y su predicado.
    1. $\forall x$ número par,$x$ es múltiplo de 2.
    2. $\forall x$ año bisiesto, $x$ tiene 366 días.
    3. $\forall (x,y)$ vector en $\mathbb{R}^2$, $\norm{x+y}\leq\norm{x}+\norm{y}$.
  3. Considera el predicado $P(x)=«x$ es múltiplo de 11». Da cuatro universos de discurso tales que los siguientes enunciados sean ciertos:
    • $\forall x P(x)$
    • $\exists x P(x)$
    • $\exists! x P(x)$
    • $\nexists x P(x)$
  4. Considera la proposición: $P(x,y,z)$ = «$x^3+y^3=z^3$». ¿Cuál de los siguientes enunciados representa la oración «No existen números enteros $x,y,z$ que cumplen $P(x,y,z)$»?:
    • $\forall x (\exists y (\exists z P(x,y,z)))$
    • $\nexists (x,y,z)P(x,y,z)$
    • $\forall x (\nexists(y,z)P(x,y,z))$
    • $\nexists x (\forall (x,y) P(x,y,z))$
  5. ¿El ejercicio anterior sólo tiene una solución? Si hay más de una opción correcta, ¿cómo argumentarías que dos enunciados representan el mismo enunciado?

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»