Archivo de la etiqueta: riemann

Cálculo Diferencial e Integral II: Definición de la integral definida

Por Moisés Morales Déciga

Deja un comentario

Introducción

En la entrada anterior se introdujo el problema de calcular el área que se encuentra en una región delimitada por ciertas líneas verticales, el eje $x$ y la gráfica de una función. Hablamos de cómo aproximar esta área cuando la función es «bien portada», pero aún no hemos dicho a qué se refiere esto. En esta entrada haremos una formalización de este concepto mediante la definición de integral definida.

La intuición que puedes tener a lo largo de la entrada es que para poder hablar de que una función sea integrable en cierto intervalo, intuitivamente necesitamos que las sumas de Riemann convergan a un valor conforme hacemos las celdas tender a cero en longitud. Esto diría que sin importar cómo hagamos la partición, las sumas de Riemann deben converger a un mismo valor conforme la partición se hace más y más fina. En particular, necesitaremos que las sumas superiores e inferiores cumplan esto. Como en ellas entendemos bien qué pasa con los refinamientos, entonces nos conviene más dar la definición en términos de ellas. Es lo más conveniente y, en particular, implica lo anterior.

Integral definida de Riemann

La definición clave que estudiaremos es la siguiente.

Definición. Sean $f:\mathbb{R}\to \mathbb{R}$ una funcion acotada y $a\leq b$ reales. Sea $\mathbf{P}$ el conjunto de las particiones de $[a,b]$. Definimos

\begin{align*}
\underline{S}(f) & = \sup \lbrace \underline{S(f,P)} \ | P \in \mathbf{P} \rbrace\\
\overline{S}(f) &= \inf \lbrace \overline{S(f,P)} \ | P \in \mathbf{P} \rbrace,
\end{align*}

es decir al supremo de las sumas inferiores y al ínfimo de las sumas superiores sobre todas las particiones posibles de $[a,b]$. Diremos que existe la integral definida de Riemann para $f$ en el intervalo $[a,b]$ si

$$ \underline{S(f)} = \overline{S(f)}.$$

En este caso, a este valor en común lo denotamos por $$\int \limits_{a}^{b} f(x) dx.$$

En otras palabras, para que $f$ sea integrable, necesitamos que el ínfimo de las sumas superiores sea igual al supremo de las sumas inferiores. A veces también decimos que $f$ es Riemann integrable en $[a,b]$ o, si el contexto es claro, simplemente que es integrable.

No todas las funciones son Riemann integrables. Hacia el final de esta unidad daremos ejemplos de funciones que no lo son. Sin embargo, por ahora nos enfocaremos en ver algunos ejemplos que sí son Riemann integrables y probar propiedades de la integral definida en los casos en los que sí exista.

Ejemplo de integral definida

Veamos un ejemplo sencillo de cómo se verifica la definición de integral definida.

Ejemplo. Tomemos la función $f:[0,1]\to \mathbb{R}$ dada por $f(x)=x$. Veamos que dicha función es integrable en el intervalo $[0,1]$. Para ello, demos la partición $P_n$ homogénea del intervalo $[0,1]$ en celdas de longitud $1/n$, con $n$ un entero positivo. Si hacemos esto, las celdas de la partición son

$$[0,1/n],[1/n,2/n],\ldots[(n-1)/n,1].$$

Los supremos de los valores de $f$ en dicho intervalo son

$$1/n, 2/n, \ldots, 1,$$

y los ínfimos son

$$0,1/n, \ldots, (n-1)/n.$$

De este modo, para esta partición la suma superior sería

\begin{align*}
\overline{S} (f,P_n) &= \frac{1}{n}\left(\frac{1}{n}+\frac{2}{n}+\ldots+\frac{n}{n}\right)\\
&=\frac{1}{n^2}(1+2+\ldots+n)\\
&=\frac{n(n+1)}{2n^2}\\
&=\frac{1}{2}+\frac{1}{2n}.
\end{align*}

y la suma inferior sería

\begin{align*}
\underline{S} (f,P_n) &= \frac{1}{n}\left(\frac{0}{n}+\frac{2}{n}+\ldots+\frac{n-1}{n}\right)\\
&=\frac{1}{n^2}(0+1+2+\ldots+(n-1))\\
&=\frac{(n-1)n}{2n^2}\\
&=\frac{1}{2}-\frac{1}{2n}.
\end{align*}

La sucesión de números $\frac{1}{2}+\frac{1}{2n}$ se acerca tanto como queramos a $\frac{1}{2}$ por arriba. Como el ínfimo $\overline{S}(f)$ que estamos buscando es cota inferior de todas las sumas inferiores, en particular es de estas que vienen de particiones homogéneas. Así, $\overline{S}(f)\leq \frac{1}{2}$. Pero además, por una proposición de la entrada anterior sabemos que cualquier suma inferior es cota inferior de todas las sumas inferiores. Como $\overline{S}(f)$ es la mayor cota inferior, tenemos que $\overline{S}(f)\geq \frac{1}{2}-\frac{1}{2n}$ para todo $n$, y entonces $\overline{S}(f)\geq \frac{1}{2}$. Todo esto nos permite concluir que $\overline{S}(f)=\frac{1}{2}$.

De manera totalmente análoga (que te sugerimos argumentar cuidadosamente), se tiene que $\underline{S}(f)=\frac{1}{2}$. Concluimos entonces que $f$ es integrable en $[0,1]$ y que $$\int_0^1 f(x)\, dx = \frac{1}{2}.$$

$\triangle$

Aunque este ejemplo tuvo un intervalo y una función muy sencillas, se volvió algo elaborado justificar la parte de los ínfimos y supremos. Es por ello que nos conviene enunciar y demostrar algunos resultados sobre funciones integrables que nos permitirán determinar la integrabilidad con más comodidad.

Integral definida mediante particiones homogéneas y la condición de Riemann

Lo primero que haremos es demostrar que para que una función sea integrable, nos basta estudiar a las particiones homogéneas.

Teorema. Sean $f:\mathbb{R}\to \mathbb{R}$ una funcion acotada y $a\leq b$ reales. Sea $P_n$ la partición homogéneas del intervalo $[a,b]$ en $n$ partes. Supongamos que se da la siguiente igualdad de límites:

$$\lim_{n\to \infty} \overline{S}(f,P_n) = \lim_{n\to \infty} \underline{S}(f,P_n).$$

Entonces, la integral existe y es igual a ese límite en común.

Demostración. $\Leftarrow)$ La demostración sigue argumentos muy parecidos al ejercicio que presentamos como ejemplo arriba. Supongamos que los límites para las particiones homogéneas existen y son iguales a $L$. Estudiemos $\overline{S}(f)$. Por ser ínfimo de todas las sumas superiores, tendríamos en particular para las particiones homogéneas que $$\overline{S}(f)\leq \overline{S}(f,P_n),$$

para todo entero positivo $n$. Haciendo tender $n$ a infinito, obtenemos $\overline{S}(f) \leq L$. Por otro lado, sabemos que cualquier suma inferior es cota inferior de cualquier suma superior, en particular, cada $\underline{S}(f,P_n)$ es una de estas cotas inferiores. Como $\overline{S}(f)$ es la mayor de las cotas inferiores, tendríamos que $$\overline{S}(f)\geq \underline{S}(f,P_n).$$

Haciendo tender $n$ a infinito, obtenemos $\overline{S}(f)\geq L$. Así, $\overline{S}(f)=L$. Un argumento análogo demuestra que $\underline{S}(f)=L$, y por lo tanto la función es integrable en $[a,b]$.

$\square$

Un siguiente resultado importante es la condición de Riemann, que nos dice que para que una función sea integrable, nos basta encontrar una partición en donde la suma superior y la inferior estén tan cerca como querramos. A esto se le conoce como la condición de Riemann.

Teorema. Sean $f:\mathbb{R}\to \mathbb{R}$ una funcion acotada y $a\leq b$ reales. Se tiene que $f$ es integrable en $[a,b]$ si y sólo si para todo $\epsilon >0$ existe una partición $P_\epsilon$ tal que:

$$\overline{S}(f,P_\epsilon) \ – \ \underline{S}(f,P_\epsilon) < \epsilon .$$

Demostración. $\Rightarrow )$ Sea $f$ integrable. Debemos mostrar que para cada $\epsilon>0$ existe una partición $P_\epsilon$ tal que $$\overline{S}(f,P_\epsilon) \ – \ \underline{S}(f,P_\epsilon) < \epsilon.$$

Para ello, tomemos $\epsilon^*=\epsilon/2$. Como $\overline{S}(f)$ es ínfimo de las sumas superiores, entonces $\overline{S}(f)+\epsilon^\ast$ ya no es cota inferior para dichas sumas superiores, por lo que existe una partición $P$ tal que $\overline{S}(f,P) < \overline{S}(f)+\epsilon^*$. Así mismo, existe una partición $P’$ tal que $\underline{S}(f,P’) > \underline{S}-\epsilon^*$. Si $P_\epsilon$ es un refinamiento mutuo de $P$ y $P’$, tendríamos entonces que

\begin{align*}
\overline{S}(f,P_\epsilon)&<\overline{S}(f,P)<\overline{S}(f)+\epsilon^*\\
\underline{S}(f,P_\epsilon)&>\underline{S}(f,Q)>\underline{S}(f)-\epsilon^*.
\end{align*}

Multiplicando la segunda igualdad por $-1$ y sumando ambas, obtenemos entonces que

\begin{align*}
\overline{S}(f,P_\epsilon) \ – \ \underline{S}(f,P_\epsilon) &< \overline{S}(f) + \epsilon^* \ – \ \underline{S}(f) + \epsilon^* \\
&= 2 \epsilon^* \\
&= \epsilon .
\end{align*}

Aquí usamos que $\overline{S}(f)=\underline{S}(f)$ por ser $f$ integrable.

$\Leftarrow)$ Supongamos ahora que para todo $\epsilon$ se puede encontrar la partición $P_\epsilon$ que satisface $\overline{S}(f,P_\epsilon) \ – \ \underline{S}(f,P_\epsilon) < \epsilon$. Veremos que a partir de esto se puede probar que $ \overline{S}(f) = \underline{S}(f) .$

Por ser $\overline{S}(f)$ el ínfimo de todas las sumas superiores, se tiene que

$$\overline{S}(f,P_\epsilon) > \overline{S}(f) .$$

$$ \underline{S}(f,P_\epsilon) < \underline{S}(f) \Longrightarrow – \underline{S}(f,P_\epsilon) > – \underline{S}(f) .$$

$$\Longrightarrow \epsilon > \overline{S}(f,P_\epsilon) \ – \ \underline{S}(f,P_\epsilon) > \overline{S}(f) \ – \ \underline{S}(f) .$$

Y $\epsilon$ es tan pequeño como lo queramos, por lo tanto.

$$ \overline{S}(f) = \underline{S}(f) .$$

$\square$

Ejemplos de integral definida con los resultados que probamos

Veamos algunos ejemplos de cómo utilizar los resultados que acabamos de mostrar para demostrar que ciertas integrales definidas existen, y para encontrar su valor.

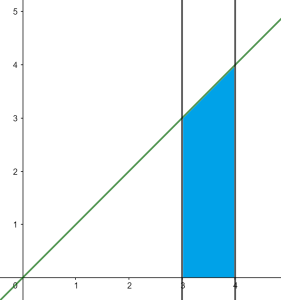
Ejemplo. Calculemos la integral de la función $f(x)=x$ en el intervalo $[3,4]$

Usaremos la técnica de los límites de las particiones homogéneas. Estudiaremos con detalle el caso de las sumas superiores y dejaremos el de las inferiores como ejercicio. Si la partición $P_n$ del intervalo $[a,b]$ es homogénea y en $n$ partes, las celdas tienen longitud $\frac{b-a}{n}$ y entonces son:

$$\left[a,a+\frac{b-a}{n}\right], \left[a+\frac{b-a}{n}, a+2\frac{b-a}{n}\right], \ldots, \left[a+(n-1)\frac{b-a}{n},b\right].$$

La función $f(x)=x$ es creciente, y entonces los máximos se alcanzan al final de cada intervalo. Así, para el intervalo $[3,4]$ tenemos:

\begin{align*}
\overline{S}(f,P_n)&=\sum_{i=1}^{n} f \left( 3+i \cdot \frac{4-1}{n} \right) \frac{4-3}{n}\\
&=\sum_{i=1}^{n} \left(3+ \frac{i}{n}\right) \frac{1}{n}\\
&=\sum_{i=1}^{n} \left(\frac{3}{n}+ \frac{i}{n^2}\right)\\
&=\sum_{i=1}^{n} \left(\frac{3}{n}\right) + \sum_{i=1}^{n} \left(\frac{i}{n^2}\right)\\
&=\frac{3}{n} \cdot n + \frac{1}{n^2} \sum_{i=1}^n i\\
&=3 + \frac{n(n+1)}{2n^2} \\
&=3 + \frac{1}{2} + \frac{1}{2n}\\
&=\frac{7}{2}+\frac{1}{2n}.
\end{align*}

De este modo,

$$\lim_{n\to\infty} \overline{S}(f,P_n) = \lim_{n\to\infty} \left(\frac{7}{2} + \frac{1}{2n}\right) = \frac{7}{2}.$$

Por tu cuenta, revisa que que también se cumple lo siguiente

$$\lim_{n\to\infty} \underline{S}(f,P_n) = \frac{7}{2}.$$

Así, por la proposición que mostarmos arriba, tenemos que la integral en el intervalo $[3,4]$ existe y por lo tanto:

$$ \int \limits_{3}^{4} x \, dx = \frac{7}{2}.$$

$\triangle$

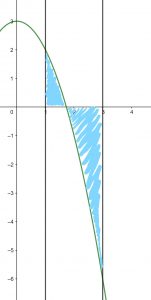
Ejemplo. Ahora calculemos la integral de la función $f(x)=-x^2 + 3$ en el intervalo $[1,3]$ . Al hacer una figura, obtenemos la siguiente gráfica.

Observa que en este caso tenemos 2 áreas: del eje $x$ y otra por debajo del eje $x$. Todo lo que hemos hecho funciona tanto para funciones positivas, como negativas. Pero obtendremos algo interesante de la conclusión de este problema.

Para ver que la integral existe, usaremos nuevamente la técnica de las particiones homogéneas. Ahora haremos las sumas inferiores. Como la función es decreciente, los valores más chicos aparecen al final de cada intervalo. Tenemos entonces que:

\begin{align*}
\underline{S}(f,P)&=\sum_{i=1}^{n} \left( – \ \left( 1+i\cdot \left(\frac{3-1}{n}\right) \right)^2+3 \right) \left(\frac{3-1}{n} \right) \\
&=\sum_{i=1}^{n} \left(- \ \left(1+i\cdot \left(\frac{2}{n}\right)\right)^2+3\right) \left(\frac{2}{n}\right)\\
&=\sum_{i=1}^{n} \left( – \ \left(1+ \frac{4i}{n} + \frac{4 i^2}{n^2}\right)+3\right) \left(\frac{2}{n}\right)\\
&=\sum_{i=1}^{n} \left(\frac{ 4}{n} – \frac{8i} {n^2} – \frac{8 i^2}{n^3}\right)\\
&=\frac{4}{n} \sum_{i=1}^{n} – \frac{8}{n^2} \sum_{i=1}^{n} i – \frac{8}{n^3}\sum_{i=1}^{n} i^2\\
&=\frac{4}{n} \cdot n – \frac{8}{n^2} \frac{n(n+1)}{2} – \frac{8}{n^3} \frac{n(n+1)(2n+1)}{6} \\
&=4 \ – \ \frac{8n^2}{2n^2} \ – \ \frac{8n}{2n^2} \ – \ \frac{8 \cdot 2n^3}{6n^3} \ – \ \frac{8 \cdot 3n^2}{6n^3} \ – \ \frac{8n}{6n^3} \\
&= – \ \frac{8}{3} \ – \ \frac{8n}{2n^2} \ – \ \frac{8 \cdot 3n^2}{6n^3} \ – \ \frac{8n}{6n^3} .
\end{align*}

Así, $$\lim_{n\to\infty} \underline{S}(f,P)=-\frac{8}{3}.$$

Se puede mostrar que el límite de las sumas superiores para las particiones homogéneas también es $-\frac{8}{3}$ (verifícalo), así que la integral buscada tiene este valor. De esta forma,

$$ \int \limits_{1}^{3} -x^2 +3 \, dx = – 8/3 .$$

$\triangle$

¿Áreas negativas?

Se comentó que la integral se utiliza para el cálculo de áreas bajo la curva, entonces, ¿Por qué el resultado del ejemplo anterior es negativo? ¿Hay áreas negativas? Intuitivamente, no debería haber áreas negativas. Sin embargo, el procedimiento que usamos para definir a la integral definida sí nos puede dar números negativos. Puedes pensarlo como sigue: el área que estamos calculando va del eje $x$ a la gráfica de la función $f$. Si esa gráfica está por debajo, entonces estámos yendo en dirección negativa. En el último ejemplo hay tanto una región por encima del eje $x$, como una por debajo. El número que nos salió es la diferencia de ambas áreas: el área por arriba del eje $x$, menos el área por debajo del eje $x$. Como el resultado que obtuvimos fue negativo, entonces el área por debajo del eje $x$ era mayor en magnitud.

Esta es una propiedad un poco antintuitiva, pero es importante preservarla. El cálculo de áreas es sólo una de las aplicaciones que tiene la integral. En otras aplicaciones, es importante que la integral mida qué tanto estuvimos por encima del eje $x$ y qué tanto estuvimos por debajo.

¿Y si queremos realmente entender la suma de las dos áreas de la figura y no la resta? En ese caso, tendremos que hacer una figura para entender cómo hacer las cuentas. Si hay área que está por debajo del eje $x$, deberemos agregar un signo $-$ para contarla correctamente como área positiva. Pero entonces tendremos que partir nuestro intervalo de integración en varios intervalos de acuerdo a cuándo la gráfica de $f$ cruza al eje $x$.

Con esto en mente, retomemos el ejemplo anterior.

Ejemplo. Encontremos el área en valor absoluto que genera la función $f(x)=-x^2 + 3$ en el intervalo $[1,3]$.

Lo primeo que haremos es obtener el punto donde la función cruza al eje $x$. Para ello, se requiere que $-x^2+3=0$, que en dicho intervalo sucede en $x=\sqrt{3}$.

Una vez encontrado el punto raíz o la raíz de la función, ahora podemos partir el área absoluta que nos interesa en dos intervalos: el $[1,\sqrt{3}]$ y el $[\sqrt{3},3]$.

Pensando en que queremos calcular el área absoluta, necesitamos dividir la formula que se planteó anteriormente en los intervalos correspondientes, y en el intervalo $[\sqrt{3},3]$ será necesario agregar un signo menos para que el área que se calcula como negativa, ahora se cuente de manera positiva. De esta manera, tendríamos:

$$ F_1^3 = \int \limits_{1}^{\sqrt 3} -x^2 +3 \, dx \ – \ \int \limits_{\sqrt 3}^{3} -x^2 +3 \, dx .$$

Ahora queda replicar el proceso que vimos en la suma anterior con estos 2 nuevos intervalos y juntarlos considerando el cambio de signo. Desarrollando los cálculos, se encuentra que el área generada por la función es de:

$$F_1^ 3= 4 \sqrt 3 \ – \ \frac{8}{3}.$$

$\triangle$

Nota. En este ejemplo partimos el intervalo en dos subintervalos, pero el intervalo puede quedar partido tantas veces como la función $f$ lo requiera, de acuerdo a la cantidad de veces que se cruza el eje $x$.

Más adelante…

En esta entrada dimos la definición formal de que una función sea integrable en cierto intervalo. O mejor dicho, que sea Riemann integrable. En cursos más avanzados de matemáticas se definen y estudian otras nociones de integrabilidad, pero por ahora esta es la que nos interesa. Para que la integral de Riemann exista, necesitamos que coindidan el ínfimo de las sumas superiores y el supremo de las sumas inferiores de la función dada. En ese caso, el valor de la integral es ese valor en común.

Ya dada la definición, dimos algunos resultados que nos ayudarán a determinar cuándo una función es integrable. En siguientes entradas daremos más propiedades que nos ayudarán entender mejor la integrabilidad y la integral. Varias entradas despuésse hablará de las integrales indefinidas y del teorema fundamental del cálculo, que daran pie a numerosas técnicas de integración.

Lo último que hicimos en esta entrada es notar que hay casos en donde el valor de la integral que se encuentra es negativo. Esto contradice un poco nuestra intuición de que la integral es un área. Sin embargo, ya platicamos qué hacer en este caso si queremos realmente el «área positiva». Seguiremos explorando esta idea de integrales negativas un poco más adelante. Por ahora, lo que puedes hacer es identificar los intervalos en los que la función tiene determinado signo.

Tarea moral

  1. Completa las cuentas que quedaron pendientes en cada uno de los ejercicios.
  2. Expresa la siguiente expresión como una integral en el intervalo $[0,\pi]$. $$\lim_{n \rightarrow \infty} \sum_{i=1}^n (x_i^3 + x_i ~ sin (x_i)) \triangle x .$$
  3. Encuentra el área delimitada por la curva $f(x)=x^2 +2 $ y el eje $x$ en el intervalo $[1,4]$.

4. Encuentra el valor del área delimitada por la gráfica de la función$f(x)= x^3-6x$ en el intervalo $[0,3]$, que es la zona sombreada. Realiza las cuentas tanto con áreas absolutas, tanto con áreas con signo.

5. Encuentra el área de la función $f(x)=\sqrt {1-x^2}$ en el intervalo $[0,1]$.

Entradas relacionadas

Álgebra Lineal I: Aplicaciones de bases ortogonales y descomposición de Fourier

Por Leonardo Ignacio Martínez Sandoval

3 respuestas

Introducción

En esta entrada continuamos hablando de bases ortogonales. Como recordatorio, para poder hablar de esto, necesitamos un espacio vectorial sobre $\mathbb{R}$ equipado con un producto interior, y por lo tanto podemos hablar de normas. Una base ortogonal de $V$ es una base en la cual cada par de vectores tiene producto interior $0$. Es ortonormal si además cada elemento es de norma $1$. Ahora veremos que dada una base ortonormal, podemos hacer una descomposición de Fourier de los vectores de $V$, que nos permite conocer varias de sus propiedades fácilmente.

La teoría que discutiremos está basada en el contenido de la Sección 10.5 del libro Essential Lineal Algebra with Applications de Titu Andreescu. Las últimas dos secciones de esta entrada son un poco abstractas, pero son la puerta a ideas matemáticas interesantes con muchas aplicaciones dentro de la matemática misma y en el mundo real.

Descomposición de Fourier

Es fácil conocer las coordenadas de un vector en términos de una base ortonormal.

Teorema. Si $V$ es un espacio Euclideano de dimensión $n$ con producto interior $\langle\cdot, \cdot\rangle$ y $B=\{e_1,\ldots,e_n\}$ es una base ortonormal con este producto interior, entonces para cualquier vector $v$, la coordenada de $v$ con respecto a $e_i$ es $\langle v, e_i \rangle$.

Demostración. Expresemos a $v$ en la base $B$ como $$v=\alpha_1e_1+\ldots+\alpha_n e_n.$$

Tomemos $j$ en $1,2,\ldots,n$. Usando la linealidad del producto interior, tenemos que
\begin{align*}
\langle v, e_j \rangle &= \left \langle \sum_{i=1}^n \alpha_i e_i, e_j \right \rangle\\
&=\sum_{i=1}^n \alpha_i \langle e_i,e_j \rangle.
\end{align*}

Como $B$ es base ortonormal, tenemos que en el lado derecho $\langle e_j,e_j\rangle = 1$ y que si $i\neq j$ entonces $\langle e_i, e_j\rangle=0$. De esta forma, el lado derecho de la expresión es $\alpha_j$, de donde concluimos que $$\langle v, e_j \rangle = \alpha_j,$$ como queríamos.

$\square$

Definición. Si $V$ es un espacio Euclideano de dimensión $n$ con producto interior $\langle\cdot, \cdot\rangle$ y $B=\{e_1,\ldots,e_n\}$ es una base ortonormal, a $$v=\sum_{i=1}^n \langle v, e_i \rangle e_i$$ le llamamos la descomposición de Fourier de $v$ con respecto a $B$.

Ejemplo. Trabajemos en el espacio vectorial $V=\mathbb{R}_2[x]$ de polinomios reales de grado a lo más $2$. Ya mostramos anteriormente (con más generalidad) que $$\langle p,q \rangle = p(-1)q(-1)+p(0)q(0)+p(1)q(1)$$ es un producto interior en $V$.

Los polinomios $\frac{1}{\sqrt{3}}$, $\frac{x}{\sqrt{2}}$ y $\frac{3x^2-2}{\sqrt{6}}$ forman una base ortonormal, lo cual se puede verificar haciendo las operaciones y queda de tarea moral. ¿Cómo expresaríamos a la base canónica $\{1,x,x^2\}$ en términos de esta base ortonormal? Los primeros dos son sencillos:
\begin{align}
1&=\sqrt{3}\cdot \frac{1}{\sqrt{3}}\\
x&=\sqrt{2}\cdot \frac{x}{\sqrt{2}}.
\end{align}

Para encontrar el tercero, usamos el teorema de descomposición de Fourier. Para ello, calculamos los siguientes productos interiores:

\begin{align*}
\left\langle x^2, \frac{1}{\sqrt{3}}\right\rangle &= \frac{2}{\sqrt{3}},\\
\left \langle x^2, \frac{x}{\sqrt{2}}\right\rangle &=0,\\
\left\langle x^2, \frac{3x^2-2}{\sqrt{6}} \right\rangle &=\frac{2}{\sqrt{6}}.
\end{align*}

De este modo, $$x^2= \frac{2}{\sqrt{3}} \cdot \frac{1}{\sqrt{3}} + \frac{2}{\sqrt{6}}\cdot \frac{3x^2-2}{\sqrt{6}}.$$

$\triangle$

Norma usando la descomposición de Fourier

Cuando tenemos bases ortogonales u ortonormales, también podemos calcular la norma de un vector fácilmente.

Teorema. Si $V$ es un espacio Euclideano de dimensión $n$ con producto interior $\langle\cdot, \cdot\rangle$ y $B=\{e_1,\ldots,e_n\}$ es una base ortogonal con este producto interior, entonces para cualquier vector $$v=\alpha_1e_1+\ldots+\alpha_ne_n,$$ tenemos que $$\norm{v}^2 = \sum_{i=1}^n \alpha_i^2 \norm{e_i}^2.$$

En particular, si $B$ es una base ortonormal, entonces $$\norm{v}^2 = \sum_{i=1}^n \langle v, e_i \rangle^2.$$

Demostración. Usando la definición de norma y la bilinealidad del producto interior, tenemos que
\begin{align*}
\norm{v}^2 &= \langle v,v \rangle\\
&=\sum_{i=1}^n \sum_{j=1}^n \alpha_i \alpha_j \langle e_i, e_j\rangle.
\end{align*}

Como $B$ es base ortogonal, los únicos sumandos que quedan a la derecha son aquellos en los que $i=j$, es decir,
\begin{align*}
\norm{v}^2&=\sum_{i=1}^n \alpha_i^2 \langle e_i, e_i\rangle\\
&=\sum_{i=1}^n \alpha_i^2 \norm{e_i}^2\\
\end{align*}

como queríamos mostrar.

Si $B$ es base ortonormal, cada $\norm{e_i}^2$ es $1$, y por el teorema anterior, $\alpha_i=\langle v, e_i\rangle$. Esto prueba la última afirmación.

$\square$

Ejemplo. Continuando con el ejemplo anterior, como ya escribimos a $x^2$ en términos de la base ortogonal, podemos encontrar fácilmente su norma. Tendríamos que
\begin{align*}
\norm{x^2}^2&=\left(\frac{2}{\sqrt{3}}\right)^2+\left(\frac{2}{\sqrt{6}}\right)^2\\
&=\frac{4}{3}+\frac{4}{6}\\
&=2.
\end{align*}

De esta forma, $\norm{x^2}=\sqrt{2}$. En efecto, esto es lo que obtendríamos si hubiéramos calculado la norma de $x^2$ con la definición.

$\triangle$

Aplicación de descomposición de Fourier a polinomios

Vamos a continuar con un ejemplo que vimos en la entrada anterior. Recordemos que estábamos trabajando en $V=\mathbb{R}_n[x]$, que habíamos elegido $n+1$ reales distintos $x_0,\ldots,x_n$, y que a partir de ellos definimos $$\langle P, Q\rangle = \sum_{i=0}^n P(x_i)Q(x_i).$$ Mostramos que $\langle \cdot , \cdot \rangle$ es un producto interior y que para $j=0,\ldots,n$ los polinomios $$L_i=\prod_{0\leq j \leq n, j\neq i} \frac{x-x_j}{x_i-x_j}$$ forman una base ortonormal de $V$.

Por el teorema de descomposición de Fourier, tenemos que cualquier polinomio $P$ de grado a lo más $n+1$ con coeficientes reales satisface que $$P=\sum_{i=0}^n \langle P, L_i \rangle L_i,$$ lo cual en otras palabras podemos escribir como sigue.

Teorema (de interpolación de Lagrange). Para $P$ un polinomio con coeficientes en los reales de grado a lo más $n$ y $x_0,x_1,\ldots,x_n$ reales distintos, tenemos que $$P(x)=\sum_{i=0}^n P(x_i) \left(\prod_{0\leq j \leq n, j\neq i} \frac{x-x_j}{x_i-x_j}\right).$$

El teorema de interpolación de Lagrange nos permite decir cuánto vale un polinomio de grado $n$ en cualquier real $x$ conociendo sus valores en $n+1$ reales distintos. Ya habíamos mostrado este teorema antes con teoría de dualidad. Esta es una demostración alternativa con teoría de bases ortogonales y descomposición de Fourier.

Aplicación de ideas de Fourier en funciones periódicas

También ya habíamos visto que $$\langle f,g \rangle = \int_{-\pi}^\pi f(x)g(x)\, dx$$ define un producto interior en el espacio vectorial $V$ de funciones $f:\mathbb{R}\to \mathbb{R}$ continuas y periódicas de periodo $2\pi$.

En ese ejemplo, definimos \begin{align*}
C_n(x)&=\frac{\cos(nx)}{\sqrt{\pi}}\\
S_n(x)&=\frac{\sin(nx)}{\sqrt{\pi}}.
\end{align*} y $C_0(x)=\frac{1}{\sqrt{2\pi}}$, y mostramos que $$\mathcal{F}:=\{C_n:n\geq 0\}\cup \{S_n:n\geq 1\}$$ era un conjunto ortonormal.

No se puede mostrar que $\mathcal{F}$ sea una base ortonormal, pues el espacio $V$ es de dimensión infinita, y es bastante más complicado que los espacios de dimensión finita. Sin embargo, la teoría de Fourier se dedica a ver que, por ejemplo, la familia $\mathcal{F}$ es buena aproximando a elementos de $V$, es decir a funciones continuas y periódicas de periodo $2\pi$. No profundizaremos mucho en esto, pero daremos algunos resultados como invitación al área.

Para empezar, restringimos a la familia $\mathcal{F}$ a una familia más pequeña:

$$\mathcal{F}_n:=\{C_m:0\leq m \leq n\}\cup \{S_m:1\leq m \leq n\}$$

Motivados en la descomposición de Fourier para espacios Euclideanos, definimos a la $n$-ésima serie parcial de Fourier de una función $f$ en $V$ a la expresión $$S_n(f)=\sum_{g\in \mathcal{F}_n} \langle f, g \rangle g.$$ Haciendo las cuentas, se puede mostrar que $$S_n(f)=\frac{a_0(f)}{2}+\sum_{k=1}^n \left(a_k(f)\cos(kx)+b_k(f)\sin(kx)\right),$$ en donde para $k\geq 1$ tenemos $$a_k=\frac{1}{\pi}\int_{-\pi}^\pi f(x)\cos(kx)\, dx$$ y $$b_k=\frac{1}{\pi}\int_{-\pi}^\pi f(x)\sin(kx)\, dx.$$

A los números $a_k$ y $b_k$ se les conoce como los $k$-ésimos coeficientes de Fourier. Aunque $\mathcal{F}$ no sea una base para $V$, sí es buena «aproximando» a elementos de $V$. Por ejemplo, un resultado lindo de Dirichlet dice que si $f$ y su derivada son continuas, entonces $$\lim_{n\to \infty} S_n(f)(x) = f(x).$$ Este tipo de teoremas de aproximación se estudian con más a detalle en un curso de análisis matemático avanzado o de análisis de Fourier.

Considera ahora $W_n$ el subespacio de $V$ generado por $\mathcal{F}_n$. Tomemos una función $f$ cualquiera en $V$. La $n$-ésima serie de Fourier de $f$ es un elemento de $W_n$. De hecho, es precisamente la proyección de $f$ en $W_n$. Por esta razón, $$\norm{f_n}^2\leq \norm{f}^2<\infty$$

Podemos calcular la norma de $f_n$, usando el resultado para espacios Euclideanos en el espacio (de dimensión finita) $W_n$. Haciendo esto, podemos reescribir la desigualdad anterior como sigue:

$$\frac{a_0(f)^2}{2}+\sum_{k=1}^n(a_k(f)^2+b_k(f)^2)\leq \frac{1}{\pi} \norm{f}^2.$$

El lado derecho es constante, y en el lado izquierdo tenemos una suma parcial de la serie $$\sum_{k\geq 1}(a_k(f)^2+b_k(f)^2).$$ Los términos son positivos y la sucesión de sumas parciales es acotada, así que la serie converge. Entonces, necesariamente la sucesión de términos debe converger a cero. Acabamos de esbozar la demostración del siguiente teorema.

Teorema (de Riemann-Lebesgue). Sea $f$ una función continua y de periodo $2\pi$. Si $a_n(f)$ y $b_n(f)$ son los coeficientes de Fourier de $f$, entonces $$\lim_{n\to \infty} a_n(f) = \lim_{n\to \infty} b_n(f) = 0.$$

De hecho, se puede mostrar que la desigualdad que mostramos se convierte en igualdad cuando $n\to \infty$. Este es un resultado bello, profundo y cuya demostración queda fuera del alcance de estas notas.

Teorema (de Plancherel). Sea $f$ una función continua y de periodo $2\pi$. Si $a_n(f)$ y $b_n(f)$ son los coeficientes de Fourier de $f$, entonces $$\frac{a_0(f)^2}{2}+\sum_{k=1}^\infty(a_k(f)^2+b_k(f)^2)= \frac{1}{\pi} \int_{-\pi}^\pi f(x)^2\, dx.$$

Aunque no daremos la demostración de este resultado, en una entrada posterior veremos cómo podemos aplicarlo.

Más adelante…

En esta entrada seguimos estudiando las bases ortogonales. Usamos este concepto para hacer una descomposición de Fourier, para conocer propiedades de V y obtener otra manera de calcular la norma de un vector. Así mismo, vimos aplicaciones de la descomposición a polinomios, viendo el teorema de la interpolación de Lagrange ya previamente demostrado mediante teoría de dualidad.

Hasta ahora solo hemos hablado de cómo ver si una base es ortonomal y algunas propiedades de estas bases y conjuntos, en la siguiente entrada hablaremos de un método pata encontrar estas bases ortonormales usando el proceso de Gram-Schmidt.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  • Verifica que los tres polinomios del ejemplo de descomposición de Fourier en efecto forman una base ortogonal.
  • Calcula la norma de $x^2$ con el producto interior del ejemplo de descomposición de Fourier usando la definición, y verifica que en efecto es $\sqrt{2}$.
  • Con la misma base ortonormal $B$ de ese ejemplo, calcula las coordenadas y la norma del polinomio $1+x+x^2$.
  • Verifica que todo lo que mencionamos se cumple con el producto punto en $\mathbb{R}^n$ y con la base canónica.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104721 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM»