Archivo de la etiqueta: relación de equivalencia

Álgebra Moderna I: Relación de equivalencia dada por un subgrupo e índice de $H$ en $G$

Por Cecilia del Carmen Villatoro Ramos

Deja un comentario

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

Como pudiste darte cuenta por el título, en esta entrada definiremos una relación de equivalencia en un grupo. Permítenos dar una motivación usando un grupo que tal vez ya hayas estudiado en cursos anteriores como el de Álgebra Superior II.

Dicho grupo tan importante, es el de los enteros con la suma $(\z, +)$. Para $a,b\in \z$ es posible establecer una relación $\thicksim$ dentro de los enteros como sigue
\begin{align*}
a \thicksim b \Leftrightarrow b-a \text{ es múltiplo de } n.
\end{align*}
Esta relación de equivalencia induce una partición de $\z$, con exáctamente $n$ conjuntos. Donde cada conjunto es una de las clases módulo $n$. En esta entrada queremos introducir una relación parecida, pero generalizada a cualquier grupo.

Comencemos modificando este ejemplo un poco. Primero, llamemos $H$ al conjunto de todos los enteros múltiplos de $n$. Así nuestra relación quedaría, para $a,b\in \z$,
\begin{align*}
a \thicksim b \Leftrightarrow b-a \in H.
\end{align*}

Luego, notemos que a pesar de que la operación que usamos para definir el grupo es la suma usual, nuestra relación está definida usando la resta. En realidad, lo que está pasando es que estamos sumando $b$ con el inverso aditivo de $a$, es decir $-a$. Entonces $b -a = b + (-a)$. Además, $(\z,+)$ es un grupo abeliano, por lo que $b + (-a) \in H \Leftrightarrow (-a) + b \in H$. Para nuestra generalización usaremos el segundo caso.

Así, tenemos que comenzar agarrando un subgrupo cualquiera de $G$, es decir, nos tomamos $H\leq G.$ Entonces nuestra relación debe quedar, dados $a,b\in G$,
\begin{align*}
a \thicksim b \Leftrightarrow a^{-1}b\in H.
\end{align*}

Ya al tener esa relación y demostrar que es una relación de equivalencia, usaremos las propiedades de grupo para descubrir que las clases de equivalencia son las clases laterales vistas en la entrada anterior.

Relación Generalizada

Lo anterior queda formalizado en la siguiente definición.

Definición. Sea $G$ un grupo y $H$ un subgrupo de $G$. Definimos una relación en $G$ del siguiente modo: dados $a,b \in G$,

\begin{align*}
a \thicksim b \Leftrightarrow a^{-1}b \in H.
\end{align*}

Ahora, demostraremos que esa relación, así como la de la introducción, es una relación de equivalencia.

Observación. La definición anterior es una relación de equivalencia.

Demostración.
Sean $G$ un grupo y $H\leq G$.

Primero, tomamos $a \in G$.
También podemos tomar $a^{-1}$ . Así $a^{-1}a = e \in H$. Por lo tanto $a \thicksim a$ y nuestra relación es reflexiva.

Ahora tomamos $a,b \in G$. Si $a \thicksim b$, entonces $a^{-1} b\in H$.

\begin{align*}
\Rightarrow b^{-1}a = (a^{-1}b)^{-1} \in H \Rightarrow b \thicksim a
\end{align*}

Por lo que nuestra relación es simétrica.

Sean $a,b,c \in G$. Si $a \thicksim b$ y $b \thicksim c$, entonces $a^{-1}b \in H$ y $b^{-1}c \in H$, entonces usando la cerradura de $H$ y asociando de otra manera, obtenemos

\begin{align*}
a^{-1}c = (a^{-1}b)(b^{-1}c) \in H \Rightarrow a \thicksim c.
\end{align*}

Así, nuestra relación es transitiva.

Por lo tanto, nuestra relación es una relación de equivalencia.

$\square$

Nótese que para probar las tres propiedades de una relación de equivalencia (reflexividad, simetría y transitividad) usamos las tres condiciones de un subgrupo (la existencia del neutro, la cerradura de los inversos y la cerradura del producto).

A continuación, veamos cómo son las clases de equivalencia:
Sea $a \in H$.

\begin{align*}
\bar{a} &= \{b \in G | a \thicksim b\} = \{b \in G | a^{-1}b \in H\} \\
&= \{b \in G | a^{-1}b = h, h \in H\} = \{b \in G | b = ah, h \in H\} \\
&= \{ah | h \in H\} = a H.
\end{align*}

Ahora veremos algunas observaciones de lo anterior.

Observación. Sean $G$ un grupo, $H\leq G$ y $a,b\in G$, entonces
\begin{align*}
a H = bH & \Leftrightarrow a^{-1}b \in H.
\end{align*}

En particular,
\begin{align*}
H = bH & \Leftrightarrow b \in H
\end{align*}

Nota. Análogamente se puede trabajar con clases laterales derechas, i.e. ($Ha = Hb \Leftrightarrow ba^{-1}\in H$).

Como $\thicksim$ es una relación de equivalencia, esta induce una partición y, como sus clases de equivalencia son las clases laterales, tenemos el siguiente teorema.

Teorema. Sea $G$ un grupo, $H$ subgrupo de $G$.

  1. $aH \neq \emptyset \quad \forall a \in G$ .
  2. Si $a,b \in G$ son tales que $aH \cap bH \neq \emptyset$, entonces $aH = bH$.
  3. $\displaystyle \bigcup_{a\in G} aH = G$

Claramente el teorema anterior enuncia las características de una partición, por lo que no hay nada que probar.

Ejemplos

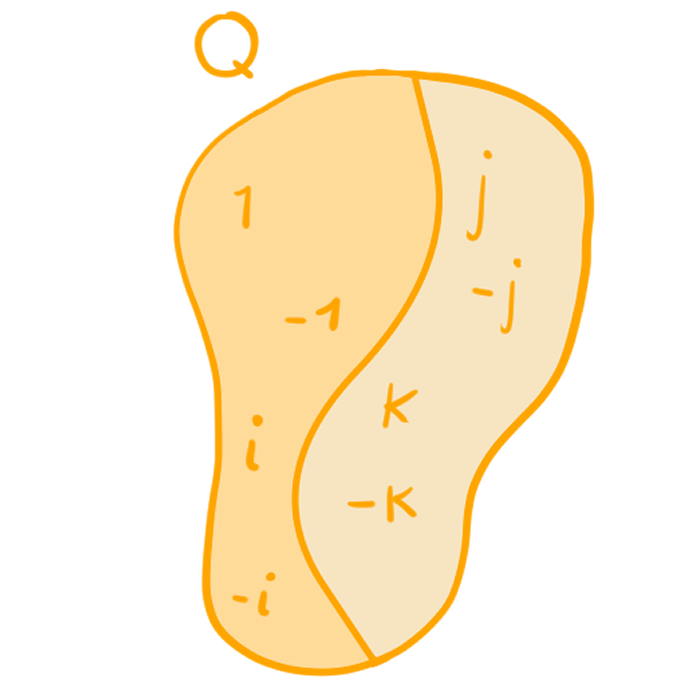
Ejemplo 1. Consideremos al grupo de los cuaternios $Q$ , tomemos el subgrupo $H = \left< i \right> = \{\pm 1 , \pm i\}$. Veamos qué sucede con sus clases laterales.
\begin{align*}
jH &= \{j(+1), j(-1), j(+i), j(-i)\}\\
&= \{j, -j, -k k\} \\
&= Hj.
\end{align*}

La última igualdad la puedes comprobar tú, multiplicando los mismos elementos por $j$, pero ahora del lado izquierdo.

Así, las clases laterales son:

  • Clases laterales izquierdas: $H, jH$.
  • Clases laterales derechas: $H, Hj$.

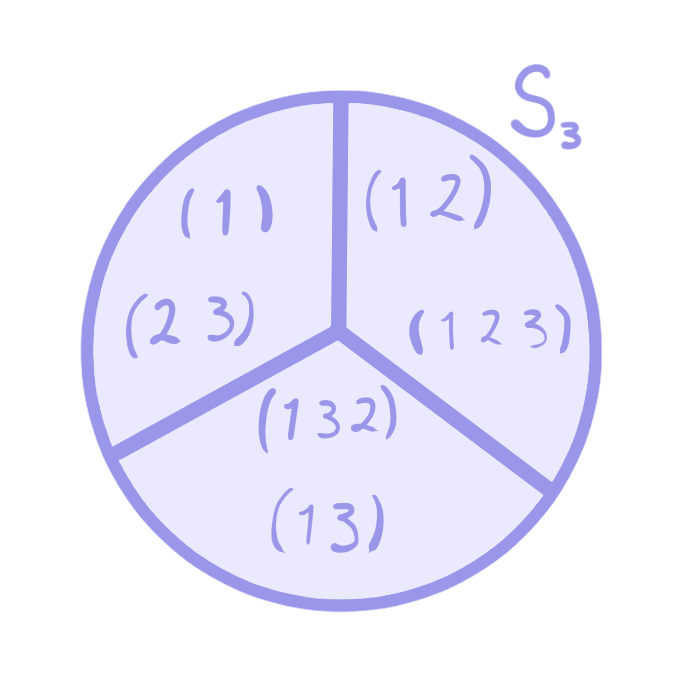
Ejemplo 2. Tomemos $S_3$ y $H = \{(1), (32)\}$.
Primero, veamos cómo se ven las clases laterales izquierdas.

Primero, tenemos la clase del neutro, es decir $(1) H = H$. Luego, tenemos que tomarnos un elemento de $S_3$ que no esté en $H$, digamos $(1\;2\;3)$, entonces,
\begin{align*}
(1\;2\;3)H &= \{(1\;2\;3)(1), (1\;2\;3)(3\;2)\}\\
&= \{(1\;2\;3), (1\;2)\}.
\end{align*}

Repetimos lo anterior, tomamos un elemento de $S_3$ que no esté $H$ y sea distinto al que ya nos tomamos para obtener una clase distinta. Esto nos da
\begin{align*}
(1\;3\;2)H &= \{(1\;3\;2)(1), (1\;3\;2)(3\;2)\} \\
& = \{(1\;3\;2)(1\;3)\}.\\
\end{align*}

Por lo que las clases laterales izquierdas son:
\begin{align*}
&(1)H = H\\
&(1\;2\;3)H = \{(1\;2\;3), (1\;2)\}\\
&(1\;3\;2)H = \{(1\;3\;2)(1\;3)\}.\\
\end{align*}

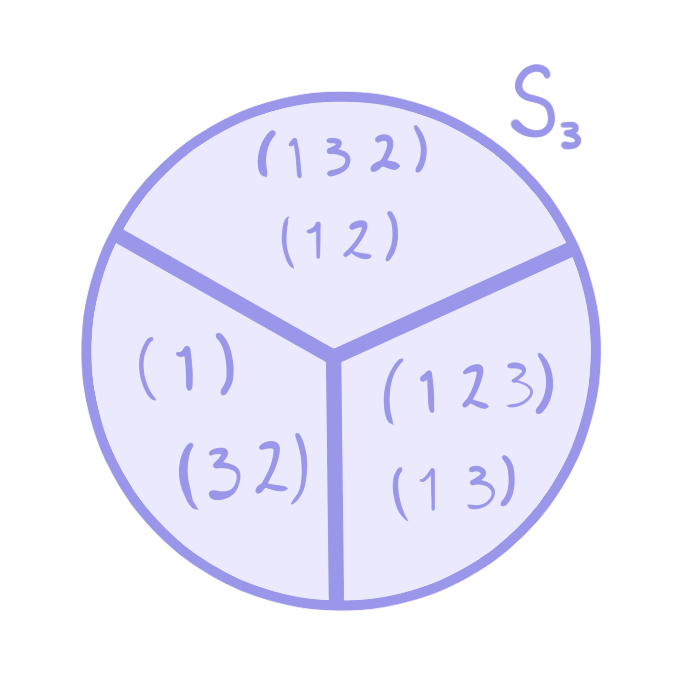
De la misma manera obtenemos las clases laterales derechas:
\begin{align*}
&H(1) = H \\
&H(1\;2\;3) = \{(1)(1\;2\;3), (3\;2)(1\;2\;3)\} = \{(1\;2\;3), (1\;3)\} \\
&H(1\;3\;2) = \{(1)(1\;3\;2), (3\;2)(1\;3\;2)\} = \{(1\;3\;2), (1\;2)\}.\\
\end{align*}

Este ejemplo nos permite ver que las clases laterales izquierdas y las clases laterales derechas no siempre coinciden.

Partición del ejemplo 1.
Partición de las clases laterales izquierdas del ejemplo 2.
Partición de las clases laterales derechas del ejemplo 2.

Número de elementos en las clases laterales

El último ejemplo nos dice que las clases laterales derechas e izquierdas no siempre coinciden, sin embargo probaremos que siempre hay la misma cantidad de ambas.

Teorema. Sea $G$ un grupo, $H$ un subgrupo de $G$. Entonces

\begin{align*}
\#\{a H | a \in G\} = \#\{Ha | a \in G\}.
\end{align*}

Demostración.

Sea $\psi: \{a H | a \in G\} \to \{Ha | a \in G\}$, definida como $\psi(aH) = Ha^{-1} \quad \forall a \in G$. Probaremos que esta función es biyectiva.

Pequeño paréntensis:

Antes de comenzar con la demostración, pongamos atención a la definición de $\psi$. En un inicio podríamos pensar ¿por qué no hacemos $\psi(aH) = Ha$? La respuesta es simple, porque esto no funcionaría. Definamos una nueva función para ejemplificar, sea $\phi: \{a H | a \in G\} \to \{Ha | a \in G\} $ tal que $\phi(aH ) = Ha$.

Tomemos $b\in G$ tal que $aH = bH$, para que $\phi$ esté bien definida, necesitaríamos que $\phi(aH) = \phi(bH)$, es decir $Ha = Hb$. Por la relación que definimos, esto implica que si $a^{-1}b \in H$, entonces $ba^{-1} \in H$, pero esto no necesariamente es cierto porque el grupo puede no ser abeliano. Lo que sí sabemos es que si $a^{-1}b\in H$, entonces $Ha^{-1}b = H$, y así $Ha^{-1} = Hb^{-1}$.

Por esto es que escogimos a $\psi$ de esa manera.

Termina paréntesis. Ahora sí comencemos con la demostración.

Sean $a,b \in G$,

\begin{align*}
aH = bH & \Leftrightarrow a^{-1}b \in H \\
&\Leftrightarrow Ha^{-1}b = H \\
& \Leftrightarrow Ha^{-1} = Hb ^{-1} \\
& \Leftrightarrow \psi (aH) = \psi (bH).
\end{align*}
Por tanto, $\psi$ está bien definida y es inyectiva.

Además, dada $Ha, a \in G$.

\begin{align*}
Ha = H(a^{–1})^{-1} = \psi(a^{-1} H)
\end{align*}

así $\psi$ es suprayectiva.

Por lo tanto $\# \{aH | a \in G\} = \# \{Ha|a\in G\}.$

$\square$

Ahora, ya sabemos que la cantidad de clases laterales izquierdas es la misma que la de clases laterales derechas. Entonces podemos nombrar esto como el índice.

Definición. Sea $G$ un grupo, $H$ un subgrupo de $G$. El índice de $H$ en $G$ es

\begin{align*}
[G:H ] = \# \{aH | a\in G\}.
\end{align*}

Ejemplos

Retomemos los ejemplos que ya hemos visto.

  1. Tomemos a $Q$ como los cuaternios, $H= \left< i \right> = \{\pm 1, \pm i\}$
    $[Q:H]= 2$.
  2. Ahora, tomemos $S_3$, $H = \{(1), (3 2)\}$. Como ya vimos,
    $[S_3:H]= 3$.
  3. Consideremos el grupo $(\z, +)$ y $H = \{6m | m \in \z\}$.
    Hay 6 clases laterales: $H, 1+H, 2+H, 3+H, 4+H, 5+H$. Que serían los múltiplos de $6$, $6+1$, $6+2$, $\dots$ respectivamente.
    Así, $[\z, H ]= 6$.

Tarea moral

  1. Analizando los ejemplos que tienes hasta ahora observa si existe alguna relación entre el orden de un grupo $G$, el orden del subgrupo $H$ y la cantidad de clases laterales de $H$ en $G$.
  2. Considera $\{\pm 1\} \leq \left< i \right> \leq Q$. Describe las clases laterales izquierdas de $\{\pm 1\}$ en $\left< i \right>$, las clases laterales izquierdas de $\left< i \right>$ en $Q$, y las clases laterales izquierdas de $\{\pm 1\}$ en $Q$. Encuentra $[Q: \{\pm 1\}]$, $[Q:\left< i \right>]$ y $[\left< i \right>: \{\pm 1\}]$.
  3. Considera $\left< (1\;2\;3) \right> \leq A_4 \leq S_4$. Describe las clases laterales izquierdas de $\left< (1\;2\;3) \right>$ en $A_4$, las clases laterales izquierdas de $A_4$ en $S_4$, y las clases laterales izquierdas de $\left< (1\;2\;3) \right>$ en $S_4$. Encuentra $[S_4:\left< (1\;2\;3) \right>]$, $[S_4: A_4]$ y $[A_4: \left< (1\;2\;3) \right>]$.
  4. Puedes checar el video de Mathologer.

Más adelante…

Ahora conoces el índice de $H$ en $G$. Recúerdalo para la siguiente entrada, porque intentaremos describir el orden de $G$ en términos del orden de $H$ y del índice. Sin hacer trampa, ¿cómo crees que se puede relacionar el orden de $G$ y el índice?

Entradas relacionadas

Nota 15. Relaciones de equivalencia y particiones.

Por Julio César Soria Ramírez

Deja un comentario

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

En esta nota veremos cómo las relaciones de equivalencia dan lugar a particiones y finalmente concluiremos que toda relación de equivalencia tiene asociada una partición y viceversa, mostrando que dicha correspondencia es una biyección. Con esta nota concluiremos la primera unidad del presente trabajo.

Teorema

Sea $A$ un conjunto, $\mathcal R$ una relación de equivalencia en $A$, entonces $\set{\overline{x}\mid x\in A}$ es una partición de $A$.

Demostración

Sea $A$ un conjunto, $\mathcal R$ una relación de equivalencia en $A$

Por demostrar que:

$\set{\overline{x}\mid x\in A}$ es una partición de $A$.

Vamos a mostrar que el conjunto $\set{\overline{x}\mid x\in A}$ cumple la definición de partición.

i) Por demostrar que $\overline{x}\neq \emptyset$, $\forall x\in A$.

Sea $x\in A$, como $\mathcal R$ es reflexiva $x\sim x$, así $x\in \overline{x}$ y entonces $\overline{x}\neq \emptyset$.

ii) Por demostrar que si $x,y\in A$ son tales que $\overline{x}\neq \overline{y} $, entonces $\overline{x}\cap \overline{y}=\emptyset$.

En la nota anterior mostramos que: $x\sim y\Longrightarrow \overline{x}=\overline{y}$, que es equivalente a: $\overline{x}\neq \overline{y} \Longrightarrow x\nsim y $ (llamada la contrapositiva de la implicación). También mostramos que $x\nsim y \Longrightarrow \overline{x}\cap \overline{y}=\emptyset$. Así, tenemos que:

$ \overline{x}\neq \overline{y} \Longrightarrow x\nsim y $

y

$x\nsim y \Longrightarrow \overline{x}\cap \overline{y}=\emptyset$

Por lo tanto se sigue que:

$\overline{x}\neq \overline{y} \Longrightarrow \overline{x}\cap \overline{y}=\emptyset $.

Así, tenemos lo que queríamos mostrar.

iii) Por demostrar que $\bigcup\limits_{x\in A} \overline{x}=A$

Prueba por doble contención.

$\subseteq$ primera contención.

Sea $z\in \bigcup\limits_{x\in A} \overline{x}$, entonces $z\in \overline{x}=\set{y\in A\mid y\sim x}$ para alguna $x\in A$, en particular $z\in A$. Por lo tanto $ \bigcup\limits_{x\in A} \overline{x}\subseteq A$.

$\supseteq$ segunda contención.

Sea $z\in A$, como $\mathcal R$ es reflexiva $z\sim z$ así $z\in \overline{z}$, concluimos que $z\in \bigcup\limits_{x\in A} \overline{x}$. Por lo tanto $A \subseteq \bigcup\limits_{x\in A} \overline{x}$.

Como se cumplen las tres condiciones para que sea una partición entonces $\set{\overline{x}\mid x\in A}$ es una partición de $A$.

Ejemplos

1. $A=\set{1,2,3,4,5}$

$\mathcal R=\set{(1,1), (2,2), (3,3), (4,4), (5,5), (1,2), (2,1), (1,5), (5,1) (2,5), (5,2) , (3,4),(4,3)}$

$\overline{1}=\set{1,2,5}$

$\overline{3}=\set{3,4}$

$\set{ \overline{1}, \overline{3}}=\set{ \set{1,2,5}, \set{3,4}} $ es la partición inducida por $\mathcal R$.

2. $A=\set{1,2,3,4,5}$

$\mathcal R$ una relación de equivalencia en $A$. Si la partición en $A$ inducida por $\mathcal R$ es:

$ \set{ \set{3}, \set{2,4}, \set{1,5} } $

¿Quién es $\mathcal R$?

Observemos que

$\mathcal R=\set{ (3,3), (2,2), (2,4), (4,4), (4,2), (1,1), (1,5), (5,5), (5,1) }$

es una relación de equivalencia que induce la partición $\set{ \overline{3}, \overline{2}, \overline{1} }=\set{ \set{3}, \set{2,4}, \set{1,5} } $.

Teorema

Sea $A$ un conjunto, consideremos:

$\mathcal R_A=\set{r\mid r \, \,es \, \, una \, \, relación \, \, de \, \, equivalencia }$

$\mathcal P_A=\set{p\mid p \, \,es \, \, una \, \, partición \, \, de \, \, A }$

Existe una biyección entre $\mathcal R_A$ y $\mathcal P_A$.

Demostración

Sea $A$ un conjunto, consideremos:

$\mathcal R_A=\set{r\mid r \, \,es \, \, una \, \, relación \, \, de \, \, equivalencia }$

$\mathcal P_A=\set{p\mid p \, \,es \, \, una \, \, partición \, \, de \, \, A }$

Definimos:

$\psi: \mathcal R_A\to \mathcal P_A$ con

$\psi(r)=\set{\overline{x}^r\mid x\in A}\, \, \, \forall r\in \mathcal R_A$

donde $ \overline{x}^r =\set{y\in A\mid (y,x)\in r} $, es decir $\psi(r)$ es la colección de clases de equivalencia dadas por la relación $r$.

Veamos que $\psi$ es inyectiva.

Sean $r,\rho\in \mathcal R_A$ tales que $\psi(r)=\psi(\rho)$.

Por demostrar que $r=\rho$.

La prueba se hará por doble contención

$\subseteq$ primera contención.

Sea $(a,b)\in r$ entonces por simetría $(b,a)\in r$ y entonces $b\in \overline{a}^r$.

Por otro lado $ \overline{a}^r\in \set{ \overline{x}^r\mid x\in A }=\psi(r)$ que por hipótesis es igual $\psi(\rho)= \set{ \overline{x}^{\rho}\mid x\in A }$ , de manera que $ \overline{a}^r = \overline{c}^{\rho}$ para alguna $c\in A$. Como $b\in \overline{a}^r$, entonces $b\in \overline{c}^{\rho}$, así $(b,c)\in \rho$, y por simetría $(c,b)\in \rho$. También $a\in \overline{a}^r= \overline{c}^{\rho}$, así $(a,c)\in \rho$. Como $(a,c)\in \rho$ y $(c,b)\in \rho$, por transitividad $(a,b)\in \rho$. Por lo tanto $r\subseteq \rho$.

$\supseteq$ segunda contención. Es análoga y se deja como ejercicio al lector.

Concluimos finalmente que $r=\rho$ y así la función $\psi: \mathcal R_A\to \mathcal P_A$ es inyectiva.

Veamos ahora que $\psi$ es suprayectiva.

Sea $p=\set{A_i\mid i\in I}$ una partición de $A$.

Definimos $r$ una relación en $A$ como:

$(x,y)\in r$ si y sólo si existe $i\in I$ tal que $(x,y)\in A_i$.

Ésta es una relación de equivalencia (demuéstralo).

Por demostrar que $\psi(r)=p$, es decir que $\set{\overline{x}^r\mid x\in A}=p$

La prueba es por doble contención.

$\subseteq$ primera contención.

Sea $\overline{a}^r\in \set{ \overline{x}^r\mid x\in A }$.

Por demostrar que $\overline{a}^r\in p$.

Como $A= \bigcup\limits_{i\in I}A_i$ entonces $a\in A_j$ para alguna $j\in I$. De hecho como $p$ es una partición, $A_j$ es el único elemento de $p$ al que pertenece $a$.

Pero

$\overline{a}^r=\set{b\in A\mid (b,a)\in r}=\set{b\in A\mid \exists i\in I \,\, tal \,\, que \,\, b,a\in A_i}=\set{b\in A\mid b\in A_j}=A_j\in p,$ y por lo tanto $\overline{a}^r\in p,$ y así $\psi(r)\subseteq p$.

$\supseteq$ segunda contención.

Sea $A_j\in p$ con $j\in I$. Sabemos que $A_j\neq \emptyset$,entonces podemos considerar $a\in A_j$, y como acabamos de ver en la primera contención, $A_j=\overline{a}^r\in \set{\overline{x}^r\mid x\in A}=\psi(r)$. Así, $p\subseteq \psi(r)$.

Con estas dos contenciones hemos probado que $p=\psi(r)$. De esta forma, dada una partición $p$ existe una relación de equivalencia que bajo $\psi$ da por resultado $p$. Por lo tanto $\psi$ es suprayectiva.

Como $\psi$ es suprayectiva e inyectiva, entonces $\psi$ es biyectiva.

$\square$

Tarea Moral

  1. Encuentra todas las posibles particiones de $\set{3,6,7,9}$, y para cada una de ellas encuentra la relación de equivalencia asociada.
  2. Considera la relación $\mathcal R$ en $\mathbb Z$, dada por: $(a,b)\in \mathcal R$ si y sólo si $4$ divide a $b-a$. Verifica que las distintas clases de equivalencia forman una partición de $\mathbb Z$.
  3. Sea $A=\set{1,2,3,4,5}$ y considera la relación dada por:
    $R=\set{(1,1),(2,3),(3,3),(4,4),(5,5),(2,4),(4,2),(2,5),(5,2),(4,5),(5,4)}$
    Encuentra la partición asociada.

Más adelante

Con esta nota hemos terminado la unidad 1 del curso de Álgebra superior I. En las siguiente nota iniciaremos la unidad 2 donde haremos un estudio de los números naturales a partir de la definición conjuntista.

Enlaces relacionados

Página principal del curso.

Nota anterior. Nota 14 Familias de conjuntos y particiones.

Nota siguiente. Nota 16. Los números naturales.

Teoría de los Conjuntos I: Conjunto cociente

Por Gabriela Hernández Aguilar

2 respuestas

Introducción

En esta entrada partimos de una relación de equivalencia y con ella definimos al conjunto cociente. Dicho conjunto tendrá como elementos a las clases de equivalencia de una relación. Además probaremos que toda relación de equivalencia induce una partición y viceversa.

Conjunto cociente

A continuación definimos un nuevo conjunto. Como parte de los ejercicios de la tarea moral, se incluye verificar que en efecto esta definición da un conjunto a partir de los axiomas.

Definición. Sea $R$ una relación de equivalencia en $A$. Definimos al conjunto cociente por la relación $R$ como el conjunto:

$A/R=\set{[a]_R: a\in A}$.

Veamos algunos ejemplos.

Ejemplo.

Sea $A=\set{1,2,3,4}$ y $R$ la relación identidad en $A$. Sabemos que $R$ es de equivalencia en $A$. Luego, siguiendo la definición de conjunto cociente tenemos que $A\diagup R=\set{[1]_R, [2]_R, [3]_R, [4]_R}$, donde $[1]_R=\set{1}$, $[2]_R=\set{2}$, $[3]_R=\set{3}$, $[4]_R=\set{4}$.

$\square$

Ejemplo.

Sean $A=\set{1,2,3,4}$ y $R=\set{(1,1), (2,2), (3,3), (4,4), (1,4), (4,1)}$. Se tiene que $R$ es una relación de equivalencia en $A$. Luego, tenemos que

$A\diagup R=\set{[1]_R, [2]_R, [3]_R, [4]_R}$,

donde

  • $[1]_R=\set{1,4}$,
  • $[2]_R=\set{2}$,
  • $[3]_R=\set{3}$,
  • $[4]_R=\set{4,1}$, pero este conjunto es igual a $[1]_R$.

Por lo tanto, $A\diagup R=\set{[1]_R, [2]_R, [3]_R}$.

$\square$

Cada relación de equivalencia induce una partición

Teorema. Sea $R$ una relación de equivalencia en $A$. El conjunto cociente $A\diagup R$ es una partición de $A$.

Demostración.

Supongamos que $R$ es una relación de equivalencia en $A$. Veamos que $A\diagup R$ es una partición de $A$.

  1. Sea $a\in A$, vimos en la entrada de particiones que $[a]_R\not=\emptyset$.
  2. Sean $[a]_R,[b]_R\in A\diagup R$ tales que $[a]_R\not=[b]_R$ y veamos que $[a]_R\cap [b]_R=\emptyset$. En la entrada anterior probamos que $aRb$ si y sólo si $[a]_R=[b]_R$ lo cual ocurre si y sólo si $[a]_R\cap[b]_R=\emptyset$. De este modo, si $[a]_R\not=[b]_R$, $[a]_R\cap[b]_R=\emptyset$.
  3. Por último, $\bigcup_{a\in A} [a]_R= A$ pues para cada $a\in A$, $a\in [a]_R$.

$\square$

Este último teorema demuestra que toda relación de equivalencia induce una partición.

Las particiones inducen una relación de equivalencia

El teorema anterior nos permitió probar que cada relación de equivalencia induce una partición y de hecho, esta partición será el conjunto cociente, Podemos preguntarnos si el resultado se cumple «de regreso», en el sentido de si dada una partición podemos inducir una relación de equivalencia. Veamos el siguiente ejemplo.

Ejemplo.

Este ejemplo es todavía algo informal, pues no hemos introducido formalmente a los números naturales, a los pares y los impares. Haremos esto más adelante. Por el momento, puedes usar lo que ya sabes de los números naturales y de su paridad.

Sea $A=\set{0,1,2, 3, \cdots}$ y sean $A_1=\set{0,2,4,\cdots}$ y $A_2=\set{1,3, 5,\cdots}$. Resulta que $\mathcal{P}$ es una partición de $A$ pues tanto $A_1$ y $A_2$ son conjuntos no vacíos, además $A_1\cap A_2=\emptyset$ y $A_1\cup A_2=A$.

Queremos ver si existe la manera de relacionar a los elementos de $A$ tal que la relación que resulte sea de equivalencia. Consideremos la relación definida como sigue:

$R_\mathcal{P}=\set{(a,b)\in A\times A: a,b\in A_1\vee a,b\in A_2}$.

Notemos que la relación $R_\mathcal{P}$ es una relación en $A$ y además relaciona a los elementos si pertenecen a un mismo conjunto de la partición.

Veamos que $R_\mathcal{P}$ es una relación de equivalencia, para ello verifiquemos si es una relación reflexiva, simétrica y transitiva.

  1. Sea $a\in A$. Si $a$ es un número par (existe $k$ tal que $a= 2k$), entonces $a\in A_1$ y por lo tanto $(a,a)\in R_\mathcal{P}$.
    Si $a$ es un número impar (existe $k$ tal que $a= 2k+1$), entonces $a\in A_2$ y por lo tanto $(a,a)\in R_\mathcal{P}$.
    Por lo tanto, $R_\mathcal{P}$ es una relación reflexiva.
  2. Supongamos que $(a,b)\in R_\mathcal{P}$ y veamos que $(b,a)\in R_\mathcal{P}$.
    Como $(a,b)\in R_\mathcal{P}$ entonces $a,b\in A_1$ o $a,b\in A_2$, lo que es equivalente a decir que $b,a\in A_1$ o $b,a\in A_2$, es decir, $(b,a)\in R_\mathcal{P}$.
    Por lo tanto, $R_\mathcal{P}$ es una relación simétrica.
  3. Supongamos que $(a,b)\in R_\mathcal{P}$ y $(b,c)\in R_\mathcal{P}$.
    Como $(a,b)\in R_\mathcal{P}$ entonces $a,b\in A_1$ o $a,b\in A_2$. Luego, como $(b,c)\in R_\mathcal{P}$ entonces $b,c\in A_1$ o $b,c\in A_2$. Si $a,b\in A_1$, entonces $b,c\in A_1$, pues de lo contrario $b,c\in A_2$ y, por tanto, $b\in A_1$ al mismo tiempo que $b\in A_2$ y así, $b$ es par e impar, lo cuál no puede ocurrir. Por lo tanto, $b,c\in A_1$, de modo que $a,c\in A_1$ y así, $(a,c)\in R_\mathcal{P}$. Análogamente, si $a,b\in A_2$, entonces, $b,c\in A_2$ y, por tanto, $a,c\in A_2$ y $(a,c)\in R_{\mathcal{P}}$. Por lo tanto $R_\mathcal{P}$ es una relación transitiva.

Por lo tanto, $R_\mathcal{P}$ es una relación de equivalencia.

$\square$

Podemos demostrar que esto ocurre para cualquier conjunto y cualquier partición. Veamos el siguiente teorema.

Teorema. Toda partición induce una relación de equivalencia.

Demostración.

Sea $A$ un conjunto y $\mathcal{P}$ una partición de $A$. Defimos a $R_\mathcal{P}$ como el siguiente conjunto:

$R_\mathcal{P}=\set{(a,b)\in A\times A: \exists p\in \mathcal{P}\ \text{tal que}\ a,b\in p}$.

Notemos que $R_\mathcal{P}$ es una relación en $A$ pues es un subconjunto de $A\times A$. Veamos que $R$ es de equivalencia, es decir, $R$ es reflexiva, simétrica y transitiva.

  1. Sea $a\in A$. Dado que $\mathcal{P}$ es una partición de $A$, entonces $A=\bigcup\mathcal{P}$. Entonces existe $p\in \mathcal{P}$ tal que $a\in p$, de donde $(a,a)\in R_\mathcal{P}$. Por lo tanto, $R_\mathcal{P}$ es una relación reflexiva.
  2. Supongamos que $(a,b)\in R_\mathcal{P}$ y veamos que $(b,a)\in R_\mathcal{P}$.
    Como $(a,b)\in R_\mathcal{P}$, existe $p\in \mathcal{P}$ tal que $a, b\in p$. Lo que es equivalente a decir que existe $p\in \mathcal{P}$ tal que $b,a\in p$, es decir, $(b,a)\in R_\mathcal{P}$. Por lo tanto, $R_\mathcal{P}$ es una relación simétrica.
  3. Supongamos que $(a,b)\in R_\mathcal{P}$ y $(b,c)\in R_\mathcal{P}$.
    Como $(a,b)\in R_\mathcal{P}$, existe $p\in \mathcal{P}$ tal que $a, b\in p$. Luego, como $(b,c)\in R_\mathcal{P}$, existe $q\in \mathcal{P}$ tal que $b,c\in q$. Además $p=q$ pues de lo contrario, $p\not= q$ y $b\in p$ al mismo tiempo que $b\in q$ y así, $b\in p\cap q$ lo cual es una contradicción a la definición de partición. Por lo tanto, $p=q$ y así $a,c\in p$, por lo que $(a,c)\in R_\mathcal{P}$. Por lo tanto, $R_\mathcal{P}$ es una relación transitiva.

Por lo tanto, $R_\mathcal{P}$ es una relación de equivalencia en $A$.

$\square$

Con este último teorema hemos probado que en efecto, así como cada relación de equivalencia induce una partición, se cumple que cada partición induce una relación de equivalencia. Además, estas correspondencias son en cierto sentido «una la inversa de la otra» como explorarás en los ejercicios a continuación.

Tarea moral

La siguiente lista de ejercicios te ayudará a reforzar el contenido de esta entrada:

  1. Demuestra mediante los axiomas que si $A$ es un conjunto y $R$ es una relación de equivalencia en $A$, entonces $A\diagup R$ es un conjunto.
  2. Sea $A=\set{1,2,3,4,5,6}$ y $R=\set{(1,1), (2,2), (3,3), (4,4), (5,5), (6,6), (5,6), (6,5), (4,6), (6,4), (4,5), (5,4)}$ relación de equivalencia en $A$. Determina al conjunto cociente de $A$ con respecto a $R$.
  3. Demuestra mediante los axiomas que $R_{\mathcal{P}}$ del último teorema en efecto es un conjunto.
  4. Demuestra lo siguiente, en términos de la notación usada en esta entrada:
    • Si $A$ es conjunto y $R$ es relación de equivalencia en $A$, entonces $R_{A\diagup R}=R$.
    • Si $A$ es conjunto $\mathcal{P}$ es partición de $A$, entonces $A\diagup R_{\mathcal{P}}=\mathcal{P}$.
  5. Si $R_1$ y $R_2$ son relaciones de equivalencia en $A$, ya demostramos que $R_1\cap R_2$ también lo es. ¿Cómo es $A\diagup (R_1\cap R_2)$ con respecto a $A\diagup R_1$ y $A\diagup R_2$?

Más adelante…

En la siguiente entrada introduciremos el concepto de orden parcial y de orden total. Estos son otro tipo especial de relaciones. Volveremos a usar las propiedades de reflexividad y transitividad. Sin embargo, tendremos que introducir otras como la asimetría, la antisimetría y la irreflexibilidad.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Álgebra Lineal II: Matrices positivas y congruencia de matrices

Por Diego Ligani Rodríguez Trejo

3 respuestas

Introducción

Ya hablamos de las matrices asociadas a formas bilineales (y sesquilineales), y de formas cuadráticas (y cuadráticas hermitianas). Así mismo, tomamos un pequeño paréntesis para recordar qué es un producto interior y un espacio euclideano. Además, vimos las nociones análogas para el caso complejo.

Lo que haremos ahora es conectar ambas ideas. Extenderemos nuestras nociones de positivo y positivo definido al mundo de las matrices. Además, veremos que estas nociones son invariantes bajo una relación de equivalencia que surge muy naturalmente de los cambios de matriz para formas bilineales (y sesquilineales).

Congruencia de matrices

En las entradas de matrices de formas bilineales y matrices de formas sesquilineales vimos cómo obtener matrices asociadas a una misma forma bilineal (o sesquilineal) usando distintas bases. Dos matrices $A$ y $A’$ representaban a la misma forma bilineal en distintas bases si y sólo si existía una matriz de cambio de base $P$ tal que $$A’= \text{ }^tP A P,$$ en el caso real, o bien tal que $$A’=P^\ast A P,$$ en el caso complejo.

Definición. Sean $A$ y $B$ matrices simétricas en $M_n(\mathbb{R})$. Diremos que $A$ es congruente a $B$ si existe una matriz invertible $P$ en $M_n(\mathbb{R})$ tal que $$A=\text{ } ^tP B P.$$

Definición. Sean $A$ y $B$ matrices hermitianas en $M_n(\mathbb{C})$. Diremos que $A$ es congruente a $B$ si existe una matriz invertible $P$ en $M_n(\mathbb{C})$ tal que $$A=P^\ast B P.$$

Las definiciones anteriores están restringidas a las matrices simétricas (o hermitianas, respectivamente). Se podrían dar definiciones un poco más generales. Sin embargo, a partir de ahora nos enfocaremos únicamente a resultados que podamos enunciar para matrices simétricas (o hermitianas, respectivamente).

Proposición. La relación «ser congruentes» es una relación de equivalencia, tanto en el caso real, como en el caso complejo.

Demostración. Daremos la demostración en el caso real. El caso complejo queda como ejercicio. Empecemos con la reflexividad. Esto es claro ya que la matriz identidad $I_n$ es invertible y se tiene la igualdad

\begin{align*} A=\text{ } ^tI_nAI_n.\end{align*}

Para la simetría, supongamos que tenemos matrices $A$ y $B$ en $M_n(\mathbb{R})$ tales que $A$ es congruente a $B$ con la matriz invertible $P$ de $M_n(\mathbb{R})$, es decir, tales que

\begin{align*} A=\text{ } ^tPBP.\end{align*}

Como $P$ es invertible, su transpuesta también. De hecho, $(^tP)^{-1}=\text{ } ^t(P^{-1})$. Así, podemos multiplicar por la inversa de $^tP$ a la izquierda y la por la inversa de $P$ a la derecha para obtener

\begin{align*} ^t(P^{-1})AP^{-1}=B.\end{align*}

Esto muestra que $B$ es congruente a $A$.

Finalmente, veamos la transitividad. Supongamos que $A$ es congruente a $B$ mediante la matriz invertible $P$ y que $B$ es congruente a $C$ mediante la matriz invertible $Q$. Tendríamos entonces las igualdades

\begin{align*}
A&= \text{ }^t PBP,\\
B&= \text{ }^t QCQ,
\end{align*}

de donde $$A= \text{ }^tP \text{ }^tQCQP= \text{ }^t (QP) C (QP).$$ Esto muestra que $A$ es congruente a $C$ mediante la matriz $QP$, que como es producto de invertibles también es invertible.

$\square$

Clasificación de matrices simétricas por congruencia

¿Será posible para cualquier matriz simétrica encontrar una matriz congruente muy sencilla? La respuesta es que sí. El siguiente teorema puede pensarse como una versión matricial del teorema de Gauss.

Teorema. Cualquier matriz simétrica en $M_n(\mathbb{R})$ es congruente a una matriz diagonal.

Demostración. Sea $A$ una matriz simétrica en $M_n(\mathbb{R})$ y sea $q$ la forma cuadrática en $\mathbb{R}^n$ asociada a $A$ en la base canónica, es decir, aquella tal que $$q(X)=\text{ }^tXAX,$$ para cualquier vector $X\in \mathbb{R}^n$.

Lo que tenemos que hacer es encontrar una base de $\mathbb{R}^n$ en la cual la matriz asociada a $q$ sea diagonal. Haremos esto mediante el teorema de Gauss. Por ese resultado, existen reales $\alpha_1,\ldots,\alpha_r$ y formas lineales linealmente independientes $l_1,\ldots,l_r$ tales que $$q(x)=\sum_{i=1}^r \alpha_i l_i(x)^2.$$

Completemos $l_1,\ldots,l_r$ a una base $l_1,\ldots,l_n$ de $(\mathbb{R}^n)^\ast$. Tomemos la base $u_1,\ldots, u_n$ de $\mathbb{R}^n$ dual a $l_1,\ldots,l_n$. Esta es la base que nos ayudará. Recordemos que la definición de base dual hace que tengamos

\begin{align*} l_i(u_j)=
\begin{cases}
1\quad \text{ si $i=j$,}\\
0\quad \text{ si $i\neq j$,}
\end{cases}
\end{align*}

y que por lo tanto las funciones $l_i$ «lean» las coordenadas de un vector en la base de las $u_i$. Tomemos un vector cualquiera $x\in \mathbb{R}^n$ y escribámoslo en la base de las $u_i$ como $x=\sum_{i=1}^n x_iu_i$. Definiendo $\alpha_{r+1}=\ldots=\alpha_n=0$, tenemos que:

\begin{align*}
q(x)&= \sum_{i=1}^n \alpha _i l_i(x)^2\\
&= \sum_{i=1}^n \alpha_i x_i^2.
\end{align*}

Esto nos dice que la matriz asociada a $q$ con respecto a la base $u_1, \ldots, u_n$ es la matriz diagonal $D$ que tiene en la diagonal a los coeficientes $\alpha_i$. Esto muestra lo que queríamos.

$\square$

El teorema también tiene una versión compleja.

Teorema. Cualquier matriz hermitiana en $M_n(\mathbb{C})$ es congruente a una matriz diagonal.

La demostración es similar. Usa el teorema de Gauss complejo. Por esta razón, queda como ejercicio.

Estos resultados parecen una curiosidad algebraica. Sin embargo, pronto veremos que tienen consecuencias importantes como la clasificación de todos los productos interiores (y los productos interiores hermitianos).

Matrices positivas y positivas definidas

En entradas anteriores definimos qué quiere decir que una forma bilineal (o sesquilineal) sea positiva o positiva definida. Podemos dar una definición análoga para matrices. Nos enfocaremos sólo en matrices simétricas (en el caso real) y en matrices hermitianas (en el caso complejo).

Definición. Una matriz simétrica $A$ en $M_n(\mathbb{R})$ es positiva si para cualquier $X\in \mathbb{R}^n$ se tiene que $^tXAX\geq 0$. Es positiva definida si se da esta desigualdad y además la igualdad sucede sólo con $X=0$.

Definición. Una matriz hermitiana $A$ en $M_n(\mathbb{C})$ es positiva si para cualquier $X\in \mathbb{C}^n$ se tiene que $X^\ast AX\geq 0$. Es positiva definida si se da esta desigualdad y además la igualdad sucede sólo con $X=0$.

Es sencillo ver que entonces una matriz $A$ real (o compleja) que sea positiva definida da un producto interior (o bien un producto interior hermitiano) en $\mathbb{R}^n$ (o bien en $\mathbb{C}^n$) dado por $\langle X,Y\rangle = \text{ } ^tX A Y$, (o bien por $\langle X,Y\rangle = X^\ast A Y$). Y viceversa, un producto interior (o producto interior hermitiano) tiene representaciones matriciales que son positivas definidas. Esto no depende de la base elegida.

Proposición. Si $A,B \in M_n(\mathbb{R})$ son matrices congruentes y $A$ es una matriz positiva, entonces $B$ también lo es.

Demostración. Supongamos que la congruencia se da mediante la matriz invertible $P$ de la siguiente manera: $$B=\text{ }^t P A P.$$

Tomemos un vector $X\in \mathbb{R}^n$. Tenemos que:

\begin{align*}
^t X B X &= \text{ }^t X \text{ } ^t P A P X\\
&=\text{ } ^t(PX) A (PX)\\
&\geq 0.
\end{align*}

En la última igualdad estamos usando que $A$ es positiva. Esto muestra lo que queremos.

$\square$

Dicho en otras palabras, en el mundo real las congruencias preservan las positividades de matrices. También puede demostrarse que las congruencias preservan las positividades definitivas. Y así mismo, se tienen resultados análogos para el caso complejo. En la sección de ejercicios viene uno de estos resultados.

Clasificación de matrices positivas

Es sencillo ver si una matriz real diagonal $D$ es positiva. Todas las entradas en su diagonal deben de ser mayores o iguales a cero. En efecto, si su $i$-ésima entrada en la diagonal fuera un número $d_{ii}<0$, entonces para el $i$-ésimo vector canónico $e_i$ de $\mathbb{R}^n$ tendríamos $^te_i D e_i=d_{ii}<0$, lo cual sería una contradicción.

Combinando esto con todo lo hecho en esta entrada, obtenemos un teorema de clasificación de matrices positivas.

Teorema. Sea $A$ una matriz simétrica en $M_n(\mathbb{R})$. Las siguientes afirmaciones son equivalentes:

  1. $A$ es positiva.
  2. $A$ es congruente a una matriz diagonal con puras entradas mayores o iguales a cero.
  3. $A$ puede ser escrita de la forma $^tBB$ para alguna matriz $B\in M_n(\mathbb{R})$.

Demostración. 1) implica 2). Sabemos que $A$ es congruente a una matriz diagonal. Como $A$ es positiva, dicha matriz diagonal también lo es. Por el comentario antes del enunciado del teorema, dicha matriz diagonal debe tener únicamente entradas mayores o iguales que 0.

2) implica 3). Supongamos que $A=\text{ }^t P D P$, en donde $P$ es invertible y $D$ tiene únicamente entradas no negativas $d_1,\ldots,d_n$ en la diagonal. Definamos a $S$ como la matriz diagonal de entradas $\sqrt{d_1}, \ldots, \sqrt{d_n}$. Tenemos que $$D=S^2=SS=\text{ }^tSS.$$ De este modo, definiendo $B=SP$ obtenemos \begin{align*}A&= \text{ }^t P D P\\ &= ( \text{ }^t P \text{ }^t S) (SP) \\&= \text{ }^t (SP) SP \\&= \text{ }^t B B,\end{align*} como queríamos.

3) implica 1). Supongamos que $A= \text{ }^t B B$ para alguna matriz $B$. Para cualquier $X\in \mathbb{R}^n$ tendríamos que $$ \text{ }^t X A X = \text{ }^t (BX) BX = \norm{BX}\geq 0.$$ Aquí la norma es con respecto al producto interior canónico de $\mathbb{R}^n$. Esto es lo que queríamos.

$\square$

También existe un teorema análogo que clasifica las matrices positivas definidas.

Teorema. Sea $A$ una matriz simétrica en $M_n(\mathbb{R})$. Las siguientes afirmaciones son equivalentes:

  1. $A$ es positiva definida.
  2. $A$ es congruente a una matriz diagonal con puras entradas diagonales positivas.
  3. $A$ puede ser escrita de la forma $^tBB$ para alguna matriz $B\in M_n(\mathbb{R})$ invertible.

Y, así mismo, existen análogos para matrices hermitianas con entradas en los complejos.

Más adelante…

En esta entrada definimos la relación de congruencia de matrices. Vimos qué son las matrices positivas y las positivas definidas. Además, vimos que la congruencia preserva estas nociones.

Podemos ser mucho más finos con nuestro análisis. Si tenemos una matriz simétrica, por los resultados de esta entrada es congruente a una matriz diagonal. Podemos fijarnos en cuántas entradas positivas, cuántas negativas y cuántas cero hay en esta diagonal. En la siguiente entrada veremos que las congruencias también preservan estas cantidades.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso. Sin embargo, sirven de ayuda para repasar los conceptos vistos en esta entrada.

  1. Demuestra que cualquier matriz hermitiana en $M_n(\mathbb{C})$ es congruente a una matriz diagonal.
  2. Demuestra que si $A$ es una matriz en $M_n(\mathbb{C})$ hermitiana y positiva definida, y $B$ es una matriz en $M_n(\mathbb{C})$ hermitiana y congruente a $A$, entonces $B$ también es positiva definida.
  3. Sea $n \geq 1$ y $A=[a_{ij}] \in M_n(\mathbb{R})$ definida por $a_{ij}=min(i,j)$, prueba que $A$ es simétrica y definida positiva.
  4. Sea $A=[a_{ij}] \in M_n(\mathbb{R})$ tal que $a_{ij}=1$ si $i \neq j$ y $a_{ii} > 1$ si $1 \leq i \leq n$. Prueba que $A$ es simétrica y definida positiva.
  5. Demuestra que una matriz hermitiana $A\in M_n(\mathbb{C})$ es positiva si y sólo si puede ser escrita de la forma $A=BB^\ast$ para alguna matriz $B\in M_n(\mathbb{C})$, y que es positiva definida si y sólo si tiene una expresión así con $B$ invertible.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»